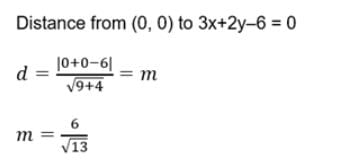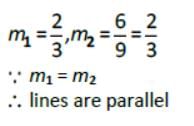All Exams >
EmSAT Achieve >
Mathematics for EmSAT Achieve >
All Questions
All questions of Conics for EmSAT Achieve Exam
The equation of a line whose perpendicular distance from the origin is 3 units and the angle made by perpendicular with positive x-axis is 30° is:- a) x + √3y = 16
- b) x + √3y = 6
- c) √3x + y + 6 = 0
- d) √3x + y - 2 = 0
Correct answer is option 'D'. Can you explain this answer?
The equation of a line whose perpendicular distance from the origin is 3 units and the angle made by perpendicular with positive x-axis is 30° is:
a)
x + √3y = 16
b)
x + √3y = 6
c)
√3x + y + 6 = 0
d)
√3x + y - 2 = 0
|
Krishna Iyer answered |
xcos 30° + y sin 30° = 3
⇒ √3x + y - 6 = 0
⇒ √3x + y - 6 = 0
For a line whose equation is √3x + y = 8, the length of the perpendicular from the origin is- a)4
- b)8
- c)16
- d)2
Correct answer is option 'A'. Can you explain this answer?
For a line whose equation is √3x + y = 8, the length of the perpendicular from the origin is
a)
4
b)
8
c)
16
d)
2
|
Rajesh Gupta answered |
√3x + y - 8
√3x + y = 8
Dividing by √[(√3)2 + (1)2]
= √[3+1]
= √4
= 2
√3x/2 + y/2 = 8/2
√3x/2 + y/2 = 4
x(√3/2) + y(1/2) = 4.....(1)
Normal form of any line : xcos w + ysin w = p....(2)
Comparing (1) and (2)
p = 4
√3x + y = 8
Dividing by √[(√3)2 + (1)2]
= √[3+1]
= √4
= 2
√3x/2 + y/2 = 8/2
√3x/2 + y/2 = 4
x(√3/2) + y(1/2) = 4.....(1)
Normal form of any line : xcos w + ysin w = p....(2)
Comparing (1) and (2)
p = 4
If A(–2, – 4), B(2, 3) and C(2, – 2) are three points, then the angle between the lines AB and AC is:- a)3π/4
- b)π/4
- c)
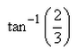
- d)
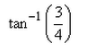
Correct answer is option 'C'. Can you explain this answer?
If A(–2, – 4), B(2, 3) and C(2, – 2) are three points, then the angle between the lines AB and AC is:
a)
3π/4
b)
π/4
c)
d)
|
Lavanya Menon answered |
Let the slope of the line AB and AC are m1 and m2 respectively.
Then,
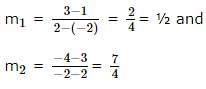
Let θ be the angle between AB and BC. Then,
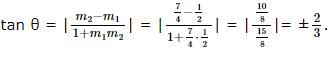
If the slope of the line passing through the points (2, 5) and (x, 1) is 2, then x = …a)-2b)0c)8d)6Correct answer is option 'B''Can you explain this answer?
|
|
Krishna Iyer answered |
Slope = Change in y coordinates÷change in x coodinates
= (5-1)÷(2-x) =2
5-1 = 4-2x
0 = 2x
x=0
= (5-1)÷(2-x) =2
5-1 = 4-2x
0 = 2x
x=0
If area of ΔABC = 0 ,three points A,B,C are- a)Coincide
- b)Collinear
- c)Non collinear
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If area of ΔABC = 0 ,three points A,B,C are
a)
Coincide
b)
Collinear
c)
Non collinear
d)
None of these
|
|
Riya Banerjee answered |
The three points A, B and C are collinear if and only if area of ΔABC = 0.
If the slope of line m = tan 0°. Therefore, the line is …… to the X-axis.- a)Perpendicular
- b)Parallel
- c)Con current
- d)Co-incident
Correct answer is option 'B'. Can you explain this answer?
If the slope of line m = tan 0°. Therefore, the line is …… to the X-axis.
a)
Perpendicular
b)
Parallel
c)
Con current
d)
Co-incident
|
Knowledge Hub answered |
Slope of x-axis is m = tan 0° = 0.
Since the inclination of every line parallel to x-axis is 0°, so its slope (m) = tan 0° = 0. Therefore, the slope of every horizontal line is 0.
Since the inclination of every line parallel to x-axis is 0°, so its slope (m) = tan 0° = 0. Therefore, the slope of every horizontal line is 0.
Let A(2, 12) and B(6,4) be two points. The slope of a line perpendicular to the line AB is:- a)2
- b)-2
- c)1/2
- d)-1/2
Correct answer is option 'C'. Can you explain this answer?
Let A(2, 12) and B(6,4) be two points. The slope of a line perpendicular to the line AB is:
a)
2
b)
-2
c)
1/2
d)
-1/2
|
Suresh Reddy answered |
Slope of the points A and B is -2 and the lines are perpendicular then
m1×m2 = -1.
∴ the slope is 1/2
What is the distance of the point (3,3) from the line 2(x-3) = 3(y+5)?- a)5/3
- b)6
- c)
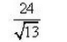
- d)
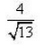
Correct answer is option 'C'. Can you explain this answer?
What is the distance of the point (3,3) from the line 2(x-3) = 3(y+5)?
a)
5/3
b)
6
c)
d)
|
Naina Sharma answered |
2(x-3) = 3(y+5)
2x - 6 = 3y + 15
2x - 3y = 21
2x - 3y - 21 = 0
Using distance formula = |ax1 + by1 + c|/(a2 + b2)1/2
= (6-9-21)/((2)2 + (3)2)1/2
= 24/(13)1/2
2x - 6 = 3y + 15
2x - 3y = 21
2x - 3y - 21 = 0
Using distance formula = |ax1 + by1 + c|/(a2 + b2)1/2
= (6-9-21)/((2)2 + (3)2)1/2
= 24/(13)1/2
+ 
= 1, and its corresponding point Q on the auxiliary circle meet on the line
For the line x+y= 1, what is the angle made with the positive direction of the x axis?- a)60°
- b)30°
- c)135°
- d)45°
Correct answer is option 'C'. Can you explain this answer?
For the line x+y= 1, what is the angle made with the positive direction of the x axis?
a)
60°
b)
30°
c)
135°
d)
45°
|
|
Krishna Iyer answered |
We have in Equation = mx+c the slope of line as m and m=tanθ, θ is the angle made by (+ve) in X-axis
Hence, y = 1 - x
Here m = -1 = tanθ
θ = 135o
Hence, y = 1 - x
Here m = -1 = tanθ
θ = 135o
Find the equation of the line parallel to the line 5x – 4y + 3 = 0 and passing through the point (2, 5) is:- a)5x – 4y + 20 = 0.
- b)5x – 4y + 10 = 0.
- c)4x – 5y + 10 = 0.
- d)4x – 5y + 20 = 0.
Correct answer is option 'B'. Can you explain this answer?
Find the equation of the line parallel to the line 5x – 4y + 3 = 0 and passing through the point (2, 5) is:
a)
5x – 4y + 20 = 0.
b)
5x – 4y + 10 = 0.
c)
4x – 5y + 10 = 0.
d)
4x – 5y + 20 = 0.
|
|
Neha Joshi answered |
5x – 4y + 3 = 0
5x – 4y = -3
(5/4)x + (-4/5)y = -3
Line is parallel m = 5/4
Points (2,5)
= 5 = (5/4)(2) + b
5 = 5/2 + b
b = 5/2
y = 5x/4 - 5/2
4y = 5x - 10
5x - 4y + 10 = 0
5x – 4y = -3
(5/4)x + (-4/5)y = -3
Line is parallel m = 5/4
Points (2,5)
= 5 = (5/4)(2) + b
5 = 5/2 + b
b = 5/2
y = 5x/4 - 5/2
4y = 5x - 10
5x - 4y + 10 = 0
The distance between the parallel lines 4x-3y+5 = 0 and 4x-3y+15 = 0 is :- a)4 units
- b)2 units
- c)3.5 units
- d)5 units
Correct answer is option 'B'. Can you explain this answer?
The distance between the parallel lines 4x-3y+5 = 0 and 4x-3y+15 = 0 is :
a)
4 units
b)
2 units
c)
3.5 units
d)
5 units
|
|
Raghav Bansal answered |
4x - 3y + 5 = 0, 4x - 3y + 15 = 0
A = 4, B = -3 c1 = 5, c2 = 15
|c1 - c2|/[A2 + B2]1/2
= |5 - 15|/[(4)2 + (-3)2]½
= 10/5
= 2
A = 4, B = -3 c1 = 5, c2 = 15
|c1 - c2|/[A2 + B2]1/2
= |5 - 15|/[(4)2 + (-3)2]½
= 10/5
= 2
A point P is in the interior of angle BAC, such that P lies on the bisector of angle BAC. What can be said about the distance of PM if PN = 2cm where PM and PN are perpendiculars from P on the lines BA and AC?- a)PM = 2 PN
- b)PM = 3 PN
- c)PM =2 cm
- d)PM =3.5 cm
Correct answer is option 'C'. Can you explain this answer?
A point P is in the interior of angle BAC, such that P lies on the bisector of angle BAC. What can be said about the distance of PM if PN = 2cm where PM and PN are perpendiculars from P on the lines BA and AC?
a)
PM = 2 PN
b)
PM = 3 PN
c)
PM =2 cm
d)
PM =3.5 cm
|
|
Krishna Iyer answered |
In Δ PAM & Δ PAN, angle (PAM) = angle (PAN) (Since AP bisects the angle (BAC)) angle (AMP) = angle (ANP) = 900
PA = PA (common)
By AAS congruence, Δ PAM and Δ PAN are congruent.
MP = NP = 2 cm
PA = PA (common)
By AAS congruence, Δ PAM and Δ PAN are congruent.
MP = NP = 2 cm
The centre of the ellipse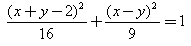 
is:- a)(0, 1)
- b)(1, 1)
- c)(0, 0)
- d)(1, 0)
Correct answer is option 'B'. Can you explain this answer?
The centre of the ellipse 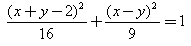is:
is:a)
(0, 1)
b)
(1, 1)
c)
(0, 0)
d)
(1, 0)
|
Lohit Matani answered |
Centre of the ellipse is the intersection point of
x+y−1=0.........(1)
x−y=0............(2)
Substituting x from equation 2 in equation 1 two equations, we get,
2y=2, y=1
Replacing, we get x=1
⇒(1,1) is the centre
x+y−1=0.........(1)
x−y=0............(2)
Substituting x from equation 2 in equation 1 two equations, we get,
2y=2, y=1
Replacing, we get x=1
⇒(1,1) is the centre
The tangent of the angle which the part of the line above the X-axis makes with the positive direction of the X-axis is:- a)Perpendicular line
- b)Slope of a line
- c)Concurrent line
- d)Parallel line
Correct answer is option 'B'. Can you explain this answer?
The tangent of the angle which the part of the line above the X-axis makes with the positive direction of the X-axis is:
a)
Perpendicular line
b)
Slope of a line
c)
Concurrent line
d)
Parallel line
|
Preeti Iyer answered |
The gradient or slope of a line (not parallel to the axis of y) is the trigonometrical tangent of the angle which the line makes with the positive direction of the x-axis. Thus, if a line makes an angle θ with the positive direction of the x-axis, then its slope will be tan θ.
A tangent having slope of _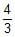
to the ellipse
+ 
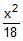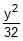= 1 intersects the major & minor axes in points A & B respectively. If C is the centre of the ellipse then the area of the triangle ABC is- a)12 sq. units
- b)24 sq. units
- c)36 sq. units
- d)48 sq. units
Correct answer is option 'B'. Can you explain this answer?
A tangent having slope of _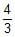 to the ellipse
to the ellipse + = 1 intersects the major & minor axes in points A & B respectively. If C is the centre of the ellipse then the area of the triangle ABC isa)
12 sq. units
b)
24 sq. units
c)
36 sq. units
d)
48 sq. units
|
|
Preeti Khanna answered |
Since the major axis is along the y-axis.
∴ Equation of tangent is x = my + [b2m2 + a]1/2
Slope of tangent = 1/m = −4/3
⇒ m = −3/4
Hence, equation of tangent is 4x+3y=24 or
x/6 + y/8 = 1
Its intercepts on the axes are 6 and 8.
Area (ΔAOB) = 1/2×6×8
= 24 sq. unit
∴ Equation of tangent is x = my + [b2m2 + a]1/2
Slope of tangent = 1/m = −4/3
⇒ m = −3/4
Hence, equation of tangent is 4x+3y=24 or
x/6 + y/8 = 1
Its intercepts on the axes are 6 and 8.
Area (ΔAOB) = 1/2×6×8
= 24 sq. unit
Can you explain the answer of this question below:The points A and B have coordinates (3, 2) and (1, 4) respectively. So, the slope of any line perpendicular to AB is- A:2
- B:1
- C:-1
- D:-2
The answer is b.
The points A and B have coordinates (3, 2) and (1, 4) respectively. So, the slope of any line perpendicular to AB is
A:
2
B:
1
C:
-1
D:
-2
|
Geetika Shah answered |
If the lines are perpendicular to each other then their slopes are in the form m1.m2 = -1.(since product of slopes of two perpendicular lines is -1) Therefore , m = 1.
The value of y, for the line passing through (3, y) and (2, 7) is parallel to the line passing through (-1 , 4) and (0, 6) is:- a)9/7
- b)3/7
- c)9
- d)3
Correct answer is option 'C'. Can you explain this answer?
The value of y, for the line passing through (3, y) and (2, 7) is parallel to the line passing through (-1 , 4) and (0, 6) is:
a)
9/7
b)
3/7
c)
9
d)
3
|
|
Suresh Reddy answered |
As A(3,y) and B(2,7) is parallel to C(-1,4) and D(0,6)
∴ Their slopes are equal
so, (y-7)/(3-1) = (4-6)/(-1-0)
y-7 = 2
y = 9
∴ Their slopes are equal
so, (y-7)/(3-1) = (4-6)/(-1-0)
y-7 = 2
y = 9
What will be the new equation of the straight line 3x + 4y = 15, if the origin gets shifted to (1,-3) ?
- a)3x+4y=4
- b)3x-4y=4
- c)4x+3y=6
- d)3x+4y=6
Correct answer is option 'D'. Can you explain this answer?
What will be the new equation of the straight line 3x + 4y = 15, if the origin gets shifted to (1,-3) ?
a)
3x+4y=4
b)
3x-4y=4
c)
4x+3y=6
d)
3x+4y=6
|
|
Neha Sharma answered |
Equation : 3x + 4y = 15
Points : (1,-3)
3(x-1) + 4(y-(-3)) = 15
3(x-1) + 4(y+3) = 15
3x - 3 + 4y + 12 = 15
3x + 4y = 6
Points : (1,-3)
3(x-1) + 4(y-(-3)) = 15
3(x-1) + 4(y+3) = 15
3x - 3 + 4y + 12 = 15
3x + 4y = 6
The equation of the line parallel to the line 2x – 3y = 1 and passing through the middle point of the line segment joining the points (1, 3) and (1, –7), is:- a)2x – 3y – 8 = 0
- b)2x + 3y – 5 = 0
- c)4x – 6y + 7 = 0
- d)3x – 2y + 8 = 0
Correct answer is option 'A'. Can you explain this answer?
The equation of the line parallel to the line 2x – 3y = 1 and passing through the middle point of the line segment joining the points (1, 3) and (1, –7), is:
a)
2x – 3y – 8 = 0
b)
2x + 3y – 5 = 0
c)
4x – 6y + 7 = 0
d)
3x – 2y + 8 = 0
|
|
Neha Joshi answered |
The midpoint of the line segment is (1+1/2, 3-7/2)
= (1,-2)
the equation of the line parallel to the line 2x-3y = 1 is of the form 2x-3y = k
since it passes through (1,-2)
2(1) - 3(-2) = k
k = 8
hence the required equation is 2x-3y=8
= (1,-2)
the equation of the line parallel to the line 2x-3y = 1 is of the form 2x-3y = k
since it passes through (1,-2)
2(1) - 3(-2) = k
k = 8
hence the required equation is 2x-3y=8
The ratio in which the point R (1, 2) divides the line segment joining points P (2, 3) and Q (3, 5) is:- a)1 : 2, externally
- b)2 : 1, externally
- c)1 : 2, internally
- d)2 : 1, internally
Correct answer is option 'A'. Can you explain this answer?
The ratio in which the point R (1, 2) divides the line segment joining points P (2, 3) and Q (3, 5) is:
a)
1 : 2, externally
b)
2 : 1, externally
c)
1 : 2, internally
d)
2 : 1, internally
|
|
Gaurav Kumar answered |
P(2,3) Q(3,5) R(1,2)
R is at centre between P and Q, using section formula for internal division
Therefore, (1,2) = ((3λ+2)/(λ+1), (5λ+3)/(λ+1))
1 = (3λ+2)/(λ+1)
(λ+1) = (3λ+2)
λ = -1/2
- sign indicates the external division
R is at centre between P and Q, using section formula for internal division
Therefore, (1,2) = ((3λ+2)/(λ+1), (5λ+3)/(λ+1))
1 = (3λ+2)/(λ+1)
(λ+1) = (3λ+2)
λ = -1/2
- sign indicates the external division
The equation of the ellipse whose one focus is at (4, 0) and whose eccentricity is 4/5 is:- a)
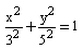
- b)
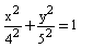
- c)
- d)
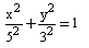
Correct answer is option 'D'. Can you explain this answer?
The equation of the ellipse whose one focus is at (4, 0) and whose eccentricity is 4/5 is:
a)
b)
c)
d)
|
Trisha Vashisht answered |
focus lies on x axis
So, the equation of ellipse is x2/a2 + y2/b2 = 1
Co-ordinate of focus(+-ae, 0)
ae = 4
e = ⅘
a = 4/e => 4/(⅘)
a = 5
(a)2 = 25
b2 = a2(1-e2)
= 25(1-16/25)
b2 = 9
Required equation : x2/(5)2 + y2/(3)2 = 1
So, the equation of ellipse is x2/a2 + y2/b2 = 1
Co-ordinate of focus(+-ae, 0)
ae = 4
e = ⅘
a = 4/e => 4/(⅘)
a = 5
(a)2 = 25
b2 = a2(1-e2)
= 25(1-16/25)
b2 = 9
Required equation : x2/(5)2 + y2/(3)2 = 1
If the curve x2 3y2 = 9 subtends an obtuse angle at the point (2α, α), then a possible value of α2 is
- a) 1
- b) 2
- c) 3
- d) 4
Correct answer is option 'A'. Can you explain this answer?
If the curve x2 3y2 = 9 subtends an obtuse angle at the point (2α, α), then a possible value of α2 is
a)
1b)
2c)
3d)
4
|
Ishan Choudhury answered |
The given curve is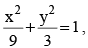 
whose director circle is x2 + y2 = 12.
For the required condition (2α, α) should lie inside the circle and outside the ellipse i.e.,
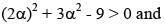
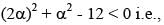
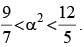
whose director circle is x2 + y2 = 12.For the required condition (2α, α) should lie inside the circle and outside the ellipse i.e.,
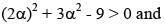
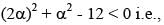
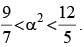
From point P (8, 27), tangent PQ and PR are drawn to the ellipse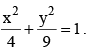 
Then the angle subtended by QR at origin is - a)
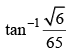
- b)
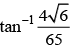
- c)
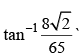
- d)
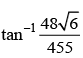
Correct answer is option 'D'. Can you explain this answer?
From point P (8, 27), tangent PQ and PR are drawn to the ellipse 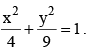Then the angle subtended by QR at origin is
Then the angle subtended by QR at origin is a)
b)
c)
d)
|
Om Desai answered |
Equation of QR is T = 0 (chord of contact)
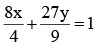
⇒ 2x + 3y = 1 .....(i)
Now, equation of the pair of lines passing through origin and points Q, R is given by
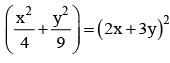
(making equation of ellipse homogeneous using Eq (i)
∴135x2 + 432xy + 320y2 = 0
⇒ 2x + 3y = 1 .....(i)
Now, equation of the pair of lines passing through origin and points Q, R is given by
(making equation of ellipse homogeneous using Eq (i)
∴135x2 + 432xy + 320y2 = 0
m1 and m2 are the slope of two perpendicular lines, if- a)m1.m2 = 1
- b)m1= m2
- c)m1 + m2 = 0
- d)1 + m1.m2 = 0
Correct answer is option 'D'. Can you explain this answer?
m1 and m2 are the slope of two perpendicular lines, if
a)
m1.m2 = 1
b)
m1= m2
c)
m1 + m2 = 0
d)
1 + m1.m2 = 0
|
|
Lakshmi Roy answered |
Explanation:
Two lines are perpendicular if the product of their slopes is -1. So, if m1 and m2 are the slopes of two perpendicular lines, then:
m1.m2 = -1
Rewriting this equation, we get:
1/m1 . 1/m2 = -1
Multiplying both sides by m1.m2, we get:
m2/m1 + m1/m2 = 0
This can be simplified as:
m1.m2 = 0
Therefore, the correct answer is option D.
Two lines are perpendicular if the product of their slopes is -1. So, if m1 and m2 are the slopes of two perpendicular lines, then:
m1.m2 = -1
Rewriting this equation, we get:
1/m1 . 1/m2 = -1
Multiplying both sides by m1.m2, we get:
m2/m1 + m1/m2 = 0
This can be simplified as:
m1.m2 = 0
Therefore, the correct answer is option D.
Find the perpendicular distance from the origin of the line x + y – 2 = 0 is:- a)√2
- b)√3
- c)5√2
- d)3√3
Correct answer is option 'A'. Can you explain this answer?
Find the perpendicular distance from the origin of the line x + y – 2 = 0 is:
a)
√2
b)
√3
c)
5√2
d)
3√3
|
|
Raghav Bansal answered |
The given point is P(0,0) and the given line is x + y - 2 = 0
Let d be the length of the perpendicular from P(0,0) to the line x + y - 2 = 0
Then,
d = |(1 × 0) + (3 × 0) − 2|/(√12 + 12)
= 2/√2
= (2/√2) * (√2/√2)
= √2
Let d be the length of the perpendicular from P(0,0) to the line x + y - 2 = 0
Then,
d = |(1 × 0) + (3 × 0) − 2|/(√12 + 12)
= 2/√2
= (2/√2) * (√2/√2)
= √2
If distance between the directrices be thrice the distance between the foci, then eccentricity of ellipse is- a)
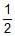
- b)
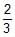
- c)
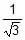
- d)
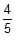
Correct answer is option 'C'. Can you explain this answer?
If distance between the directrices be thrice the distance between the foci, then eccentricity of ellipse is
a)
b)
c)
d)
|
|
Trisha Vashisht answered |
Distance between the directrices is 2a/e
Distance between the foci is 2ae
Given: 2a/e = 3∗2ae
Or,e2 = 1/3
∴ e=1/√3
Distance between the foci is 2ae
Given: 2a/e = 3∗2ae
Or,e2 = 1/3
∴ e=1/√3
The line through the points (a , b) and (- a , - b) passes through the point- a)(1 , 1)
- b)(a2,ab)
- c)(3a , - 2b)
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The line through the points (a , b) and (- a , - b) passes through the point
a)
(1 , 1)
b)
(a2,ab)
c)
(3a , - 2b)
d)
none of these
|
|
Naina Sharma answered |
Slope of line passing through (a,b) and (−a,−b) is given by (b+b)/(a+a) = b/a
So equation of line passing is given by (using slope point form)
y−b = b/a(x−a)
⇒ ay − ab = bx − ab
⇒ ay = bx
Clearly the point (a2,ab) lie on the above line
So equation of line passing is given by (using slope point form)
y−b = b/a(x−a)
⇒ ay − ab = bx − ab
⇒ ay = bx
Clearly the point (a2,ab) lie on the above line
Two lines 3x+4y=8 and lx+my=n are perpendicular. Which of the following is true?- a)3m+4l=0
- b)3m-4l=0
- c)3l-4m=0
- d)3l+4m=0
Correct answer is option 'D'. Can you explain this answer?
Two lines 3x+4y=8 and lx+my=n are perpendicular. Which of the following is true?
a)
3m+4l=0
b)
3m-4l=0
c)
3l-4m=0
d)
3l+4m=0
|
|
Preeti Iyer answered |
In perpendicular, the slope of product = -1
Slope of L1 * slope of L2 = -1
-3/4 * (-l/m) = -1
=> 3l/4m = -1
=> 3l = -4m
= 3l + 4m = 0
Slope of L1 * slope of L2 = -1
-3/4 * (-l/m) = -1
=> 3l/4m = -1
=> 3l = -4m
= 3l + 4m = 0
The eccentricity of an ellipse whose latus rectum is equal to distance between foci is:- a)
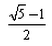
- b)
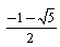
- c)
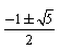
- d)
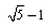
Correct answer is option 'A'. Can you explain this answer?
The eccentricity of an ellipse whose latus rectum is equal to distance between foci is:
a)
b)
c)
d)
|
|
Suresh Reddy answered |
Distance between the foci of an ellipse = length of latus rectum
i.e. (2b2)/a=2ae
e=b2/a2
But e=[1−b2/a2]1/2
Then e=(1−e)1/2
Squaring both sides, we get
e2 +e−1=0
e=−1 ± (1 + 4)1/2]/2
(∵ Eccentricity cannot be negative)
e=[(5)1/2 − 1]/2
i.e. (2b2)/a=2ae
e=b2/a2
But e=[1−b2/a2]1/2
Then e=(1−e)1/2
Squaring both sides, we get
e2 +e−1=0
e=−1 ± (1 + 4)1/2]/2
(∵ Eccentricity cannot be negative)
e=[(5)1/2 − 1]/2
What will be the value of ‘p” if the equation of the straight line 3x + 5y = 10 gets changed to 3x + 5y = p after shifting the origin at (2,2) ?- a)6
- b)-6
- c)26
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
What will be the value of ‘p” if the equation of the straight line 3x + 5y = 10 gets changed to 3x + 5y = p after shifting the origin at (2,2) ?
a)
6
b)
-6
c)
26
d)
none of these
|
|
Krishna Iyer answered |
3x + 5y = 10, at origin
But now, it’s (2,2),
3(x-2) + 5(y-2) = 10
Hence, 3x - 6 + 5y - 10 = 10
3x + 5y = 26
So, 3x + 5y = p
=> p = 26.
But now, it’s (2,2),
3(x-2) + 5(y-2) = 10
Hence, 3x - 6 + 5y - 10 = 10
3x + 5y = 26
So, 3x + 5y = p
=> p = 26.
The distance of (2,3) from x+y=1 is- a)2 units
- b)3√2 units
- c)4√2 units
- d)2√2 units
Correct answer is option 'D'. Can you explain this answer?
The distance of (2,3) from x+y=1 is
a)
2 units
b)
3√2 units
c)
4√2 units
d)
2√2 units
|
|
Lavanya Menon answered |
Given circle = (2,3)
Given line (x+y-1) = 0
Distance between point to line is:
d = |ax1 + by1 + c|/√(a2 + b2)
where a = 1, b = 1, c = -1 and x1 = 2, y1 = 3
d = |1(2) + 1(3) - 1|/√(1+1)
d = 4/(√2)
d = 2√2
Given line (x+y-1) = 0
Distance between point to line is:
d = |ax1 + by1 + c|/√(a2 + b2)
where a = 1, b = 1, c = -1 and x1 = 2, y1 = 3
d = |1(2) + 1(3) - 1|/√(1+1)
d = 4/(√2)
d = 2√2
The radius of the circle given by 2x2 + 2y2 – x = 0 is- a)1/4
- b)1
- c)2
- d)1/2
Correct answer is option 'A'. Can you explain this answer?
The radius of the circle given by 2x2 + 2y2 – x = 0 is
a)
1/4
b)
1
c)
2
d)
1/2
|
|
Geetika Shah answered |
2x² + 2y² - x = 0 .
==> 2 ( x² + y² - x/2 ) = 0 .
==> 2/2 ( x² + y² - x/2 ) = 0/2 .
==> x² - x/2 + y² = 0 .
==> ( x² - x/2 + (1/4)² ) + y² = (1/4)² .
==> ( x - 1/4 )² + ( y - 0 )² = (1/4)²
Centre (-¼, 0) radius(¼)
==> 2 ( x² + y² - x/2 ) = 0 .
==> 2/2 ( x² + y² - x/2 ) = 0/2 .
==> x² - x/2 + y² = 0 .
==> ( x² - x/2 + (1/4)² ) + y² = (1/4)² .
==> ( x - 1/4 )² + ( y - 0 )² = (1/4)²
Centre (-¼, 0) radius(¼)
The equation of the parabola with vertex at (0, 0) and focus at (0, – 2) is:- a)y2 = – 2x
- b)x2 = – 8y
- c)y2 = – 8x
- d)x2 = – 4y
Correct answer is option 'B'. Can you explain this answer?
The equation of the parabola with vertex at (0, 0) and focus at (0, – 2) is:
a)
y2 = – 2x
b)
x2 = – 8y
c)
y2 = – 8x
d)
x2 = – 4y
|
Praveen Kumar answered |
Given the vertex of the parabola is (0,0) and focus is at (0,-2).
This gives the axis of the parabola is the positive y− axis.
Then the equation of the parabola will be x^2 = 4ay where a = -2.
So the equation of the parabola is x2 = -8y.
This gives the axis of the parabola is the positive y− axis.
Then the equation of the parabola will be x^2 = 4ay where a = -2.
So the equation of the parabola is x2 = -8y.
The equation of a line whose perpendicular distance from the origin is 8 units and the angle made by perpendicular with positive x-axis is 60 degree is:- a)5x - 3y + 6 = 0
- b)x + √3y = 16
- c)√3x + y - 2 = 0
- d)√3x + √2y - 5 = 0
Correct answer is option 'B'. Can you explain this answer?
The equation of a line whose perpendicular distance from the origin is 8 units and the angle made by perpendicular with positive x-axis is 60 degree is:
a)
5x - 3y + 6 = 0
b)
x + √3y = 16
c)
√3x + y - 2 = 0
d)
√3x + √2y - 5 = 0
|
|
Gaurav Kumar answered |
If p isthe length of the normal from the origin to a line and ωis the angle made by the normal with the positive direction of thex-axis,then the equation of the line is given by xcosω +ysinω= p.
Here, p = 8 units and ω= 60°
Thus, therequired equation of the given line is
xcos 60° + y sin 60° = 8
x(1/2) + y(√3/2) = 8
x/2 + √3y/2 = 8
x + √3y = 16
Here, p = 8 units and ω= 60°
Thus, therequired equation of the given line is
xcos 60° + y sin 60° = 8
x(1/2) + y(√3/2) = 8
x/2 + √3y/2 = 8
x + √3y = 16
The acute angle between the lines ax + by + c = 0 and (a + b)x = (a – b)y , a ≠ b , is- a)450
- b)300
- c)600
- d)150
Correct answer is option 'A'. Can you explain this answer?
The acute angle between the lines ax + by + c = 0 and (a + b)x = (a – b)y , a ≠ b , is
a)
450
b)
300
c)
600
d)
150
|
Aryan Khanna answered |
ax + by + c = 0 and (a + b)x = (a – b)y
m1 = -a/b, m2 = (a+b)/(a-b)
tanx = [(m1-m2)/(1+m1×m2)]
=> {(-a/b)- (a+b)/(a-b)}/{1+(-a/b)[(a+b)/(a-b)]}
=> {-a2+ab-ab-b2}/{b(a-b)} * {ba-b2-a2-ab}/{b(a-b)}
=> (-a2-b2)/{1/(-a2-b2)
tanx = 1
x = tan-1(1)
Angle = 45o
m1 = -a/b, m2 = (a+b)/(a-b)
tanx = [(m1-m2)/(1+m1×m2)]
=> {(-a/b)- (a+b)/(a-b)}/{1+(-a/b)[(a+b)/(a-b)]}
=> {-a2+ab-ab-b2}/{b(a-b)} * {ba-b2-a2-ab}/{b(a-b)}
=> (-a2-b2)/{1/(-a2-b2)
tanx = 1
x = tan-1(1)
Angle = 45o
A variable chord PQ of the parabola y = 4x2 substends a right angle at the vertex. Then the locus of points of intersection of the tangents at P and Q is- a)4y + 1= 16x2
- b)y + 4 = 0
- c)4y + 4 = 4x2
- d)4y + 1 = 0
Correct answer is option 'D'. Can you explain this answer?
A variable chord PQ of the parabola y = 4x2 substends a right angle at the vertex. Then the locus of points of intersection of the tangents at P and Q is
a)
4y + 1= 16x2
b)
y + 4 = 0
c)
4y + 4 = 4x2
d)
4y + 1 = 0
|
|
Krishna Iyer answered |
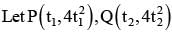
Slope of OP x slope of OQ = -1
⇒ 4t1.4t2 = -1
Eq of tangent at
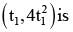
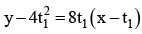
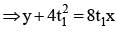
Eq of tangent at
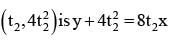
Let (x1 , y1) is the point of intersection
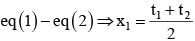
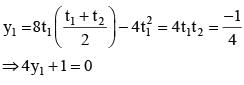
The length of the semi-latus-rectum of an ellipse is one third of its major axis, its eccentricity would be
- a)
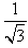
- b)
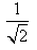
- c)2/3
- d)
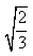
Correct answer is option 'A'. Can you explain this answer?
The length of the semi-latus-rectum of an ellipse is one third of its major axis, its eccentricity would be
a)
b)
c)
2/3
d)
|
|
Suresh Iyer answered |
Correct Answer :- a
Explanation : Semi latus rectum of ellipse = one half the last rectum
b2/a = 1/3*2a
b2 = 2a2/3
b = (2a/3)1/2...........(1)
So, b2/a = a(1-e2)
b2 = a2(1-e2)
Substituting from (1)
2a2/3 = a2(1-e2)
e2 = 1-2/3
e2 = 1/(3)1/2
The vertices of a triangle are (0 , 3) , (- 3 , 0) and (3 , 0). The orthocenter of the triangle is- a)(0 , 3)
- b)(- 3 , 0)
- c)(3 , 0)
- d)none of these.
Correct answer is option 'A'. Can you explain this answer?
The vertices of a triangle are (0 , 3) , (- 3 , 0) and (3 , 0). The orthocenter of the triangle is
a)
(0 , 3)
b)
(- 3 , 0)
c)
(3 , 0)
d)
none of these.
|
Dipika Choudhury answered |
Method to Solve :Triangle ABC, vertices are A(3,4), B(0,0), C(4,0)O is the Orthocentre of the triangleBy considering the coordinates of B, C, A ,we can conclude that:Equation of BC is y=0………..(1)Equati
Any point on the parabola whose focus is (0,1) and the directrix is x + 2 = 0 is given by- a)(t2 + 1, 2t – 1)
- b)(t2, 2t)
- c)(t2 + 1, 2t + 1)
- d)(t2 – 1, 2t + 1)
Correct answer is option 'D'. Can you explain this answer?
Any point on the parabola whose focus is (0,1) and the directrix is x + 2 = 0 is given by
a)
(t2 + 1, 2t – 1)
b)
(t2, 2t)
c)
(t2 + 1, 2t + 1)
d)
(t2 – 1, 2t + 1)
|
|
Pooja Shah answered |
f(0,1),d(x+2=0)
Distance of any point on parabola and focus is equal to distance of point and directrix.
fP=(h−0)2+(k−1)2= (h2+k2+1−2k)1/2
Distance of point (h,k) and line x+2=0
Using point line distance formula.
dP=h+2
[h2+k2+1−2k]1/2=h+2
h2+k2+1−2k = h2+4+4h
k2−2k+1−4−4h=0
replacing h→x,k→y y2−2y+1−4−4x=0
(y−1)2=4(x+1) …(1)
Let Y=y−1,X=x+1 then (1) becomes
Y^2=4aX2
Here a=1 any point on this parabola will be of the form (at2,2at)=(t2,2at)
⇒X=t2 ⇒x+1=t2
⇒x=t2−1
⇒Y2=2t
⇒y−1 = 2t ⇒ y = 2t+1
∴ Any point on the parabola (y−1)2=4(x+1) is
= (t2−1,2t+1)
Distance of any point on parabola and focus is equal to distance of point and directrix.
fP=(h−0)2+(k−1)2= (h2+k2+1−2k)1/2
Distance of point (h,k) and line x+2=0
Using point line distance formula.
dP=h+2
[h2+k2+1−2k]1/2=h+2
h2+k2+1−2k = h2+4+4h
k2−2k+1−4−4h=0
replacing h→x,k→y y2−2y+1−4−4x=0
(y−1)2=4(x+1) …(1)
Let Y=y−1,X=x+1 then (1) becomes
Y^2=4aX2
Here a=1 any point on this parabola will be of the form (at2,2at)=(t2,2at)
⇒X=t2 ⇒x+1=t2
⇒x=t2−1
⇒Y2=2t
⇒y−1 = 2t ⇒ y = 2t+1
∴ Any point on the parabola (y−1)2=4(x+1) is
= (t2−1,2t+1)
Find the equation of the line whose intercepts on X and Y-axes are a2 and b2 respectively- a)bx + ay = ab
- b)b2x + a2b2y = a2
- c)b2a2x + a2y = b2
- d)b2x + a2y = a2b2
Correct answer is option 'D'. Can you explain this answer?
Find the equation of the line whose intercepts on X and Y-axes are a2 and b2 respectively
a)
bx + ay = ab
b)
b2x + a2b2y = a2
c)
b2a2x + a2y = b2
d)
b2x + a2y = a2b2
|
Defence Exams answered |
Consider the given points. (a2,0) and (0,b2)
We know that the equation of the line which is passing through the points
y−y1 =[ (y2−y1) / (x2−x1)] (x−x1)
So, y−0 = b2−0/0-a2(x-a2)
-ya2 - b2x = -b2a2
xb2 +ya2 = b2a2
We know that the equation of the line which is passing through the points
y−y1 =[ (y2−y1) / (x2−x1)] (x−x1)
So, y−0 = b2−0/0-a2(x-a2)
-ya2 - b2x = -b2a2
xb2 +ya2 = b2a2
The equation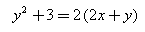 
represents a parabola with the vertex at- a)
- b)
- c)
- d)
Correct answer is option 'C'. Can you explain this answer?
The equation 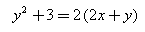represents a parabola with the vertex at
represents a parabola with the vertex ata)
b)
c)
d)
|
|
Gaurav Kumar answered |
y2+3=2(2x+y) represents parabola.
y2+3=4x+2y
y2−2y+3=4x
y2−2y+1+3=4x+1
(y−1)2=4x−2
(y−1)2=4(x−1/2)
So, the vertex of parabola=(1/2,1) and axis is parallel to x axis.
a=1
Focus=(1/2+1,1)
=(3/2,1)
y2+3=4x+2y
y2−2y+3=4x
y2−2y+1+3=4x+1
(y−1)2=4x−2
(y−1)2=4(x−1/2)
So, the vertex of parabola=(1/2,1) and axis is parallel to x axis.
a=1
Focus=(1/2+1,1)
=(3/2,1)
The line 4x – 7y + 10 = 0 intersects the parabola, y2 = 4x at the points A & B. The co-ordinates of the point of intersection of the tangents drawn at the points A & B are- a)
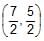
- b)
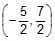
- c)
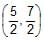
- d)
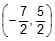
Correct answer is option 'C'. Can you explain this answer?
The line 4x – 7y + 10 = 0 intersects the parabola, y2 = 4x at the points A & B. The co-ordinates of the point of intersection of the tangents drawn at the points A & B are
a)
b)
c)
d)
|
Manish Aggarwal answered |
ky=[4(x+h)]/2
=> 2ky=2(x+h)
2ky=4x+4h =>4x−2ky+4h=0
4x−7y+10=0
4h=10 => h=5/2
2k=7 => k=7/2
point of intersection of tangent at p and q is (5/2,7/2)
=> 2ky=2(x+h)
2ky=4x+4h =>4x−2ky+4h=0
4x−7y+10=0
4h=10 => h=5/2
2k=7 => k=7/2
point of intersection of tangent at p and q is (5/2,7/2)
What will be the new equation of the straight line 5x + 8y = 10, if the origin gets shifted to (2,-3) ?- a)5x + 8y = -4
- b)5x + 8y = – 14
- c)5x – 8y = 14
- d)8x + 5y = 24
Correct answer is option 'A'. Can you explain this answer?
What will be the new equation of the straight line 5x + 8y = 10, if the origin gets shifted to (2,-3) ?
a)
5x + 8y = -4
b)
5x + 8y = – 14
c)
5x – 8y = 14
d)
8x + 5y = 24
|
|
Rajesh Gupta answered |
Equation : 5x + 8y = 10
Points (2, -3)
(x-2, y+3)
⇒ 5(x-2) + 8(y+3) = 10
= 5x - 10 + 8y + 24 = 10
⇒ 5x + 8 = - 4
Points (2, -3)
(x-2, y+3)
⇒ 5(x-2) + 8(y+3) = 10
= 5x - 10 + 8y + 24 = 10
⇒ 5x + 8 = - 4
Find the equation of line passing through the mid-point of line joining the points (3, 4) and (5, 6) and perpendicular to the equation of line 2x + 3y = 5.- a)2x – 3y – 2 = 0
- b)5x – 7y + 4 = 0
- c)3x – 2y – 2 = 0
- d)4x – 5y + 13 = 0
Correct answer is option 'C'. Can you explain this answer?
Find the equation of line passing through the mid-point of line joining the points (3, 4) and (5, 6) and perpendicular to the equation of line 2x + 3y = 5.
a)
2x – 3y – 2 = 0
b)
5x – 7y + 4 = 0
c)
3x – 2y – 2 = 0
d)
4x – 5y + 13 = 0
|
|
Suresh Iyer answered |
Mid Point [(3+5)/2, (4+6)/2]
= [8/2, 10/2]
= (4,5)
Perpendicular to the equation : 2x + 3y - 5 = 10
3x - 2y + k = 0
3(4) - 2(5) + k = 0
12 - 10 + k 0
k = -2
Therefore the equation is : 3x - 2y - 2 = 0
= [8/2, 10/2]
= (4,5)
Perpendicular to the equation : 2x + 3y - 5 = 10
3x - 2y + k = 0
3(4) - 2(5) + k = 0
12 - 10 + k 0
k = -2
Therefore the equation is : 3x - 2y - 2 = 0
Chapter doubts & questions for Conics - Mathematics for EmSAT Achieve 2025 is part of EmSAT Achieve exam preparation. The chapters have been prepared according to the EmSAT Achieve exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for EmSAT Achieve 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Conics - Mathematics for EmSAT Achieve in English & Hindi are available as part of EmSAT Achieve exam.
Download more important topics, notes, lectures and mock test series for EmSAT Achieve Exam by signing up for free.
Mathematics for EmSAT Achieve
146 videos|222 docs|220 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily