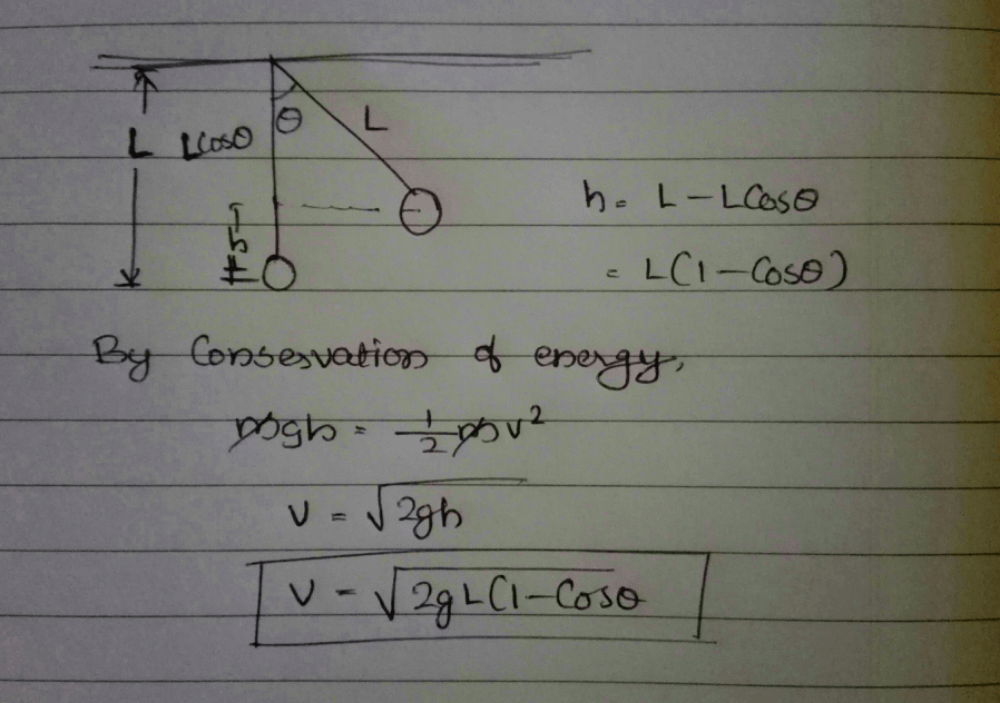All Exams >
EmSAT Achieve >
Physics for EmSAT Achieve >
All Questions
All questions of Undamped Simple Harmonic Motion for EmSAT Achieve Exam
Two identical spring, each of stiffness k are welded to each other at point P. The other two ends are fixed to the edge of a smooth horizontal tube as shown. A particle of mass m is welded at P. The entire system is horizontal. The period of oscillation of the particle in the direction of x is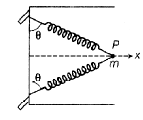 
- a)
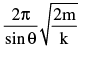
- b)
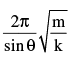
- c)
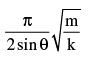
- d)
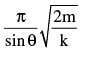
Correct answer is option 'D'. Can you explain this answer?
Two identical spring, each of stiffness k are welded to each other at point P. The other two ends are fixed to the edge of a smooth horizontal tube as shown. A particle of mass m is welded at P. The entire system is horizontal. The period of oscillation of the particle in the direction of x is
a)
b)
c)
d)
|
Mohit Rajpoot answered |
Let us assume a force dF is applied at P in positive x - direction. This will stretch each spring by dl inducing a spring force dFs in each spring.
Let the static deformation of the system is dx (along the x-direction). The particle is in equilibrium. So,
Using Pythagoras theorem,
Here y is constant.
What is the maximum Kinetic energy and minimum potential energy of a harmonic oscillator with amplitude 0.03m, force constant 4×105 N/m and total mechanical energy of 230 J.- a)200J, 40J
- b)180J,50J
- c)190J, 60J
- d)210J,60J
Correct answer is option 'B'. Can you explain this answer?
What is the maximum Kinetic energy and minimum potential energy of a harmonic oscillator with amplitude 0.03m, force constant 4×105 N/m and total mechanical energy of 230 J.
a)
200J, 40J
b)
180J,50J
c)
190J, 60J
d)
210J,60J
|
Infinity Academy answered |
K. Σ=1/2 K(A2-x2)
Max of mean position,
K. Σ=1/2 KA2
=1/2 x4x105x(3x10-2)2
=180J
T.M. Σ=180+P.Σ
230=180+P.Σ
P.Σ=230-180
P.Σ=50J
Max of mean position,
K. Σ=1/2 KA2
=1/2 x4x105x(3x10-2)2
=180J
T.M. Σ=180+P.Σ
230=180+P.Σ
P.Σ=230-180
P.Σ=50J
The work done by the string of a simple pendulum in S.H.M is- a)zero
- b)equal to total energy of system
- c)mg
- d)equal to kinetic energy of the system
Correct answer is option 'A'. Can you explain this answer?
The work done by the string of a simple pendulum in S.H.M is
a)
zero
b)
equal to total energy of system
c)
mg
d)
equal to kinetic energy of the system
|
Dilip Chaurasiya answered |
Zero becz. Tension and disp. Is at 90 degree.
The dimensions and unit of phase constant Φ is- a)dinensionless,rad
- b)[T]-1 ,s-1
- c)dinensionless, no units
- d)[T] , s
Correct answer is option 'A'. Can you explain this answer?
The dimensions and unit of phase constant Φ is
a)
dinensionless,rad
b)
[T]-1 ,s-1
c)
dinensionless, no units
d)
[T] , s
|
Suresh Reddy answered |
Mathematical constants don't have any dimensions hence, it is dimensionless and phase constant is in angle therefore, the unit is radian.
A mass m = 2.0 kg is attached to a spring having a force constant k = 290 N/m as in the figure. The mass is displaced from its equilibrium position and released. Its frequency of oscillation (in Hz) is approximately:
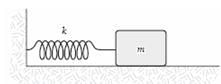
- a)12
- b)0.50
- c)1.9
- d)0.01
Correct answer is option 'C'. Can you explain this answer?
A mass m = 2.0 kg is attached to a spring having a force constant k = 290 N/m as in the figure. The mass is displaced from its equilibrium position and released. Its frequency of oscillation (in Hz) is approximately:
a)
12
b)
0.50
c)
1.9
d)
0.01
|
Riya Banerjee answered |
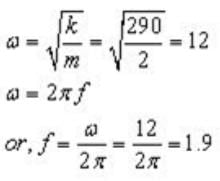
The amplitude A of a simple harmonic oscillator (with period, T and energy, E) is tripled. What would happen to T and E?
- a)T and E triples
- b)T and E doubles
- c)T remains same and E becomes nine times
- d)T gets tripled and E becomes zero
Correct answer is option 'C'. Can you explain this answer?
The amplitude A of a simple harmonic oscillator (with period, T and energy, E) is tripled. What would happen to T and E?
a)
T and E triples
b)
T and E doubles
c)
T remains same and E becomes nine times
d)
T gets tripled and E becomes zero
|
Preeti Iyer answered |
E α A2 and hence the energy will become 9 times.
T is independent of A and hence no change will occur.
Hence C is the correct answer.
T is independent of A and hence no change will occur.
Hence C is the correct answer.
A body of mass 5.0 kg is suspended by a spring which stretches 10 cm when the mass is attached. It is then displaced downward an additional 5.0 cm and released. Its position as a function of time is approximately:- a)y = .10 cos (9.9t + .1)
- b)y = .10 sin 9.9t
- c)y = .10 cos 9.9t
- d)y = .05 cos 9.9t
Correct answer is option 'D'. Can you explain this answer?
A body of mass 5.0 kg is suspended by a spring which stretches 10 cm when the mass is attached. It is then displaced downward an additional 5.0 cm and released. Its position as a function of time is approximately:
a)
y = .10 cos (9.9t + .1)
b)
y = .10 sin 9.9t
c)
y = .10 cos 9.9t
d)
y = .05 cos 9.9t
|
Nandini Iyer answered |
a. y
= .10 sin 9.9t
b. y
= .10 cos 9.9t
c. y
= .10 cos (9.9t + .1)
d. y
= .10 sin (9.9t + 5)
e. y
= .05 cos 9.9t
Answer: e.
y = 0.5 . cos 9.9 t
If the sign in equation F = -kx is changed what would happen to the motion of the oscillating body?- a)Motion would be linearly accelerated motion
- b)Body would come at rest
- c)Body would slow down
- d)Motion would be oscillating accelerated
Correct answer is option 'A'. Can you explain this answer?
If the sign in equation F = -kx is changed what would happen to the motion of the oscillating body?
a)
Motion would be linearly accelerated motion
b)
Body would come at rest
c)
Body would slow down
d)
Motion would be oscillating accelerated
|
Imk Pathsala answered |
If the sign is changed in F=-kx then the force and hence acceleration will not be opposite to the displacement. Due to this the particle will not oscillate and would accelerate in the direction of displacement. Hence the motion of the body will become linearly accelerated motion.
A simple pendulum with length l and bob of mass m is executing S.H.M of small amplitude a. The expression for maximum tension in the string will be- a)mg
- b)
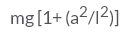
- c)
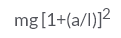
- d)mg[1 + (a/l) ]
Correct answer is option 'B'. Can you explain this answer?
A simple pendulum with length l and bob of mass m is executing S.H.M of small amplitude a. The expression for maximum tension in the string will be
a)
mg
b)
c)
d)
mg[1 + (a/l) ]
|
|
Nandini Patel answered |
The tension in the string would be maximum when bob will be passing mean position.
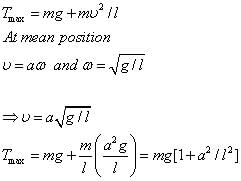
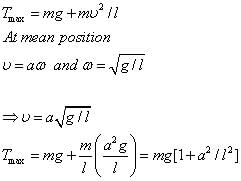
What provides the restoring force for SHM in case of column of mercury in U-tube?- a)Temperature
- b)Weight of mercury
- c)Height of column
- d)Elasticity
Correct answer is option 'B'. Can you explain this answer?
What provides the restoring force for SHM in case of column of mercury in U-tube?
a)
Temperature
b)
Weight of mercury
c)
Height of column
d)
Elasticity
|
|
Riya Banerjee answered |
Weight of mercury provides the restoring force for SHM in case of column of mercury in U-tube.
In the figure shown pulley is massless. Initially the blocks are held at a height such that spring is in its natural length. The amplitude and velocity amplitude of block B1 respectively are (there is no slipping anywhere)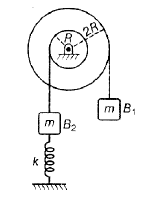
- a)
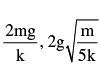
- b)
- c)
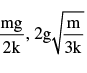
- d)
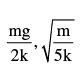
Correct answer is option 'A'. Can you explain this answer?
In the figure shown pulley is massless. Initially the blocks are held at a height such that spring is in its natural length. The amplitude and velocity amplitude of block B1 respectively are (there is no slipping anywhere)
a)
b)
c)
d)
|
Muskaan Mishra answered |
Decrease in GPE of B1 = Increase in Gravitational PE of B2 + Increase in elastic PE of spring.
Again applying law of conservation of mechanical energy at the mean position we get
The motion of simple pendulum is said to be S.H.M when its angle θ¸ through which bob is displaced from its equilibrium position is- a)θ is very small
- b)θ is zero
- c)θ is very large
- d)θ = cosθ
Correct answer is option 'A'. Can you explain this answer?
The motion of simple pendulum is said to be S.H.M when its angle θ¸ through which bob is displaced from its equilibrium position is
a)
θ is very small
b)
θ is zero
c)
θ is very large
d)
θ = cosθ
|
|
Priya Patel answered |
Consider a simple pendulum having mass 'm', length L and displaced by a small angle Θ with the vertical. Thus, it oscillates about its mean position. In the displaced position, two forces are acting on the bob, Gravitational force, which is the weight of the bob – 'mg' acting in the downward direction.
If the reference particle P moves in uniform circular motion, its projection along a diameter of the circle executes- a)motion along x axis
- b)motion along y axis
- c)circular motion
- d)Simple Harmonic motion
Correct answer is option 'D'. Can you explain this answer?
If the reference particle P moves in uniform circular motion, its projection along a diameter of the circle executes
a)
motion along x axis
b)
motion along y axis
c)
circular motion
d)
Simple Harmonic motion
|
|
Raghav Bansal answered |
SHM is a 1D projection of 2D UCM.
A particle starts S.H.M. from the mean position. Its amplitude is A and time period is T. At the time when its speed is half of the maximum speed, its displacement y is- a)A√3/2
- b)2A/√3
- c)A/2
- d)A/√2
Correct answer is option 'A'. Can you explain this answer?
A particle starts S.H.M. from the mean position. Its amplitude is A and time period is T. At the time when its speed is half of the maximum speed, its displacement y is
a)
A√3/2
b)
2A/√3
c)
A/2
d)
A/√2
|
|
Rajesh Gupta answered |
The relation between angular frequency and displacement is given as
v=ω√A2−x2
Suppose
x=A sinω t
On differentiating the above equation w.r.t. time we get
dx/dt=Aωcosωt
The maximum value of velocity will be [{v{\max }} = A\omega \]
The displacement for the time when speed is half the maximum is given as
v=Aω/2
A2ω2=4ω(A2−x2)
By substituting the value in (1) we get the displacement as
x=A√3/2
v=ω√A2−x2
Suppose
x=A sinω t
On differentiating the above equation w.r.t. time we get
dx/dt=Aωcosωt
The maximum value of velocity will be [{v{\max }} = A\omega \]
The displacement for the time when speed is half the maximum is given as
v=Aω/2
A2ω2=4ω(A2−x2)
By substituting the value in (1) we get the displacement as
x=A√3/2
At what distance from the mean position would the K.E of a particle in simple harmonic motion be equal to its potential energy?- a)a/√2
- b)a/2
- c)2√a
- d)a
Correct answer is option 'A'. Can you explain this answer?
At what distance from the mean position would the K.E of a particle in simple harmonic motion be equal to its potential energy?
a)
a/√2
b)
a/2
c)
2√a
d)
a
|
|
Raghav Bansal answered |
Let say from some distance x, the KE = PE and as total energy must be conserved and TE = -½ kA2
Thus we get 2PE = ½ kA2
Thus we get 2kx2 = kA2
We get x = A / √2
Thus we get 2PE = ½ kA2
Thus we get 2kx2 = kA2
We get x = A / √2
The equation of motion of a particle is x= 3cos(0.45t+π/4)m. Its maximum acceleration is
- a)0.60 ms-2
- b)0.50 ms-2
- c)0.55 ms-2
- d)0.45 ms-2
Correct answer is option 'A'. Can you explain this answer?
The equation of motion of a particle is x= 3cos(0.45t+π/4)m. Its maximum acceleration is
a)
0.60 ms-2
b)
0.50 ms-2
c)
0.55 ms-2
d)
0.45 ms-2
|
Nilotpal Singh answered |
+ 2) meters.
We can find the velocity and acceleration functions by taking the first and second derivatives of x with respect to time:
velocity v(t) = dx/dt = -3(0.45)sin(0.45t + 2)
acceleration a(t) = d^2x/dt^2 = -3(0.45)^2cos(0.45t + 2)
To find the maximum velocity, we set v(t) equal to zero and solve for t:
0 = -3(0.45)sin(0.45t + 2)
sin(0.45t + 2) = 0
0.45t + 2 = nπ, where n is an integer
t = (nπ - 2)/0.45
To find the maximum acceleration, we set a(t) equal to zero and solve for t:
0 = -3(0.45)^2cos(0.45t + 2)
cos(0.45t + 2) = 0
0.45t + 2 = (n + 0.5)π, where n is an integer
t = [(n + 0.5)π - 2]/0.45
Note that there are infinitely many solutions for both t_max_v and t_max_a, as there are infinitely many values of n.
To find the values of maximum velocity and maximum acceleration, we can substitute the values of t_max_v and t_max_a into the corresponding velocity and acceleration functions:
v_max = -3(0.45)sin(0.45t_max_v + 2)
a_max = -3(0.45)^2cos(0.45t_max_a + 2)
However, since there are infinitely many solutions for t_max_v and t_max_a, we cannot find a unique value for v_max and a_max without additional information.
We can find the velocity and acceleration functions by taking the first and second derivatives of x with respect to time:
velocity v(t) = dx/dt = -3(0.45)sin(0.45t + 2)
acceleration a(t) = d^2x/dt^2 = -3(0.45)^2cos(0.45t + 2)
To find the maximum velocity, we set v(t) equal to zero and solve for t:
0 = -3(0.45)sin(0.45t + 2)
sin(0.45t + 2) = 0
0.45t + 2 = nπ, where n is an integer
t = (nπ - 2)/0.45
To find the maximum acceleration, we set a(t) equal to zero and solve for t:
0 = -3(0.45)^2cos(0.45t + 2)
cos(0.45t + 2) = 0
0.45t + 2 = (n + 0.5)π, where n is an integer
t = [(n + 0.5)π - 2]/0.45
Note that there are infinitely many solutions for both t_max_v and t_max_a, as there are infinitely many values of n.
To find the values of maximum velocity and maximum acceleration, we can substitute the values of t_max_v and t_max_a into the corresponding velocity and acceleration functions:
v_max = -3(0.45)sin(0.45t_max_v + 2)
a_max = -3(0.45)^2cos(0.45t_max_a + 2)
However, since there are infinitely many solutions for t_max_v and t_max_a, we cannot find a unique value for v_max and a_max without additional information.
The instantaneous displacement of a simple harmonic oscillator is given by y = A cos (ωt + n/4). Its speed will be maximum at the time:). Its speed will be maximum at the time:- a)n/4ω
- b)ω/n
- c)ω/2n
- d)2n/ω
Correct answer is option 'A'. Can you explain this answer?
The instantaneous displacement of a simple harmonic oscillator is given by y = A cos (ωt + n/4). Its speed will be maximum at the time:). Its speed will be maximum at the time:
a)
n/4ω
b)
ω/n
c)
ω/2n
d)
2n/ω
|
|
Nandini Iyer answered |
The instantaneous displacement of a simple pendulum oscillator is given as y = acos(ωt + π/4)
differentiating with respect to time,
dy/dt = -ωasin(ωt + π/4)
here, dy/dt is the velocity of a particle executing SHM.
so, speed of particle = | dy/dt | = ωasin(ωt + π/4)
so, dy/dt will be maximum when sin(ωt + π/4) will be maximum i.e., 1
so, sin(ωt + π/4) = 1 = sin(π/2)
⇒ωt + π/4 = π/2
⇒ωt = π/4
⇒t = π/(4ω)
hence, at t = π/(4ω) , speed of the particle will be maximum.
differentiating with respect to time,
dy/dt = -ωasin(ωt + π/4)
here, dy/dt is the velocity of a particle executing SHM.
so, speed of particle = | dy/dt | = ωasin(ωt + π/4)
so, dy/dt will be maximum when sin(ωt + π/4) will be maximum i.e., 1
so, sin(ωt + π/4) = 1 = sin(π/2)
⇒ωt + π/4 = π/2
⇒ωt = π/4
⇒t = π/(4ω)
hence, at t = π/(4ω) , speed of the particle will be maximum.
Two light springs of force constants k1 and k2, loaded with equal masses undergo vertical oscillations. If the maximum velocities of the masses are the same, the ratio of the amplitudes of oscillations is:- a)k1 /k2
- b)1
- c)√(k2 /k1)
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Two light springs of force constants k1 and k2, loaded with equal masses undergo vertical oscillations. If the maximum velocities of the masses are the same, the ratio of the amplitudes of oscillations is:
a)
k1 /k2
b)
1
c)
√(k2 /k1)
d)
none of these
|
Lavanya Menon answered |
As the maximum velocities are equal
a1ω1 = a2ω2
a1/a2 = ω2/ω1 ----- (1)
as, k1 = mω12 ----- (2)
k2 = mω22 ----- (3)
substituting eq 2 and eq 3 in eq 1 ,we get
a1/a2 = (k1/k2)1/2
a1ω1 = a2ω2
a1/a2 = ω2/ω1 ----- (1)
as, k1 = mω12 ----- (2)
k2 = mω22 ----- (3)
substituting eq 2 and eq 3 in eq 1 ,we get
a1/a2 = (k1/k2)1/2
A particle of mass 0.1 kg is executing SHM of amplitude 0.1 m. When the particle passes through the mean position, its KE is 8 ×10-3 J. Find the equation of motion of the particle if the initial phase of oscillation is 45˚- a)y = 0.1 cos(3t + (π/4))
- b)y = 0.1 sin(6t + (π/4))
- c)y = 0.1 sin(4t + (π/4))
- d)y=0.1 cos(4t + (π/4))
Correct answer is option 'C'. Can you explain this answer?
A particle of mass 0.1 kg is executing SHM of amplitude 0.1 m. When the particle passes through the mean position, its KE is 8 ×10-3 J. Find the equation of motion of the particle if the initial phase of oscillation is 45˚
a)
y = 0.1 cos(3t + (π/4))
b)
y = 0.1 sin(6t + (π/4))
c)
y = 0.1 sin(4t + (π/4))
d)
y=0.1 cos(4t + (π/4))
|
Arun Khanna answered |
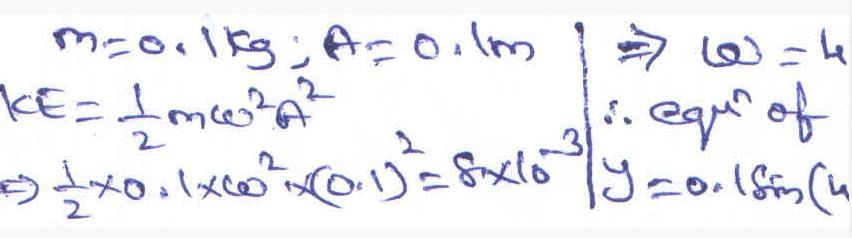Option C CorrectA pendulum has time period T for small oscillations. Now, an obstacle is situated below the
point of suspension O at a distance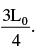 
The pendulum is released from rest. Throughout the motion, the moving string makes small angle with vertical. Time after which the pendulum returns back to its initial position is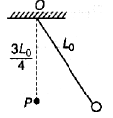
- a)T
- b)4/3T
- c)2/3T
- d)3/4T
Correct answer is option 'D'. Can you explain this answer?
A pendulum has time period T for small oscillations. Now, an obstacle is situated below the
point of suspension O at a distance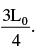 The pendulum is released from rest. Throughout the motion, the moving string makes small angle with vertical. Time after which the pendulum returns back to its initial position is
point of suspension O at a distance
The pendulum is released from rest. Throughout the motion, the moving string makes small angle with vertical. Time after which the pendulum returns back to its initial position isa)
T
b)
4/3T
c)
2/3T
d)
3/4T
|
Amrita Kumar answered |
For the right (half) oscillation,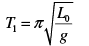 
For the left (half) oscillation,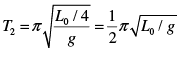 
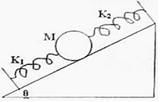
A sphere of mass M is arranged on a smooth inclined plane of angle θ, in between two springs of spring constants K1 and K2 . The springs are joined to rigid supports on the inclined plane and to the sphere (Fig). When the sphere is displaced slightly, it executes simple harmonic motion. What is the period of this motion?
- a)
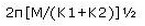
- b)
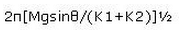
- c)
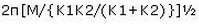
- d)
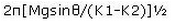
Correct answer is option 'A'. Can you explain this answer?
A sphere of mass M is arranged on a smooth inclined plane of angle θ, in between two springs of spring constants K1 and K2 . The springs are joined to rigid supports on the inclined plane and to the sphere (Fig). When the sphere is displaced slightly, it executes simple harmonic motion. What is the period of this motion?
a)
b)
c)
d)
|
|
Preeti Iyer answered |
Compression and expansion in both the springs will be same. Hence, F = k1x= k2x. Fn=F + F. Therefore, kn = k1 + k2.
T = 2π [m / kn]½
T = 2π [m / (k1+k2)]½
Hence A is correct.
T = 2π [m / kn]½
T = 2π [m / (k1+k2)]½
Hence A is correct.
A simple pendulum is arranged using a small metallic bob of mass ‘m’and a light rubber cord of length ‘L’ (on suspending the bob), area of cross section ‘A’ and Young’s modulus ‘Y’. [One should use inextensible cord only for simple pendulum!]. When this unconventional pendulum is at rest in its mean position, the bob is pulled slightly down and is released. Then, the period of the vertical oscillation of the bob is (assuming that the size of the bob is negligible compared to the length of the cord):- a)
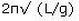
- b)
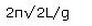
- c)
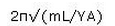
- d)
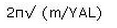
Correct answer is option 'C'. Can you explain this answer?
A simple pendulum is arranged using a small metallic bob of mass ‘m’and a light rubber cord of length ‘L’ (on suspending the bob), area of cross section ‘A’ and Young’s modulus ‘Y’. [One should use inextensible cord only for simple pendulum!]. When this unconventional pendulum is at rest in its mean position, the bob is pulled slightly down and is released. Then, the period of the vertical oscillation of the bob is (assuming that the size of the bob is negligible compared to the length of the cord):
a)
b)
c)
d)
|
Ciel Knowledge answered |
The period as usual is given by T = 2n√(m/k). Here `m' is the same as the mass of the bob. The force constant can be found by writing the expression for Young's modulus (since it arises from the elastic force in the cord): V = FL/A(δL) where 6L is the increase in the length of the cord on pulling the bob down with a force F. Therefore, the force constant, F/(δL) = YA/L. On substituting this value, the period is 2m✓(mL/YA).
Two pendulums of length 100 cm and 121 cm starts oscillating. At some instant, the two are at the mean position in the same phase. After how many oscillations of the longer pendulum will the two be in the same phase at the mean position again- a)11
- b)10
- c)21
- d)20
Correct answer is option 'B'. Can you explain this answer?
Two pendulums of length 100 cm and 121 cm starts oscillating. At some instant, the two are at the mean position in the same phase. After how many oscillations of the longer pendulum will the two be in the same phase at the mean position again
a)
11
b)
10
c)
21
d)
20
|
|
Mira Sharma answered |
Three masses of 500 g, 300 g and 100 g are suspended at the end of an ideal spring as shown and are in equilibrium. When the 500 g mass is suddenly removed, the system oscillated with a period of 2 s. When 300 g mass is also removed, it will oscillate with the period- a)1.75 s
- b)1.25 s
- c)1.5 s
- d)1 s
Correct answer is option 'D'. Can you explain this answer?
Three masses of 500 g, 300 g and 100 g are suspended at the end of an ideal spring as shown and are in equilibrium. When the 500 g mass is suddenly removed, the system oscillated with a period of 2 s. When 300 g mass is also removed, it will oscillate with the period
a)
1.75 s
b)
1.25 s
c)
1.5 s
d)
1 s
|
Tejas Joshi answered |
When 500 g is removed, m = (100 + 300)g = 0.4 kg
When 300 g is also removed,
A particle of mass m is executing oscillation about the origin on X-axis. Its potential energy is V(x)=K∣x∣3. Where K is a positive constant. If the amplitude of oscillation is a, then its time period T is proportional to.- a) 1/√a
- b)a
- c)√a
- d) a3/2
Correct answer is option 'A'. Can you explain this answer?
A particle of mass m is executing oscillation about the origin on X-axis. Its potential energy is V(x)=K∣x∣3. Where K is a positive constant. If the amplitude of oscillation is a, then its time period T is proportional to.
a)
1/√a
b)
a
c)
√a
d)
a3/2
|
Sravya Sarkar answered |
1/√a^3
Due to what force a simple pendulum remains in simple harmonic motion?- a)y, displacement
- b)mg sinθ, component of weight due to gravitational force
- c)a, acceleration
- d)mg , weight
Correct answer is option 'B'. Can you explain this answer?
Due to what force a simple pendulum remains in simple harmonic motion?
a)
y, displacement
b)
mg sinθ, component of weight due to gravitational force
c)
a, acceleration
d)
mg , weight
|
|
Preeti Iyer answered |
For the pendulum, we can use Newton's second law to write an equation for the forces on the pendulum. The only force responsible for the oscillating motion of the pendulum is the x-component of the weight, so the restoring force on a pendulum is:
F=−mg sinθ
For angles under about 15°, we can approximate sinθ as θ and the restoring force simplifies to:
F ≈ −mgθ
Thus, simple pendulums are simple harmonic oscillators for small displacement angles.
F=−mg sinθ
For angles under about 15°, we can approximate sinθ as θ and the restoring force simplifies to:
F ≈ −mgθ
Thus, simple pendulums are simple harmonic oscillators for small displacement angles.
The velocity and acceleration amplitudes of body executing simple harmonic motion is- a)ω2A , ωA
- b)A , A
- c)ω2/A , ω/A
- d) ωA , ω2A
Correct answer is option 'D'. Can you explain this answer?
The velocity and acceleration amplitudes of body executing simple harmonic motion is
a)
ω2A , ωA
b)
A , A
c)
ω2/A , ω/A
d)
ωA , ω2A
|
Jayant Mishra answered |
Maximum velocity :-
V = ωa ,where ω is uniform angular velocity and a is the radius of the circle in which a reference particle executing S.H.M.
Velocity is maximum at mean positions. The maximum value of velocity is called velocity amplitude in SHM.
Acceleration is maximum at extreme position given by A = - ω 2a. The maximum value of acceleration is called acceleration amplitude in SHM.
Two simple pendulums of length 1m and 25 m, respectively, are both given small displacements in the same direction at the same instant.If they are in phase after the shorter pendulum has completed n oscillation, n is equal to - a)4/3
- b)5/4
- c)7/5
- d)8/7
Correct answer is option 'B'. Can you explain this answer?
Two simple pendulums of length 1m and 25 m, respectively, are both given small displacements in the same direction at the same instant.If they are in phase after the shorter pendulum has completed n oscillation, n is equal to
a)
4/3
b)
5/4
c)
7/5
d)
8/7
|
Arya Reddy answered |
∴ T ∝ √L , as time period decreases when the length of pendulum decreases, the time period of shorter pendulum (Ts) is smaller than that of longer pendulum (Tl). That means shorter pendulum performs more oscillations in a given time.
It is given that after n oscillations of shorter pendulum, both are again in phase. So, by this time longer pendulum must have made (n – 1) oscillations.
So, the two pendulum shall be in the same phase for the first time when the shorter pendulum has
completed 5/4 oscillation
completed 5/4 oscillation
A particle of mass m is executing oscillations about the origin on the X-axis with amplitude A. Its potential energy is given as U(x) = βx4 where β is a positive constant. The x- cordinate of the particle, when the potential energy is one- third of the kinetic energy, is- a)
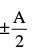
- b)
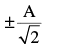
- c)
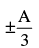
- d)
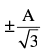
Correct answer is option 'B'. Can you explain this answer?
A particle of mass m is executing oscillations about the origin on the X-axis with amplitude A. Its potential energy is given as U(x) = βx4 where β is a positive constant. The x- cordinate of the particle, when the potential energy is one- third of the kinetic energy, is
a)
b)
c)
d)
|
Sai Mishra answered |
A weight of mass m is at rest at O when suspended from a spring, as shown. When it is pulled down and released, it oscillates between positions A and B. Which statement about the system consisting of the spring and the mass is correct?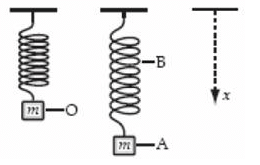
- a)The rate of change of momentum has its greatest magnitude at A and B
- b)The rate of change of gravitational potential energy is smallest at O
- c)The gravitational potential energy of the system is greatest at A
- d)The elastic potential energy of the system is greatest at O
Correct answer is option 'A'. Can you explain this answer?
A weight of mass m is at rest at O when suspended from a spring, as shown. When it is pulled down and released, it oscillates between positions A and B. Which statement about the system consisting of the spring and the mass is correct?
a)
The rate of change of momentum has its greatest magnitude at A and B
b)
The rate of change of gravitational potential energy is smallest at O
c)
The gravitational potential energy of the system is greatest at A
d)
The elastic potential energy of the system is greatest at O
|
|
User2408930 answered |
A uniform disc of mass m and radius R is pivoted smoothly at P,.If a uniform thin ring of mass m and radius R is welded at the lower point of the disc, find the period of SHM of the system (disc + ring).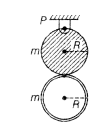
- a)
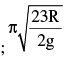
- b)
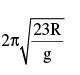
- c)
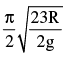
- d)
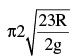
Correct answer is option 'A'. Can you explain this answer?
A uniform disc of mass m and radius R is pivoted smoothly at P,.If a uniform thin ring of mass m and radius R is welded at the lower point of the disc, find the period of SHM of the system (disc + ring).
a)
b)
c)
d)
|
Ishani Mehta answered |
The time period of a physical pendulum is
where, I = MI of the system about point of sduspension
M = mass of the system and
l = distance between COM of the system and point suspension
Now, M = m + m = 2m
A particle of mass m is allowed to oscillate on a smooth parabola x2 = 4ay, a > 0, about the origin O (see figure). For small oscillations, find the angular frequency ( ω )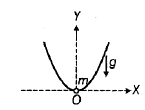
- a)
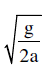
- b)
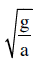
- c)
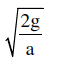
- d)
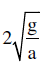
Correct answer is option 'A'. Can you explain this answer?
A particle of mass m is allowed to oscillate on a smooth parabola x2 = 4ay, a > 0, about the origin O (see figure). For small oscillations, find the angular frequency ( ω )
a)
b)
c)
d)
|
Anushka Desai answered |
During its oscillations, at a particular instant let the coordinates of the particle are (x, y) The total energy of the particle is
As oscillations are very small, we can ignore the middle term.
A particle of mass m is located in a unidimensional potential field, where the potential
energy of the particle depends on the coordinate x as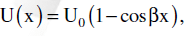 
where U0 and b are constant. Find the time period of small oscillations that the particle performs about the equilibrium position (solve the problem by Taylor’s method)- a)
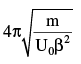
- b)
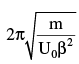
- c)
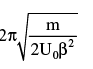
- d)
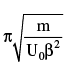
Correct answer is option 'B'. Can you explain this answer?
A particle of mass m is located in a unidimensional potential field, where the potential
energy of the particle depends on the coordinate x as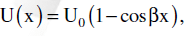where U0 and b are constant. Find the time period of small oscillations that the particle performs about the equilibrium position (solve the problem by Taylor’s method)
energy of the particle depends on the coordinate x as
where U0 and b are constant. Find the time period of small oscillations that the particle performs about the equilibrium position (solve the problem by Taylor’s method)a)
b)
c)
d)
|
|
Rhea Choudhary answered |
An air chamber of volume V, has a long neck of cross-sectional area A. A ball of mass m is fitted smoothly in the neck. The bulk modulus of air is B. If the ball is pressed down slightly and released, the time period of its oscillation is- a)
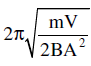
- b)
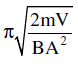
- c)
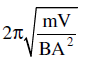
- d)
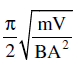
Correct answer is option 'C'. Can you explain this answer?
An air chamber of volume V, has a long neck of cross-sectional area A. A ball of mass m is fitted smoothly in the neck. The bulk modulus of air is B. If the ball is pressed down slightly and released, the time period of its oscillation is
a)
b)
c)
d)
|
Sounak Chaudhary answered |
Let the ball is pressed down by a small y, then the value of air decreased by Ay.
Then, excess pressure is
Two particles executing SHM with same angular frequency and amplitude A and 2A same
straight line with same position cross other in opposite direction at a distance A/3 from mean position. The phase difference between the two SHM’s is- a)
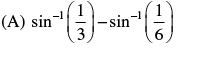
- b)zero
- c)
- d)
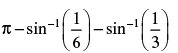
Correct answer is option 'D'. Can you explain this answer?
Two particles executing SHM with same angular frequency and amplitude A and 2A same
straight line with same position cross other in opposite direction at a distance A/3 from mean position. The phase difference between the two SHM’s is
straight line with same position cross other in opposite direction at a distance A/3 from mean position. The phase difference between the two SHM’s is
a)
b)
zero
c)
d)
|
|
Muskaan Mishra answered |
Let particle (1) is moving towards right and particle (2) is moving towards left art this instant, 1 = 0
A linear harmonic oscillator of force constant 2 x 106 Nm–1 and amplitude 0.01 m has a total mechanical energy 160 J. Among the following statements, which are correct?
- a)Both I and II
- b)Both II and III
- c)Both II and IV
- d)None
Correct answer is option 'B'. Can you explain this answer?
A linear harmonic oscillator of force constant 2 x 106 Nm–1 and amplitude 0.01 m has a total mechanical energy 160 J. Among the following statements, which are correct?
a)
Both I and II
b)
Both II and III
c)
Both II and IV
d)
None
|
Rahul Chaudhary answered |
Total mechanical energy is 160
ET = J
∴ U max = 160 J
ET = J
∴ U max = 160 J
At extreme position KE is zero. Work done by spring force from extreme position to mean position is
Find the frequency of small oscillations of a thin uniform vertical rod of mass m and length L hinged at the point O as shown in the figure. The stiffness of each spring is k. Mass of the springs is negligible. The figure shows equilibrium position.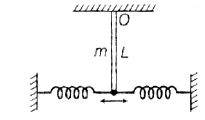
- a)
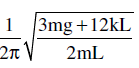
- b)
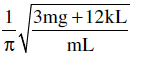
- c)
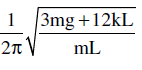
- d)
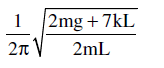
Correct answer is option 'A'. Can you explain this answer?
Find the frequency of small oscillations of a thin uniform vertical rod of mass m and length L hinged at the point O as shown in the figure. The stiffness of each spring is k. Mass of the springs is negligible. The figure shows equilibrium position.
a)
b)
c)
d)
|
Krithika Kulkarni answered |
A 7 kg disc is free to rotate about a horizontal axis passing through its centre O (see figure). The radius of the disc is 10 cm and spring constant of both the spring is 600 Nm-1 There is no slipping between the disc and the string. The time period of small oscillations of the disc is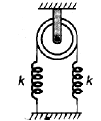
- a).12 s
- b)0.34s
- c)0.25 s
- d)0.48 s
Correct answer is option 'B'. Can you explain this answer?
A 7 kg disc is free to rotate about a horizontal axis passing through its centre O (see figure). The radius of the disc is 10 cm and spring constant of both the spring is 600 Nm-1 There is no slipping between the disc and the string. The time period of small oscillations of the disc is
a)
.12 s
b)
0.34s
c)
0.25 s
d)
0.48 s
|
Shubham Nambiar answered |
When the angular displacement of the disc is θ the deformation (elongation and compression) in each spring is x = Rθ .
The potential energy between two atoms in a diatomic molecule varies with x as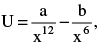 
where a and b are positive constants. Find the equivalent spring constant forthe oscillation of one atom if the other atom is kept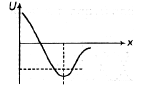 
- a)
- b)
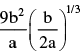
- c)
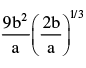
- d)
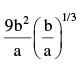
Correct answer is option 'B'. Can you explain this answer?
The potential energy between two atoms in a diatomic molecule varies with x as 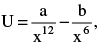where a and b are positive constants. Find the equivalent spring constant for
where a and b are positive constants. Find the equivalent spring constant forthe oscillation of one atom if the other atom is kept
a)
b)
c)
d)
|
|
Rhea Choudhary answered |
A solid uniform cylinder of mass m performs small oscillations in horizontal plane if slightly displaced from its mean position shown in the figure. Initially springs are in naturals and cylinder does not slip on ground during oscillations due to friction between ground and cylinder. Force constant of each spring is k. The time period of oscillation is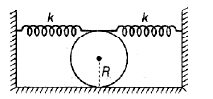
- a)
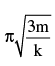
- b)
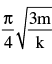
- c)
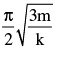
- d)
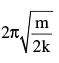
Correct answer is option 'C'. Can you explain this answer?
A solid uniform cylinder of mass m performs small oscillations in horizontal plane if slightly displaced from its mean position shown in the figure. Initially springs are in naturals and cylinder does not slip on ground during oscillations due to friction between ground and cylinder. Force constant of each spring is k. The time period of oscillation is
a)
b)
c)
d)
|
|
Sai Mishra answered |
A snapshot during oscillations of the cylinder is shown in the figure. Its displacement is x and velocity v.
Its angular velocity is ω = V/R(Due to pure rolling)
Its angular velocity is ω = V/R(Due to pure rolling)
As the centre of the cylinder is at a distance x from the initial position, the spring which are connected at a
point on its rim must be compressed and stretched by a distance 2x. Thus, at this intermediate position total
energy of the oscillation system can be given as
point on its rim must be compressed and stretched by a distance 2x. Thus, at this intermediate position total
energy of the oscillation system can be given as
A uniform semicircular cylinder of radius R and mass m is displaced through a small angle
θ from its equilibrium position. It rolls without slipping during oscillations. The time period
of small oscillation is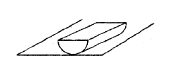
- a)
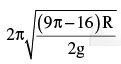
- b)
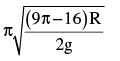
- c)
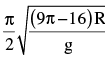
- d)
Correct answer is option 'B'. Can you explain this answer?
A uniform semicircular cylinder of radius R and mass m is displaced through a small angle
θ from its equilibrium position. It rolls without slipping during oscillations. The time period
of small oscillation is
θ from its equilibrium position. It rolls without slipping during oscillations. The time period
of small oscillation is
a)
b)
c)
d)
|
|
Ruchi Basak answered |
Restoring torque is τ = mg ( O ' P ) = − I0 α
In the figure, θ is very small
In the figure is shown a small block B of mass m resting on a smooth horizontal floor and the block is attached to an ideal spring (of force constant k). The spring is attached to vertical wall W1. At a distance d from the block, right side of it, is present the vertical wall W2. Now, the block is compressed by a distance 5d/3 and released. It starts oscillating. If the collision of the block with W2 are perfectly elastic, the time period of oscillation of the block is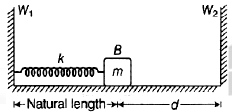
- a)
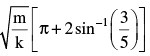
- b)
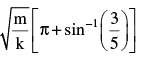
- c)
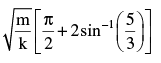
- d)
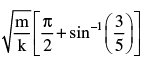
Correct answer is option 'A'. Can you explain this answer?
In the figure is shown a small block B of mass m resting on a smooth horizontal floor and the block is attached to an ideal spring (of force constant k). The spring is attached to vertical wall W1. At a distance d from the block, right side of it, is present the vertical wall W2. Now, the block is compressed by a distance 5d/3 and released. It starts oscillating. If the collision of the block with W2 are perfectly elastic, the time period of oscillation of the block is
a)
b)
c)
d)
|
|
Gargi Sharma answered |
absence of wall W2, the time period of block would have been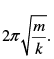 
But due to the presence of W2, it alters. But for the left part of oscillation (from the mean position shown), the period will be 
But due to the presence of W2, it alters. But for the left part of oscillation (from the mean position shown), the period will be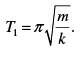 For the right side part, d = A sinω t [from x = A sinω t ]
This is the time taken by the block to reach W2 from mean position. Collision with W2 is perfectly elastic (given).
Time taken for right side part of oscillation will be
∴ Total time period is
The distance travelled by a particle executing SHM in 10 s, if the time period is 3 s, is
(It is given that the body starts from A√3/3 from equilibrium position, moves is positive direction at t = 0) - a)
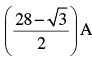
- b)
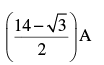
- c)
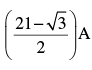
- d)
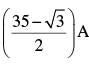
Correct answer is option 'A'. Can you explain this answer?
The distance travelled by a particle executing SHM in 10 s, if the time period is 3 s, is
(It is given that the body starts from A√3/3 from equilibrium position, moves is positive direction at t = 0)
(It is given that the body starts from A√3/3 from equilibrium position, moves is positive direction at t = 0)
a)
b)
c)
d)
|
|
Ruchi Basak answered |
In 9s, the distance travelled = 4A × 3 = 12A
Imagine, now it is at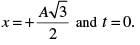
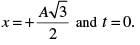
The displacement of the motion of a particle is represented (in metre) by the equation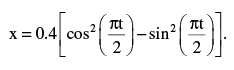 
The motion of the particle is - a)oscillatory but not SHM
- b)SHM with amplitude 0.4 m
- c)SHM with amplitude 0.4√2 m
- d)SHM with amplitude 0.8 m
Correct answer is option 'B'. Can you explain this answer?
The displacement of the motion of a particle is represented (in metre) by the equation 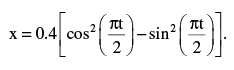The motion of the particle is
The motion of the particle is a)
oscillatory but not SHM
b)
SHM with amplitude 0.4 m
c)
SHM with amplitude 0.4√2 m
d)
SHM with amplitude 0.8 m
|
|
Amrita Kumar answered |
∴ Amplitude is 0.4 m and motion is SHM.
A cylinder of radius r and mass m rests on a curved path of radius R as shown in the figure. It is slightly displaced to its left. Thus, the cylinder makes oscillation about the mean position. The period of oscillations is (the cylinder rolls without slipping)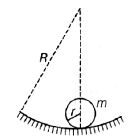
- a)
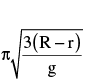
- b)
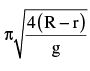
- c)
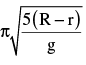
- d)
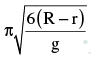
Correct answer is option 'D'. Can you explain this answer?
A cylinder of radius r and mass m rests on a curved path of radius R as shown in the figure. It is slightly displaced to its left. Thus, the cylinder makes oscillation about the mean position. The period of oscillations is (the cylinder rolls without slipping)
a)
b)
c)
d)
|
Rithika Mukherjee answered |
Chapter doubts & questions for Undamped Simple Harmonic Motion - Physics for EmSAT Achieve 2025 is part of EmSAT Achieve exam preparation. The chapters have been prepared according to the EmSAT Achieve exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for EmSAT Achieve 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Undamped Simple Harmonic Motion - Physics for EmSAT Achieve in English & Hindi are available as part of EmSAT Achieve exam.
Download more important topics, notes, lectures and mock test series for EmSAT Achieve Exam by signing up for free.
Physics for EmSAT Achieve
208 videos|329 docs|212 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily