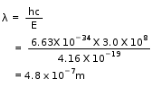All Exams >
EmSAT Achieve >
Chemistry for EmSAT Achieve >
All Questions
All questions of Waves for EmSAT Achieve Exam
Direction (Q. Nos. 12 and 13) This section contains a paragraph, wach describing theory, experiments, data etc. three Questions related to paragraph have been given.Each question have only one correct answer among the four given ptions (a),(b),(c),(d)A hypothetical electromagnetic wave is pictured here.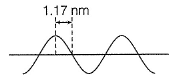 Q. Energy associated with this wave is
Q. Energy associated with this wave is- a)4.24 x 10-19J
- b)2.12 x 10-19J
- c)1.06 x 10-19J
- d)8.49 x 10-19J
Correct answer is option 'A'. Can you explain this answer?
Direction (Q. Nos. 12 and 13) This section contains a paragraph, wach describing theory, experiments, data etc. three Questions related to paragraph have been given.Each question have only one correct answer among the four given ptions (a),(b),(c),(d)
A hypothetical electromagnetic wave is pictured here.
Q. Energy associated with this wave is
a)
4.24 x 10-19J
b)
2.12 x 10-19J
c)
1.06 x 10-19J
d)
8.49 x 10-19J
|
|
Hansa Sharma answered |
A to E makes one complete wave.
The de Broglie wavelength of a particle is given by.- a)h/mv
- b)h + mv
- c)hmv
- d)mv/c
Correct answer is option 'A'. Can you explain this answer?
The de Broglie wavelength of a particle is given by.
a)
h/mv
b)
h + mv
c)
hmv
d)
mv/c

|
Ambition Institute answered |
According to De Broglie, a moving small particle like electron, proton, neutron, dust particle, a small ball etc. has the properties of a wave (Dual nature of matter).
The wave length of a moving particle may be calculated as
λ=h/mv =h/p
De Broglie equation
λ =wave length
h= planck’s constt.
m=mass of particle
v=velocity of particle
p=momentum of the particle
The de – Broglie wavelength of an electron is 600 nm. The velocity of the electron having the mass 9.1 X 10-31 Kg is- a)0.0012 x 10+4 m/s
- b)0.0012 x 10+3 m/s
- c)0.0012 x 10+6 m/s
- d)0.0012 x 10+2 m/s
Correct answer is option 'C'. Can you explain this answer?
The de – Broglie wavelength of an electron is 600 nm. The velocity of the electron having the mass 9.1 X 10-31 Kg is
a)
0.0012 x 10+4 m/s
b)
0.0012 x 10+3 m/s
c)
0.0012 x 10+6 m/s
d)
0.0012 x 10+2 m/s
|
|
Arjun Gupta answered |
1nm= 10^-9m.
wavelength= 600nm= 600 ×10-9m
wavelength= h/p.
wavelength= h/mv
v= h/ m wavelength
v=6.625×10^-34/9.1×10^-31×600× 10-9.
v= 6.625 × 10+4/9.1 ×6.
v= 6.625× 10+4/9.1×6.
v= 6.625 ×104/54.6.
v= 0.12 × 104.
v= 0.0012 × 10+6 .
wavelength= 600nm= 600 ×10-9m
wavelength= h/p.
wavelength= h/mv
v= h/ m wavelength
v=6.625×10^-34/9.1×10^-31×600× 10-9.
v= 6.625 × 10+4/9.1 ×6.
v= 6.625× 10+4/9.1×6.
v= 6.625 ×104/54.6.
v= 0.12 × 104.
v= 0.0012 × 10+6 .
The de Broglie wavelength of an electron is 8.7 x 10-11 m. The mass of an electron is 9.1 x 10-31 kg. The velocity of this electron is:- a)0.0837 × 108 m/s
- b)6.9 × 10-5 m/s
- c)8.4 × 103 m/s
- d)1.2 × 10-7 m/s
Correct answer is option 'A'. Can you explain this answer?
The de Broglie wavelength of an electron is 8.7 x 10-11 m. The mass of an electron is 9.1 x 10-31 kg. The velocity of this electron is:
a)
0.0837 × 108 m/s
b)
6.9 × 10-5 m/s
c)
8.4 × 103 m/s
d)
1.2 × 10-7 m/s
|
|
Suresh Reddy answered |
Wavelength = h/p = h/ mv.
v= h/ m.wavelength
v= 6.625 × 10-34/9.1×10-31 × 8.7 × 10-11
v= 6.625 × 108/ 9.1× 8.7
v= 0.08367 ×108.
v= h/ m.wavelength
v= 6.625 × 10-34/9.1×10-31 × 8.7 × 10-11
v= 6.625 × 108/ 9.1× 8.7
v= 0.08367 ×108.
Uncertainty in the position of an electron (mass 9.1 x 10-31 kg) moving with a velocity of 300 ms-1, accurate upto 0.001% will be:
- a)1.92 x 10-2 m
- b)3.84 x 10-2 m
- c)19.2 x 10-2 m
- d)5.76 x 10-2 m
Correct answer is option 'C'. Can you explain this answer?
Uncertainty in the position of an electron (mass 9.1 x 10-31 kg) moving with a velocity of 300 ms-1, accurate upto 0.001% will be:
a)
1.92 x 10-2 m
b)
3.84 x 10-2 m
c)
19.2 x 10-2 m
d)
5.76 x 10-2 m
|
|
Lavanya Menon answered |
Change in position (X),
P= momentum,
P=mv.
X ×P = h/4π.
X× m v = h/4π.
X= h/4πmv.
X=6.625×10-34/4 ×3.14×9.1×10^-31×300.
X=6.625×10-5/342.8.
X=0.0192×10^-5.
X= 19.2× 10-7.
in question it is given to take accurate up to 0.001%.= 1×10-3/100=1 ×10-5.
X= 19.2 ×10-7/10-5.
X=19.2 × 10-2.
P= momentum,
P=mv.
X ×P = h/4π.
X× m v = h/4π.
X= h/4πmv.
X=6.625×10-34/4 ×3.14×9.1×10^-31×300.
X=6.625×10-5/342.8.
X=0.0192×10^-5.
X= 19.2× 10-7.
in question it is given to take accurate up to 0.001%.= 1×10-3/100=1 ×10-5.
X= 19.2 ×10-7/10-5.
X=19.2 × 10-2.
Energy of a mole of radio wave photons with a frequency of 909 kHz is- a)6.02 x 10-28 J
- b)3.62 x 10-4 J
- c)1.00 x 10-4 J
- d)6.02 x 10-31 J
Correct answer is option 'B'. Can you explain this answer?
Energy of a mole of radio wave photons with a frequency of 909 kHz is
a)
6.02 x 10-28 J
b)
3.62 x 10-4 J
c)
1.00 x 10-4 J
d)
6.02 x 10-31 J
|
|
Rajeev Nair answered |
E = N0hv
= 6.02 x 1023 x 6.62 x 10-34 Js x 909 x103 s-1
= 3.62 x 10-4 J
= 3.62 x 10-4 J
In the relationship ∆x. ∆p = 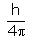 , ∆p is:
, ∆p is:- a)Certainty in momentum
- b)Certainty in position
- c)Uncertainty in momentum
- d)Uncertainty in position
Correct answer is option 'C'. Can you explain this answer?
In the relationship ∆x. ∆p = 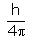 , ∆p is:
, ∆p is:
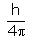 , ∆p is:
, ∆p is:a)
Certainty in momentum
b)
Certainty in position
c)
Uncertainty in momentum
d)
Uncertainty in position
|
|
Hansa Sharma answered |
The uncertainty principle is alternatively expressed in terms of a particle’s momentum and position. The momentum of a particle is equal to the product of its mass times its velocity. Thus, the product of the uncertainties in the momentum and the position of a particle equals h/(4π)
Direction (Q. Nos. 11 and 12) This section contains a paragraph, wach describing theory, experiments, data etc. three Questions related to paragraph have been given.Each question have only one correct answer among the four given ptions (a),(b),(c),(d)Photoelectric effect can be expressed in terms of the following graph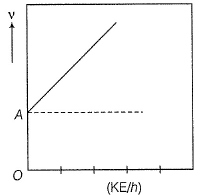
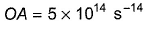 Q. What is work function for this photoelectric emission of electrons?
Q. What is work function for this photoelectric emission of electrons?- a)199.262 kJ mol-1
- b)199.262 J mol-1
- c)3.3 kJ mol-1
- d)3.3 x 10-19 kJ mol-1
Correct answer is option 'A'. Can you explain this answer?
Direction (Q. Nos. 11 and 12) This section contains a paragraph, wach describing theory, experiments, data etc. three Questions related to paragraph have been given.Each question have only one correct answer among the four given ptions (a),(b),(c),(d)
Photoelectric effect can be expressed in terms of the following graph
Q. What is work function for this photoelectric emission of electrons?
a)
199.262 kJ mol-1
b)
199.262 J mol-1
c)
3.3 kJ mol-1
d)
3.3 x 10-19 kJ mol-1
|
|
Gaurav Kumar answered |
Photoelectric effect is represented by
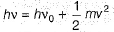
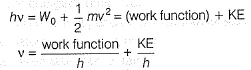


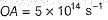
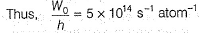
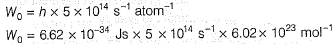
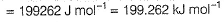
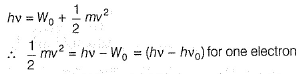
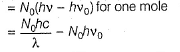
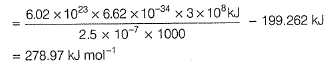
The position of both, an electron and a helium atom is known within 1.0 mm. Further more the momentum of the electron is known within 5.0 x 10-26 kg ms-1. The minimum uncertainty in the measurement of the momentum of the helium atom is- a)50.0 kg ms-1
- b)80.0 kg ms-1
- c)80.0 x 10-26 kg ms-1
- d)5.0 x 10-26 kg ms-1
Correct answer is option 'D'. Can you explain this answer?
The position of both, an electron and a helium atom is known within 1.0 mm. Further more the momentum of the electron is known within 5.0 x 10-26 kg ms-1. The minimum uncertainty in the measurement of the momentum of the helium atom is
a)
50.0 kg ms-1
b)
80.0 kg ms-1
c)
80.0 x 10-26 kg ms-1
d)
5.0 x 10-26 kg ms-1

|
Nabanita Singh answered |
Given,
Position of both an electron and a Helium atom = 1 nm
The momentum of an electron =
Uncertainty principle: It is defined as the position and the momentum both can not be determined simultaneously.
According to the Uncertainty principle,

h = Planck`s constant
When the position of an electron and helium atom is the same and the momentum of an electron is known then the momentum of the helium atom is equal to the momentum of an electron.
Therefore, the momentum of the Helium atom is 5.0 x 10-26 kg ms-1
Direction (Q. Nos. 1-8) This section contains 8 multiple choice questions. Each question has four choices (a), (b), (c) and (d), out of which ONLY ONE option is correct.
Q. FM radio broadcasts at 900 kHz. What wavelength does this corresponds to?- a)333 m
- b)3.03 x 10-3m
- c)330 m
- d)3300 m
Correct answer is 'A'. Can you explain this answer?
Direction (Q. Nos. 1-8) This section contains 8 multiple choice questions. Each question has four choices (a), (b), (c) and (d), out of which ONLY ONE option is correct.
Q. FM radio broadcasts at 900 kHz. What wavelength does this corresponds to?
a)
333 m
b)
3.03 x 10-3m
c)
330 m
d)
3300 m
|
|
Soumya Mukherjee answered |
Understanding FM Radio Frequency and Wavelength
FM radio broadcasts at a frequency of 900 kHz. To find the corresponding wavelength, we can use the formula that relates frequency and wavelength in a vacuum:
Formula for Wavelength
Wavelength (λ) = Speed of Light (c) / Frequency (f)
Where:
- Speed of Light (c) ≈ 3 x 10^8 meters per second
- Frequency (f) = 900 kHz = 900,000 Hz (since 1 kHz = 1,000 Hz)
Calculating the Wavelength
Using the values:
- λ = (3 x 10^8 m/s) / (900,000 Hz)
- λ = (3 x 10^8) / (9 x 10^5)
- λ = 333.33 meters
Thus, the wavelength that corresponds to a frequency of 900 kHz is approximately 333 meters.
Conclusion
So, the correct answer to the question is:
- Option (a): 333 m
This calculation illustrates how the frequency of radio waves is inversely related to their wavelength; as frequency increases, wavelength decreases.
FM radio broadcasts at a frequency of 900 kHz. To find the corresponding wavelength, we can use the formula that relates frequency and wavelength in a vacuum:
Formula for Wavelength
Wavelength (λ) = Speed of Light (c) / Frequency (f)
Where:
- Speed of Light (c) ≈ 3 x 10^8 meters per second
- Frequency (f) = 900 kHz = 900,000 Hz (since 1 kHz = 1,000 Hz)
Calculating the Wavelength
Using the values:
- λ = (3 x 10^8 m/s) / (900,000 Hz)
- λ = (3 x 10^8) / (9 x 10^5)
- λ = 333.33 meters
Thus, the wavelength that corresponds to a frequency of 900 kHz is approximately 333 meters.
Conclusion
So, the correct answer to the question is:
- Option (a): 333 m
This calculation illustrates how the frequency of radio waves is inversely related to their wavelength; as frequency increases, wavelength decreases.
Can you explain the answer of this question below:The threshold frequency v0 for a metal is 7.0 x 1014 s-1. Radiation of frequency v = 1.0 x 1015 s-1 hits the metal. Kinetic energy of the emitted electron is
- A:
2.0 x 10-18 J
- B:
1.60 x 10-17 J
- C:
1.60 x 10-19 J
- D:
2.0 x 10-19 J
The answer is d.
The threshold frequency v0 for a metal is 7.0 x 1014 s-1. Radiation of frequency v = 1.0 x 1015 s-1 hits the metal. Kinetic energy of the emitted electron is
2.0 x 10-18 J
1.60 x 10-17 J
1.60 x 10-19 J
2.0 x 10-19 J
|
|
Suresh Reddy answered |
By photoelectric effect
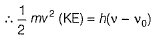
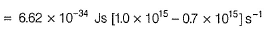
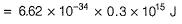
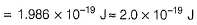
Can you explain the answer of this question below: If uncertainity in the position of an electron is zero, the uncertainity in its momentum would be
- A:
Zero
- B:
< h / 4π
- C:
Infinite
- D:
≤ h / 4π
The answer is c.
If uncertainity in the position of an electron is zero, the uncertainity in its momentum would be
Zero
< h / 4π
Infinite
≤ h / 4π

|
Ayush Joshi answered |
Actually, according to uncertainty principle,
Δx.Δp ≥ h/4π
or Δx.Δp ≈ h/4n
where, Δx, is uncertainty in position and Δp is uncertainty in momentum.
So, if Δx = 0
Hence, uncertainty in momentum Δp = h/4π x 0 = Infinity
Photoelectric effect can be expressed in terms of the following graph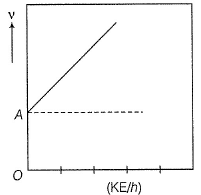
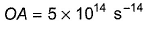 Q. Kinetic energy imparted to the moving electron at a wavelength of 2.5 x 10-7 m is
Q. Kinetic energy imparted to the moving electron at a wavelength of 2.5 x 10-7 m is- a)-278.97 kJ mol-1
- b)278.97 kJmol-1
- c)168.23 kJmol-1
- d)-168.23 kJ mol-1
Correct answer is option 'B'. Can you explain this answer?
Photoelectric effect can be expressed in terms of the following graph
Q. Kinetic energy imparted to the moving electron at a wavelength of 2.5 x 10-7 m is
a)
-278.97 kJ mol-1
b)
278.97 kJmol-1
c)
168.23 kJmol-1
d)
-168.23 kJ mol-1

|
Pioneer Academy answered |
Photoelectric effect is represented by
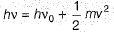



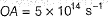
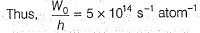
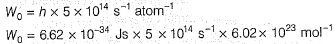
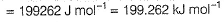
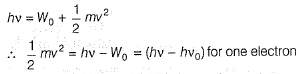
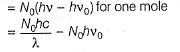
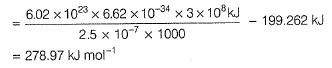
Statement I : It is impossible to determine position and momentum of the moving electron simultaneously with same accuracy.Statement II : The path of an electron in an atom is clearly defined.- a)Both Statement I and Statement II are correct and Statement II is the correct explanation of Statement I
- b)Both Statement I and Statement II are correct and Statement II is not the correct explanation of Statement I
- c)Statement I is correct but Statement II is incorrect
- d)Statement II is correct but Statement I is incorrect
Correct answer is option 'C'. Can you explain this answer?
Statement I : It is impossible to determine position and momentum of the moving electron simultaneously with same accuracy.
Statement II : The path of an electron in an atom is clearly defined.
a)
Both Statement I and Statement II are correct and Statement II is the correct explanation of Statement I
b)
Both Statement I and Statement II are correct and Statement II is not the correct explanation of Statement I
c)
Statement I is correct but Statement II is incorrect
d)
Statement II is correct but Statement I is incorrect
|
|
Neha Joshi answered |
Statement 1 is uncertainty principle, according to which we can't locate a moving electron accurately at any instant, which implies there must me certain uncertainty in its path, as path basically gives us the position of electron at various instances.
A gas absorbs photon of wavelength 355 nm and emits at two wavelengths. If one of the emissions is at 680 nm, the other is at[AlEEE 2011]- a)1035nm
- b)325 nm
- c)743 nm
- d)518 nm
Correct answer is option 'C'. Can you explain this answer?
A gas absorbs photon of wavelength 355 nm and emits at two wavelengths. If one of the emissions is at 680 nm, the other is at
[AlEEE 2011]
a)
1035nm
b)
325 nm
c)
743 nm
d)
518 nm
|
|
Nandini Patel answered |
1/λ = 1/λ1 + 1/λ2
1355 = 1680 + 1λ2
1/λ2 = (680 − 355/680 x 355)
⇒ λ2 = 743nm.
The uncertainty principle states that- a)it is impossible to know anything with certainty
- b)there can only be one uncertain digit in a reported number
- c)it is impossible to know the exact position and momentum of an electron simultaneously
- d)it is impossible to determine mass of light particles
Correct answer is option 'C'. Can you explain this answer?
The uncertainty principle states that
a)
it is impossible to know anything with certainty
b)
there can only be one uncertain digit in a reported number
c)
it is impossible to know the exact position and momentum of an electron simultaneously
d)
it is impossible to determine mass of light particles

|
Swara Mukherjee answered |
The Heisenberg uncertainty principle states that the exact position and momentum of an electron cannot be simultaneously determined. This is because electrons simply don't have a definite position, and direction of motion, at the same time!
If the uncertainties in the measurements of position and momentum are equal, calculate the uncertainty in the measurement of velocity (in ms-1) of particle of mass 1.21 x 10-18 kg
Correct answer is '6'. Can you explain this answer?
If the uncertainties in the measurements of position and momentum are equal, calculate the uncertainty in the measurement of velocity (in ms-1) of particle of mass 1.21 x 10-18 kg

|
Arnav Kulkarni answered |
Uncertainty principle:
The uncertainty principle states that it is impossible to simultaneously measure the exact position and momentum of a particle with complete accuracy. The more precisely we try to measure one of these quantities, the less precisely we can know the other.
Given information:
- The uncertainties in the measurements of position and momentum are equal.
- The mass of the particle is 1.21 x 10^-18 kg.
Mathematical representation:
The uncertainty principle is mathematically represented as Δx * Δp ≥ h/(4π), where Δx is the uncertainty in position, Δp is the uncertainty in momentum, and h is the Planck's constant (6.626 x 10^-34 Js).
Equal uncertainties:
Since the uncertainties in position and momentum are equal, we can write Δx = Δp.
Calculating the uncertainty in velocity:
Velocity is defined as the rate of change of position with respect to time. It is given by the equation v = Δx/Δt, where v is velocity, Δx is the change in position, and Δt is the change in time.
We can rearrange this equation to express the change in position as Δx = v * Δt.
Substituting the value of Δx in the uncertainty principle equation, we get Δp * v * Δt ≥ h/(4π).
Since Δp = Δx, we can rewrite the equation as Δx * v * Δt ≥ h/(4π).
Simplifying further, we have v * Δt ≥ h/(4πΔx).
The uncertainty in velocity is given by Δv = v * Δt.
Substituting the value of Δt in the equation, we get Δv = v * (h/(4πΔx))/v.
Simplifying further, we have Δv = h/(4πΔx).
Substituting Δx = Δp, we have Δv = h/(4πΔp).
Substituting the value of h and Δp, we get Δv = (6.626 x 10^-34 Js)/(4πΔp).
Since Δp = Δx, we can write Δv = (6.626 x 10^-34 Js)/(4πΔx).
Given that Δx = Δp, we can further simplify the equation to Δv = (6.626 x 10^-34 Js)/(4πΔp) = (6.626 x 10^-34 Js)/(4πΔx).
Calculating the uncertainty in velocity:
Substituting the value of Δx = Δp = Δv, we get Δv = (6.626 x 10^-34 Js)/(4πΔv).
Simplifying further, we have Δv^2 = (6.626 x 10^-34 Js)/(4π).
Taking the square root of both sides, we have Δv = √[(6.626 x 10^-34 Js)/(4π)].
Calculating the numerical value, we find Δv ≈ 6 m/s.
Therefore, the uncertainty in the measurement of velocity is approximately 6 m/s.
The uncertainty principle states that it is impossible to simultaneously measure the exact position and momentum of a particle with complete accuracy. The more precisely we try to measure one of these quantities, the less precisely we can know the other.
Given information:
- The uncertainties in the measurements of position and momentum are equal.
- The mass of the particle is 1.21 x 10^-18 kg.
Mathematical representation:
The uncertainty principle is mathematically represented as Δx * Δp ≥ h/(4π), where Δx is the uncertainty in position, Δp is the uncertainty in momentum, and h is the Planck's constant (6.626 x 10^-34 Js).
Equal uncertainties:
Since the uncertainties in position and momentum are equal, we can write Δx = Δp.
Calculating the uncertainty in velocity:
Velocity is defined as the rate of change of position with respect to time. It is given by the equation v = Δx/Δt, where v is velocity, Δx is the change in position, and Δt is the change in time.
We can rearrange this equation to express the change in position as Δx = v * Δt.
Substituting the value of Δx in the uncertainty principle equation, we get Δp * v * Δt ≥ h/(4π).
Since Δp = Δx, we can rewrite the equation as Δx * v * Δt ≥ h/(4π).
Simplifying further, we have v * Δt ≥ h/(4πΔx).
The uncertainty in velocity is given by Δv = v * Δt.
Substituting the value of Δt in the equation, we get Δv = v * (h/(4πΔx))/v.
Simplifying further, we have Δv = h/(4πΔx).
Substituting Δx = Δp, we have Δv = h/(4πΔp).
Substituting the value of h and Δp, we get Δv = (6.626 x 10^-34 Js)/(4πΔp).
Since Δp = Δx, we can write Δv = (6.626 x 10^-34 Js)/(4πΔx).
Given that Δx = Δp, we can further simplify the equation to Δv = (6.626 x 10^-34 Js)/(4πΔp) = (6.626 x 10^-34 Js)/(4πΔx).
Calculating the uncertainty in velocity:
Substituting the value of Δx = Δp = Δv, we get Δv = (6.626 x 10^-34 Js)/(4πΔv).
Simplifying further, we have Δv^2 = (6.626 x 10^-34 Js)/(4π).
Taking the square root of both sides, we have Δv = √[(6.626 x 10^-34 Js)/(4π)].
Calculating the numerical value, we find Δv ≈ 6 m/s.
Therefore, the uncertainty in the measurement of velocity is approximately 6 m/s.
Frequency of a matter wave is equal to- a)

- b)
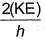
- c)
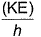
- d)
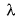
Correct answer is option 'B'. Can you explain this answer?
Frequency of a matter wave is equal to
a)
b)
c)
d)
|
|
Chirag Verma answered |
By de-Broglie equation
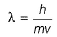
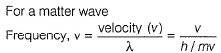
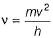
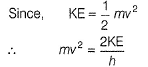
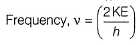
If the photon of the wavelength 150 pm strikes an atom and one of its inner bound electrons is ejected out with a velocity of 1.5 x 107 ms-1, then binding energy by which electron is bound to nucleus is- a)1.223 x10-15 J
- b)-1.223x 10-15 J
- c)2.345 x10-15 J
- d)1.428 x10-15 J
Correct answer is option 'B'. Can you explain this answer?
If the photon of the wavelength 150 pm strikes an atom and one of its inner bound electrons is ejected out with a velocity of 1.5 x 107 ms-1, then binding energy by which electron is bound to nucleus is
a)
1.223 x10-15 J
b)
-1.223x 10-15 J
c)
2.345 x10-15 J
d)
1.428 x10-15 J
|
|
Shreya Gupta answered |

Direction (Q. Nos. 1-10) This section contains 10 multiple choice questions. Each question has four choices (a), (b), (c) and (d), out of which ONLY ONE option is correct.Which of the following properties of atom could be explained correctly by Thomson Model of atom?- a)Overall neutrality of atom.
- b)Spectra of hydrogen atom.
- c)Position of electrons, protons and neutrons in atom.
- d)Stability of atom.
Correct answer is option 'A'. Can you explain this answer?
Direction (Q. Nos. 1-10) This section contains 10 multiple choice questions. Each question has four choices (a), (b), (c) and (d), out of which ONLY ONE option is correct.
Which of the following properties of atom could be explained correctly by Thomson Model of atom?
a)
Overall neutrality of atom.
b)
Spectra of hydrogen atom.
c)
Position of electrons, protons and neutrons in atom.
d)
Stability of atom.
|
|
Anjana Sharma answered |
According to Thomson model of atom, the mass of the atom is assumed to be uniformly distributed over the atom. This model was able to explain the overall neutrality of the atom.
Select the incorrect statement about cathode rays.- a)They travel from cathode to anode
- b)They travel in a straight line in the absence of an external electrical or magnetic field
- c)Their nature is independent of the materials of cathode
- d)Their nature is dependent on the nature of the gas present
Correct answer is option 'D'. Can you explain this answer?
Select the incorrect statement about cathode rays.
a)
They travel from cathode to anode
b)
They travel in a straight line in the absence of an external electrical or magnetic field
c)
Their nature is independent of the materials of cathode
d)
Their nature is dependent on the nature of the gas present

|
Amrita Sarkar answered |
(a) Cathode rays travel from cathode (source) to anode. True
(b) In the absence of these fields, they are not deflected but in the presence of electrical field, they are deflected indicating that they are charged. Thus, True
(c) Their nature is independent of the material of cathode. True
(d) Their nature is independent of the nature of the gas.
Thus, given statement is false.
(b) In the absence of these fields, they are not deflected but in the presence of electrical field, they are deflected indicating that they are charged. Thus, True
(c) Their nature is independent of the material of cathode. True
(d) Their nature is independent of the nature of the gas.
Thus, given statement is false.
Select the correct statement(s).
- a)The ideal body, which emits and absorbs all frequencies is called a black body
- b)The exact frequency distribution of the emitted radiation from a black body depends upon its temperature
- c)The radiation emitted goes from a lower frequency to higher frequency as the temperature increases
- d)In vacuum, all types of electromagnetic radiation travel at the same speed
Correct answer is option 'A,B,C,D'. Can you explain this answer?
Select the correct statement(s).
a)
The ideal body, which emits and absorbs all frequencies is called a black body
b)
The exact frequency distribution of the emitted radiation from a black body depends upon its temperature
c)
The radiation emitted goes from a lower frequency to higher frequency as the temperature increases
d)
In vacuum, all types of electromagnetic radiation travel at the same speed

|
Sushant Khanna answered |
(a) Correct
(b) As temperature increases, distribution of frequency (and energy) increases. Thus, correct.
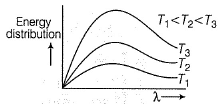
(c) As temperature increases, radiation emitted is shifted to lower wavelength, i.e. higher frequency. Correct
(d) All types of radiations have same speed 3 x 108 ms-1. Correct
(b) As temperature increases, distribution of frequency (and energy) increases. Thus, correct.
(c) As temperature increases, radiation emitted is shifted to lower wavelength, i.e. higher frequency. Correct
(d) All types of radiations have same speed 3 x 108 ms-1. Correct
Direction (Q. Nos. 15 and 16) This section contains 2 questions. when worked out will result in an integer from 0 to 9 (both inclusive)Q. In Millikan’s experiment, static electric charge on the oil drops has been obtained by shining X-rays. If the static electric charge on the oil drop is -1.282x 10-18 C, calculate the number of electrons present on it.
Correct answer is '8'. Can you explain this answer?
Direction (Q. Nos. 15 and 16) This section contains 2 questions. when worked out will result in an integer from 0 to 9 (both inclusive)
Q. In Millikan’s experiment, static electric charge on the oil drops has been obtained by shining X-rays. If the static electric charge on the oil drop is -1.282x 10-18 C, calculate the number of electrons present on it.

|
Manisha Mehta answered |
Charge on one electron = - 1.6022 x 10-19C
Let, number of electrons = N
Then total charge = - N x 1.6022 x 10-19C
Given, total charge = -1.282 x 10-18 C
Thus, - N x 1.6022 x 10-19 C = - 1. 282 x 10-18C
Let, number of electrons = N
Then total charge = - N x 1.6022 x 10-19C
Given, total charge = -1.282 x 10-18 C
Thus, - N x 1.6022 x 10-19 C = - 1. 282 x 10-18C
∴ N = 8
Wavelength associated with an electron having KE 3.0 x 10-25 J is x *10-7 m.Q. What is the value of x? (Round of to nearest integer)Correct answer is '9'. Can you explain this answer?
Wavelength associated with an electron having KE 3.0 x 10-25 J is x *10-7 m.
Q. What is the value of x? (Round of to nearest integer)
|
|
Ashish Chaudhary answered |
Understanding the Problem
To find the wavelength of an electron with a given kinetic energy (KE), we will use the de Broglie wavelength formula. The kinetic energy is provided as 3.0 x 10-25 J.
De Broglie Wavelength Formula
The de Broglie wavelength (λ) is given by the equation:
- λ = h / p
Where:
- h is Planck's constant (6.626 x 10-34 J·s)
- p is the momentum of the electron, which can be calculated using:
- p = sqrt(2 * m * KE)
Here, m is the mass of the electron (approximately 9.11 x 10-31 kg).
Calculating the Momentum
- Substitute the known values:
- KE = 3.0 x 10-25 J
- m = 9.11 x 10-31 kg
- Calculate p:
- p = sqrt(2 * 9.11 x 10-31 kg * 3.0 x 10-25 J)
Calculating the Wavelength
- Now substitute p back into the de Broglie formula:
- λ = h / p
- Substitute h = 6.626 x 10-34 J·s and the calculated momentum to find λ.
Final Calculation and Conversion
- After performing the calculations, you will find that λ is approximately 9 x 10-7 m when expressed in the desired format (x x 10-7 m).
Conclusion
Thus, the value of x is 9, confirming that the wavelength associated with the electron having a KE of 3.0 x 10-25 J is indeed 9 x 10-7 m.
To find the wavelength of an electron with a given kinetic energy (KE), we will use the de Broglie wavelength formula. The kinetic energy is provided as 3.0 x 10-25 J.
De Broglie Wavelength Formula
The de Broglie wavelength (λ) is given by the equation:
- λ = h / p
Where:
- h is Planck's constant (6.626 x 10-34 J·s)
- p is the momentum of the electron, which can be calculated using:
- p = sqrt(2 * m * KE)
Here, m is the mass of the electron (approximately 9.11 x 10-31 kg).
Calculating the Momentum
- Substitute the known values:
- KE = 3.0 x 10-25 J
- m = 9.11 x 10-31 kg
- Calculate p:
- p = sqrt(2 * 9.11 x 10-31 kg * 3.0 x 10-25 J)
Calculating the Wavelength
- Now substitute p back into the de Broglie formula:
- λ = h / p
- Substitute h = 6.626 x 10-34 J·s and the calculated momentum to find λ.
Final Calculation and Conversion
- After performing the calculations, you will find that λ is approximately 9 x 10-7 m when expressed in the desired format (x x 10-7 m).
Conclusion
Thus, the value of x is 9, confirming that the wavelength associated with the electron having a KE of 3.0 x 10-25 J is indeed 9 x 10-7 m.
Which of the following rules/principles is responsible to rule out the existence of definite paths or trajectories of electrons?- a)Aufbau (ascending energy) rule
- b)Hund’s rule of maximum multiples
- c)Pauli’s exclusion principle
- d)Heisenberg’s uncertainty principle
Correct answer is option 'D'. Can you explain this answer?
Which of the following rules/principles is responsible to rule out the existence of definite paths or trajectories of electrons?
a)
Aufbau (ascending energy) rule
b)
Hund’s rule of maximum multiples
c)
Pauli’s exclusion principle
d)
Heisenberg’s uncertainty principle
|
|
Anjana Sharma answered |
According to Heisenberg’s uncertainty principle, the position and velocity of an electron cannot be determined simultaneously with accuracy which rules out the existence of fixed paths.
Which of the following conclusions could not be derived from Rutherford’s α-particle scattering experiment?- a)Electrons and nucleus are held together by electrostatic forces of attraction
- b)The radius of the atom is larger than that of the nucleus
- c)Most of the space in the atom is empty
- d)Electrons move in a circular path of fixed energy. Circular paths are called orbits
Correct answer is option 'D'. Can you explain this answer?
Which of the following conclusions could not be derived from Rutherford’s α-particle scattering experiment?
a)
Electrons and nucleus are held together by electrostatic forces of attraction
b)
The radius of the atom is larger than that of the nucleus
c)
Most of the space in the atom is empty
d)
Electrons move in a circular path of fixed energy. Circular paths are called orbits

|
Dipika Choudhury answered |
(a) Electrons (-) and nucleus (+) are held togeather by electrostatic forces of attractions. Thus. true.
(b) Radius of the atom (= 10-10m) > radiue of the nucleus (10-15m). Thus true
(c) Most of the space is empty as given by radius of the nucleus and atom. Thus, true.
(d) As electron moves in a circular paith, it emits energy and ultimately false into nucleus. Thus, false.
(b) Radius of the atom (= 10-10m) > radiue of the nucleus (10-15m). Thus true
(c) Most of the space is empty as given by radius of the nucleus and atom. Thus, true.
(d) As electron moves in a circular paith, it emits energy and ultimately false into nucleus. Thus, false.
What experimental result did Albert Einstein cite as evidence that light has particle-like properties?- a)The fact that electrons posses both particle and wave-like properties.
- b)The orbits of electrons within the hydrogen atom could have only certain radii.
- c)The ejection of electrons from a metal surface by light depends only on the frequency of the light used.
- d)The pattern of light and dark bands produced when light was passed through a pair of narrow slits.
Correct answer is option 'C'. Can you explain this answer?
What experimental result did Albert Einstein cite as evidence that light has particle-like properties?
a)
The fact that electrons posses both particle and wave-like properties.
b)
The orbits of electrons within the hydrogen atom could have only certain radii.
c)
The ejection of electrons from a metal surface by light depends only on the frequency of the light used.
d)
The pattern of light and dark bands produced when light was passed through a pair of narrow slits.
|
|
Arun Khanna answered |
Einstein's explanation of photoelectric effect using the concept of photons. In 1905, Albert Einstein provided an explanation of the photoelectric effect, an experiment that the wave theory of light failed to explain. He did so by postulating the existence of photons, quanta of light energy with particulate qualities.
A hypothetical electromagnetic wave is pictured here. Q. A standing wave in a string 42 cm long has a total of six nodes (including those at the ends). Wavelength of the standing wave is
Q. A standing wave in a string 42 cm long has a total of six nodes (including those at the ends). Wavelength of the standing wave is- a)7.0 cm
- b)16.8 cm
- c)10.5 cm
- d)5.25 cm
Correct answer is option 'B'. Can you explain this answer?
A hypothetical electromagnetic wave is pictured here.
Q. A standing wave in a string 42 cm long has a total of six nodes (including those at the ends). Wavelength of the standing wave is
a)
7.0 cm
b)
16.8 cm
c)
10.5 cm
d)
5.25 cm

|
Ayush Joshi answered |
If there are 6 nodes, then there are 5 segments between nodes, and the wavelength of the underlying wave is 2 of those (because they look similar when they’re moving but if you freeze-frame, every second one is the opposite direction), so I make it 2*42/5 = 16.8 cm.
Direction (Q. Nos. 13) Choice the correct combination of elements and column I and coloumn II are given as option (a), (b), (c) and (d), out of which ONE option is correct.Q. Neon gas is generally used in sign boards. It emits radiations at wavelength 616 nm.
Match the values derived given in Column II with the corresponding parameter given in Column I.

- a)a
- b)b
- c)c
- d)d
Correct answer is option 'B'. Can you explain this answer?
Direction (Q. Nos. 13) Choice the correct combination of elements and column I and coloumn II are given as option (a), (b), (c) and (d), out of which ONE option is correct.
Q.
Neon gas is generally used in sign boards. It emits radiations at wavelength 616 nm.
Match the values derived given in Column II with the corresponding parameter given in Column I.
Match the values derived given in Column II with the corresponding parameter given in Column I.
a)
a
b)
b
c)
c
d)
d
|
|
Abhijeet Chauhan answered |
Direction (Q. Nos. 14 - 16) This section contains 2 questions. when worked out will result in an integer from 0 to 9 (both inclusive)Q. The work function (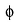 ) of some metals is listed below. The number of metals which will show photoelectric effect when light of 300 nm wavelength falls on the metal i s ........
) of some metals is listed below. The number of metals which will show photoelectric effect when light of 300 nm wavelength falls on the metal i s ........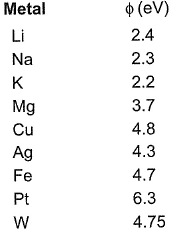
Correct answer is '4'. Can you explain this answer?
Direction (Q. Nos. 14 - 16) This section contains 2 questions. when worked out will result in an integer from 0 to 9 (both inclusive)
Q.
The work function (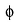 ) of some metals is listed below. The number of metals which will show photoelectric effect when light of 300 nm wavelength falls on the metal i s ........
) of some metals is listed below. The number of metals which will show photoelectric effect when light of 300 nm wavelength falls on the metal i s ........

|
Akshay Sharma answered |
Thus, any metal with energy less than 4.14 eV will emit photons thus, showing photoelectric effect. (Li, Na, K, Mg)
In an atom, an electron is moving with a speed of 600 ms-1 with an accuracy of 0.005%. Certainty with which the position of the electron can be located is [AIEEE2009]
[AIEEE2009]- a)1.52x 10-4 m
- b)5.10 x 10-3 m
- c)1.92 x 10-3 m
- d)3.84 x 10-3 m
Correct answer is option 'C'. Can you explain this answer?
In an atom, an electron is moving with a speed of 600 ms-1 with an accuracy of 0.005%. Certainty with which the position of the electron can be located is
[AIEEE2009]
a)
1.52x 10-4 m
b)
5.10 x 10-3 m
c)
1.92 x 10-3 m
d)
3.84 x 10-3 m

|
Nilesh Saini answered |
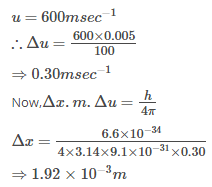
Direction (Q. Nos. 14) Choice the correct combination of elements and column I and coloumn II are given as option (a), (b), (c) and (d), out of which ONE option is correct. Q. The colours of visible light are at different wavelength. Match the wavelengths in Column I with their colours in Column II.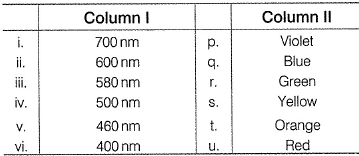
- a)a
- b)b
- c)c
- d)d
Correct answer is option 'B'. Can you explain this answer?
Direction (Q. Nos. 14) Choice the correct combination of elements and column I and coloumn II are given as option (a), (b), (c) and (d), out of which ONE option is correct.
Q. The colours of visible light are at different wavelength. Match the wavelengths in Column I with their colours in Column II.
a)
a
b)
b
c)
c
d)
d

|
Ishita Reddy answered |
Thus, (i)(700nm) Red (u)
(ii) (600 nm) - Orange (t)
(iii) (580 nm) - Yellow (s)
(iv) (500nm) - Green (r)
(v) (460 nm) - Blue (q)
(vi) (400 nm) - Violet (p)
(ii) (600 nm) - Orange (t)
(iii) (580 nm) - Yellow (s)
(iv) (500nm) - Green (r)
(v) (460 nm) - Blue (q)
(vi) (400 nm) - Violet (p)
Chapter doubts & questions for Waves - Chemistry for EmSAT Achieve 2025 is part of EmSAT Achieve exam preparation. The chapters have been prepared according to the EmSAT Achieve exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for EmSAT Achieve 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Waves - Chemistry for EmSAT Achieve in English & Hindi are available as part of EmSAT Achieve exam.
Download more important topics, notes, lectures and mock test series for EmSAT Achieve Exam by signing up for free.
Chemistry for EmSAT Achieve
191 videos|265 docs|160 tests
|