All Exams >
Grade 12 >
Mathematics for Grade 12 >
All Questions
All questions of Probability for Grade 12 Exam
Probability of getting a number between 1 and 100, which is divisible by 1 and itself only, is- a)25/99
- b)1/4
- c)25/98
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Probability of getting a number between 1 and 100, which is divisible by 1 and itself only, is
a)
25/99
b)
1/4
c)
25/98
d)
none of these
|
|
Nandini Iyer answered |
The prime numbers between 1 and 100 are :2, 3, 5, ... more7, 11,
A box contains 15 red marbles, 15 blue marbles and 30 green marbles. 5 marbles are drawn from the box, what is the probability that atleast one will be green?- a)
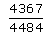
- b)
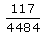
- c) zero
- d)1
Correct answer is option 'A'. Can you explain this answer?
A box contains 15 red marbles, 15 blue marbles and 30 green marbles. 5 marbles are drawn from the box, what is the probability that atleast one will be green?
a)
b)
c)
zero
d)
1

|
Shashwat Singh answered |
It's like doing the question orally... (don't get into maths... as I was also stuck in the middle) but by common sense (which is very uncommon) it can be said as 1-probablity of not getting any green in 5 balls... in this case we can see the answer aproaches to 1 which can be seen in option a) .... hope it helps... but with maths a can see a nightmare coming...
The probability that a man will live for 10 more years is 1/4 and that his wife will live 10 more years is 1/3. The probability that neither will be alive in 10 years is- a)5/12
- b)1/2
- c)11/12
- d)7/12
Correct answer is option 'B'. Can you explain this answer?
The probability that a man will live for 10 more years is 1/4 and that his wife will live 10 more years is 1/3. The probability that neither will be alive in 10 years is
a)
5/12
b)
1/2
c)
11/12
d)
7/12
|
|
Mayank Dasgupta answered |
Given probabilities:
- Probability that the man will live for 10 more years = 1/4
- Probability that his wife will live for 10 more years = 1/3
To find: Probability that neither will be alive in 10 years
Solution:
Let A be the event that the man will be alive in 10 years, and B be the event that his wife will be alive in 10 years. Then, the probability that neither will be alive in 10 years is the probability of the complement of the union of A and B, i.e., P((A ∪ B)').
Using the formula for the probability of the union of two events, we have:
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
where P(A ∩ B) is the probability that both the man and his wife will be alive in 10 years.
Substituting the given probabilities, we get:
P(A ∪ B) = 1/4 + 1/3 - P(A ∩ B)
Simplifying, we get:
P(A ∩ B) = 7/12 - P((A ∪ B)')
Now, we know that the probability of the man being alive in 10 years is 1/4, which means the probability of him not being alive in 10 years is 3/4. Similarly, the probability of his wife not being alive in 10 years is 2/3.
Using the product rule of probability, we can find the probability of both of them not being alive in 10 years:
P((A ∪ B)') = P(A' ∩ B') = P(A') × P(B') = (3/4) × (2/3) = 1/2
Substituting this value in the above equation, we get:
P(A ∩ B) = 7/12 - 1/2 = 1/12
Therefore, the probability that neither the man nor his wife will be alive in 10 years is:
P((A ∪ B)') = 1 - P(A ∪ B) = 1 - (1/4 + 1/3 - 1/12) = 1/2
Hence, the correct option is (B).
- Probability that the man will live for 10 more years = 1/4
- Probability that his wife will live for 10 more years = 1/3
To find: Probability that neither will be alive in 10 years
Solution:
Let A be the event that the man will be alive in 10 years, and B be the event that his wife will be alive in 10 years. Then, the probability that neither will be alive in 10 years is the probability of the complement of the union of A and B, i.e., P((A ∪ B)').
Using the formula for the probability of the union of two events, we have:
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
where P(A ∩ B) is the probability that both the man and his wife will be alive in 10 years.
Substituting the given probabilities, we get:
P(A ∪ B) = 1/4 + 1/3 - P(A ∩ B)
Simplifying, we get:
P(A ∩ B) = 7/12 - P((A ∪ B)')
Now, we know that the probability of the man being alive in 10 years is 1/4, which means the probability of him not being alive in 10 years is 3/4. Similarly, the probability of his wife not being alive in 10 years is 2/3.
Using the product rule of probability, we can find the probability of both of them not being alive in 10 years:
P((A ∪ B)') = P(A' ∩ B') = P(A') × P(B') = (3/4) × (2/3) = 1/2
Substituting this value in the above equation, we get:
P(A ∩ B) = 7/12 - 1/2 = 1/12
Therefore, the probability that neither the man nor his wife will be alive in 10 years is:
P((A ∪ B)') = 1 - P(A ∪ B) = 1 - (1/4 + 1/3 - 1/12) = 1/2
Hence, the correct option is (B).
The sample space of an experiment is S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} and A = {TTT}, B = {HTT, THT, TTH}, C = {HHT, HTH, THH, HHH},
then A, B and C form a set of?- a)Mutually exclusive but not exhaustive events
- b)Exhaustive but not mutually exclusive events
- c)Mutually exclusive and exhaustive events
- d)Neither mutually exclusive nor exhaustive events
Correct answer is option 'C'. Can you explain this answer?
The sample space of an experiment is S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} and A = {TTT}, B = {HTT, THT, TTH}, C = {HHT, HTH, THH, HHH},
then A, B and C form a set of?
then A, B and C form a set of?
a)
Mutually exclusive but not exhaustive events
b)
Exhaustive but not mutually exclusive events
c)
Mutually exclusive and exhaustive events
d)
Neither mutually exclusive nor exhaustive events
|
|
Suresh Reddy answered |
Above information has no common element in three of them and U of three sets forms sample set . Therefore option C is correct.
If 2/7 is the probability of an event, then the probability of the event ‘not A’ is:- a)5/7
- b)6/7
- c)2/7
- d)3/7
Correct answer is option 'A'. Can you explain this answer?
If 2/7 is the probability of an event, then the probability of the event ‘not A’ is:
a)
5/7
b)
6/7
c)
2/7
d)
3/7
|
|
Geetika Shah answered |
If 2/7 is probability of event A then the probability of an event not A is 1-(2/7) i.e., probability of not A is 5/7
If an event has more than one sample point, it is called a ………- a)Exhaustive event
- b)Compound event
- c)Simple event
- d)Mutually exclusive event
Correct answer is option 'B'. Can you explain this answer?
If an event has more than one sample point, it is called a ………
a)
Exhaustive event
b)
Compound event
c)
Simple event
d)
Mutually exclusive event

|
Infinity Academy answered |
Compound Event If an event has more than one sample point it is called a compound event, for example, S = {HH, HT} is a compound event.
Two students Amit and Priyanka appeared in an examination. The probability that Amit will qualify the examination is 0.06 and that Priyanka will qualify the examination is 0.12. The probability that both will qualify the examination is 0.02. Then, the probability that both Amit and Priyanka will not qualify the examination is:- a)0.91
- b)0.12
- c)0.84
- d)0.45
Correct answer is option 'C'. Can you explain this answer?
Two students Amit and Priyanka appeared in an examination. The probability that Amit will qualify the examination is 0.06 and that Priyanka will qualify the examination is 0.12. The probability that both will qualify the examination is 0.02. Then, the probability that both Amit and Priyanka will not qualify the examination is:
a)
0.91
b)
0.12
c)
0.84
d)
0.45
|
|
Naina Sharma answered |
Probability that Amit will qualify the exam(E) = 0.06
Probability that Priyanka will qualify the exam(F) = 0.12
Probability that both will qualify the exam P(E⋂F) = 0.02
P(EUF) = P(E) + P(F) - P(EUF)
= 0.06 + 0.12 - 0.02 = 0.16
P(E’⋂F’) = 1 - P(EUF)
⇒ 1 - 0.16
= 0.84
Probability that Priyanka will qualify the exam(F) = 0.12
Probability that both will qualify the exam P(E⋂F) = 0.02
P(EUF) = P(E) + P(F) - P(EUF)
= 0.06 + 0.12 - 0.02 = 0.16
P(E’⋂F’) = 1 - P(EUF)
⇒ 1 - 0.16
= 0.84
Five marbles are drawn from a bag which contains 6 blue marbles and 7 green marbles. Then, the probability that 3 will be blue and 2 green is:- a)213/429
- b)140/429
- c)117/429
- d)167/429
Correct answer is option 'B'. Can you explain this answer?
Five marbles are drawn from a bag which contains 6 blue marbles and 7 green marbles. Then, the probability that 3 will be blue and 2 green is:
a)
213/429
b)
140/429
c)
117/429
d)
167/429
|
|
Naina Sharma answered |
Blue = 6
Green = 7
Number of ways 3 blue marbles can be drawn = 6C3
number of ways 2 green marbles can be drawn = 7C2
total ways of drawing 5 marbles = 13C5
=> probability = (6C3 * 7C2)/13C5
= 140/429
Green = 7
Number of ways 3 blue marbles can be drawn = 6C3
number of ways 2 green marbles can be drawn = 7C2
total ways of drawing 5 marbles = 13C5
=> probability = (6C3 * 7C2)/13C5
= 140/429
The letters of the word ‘ASSASSIN ‘ are written at random in a row. The chance that all the similar letters occur together is- a)1/35
- b)1/14
- c)34/35
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The letters of the word ‘ASSASSIN ‘ are written at random in a row. The chance that all the similar letters occur together is
a)
1/35
b)
1/14
c)
34/35
d)
none of these
|
|
Ankita Chavan answered |
There is no specific word mentioned in your question. Please provide the word you are referring to.
8 coins are tossed at a time. The probability of getting 6 heads up is- a)57/64
- b)7/64
- c)37/256
- d)229/256
Correct answer is option 'C'. Can you explain this answer?
8 coins are tossed at a time. The probability of getting 6 heads up is
a)
57/64
b)
7/64
c)
37/256
d)
229/256
|
|
Koyna Jatwar answered |
The required probability =8C6(1/2)^6.(1/2)^2+8C7(1/2)^7(1/2)+8C8(1/2)^8. =1/256(28+8+1)=37/256
The letters of the word ‘MALENKOV‘are arranged in all possible ways. The chance that there are exactly four letters between M and E is- a)3/28
- b)3/14
- c)1/14
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The letters of the word ‘MALENKOV‘are arranged in all possible ways. The chance that there are exactly four letters between M and E is
a)
3/28
b)
3/14
c)
1/14
d)
none of these
|
|
Shilpa Rane answered |
"algorithm" can be rearranged in 9! (362,880) different ways.
The probability that a card drawn at random from a pack of 52 cards is a king or a heart is- a)16/52
- b)1/13
- c)1/52
- d)1/4
Correct answer is option 'A'. Can you explain this answer?
The probability that a card drawn at random from a pack of 52 cards is a king or a heart is
a)
16/52
b)
1/13
c)
1/52
d)
1/4

|
Er Aarif answered |
The number of kings in a deck are 4
Number of hearts in the deck are 13, including the king of hearts
Probability of getting either a king or a heart is, P = 4+(13–1) / 52
P = 16/52
Number of hearts in the deck are 13, including the king of hearts
Probability of getting either a king or a heart is, P = 4+(13–1) / 52
P = 16/52
From a pack of 52 cards, the cards are drawn one by one till an ace appears. The chance that an ace does not come up in first 26 cards is- a)109/153
- b)23/27
- c)46/153
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
From a pack of 52 cards, the cards are drawn one by one till an ace appears. The chance that an ace does not come up in first 26 cards is
a)
109/153
b)
23/27
c)
46/153
d)
none of these
|
|
Madhavan Chatterjee answered |
There are 4 aces in a pack. So, the probability of drawing an ace = 4/52
= 1/13
and the probability of drawing a card other than ace = 12/13.
Hence, the probability that ace doesn't appear in first 26 draws = (12/13)26
= 1/13
and the probability of drawing a card other than ace = 12/13.
Hence, the probability that ace doesn't appear in first 26 draws = (12/13)26
A fair coin is tossed a fixed number of times. If the probability of getting 4 heads is equal to the probability of getting 7 heads, then the probability of getting 2 heads is- a)55/2048
- b)3/4096
- c)1/1024
- d)3/1024
Correct answer is option 'A'. Can you explain this answer?
A fair coin is tossed a fixed number of times. If the probability of getting 4 heads is equal to the probability of getting 7 heads, then the probability of getting 2 heads is
a)
55/2048
b)
3/4096
c)
1/1024
d)
3/1024
|
|
Sanchita Khanna answered |
Given, probability of getting 4 heads = probability of getting 7 heads
Let the number of tosses be n. Then,
Probability of getting 4 heads = Probability of getting (n-4) tails = (1/2)^n * nC4
Probability of getting 7 heads = Probability of getting (n-7) tails = (1/2)^n * nC7
Equating the two probabilities, we get
nC4 = nC7/35
Solving this equation, we get n = 11
So, the number of tosses is 11.
Now, we need to find the probability of getting 2 heads.
Probability of getting 2 heads = Probability of getting (11-2) tails = (1/2)^11 * nC2
= (1/2)^11 * 55
= 55/2048
Therefore, the correct option is A) 55/2048.
Let the number of tosses be n. Then,
Probability of getting 4 heads = Probability of getting (n-4) tails = (1/2)^n * nC4
Probability of getting 7 heads = Probability of getting (n-7) tails = (1/2)^n * nC7
Equating the two probabilities, we get
nC4 = nC7/35
Solving this equation, we get n = 11
So, the number of tosses is 11.
Now, we need to find the probability of getting 2 heads.
Probability of getting 2 heads = Probability of getting (11-2) tails = (1/2)^11 * nC2
= (1/2)^11 * 55
= 55/2048
Therefore, the correct option is A) 55/2048.
An experiment involves rolling a pair of dice and recording the number that comes up. Suppose,
A: the sum is greater than 8.
B: 2 occurs on either die. Then A and B are ……. events.- a)Random experiment
- b)Mutually exclusive events
- c)Exhaustive events
- d)Favorable events
Correct answer is option 'B'. Can you explain this answer?
An experiment involves rolling a pair of dice and recording the number that comes up. Suppose,
A: the sum is greater than 8.
B: 2 occurs on either die. Then A and B are ……. events.
A: the sum is greater than 8.
B: 2 occurs on either die. Then A and B are ……. events.
a)
Random experiment
b)
Mutually exclusive events
c)
Exhaustive events
d)
Favorable events

|
Advait Ghoshal answered |
A pair of dice is rolled
Therefore the sample space S will be

Pairs which are mutually exclusive :
A∩B=ϕ⇒ A and B are mutually exclusive.
B∩C=ϕ⇒ B and C are mutually exclusive.
A∩C=ϕ⇒ They are not mutually exclusive.
∴A∩B and B∩C are mutually exclusive.
A drawer contains 5 black socks and 4 blue socks well mixed. A person searches the drawer and pulls out 2 socks at random. The probability that they match is- a)41/81
- b)5/8
- c)4/9
- d)5/9
Correct answer is option 'C'. Can you explain this answer?
A drawer contains 5 black socks and 4 blue socks well mixed. A person searches the drawer and pulls out 2 socks at random. The probability that they match is
a)
41/81
b)
5/8
c)
4/9
d)
5/9
|
|
Jaya Deshpande answered |
Out of 9 socks, 2 can be drawn in 9C2 ways.
Therefore, the total number of cases is 9C2.
Two socks drawn from the drawer will match if either both are black or both are blue.
Therefore, favorable number of cases is 5C2+ 4C2.
Hence, the required probability is
(5C2+ 4C2.)/ 9C2
= 4/9
Three of the 6 vertices of a regular hexagon are chosen at random.The probability that the triangle with these vertices is equilateral is- a)1/10
- b)1/20
- c)1/5
- d)1/2
Correct answer is option 'A'. Can you explain this answer?
Three of the 6 vertices of a regular hexagon are chosen at random.The probability that the triangle with these vertices is equilateral is
a)
1/10
b)
1/20
c)
1/5
d)
1/2
|
|
Kurakula Suryateja answered |
Rules of Triangle …..
Total possible cases = 6 C 3
Favourable cases =2
So the probability is = 2/6 C 3 =1/10.
Because there can be 2 22 equilateral triangles possible and total number of triangles possible would be (6/3) the answer is 1/10.
Total possible cases = 6 C 3
Favourable cases =2
So the probability is = 2/6 C 3 =1/10.
Because there can be 2 22 equilateral triangles possible and total number of triangles possible would be (6/3) the answer is 1/10.
A cubical dice has 3 on three faces, 2 on two faces and 1 on the 6 thth face .It is tossed twice. The chance that both the tosses show an even number is- a)1/4
- b)1/9
- c)1/36
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
A cubical dice has 3 on three faces, 2 on two faces and 1 on the 6 thth face .It is tossed twice. The chance that both the tosses show an even number is
a)
1/4
b)
1/9
c)
1/36
d)
none of these
|
|
Priya Mishra answered |
The correct option is B.
Since we have only even number 2,so when the dice is rolled twice we have (2,2) four times which means 2 on first dice pairs with both the twos on the second dice , similarly second two on first dice pairs with both the twos on the second dice
Hence the probability = 4/36 = 1/9
A bag contains 5 white, 7 red and 4 black balls. Four balls are drawn one by one with replacement. The chance that atleast two balls are black is- a)243/256
- b)67/256
- c)54/256
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
A bag contains 5 white, 7 red and 4 black balls. Four balls are drawn one by one with replacement. The chance that atleast two balls are black is
a)
243/256
b)
67/256
c)
54/256
d)
none of these
|
|
Riya Banerjee answered |
Let A, B, C, D denote the events of not getting a white ball in first, second, third and fourth draw respectively.
Since the balls are drawn with replacement, therefore, A, B, C, D are independent events such that P (A) = P (B) = P (C) = P (D).
Since out of 16 balls, 11 are not white, therefore, P (A) = 11/16
∴ Required probability = P (A) . P (B) . P (C) . P (D)
=> (11/16) x (11/16) x (11/16) x (11/16) = (11/16)^4.
A four digit number is formed by using the digits 1,2,3,4,5,6,7 without repetition. What is the probability that it’s divisible by 2?- a)3/7
- b)4/7
- c)2/7
- d)1/7
Correct answer is option 'A'. Can you explain this answer?
A four digit number is formed by using the digits 1,2,3,4,5,6,7 without repetition. What is the probability that it’s divisible by 2?
a)
3/7
b)
4/7
c)
2/7
d)
1/7

|
Anushka Ahuja answered |
The total number of possible four-digit numbers using the digits 1, 2, 3, 4, 5, 6, 7 without repetition is 7P4 = 7!/3! = 7*6*5*4 = 840.
To find the probability of the number being divisible by 4, we need to find the number of four-digit numbers using these digits that are divisible by 4.
A number is divisible by 4 if the last two digits form a number divisible by 4.
The possible two-digit numbers that are divisible by 4 are 12, 16, 24, 32, 36, 52, 56, 64, 72, and 76.
For each of these two-digit numbers, there are 5 choices for the first digit (excluding the last two digits used), and 4 choices for the remaining digit.
So, the total number of four-digit numbers using these digits that are divisible by 4 is 10 * 5 * 4 = 200.
Therefore, the probability of a random four-digit number using the digits 1, 2, 3, 4, 5, 6, 7 without repetition being divisible by 4 is 200/840 = 5/21.
To find the probability of the number being divisible by 4, we need to find the number of four-digit numbers using these digits that are divisible by 4.
A number is divisible by 4 if the last two digits form a number divisible by 4.
The possible two-digit numbers that are divisible by 4 are 12, 16, 24, 32, 36, 52, 56, 64, 72, and 76.
For each of these two-digit numbers, there are 5 choices for the first digit (excluding the last two digits used), and 4 choices for the remaining digit.
So, the total number of four-digit numbers using these digits that are divisible by 4 is 10 * 5 * 4 = 200.
Therefore, the probability of a random four-digit number using the digits 1, 2, 3, 4, 5, 6, 7 without repetition being divisible by 4 is 200/840 = 5/21.
Both A and B throw a dice. The chance that B throws a number not less than that thrown by A is- a)1/2
- b)15/36
- c)21/36
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Both A and B throw a dice. The chance that B throws a number not less than that thrown by A is
a)
1/2
b)
15/36
c)
21/36
d)
none of these
|
|
Nandini Patel answered |
c) 21/36
If both A and B throw a dice, there are 36 possible outcomes in total: 6 possibilities for what A throws and 6 possibilities for what B throws. Of these 36 outcomes, 15 of them result in B throwing a number that is not less than the number thrown by A. Therefore, the probability that B throws a number not less than that thrown by A is 15/36, which is approximately 41.7%.
To find the probability of this event, we can consider each of the possible outcomes separately. For example, if A throws a 1 and B throws a 2, then B has thrown a number not less than that thrown by A. If A throws a 3 and B throws a 3, then B has thrown a number not less than that thrown by A. If A throws a 4 and B throws a 6, then B has thrown a number not less than that thrown by A. There are a total of 15 such outcomes.
The probability that B throws a number less than that thrown by A is 21/36, or approximately 58.3%. This is the complementary probability to the probability that B throws a number not less than that thrown by A. The complementary probability is the probability of the event not occurring. In this case, the event "B throws a number not less than that thrown by A" is not occurring if B throws a number less than that thrown by A. The sum of the probability of an event occurring and the probability of the event not occurring is always 1, so the probability of an event occurring plus the complementary probability of the event is always equal to 1.
When the sets A and B are two events associated with a sample space, then "A ∩ B " is the event common to
- a)Either A or B or both
- b)Only one of the two, A or B
- c)Both A and B
- d)Neither A nor B
Correct answer is option 'C'. Can you explain this answer?
When the sets A and B are two events associated with a sample space, then "A ∩ B " is the event common to
a)
Either A or B or both
b)
Only one of the two, A or B
c)
Both A and B
d)
Neither A nor B
|
|
Chirag Verma answered |
Intersection of two sets A ∩ B is the set of those elements which are common to both A and B. i.e., which belong to both ‘A and B’.
If A and B are two events, then the set A ∩ B denotes the event ‘A and B’.
If A and B are two events, then the set A ∩ B denotes the event ‘A and B’.
The sample space associated to thrown a dice is- a)(1, 2, 3)
- b)(1, 2, 3, 4, 5, 6)
- c)(1, 3, 5)
- d)(2, 4, 6)
Correct answer is option 'B'. Can you explain this answer?
The sample space associated to thrown a dice is
a)
(1, 2, 3)
b)
(1, 2, 3, 4, 5, 6)
c)
(1, 3, 5)
d)
(2, 4, 6)

|
Kamali Anandbabu answered |
The size of the sample space is the total number of possible outcomes. So one dice has 6 sides which has sample space of 1,2,3,4,5 and 6.
In a certain town, 40% persons have brown hair, 25% have brown eyes, and 15% have both. If a person selected at random has brown hair, the chance that a person selected at random with brown hair is with brown eyes- a)3/8
- b)1/3
- c)3/20
- d)2/3
Correct answer is option 'A'. Can you explain this answer?
In a certain town, 40% persons have brown hair, 25% have brown eyes, and 15% have both. If a person selected at random has brown hair, the chance that a person selected at random with brown hair is with brown eyes
a)
3/8
b)
1/3
c)
3/20
d)
2/3
|
|
Rhea Basak answered |
Solution:
Given that 40% of persons have brown hair, 25% have brown eyes, and 15% have both.
Let A be the event that a person has brown hair, and B be the event that a person has brown eyes.
Then, P(A) = 0.40, P(B) = 0.25, and P(A ∩ B) = 0.15.
We are asked to find the probability that a person selected at random with brown hair is also with brown eyes, i.e., P(B|A).
Using Bayes' theorem, we have:
P(B|A) = P(A ∩ B) / P(A)
Substituting the given values, we get:
P(B|A) = 0.15 / 0.40
Simplifying, we get:
P(B|A) = 3/8
Therefore, the answer is option (A).
Given that 40% of persons have brown hair, 25% have brown eyes, and 15% have both.
Let A be the event that a person has brown hair, and B be the event that a person has brown eyes.
Then, P(A) = 0.40, P(B) = 0.25, and P(A ∩ B) = 0.15.
We are asked to find the probability that a person selected at random with brown hair is also with brown eyes, i.e., P(B|A).
Using Bayes' theorem, we have:
P(B|A) = P(A ∩ B) / P(A)
Substituting the given values, we get:
P(B|A) = 0.15 / 0.40
Simplifying, we get:
P(B|A) = 3/8
Therefore, the answer is option (A).
A determinant is chosen at random from the set of all determinants of order 2 with elements 0 or 1 only. The probability that the value of the determinant chosen is positive is- a)1/4
- b)1/16
- c)2/16
- d)3/16
Correct answer is option 'D'. Can you explain this answer?
A determinant is chosen at random from the set of all determinants of order 2 with elements 0 or 1 only. The probability that the value of the determinant chosen is positive is
a)
1/4
b)
1/16
c)
2/16
d)
3/16
|
|
Hansa Sharma answered |
Total number of determinant =2 ^ 4 =16
The positive determinants are [1 1 0 1 ], [1 0 1 1], [1 0 0 1]
Therefore required probability = 3/16
A coin is tossed. If head comes up a die is thrown but if tail comes up, the coin is tossed again. The probability of obtaining head and number 6 is:- a)1/8
- b)5/8
- c)7/8
- d)3/8
Correct answer is option 'A'. Can you explain this answer?
A coin is tossed. If head comes up a die is thrown but if tail comes up, the coin is tossed again. The probability of obtaining head and number 6 is:
a)
1/8
b)
5/8
c)
7/8
d)
3/8
|
|
Sanchita Mukherjee answered |
Sample space = {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6), (T, H), (T, T)}
n(Sample space) = 8
P(obtaining head and number 6) = P(H, 6) = 1/8
n(Sample space) = 8
P(obtaining head and number 6) = P(H, 6) = 1/8
A possible result of a random experiment is called its ……- a)Favorable outcomes
- b)Event
- c)Outcome
- d)Experiment
Correct answer is option 'C'. Can you explain this answer?
A possible result of a random experiment is called its ……
a)
Favorable outcomes
b)
Event
c)
Outcome
d)
Experiment
|
|
Mehul Rane answered |
Understanding Random Experiments
In probability theory, a random experiment is any procedure or action that results in one or more outcomes that cannot be predicted with certainty. A key aspect of this is understanding the terminology associated with its possible results.
What is an Outcome?
- An outcome is a specific result of a random experiment.
- For example, when tossing a coin, the possible outcomes are "heads" or "tails."
- Each outcome represents a unique, observable result of the experiment.
Other Terms Explained
- Favorable Outcomes: These refer to outcomes that align with a specific event we are interested in. For instance, if we want to know the probability of rolling an even number on a die, the favorable outcomes would be 2, 4, and 6.
- Event: This is a set of outcomes. An event can consist of one or more outcomes. For example, getting a "head" when tossing a coin is an event consisting of a single outcome.
- Experiment: This is the process or action through which outcomes are generated. The term encompasses the entire procedure, such as rolling a die or drawing a card from a deck.
Conclusion
Given these definitions, the correct answer to the question is option C: an outcome, as it specifically refers to the result of a random experiment. Understanding these terms is crucial for grasping the foundational concepts of probability and statistics, which are essential for success in JEE and other competitive exams.
In probability theory, a random experiment is any procedure or action that results in one or more outcomes that cannot be predicted with certainty. A key aspect of this is understanding the terminology associated with its possible results.
What is an Outcome?
- An outcome is a specific result of a random experiment.
- For example, when tossing a coin, the possible outcomes are "heads" or "tails."
- Each outcome represents a unique, observable result of the experiment.
Other Terms Explained
- Favorable Outcomes: These refer to outcomes that align with a specific event we are interested in. For instance, if we want to know the probability of rolling an even number on a die, the favorable outcomes would be 2, 4, and 6.
- Event: This is a set of outcomes. An event can consist of one or more outcomes. For example, getting a "head" when tossing a coin is an event consisting of a single outcome.
- Experiment: This is the process or action through which outcomes are generated. The term encompasses the entire procedure, such as rolling a die or drawing a card from a deck.
Conclusion
Given these definitions, the correct answer to the question is option C: an outcome, as it specifically refers to the result of a random experiment. Understanding these terms is crucial for grasping the foundational concepts of probability and statistics, which are essential for success in JEE and other competitive exams.
Two players toss four coins each. The probability that both obtain the same number of heads is- a)1/16
- b)5/256
- c)35/128
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Two players toss four coins each. The probability that both obtain the same number of heads is
a)
1/16
b)
5/256
c)
35/128
d)
none of these

|
Rahul Chaudhary answered |
The tossing of coin by each of the two players is independent. So we can multiply the respective probabilities and get the required probability.


There are five cases:


If three dice are thrown, then the probability that they show the numbers in A.P. is- a)1/12
- b)7/36
- c)1/36
- d)1/18
Correct answer is option 'D'. Can you explain this answer?
If three dice are thrown, then the probability that they show the numbers in A.P. is
a)
1/12
b)
7/36
c)
1/36
d)
1/18
|
|
Anagha Dey answered |
A.P. with common diff one are =4=(123)(234)(345)(456)
A.P. with common diff 2 are =2=(135)(246)
A.P. with common diff 0 are =6
⇒P=2+4+6/216=1/18
A.P. with common diff 2 are =2=(135)(246)
A.P. with common diff 0 are =6
⇒P=2+4+6/216=1/18
If E1 and E2 are two independent events, then P (E1∩E2) is equal to- a)P(E1)+(E2)
- b)P(E1)P(E2)
- c)P(E1)+P(E2)+P(E1+∪E2)
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
If E1 and E2 are two independent events, then P (E1∩E2) is equal to
a)
P(E1)+(E2)
b)
P(E1)P(E2)
c)
P(E1)+P(E2)+P(E1+∪E2)
d)
none of these
|
|
Geetika Mehta answered |
Explanation:
Independence of Events:
When two events E1 and E2 are independent, it means that the occurrence of one event does not affect the probability of the other event. Mathematically, this can be represented as:
P(E1 ∩ E2) = P(E1) * P(E2)
Calculating P(E1 ∩ E2):
To find the probability of both events E1 and E2 happening, we use the formula for independent events:
P(E1 ∩ E2) = P(E1) * P(E2)
Therefore, option B is correct:
b) P(E1) * P(E2)
Independence of Events:
When two events E1 and E2 are independent, it means that the occurrence of one event does not affect the probability of the other event. Mathematically, this can be represented as:
P(E1 ∩ E2) = P(E1) * P(E2)
Calculating P(E1 ∩ E2):
To find the probability of both events E1 and E2 happening, we use the formula for independent events:
P(E1 ∩ E2) = P(E1) * P(E2)
Therefore, option B is correct:
b) P(E1) * P(E2)
The probability of having atleast one head in 5 throws of a coin is- a)1/32
- b)5/32
- c)31/32
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The probability of having atleast one head in 5 throws of a coin is
a)
1/32
b)
5/32
c)
31/32
d)
none of these
|
|
Jyoti Tiwari answered |
**Solution:**
When we toss a coin, the possible outcomes are head (H) or tail (T).
- The probability of getting a head on any one toss of a fair coin is 1/2.
So, the probability of getting a tail on any one toss of a fair coin is also 1/2.
**Finding the probability of having at least one head in 5 throws:**
To find the probability of having at least one head in 5 throws of a coin, we can use the concept of complementary events.
- The complementary event of having at least one head in 5 throws is having no heads in 5 throws.
The probability of having no heads in 5 throws is:
- (1/2) x (1/2) x (1/2) x (1/2) x (1/2) = 1/32
Therefore, the probability of having at least one head in 5 throws is:
- 1 - 1/32 = 31/32
Hence, the correct option is (c) 31/32.
When we toss a coin, the possible outcomes are head (H) or tail (T).
- The probability of getting a head on any one toss of a fair coin is 1/2.
So, the probability of getting a tail on any one toss of a fair coin is also 1/2.
**Finding the probability of having at least one head in 5 throws:**
To find the probability of having at least one head in 5 throws of a coin, we can use the concept of complementary events.
- The complementary event of having at least one head in 5 throws is having no heads in 5 throws.
The probability of having no heads in 5 throws is:
- (1/2) x (1/2) x (1/2) x (1/2) x (1/2) = 1/32
Therefore, the probability of having at least one head in 5 throws is:
- 1 - 1/32 = 31/32
Hence, the correct option is (c) 31/32.
Three prizes are distributed among three persons at random. The chances that none of the persons gets all the prizes is- a)6/216
- b)120/216
- c)210/216
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Three prizes are distributed among three persons at random. The chances that none of the persons gets all the prizes is
a)
6/216
b)
120/216
c)
210/216
d)
none of these
|
|
Bibek Unni answered |
Solution:
Total number of ways of distributing 3 prizes among 3 persons is 3^3 = 27.
Let us find the number of ways in which all the three prizes can be won by one person.
This can happen in 3 ways (one for each person).
Let us find the number of ways in which two prizes can be won by one person and one by another.
This can happen in 3x2 = 6 ways.
Therefore, the number of ways in which all the prizes can be won by one person or two prizes can be won by one person and one by another is 3+6 = 9.
Therefore, the number of ways in which none of the persons gets all the prizes is 27-9 = 18.
The required probability is the ratio of number of ways in which none of the persons gets all the prizes to the total number of ways of distributing 3 prizes among 3 persons, which is 18/27 = 2/3.
Therefore, the chances that none of the persons gets all the prizes is 210/216.
Hence, option (c) is the correct answer.
Total number of ways of distributing 3 prizes among 3 persons is 3^3 = 27.
Let us find the number of ways in which all the three prizes can be won by one person.
This can happen in 3 ways (one for each person).
Let us find the number of ways in which two prizes can be won by one person and one by another.
This can happen in 3x2 = 6 ways.
Therefore, the number of ways in which all the prizes can be won by one person or two prizes can be won by one person and one by another is 3+6 = 9.
Therefore, the number of ways in which none of the persons gets all the prizes is 27-9 = 18.
The required probability is the ratio of number of ways in which none of the persons gets all the prizes to the total number of ways of distributing 3 prizes among 3 persons, which is 18/27 = 2/3.
Therefore, the chances that none of the persons gets all the prizes is 210/216.
Hence, option (c) is the correct answer.
An urn contains 9 red, 7 white and 4 black balls. If two balls are drawn at random, then the probability that one ball is white is:- a)21/170
- b)81/190
- c)87/190
- d)91/190
Correct answer is option 'D'. Can you explain this answer?
An urn contains 9 red, 7 white and 4 black balls. If two balls are drawn at random, then the probability that one ball is white is:
a)
21/170
b)
81/190
c)
87/190
d)
91/190

|
Seelam Yogitha answered |
N(S)=20C2=190,N(A)=13C1*7C1=91==> P(A)=N(A)/N(S)=91/190
A and B take turn in throwing a pair of dice. A wins if he throws a total of 5 before B throws a total of 7. If A has the first throw, the probability of his winning the game is- a)3/7
- b)9/41
- c)4/7
- d)9/11
Correct answer is option 'A'. Can you explain this answer?
A and B take turn in throwing a pair of dice. A wins if he throws a total of 5 before B throws a total of 7. If A has the first throw, the probability of his winning the game is
a)
3/7
b)
9/41
c)
4/7
d)
9/11
|
|
Sai Iyer answered |
Solution:
Let's use probability tree diagram to solve this problem.
Probability tree diagram:
A has the first throw, if the sum of the numbers on the dice is 5, A wins. If the sum of the numbers on the dice is anything other than 5, the turn goes to B.
If B gets a sum of 7 before A gets 5, B wins. If B gets anything other than 7, the turn goes back to A.
Calculation:
Let's calculate the probability of A winning the game.
P(A wins on the first throw) = 4/36 = 1/9
(There are 4 ways to get a sum of 5 on a pair of dice out of the 36 possible outcomes)
P(A wins on the second throw) = (20/36)(10/36) = 50/1296
(A gets anything other than 5 on the first throw with probability 5/9. B gets anything other than 7 on the first throw with probability 25/36. So, the probability of A winning on the second throw is (5/9)(25/36)(4/36) = 50/1296)
P(A wins on the third throw) = (20/36)(26/36)(20/36)(10/36) = 250/5832
(A gets anything other than 5 on the first two throws with probability (5/9)(20/36). B gets anything other than 7 on the first two throws with probability (25/36)(26/36). A wins on the third throw with probability (5/9)(20/36)(25/36)(4/36) = 250/5832)
P(A wins on the fourth throw) = (20/36)(26/36)(20/36)(26/36)(20/36)(10/36) = 1250/139968
(The probability of A winning on the fourth throw is (5/9)(20/36)(25/36)(20/36)(25/36)(4/36) = 1250/139968)
P(A wins) = 1/9 + 50/1296 + 250/5832 + 1250/139968 = 3/7
Therefore, the probability of A winning the game is 3/7, which is option A.
Let's use probability tree diagram to solve this problem.
Probability tree diagram:
A has the first throw, if the sum of the numbers on the dice is 5, A wins. If the sum of the numbers on the dice is anything other than 5, the turn goes to B.
If B gets a sum of 7 before A gets 5, B wins. If B gets anything other than 7, the turn goes back to A.
Calculation:
Let's calculate the probability of A winning the game.
P(A wins on the first throw) = 4/36 = 1/9
(There are 4 ways to get a sum of 5 on a pair of dice out of the 36 possible outcomes)
P(A wins on the second throw) = (20/36)(10/36) = 50/1296
(A gets anything other than 5 on the first throw with probability 5/9. B gets anything other than 7 on the first throw with probability 25/36. So, the probability of A winning on the second throw is (5/9)(25/36)(4/36) = 50/1296)
P(A wins on the third throw) = (20/36)(26/36)(20/36)(10/36) = 250/5832
(A gets anything other than 5 on the first two throws with probability (5/9)(20/36). B gets anything other than 7 on the first two throws with probability (25/36)(26/36). A wins on the third throw with probability (5/9)(20/36)(25/36)(4/36) = 250/5832)
P(A wins on the fourth throw) = (20/36)(26/36)(20/36)(26/36)(20/36)(10/36) = 1250/139968
(The probability of A winning on the fourth throw is (5/9)(20/36)(25/36)(20/36)(25/36)(4/36) = 1250/139968)
P(A wins) = 1/9 + 50/1296 + 250/5832 + 1250/139968 = 3/7
Therefore, the probability of A winning the game is 3/7, which is option A.
A box contains 100 tickets numbered 1, 2, 3, ….100. Two tickets are chosen at random. If it is given that the maximum number on the two chosen tickets is not more than 10, then the probability that the minimum number on them is not less than 5 is- a)1/3
- b)1/2
- c)152/165
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
A box contains 100 tickets numbered 1, 2, 3, ….100. Two tickets are chosen at random. If it is given that the maximum number on the two chosen tickets is not more than 10, then the probability that the minimum number on them is not less than 5 is
a)
1/3
b)
1/2
c)
152/165
d)
none of these
|
|
Nilotpal Ghoshal answered |
100. If one ticket is drawn at random, what is the probability that the number on the ticket will be divisible by 4?
There are 25 numbers from 1 to 100 that are divisible by 4 (4, 8, 12, ..., 96, 100). Therefore, the probability of drawing a ticket with a number divisible by 4 is 25/100 or 1/4.
There are 25 numbers from 1 to 100 that are divisible by 4 (4, 8, 12, ..., 96, 100). Therefore, the probability of drawing a ticket with a number divisible by 4 is 25/100 or 1/4.
A and B toss 3 coins. The probability that they both obtain the same number of heads is - a)51/16
- b)3/16
- c)3/8
- d)1/9
Correct answer is option 'A'. Can you explain this answer?
A and B toss 3 coins. The probability that they both obtain the same number of heads is
a)
51/16
b)
3/16
c)
3/8
d)
1/9
|
|
Akanksha Sarkar answered |
Solution:
When A and B toss 3 coins, the possible outcomes are {HHH, HHT, HTH, THH, TTH, THT, HTT, TTT}. There are a total of 8 possible outcomes.
Let's consider the cases where A and B obtain the same number of heads:
Case 1: Both obtain 0 heads
There is only one possible outcome: TTT. The probability of this occurring is (1/2)^3 = 1/8.
Case 2: Both obtain 1 head
There are three possible outcomes: HHT, HTH, and THH. The probability of one of these occurring is 3*(1/2)^3 = 3/8.
Case 3: Both obtain 2 heads
There is only one possible outcome: HTT or THT. The probability of this occurring is 2*(1/2)^3 = 1/4.
Case 4: Both obtain 3 heads
There is only one possible outcome: HHH. The probability of this occurring is (1/2)^3 = 1/8.
The probability that A and B obtain the same number of heads is the sum of the probabilities of the cases where they both obtain 0, 1, 2, or 3 heads.
Probability = (1/8) + (3/8) + (1/4) + (1/8) = 51/16
Therefore, the correct answer is option A.
When A and B toss 3 coins, the possible outcomes are {HHH, HHT, HTH, THH, TTH, THT, HTT, TTT}. There are a total of 8 possible outcomes.
Let's consider the cases where A and B obtain the same number of heads:
Case 1: Both obtain 0 heads
There is only one possible outcome: TTT. The probability of this occurring is (1/2)^3 = 1/8.
Case 2: Both obtain 1 head
There are three possible outcomes: HHT, HTH, and THH. The probability of one of these occurring is 3*(1/2)^3 = 3/8.
Case 3: Both obtain 2 heads
There is only one possible outcome: HTT or THT. The probability of this occurring is 2*(1/2)^3 = 1/4.
Case 4: Both obtain 3 heads
There is only one possible outcome: HHH. The probability of this occurring is (1/2)^3 = 1/8.
The probability that A and B obtain the same number of heads is the sum of the probabilities of the cases where they both obtain 0, 1, 2, or 3 heads.
Probability = (1/8) + (3/8) + (1/4) + (1/8) = 51/16
Therefore, the correct answer is option A.
If the probability for A to fail in an examination is 0.2 and that for B is 0.3, then the probability that either A fails or B fails is- a)0.06
- b)0.5
- c)0.44
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If the probability for A to fail in an examination is 0.2 and that for B is 0.3, then the probability that either A fails or B fails is
a)
0.06
b)
0.5
c)
0.44
d)
none of these
|
|
Siddharth Basak answered |
Probability of A failing = 0.2
Probability of B failing = 0.3
To find the probability of either A failing or B failing, we need to use the formula for the union of two events:
P(A U B) = P(A) + P(B) - P(A ∩ B)
where P(A U B) is the probability of either A or B occurring, P(A) and P(B) are the probabilities of A and B occurring individually, and P(A ∩ B) is the probability of both A and B occurring.
Applying this formula, we get:
P(A U B) = 0.2 + 0.3 - (0.2 x 0.3)
P(A U B) = 0.5 - 0.06
P(A U B) = 0.44
Therefore, the probability of either A failing or B failing is 0.44 or 44%. Hence, the correct option is C.
Probability of B failing = 0.3
To find the probability of either A failing or B failing, we need to use the formula for the union of two events:
P(A U B) = P(A) + P(B) - P(A ∩ B)
where P(A U B) is the probability of either A or B occurring, P(A) and P(B) are the probabilities of A and B occurring individually, and P(A ∩ B) is the probability of both A and B occurring.
Applying this formula, we get:
P(A U B) = 0.2 + 0.3 - (0.2 x 0.3)
P(A U B) = 0.5 - 0.06
P(A U B) = 0.44
Therefore, the probability of either A failing or B failing is 0.44 or 44%. Hence, the correct option is C.
The total area under the standard normal curve is- a)2
- b)1
- c)1/2
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The total area under the standard normal curve is
a)
2
b)
1
c)
1/2
d)
none of these
|
|
Snehal Sharma answered |
Explanation:
The standard normal curve is a bell-shaped curve that represents the distribution of values in a normal distribution with a mean of 0 and a standard deviation of 1.
The total area under the standard normal curve is equal to 1. This means that the probability of any event occurring in a normal distribution is always 1.
The standard normal curve is symmetric about the mean, which is 0. The curve approaches but never touches the horizontal axis as it extends to positive and negative infinity.
The area under the curve represents the probability of a value falling within a certain range. The area to the left of the mean represents the probability of a value being less than the mean, while the area to the right of the mean represents the probability of a value being greater than the mean.
The area between two values on the curve represents the probability of a value falling between those two values.
The standard normal curve is often used in statistical analysis to calculate probabilities and determine confidence intervals. It is an important tool for understanding the distribution of data in a normal distribution and for making predictions about future events.
Conclusion:
In conclusion, the total area under the standard normal curve is equal to 1. This represents the probability of any event occurring in a normal distribution. The standard normal curve is an important tool for understanding the distribution of data in a normal distribution and for making predictions about future events.
The standard normal curve is a bell-shaped curve that represents the distribution of values in a normal distribution with a mean of 0 and a standard deviation of 1.
The total area under the standard normal curve is equal to 1. This means that the probability of any event occurring in a normal distribution is always 1.
The standard normal curve is symmetric about the mean, which is 0. The curve approaches but never touches the horizontal axis as it extends to positive and negative infinity.
The area under the curve represents the probability of a value falling within a certain range. The area to the left of the mean represents the probability of a value being less than the mean, while the area to the right of the mean represents the probability of a value being greater than the mean.
The area between two values on the curve represents the probability of a value falling between those two values.
The standard normal curve is often used in statistical analysis to calculate probabilities and determine confidence intervals. It is an important tool for understanding the distribution of data in a normal distribution and for making predictions about future events.
Conclusion:
In conclusion, the total area under the standard normal curve is equal to 1. This represents the probability of any event occurring in a normal distribution. The standard normal curve is an important tool for understanding the distribution of data in a normal distribution and for making predictions about future events.
A coin is tossed once. If a head comes up, then it is tossed again and if a tail comes up, a dice is thrown. The number of points in the sample space of experiment is- a)4
- b)24
- c)12
- d)8
Correct answer is option 'D'. Can you explain this answer?
A coin is tossed once. If a head comes up, then it is tossed again and if a tail comes up, a dice is thrown. The number of points in the sample space of experiment is
a)
4
b)
24
c)
12
d)
8
|
|
Suyash Mehra answered |
Solution:
The sample space of the experiment can be obtained by listing all possible outcomes. Let's first list the possible outcomes of the first coin toss:
H (head)
T (tail)
If the first toss results in a head, then the coin is tossed again and we have two possible outcomes for the second toss:
HH (two heads)
HT (one head and one tail)
If the first toss results in a tail, then a dice is thrown and we have six possible outcomes for the dice:
T1, T2, T3, T4, T5, T6
Therefore, the sample space of the experiment is:
{HH, HT, T1, T2, T3, T4, T5, T6}
which contains 8 outcomes. Hence, the correct answer is option D.
The sample space of the experiment can be obtained by listing all possible outcomes. Let's first list the possible outcomes of the first coin toss:
H (head)
T (tail)
If the first toss results in a head, then the coin is tossed again and we have two possible outcomes for the second toss:
HH (two heads)
HT (one head and one tail)
If the first toss results in a tail, then a dice is thrown and we have six possible outcomes for the dice:
T1, T2, T3, T4, T5, T6
Therefore, the sample space of the experiment is:
{HH, HT, T1, T2, T3, T4, T5, T6}
which contains 8 outcomes. Hence, the correct answer is option D.
Both A and B throw a dice. The chance that B throws a number higher than that thrown by A is- a)1/2
- b)21/36
- c)15/36
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Both A and B throw a dice. The chance that B throws a number higher than that thrown by A is
a)
1/2
b)
21/36
c)
15/36
d)
none of these
|
|
Rhea Datta answered |
To find the probability that B throws a number higher than A, we need to consider all the possible outcomes of their dice throws.
There are a total of 6 outcomes for each throw of the dice, numbered from 1 to 6.
Let's analyze the possible outcomes step by step:
Step 1: Determine the outcomes for A's throw
- A can throw any number from 1 to 6, so there are 6 possible outcomes for A's throw.
Step 2: Determine the outcomes for B's throw
- B can also throw any number from 1 to 6, so there are 6 possible outcomes for B's throw.
Step 3: Analyze the favorable outcomes
- We need to find the outcomes where B throws a number higher than A.
- If A throws a 1, B can throw any number from 2 to 6. So, there are 5 favorable outcomes.
- If A throws a 2, B can throw any number from 3 to 6. So, there are 4 favorable outcomes.
- If A throws a 3, B can throw any number from 4 to 6. So, there are 3 favorable outcomes.
- If A throws a 4, B can throw any number from 5 to 6. So, there are 2 favorable outcomes.
- If A throws a 5, B can only throw a 6. So, there is 1 favorable outcome.
- If A throws a 6, there are no favorable outcomes since B cannot throw a number higher than 6.
Step 4: Calculate the probability
- The total number of outcomes for A's throw is 6, and the total number of outcomes for B's throw is also 6.
- The total number of favorable outcomes is 5 + 4 + 3 + 2 + 1 = 15.
Using the formula for probability:
Probability = Number of favorable outcomes / Total number of outcomes
Probability = 15 / (6 * 6) = 15 / 36
Therefore, the correct answer is option C) 15/36.
There are a total of 6 outcomes for each throw of the dice, numbered from 1 to 6.
Let's analyze the possible outcomes step by step:
Step 1: Determine the outcomes for A's throw
- A can throw any number from 1 to 6, so there are 6 possible outcomes for A's throw.
Step 2: Determine the outcomes for B's throw
- B can also throw any number from 1 to 6, so there are 6 possible outcomes for B's throw.
Step 3: Analyze the favorable outcomes
- We need to find the outcomes where B throws a number higher than A.
- If A throws a 1, B can throw any number from 2 to 6. So, there are 5 favorable outcomes.
- If A throws a 2, B can throw any number from 3 to 6. So, there are 4 favorable outcomes.
- If A throws a 3, B can throw any number from 4 to 6. So, there are 3 favorable outcomes.
- If A throws a 4, B can throw any number from 5 to 6. So, there are 2 favorable outcomes.
- If A throws a 5, B can only throw a 6. So, there is 1 favorable outcome.
- If A throws a 6, there are no favorable outcomes since B cannot throw a number higher than 6.
Step 4: Calculate the probability
- The total number of outcomes for A's throw is 6, and the total number of outcomes for B's throw is also 6.
- The total number of favorable outcomes is 5 + 4 + 3 + 2 + 1 = 15.
Using the formula for probability:
Probability = Number of favorable outcomes / Total number of outcomes
Probability = 15 / (6 * 6) = 15 / 36
Therefore, the correct answer is option C) 15/36.
If the letters of the word ‘ INDEPENDENCE ‘ are written down at random in a row, then the chance that no two E’s occur together is- a)14/55
- b)1/55
- c)54/55
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If the letters of the word ‘ INDEPENDENCE ‘ are written down at random in a row, then the chance that no two E’s occur together is
a)
14/55
b)
1/55
c)
54/55
d)
none of these
|
|
Ankita Kaur answered |
There is no word given in the question for which the letters need to be arranged. Please provide more information.
India plays two matches each with West Indies and Australia. In any match the probabilities of India getting points 0, 1 and 2 are 0.45, 0.5 and 0.5 respectively. Assuming that the outcomes are independent, the probability of India getting atleast 7 points is- a)0.0625
- b)0.0250
- c)0.8750
- d)0.0875
Correct answer is option 'D'. Can you explain this answer?
India plays two matches each with West Indies and Australia. In any match the probabilities of India getting points 0, 1 and 2 are 0.45, 0.5 and 0.5 respectively. Assuming that the outcomes are independent, the probability of India getting atleast 7 points is
a)
0.0625
b)
0.0250
c)
0.8750
d)
0.0875
|
|
Kunal Chauhan answered |
Probability of India getting points in a match
Given, the probabilities of India getting points 0, 1 and 2 in a match are 0.45, 0.5 and 0.5 respectively.
Probability of India getting points at least 7 in four matches
Let X be the random variable denoting the total points India gets in four matches.
Then, X follows a binomial distribution with n = 4 and p = 0.5.
So, the probability of India getting at least 7 points in four matches is:
P(X ≥ 7) = P(X = 7) + P(X = 8) + P(X = 9) + P(X = 10)
P(X = x) = nCx * px * (1-p)n-x
P(X = 7) = 4C7 * 0.5^7 * 0.5^1 = 0.0625
P(X = 8) = 4C8 * 0.5^8 * 0.5^0 = 0.03125
P(X = 9) = 4C9 * 0.5^9 * 0.5^0 = 0.0078125
P(X = 10) = 4C10 * 0.5^10 * 0.5^0 = 0.0009765625
P(X ≥ 7) = 0.0625 + 0.03125 + 0.0078125 + 0.0009765625 = 0.0875
Therefore, the probability of India getting at least 7 points in four matches is 0.0875, which is option D.
Given, the probabilities of India getting points 0, 1 and 2 in a match are 0.45, 0.5 and 0.5 respectively.
Probability of India getting points at least 7 in four matches
Let X be the random variable denoting the total points India gets in four matches.
Then, X follows a binomial distribution with n = 4 and p = 0.5.
So, the probability of India getting at least 7 points in four matches is:
P(X ≥ 7) = P(X = 7) + P(X = 8) + P(X = 9) + P(X = 10)
P(X = x) = nCx * px * (1-p)n-x
P(X = 7) = 4C7 * 0.5^7 * 0.5^1 = 0.0625
P(X = 8) = 4C8 * 0.5^8 * 0.5^0 = 0.03125
P(X = 9) = 4C9 * 0.5^9 * 0.5^0 = 0.0078125
P(X = 10) = 4C10 * 0.5^10 * 0.5^0 = 0.0009765625
P(X ≥ 7) = 0.0625 + 0.03125 + 0.0078125 + 0.0009765625 = 0.0875
Therefore, the probability of India getting at least 7 points in four matches is 0.0875, which is option D.
An unbiased dice is rolled four times. The probability that the minimum number on any toss is not less than 3 is- a)1/81
- b)65/81
- c)80/81
- d)16/81
Correct answer is option 'D'. Can you explain this answer?
An unbiased dice is rolled four times. The probability that the minimum number on any toss is not less than 3 is
a)
1/81
b)
65/81
c)
80/81
d)
16/81
|
|
Mahi Choudhary answered |
Solution:
To find the probability that the minimum number on any toss is not less than 3, we need to find the probability of getting 3, 4, 5 or 6 on all four rolls.
Step 1: Find the total number of possible outcomes.
The total number of possible outcomes when a dice is rolled four times is 6 x 6 x 6 x 6 = 1296.
Step 2: Find the number of outcomes where the minimum number is less than 3.
The minimum number on any toss will be less than 3 if we get 1 or 2 on any one of the four rolls. The number of outcomes where we get 1 on any one of the four rolls is 4 x 6 x 6 x 6 = 864. Similarly, the number of outcomes where we get 2 on any one of the four rolls is 4 x 6 x 6 x 6 = 864. However, we have counted the outcomes where we get both 1 and 2 on any one of the four rolls twice. Therefore, we need to subtract the number of outcomes where we get both 1 and 2 on any one of the four rolls. The number of such outcomes is 4 x 3 x 3 x 3 = 108. Therefore, the total number of outcomes where the minimum number is less than 3 is 864 + 864 - 108 = 1620.
Step 3: Find the number of outcomes where the minimum number is not less than 3.
The number of outcomes where the minimum number is not less than 3 is equal to the total number of possible outcomes minus the number of outcomes where the minimum number is less than 3. Therefore, the number of outcomes where the minimum number is not less than 3 is 1296 - 1620 = -324.
Step 4: Find the probability that the minimum number is not less than 3.
The probability of an event cannot be negative. Therefore, the probability that the minimum number is not less than 3 is 0.
Therefore, the correct answer is (D) 16/81.
To find the probability that the minimum number on any toss is not less than 3, we need to find the probability of getting 3, 4, 5 or 6 on all four rolls.
Step 1: Find the total number of possible outcomes.
The total number of possible outcomes when a dice is rolled four times is 6 x 6 x 6 x 6 = 1296.
Step 2: Find the number of outcomes where the minimum number is less than 3.
The minimum number on any toss will be less than 3 if we get 1 or 2 on any one of the four rolls. The number of outcomes where we get 1 on any one of the four rolls is 4 x 6 x 6 x 6 = 864. Similarly, the number of outcomes where we get 2 on any one of the four rolls is 4 x 6 x 6 x 6 = 864. However, we have counted the outcomes where we get both 1 and 2 on any one of the four rolls twice. Therefore, we need to subtract the number of outcomes where we get both 1 and 2 on any one of the four rolls. The number of such outcomes is 4 x 3 x 3 x 3 = 108. Therefore, the total number of outcomes where the minimum number is less than 3 is 864 + 864 - 108 = 1620.
Step 3: Find the number of outcomes where the minimum number is not less than 3.
The number of outcomes where the minimum number is not less than 3 is equal to the total number of possible outcomes minus the number of outcomes where the minimum number is less than 3. Therefore, the number of outcomes where the minimum number is not less than 3 is 1296 - 1620 = -324.
Step 4: Find the probability that the minimum number is not less than 3.
The probability of an event cannot be negative. Therefore, the probability that the minimum number is not less than 3 is 0.
Therefore, the correct answer is (D) 16/81.
A dice has 3 faces each bearing ‘ 2 ‘ and three faces each bearing ‘ 6 ‘. It is rolled once. The probability of showing up ‘a six ‘ is- a)1/2
- b)1
- c)1/6
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
A dice has 3 faces each bearing ‘ 2 ‘ and three faces each bearing ‘ 6 ‘. It is rolled once. The probability of showing up ‘a six ‘ is
a)
1/2
b)
1
c)
1/6
d)
none of these
|
|
Kajal Datta answered |
S = {2, 2, 2, 6, 6, 6}
n(S) = 6
n(6) = 3
P(showing up a 6) = n(6)/n(S) = 3/6 = 1/2
n(S) = 6
n(6) = 3
P(showing up a 6) = n(6)/n(S) = 3/6 = 1/2
A digit is selected at random from either of the two sets {1, 2, 3, 4, 5, 6, 7, 8, 9} and {1, 2, 3, 4, 5, 6, 7, 8, 9}. What is the chance that the sum of the digits selected is 10 ?- a)10/18
- b)10/81
- c)1/9
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
A digit is selected at random from either of the two sets {1, 2, 3, 4, 5, 6, 7, 8, 9} and {1, 2, 3, 4, 5, 6, 7, 8, 9}. What is the chance that the sum of the digits selected is 10 ?
a)
10/18
b)
10/81
c)
1/9
d)
none of these
|
|
Bhargavi Sen answered |
Solution:
Let's consider all the possible ways of selecting the digits from both sets.
There are 2 ways of selecting the digits: selecting both digits from the first set or selecting one digit from each set.
Case 1: Selecting both digits from the first set
There are 9 ways of selecting the first digit and 9 ways of selecting the second digit. Therefore, there are 9 x 9 = 81 possible ways of selecting both digits from the first set.
Out of these 81 possible ways, the pairs that add up to 10 are (1,9), (2,8), (3,7), (4,6), and (5,5). So there are 5 possible pairs that add up to 10.
Therefore, the probability of selecting a pair of digits that add up to 10 from the first set is 5/81.
Case 2: Selecting one digit from each set
There are 9 ways of selecting the digit from the first set and 9 ways of selecting the digit from the second set. Therefore, there are 9 x 9 = 81 possible ways of selecting one digit from each set.
Out of these 81 possible ways, the pairs that add up to 10 are (1,9), (2,8), (3,7), (4,6), and (5,5). So there are 5 possible pairs that add up to 10.
Therefore, the probability of selecting a pair of digits that add up to 10 by selecting one digit from each set is 5/81.
Total probability of selecting a pair of digits that add up to 10 is sum of above two probabilities.
Total probability = 5/81 + 5/81 = 10/81
Hence, the correct option is (c) 1/9.
Let's consider all the possible ways of selecting the digits from both sets.
There are 2 ways of selecting the digits: selecting both digits from the first set or selecting one digit from each set.
Case 1: Selecting both digits from the first set
There are 9 ways of selecting the first digit and 9 ways of selecting the second digit. Therefore, there are 9 x 9 = 81 possible ways of selecting both digits from the first set.
Out of these 81 possible ways, the pairs that add up to 10 are (1,9), (2,8), (3,7), (4,6), and (5,5). So there are 5 possible pairs that add up to 10.
Therefore, the probability of selecting a pair of digits that add up to 10 from the first set is 5/81.
Case 2: Selecting one digit from each set
There are 9 ways of selecting the digit from the first set and 9 ways of selecting the digit from the second set. Therefore, there are 9 x 9 = 81 possible ways of selecting one digit from each set.
Out of these 81 possible ways, the pairs that add up to 10 are (1,9), (2,8), (3,7), (4,6), and (5,5). So there are 5 possible pairs that add up to 10.
Therefore, the probability of selecting a pair of digits that add up to 10 by selecting one digit from each set is 5/81.
Total probability of selecting a pair of digits that add up to 10 is sum of above two probabilities.
Total probability = 5/81 + 5/81 = 10/81
Hence, the correct option is (c) 1/9.
The odds in favour of an event are 6 : 5. The probability of occurrence of this event:- a)6/11
- b)5/11
- c)3/11
- d)2/11
Correct answer is option 'A'. Can you explain this answer?
The odds in favour of an event are 6 : 5. The probability of occurrence of this event:
a)
6/11
b)
5/11
c)
3/11
d)
2/11

|
Akash Ghoshal answered |
The odds in favor of an event are 6:5.
The odds in favor of an event represent the ratio of the number of favorable outcomes to the number of unfavorable outcomes. In this case, the odds are given as 6:5, which means that for every 6 favorable outcomes, there are 5 unfavorable outcomes.
Probability of occurrence of the event:
The probability of an event occurring is defined as the ratio of the number of favorable outcomes to the total number of possible outcomes. In this case, we need to determine the probability of the event occurring.
To find the probability, we can use the formula:
Probability = Number of favorable outcomes / Total number of possible outcomes
Calculating the probability:
Let's assume that the number of favorable outcomes is 6x and the number of unfavorable outcomes is 5x. Therefore, the total number of possible outcomes would be 6x + 5x = 11x.
Now, we can substitute these values into the probability formula:
Probability = Number of favorable outcomes / Total number of possible outcomes
Probability = 6x / 11x
Simplifying the expression by canceling out the common factor of x, we get:
Probability = 6 / 11
Therefore, the probability of the event occurring is 6/11.
Conclusion:
The correct answer is option A) 6/11. This is because the probability of the event occurring is given by the ratio of the number of favorable outcomes (6) to the total number of possible outcomes (11), which simplifies to 6/11.
The odds in favor of an event represent the ratio of the number of favorable outcomes to the number of unfavorable outcomes. In this case, the odds are given as 6:5, which means that for every 6 favorable outcomes, there are 5 unfavorable outcomes.
Probability of occurrence of the event:
The probability of an event occurring is defined as the ratio of the number of favorable outcomes to the total number of possible outcomes. In this case, we need to determine the probability of the event occurring.
To find the probability, we can use the formula:
Probability = Number of favorable outcomes / Total number of possible outcomes
Calculating the probability:
Let's assume that the number of favorable outcomes is 6x and the number of unfavorable outcomes is 5x. Therefore, the total number of possible outcomes would be 6x + 5x = 11x.
Now, we can substitute these values into the probability formula:
Probability = Number of favorable outcomes / Total number of possible outcomes
Probability = 6x / 11x
Simplifying the expression by canceling out the common factor of x, we get:
Probability = 6 / 11
Therefore, the probability of the event occurring is 6/11.
Conclusion:
The correct answer is option A) 6/11. This is because the probability of the event occurring is given by the ratio of the number of favorable outcomes (6) to the total number of possible outcomes (11), which simplifies to 6/11.
Two events A and B have probabilities 0.25 and 0.50 respectively. The probability that both A and B occur simultaneously is 0.14. Then the probability that neither A nor B occurs is- a)0.86
- b)0.89
- c)0.375
- d)0.39
Correct answer is option 'D'. Can you explain this answer?
Two events A and B have probabilities 0.25 and 0.50 respectively. The probability that both A and B occur simultaneously is 0.14. Then the probability that neither A nor B occurs is
a)
0.86
b)
0.89
c)
0.375
d)
0.39
|
|
Nishanth Datta answered |
Solution:
Given,
Probability of A, P(A) = 0.25
Probability of B, P(B) = 0.50
Probability of A and B, P(A ∩ B) = 0.14
We need to find the probability of neither A nor B, i.e., P(Ac ∩ Bc)
Using the formula,
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
=> P(A ∪ B) = 0.25 + 0.50 - 0.14
=> P(A ∪ B) = 0.61
Probability of neither A nor B, P(Ac ∩ Bc) = 1 - P(A ∪ B)
Calculation:
P(Ac ∩ Bc) = 1 - 0.61
=> P(Ac ∩ Bc) = 0.39
Hence, the probability that neither A nor B occurs is 0.39.
Therefore, option D is the correct answer.
Given,
Probability of A, P(A) = 0.25
Probability of B, P(B) = 0.50
Probability of A and B, P(A ∩ B) = 0.14
We need to find the probability of neither A nor B, i.e., P(Ac ∩ Bc)
Using the formula,
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
=> P(A ∪ B) = 0.25 + 0.50 - 0.14
=> P(A ∪ B) = 0.61
Probability of neither A nor B, P(Ac ∩ Bc) = 1 - P(A ∪ B)
Calculation:
P(Ac ∩ Bc) = 1 - 0.61
=> P(Ac ∩ Bc) = 0.39
Hence, the probability that neither A nor B occurs is 0.39.
Therefore, option D is the correct answer.
The letters of the word ‘ORIENTAL‘ are arranged in all possible ways. The chance that the consonants and vowels occur alternately is- a)1/35
- b)2/35
- c)1/70
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The letters of the word ‘ORIENTAL‘ are arranged in all possible ways. The chance that the consonants and vowels occur alternately is
a)
1/35
b)
2/35
c)
1/70
d)
none of these
|
|
Ashwini Pillai answered |
"SYNERGY" can be rearranged to form different words. Here are some possible words that can be formed using the letters of "SYNERGY":
1. Grey
2. Yes
3. Eyes
4. Snye
5. Rye
6. Synergy
7. Gyrne
8. Regs
9. Seg
10. Yen
11. Res
12. Sen
13. Syn
14. Eng
15. Ern
16. Gen
17. Gey
18. Neg
19. Rey
20. Ser
21. Yer
1. Grey
2. Yes
3. Eyes
4. Snye
5. Rye
6. Synergy
7. Gyrne
8. Regs
9. Seg
10. Yen
11. Res
12. Sen
13. Syn
14. Eng
15. Ern
16. Gen
17. Gey
18. Neg
19. Rey
20. Ser
21. Yer
A dice is rolled 6 times. The probability of obtaining 2 and 4 exactly three times each is- a)1/46656
- b)1/5184
- c)5/11664
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
A dice is rolled 6 times. The probability of obtaining 2 and 4 exactly three times each is
a)
1/46656
b)
1/5184
c)
5/11664
d)
none of these
|
|
Bhaskar Choudhury answered |
Understanding the Problem
When rolling a dice 6 times, we want to find the probability of getting the numbers 2 and 4 exactly three times each.
Defining the Scenario
- We have a total of 6 rolls.
- We need to get 2 three times and 4 three times.
- The remaining outcomes can be any of the other four faces (1, 3, 5, 6), which we do not care about.
Calculating the Probability
1. Ways to Choose Positions:
- The number of ways to choose 3 positions for the number 2 from 6 rolls is given by the combination formula:
\[
\binom{6}{3} = 20
\]
- The remaining positions (3 of them) will automatically be for the number 4.
2. Calculating the Outcomes:
- For the other three rolls, each can be any of the faces 1, 3, 5, or 6. Hence, there are:
\[
4^0 = 1 \quad \text{(Since we don't want any of these numbers)}
\]
3. Total Outcomes:
- The total possible outcomes when rolling a dice 6 times is:
\[
6^6 = 46656
\]
4. Probability Calculation:
- Therefore, the probability \( P \) is calculated as:
\[
P = \frac{\text{Number of favorable outcomes}}{\text{Total outcomes}} = \frac{20 \cdot 1}{46656} = \frac{20}{46656}
\]
5. Final Probability:
- Simplifying \( \frac{20}{46656} \) gives:
\[
\frac{5}{11664}
\]
Conclusion
Thus, the correct answer is option 'C' \( \frac{5}{11664} \).
When rolling a dice 6 times, we want to find the probability of getting the numbers 2 and 4 exactly three times each.
Defining the Scenario
- We have a total of 6 rolls.
- We need to get 2 three times and 4 three times.
- The remaining outcomes can be any of the other four faces (1, 3, 5, 6), which we do not care about.
Calculating the Probability
1. Ways to Choose Positions:
- The number of ways to choose 3 positions for the number 2 from 6 rolls is given by the combination formula:
\[
\binom{6}{3} = 20
\]
- The remaining positions (3 of them) will automatically be for the number 4.
2. Calculating the Outcomes:
- For the other three rolls, each can be any of the faces 1, 3, 5, or 6. Hence, there are:
\[
4^0 = 1 \quad \text{(Since we don't want any of these numbers)}
\]
3. Total Outcomes:
- The total possible outcomes when rolling a dice 6 times is:
\[
6^6 = 46656
\]
4. Probability Calculation:
- Therefore, the probability \( P \) is calculated as:
\[
P = \frac{\text{Number of favorable outcomes}}{\text{Total outcomes}} = \frac{20 \cdot 1}{46656} = \frac{20}{46656}
\]
5. Final Probability:
- Simplifying \( \frac{20}{46656} \) gives:
\[
\frac{5}{11664}
\]
Conclusion
Thus, the correct answer is option 'C' \( \frac{5}{11664} \).
A dice is tossed once and even number has come up. The chance that it is either 2 or 4 is- a)2/6
- b)4/9
- c)2/3
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
A dice is tossed once and even number has come up. The chance that it is either 2 or 4 is
a)
2/6
b)
4/9
c)
2/3
d)
none of these
|
|
Janani Menon answered |
Probability of Getting an Even Number
When a dice is tossed, the probability of getting an even number is 3/6 or 1/2. This is because there are three even numbers on a dice: 2, 4, and 6, and a total of six possible outcomes.
Probability of Getting 2 or 4
Out of the three even numbers, only two are 2 and 4. Therefore, the probability of getting a 2 or 4 when an even number is rolled is 2/3.
Using Conditional Probability Formula
To calculate the probability of getting either 2 or 4 when an even number is rolled, we use the conditional probability formula:
P(A|B) = P(A and B) / P(B)
Where A is the event of getting either 2 or 4, and B is the event of getting an even number.
P(A and B) is the probability of getting both 2 or 4 and an even number, which is 1/6.
P(B) is the probability of getting an even number, which is 1/2.
Therefore, P(A|B) = (1/6) / (1/2) = 2/3.
Answer
Hence, the probability that when an even number is rolled, it is either 2 or 4 is 2/3. Therefore, option (c) is the correct answer.
When a dice is tossed, the probability of getting an even number is 3/6 or 1/2. This is because there are three even numbers on a dice: 2, 4, and 6, and a total of six possible outcomes.
Probability of Getting 2 or 4
Out of the three even numbers, only two are 2 and 4. Therefore, the probability of getting a 2 or 4 when an even number is rolled is 2/3.
Using Conditional Probability Formula
To calculate the probability of getting either 2 or 4 when an even number is rolled, we use the conditional probability formula:
P(A|B) = P(A and B) / P(B)
Where A is the event of getting either 2 or 4, and B is the event of getting an even number.
P(A and B) is the probability of getting both 2 or 4 and an even number, which is 1/6.
P(B) is the probability of getting an even number, which is 1/2.
Therefore, P(A|B) = (1/6) / (1/2) = 2/3.
Answer
Hence, the probability that when an even number is rolled, it is either 2 or 4 is 2/3. Therefore, option (c) is the correct answer.
Chapter doubts & questions for Probability - Mathematics for Grade 12 2025 is part of Grade 12 exam preparation. The chapters have been prepared according to the Grade 12 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Grade 12 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Probability - Mathematics for Grade 12 in English & Hindi are available as part of Grade 12 exam.
Download more important topics, notes, lectures and mock test series for Grade 12 Exam by signing up for free.
Mathematics for Grade 12
99 videos|124 docs|82 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup










