All Exams >
Mechanical Engineering >
General Aptitude for GATE >
All Questions
All questions of Series for Mechanical Engineering Exam
A bacteria gives birth to two new bacteria in each second and the life span of each bacteria is 5 seconds. The process of the reproduction is continuous until the death of the bacteria. initially there is one newly born bacteria at time t = 0, the find the total number of live bacteria just after 10 seconds :- a)310 /2
- b)310 - 210
- c)243 *(35 -1)
- d)310 -25
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A bacteria gives birth to two new bacteria in each second and the life span of each bacteria is 5 seconds. The process of the reproduction is continuous until the death of the bacteria. initially there is one newly born bacteria at time t = 0, the find the total number of live bacteria just after 10 seconds :
a)
310 /2
b)
310 - 210
c)
243 *(35 -1)
d)
310 -25
e)
None of these

|
Pallabi Deshpande answered |
Total number of bacteria after 10 seconds,
= 3^10 - 3^5
= 3^5 *(3^5 -1)
= 243 *(3^5 -1)
Since, just after 10 seconds all the bacterias (i.e. 3^5 ) are dead after living 5 seconds each.
After striking the floor, a rubber ball rebounds to 4/5th of the height from which it has fallen. Find the total distance that it travels before coming to rest if it has been gently dropped from a height of 120 metres.- a)540 m
- b)960 m
- c)1080 m
- d)1020 m
- e)1120 m
Correct answer is option 'C'. Can you explain this answer?
After striking the floor, a rubber ball rebounds to 4/5th of the height from which it has fallen. Find the total distance that it travels before coming to rest if it has been gently dropped from a height of 120 metres.
a)
540 m
b)
960 m
c)
1080 m
d)
1020 m
e)
1120 m
|
|
Vikas Choudhury answered |
The first drop is 120 metres. After this the ball will rise by 96 metres and fall by 96 metres. This process will continue in the form of infinite GP with common ratio 0.8 and first term 96. The required answer is given by the formula:
a/(1-r)
Now,
[{120/(1/5)}+{96/(1/5)}]
= 1080 m.
There are three numbers in an arithmetic progression. If the two larger numbers are increased by one, then the resulting numbers are prime. The product of these two primes and the smallest of the original numbers is 598. Find the sum of the three numbers.- a)45
- b)29
- c)42
- d)36
Correct answer is option 'C'. Can you explain this answer?
There are three numbers in an arithmetic progression. If the two larger numbers are increased by one, then the resulting numbers are prime. The product of these two primes and the smallest of the original numbers is 598. Find the sum of the three numbers.
a)
45
b)
29
c)
42
d)
36
|
|
Krishna Iyer answered |
Let three numbers are 2,12,22
Two larger numbers are increased by 1 : 13,23
New three numbers : 2,13,23
Product of these numbers is equal to 598.
=> 2*13*23 = 598
Sum of the three numbers = 2+13+23
= 36
Two larger numbers are increased by 1 : 13,23
New three numbers : 2,13,23
Product of these numbers is equal to 598.
=> 2*13*23 = 598
Sum of the three numbers = 2+13+23
= 36
In how many ways can we select three natural numbers out of the first 10 natural numbers so that they are in a geometric progression with the common ratio greater than 1?- a)2 ways
- b)3 ways
- c)4 ways
- d)5 ways
Correct answer is option 'B'. Can you explain this answer?
In how many ways can we select three natural numbers out of the first 10 natural numbers so that they are in a geometric progression with the common ratio greater than 1?
a)
2 ways
b)
3 ways
c)
4 ways
d)
5 ways

|
Kirti Kumar answered |
Make pair of three numbers. Only sequence with 2 and 3 as the common ratio is possible.
Find the 15th term of the sequence 20, 15, 10....- a)-45
- b)-55
- c)-50
- d)0
Correct answer is option 'C'. Can you explain this answer?
Find the 15th term of the sequence 20, 15, 10....
a)
-45
b)
-55
c)
-50
d)
0
|
|
Santosh Jaiswal answered |
Since above sequence is in A.P with common difference of -5 and first term 20.
Then applying formula of AP we get 15 term as
20 + (n-1) d.
15 term is 20 + (15-1) -5 i.e. -50
Then applying formula of AP we get 15 term as
20 + (n-1) d.
15 term is 20 + (15-1) -5 i.e. -50
Four angles of a quadrilateral are in G.P. Whose common ratio is an intiger. Two of the angles are acute while the other two are obtuse. The measure of the smallest angle of the quadrilateral is- a)12
- b)24
- c)36
- d)48
Correct answer is option 'B'. Can you explain this answer?
Four angles of a quadrilateral are in G.P. Whose common ratio is an intiger. Two of the angles are acute while the other two are obtuse. The measure of the smallest angle of the quadrilateral is
a)
12
b)
24
c)
36
d)
48
|
|
Kavya Saxena answered |
Let the angles be a, ar, ar 2, ar 3.
Sum of the angles = a ( r 4- 1 ) /r -1 = a ( r 2 + 1 ) ( r + 1 ) = 360
a< 90 , and ar< 90, Therefore, a ( 1 + r ) < 180, or ( r 2 + 1 ) > 2
Therefore, r is not equal to 1. Trying for r = 2 we get a = 24 Therefore, The angles are 24, 48, 96 and 192.
Sum of the angles = a ( r 4- 1 ) /r -1 = a ( r 2 + 1 ) ( r + 1 ) = 360
a< 90 , and ar< 90, Therefore, a ( 1 + r ) < 180, or ( r 2 + 1 ) > 2
Therefore, r is not equal to 1. Trying for r = 2 we get a = 24 Therefore, The angles are 24, 48, 96 and 192.
How many natural numbers between 300 to 500 are multiples of 7?- a)29
- b)28
- c)27
- d)30
Correct answer is option 'A'. Can you explain this answer?
How many natural numbers between 300 to 500 are multiples of 7?
a)
29
b)
28
c)
27
d)
30

|
Disha Sengupta answered |
The series will be 301, 308, …….. 497
Find the 15th term of an arithmetic progression whose first term is 2 and the common difference is 3
- a)45
- b)38
- c)44
- d)40
Correct answer is option 'C'. Can you explain this answer?
Find the 15th term of an arithmetic progression whose first term is 2 and the common difference is 3
a)
45
b)
38
c)
44
d)
40
|
|
Aisha Gupta answered |
Method to Solve :
A ( first term ) :- 2
d ( common difference ) :- 3
n = 15
To find nth term we have formula as
an = a + ( n - 1 )d
a15 = 2 + 14 � 3
a15 = 2 + 42
a15 = 44
d ( common difference ) :- 3
n = 15
To find nth term we have formula as
an = a + ( n - 1 )d
a15 = 2 + 14 � 3
a15 = 2 + 42
a15 = 44
How many terms are there in 20, 25, 30......... 140- a)22
- b)25
- c)23
- d)24
Correct answer is option 'B'. Can you explain this answer?
How many terms are there in 20, 25, 30......... 140
a)
22
b)
25
c)
23
d)
24
|
|
Anaya Patel answered |
Number of terms = { (1st term - last term) / common difference} + 1
= {(140-20) / 5} + 1
⇒ (120/5) + 1
⇒ 24 + 1 = 25.
= {(140-20) / 5} + 1
⇒ (120/5) + 1
⇒ 24 + 1 = 25.
Find the first term of an AP whose 8th and 12th terms are respectively 39 and 59.- a)5
- b)6
- c)4
- d)3
- e)7
Correct answer is 'C'. Can you explain this answer?
Find the first term of an AP whose 8th and 12th terms are respectively 39 and 59.
a)
5
b)
6
c)
4
d)
3
e)
7
|
|
Disha Dasgupta answered |
Solution: 1st Method:
8th term = a+7d = 39 ........... (i)
12th term = a+11d = 59 ........... (ii)
(i)-(ii);
Or, a+7d-a-11d = 39-59; Or, 4d = 20;
Or, d = 5;
Hence, a+7*5 = 39;
Thus, a = 39-35 = 4.
2nd Method (Thought Process):
8th term = 39;
And, 12th term = 59;
Here, we see that 20 is added to 8th term 39 to get 12th term 59 i.e. 4 times the common difference is added to 39.
So, CD = 20/4 = 5.
Hence, 7 times CD is added to 1st term to get 39. That means 4 is the 1st term of the AP.
8th term = a+7d = 39 ........... (i)
12th term = a+11d = 59 ........... (ii)
(i)-(ii);
Or, a+7d-a-11d = 39-59; Or, 4d = 20;
Or, d = 5;
Hence, a+7*5 = 39;
Thus, a = 39-35 = 4.
2nd Method (Thought Process):
8th term = 39;
And, 12th term = 59;
Here, we see that 20 is added to 8th term 39 to get 12th term 59 i.e. 4 times the common difference is added to 39.
So, CD = 20/4 = 5.
Hence, 7 times CD is added to 1st term to get 39. That means 4 is the 1st term of the AP.
How many terms are there in the AP 20, 25, 30,… 130.- a)22
- b)23
- c)21
- d)24
Correct answer is option 'B'. Can you explain this answer?
How many terms are there in the AP 20, 25, 30,… 130.
a)
22
b)
23
c)
21
d)
24

|
Arnav Rane answered |
In order to count the number of terms in the AP, use the short cut:
[(last term – first term)/ common difference] + 1. In this case it would become:
[(130 – 20)/5] +1 = 23. Option (b) is correct.
[(last term – first term)/ common difference] + 1. In this case it would become:
[(130 – 20)/5] +1 = 23. Option (b) is correct.
The sum of the first four terms of an AP is 28 and sum of the first eight terms of the same AP is 88.Find the sum of the first 16 terms of the AP?- a)346
- b)340
- c)304
- d)268
Correct answer is option 'C'. Can you explain this answer?
The sum of the first four terms of an AP is 28 and sum of the first eight terms of the same AP is 88.Find the sum of the first 16 terms of the AP?
a)
346
b)
340
c)
304
d)
268
|
|
Abhay Shah answered |
Think like this:
The average of the first 4 terms is 7, while the average of the first 8 terms must be 11.
Now visualize this :
The average of the first 4 terms is 7, while the average of the first 8 terms must be 11.
Now visualize this :
Hence, d = 4/2 = 2 [Note: understand this as a property of an A.P.]
Hence, the average of the 6th and 7th terms = 15 and the average of the 8th and 9th term = 19
But this (19) also represents the average of the 16 term A.P.
Hence, required answer = 16 × 19 = 304.
Hence, the average of the 6th and 7th terms = 15 and the average of the 8th and 9th term = 19
But this (19) also represents the average of the 16 term A.P.
Hence, required answer = 16 × 19 = 304.
The sum of 5 numbers in AP is 30 and the sum of their squares is 220. Which of the following is the third term?- a)5
- b)6
- c)8
- d)9
Correct answer is option 'B'. Can you explain this answer?
The sum of 5 numbers in AP is 30 and the sum of their squares is 220. Which of the following is the third term?
a)
5
b)
6
c)
8
d)
9

|
Isha Mukherjee answered |
Since the sum of 5 numbers in AP is 30, their average would be 6. The average of 5 terms in AP is
also equal to the value of the 3rd term (logic of the middle term of an AP). Hence, the third term’s
value would be 6. Option (b) is correct.
also equal to the value of the 3rd term (logic of the middle term of an AP). Hence, the third term’s
value would be 6. Option (b) is correct.
How many terms are there in the GP 5, 20, 80, 320........... 20480?- a)5
- b)6
- c)8
- d)9
- e)7
Correct answer is option 'E'. Can you explain this answer?
How many terms are there in the GP 5, 20, 80, 320........... 20480?
a)
5
b)
6
c)
8
d)
9
e)
7

|
Sameer Rane answered |
Common ratio, r = 20/5 = 4;
Last term or nth term of GP = ar^[n-1].
20480 = 5*[4^(n-1)];
Or, 4^(n-1) = 20480/5 = 4^8;
So, comparing the power,
Thus, n-1 = 8;
Or, n = 7;
Number of terms = 7.
A boy agrees to work at the rate of one rupee on the first day, two rupees on the second day, and four rupees on third day and so on. How much will the boy get if he started working on the 1st of February and finishes on the 20th of February?a) 2^20b) 2^20-1c) 2^19-1d) 2^19e) None of theseCorrect answer is option 'B'. Can you explain this answer?

|
Manoj Ghosh answered |
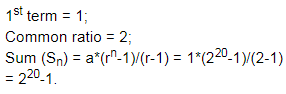
The sum of the first 100 numbers, 1 to 100 is divisible by- a)1,2,4,8
- b)2 and 4
- c)2
- d)none
Correct answer is option 'C'. Can you explain this answer?
The sum of the first 100 numbers, 1 to 100 is divisible by
a)
1,2,4,8
b)
2 and 4
c)
2
d)
none
|
|
Sagar Sharma answered |
The sum of the first 100 numbers, 1 to 100, can be calculated using the formula for the sum of an arithmetic series. The formula is given by:
S = (n/2)(a + l)
where S is the sum of the series, n is the number of terms, a is the first term, and l is the last term.
In this case, we have n = 100, a = 1, and l = 100. Plugging these values into the formula, we get:
S = (100/2)(1 + 100)
S = 50(101)
S = 5050
Therefore, the sum of the first 100 numbers is 5050.
To determine which options this sum is divisible by, we can perform the division:
5050 ÷ 1 = 5050
5050 ÷ 2 = 2525
5050 ÷ 4 = 1262.5
5050 ÷ 8 = 631.25
Therefore, the sum of the first 100 numbers is divisible by 1, 2, and 4.
Now, let's analyze the given options:
a) 1, 2, 4, 8: This option is incorrect because the sum of the first 100 numbers is not divisible by 8.
b) 2 and 4: This option is incorrect because the sum of the first 100 numbers is divisible by 1 and 4, but not just by 2.
c) 2: This option is correct because the sum of the first 100 numbers is divisible by 2.
d) None: This option is incorrect because the sum of the first 100 numbers is divisible by 2.
Therefore, the correct answer is option 'C', which states that the sum of the first 100 numbers is divisible by 2.
S = (n/2)(a + l)
where S is the sum of the series, n is the number of terms, a is the first term, and l is the last term.
In this case, we have n = 100, a = 1, and l = 100. Plugging these values into the formula, we get:
S = (100/2)(1 + 100)
S = 50(101)
S = 5050
Therefore, the sum of the first 100 numbers is 5050.
To determine which options this sum is divisible by, we can perform the division:
5050 ÷ 1 = 5050
5050 ÷ 2 = 2525
5050 ÷ 4 = 1262.5
5050 ÷ 8 = 631.25
Therefore, the sum of the first 100 numbers is divisible by 1, 2, and 4.
Now, let's analyze the given options:
a) 1, 2, 4, 8: This option is incorrect because the sum of the first 100 numbers is not divisible by 8.
b) 2 and 4: This option is incorrect because the sum of the first 100 numbers is divisible by 1 and 4, but not just by 2.
c) 2: This option is correct because the sum of the first 100 numbers is divisible by 2.
d) None: This option is incorrect because the sum of the first 100 numbers is divisible by 2.
Therefore, the correct answer is option 'C', which states that the sum of the first 100 numbers is divisible by 2.
If the roots of x3 - 12x2 + 39x - 28 = 0 are in an AP then their common difference is
- a)± 1
- b)± 2
- c)± 3
- d)± 4
Correct answer is option 'C'. Can you explain this answer?
If the roots of x3 - 12x2 + 39x - 28 = 0 are in an AP then their common difference is
a)
± 1
b)
± 2
c)
± 3
d)
± 4

|
Gowri Chakraborty answered |
Factorize the equation and we get ( x - 1 ) ( x - 4 ) ( x - 7 )
Explanation:
Given Equation: x³ - 12x² + 39x - 28 = 0
Roots in an AP:
Let the roots of the equation be a - d, a, a + d, where d is the common difference.
Sum of roots: = -b/a
Sum of roots = a - d + a + a + d = 3a
From the equation, we know that sum of roots = -(-12) = 12
Therefore, 3a = 12
a = 4
Product of roots: = -d/a
Product of roots = (a - d)(a)(a + d) = 4(a2 - d2) = 28
Substitute a = 4 in the equation:
42 - d² = 7
16 - d² = 7
d² = 9
d = ±3
Therefore, the correct answer is C: ±3.
Explanation:
Given Equation: x³ - 12x² + 39x - 28 = 0
Roots in an AP:
Let the roots of the equation be a - d, a, a + d, where d is the common difference.
Sum of roots: = -b/a
Sum of roots = a - d + a + a + d = 3a
From the equation, we know that sum of roots = -(-12) = 12
Therefore, 3a = 12
a = 4
Product of roots: = -d/a
Product of roots = (a - d)(a)(a + d) = 4(a2 - d2) = 28
Substitute a = 4 in the equation:
42 - d² = 7
16 - d² = 7
d² = 9
d = ±3
Therefore, the correct answer is C: ±3.
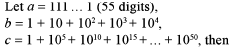
- a)a = b + c
- b)a = bc
- c)b = ac
- d)c = ab
Correct answer is option 'B'. Can you explain this answer?
a)
a = b + c
b)
a = bc
c)
b = ac
d)
c = ab

|
Hetal Purohit answered |
The question is wrong
The mid-points of the adjacent sides of a square are joined. Again the mid-points of the adjacent sides of the newly formed figure are connected and this process is repeated again and again. Calculate the sum of the areas of all such figures given that the diagonal of outermost square is 6√2cm.- a)35 cm2
- b)44 cm2
- c)72 cm2
- d)58 cm2
Correct answer is option 'C'. Can you explain this answer?
The mid-points of the adjacent sides of a square are joined. Again the mid-points of the adjacent sides of the newly formed figure are connected and this process is repeated again and again. Calculate the sum of the areas of all such figures given that the diagonal of outermost square is 6√2cm.
a)
35 cm2
b)
44 cm2
c)
72 cm2
d)
58 cm2

|
Hridoy Roy answered |
The side of the outermost square is 6 cm. Area of the square one in G.P with first term 36 and common ratio = 1/2
If a man saves ` 4 more each year than he did the year before and if he saves ` 20 in the first year,after how many years will his savings be more than ` 1000 altogether?- a)19 years
- b)20 years
- c)21years
- d)18 years
Correct answer is option 'A'. Can you explain this answer?
If a man saves ` 4 more each year than he did the year before and if he saves ` 20 in the first year,after how many years will his savings be more than ` 1000 altogether?
a)
19 years
b)
20 years
c)
21years
d)
18 years
|
|
Aarav Sharma answered |
Solution:
To solve this problem, we can use the formula for the sum of an arithmetic progression:
Sn = n/2[2a + (n-1)d]
where Sn is the sum of the first n terms, a is the first term, d is the common difference, and n is the number of terms.
We know that the man saves 4 more each year than he did the year before, so the common difference is d = 4.
We also know that he saves `20 in the first year, so the first term is a = 20.
We want to find out after how many years his savings will be more than `1000 altogether, so we want to find the value of n that satisfies the inequality Sn > 1000.
Substituting the values that we know into the formula, we get:
Sn = n/2[2a + (n-1)d]
Sn = n/2[2(20) + (n-1)(4)]
Sn = n/2[40 + 4n - 4]
Sn = n/2[36 + 4n]
Sn = 18n + 2n^2
Now we can set up the inequality:
Sn > 1000
18n + 2n^2 > 1000
2n^2 + 18n - 1000 > 0
We can solve this quadratic inequality by factoring or using the quadratic formula, but we can also estimate the value of n by looking at the options given.
Option A is 19 years, which means that the man's savings would be:
S19 = 19/2[2(20) + (19-1)(4)]
S19 = 19/2[40 + 72]
S19 = 19/2[112]
S19 = 1064
This is more than `1000, so option A is the correct answer.
We can also check the other options:
Option B: S20 = 20/2[2(20) + (20-1)(4)] = 1120
Option C: S21 = 21/2[2(20) + (21-1)(4)] = 1204
Option D: S18 = 18/2[2(20) + (18-1)(4)] = 988
Therefore, the correct answer is option A, 19 years.
To solve this problem, we can use the formula for the sum of an arithmetic progression:
Sn = n/2[2a + (n-1)d]
where Sn is the sum of the first n terms, a is the first term, d is the common difference, and n is the number of terms.
We know that the man saves 4 more each year than he did the year before, so the common difference is d = 4.
We also know that he saves `20 in the first year, so the first term is a = 20.
We want to find out after how many years his savings will be more than `1000 altogether, so we want to find the value of n that satisfies the inequality Sn > 1000.
Substituting the values that we know into the formula, we get:
Sn = n/2[2a + (n-1)d]
Sn = n/2[2(20) + (n-1)(4)]
Sn = n/2[40 + 4n - 4]
Sn = n/2[36 + 4n]
Sn = 18n + 2n^2
Now we can set up the inequality:
Sn > 1000
18n + 2n^2 > 1000
2n^2 + 18n - 1000 > 0
We can solve this quadratic inequality by factoring or using the quadratic formula, but we can also estimate the value of n by looking at the options given.
Option A is 19 years, which means that the man's savings would be:
S19 = 19/2[2(20) + (19-1)(4)]
S19 = 19/2[40 + 72]
S19 = 19/2[112]
S19 = 1064
This is more than `1000, so option A is the correct answer.
We can also check the other options:
Option B: S20 = 20/2[2(20) + (20-1)(4)] = 1120
Option C: S21 = 21/2[2(20) + (21-1)(4)] = 1204
Option D: S18 = 18/2[2(20) + (18-1)(4)] = 988
Therefore, the correct answer is option A, 19 years.
If Sn denotes the sum of the first n terms in an Arithmetic Progression and S1: S4 = 1: 10Then the ratio of first term to fourth term is:- a)1 : 3
- b)2 : 3
- c)1 : 4
- d)1 : 5
Correct answer is option 'C'. Can you explain this answer?
If Sn denotes the sum of the first n terms in an Arithmetic Progression and S1: S4 = 1: 10
Then the ratio of first term to fourth term is:
a)
1 : 3
b)
2 : 3
c)
1 : 4
d)
1 : 5

|
Gowri Chakraborty answered |
Use Sn = (n/2)[ 2a + (n-1)d] and Tn = a + (n – 1) d
S1/S4 = 1/10 = a/ (4/2) [2a + 3d]
6a = 6d or a = d
Therefore T1/T4 = a/ (a+ 3d) = a/4a = 1/4
If a geometric mean of two non-negative numbers is equal to their harmonic mean, then which of the following is necessarily true?I. One of the numbers is zero.II. Both the numbers are equal.III. One of the numbers is one.- a)I and III only
- b)Either I or III
- c)III only
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
If a geometric mean of two non-negative numbers is equal to their harmonic mean, then which of the following is necessarily true?I. One of the numbers is zero.II. Both the numbers are equal.III. One of the numbers is one.
a)
I and III only
b)
Either I or III
c)
III only
d)
None of these

|
Hridoy Roy answered |
A series in which any term is the sum of the preceding two terms is called a Fibonacci series. The first two terms are given initially and together they determine the entire series. If the difference of the squares of the ninth and the eighth terms of a Fibonacci series is 715 then, what is the 12th term of that series?- a)157
- b)142
- c)144
- d)Cannot be determined
Correct answer is option 'C'. Can you explain this answer?
A series in which any term is the sum of the preceding two terms is called a Fibonacci series. The first two terms are given initially and together they determine the entire series. If the difference of the squares of the ninth and the eighth terms of a Fibonacci series is 715 then, what is the 12th term of that series?
a)
157
b)
142
c)
144
d)
Cannot be determined

|
Asha Basak answered |
The series is like 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144...
The difference is 715 and the 12th term is 144.
The difference is 715 and the 12th term is 144.
A sum of money kept in a bank amounts to ` 1240 in 4 years and ` 1600 in 10 years at simpleInterest. Find the sum.- a)` 800
- b)` 900
- c)` 1150
- d)` 1000
Correct answer is option 'D'. Can you explain this answer?
A sum of money kept in a bank amounts to ` 1240 in 4 years and ` 1600 in 10 years at simpleInterest. Find the sum.
a)
` 800
b)
` 900
c)
` 1150
d)
` 1000

|
Debanshi Sarkar answered |
The difference between the amounts at the end of 4 years and 10 years will be the simple interest
on the initial capital for 6 years.
Hence, 360/6 = 60 =(simple interest.)
Also, the Simple Interest for 4 years when added to the sum gives 1240 as the amount.
Hence, the original sum must be 1000.
on the initial capital for 6 years.
Hence, 360/6 = 60 =(simple interest.)
Also, the Simple Interest for 4 years when added to the sum gives 1240 as the amount.
Hence, the original sum must be 1000.
The first term of an AP = the common ratio of a GP and the first term of the GP = common difference of the AP. If the sum of the first two terms of the GP is equal to the sum of the first 2 terms of the AP, then the ratio of the first term of the GP to the first term of an AP is- a)>1
- b)Independent of first term of AP
- c)Independent of first term of GP
- d)< 1
Correct answer is option 'C'. Can you explain this answer?
The first term of an AP = the common ratio of a GP and the first term of the GP = common difference of the AP. If the sum of the first two terms of the GP is equal to the sum of the first 2 terms of the AP, then the ratio of the first term of the GP to the first term of an AP is
a)
>1
b)
Independent of first term of AP
c)
Independent of first term of GP
d)
< 1

|
Hridoy Roy answered |
This is independent of the first term of GP.
The sum of the three numbers in A.P is 21 and the product of their extremes is 45. Find the numbers.- a)9, 7 and 5
- b)5, 7 and 9
- c)Both (1) and (2)
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The sum of the three numbers in A.P is 21 and the product of their extremes is 45. Find the numbers.
a)
9, 7 and 5
b)
5, 7 and 9
c)
Both (1) and (2)
d)
None of these

|
Arya Roy answered |
The correct answer is c.
Let the numbers are be a - d, a, a + d
Let the numbers are be a - d, a, a + d
Then a-d+a+a+d= 21
3a = 21
a = 7
and (a - d) (a + d) = 45
a^2 - d^2 = 45
d^2=4
d = 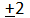
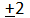
Hence, the numbers are 5, 7 and 9 when d = 2 and 9, 7 and 5 when d = -2. In both the cases numbers are the same.
There is an AP 1, 3, 5…. Which term of this AP is 55?- a)27th
- b)26th
- c)25th
- d)28th
Correct answer is option 'D'. Can you explain this answer?
There is an AP 1, 3, 5…. Which term of this AP is 55?
a)
27th
b)
26th
c)
25th
d)
28th

|
Disha Sengupta answered |
The number of terms in a series are found by:
How many terms are there in the GP 5, 20, 80, 320,… 20480?- a)6
- b)5
- c)7
- d)8
Correct answer is option 'C'. Can you explain this answer?
How many terms are there in the GP 5, 20, 80, 320,… 20480?
a)
6
b)
5
c)
7
d)
8

|
Saanvi Sarkar answered |
The series would be 5, 20, 80, 320, 1280, 5120, 20480. Thus, there are a total of 7 terms in the
series. Option (c) is correct.
series. Option (c) is correct.
Find the lowest number in an AP such that the sum of all the terms is 105 and greatest term is 6 times the least.- a)5
- b)10
- c)15
- d)(a), (b) & (c)
Correct answer is option 'D'. Can you explain this answer?
Find the lowest number in an AP such that the sum of all the terms is 105 and greatest term is 6 times the least.
a)
5
b)
10
c)
15
d)
(a), (b) & (c)

|
Akash Sengupta answered |
Trying Option (a),
We get least term 5 and largest term 30 (since the largest term is 6 times the least term).
The average of the A.P becomes (5 + 30)/2 = 17.5
Thus, 17.5 × n = 105 gives us:
to get a total of 105 we need n = 6 i.e. 6 terms in this A.P. That means the A.P. should look like:
5, _ , _ , _, _, 30.
It can be easily seen that the common difference should be 5. The A.P, 5, 10, 15, 20, 25, 30 fits the
situation.
The same process used for option (b) gives us the A.P. 10, 35, 60. (10 + 35 + 60 = 105) and in the
third option 15, 90 (15 + 90 = 105).
Hence, all the three options are correct.
We get least term 5 and largest term 30 (since the largest term is 6 times the least term).
The average of the A.P becomes (5 + 30)/2 = 17.5
Thus, 17.5 × n = 105 gives us:
to get a total of 105 we need n = 6 i.e. 6 terms in this A.P. That means the A.P. should look like:
5, _ , _ , _, _, 30.
It can be easily seen that the common difference should be 5. The A.P, 5, 10, 15, 20, 25, 30 fits the
situation.
The same process used for option (b) gives us the A.P. 10, 35, 60. (10 + 35 + 60 = 105) and in the
third option 15, 90 (15 + 90 = 105).
Hence, all the three options are correct.
A group of friends have some money which was in an increasing GP. The total money with the first and the last friend was Rs 66 and the product of the money that the second friend had and that the last but one friend had was Rs 128. If the total money with all of them together was Rs 126, then how many friends were there?- a)6
- b)5
- c)3
- d)Cannot be determined
Correct answer is option 'A'. Can you explain this answer?
A group of friends have some money which was in an increasing GP. The total money with the first and the last friend was Rs 66 and the product of the money that the second friend had and that the last but one friend had was Rs 128. If the total money with all of them together was Rs 126, then how many friends were there?
a)
6
b)
5
c)
3
d)
Cannot be determined

|
Prasenjit Basu answered |
The sum of money with the first and the last friend = 66. This can be used as a hint. Let us assume the first friend was having Rs 2 and the last friend was having Rs 64. So, the money can be in the sequence 2, 4, 8, 16, 32, 64. It satisfies the given conditions. Alternatively, this can be done by using the formula for tn of GP also.
Given that (m +1l)th, (n + 1)th and (r +1l)th term of an AP are in GP and m , n , r are in HP, then find the ratio of the first term of the AP to its common difference in terms of n.- a)2 : n
- b)n : 2
- c)2n : 3
- d)3 : 4n
Correct answer is option 'B'. Can you explain this answer?
Given that (m +1l)th, (n + 1)th and (r +1l)th term of an AP are in GP and m , n , r are in HP, then find the ratio of the first term of the AP to its common difference in terms of n.
a)
2 : n
b)
n : 2
c)
2n : 3
d)
3 : 4n

|
Mahesh Mehta answered |
Since the (m + 1)th, (n + 1)th and (r + 1)th term of an A.P are in G.P. so,
A GP consists of 1000 terms. The sum of the terms occupying the odd places is Pj and the sum of the terms occupying the even places is P2. Find the common ratio of this GP.
- a)P2/P1
- b) P1/P2
- c)(P2 - P1)/P1
- d) (P2+ P1)/P2
Correct answer is option 'A'. Can you explain this answer?
A GP consists of 1000 terms. The sum of the terms occupying the odd places is Pj and the sum of the terms occupying the even places is P2. Find the common ratio of this GP.
a)
P2/P1
b)
P1/P2
c)
(P2 - P1)/P1
d)
(P2+ P1)/P2

|
Debanshi Reddy answered |

The least value of n for which the sum of the series 5 + 8 + 11… n terms is not less than 670 is- a)20
- b)19
- c)22
- d)21
Correct answer is option 'A'. Can you explain this answer?
The least value of n for which the sum of the series 5 + 8 + 11… n terms is not less than 670 is
a)
20
b)
19
c)
22
d)
21

|
Isha Mukherjee answered |
Solve this question through trial and error by using values of n from the options:
For 19 terms, the series would be 5 + 8 + 11 + …. + 59 which would give us a sum for the series
as 19 × 32 = 608. The next term (20th term of the series) would be 62. Thus, 608 + 62 = 670
would be the sum to 20 terms. It can thus be concluded that for 20 terms the value of the sum of the
series is not less than 670. Option (a) is correct.
For 19 terms, the series would be 5 + 8 + 11 + …. + 59 which would give us a sum for the series
as 19 × 32 = 608. The next term (20th term of the series) would be 62. Thus, 608 + 62 = 670
would be the sum to 20 terms. It can thus be concluded that for 20 terms the value of the sum of the
series is not less than 670. Option (a) is correct.
Find the 1st term of an AP whose 8th and 12th terms are respectively 39 and 59.- a)5
- b)6
- c)4
- d)3
Correct answer is option 'C'. Can you explain this answer?
Find the 1st term of an AP whose 8th and 12th terms are respectively 39 and 59.
a)
5
b)
6
c)
4
d)
3

|
Isha Mukherjee answered |
Since the 8th and the 12th terms of the AP are given as 39 and 59 respectively, the difference
between the two terms would equal 4 times the common difference. Thus we get 4d = 59 – 39 =
20. This gives us d = 5. Also, the 8th term in the AP is represented by a + 7d, we get:
a + 7d = 39 Æ a + 7 × 5 = 39 Æ a = 4. Option (c) is correct.
between the two terms would equal 4 times the common difference. Thus we get 4d = 59 – 39 =
20. This gives us d = 5. Also, the 8th term in the AP is represented by a + 7d, we get:
a + 7d = 39 Æ a + 7 × 5 = 39 Æ a = 4. Option (c) is correct.
If the fifth term of a GP is 81 and first term is 16, what will be the 4th term of the GP?- a)36
- b)18
- c)54
- d)24
- e)27
Correct answer is option 'C'. Can you explain this answer?
If the fifth term of a GP is 81 and first term is 16, what will be the 4th term of the GP?
a)
36
b)
18
c)
54
d)
24
e)
27

|
Gowri Chakraborty answered |
5th term of GP = ar5-1 = 16*r4 = 81;
Or, r = (81/16)1/4 = 3/2;
4th term of GP = ar4-1 = 16*(3/2)3 = 54.
The sum of three numbers in a GP is 14 and the sum of their squares is 84. Find the largestnumber.- a)8
- b)6
- c)4
- d)12
Correct answer is option 'A'. Can you explain this answer?
The sum of three numbers in a GP is 14 and the sum of their squares is 84. Find the largestnumber.
a)
8
b)
6
c)
4
d)
12

|
Krithika Sengupta answered |
Visualising the squares below 84, we can see that the only way to get the sum of 3 squares as 84
is: 22 + 42 + 82 = 4 + 16 + 64. The largest number is 8. Option (a) is correct.
is: 22 + 42 + 82 = 4 + 16 + 64. The largest number is 8. Option (a) is correct.
The sum of the first 16 terms of an AP whose first term and third term are 5 and 15 respectively is- a)600
- b)765
- c)640
- d)680
- e)690
Correct answer is option 'D'. Can you explain this answer?
The sum of the first 16 terms of an AP whose first term and third term are 5 and 15 respectively is
a)
600
b)
765
c)
640
d)
680
e)
690

|
Arya Roy answered |
1st Method:
1st term = 5;
3rd term = 15;
Then, d = 5;
16th term = a+15d = 5+15*5 = 80;
Sum = {n*(a+L)/2} = {No. of terms*(first term + last term)/2}.
Thus, sum = {16*(5+80)/2} = 680.
2nd Method (Thought Process):
Sum = Number of terms * Average of that AP.
Sum = 16* {(5+80)/2} = 16*45 = 680.
If(12+22+32+…..+102)=385,then the value of (22+42+62 + …+202) is :
- a)770
- b)1155
- c)1540
- d)(385*385)
Correct answer is option 'C'. Can you explain this answer?
If(12+22+32+…..+102)=385,then the value of (22+42+62 + …+202) is :
a)
770
b)
1155
c)
1540
d)
(385*385)

|
Gowri Chakraborty answered |
(1^2+2^2+3^2+....10^2)=385
(2^2+4^2+6^2+....+20^2)=2^2(1^2+2^2+ 3^2+....+10^2 )
=4(385)
=1540
If the fifth term of a GP is 81 and first term is 16, what will be the 4th term of the GP?- a)36
- b)18
- c)54
- d)24
Correct answer is option 'C'. Can you explain this answer?
If the fifth term of a GP is 81 and first term is 16, what will be the 4th term of the GP?
a)
36
b)
18
c)
54
d)
24

|
Saanvi Sarkar answered |
16r4 = 81 Æ r4 = 81/16 Æ r = 3/2. Thus, 4th term = ar3 = 16 × (3/2)3 = 54. Option (c) is correct
If a, b and c are positive integers, then find the product of (a + b) (b + c) (c + a).- a)> 8 abc
- b)<8 abc
- c)=8 abc
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If a, b and c are positive integers, then find the product of (a + b) (b + c) (c + a).
a)
> 8 abc
b)
<8 abc
c)
=8 abc
d)
None of these

|
Pranavi Dey answered |
Put a= l, b = 2 c = 3 and check through options.
What is the sum of the first 15 terms of an A.P whose 11 th and 7 th terms are 5.25 and 3.25 respectively- a)56.25
- b)60
- c)52.5
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
What is the sum of the first 15 terms of an A.P whose 11 th and 7 th terms are 5.25 and 3.25 respectively
a)
56.25
b)
60
c)
52.5
d)
none of these

|
Ishani Rane answered |
a +10d = 5.25, a+6d = 3.25, 4d = 2, d = 1/4
a +5 = 5.25, a = 0.25 = 1/4, s 15 = 15/2 ( 2 * 1/4 + 14 * 1/4 )
= 15/2 (1/2 +14/2 ) = 15/2 *15/2 =225/ 4 = 56.25
In an arithmetic series consisting of 51 terms, the sum of the first three terms is 65 and the sum of the middle three terms is 129. What is the first term and the common difference of the series?- a)64, 9/8
- b)32, 8/9
- c)187/9, 8/9
- d)72, 9/8
Correct answer is option 'C'. Can you explain this answer?
In an arithmetic series consisting of 51 terms, the sum of the first three terms is 65 and the sum of the middle three terms is 129. What is the first term and the common difference of the series?
a)
64, 9/8
b)
32, 8/9
c)
187/9, 8/9
d)
72, 9/8

|
Manoj Ghosh answered |
Given a + (a + d) + (a + 2d)= 65
=> 3a + 3d =65…. (1)
The middle terms are 25th , 26th and 27th terms
=> a + 24d + a + 25d + a + 26d = 129
=> 3a + 75d
129 ….(2)
From (1) and (2) d= 8/9 =>a= 187/9
The 4th and 10th term of an GP are 1/3 and 243 respectively. Find the 2nd term.- a)3
- b)1
- c)1/27
- d)1/9
Correct answer is option 'C'. Can you explain this answer?
The 4th and 10th term of an GP are 1/3 and 243 respectively. Find the 2nd term.
a)
3
b)
1
c)
1/27
d)
1/9
|
|
Aarav Sharma answered |
Given, 4th term = 1/3 and 10th term = 243.
Let the first term be 'a' and the common ratio be 'r'.
We know that the nth term of a GP is given by ar^(n-1).
So, we can write:
ar^3 = 1/3 ...(1)
ar^9 = 243 ...(2)
Dividing equation (2) by equation (1), we get:
r^6 = 729
r = 3
Substituting this value of r in equation (1), we get:
a(3^3) = 1/3
a = 1/27
Therefore, the first term of the GP is 1/27 and the second term can be found using the formula:
ar = (1/27)*3 = 1/9
Hence, the correct answer is option (c) 1/27.
Let the first term be 'a' and the common ratio be 'r'.
We know that the nth term of a GP is given by ar^(n-1).
So, we can write:
ar^3 = 1/3 ...(1)
ar^9 = 243 ...(2)
Dividing equation (2) by equation (1), we get:
r^6 = 729
r = 3
Substituting this value of r in equation (1), we get:
a(3^3) = 1/3
a = 1/27
Therefore, the first term of the GP is 1/27 and the second term can be found using the formula:
ar = (1/27)*3 = 1/9
Hence, the correct answer is option (c) 1/27.
The AM o f two given positive numbers is 2. I f the larger number is increased by 1, the GM of the numbers becomes equal to the AM of the given numbers. Then the HM of the given numbers is- a)3/2
- b)2/3
- c)1/2
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The AM o f two given positive numbers is 2. I f the larger number is increased by 1, the GM of the numbers becomes equal to the AM of the given numbers. Then the HM of the given numbers is
a)
3/2
b)
2/3
c)
1/2
d)
None of these

|
Mahesh Mehta answered |
Take two numbers such that their AM is 2 like 1 and 3. And go according to the conditions given in the question.
The sum of the first 16 terms of an AP whose first term and third term are 5 and 15 respectively is- a)600
- b)765
- c)640
- d)680
Correct answer is option 'D'. Can you explain this answer?
The sum of the first 16 terms of an AP whose first term and third term are 5 and 15 respectively is
a)
600
b)
765
c)
640
d)
680

|
Akash Sengupta answered |
a = 5, a + 2d = 15 means d = 5. The 16th term would be a + 15d = 5 + 75 = 80. The sum of the
series would be given by:
[16/2] × [5 + 80] = 16 × 42.5 = 680. Option (d) is correct.
series would be given by:
[16/2] × [5 + 80] = 16 × 42.5 = 680. Option (d) is correct.
Chapter doubts & questions for Series - General Aptitude for GATE 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Series - General Aptitude for GATE in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
General Aptitude for GATE
194 videos|167 docs|152 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup












