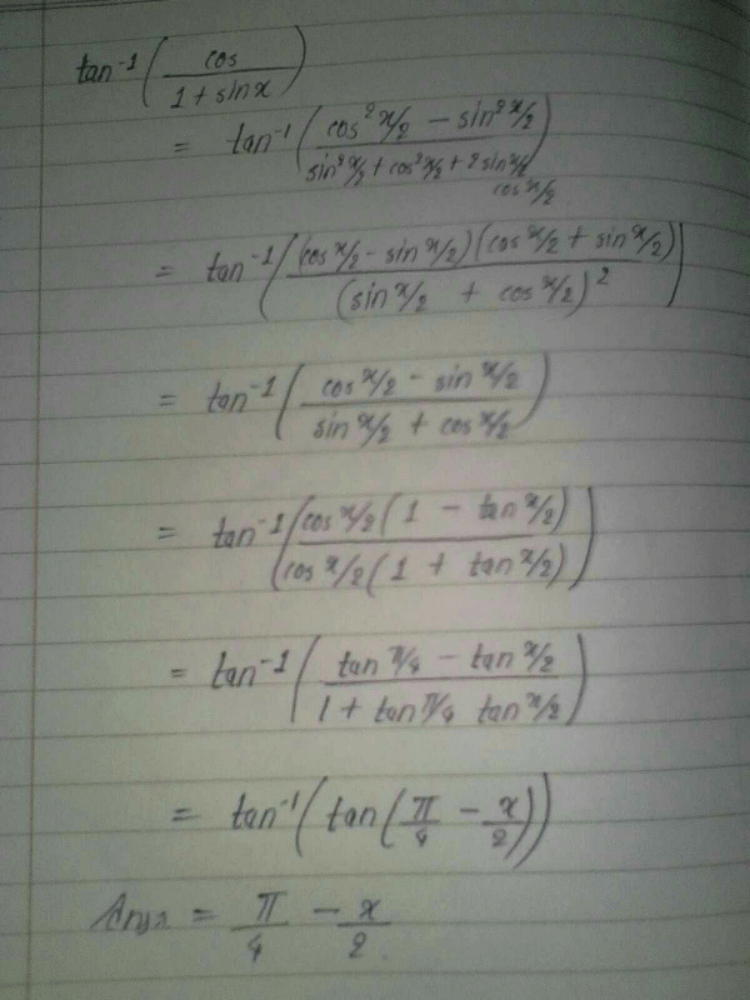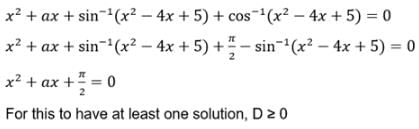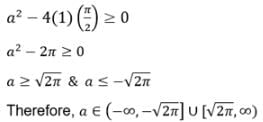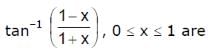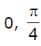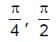All Exams >
JEE >
Chapter-wise Tests for JEE Main & Advanced >
All Questions
All questions of Inverse Trigonometric Functions for JEE Exam
Can you explain the answer of this question below: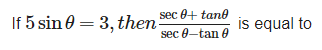
- A:
4
- B:
1/4
- C:
2
- D:
none of these.
The answer is a.
4
1/4
2
none of these.

|
Divey Sethi answered |
sin θ is 3/5.
on simplifying:
(secθ + tanθ)/(secθ - tanθ)
We get, (1+sin θ)/(1-sin θ)
=(1+3/5)/(1-3/5)
=(8/2)
=4
on simplifying:
(secθ + tanθ)/(secθ - tanθ)
We get, (1+sin θ)/(1-sin θ)
=(1+3/5)/(1-3/5)
=(8/2)
=4
If xy + yz + zx = 1, then, tan–1x + tan–1y + tan–1z =- a)π
- b)π/2
- c)1
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
If xy + yz + zx = 1, then, tan–1x + tan–1y + tan–1z =
a)
π
b)
π/2
c)
1
d)
None of these
|
|
Aryan Khanna answered |
If xy + yz + zx = 1,
Then, 1 – xy – yz – zx = 0 ----- eqn1
tan-1x + tan-1y = tan-1((x+y)/(1-xy))
tan-1x + tan-1y + tan-1z = tan-1((x+y)/(1-xy)) + tan-1z
= tan-1( ( ((x+y)/(1-xy)) + z ) / (1 – ((x+y)*z)/(1+xy)))
= tan-1((x+y+z-xyz)/(1-xy-yz-zx))
= tan-1((x+y+z-xyz)/0) [From eqn1]
= π/2
Then, 1 – xy – yz – zx = 0 ----- eqn1
tan-1x + tan-1y = tan-1((x+y)/(1-xy))
tan-1x + tan-1y + tan-1z = tan-1((x+y)/(1-xy)) + tan-1z
= tan-1( ( ((x+y)/(1-xy)) + z ) / (1 – ((x+y)*z)/(1+xy)))
= tan-1((x+y+z-xyz)/(1-xy-yz-zx))
= tan-1((x+y+z-xyz)/0) [From eqn1]
= π/2
Value of 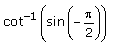
- a)
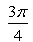
- b)
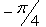
- c)-1
- d)
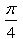
Correct answer is option 'A'. Can you explain this answer?
Value of 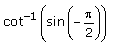
a)
b)
c)
-1
d)
|
|
Aravind Rane answered |
Cot-1[sin(-90)] =cot-1(-1) =π-cot-1(1) =π-π/4 =3π/4
The simplest form of 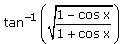 for x > 0 is …
for x > 0 is …- a)x
- b)-x/2
- c)2x
- d)x/2
Correct answer is option 'D'. Can you explain this answer?
The simplest form of 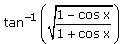 for x > 0 is …
for x > 0 is …
a)
x
b)
-x/2
c)
2x
d)
x/2
|
|
Mira Joshi answered |
tan-1(1-cosx/1+cosx)½
= tan-1{(2sin2 x/2) / (2cos2 x/2)}½
= tan-1{(2sin2 x/2) / (2cos2 x/2)}
= tan-1(tan x/2)
= x/2
= tan-1{(2sin2 x/2) / (2cos2 x/2)}½
= tan-1{(2sin2 x/2) / (2cos2 x/2)}
= tan-1(tan x/2)
= x/2
Evaluate sin(3 sin–10.4)a)0.56b)0.31c)0.64d)0.9Correct answer is 'D'. Can you explain this answer?
|
|
Subhankar Choudhary answered |
3sin^-1(x) = sin^-1(3x - 4x^3) when -1/2<=x<=1/2
Definitely 0.4 comes in this range of x and so
Definitely 0.4 comes in this range of x and so
3sin^-1(0.4) = sin^-1[3*0.4 - 4*0.4^3]
3sin^-1(0.4) = sin^-1[1.2 - 4*0.064]
3sin^-1(0.4) = sin^-1[1.2 - 0.256]
3sin^-1(0.4) = sin^-1[0.944]
3sin^-1(0.4) = sin^-1[1.2 - 4*0.064]
3sin^-1(0.4) = sin^-1[1.2 - 0.256]
3sin^-1(0.4) = sin^-1[0.944]
Finally , sin(3sin^-1(0.4)) = sin{sin^-1(0.944)} = 0.944
The maximum value of sin x + cos x is- a)1
- b)2
- c)√2
- d)
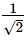
Correct answer is option 'C'. Can you explain this answer?
The maximum value of sin x + cos x is
a)
1
b)
2
c)
√2
d)
|
|
Shreya Gupta answered |
sinx + cosx=sinx + sin(90-x)=2sin{(x+90-x)/2}cos{(... morex-90+x)/2}using the formula
The value of tan–1(1) + cos–1(–1/2) + sin–1(–1/2) is equal to -
- a)3π/4
- b)5π/12
- c)π/4
- d)13π/12
Correct answer is option 'C'. Can you explain this answer?
The value of tan–1(1) + cos–1(–1/2) + sin–1(–1/2) is equal to -
a)
3π/4
b)
5π/12
c)
π/4
d)
13π/12

|
Bs Academy answered |
Since, here we are considering only principle solutions
tan-1(1) = π/4
cos-1(-1/2) = 2π/3
sin-1(-1/2) = -π/6
Sol : π/4 +2π/3 -π/6
: 3π/4
Can you explain the answer of this question below:Value of 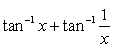 is
is
- A:
π/2
- B:
1/x
- C:
x
- D:
π
The answer is a.
Value of is
π/2
1/x
x
π

|
Case Studies answered |
Tan-1(1/x) = cot-1(x) and tan-1(x) + cot-1(x) =90degree
If sin-1 x + sin-1 y + sin-1z = 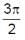 , then
, then - a)

- b)x22 + y42 + z62 - x220- y420 - z620 = 0
- c)x50 + y25 + z5 = 0
- d)
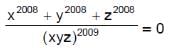
Correct answer is option 'A,B'. Can you explain this answer?
If sin-1 x + sin-1 y + sin-1z = 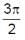 , then
, then
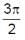 , then
, then a)

b)
x22 + y42 + z62 - x220- y420 - z620 = 0
c)
x50 + y25 + z5 = 0
d)
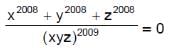

|
Vikash Yadav answered |
Put x = y = z = 1
This will satisfy the eqns
Can you explain the answer of this question below:Domain of f(x) = cos–1 x + cot–1 x + cosec–1 x is
- A:
[–1, 1]
- B:
R
- C:
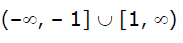
- D:
{–1, 1}
The answer is D.
Domain of f(x) = cos–1 x + cot–1 x + cosec–1 x is
[–1, 1]
R
{–1, 1}
|
|
Suresh Iyer answered |
Domain of cos-1x = [-1 ,1]
Domain of cot-1x = R
Domain of cosec-1x = R - (-1,1)
So taking intersection of domains of all three we have only {-1 ,1}
As cos-1x is confined between [-1,1] and cosec-1x is not defined between (-1,1), So only -1 and 1 are left.
Domain of cot-1x = R
Domain of cosec-1x = R - (-1,1)
So taking intersection of domains of all three we have only {-1 ,1}
As cos-1x is confined between [-1,1] and cosec-1x is not defined between (-1,1), So only -1 and 1 are left.
The value ofcos150−sin150 is- a)

- b)

- c)0
- d)

Correct answer is option 'D'. Can you explain this answer?
The value ofcos150−sin150 is
a)
b)
c)
0
d)

|
Poojan Angiras answered |
Heyy!!! write cos 15 and sin 15 as cos(60-45) and sin(60-45) respectively.And then apply formula of cos(a+b) and sin(a+b).Proceed as the question u will get correct answer :-):-)^_^
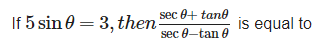
- a)4
- b)1/4
- c)2
- d)none of these.
Correct answer is option 'A'. Can you explain this answer?
a)
4
b)
1/4
c)
2
d)
none of these.
|
|
Krishna Iyer answered |
sin θ is 3/5.
on simplifying:
(secθ + tanθ)/(secθ - tanθ)
We get, (1+sin θ)/(1-sin θ)
=(1+3/5)/(1-3/5)
=(8/2)
=4
on simplifying:
(secθ + tanθ)/(secθ - tanθ)
We get, (1+sin θ)/(1-sin θ)
=(1+3/5)/(1-3/5)
=(8/2)
=4
Evaluate :cos (tan–1 x)- a)
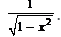
- b)
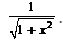
- c)
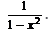
- d)
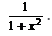
Correct answer is option 'B'. Can you explain this answer?
Evaluate :cos (tan–1 x)
a)
b)
c)
d)

|
Ishita Kaushik answered |
In this question you have to convert tan into cos by Pythagoras theorm and the you will get the answer ...I am not able to attach the picture of the answer but I think I have explained it well if you have any query in question you can ask
If ab + bc + ca = 0, then find 1/a2-bc + 1/b2 – ca + 1/c2- ab- a)π
- b)0
- c)-1
- d)2π
Correct answer is option 'B'. Can you explain this answer?
If ab + bc + ca = 0, then find 1/a2-bc + 1/b2 – ca + 1/c2- ab
a)
π
b)
0
c)
-1
d)
2π
|
|
Preeti Iyer answered |
Given ab+bc+ca=0 and asked to find value 1/(a2-bc ... more) + 1/(c2-ab) + 1/(a2-bc)Put -ac = ab + bc ; -ab = ac+ bc and -bc =ab +
If x< 0 then value of tan-1(x) + tan-1 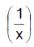 is equal to
is equal to - a)π/2
- b)–π/2
- c)0
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If x< 0 then value of tan-1(x) + tan-1 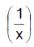 is equal to
is equal to
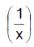 is equal to
is equal to a)
π/2
b)
–π/2
c)
0
d)
None of these
|
|
Lavanya Menon answered |
Let y = tan-1 x
x = tan y
⇒ 1/x = 1/tan y
⇒ 1/x = cot y
⇒ 1/x = tan(π/2 - y)
⇒ π/2 - y = tan-1 (1/x)
As we know that y = tan-1 x
π/2 = tan-1(x) + tan-1(1/x)
x = tan y
⇒ 1/x = 1/tan y
⇒ 1/x = cot y
⇒ 1/x = tan(π/2 - y)
⇒ π/2 - y = tan-1 (1/x)
As we know that y = tan-1 x
π/2 = tan-1(x) + tan-1(1/x)
If sin A + cos A = 1, then sin 2A is equal to- a)2
- b)1/2
- c)0
- d)1
Correct answer is option 'C'. Can you explain this answer?
If sin A + cos A = 1, then sin 2A is equal to
a)
2
b)
1/2
c)
0
d)
1
|
|
Suresh Iyer answered |
(Sin A + Cos A)2 = sin2A + cos2A + 2 sinAcosA
1 = 1 + Sin 2A
so, Sin 2A = 0
Hence A = 0
Range of f(x) = sin–1 x + tan–1 x + sec–1 x is- a)
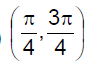
- b)

- c)
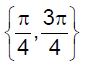
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Range of f(x) = sin–1 x + tan–1 x + sec–1 x is
a)
b)
c)
d)
None of these
|
|
Tanuja Kapoor answered |
The function f is defined for x = ±1
Now, f(1) = sin-1(1) + sec-1(1) + tan-1(1)
= π/2 + 0 + π/4 = 3π/4
Also, f(-1) = sin-1(-1) + sec-1(-1) + tan-1(-1)
= - π/2 + π - 0 - π/4
= 3π/4
Range = { π/4, 3π/4}
Now, f(1) = sin-1(1) + sec-1(1) + tan-1(1)
= π/2 + 0 + π/4 = 3π/4
Also, f(-1) = sin-1(-1) + sec-1(-1) + tan-1(-1)
= - π/2 + π - 0 - π/4
= 3π/4
Range = { π/4, 3π/4}
The number of solutions of the equation sin-1 x - cos-1 x = sin-1(1/2) is
a) 3
b) 1
c) 2
d) infinite.
Correct answer is option 'B'. Can you explain this answer?
|
|
Raghavendra Ghoshal answered |
Solution:
Given equation is sin^-1(x) - cos^-1(x) = sin^-1(1/2)
We know that sin(x) + cos(x) = √2 cos(x - π/4)
So, sin^-1(x) - cos^-1(x) = π/2 - sin^-1(√2x)
Therefore, the given equation becomes π/2 - sin^-1(√2x) = sin^-1(1/2)
sin(sin^-1(x)) = xsin(π/2 - sin^-1(√2x)) = √[1 - 2x^2]
√[1 - 2x^2] = 1/2
2x^2 = 3/4
x = ±√3/2
Therefore, the given equation has only 1 solution, which is x = √3/2 or x = -√3/2.
Hence, the correct answer is option B.
Given equation is sin^-1(x) - cos^-1(x) = sin^-1(1/2)
We know that sin(x) + cos(x) = √2 cos(x - π/4)
So, sin^-1(x) - cos^-1(x) = π/2 - sin^-1(√2x)
Therefore, the given equation becomes π/2 - sin^-1(√2x) = sin^-1(1/2)
sin(sin^-1(x)) = xsin(π/2 - sin^-1(√2x)) = √[1 - 2x^2]
√[1 - 2x^2] = 1/2
2x^2 = 3/4
x = ±√3/2
Therefore, the given equation has only 1 solution, which is x = √3/2 or x = -√3/2.
Hence, the correct answer is option B.

- a) tan-1 (9/5√10)
- b)cos-1(9/5√10)
- c)tan-1(9/14)
- d)sin-1(9/5√10)
Correct answer is option 'D'. Can you explain this answer?

a)
tan-1 (9/5√10)
b)
cos-1(9/5√10)
c)
tan-1(9/14)
d)
sin-1(9/5√10)

|
Defence Exams answered |
Given α = cos-1(⅗)
cos α = 3/5
sin α = ⅘
tan α = 4/3
Also β = tan-1(⅓)
So tan β = 1/3
tan (α-β) = (tan α – tan β)/(1 + tan α tan β)
= (4/3 – ⅓)/(1 + 4/9)
= 1/(13/9)
= 9/13
So (α-β) = tan-1 (9/13)
= sin-1(9/5√10)
Hence option d is the answer.
The principal value of 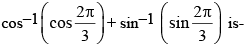
- a)π
- b)π/2
- c)π/3
- d)4π/3
Correct answer is option 'A'. Can you explain this answer?
The principal value of 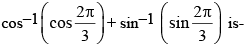
a)
π
b)
π/2
c)
π/3
d)
4π/3
|
|
Leelu Bhai answered |
We know that the principle value of cos -¹x is [0,... moreπ] and
The complete solution set of the inequality [cot–1 x]2 – 6[cot–1 x] + 9 ≤0 is (where [ * ] denotes the greatest integer function)- a)(– ∞, cot 3]
- b) [cot 3, cot 2]
- c) [cot 3, ∞)
- d)None of these
Correct answer is 'A'. Can you explain this answer?
The complete solution set of the inequality [cot–1 x]2 – 6[cot–1 x] + 9 ≤0 is (where [ * ] denotes the greatest integer function)
a)
(– ∞, cot 3]
b)
[cot 3, cot 2]
c)
[cot 3, ∞)
d)
None of these
|
|
Janani Roy answered |
Since $\cot x>0$ for $0< /><\pi $,="" the="" given="" inequality="" is="" equivalent="" to=""><\frac{\pi}{4}$, or=""><\frac{\pi}{2}$. thus,="" the="" solution="" set="" is="">< /><\frac{\pi}{2}.$$>
Evaluate sin(3 sin–1 0.4)- a)0.9
- b)0.31
- c)0.64
- d)0.56
Correct answer is option 'D'. Can you explain this answer?
Evaluate sin(3 sin–1 0.4)
a)
0.9
b)
0.31
c)
0.64
d)
0.56

|
Mohit Rajpoot answered |
3sin^-1(x) = sin^-1(3x - 4x^3) when -1/2<=x<=1/2
Definitely 0.4 comes in this range of x and so
Definitely 0.4 comes in this range of x and so
3sin^-1(0.4) = sin^-1[3*0.4 - 4*0.4^3]
3sin^-1(0.4) = sin^-1[1.2 - 4*0.064]
3sin^-1(0.4) = sin^-1[1.2 - 0.256]
3sin^-1(0.4) = sin^-1[0.944]
3sin^-1(0.4) = sin^-1[1.2 - 4*0.064]
3sin^-1(0.4) = sin^-1[1.2 - 0.256]
3sin^-1(0.4) = sin^-1[0.944]
Finally , sin(3sin^-1(0.4)) = sin{sin^-1(0.944)} = 0.944
The value of 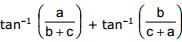 , if ∠C = 900 in triangle ABC, is
, if ∠C = 900 in triangle ABC, is - a)π/4
- b)π/3
- c)π/2
- d)π
Correct answer is option 'A'. Can you explain this answer?
The value of 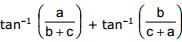 , if ∠C = 900 in triangle ABC, is
, if ∠C = 900 in triangle ABC, is
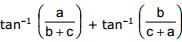 , if ∠C = 900 in triangle ABC, is
, if ∠C = 900 in triangle ABC, is a)
π/4
b)
π/3
c)
π/2
d)
π
|
|
Swati Verma answered |
a2 + b2 = c2
tan-1 A + tan-1 B = tan(A + B)/(1 - AB)
=> tan-1 (a/(b+c)) + tan-1 (b/(c+a))
tan-1 [(a/(b+c) + b/(c+a))/(1 - ab/(b+c)(c+a))]
=> tan-1(ac + a2 + b2 + bc)/(bc + ab + c2 + ac - ab)
= tan-1 (ac + bc + a2 + b2)/(ac + bc + c2)
= tan-1 (ac + bc + c2)/(ac + bc + c2) As we know that {a2 + b2 = c2}
= tan-1(1)
= π/4
tan-1 A + tan-1 B = tan(A + B)/(1 - AB)
=> tan-1 (a/(b+c)) + tan-1 (b/(c+a))
tan-1 [(a/(b+c) + b/(c+a))/(1 - ab/(b+c)(c+a))]
=> tan-1(ac + a2 + b2 + bc)/(bc + ab + c2 + ac - ab)
= tan-1 (ac + bc + a2 + b2)/(ac + bc + c2)
= tan-1 (ac + bc + c2)/(ac + bc + c2) As we know that {a2 + b2 = c2}
= tan-1(1)
= π/4
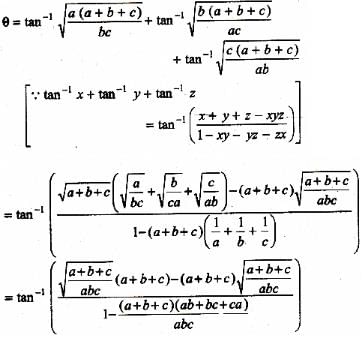
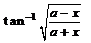 is equal to
is equal to- a)
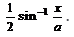
- b)
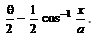
- c)
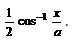
- d)
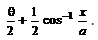
Correct answer is 'C'. Can you explain this answer?
a)
b)
c)
d)
|
|
Nikita Singh answered |
Let y = tan−1[(a−x)/(a+x)]1/2
put x = a cos θ
Now, y = tan−1[(a − a cos θ)/(a + a cos θ)]1/2
⇒ y = tan−1((1 − cos θ)/(1 + cos θ))1/2
⇒ y = tan−1[[(1−cos θ)(1−cos θ)]/(1+cos θ)(1−cos θ)]1/2
⇒ y = tan−1[(1−cos θ)2/1 − cos2θ]1/2
⇒ y = tan−1[(1 − cos θ)/sin θ]
⇒ y = tan−1[2 sin2(θ/2)/2 sin(θ/2) . cos(θ/2)]
⇒ y = tan−1[tan(θ/2)]
⇒ y = θ/2
⇒ y = 1/2 cos−1(x/a)
put x = a cos θ
Now, y = tan−1[(a − a cos θ)/(a + a cos θ)]1/2
⇒ y = tan−1((1 − cos θ)/(1 + cos θ))1/2
⇒ y = tan−1[[(1−cos θ)(1−cos θ)]/(1+cos θ)(1−cos θ)]1/2
⇒ y = tan−1[(1−cos θ)2/1 − cos2θ]1/2
⇒ y = tan−1[(1 − cos θ)/sin θ]
⇒ y = tan−1[2 sin2(θ/2)/2 sin(θ/2) . cos(θ/2)]
⇒ y = tan−1[tan(θ/2)]
⇒ y = θ/2
⇒ y = 1/2 cos−1(x/a)
cos2θ is not equal to- a)1−2sin2θ
- b)2cos2θ−1
- c)
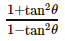
- d)
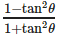
Correct answer is option 'C'. Can you explain this answer?
cos2θ is not equal to
a)
1−2sin2θ
b)
2cos2θ−1
c)
d)
|
|
Priyanka Sharma answered |
cos 2θ is equal to cos2θ - sin2θ = 2cos2θ - 1
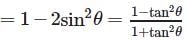
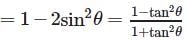
tan–1 a + tan–1b, where a > 0, b > 0, ab > 1, is equal to- a)
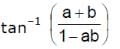
- b)
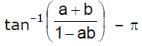
- c)
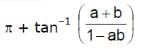
- d)
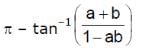
Correct answer is option 'C'. Can you explain this answer?
tan–1 a + tan–1b, where a > 0, b > 0, ab > 1, is equal to
a)
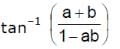
b)
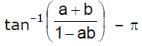
c)
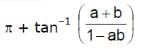
d)
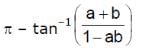
|
|
Geetika Shah answered |
tan-1 a + tan-1 b = tan-1[(a+b)/(1 - ab)] (ab>1)
tan-1[-(a+b)/(1 - ab)]
π - tan-1[(a+b)/(1 - ab)]
tan-1[-(a+b)/(1 - ab)]
π - tan-1[(a+b)/(1 - ab)]
The number of real solution of 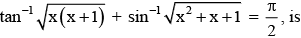
- a)zero
- b)one
- c)two
- d)infinite
Correct answer is option 'C'. Can you explain this answer?
The number of real solution of 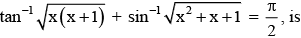
a)
zero
b)
one
c)
two
d)
infinite

|
Pallavi Desai answered |
From function it is clear that
(1) x(x + 1) > 0 ∴ Domain of square root function.
(2) x2 + x + 1>0 ∴ Domain of square root function.
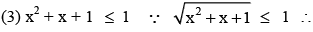 Domain of sin-1 function. From (2) and (3)
Domain of sin-1 function. From (2) and (3)
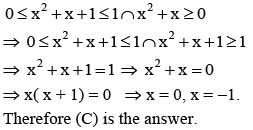
(1) x(x + 1) > 0 ∴ Domain of square root function.
(2) x2 + x + 1>0 ∴ Domain of square root function.
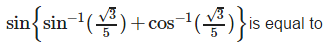
- a)

- b)1
- c)0
- d)none of these.
Correct answer is option 'B'. Can you explain this answer?
a)
b)
1
c)
0
d)
none of these.
|
|
Nikita Singh answered |
sin-1√3/5 = A
Sin A = √3/5 , cos A = √22/5
Therefore Cos-1√3/5 = B
Cos B = √3/5 , sin B = √22/5
sin(A+B) = sinA cosB + cosA sinB
= √3/5 * √3/5 + √22/5 * √22/5
= 3/25 * 22/25
= 25/25
= 1
Sin A = √3/5 , cos A = √22/5
Therefore Cos-1√3/5 = B
Cos B = √3/5 , sin B = √22/5
sin(A+B) = sinA cosB + cosA sinB
= √3/5 * √3/5 + √22/5 * √22/5
= 3/25 * 22/25
= 25/25
= 1
The value of sin-1[cos{cos-1 (cos x) + sin-1(sin x)}], where x 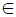
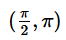
- a)π/2
- b)π/4
- c)–π/4
- d)–π/2
Correct answer is option 'D'. Can you explain this answer?
The value of sin-1[cos{cos-1 (cos x) + sin-1(sin x)}], where x 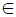
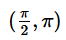
a)
π/2
b)
π/4
c)
–π/4
d)
–π/2
|
|
Riya Banerjee answered |
x implies(pi/2, pi)
= sin-1(cos(cos-1(cosx) + sin-1(sinx)))
= sin-1(cos(x + π - x)
= sin-1(cos π)
= sin-1(-1)
= -π/2
= sin-1(cos(cos-1(cosx) + sin-1(sinx)))
= sin-1(cos(x + π - x)
= sin-1(cos π)
= sin-1(-1)
= -π/2
The value of x for which sin [cot–1(1+x)] = cos(tan–1x)- a)1/2
- b)1
- c)0
- d)-1/2
Correct answer is option 'D'. Can you explain this answer?
The value of x for which sin [cot–1(1+x)] = cos(tan–1x)
a)
1/2
b)
1
c)
0
d)
-1/2
|
|
Nandini Iyer answered |
sin[cot−1(x+1)] = cos(tan−1x)
⇒ sin[sin^−1(1/√1+(x+1)2)] = cos[ cos−1(1/√1+x2)]
⇒ 1/(√1+(x+1)2) = 1/(√1+x2)
⇒ 1/(x2+2x+2) = 1/(√x2+1)
⇒ x2+2x+2 = x2+1
⇒ 2x + 2 = 1
⇒ 2x = 1 − 2
⇒ 2x = −1
⇒ x = −1/2
⇒ sin[sin^−1(1/√1+(x+1)2)] = cos[ cos−1(1/√1+x2)]
⇒ 1/(√1+(x+1)2) = 1/(√1+x2)
⇒ 1/(x2+2x+2) = 1/(√x2+1)
⇒ x2+2x+2 = x2+1
⇒ 2x + 2 = 1
⇒ 2x = 1 − 2
⇒ 2x = −1
⇒ x = −1/2
Chapter doubts & questions for Inverse Trigonometric Functions - Chapter-wise Tests for JEE Main & Advanced 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Inverse Trigonometric Functions - Chapter-wise Tests for JEE Main & Advanced in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily
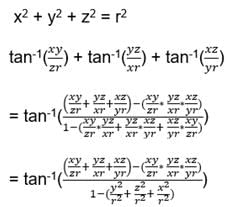
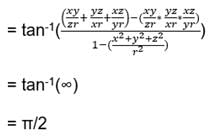

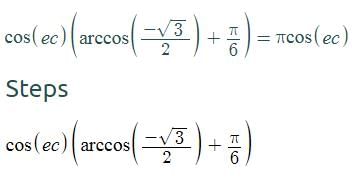

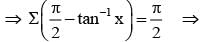
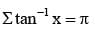

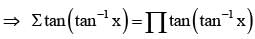



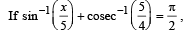 then the values of x is
then the values of x is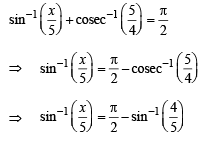

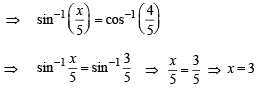
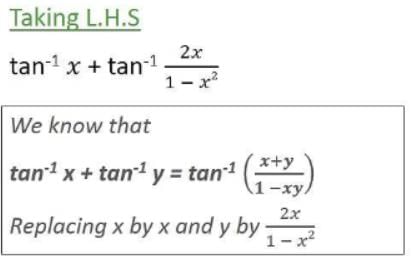
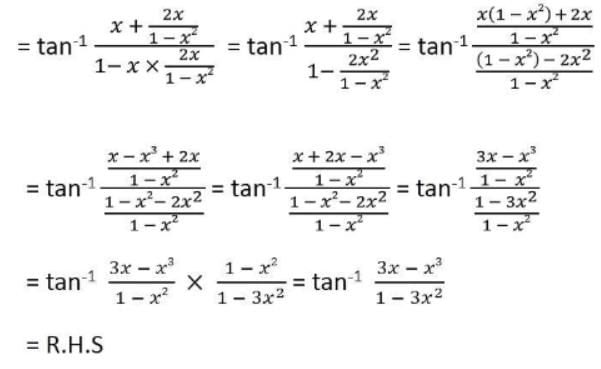
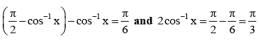
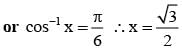
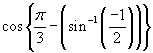 is given by
is given by