All Exams >
Class 10 >
Mathematics (Maths) Class 10 >
All Questions
All questions of Polynomials for Class 10 Exam
If one of the factors of x2 + x – 20 is (x + 5), then other factor is- a)(x – 4)
- b)(x – 5)
- c)(x – 6)
- d)(x – 7)
Correct answer is 'A'. Can you explain this answer?
If one of the factors of x2 + x – 20 is (x + 5), then other factor is
a)
(x – 4)
b)
(x – 5)
c)
(x – 6)
d)
(x – 7)
|
|
Arun Sharma answered |
Using mid-term splitting,
x2+x-20=x2+5x-4x-20=x(x+5)-4(x+5)
Taking common x+5
(x+5)(x-4) , so the other factor is x-4
x2+x-20=x2+5x-4x-20=x(x+5)-4(x+5)
Taking common x+5
(x+5)(x-4) , so the other factor is x-4
If the graph of a polynomial intersects the x – axis at three points, then the number of zeroes =- a)3
- b)0
- c)at most three
- d)at least three
Correct answer is option 'A'. Can you explain this answer?
If the graph of a polynomial intersects the x – axis at three points, then the number of zeroes =
a)
3
b)
0
c)
at most three
d)
at least three

|
Megha Roy answered |
If the graph of a polynomial intersects the x-axis at three points, then the number of zeroes are 3 because number of zeroes of the polynomial are the number of the coordinates of the points where its graph intersects the x-axis.
If p and q are the zeroes of the polynomial x2- 5x + k. Such that p - q = 1, find the value of K
- a)6
- b)7
- c)8
- d)9
Correct answer is option 'A'. Can you explain this answer?
If p and q are the zeroes of the polynomial x2- 5x + k. Such that p - q = 1, find the value of K
a)
6
b)
7
c)
8
d)
9
|
|
Zachary Foster answered |
Given α and β are the zeroes of the polynomial x2 − 5x + k
Also given that α − β = 1 → (1)
Recall that sum of roots (α + β) = −(b/a)
∴ α + β = 5 → (2)
Add (1) and (2), we get
α − β = 1
α + β = 5
2α = 6
∴ α = 3
Put α = 3 in α + β = 5
3 + β = 5
∴ β = 2
Hence 3 and 2 are zeroes of the given polynomial
Put x = 2 in the given polynomial to find the value of k ( Since 2 is a zero of the polynomial, f(2) will be 0 )
x2 − 5x + k = 0
⇒ 22 − 5(2) + k = 0
⇒ 4 − 10 + k = 0
⇒ − 6 + k = 0
∴ k = 6
Also given that α − β = 1 → (1)
Recall that sum of roots (α + β) = −(b/a)
∴ α + β = 5 → (2)
Add (1) and (2), we get
α − β = 1
α + β = 5
2α = 6
∴ α = 3
Put α = 3 in α + β = 5
3 + β = 5
∴ β = 2
Hence 3 and 2 are zeroes of the given polynomial
Put x = 2 in the given polynomial to find the value of k ( Since 2 is a zero of the polynomial, f(2) will be 0 )
x2 − 5x + k = 0
⇒ 22 − 5(2) + k = 0
⇒ 4 − 10 + k = 0
⇒ − 6 + k = 0
∴ k = 6
The number of zeroes of a cubic polynomial is- a)3
- b)at least 3
- c)2
- d)at most 3
Correct answer is option 'D'. Can you explain this answer?
The number of zeroes of a cubic polynomial is
a)
3
b)
at least 3
c)
2
d)
at most 3
|
|
Nilima singh answered |
The number of zeroes of a cubic polynomial is at most 3 because the highest power of the variable in cubic polynomial is 3, i.e. ax3+bx2+cx+d
If 5 is a zero of the quadratic polynomial, (x^2) - kx - 15 then the value of k isa) 2b)-2c) 4d)- 4Correct answer is option 'A'. Can you explain this answer?- 4
If 5 is a zero of the quadratic polynomial, (x^2) - kx - 15 then the value of k is
a) 2
b)-2
c) 4
d)- 4
Correct answer is option 'A'. Can you explain this answer?
|
|
Rohit Sharma answered |
p(x) = x2- kx - 15
Given: p(5) = 0
⇒ (5)2- k(5) - 15 = 0
⇒ 25 - 5k - 15 = 0
⇒ 5k = 10
⇒ k = 10/5 = 2
⇒ (5)2- k(5) - 15 = 0
⇒ 25 - 5k - 15 = 0
⇒ 5k = 10
⇒ k = 10/5 = 2
Thus, Value of k is 2
If α,β be the zeros of the quadratic polynomial 2 – 3x – x2, then α + β =- a)2
- b)3
- c)1
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
If α,β be the zeros of the quadratic polynomial 2 – 3x – x2, then α + β =
a)
2
b)
3
c)
1
d)
None of these
|
|
Pooja Shah answered |
If α and β are the zeros of the polynomial then
(x−α)(x−β) are the factors of the polynomial
Thus, (x−α)(x−β) is the polynomial.
So, the polynomial =x2 − αx − βx + αβ
=x2 − (α + β)x + αβ....(i)
Now,the quadratic polynomial is
2 − 3x − x2 = x2 + 3x − 2....(ii)
(x−α)(x−β) are the factors of the polynomial
Thus, (x−α)(x−β) is the polynomial.
So, the polynomial =x2 − αx − βx + αβ
=x2 − (α + β)x + αβ....(i)
Now,the quadratic polynomial is
2 − 3x − x2 = x2 + 3x − 2....(ii)
Now, comparing equation (i) and (ii),we get,
−(α + β) = 3
α + β = −3
−(α + β) = 3
α + β = −3
If one of the zeroes of the cubic polynomial x3−7x+6 is 2, then the product of the other two zeroes is- a)2
- b)3
- c)– 3
- d)– 2
Correct answer is 'C'. Can you explain this answer?
If one of the zeroes of the cubic polynomial x3−7x+6 is 2, then the product of the other two zeroes is
a)
2
b)
3
c)
– 3
d)
– 2

|
Navya Patel answered |
Let α,β,γ are the zeroes of the given polynomial. Given: α = 2
Since αβγ = -d/a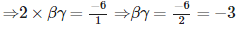
Since αβγ = -d/a
A polynomial of degree ____ is called a quadratic polynomial.- a)0
- b)2
- c)1
- d)3
Correct answer is option 'B'. Can you explain this answer?
A polynomial of degree ____ is called a quadratic polynomial.
a)
0
b)
2
c)
1
d)
3

|
Abhiram Gupta answered |
A polynomial of degree 2 is called a quadratic polynomial.
Quadratic polynomial having sum of it's zeros 5 and product of it's zeros – 14 is –- a)x2 – 5x – 14
- b)x2 – 10x – 14
- c)x2 – 5x + 14
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Quadratic polynomial having sum of it's zeros 5 and product of it's zeros – 14 is –
a)
x2 – 5x – 14
b)
x2 – 10x – 14
c)
x2 – 5x + 14
d)
None of these
|
|
Amit Kumar answered |
The quadratic equation is of the form x2 - (sum of zeros) x + (product of zeros)
=x2 - 5x - 14
=x2 - 5x - 14
If one root of the polynomial p(y) = 5y2 + 13y + m is reciprocal of other, then the value of m is- a)6
- b)0
- c)5
- d)1/5
Correct answer is option 'C'. Can you explain this answer?
If one root of the polynomial p(y) = 5y2 + 13y + m is reciprocal of other, then the value of m is
a)
6
b)
0
c)
5
d)
1/5
|
|
Vivek Rana answered |
Let the roots be α and 1/α.
Product of roots = α(1/α) = 1
⇒ m/5 = 1
⇒ m = 5
⇒ m/5 = 1
⇒ m = 5
If the zeroes of the quadratic polynomial x2 + (a + 1) x + b are 2 and -3, the- a)a = -7, b = -1
- b)a = 5, b = -1
- c)a = 2, b = -6
- d)a = 0, b = -6
Correct answer is option 'D'. Can you explain this answer?
If the zeroes of the quadratic polynomial x2 + (a + 1) x + b are 2 and -3, the
a)
a = -7, b = -1
b)
a = 5, b = -1
c)
a = 2, b = -6
d)
a = 0, b = -6
|
|
Amit Sharma answered |
p(x) = x2 + (a + 1)x + b
Given: zeros of polynomial is 2, -3
For x = 2
(2)2 + (a + 1)2 + b = 0
⇒ 4 + 2a + 2 + b = 0
⇒ 2a + b = -6 ...(i)
Given: zeros of polynomial is 2, -3
For x = 2
(2)2 + (a + 1)2 + b = 0
⇒ 4 + 2a + 2 + b = 0
⇒ 2a + b = -6 ...(i)
For x = -3
(-3)2 + (a + 1) (-3) + b = 0
⇒ 9 - 3a - 3 + b = 0
⇒ -3a + b = -6 ..(ii)
(-3)2 + (a + 1) (-3) + b = 0
⇒ 9 - 3a - 3 + b = 0
⇒ -3a + b = -6 ..(ii)
Solving (i) and (ii), we get 5a = 0
⇒ a = 0 and b = -6
⇒ a = 0 and b = -6
Alternative method:
p(x) = x2 + (a + 1)x + b
Given: zeros of polynomial is 2, -3
Given: zeros of polynomial is 2, -3
Sum of zeros: -(a+1) = 2-3
⇒ a = 0
Product of zeros: b = 2.(-3) = -6
⇒ a = 0
Product of zeros: b = 2.(-3) = -6
Which of the following is not the graph of a quadratic polynomial ?- a)
- b)
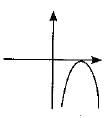
- c)
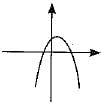
- d)
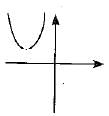
Correct answer is option 'A'. Can you explain this answer?
Which of the following is not the graph of a quadratic polynomial ?
a)

b)

c)

d)


|
Dr Manju Sen answered |
For any quadratic polynomial ax2 + bx + c, a≠0, graph for the corresponding equation:
- Has one of the two shapes either open upwards like ∪ or open downwards like ∩ depending on whether a > 0 or a < 0. These curves are called parabolas.
- The curve of a quadratic polynomial crosses the X-axis on at most two points.
Thus, option A is correct.
If x = 2 and x = 3 are zeros of the quadratic polynomial x2 + ax + b, the values of a and b respectively are :- a)5, 6
- b)- 5, - 6
- c)- 5, 6
- d)5, - 6
Correct answer is option 'C'. Can you explain this answer?
If x = 2 and x = 3 are zeros of the quadratic polynomial x2 + ax + b, the values of a and b respectively are :
a)
5, 6
b)
- 5, - 6
c)
- 5, 6
d)
5, - 6
|
|
Gaurav Kumar answered |
Zeros of the polynomials are the values which gives zero when their value is substituted in the polynomial
When x=2,
x2+ax+b =(2)2+a*2+b=0
4+2a+b=0
b=-4-2a ….1
When x=3,
(3)2+ 3a + b=0
9 + 3a + b=0
Substituting
9 + 3a - 4 - 2a =0
5 + a =0
a = -5
b = 6
When x=2,
x2+ax+b =(2)2+a*2+b=0
4+2a+b=0
b=-4-2a ….1
When x=3,
(3)2+ 3a + b=0
9 + 3a + b=0
Substituting
9 + 3a - 4 - 2a =0
5 + a =0
a = -5
b = 6
The number of polynomials having zeros as - 2 and 5 is- a)1
- b)2
- c)3
- d)more than 3
Correct answer is option 'D'. Can you explain this answer?
The number of polynomials having zeros as - 2 and 5 is
a)
1
b)
2
c)
3
d)
more than 3

|
Shubham Mukherjee answered |
let - 2 and 5 are the zeroes of the polynomials of the formp(x) = ax^2 + bx + c.
sum of the zeroes = - (coefficient of x) � coefficient of x^2 i.e.
Sum of the zeroes = - b/a
- 2 + 5 = - b/a
3 = - b/a
⇒ b = - 3 and a = 1
Product of the zeroes = constant term � coefficient of x^2 i.e.
Product of zeroes = c/a
(- 2)5 = c/a
- 10 = c
Put the values of a, b and c in the polynomial p(x) = ax^2 + bx + c.
∴ The equation is x^2 - 3x - 10
OR
The equation of a quadratic polynomial is given by x^2 - (sum of the zeroes)x + (product of the zeroes) where,
Sum of the zeroes = - (coefficient of x) � coefficient of x^2 and
Product of the zeroes = constant term � coefficient of x^2
∴ Sum of the zeroes = - 2 + 5 and product of the zeroes = (- 2)5
= 3 = - 10
∴ the equation is x^2 - 3x - 10
We know, the zeroes do not change if the polynomial is divided or multiplied by a constant
⇒ kx^2 - 3kx - 10k will also have - 2 and 5 as their zeroes.
As k can take any real value, there can be many polynomials having - 2 and 5 as their zeroes.
Can you explain the answer of this question below:The sum of two zeroes of the polynomial f(x) = 2x2+(p+3) x+5 is zero, then the value of ‘p’ is
- A:
4
- B:
– 4
- C:
3
- D:
– 3
The answer is d.
The sum of two zeroes of the polynomial f(x) = 2x2+(p+3) x+5 is zero, then the value of ‘p’ is
4
– 4
3
– 3

|
Shubham Mukherjee answered |
Let one zeroes of the given polynomial be α and β. According to the question,

If p(x) is a polynomial of at least degree one and p(k) = 0, then k is known as- a)value of p(x)
- b)zero of p(x)
- c)constant term of p(x)
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
If p(x) is a polynomial of at least degree one and p(k) = 0, then k is known as
a)
value of p(x)
b)
zero of p(x)
c)
constant term of p(x)
d)
none of these
|
|
Ishan Choudhury answered |
Let p(x) = ax + b
p(k) = ak + b = 0
∴ k is zero of p(x)
p(k) = ak + b = 0
∴ k is zero of p(x)
If one zero of the quadratic polynomial x2+ 3x + k is 2, then the value of ‘k’ is- a)– 10
- b)5
- c)– 5
- d)10
Correct answer is option 'A'. Can you explain this answer?
If one zero of the quadratic polynomial x2+ 3x + k is 2, then the value of ‘k’ is
a)
– 10
b)
5
c)
– 5
d)
10
|
|
Rajiv Gupta answered |
Let the given quadratic polynomial be p(x) = x^2 + 3x + k
Given one of the zero of the quadratic polynomial is 2.
Hence p(2) = 0
Put x = 2 in p(x), we get
p(2) = 2^2 + 3(2) + k
⇒ 0 = 4 + 6 + k
⇒ 0 = 10 + k
∴ k = – 10
The number of polynomials having zeroes as -2 and 5 is:- a)1
- b)2
- c)3
- d)More than 3
Correct answer is option 'D'. Can you explain this answer?
The number of polynomials having zeroes as -2 and 5 is:
a)
1
b)
2
c)
3
d)
More than 3

|
Kamna Science Academy answered |
The polynomials x2-3x-10, 2x2-6x-20, (1/2)x2-(3/2)x-5, 3x2-9x-30, have zeroes as -2 and 5.
The quadratic polynomial whose sum of zeroes is 3 and product of zeroes is –2 is :- a) x2 + 3x – 2
- b)x2 – 2x + 3
- c)x2 – 3x + 2
- d)x2 – 3x – 2
Correct answer is 'C'. Can you explain this answer?
The quadratic polynomial whose sum of zeroes is 3 and product of zeroes is –2 is :
a)
x2 + 3x – 2
b)
x2 – 2x + 3
c)
x2 – 3x + 2
d)
x2 – 3x – 2
|
|
Pooja Shah answered |
Sum of zeros = 3/1
-b/a = 3/1
Product of zeros = 2/1
c/a = 2/1
This gives
a = 1
b = -3
c = -2,
The required quadratic equation is
ax2+bx+c
So, x2-3x+2
-b/a = 3/1
Product of zeros = 2/1
c/a = 2/1
This gives
a = 1
b = -3
c = -2,
The required quadratic equation is
ax2+bx+c
So, x2-3x+2
The sum and product of the zeroes of the polynomial f(x) = 4x2−27x+3k2 are equal, then the value of ‘k’ is- a)±3
- b)0
- c)±2
- d)±1
Correct answer is option 'A'. Can you explain this answer?
The sum and product of the zeroes of the polynomial f(x) = 4x2−27x+3k2 are equal, then the value of ‘k’ is
a)
±3
b)
0
c)
±2
d)
±1
|
|
Vikram Kapoor answered |
Let α,β are the zeroes of the given polynomial.
Given: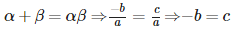
⇒ −(−27) = 3k2 ⇒ k2 = 0 ⇒ k= ±3
Given:
⇒ −(−27) = 3k2 ⇒ k2 = 0 ⇒ k= ±3
If one zero of the polynomial p(x)=(k+4)x2+13x+3k is reciprocal of the other, then the value of ‘k’ is- a)3
- b)4
- c)5
- d)2
Correct answer is option 'D'. Can you explain this answer?
If one zero of the polynomial p(x)=(k+4)x2+13x+3k is reciprocal of the other, then the value of ‘k’ is
a)
3
b)
4
c)
5
d)
2
|
|
Neha Patel answered |
Let the roots of (k2 + 4) x2 + 13x + 4k be p and 1/p.
Product of the roots = p x 1/p = (constant term) / coefficient of x2
⇒ (4k) / (k2 + 4) = p x 1/p
⇒ (4k) / (k2 + 4) = 1
⇒ k2 - 4k + 4 = 0
⇒ (k - 2)2 = 0
⇒ k - 2 = 0
⇒ k = 2
Therefore, the value of k is 2.
If α,β be the zeros of the quadratic polynomial 2x2 + 5x + 1, then value of α + β + αβ =- a)- 2
- b)- 1
- c)1
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If α,β be the zeros of the quadratic polynomial 2x2 + 5x + 1, then value of α + β + αβ =
a)
- 2
b)
- 1
c)
1
d)
None of these
|
|
Naina Sharma answered |
P(x) = 2x² + 5x + 1
Sum of roots = -5/2
Product of roots = 1/2
Therefore substituting these values,
α + β +αβ
=(α + β) + αβ
= -5/2 + 1/2
= -4/2
= -2
Sum of roots = -5/2
Product of roots = 1/2
Therefore substituting these values,
α + β +αβ
=(α + β) + αβ
= -5/2 + 1/2
= -4/2
= -2
The sum and product of the zeroes of the polynomial x2−6x+8 are respectively- a)-3/2 and – 1
- b)6 and 8
- c)-3/2 and 1
- d)3/2 and 1
Correct answer is option 'B'. Can you explain this answer?
The sum and product of the zeroes of the polynomial x2−6x+8 are respectively
a)
-3/2 and – 1
b)
6 and 8
c)
-3/2 and 1
d)
3/2 and 1
|
|
Abhi Prajapati answered |
Given,
a =1
b=-6
c=+8
Sum of zeroes are
alpha + beta = - b/a
Alpha + beta =. - (-6)/1. = 6
Products of zeroes
alpha × beta = c/a
alpha × beta = 8 / 1 = 8
a =1
b=-6
c=+8
Sum of zeroes are
alpha + beta = - b/a
Alpha + beta =. - (-6)/1. = 6
Products of zeroes
alpha × beta = c/a
alpha × beta = 8 / 1 = 8
If ‘α ’ and ‘β ’ are the zeroes of a quadratic polynomial x2−− 5x k and α −− β = 1 , then the value of ‘k’ is- a)– 5
- b)6
- c)5
- d)– 6
Correct answer is option 'B'. Can you explain this answer?
If ‘α ’ and ‘β ’ are the zeroes of a quadratic polynomial x2−− 5x k and α −− β = 1 , then the value of ‘k’ is
a)
– 5
b)
6
c)
5
d)
– 6
|
|
Arun Yadav answered |
x^2-5x+k
Here, a=1, b=-5 and c=k
Now, α+ β = -b/a= -(-5)/1= 5
α*β = c/a= k/7= k
Now,α - β =1
Squaring both sides, we get,
(α - β)^2=1^2
⇒ α^2 + β^2 - 2αβ = 1
⇒ (α^2 + β^2 + 2αβ) - 4αβ = 1
⇒ (α +β)^2 -4αβ =1
⇒ (5)^2-4k=1
⇒ -4k= 7-25
⇒ -4k= -24
⇒ k=6 So the value of k is 6.
Assertion (A): A polynomial of degree n cannot have more than n terms.
Reason (R): The number of coefficients in a polynomial is always one more than its degree.- a)Both Assertion and Reason are correct, and Reason is the correct explanation of Assertion.
- b)Both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
- c)The assertion is correct, but the Reason is incorrect.
- d)Assertion is incorrect, but Reason is correct.
Correct answer is option 'D'. Can you explain this answer?
Assertion (A): A polynomial of degree n cannot have more than n terms.
Reason (R): The number of coefficients in a polynomial is always one more than its degree.
Reason (R): The number of coefficients in a polynomial is always one more than its degree.
a)
Both Assertion and Reason are correct, and Reason is the correct explanation of Assertion.
b)
Both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
c)
The assertion is correct, but the Reason is incorrect.
d)
Assertion is incorrect, but Reason is correct.
|
|
Khusboo shah answered |
Understanding the Assertion and Reason
The assertion (A) states that a polynomial of degree n cannot have more than n terms. The reason (R) states that the number of coefficients in a polynomial is always one more than its degree. Let's break down these statements.
Assertion (A): Analysis
- A polynomial of degree n is defined as a mathematical expression of the form:
- a_n * x^n + a_(n-1) * x^(n-1) + ... + a_1 * x + a_0
- The degree of a polynomial is determined by the highest power of the variable x.
- A polynomial can indeed have fewer than n terms (e.g., x^n + x^2 has 2 terms but is still degree n).
- Therefore, the assertion is incorrect as a polynomial can have more than n terms, as long as terms are combined appropriately.
Reason (R): Analysis
- The reason correctly states that the number of coefficients in a polynomial is always one more than its degree.
- This is because each term has a coefficient, including the constant term (a_0).
- For example, a polynomial of degree 3 (like x^3 + 2x^2 + 3x + 4) has 4 coefficients (a_3, a_2, a_1, and a_0).
Conclusion
- The assertion is incorrect, but the reason is correct.
- Thus, the correct option is D: Assertion is incorrect, but Reason is correct.
This analysis highlights the importance of understanding polynomials and their properties in mathematics.
The assertion (A) states that a polynomial of degree n cannot have more than n terms. The reason (R) states that the number of coefficients in a polynomial is always one more than its degree. Let's break down these statements.
Assertion (A): Analysis
- A polynomial of degree n is defined as a mathematical expression of the form:
- a_n * x^n + a_(n-1) * x^(n-1) + ... + a_1 * x + a_0
- The degree of a polynomial is determined by the highest power of the variable x.
- A polynomial can indeed have fewer than n terms (e.g., x^n + x^2 has 2 terms but is still degree n).
- Therefore, the assertion is incorrect as a polynomial can have more than n terms, as long as terms are combined appropriately.
Reason (R): Analysis
- The reason correctly states that the number of coefficients in a polynomial is always one more than its degree.
- This is because each term has a coefficient, including the constant term (a_0).
- For example, a polynomial of degree 3 (like x^3 + 2x^2 + 3x + 4) has 4 coefficients (a_3, a_2, a_1, and a_0).
Conclusion
- The assertion is incorrect, but the reason is correct.
- Thus, the correct option is D: Assertion is incorrect, but Reason is correct.
This analysis highlights the importance of understanding polynomials and their properties in mathematics.
The sum and product of zeros of the quadratic polynomial are – 5 and 3 respectively the quadratic polynomial is equal to –- a)x2 + 2x + 3
- b)x2 – 5x + 3
- c)x2 + 5x + 3
- d)x2 + 3x – 5
Correct answer is option 'C'. Can you explain this answer?
The sum and product of zeros of the quadratic polynomial are – 5 and 3 respectively the quadratic polynomial is equal to –
a)
x2 + 2x + 3
b)
x2 – 5x + 3
c)
x2 + 5x + 3
d)
x2 + 3x – 5
|
|
Bhaskar Dasgupta answered |
If α, β be the zeros of the quadratic polynomial ,then
(x−α)(x−β) is the quadratic polynomial.
Thus, (x−α)(x−β) is the polynomial.
=x^2−αx−βx+αβ
=x^2−x(α+β)+αβ(i)
(α+β)=−5αβ=3
Now putting the value of (α+β),αβ in equation (i) we get,
x^2−x(−5)+3
=x^2+5x+3
A quadratic polynomial whose product and sum of zeroes are 1/3 and √2 respectively is- a)3x2−3√2x+1
- b)3x2−x+3√2
- c)3x2+x−3√2
- d)3x2+3√2x+1
Correct answer is option 'A'. Can you explain this answer?
A quadratic polynomial whose product and sum of zeroes are 1/3 and √2 respectively is
a)
3x2−3√2x+1
b)
3x2−x+3√2
c)
3x2+x−3√2
d)
3x2+3√2x+1

|
Rishika Rane answered |
Given: 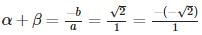

On comparing, we get,a = 3,b = −3√2–,c = 1
Putting these values in general form of a quadratic polynomial ax2+bx+c, we have 3x2−3√2x+1
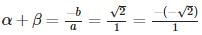

On comparing, we get,a = 3,b = −3√2–,c = 1
Putting these values in general form of a quadratic polynomial ax2+bx+c, we have 3x2−3√2x+1
If p(x) is a polynomial of degree one and p(a) = 0, then a is said to be:- a)Zero of p(x)
- b)Value of p(x)
- c)Constant of p(x)
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
If p(x) is a polynomial of degree one and p(a) = 0, then a is said to be:
a)
Zero of p(x)
b)
Value of p(x)
c)
Constant of p(x)
d)
None of the above

|
Aniket Yadav answered |
Understanding Zero of a Polynomial
When we say that p(x) is a polynomial of degree one, it can be expressed in the form:
p(x) = mx + b,
where m is the slope and b is the y-intercept.
When we find that p(a) = 0, we are essentially finding the value of x for which the polynomial equals zero.
Definition of Zero of a Polynomial
- A zero of a polynomial is a value of x that makes the polynomial equal to zero.
- In this case, since p(a) = 0, 'a' is the value at which the polynomial intersects the x-axis.
Why Option A is Correct
- Since p(a) = 0, it directly indicates that 'a' is a solution to the equation p(x) = 0.
- Therefore, 'a' is indeed referred to as a "zero" of the polynomial p(x).
Other Options Explained
- Option B: Value of p(x)
This is incorrect because p(a) = 0 indicates the value of the polynomial at 'a', not 'a' itself.
- Option C: Constant of p(x)
This option is misleading since there is no constant term being referred to here; it's about the root or zero of the polynomial.
- Option D: None of the above
This is incorrect as we have already established that 'a' is indeed a zero of p(x).
In summary, when p(a) = 0 for a polynomial p(x) of degree one, 'a' is correctly termed as a zero of p(x), confirming that option A is the right answer.
When we say that p(x) is a polynomial of degree one, it can be expressed in the form:
p(x) = mx + b,
where m is the slope and b is the y-intercept.
When we find that p(a) = 0, we are essentially finding the value of x for which the polynomial equals zero.
Definition of Zero of a Polynomial
- A zero of a polynomial is a value of x that makes the polynomial equal to zero.
- In this case, since p(a) = 0, 'a' is the value at which the polynomial intersects the x-axis.
Why Option A is Correct
- Since p(a) = 0, it directly indicates that 'a' is a solution to the equation p(x) = 0.
- Therefore, 'a' is indeed referred to as a "zero" of the polynomial p(x).
Other Options Explained
- Option B: Value of p(x)
This is incorrect because p(a) = 0 indicates the value of the polynomial at 'a', not 'a' itself.
- Option C: Constant of p(x)
This option is misleading since there is no constant term being referred to here; it's about the root or zero of the polynomial.
- Option D: None of the above
This is incorrect as we have already established that 'a' is indeed a zero of p(x).
In summary, when p(a) = 0 for a polynomial p(x) of degree one, 'a' is correctly termed as a zero of p(x), confirming that option A is the right answer.
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : Zeroes of f(x) = x2 - 4x - 5 are 5, - 1
Reason : The polynomial whose zeroes are 2 + √3, 2 - √3 is x2 - 4x + 7.- a)Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
- b)Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
- c)Assertion (A) is true but reason (R) is false.
- d)Assertion (A) is false but reason (R) is true.
Correct answer is option 'C'. Can you explain this answer?
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : Zeroes of f(x) = x2 - 4x - 5 are 5, - 1
Reason : The polynomial whose zeroes are 2 + √3, 2 - √3 is x2 - 4x + 7.
Assertion : Zeroes of f(x) = x2 - 4x - 5 are 5, - 1
Reason : The polynomial whose zeroes are 2 + √3, 2 - √3 is x2 - 4x + 7.
a)
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
b)
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
c)
Assertion (A) is true but reason (R) is false.
d)
Assertion (A) is false but reason (R) is true.
|
|
Anita Menon answered |
Zeroes of f(x) = x2 − 4x − 5 are obtained by solving:
x2 − 4x − 5 = 0, which implies
x2 − 5x + x − 5 = 0 or, x(x − 5) + 1(x − 5) = 0
which means x = 5 or x = −1
Thus the assertion is correct.
However, the reason is incorrect.
The numbers given are not the zeroes of x2 − 4x + 7
x2 − 4x − 5 = 0, which implies
x2 − 5x + x − 5 = 0 or, x(x − 5) + 1(x − 5) = 0
which means x = 5 or x = −1
Thus the assertion is correct.
However, the reason is incorrect.
The numbers given are not the zeroes of x2 − 4x + 7
A quadratic polynomial, whose zeroes are –3 and 4, is- a)x2 – x + 12
- b)x2 + x + 12
- c)(x2/2) – (x/2) – 6
- d)2x2 + 2x – 24
Correct answer is option 'C'. Can you explain this answer?
A quadratic polynomial, whose zeroes are –3 and 4, is
a)
x2 – x + 12
b)
x2 + x + 12
c)
(x2/2) – (x/2) – 6
d)
2x2 + 2x – 24
|
|
Aditi bajaj answered |
Understanding Quadratic Polynomials
A quadratic polynomial can be expressed in the form of ax² + bx + c, where a, b, and c are constants. The roots (or zeroes) of the polynomial are the values of x that make the polynomial equal to zero.
Finding the Polynomial with Given Zeroes
Given the zeroes -3 and 4, we can use the fact that if p and q are the zeroes of a quadratic polynomial, it can be expressed as:
- P(x) = a(x - p)(x - q)
Substituting the zeroes:
- P(x) = a(x + 3)(x - 4)
Expanding the Expression
Now, let's expand this expression:
1. P(x) = a[(x + 3)(x - 4)]
2. P(x) = a[x² - 4x + 3x - 12]
3. P(x) = a[x² - x - 12]
Choosing the Value of a
To find a suitable form, we can choose a = 1 for simplicity, giving:
- P(x) = x² - x - 12
However, we need to check the options presented.
Evaluating the Options
- Option a: x² - x + 12 (Incorrect, does not match)
- Option b: x² + x + 12 (Incorrect, does not match)
- Option c: (x²/2) - (x/2) - 6 (Let’s analyze)
- Option d: 2x² + 2x - 24 (Incorrect, does not match)
Verifying Option C
To verify option c:
1. Multiply the entire expression by 2 to eliminate the fraction:
- 2[(x²/2) - (x/2) - 6] = x² - x - 12
This matches our previously derived polynomial.
Conclusion
Thus, the correct answer is option c: (x²/2) - (x/2) - 6, as it is equivalent to the polynomial derived from the given zeroes -3 and 4.
A quadratic polynomial can be expressed in the form of ax² + bx + c, where a, b, and c are constants. The roots (or zeroes) of the polynomial are the values of x that make the polynomial equal to zero.
Finding the Polynomial with Given Zeroes
Given the zeroes -3 and 4, we can use the fact that if p and q are the zeroes of a quadratic polynomial, it can be expressed as:
- P(x) = a(x - p)(x - q)
Substituting the zeroes:
- P(x) = a(x + 3)(x - 4)
Expanding the Expression
Now, let's expand this expression:
1. P(x) = a[(x + 3)(x - 4)]
2. P(x) = a[x² - 4x + 3x - 12]
3. P(x) = a[x² - x - 12]
Choosing the Value of a
To find a suitable form, we can choose a = 1 for simplicity, giving:
- P(x) = x² - x - 12
However, we need to check the options presented.
Evaluating the Options
- Option a: x² - x + 12 (Incorrect, does not match)
- Option b: x² + x + 12 (Incorrect, does not match)
- Option c: (x²/2) - (x/2) - 6 (Let’s analyze)
- Option d: 2x² + 2x - 24 (Incorrect, does not match)
Verifying Option C
To verify option c:
1. Multiply the entire expression by 2 to eliminate the fraction:
- 2[(x²/2) - (x/2) - 6] = x² - x - 12
This matches our previously derived polynomial.
Conclusion
Thus, the correct answer is option c: (x²/2) - (x/2) - 6, as it is equivalent to the polynomial derived from the given zeroes -3 and 4.
Consider the following statement about the role of press and literature in the 19th century.
1. The press never criticised official Policies but urged the people to unite
2. There was the prolonged growth of Indian owned Vernacular newspapers because of numerous restrictions imposed on the press by the colonial rulers
Which of these statements is/are correct?
- a)1 Only
- b)Neither of them
- c)Both of them
- d)2 Only
Correct answer is option 'D'. Can you explain this answer?
Consider the following statement about the role of press and literature in the 19th century.
1. The press never criticised official Policies but urged the people to unite
2. There was the prolonged growth of Indian owned Vernacular newspapers because of numerous restrictions imposed on the press by the colonial rulers
Which of these statements is/are correct?
a)
1 Only
b)
Neither of them
c)
Both of them
d)
2 Only
|
|
Shruti Desai answered |
Explanation:
The given statement talks about the role of press and literature in the 19th century in India. Let's break down each statement and see if it is correct or not:
1. The press never criticised official Policies but urged the people to unite.
This statement is not entirely accurate. The press did criticize official policies, but they had to do it carefully because of the restrictions imposed by the colonial rulers. The press played a crucial role in shaping public opinion and creating awareness about the injustices of the colonial rule. They urged people to unite and fight for their rights. However, they had to do it without crossing the line and inviting censorship or prosecution.
2. There was the prolonged growth of Indian owned Vernacular newspapers because of numerous restrictions imposed on the press by the colonial rulers.
This statement is partially correct. Indian owned Vernacular newspapers did grow during the 19th century because they could cater to the local audience and address their concerns. However, the growth of these newspapers was not entirely due to the restrictions imposed by the colonial rulers. The vernacular press had to face numerous challenges, such as the lack of funds, illiteracy, and censorship. It was only after the Indian National Congress was formed in 1885 that the vernacular press gained momentum and started playing a more active role in the freedom struggle.
Therefore, neither of the given statements is entirely correct. The press did criticize official policies, but they had to do it cautiously. The growth of the vernacular press was not solely due to the restrictions imposed by the colonial rulers. It was a combination of various factors that contributed to its growth.
In conclusion, it is essential to understand the role of the press and literature in shaping public opinion and creating awareness about the injustices of the colonial rule. The press had to operate under challenging circumstances, but they managed to play a crucial role in the freedom struggle.
The given statement talks about the role of press and literature in the 19th century in India. Let's break down each statement and see if it is correct or not:
1. The press never criticised official Policies but urged the people to unite.
This statement is not entirely accurate. The press did criticize official policies, but they had to do it carefully because of the restrictions imposed by the colonial rulers. The press played a crucial role in shaping public opinion and creating awareness about the injustices of the colonial rule. They urged people to unite and fight for their rights. However, they had to do it without crossing the line and inviting censorship or prosecution.
2. There was the prolonged growth of Indian owned Vernacular newspapers because of numerous restrictions imposed on the press by the colonial rulers.
This statement is partially correct. Indian owned Vernacular newspapers did grow during the 19th century because they could cater to the local audience and address their concerns. However, the growth of these newspapers was not entirely due to the restrictions imposed by the colonial rulers. The vernacular press had to face numerous challenges, such as the lack of funds, illiteracy, and censorship. It was only after the Indian National Congress was formed in 1885 that the vernacular press gained momentum and started playing a more active role in the freedom struggle.
Therefore, neither of the given statements is entirely correct. The press did criticize official policies, but they had to do it cautiously. The growth of the vernacular press was not solely due to the restrictions imposed by the colonial rulers. It was a combination of various factors that contributed to its growth.
In conclusion, it is essential to understand the role of the press and literature in shaping public opinion and creating awareness about the injustices of the colonial rule. The press had to operate under challenging circumstances, but they managed to play a crucial role in the freedom struggle.
A polynomial of degree n has:- a)Only one zero
- b)At least n zeroes
- c)More than n zeroes
- d)At most n zeroes
Correct answer is option 'D'. Can you explain this answer?
A polynomial of degree n has:
a)
Only one zero
b)
At least n zeroes
c)
More than n zeroes
d)
At most n zeroes
|
|
Anjali garg answered |
Understanding Polynomial Zeros
Polynomials are mathematical expressions that involve variables raised to whole number powers. The degree of a polynomial is defined as the highest power of the variable in the expression.
Key Concept: The Fundamental Theorem of Algebra
- This theorem states that a polynomial of degree n has exactly n roots (or zeros) in the complex number system, counting multiplicities.
Option Analysis
- Option A: Only one zero
- This is not always true; a polynomial can have multiple zeros or none.
- Option B: At least n zeros
- While a polynomial has exactly n roots, some could be repeated (counted multiple times), but they don’t guarantee distinct zeros.
- Option C: More than n zeros
- This is incorrect. A polynomial of degree n cannot have more than n roots.
- Option D: At most n zeros
- This is the correct answer. A polynomial can have anywhere from 0 to n zeros. Zeros can be real or complex. For example:
- A quadratic polynomial (degree 2) can have 0, 1, or 2 real roots.
- A cubic polynomial (degree 3) can have 0, 1, 2, or 3 real roots.
Conclusion
In summary, a polynomial of degree n can have at most n zeros, which may include repeated roots and complex solutions. This is a fundamental principle in algebra that helps in understanding the behavior of polynomial functions.
Polynomials are mathematical expressions that involve variables raised to whole number powers. The degree of a polynomial is defined as the highest power of the variable in the expression.
Key Concept: The Fundamental Theorem of Algebra
- This theorem states that a polynomial of degree n has exactly n roots (or zeros) in the complex number system, counting multiplicities.
Option Analysis
- Option A: Only one zero
- This is not always true; a polynomial can have multiple zeros or none.
- Option B: At least n zeros
- While a polynomial has exactly n roots, some could be repeated (counted multiple times), but they don’t guarantee distinct zeros.
- Option C: More than n zeros
- This is incorrect. A polynomial of degree n cannot have more than n roots.
- Option D: At most n zeros
- This is the correct answer. A polynomial can have anywhere from 0 to n zeros. Zeros can be real or complex. For example:
- A quadratic polynomial (degree 2) can have 0, 1, or 2 real roots.
- A cubic polynomial (degree 3) can have 0, 1, 2, or 3 real roots.
Conclusion
In summary, a polynomial of degree n can have at most n zeros, which may include repeated roots and complex solutions. This is a fundamental principle in algebra that helps in understanding the behavior of polynomial functions.
If one zero of the quadratic polynomial x2 + 3x + k is 2, then the value of k is- a)10
- b)–10
- c)5
- d)–5
Correct answer is option 'B'. Can you explain this answer?
If one zero of the quadratic polynomial x2 + 3x + k is 2, then the value of k is
a)
10
b)
–10
c)
5
d)
–5
|
|
Sheetal jain answered |
Given Problem
We have the quadratic polynomial:
x² + 3x + k, where one of the zeros is 2. We need to find the value of k.
Understanding Zeros of a Polynomial
- A zero (root) of a polynomial is a value of x that makes the polynomial equal to zero.
- If 2 is a zero, we can substitute x = 2 into the polynomial and set it equal to zero.
Substituting the Zero
Let's substitute x = 2 into the polynomial:
- 2² + 3(2) + k = 0
Now, calculate:
- 4 + 6 + k = 0
Simplifying the Equation
- Combine the constants:
10 + k = 0
- Now, isolate k:
k = -10
Conclusion
The value of k that satisfies the condition that one zero of the polynomial is 2 is k = -10.
Thus, the correct answer is option 'B'.
We have the quadratic polynomial:
x² + 3x + k, where one of the zeros is 2. We need to find the value of k.
Understanding Zeros of a Polynomial
- A zero (root) of a polynomial is a value of x that makes the polynomial equal to zero.
- If 2 is a zero, we can substitute x = 2 into the polynomial and set it equal to zero.
Substituting the Zero
Let's substitute x = 2 into the polynomial:
- 2² + 3(2) + k = 0
Now, calculate:
- 4 + 6 + k = 0
Simplifying the Equation
- Combine the constants:
10 + k = 0
- Now, isolate k:
k = -10
Conclusion
The value of k that satisfies the condition that one zero of the polynomial is 2 is k = -10.
Thus, the correct answer is option 'B'.
The zeroes of x2– 2x – 8 are:- a)(2, -4)
- b)(4, -2)
- c)(-2, -2)
- d)(-4, -4)
Correct answer is option 'B'. Can you explain this answer?
The zeroes of x2– 2x – 8 are:
a)
(2, -4)
b)
(4, -2)
c)
(-2, -2)
d)
(-4, -4)

|
EduRev Class 10 answered |
x2 – 2x – 8 = x2 – 4x + 2x – 8
= x(x – 4) + 2(x – 4)
= (x - 4)(x + 2)
Therefore, x = 4, -2.
= x(x – 4) + 2(x – 4)
= (x - 4)(x + 2)
Therefore, x = 4, -2.
If 2 and (- 1/2) as the sum and product of its zeros respectively then the quadratic polynomial f(x) is –- a)x2 – 2x – 4
- b)4x2 – 2x + 1
- c)2x2 + 4x – 1
- d)2x2 – 4x – 1
Correct answer is option 'D'. Can you explain this answer?
If 2 and (- 1/2) as the sum and product of its zeros respectively then the quadratic polynomial f(x) is –
a)
x2 – 2x – 4
b)
4x2 – 2x + 1
c)
2x2 + 4x – 1
d)
2x2 – 4x – 1

|
Kamna Science Academy answered |
Given that the sum of the zeros is 2 and the product is 4, the quadratic equation has the form:
f(x) = a(x2 - 2x + 4)
Setting a = 2 (to match the coefficients), we get:
f(x) = 2(x2 - 2x + 4) = 2x2 - 4x - 1
So, the correct answer is:
d) 2x2 - 4x - 1.
f(x) = a(x2 - 2x + 4)
Setting a = 2 (to match the coefficients), we get:
f(x) = 2(x2 - 2x + 4) = 2x2 - 4x - 1
So, the correct answer is:
d) 2x2 - 4x - 1.
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:Assertion : (2 - √3) is one zero of the quadratic polynomial then other zero will be (2 + √3).Reason : Irrational zeros (roots) always occurs in pairs.- a)Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
- b)Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
- c)Assertion (A) is true but reason (R) is false.
- d)Assertion (A) is false but reason (R) is true.
Correct answer is option 'A'. Can you explain this answer?
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : (2 - √3) is one zero of the quadratic polynomial then other zero will be (2 + √3).
Reason : Irrational zeros (roots) always occurs in pairs.
a)
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
b)
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
c)
Assertion (A) is true but reason (R) is false.
d)
Assertion (A) is false but reason (R) is true.
|
|
Kiran Mehta answered |
As irrational roots/zeros always occurs in pairs therefore, when one zero is (2 - √3) then other will be (2 + √3). So, both A and R are correct and R explains A.
Assertion (A): A polynomial of degree 3 can have at most two real roots.Reason (R): According to the Fundamental Theorem of Algebra, a polynomial of degree n has exactly n roots, which can be real or complex.- a)Both Assertion and Reason are correct, and Reason is the correct explanation of Assertion.
- b)Both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
- c)Assertion is correct, but Reason is incorrect.
- d)Assertion is incorrect, but Reason is correct.
Correct answer is option 'D'. Can you explain this answer?
Assertion (A): A polynomial of degree 3 can have at most two real roots.
Reason (R): According to the Fundamental Theorem of Algebra, a polynomial of degree n has exactly n roots, which can be real or complex.
a)
Both Assertion and Reason are correct, and Reason is the correct explanation of Assertion.
b)
Both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
c)
Assertion is correct, but Reason is incorrect.
d)
Assertion is incorrect, but Reason is correct.

|
Kds Coaching answered |
Answer: d) Assertion is incorrect, but Reason is correct.
Explanation:
A polynomial of degree 3 can have at most three real roots. The assertion stating that it can have at most two real roots is incorrect.
A polynomial of degree 3 can have at most three real roots. The assertion stating that it can have at most two real roots is incorrect.
Assertion (A): The polynomial x2−5x + 6 can be factored as (x−2) (x−3)
Reason (R): The roots of the polynomial are 2 and 3, which can be used to express the polynomial in its factored form.- a)Both Assertion and Reason are correct, and Reason is the correct explanation of Assertion.
- b)Both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
- c)Assertion is correct, but Reason is incorrect.
- d)Assertion is incorrect, but Reason is correct.
Correct answer is option 'A'. Can you explain this answer?
Assertion (A): The polynomial x2−5x + 6 can be factored as (x−2) (x−3)
Reason (R): The roots of the polynomial are 2 and 3, which can be used to express the polynomial in its factored form.
Reason (R): The roots of the polynomial are 2 and 3, which can be used to express the polynomial in its factored form.
a)
Both Assertion and Reason are correct, and Reason is the correct explanation of Assertion.
b)
Both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
c)
Assertion is correct, but Reason is incorrect.
d)
Assertion is incorrect, but Reason is correct.

|
Krithika Iyer answered |
Understanding the Assertion and Reason
The given assertion and reason relate to the polynomial x^2 - 5x + 6 and its factored form.
Assertion (A):
- The polynomial x^2 - 5x + 6 can be factored as (x - 2)(x - 3).
Reason (R):
- The roots of the polynomial are 2 and 3, which can be used to express the polynomial in its factored form.
Explanation of Assertion (A):
- To factor the polynomial x^2 - 5x + 6, we look for two numbers that add up to -5 (the coefficient of x) and multiply to 6 (the constant term).
- The numbers -2 and -3 satisfy these conditions:
- (-2) + (-3) = -5
- (-2) * (-3) = 6
- Thus, the polynomial can indeed be expressed as (x - 2)(x - 3).
Explanation of Reason (R):
- The roots of the polynomial can be found by setting x^2 - 5x + 6 = 0.
- Solving, we find the roots are x = 2 and x = 3.
- These roots confirm that the polynomial can be factored as (x - 2)(x - 3).
Conclusion:
- Both the assertion and the reason are correct.
- The reason directly explains why the assertion holds true, as the roots of the polynomial provide the necessary factors.
Thus, the correct answer is option 'A': Both Assertion and Reason are correct, and Reason is the correct explanation of Assertion.
The given assertion and reason relate to the polynomial x^2 - 5x + 6 and its factored form.
Assertion (A):
- The polynomial x^2 - 5x + 6 can be factored as (x - 2)(x - 3).
Reason (R):
- The roots of the polynomial are 2 and 3, which can be used to express the polynomial in its factored form.
Explanation of Assertion (A):
- To factor the polynomial x^2 - 5x + 6, we look for two numbers that add up to -5 (the coefficient of x) and multiply to 6 (the constant term).
- The numbers -2 and -3 satisfy these conditions:
- (-2) + (-3) = -5
- (-2) * (-3) = 6
- Thus, the polynomial can indeed be expressed as (x - 2)(x - 3).
Explanation of Reason (R):
- The roots of the polynomial can be found by setting x^2 - 5x + 6 = 0.
- Solving, we find the roots are x = 2 and x = 3.
- These roots confirm that the polynomial can be factored as (x - 2)(x - 3).
Conclusion:
- Both the assertion and the reason are correct.
- The reason directly explains why the assertion holds true, as the roots of the polynomial provide the necessary factors.
Thus, the correct answer is option 'A': Both Assertion and Reason are correct, and Reason is the correct explanation of Assertion.
What is the quadratic polynomial whose sum and the product of zeroes is √2, 1/3 respectively?- a)3x2 - 3√2x +1
- b)3x2 + 3√2x +1
- c)3x2 + 3√2x -1
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
What is the quadratic polynomial whose sum and the product of zeroes is √2, 1/3 respectively?
a)
3x2 - 3√2x +1
b)
3x2 + 3√2x +1
c)
3x2 + 3√2x -1
d)
None of the above

|
Gowri Mehta answered |
Understanding the Problem
To find the quadratic polynomial based on the given sum and product of its zeroes, we can use Vieta's formulas. For a quadratic polynomial in the form of ax² + bx + c, the relationships are:
- Sum of zeroes (α + β) = -b/a
- Product of zeroes (αβ) = c/a
In this case, we have:
- Sum of zeroes = √2
- Product of zeroes = 1/3
Formulating the Polynomial
1. Using Vieta's Formulas:
- From the sum of zeroes: α + β = √2
- Hence, -b/a = √2
- From the product of zeroes: αβ = 1/3
- Hence, c/a = 1/3
2. Choosing a Value for 'a':
- Let's choose a = 3 (to eliminate fractions easily).
- Then, -b/3 = √2 implies b = -3√2.
- For c, we have c/3 = 1/3, leading to c = 1.
Constructing the Polynomial
Now substituting the values of a, b, and c into the quadratic polynomial form:
- The polynomial becomes:
3x² - 3√2x + 1
Conclusion
The required quadratic polynomial is:
3x² - 3√2x + 1
Thus, the correct answer is option 'A'.
To find the quadratic polynomial based on the given sum and product of its zeroes, we can use Vieta's formulas. For a quadratic polynomial in the form of ax² + bx + c, the relationships are:
- Sum of zeroes (α + β) = -b/a
- Product of zeroes (αβ) = c/a
In this case, we have:
- Sum of zeroes = √2
- Product of zeroes = 1/3
Formulating the Polynomial
1. Using Vieta's Formulas:
- From the sum of zeroes: α + β = √2
- Hence, -b/a = √2
- From the product of zeroes: αβ = 1/3
- Hence, c/a = 1/3
2. Choosing a Value for 'a':
- Let's choose a = 3 (to eliminate fractions easily).
- Then, -b/3 = √2 implies b = -3√2.
- For c, we have c/3 = 1/3, leading to c = 1.
Constructing the Polynomial
Now substituting the values of a, b, and c into the quadratic polynomial form:
- The polynomial becomes:
3x² - 3√2x + 1
Conclusion
The required quadratic polynomial is:
3x² - 3√2x + 1
Thus, the correct answer is option 'A'.
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:Assertion (A): The graph of y = p(x), where p(x) is a polynomial in variable x, is as follows: The number of zeroes of p(x) is 5.Reason (R): If the graph of a polynomial intersects the x-axis at exactly two points, it need not be a quadratic polynomial.
The number of zeroes of p(x) is 5.Reason (R): If the graph of a polynomial intersects the x-axis at exactly two points, it need not be a quadratic polynomial.- a)Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
- b)Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
- c)Assertion (A) is true but reason (R) is false.
- d)Assertion (A) is false but reason (R) is true.
Correct answer is option 'B'. Can you explain this answer?
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion (A): The graph of y = p(x), where p(x) is a polynomial in variable x, is as follows:

The number of zeroes of p(x) is 5.
Reason (R): If the graph of a polynomial intersects the x-axis at exactly two points, it need not be a quadratic polynomial.
a)
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
b)
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
c)
Assertion (A) is true but reason (R) is false.
d)
Assertion (A) is false but reason (R) is true.
|
|
Ishan Choudhury answered |
In case of assertion: Since the graph touches the x-axis 5 times, So, the number of zeroes of p(x) is 5.
∴ Given statement is correct.
In case of reason:
If a polynomial of degree more than two has two real zeroes and other zeroes are not real or are imaginary, and then graph of the polynomial will intersect at two points on x-axis.
∴ Given statement is correct:
Thus, both assertion and reason are correct but reason is not the correct explanation for assertion.
Assertion (A): The zeroes of the polynomial p(x) = (x - 1)(x - 2)(x - 3) are 1, 2, and 3.
Reason (R): The zeroes of a polynomial are the x-coordinates of the points where the graph of the polynomial intersects or touches the x-axis or the points on the graph where p(x) = 0 - a)Both A and R are true and R is the correct explanation for A.
- b)Both A and R are true and R is not the correct explanation for A.
- c)A is true but R is false.
- d) A is false but R is true.
Correct answer is option 'A'. Can you explain this answer?
Assertion (A): The zeroes of the polynomial p(x) = (x - 1)(x - 2)(x - 3) are 1, 2, and 3.
Reason (R): The zeroes of a polynomial are the x-coordinates of the points where the graph of the polynomial intersects or touches the x-axis or the points on the graph where p(x) = 0
Reason (R): The zeroes of a polynomial are the x-coordinates of the points where the graph of the polynomial intersects or touches the x-axis or the points on the graph where p(x) = 0
a)
Both A and R are true and R is the correct explanation for A.
b)
Both A and R are true and R is not the correct explanation for A.
c)
A is true but R is false.
d)
A is false but R is true.

|
Kamna Science Academy answered |
Option A: Both A and R are true and R is the correct explanation for A.
The polynomial p(x) = (x - 1)(x - 2)(x - 3) \) is factored into three linear factors: (x - 1) , (x - 2) , and (x - 3) .
The zeroes of a polynomial are the values of x for which p(x) = 0. Setting each factor equal to zero gives the zeroes as x = 1 , x = 2 , and x = 3 , which confirms Assertion (A) as correct.
The reason (R) correctly explains the concept that the zeroes of a polynomial are the x-coordinates where the polynomial graph intersects or touches the x-axis, or where p(x) = 0.
Therefore, both the assertion and reason are correct, and the reason provides the correct explanation for the assertion.
Directions: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion: If the sum of the zeroes of the quadratic polynomial x2-2kx+8 is 2 then value of k is 1.
Reason: Sum of zeroes of a quadratic polynomial ax2+bx+c is -b/a
- a)Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
- b)Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
- c)Assertion (A) is true but reason (R) is false.
- d)Assertion (A) is false but reason (R) is true.
Correct answer is option 'A'. Can you explain this answer?
Directions: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion: If the sum of the zeroes of the quadratic polynomial x2-2kx+8 is 2 then value of k is 1.
Reason: Sum of zeroes of a quadratic polynomial ax2+bx+c is -b/a
Reason: Sum of zeroes of a quadratic polynomial ax2+bx+c is -b/a
a)
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
b)
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
c)
Assertion (A) is true but reason (R) is false.
d)
Assertion (A) is false but reason (R) is true.
|
|
Rohit rana answered |
Assertion and Reasoning
Assertion: P(x) = 4x3 – x2 + 5x4 + 3x – 2 is a polynomial of degree 3.
Reason: The highest power of x in the polynomial P(x) is the degree of the polynomial.
Explanation
A polynomial is an expression consisting of variables and coefficients, which are combined using operations of addition, subtraction, multiplication, and non-negative integer exponents. The degree of a polynomial is the highest power of the variable in the polynomial.
In the given assertion, the polynomial P(x) is represented as:
P(x) = 4x3 – x2 + 5x4 + 3x – 2
To find the degree of the polynomial P(x), we need to determine the highest power of x in the polynomial.
Here, the term with the highest power of x is 5x4. Therefore, the degree of the polynomial P(x) is 4, not 3.
Hence, the assertion is false, and the reason is true.
Option D is the correct answer.
Assertion: P(x) = 4x3 – x2 + 5x4 + 3x – 2 is a polynomial of degree 3.
Reason: The highest power of x in the polynomial P(x) is the degree of the polynomial.
Explanation
A polynomial is an expression consisting of variables and coefficients, which are combined using operations of addition, subtraction, multiplication, and non-negative integer exponents. The degree of a polynomial is the highest power of the variable in the polynomial.
In the given assertion, the polynomial P(x) is represented as:
P(x) = 4x3 – x2 + 5x4 + 3x – 2
To find the degree of the polynomial P(x), we need to determine the highest power of x in the polynomial.
Here, the term with the highest power of x is 5x4. Therefore, the degree of the polynomial P(x) is 4, not 3.
Hence, the assertion is false, and the reason is true.
Option D is the correct answer.
The zeroes of the quadratic polynomial x2 + 99x + 127 are- a)both positive
- b)both negative
- c)one positive and one negative
- d)both equal
Correct answer is option 'B'. Can you explain this answer?
The zeroes of the quadratic polynomial x2 + 99x + 127 are
a)
both positive
b)
both negative
c)
one positive and one negative
d)
both equal

|
EduRev Class 10 answered |
Given quadratic polynomial is x2 + 99x + 127.
By comparing with the standard form, we get;
a = 1, b = 99 and c = 127
a > 0, b > 0 and c > 0
We know that in any quadratic polynomial, if all the coefficients have the same sign, then the zeroes of that polynomial will be negative.
Therefore, the zeroes of the given quadratic polynomial are negative.
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:Assertion : If one zero of poly-nominal p(x) = (k2 + 4)x2 + 13x + 4k is reciprocal of other, then k = 2.Reason : If (x – a) is a factor of p(x), then p(a) = 0 i.e. a is a zero of p(x).- a)Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
- b)Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
- c)Assertion (A) is true but reason (R) is false.
- d)Assertion (A) is false but reason (R) is true.
Correct answer is option 'B'. Can you explain this answer?
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : If one zero of poly-nominal p(x) = (k2 + 4)x2 + 13x + 4k is reciprocal of other, then k = 2.
Reason : If (x – a) is a factor of p(x), then p(a) = 0 i.e. a is a zero of p(x).
a)
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
b)
Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
c)
Assertion (A) is true but reason (R) is false.
d)
Assertion (A) is false but reason (R) is true.
|
|
Shobha dubey answered |
Explanation:
Assertion (A) and Reason (R) Analysis:
- The assertion states that if one zero of polynomial p(x) = (k2 + 4)x2 + 13x + 4k is the reciprocal of the other, then k = 2.
- The reason provided is that if (x – a) is a factor of p(x), then p(a) = 0, meaning a is a zero of p(x).
Evaluation of Assertion and Reason:
- The assertion is true because if one zero is the reciprocal of the other, it implies that the product of the zeros is 1 (for a quadratic polynomial).
- However, the reason is not directly related to the assertion. While it is true that if (x – a) is a factor of p(x), then p(a) = 0, this does not directly explain why k = 2 in this specific scenario.
Conclusion:
- Both assertion (A) and reason (R) are true, but the reason does not provide a correct explanation for the assertion. Therefore, the correct choice is option 'B' - Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
Assertion (A) and Reason (R) Analysis:
- The assertion states that if one zero of polynomial p(x) = (k2 + 4)x2 + 13x + 4k is the reciprocal of the other, then k = 2.
- The reason provided is that if (x – a) is a factor of p(x), then p(a) = 0, meaning a is a zero of p(x).
Evaluation of Assertion and Reason:
- The assertion is true because if one zero is the reciprocal of the other, it implies that the product of the zeros is 1 (for a quadratic polynomial).
- However, the reason is not directly related to the assertion. While it is true that if (x – a) is a factor of p(x), then p(a) = 0, this does not directly explain why k = 2 in this specific scenario.
Conclusion:
- Both assertion (A) and reason (R) are true, but the reason does not provide a correct explanation for the assertion. Therefore, the correct choice is option 'B' - Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
Chapter doubts & questions for Polynomials - Mathematics (Maths) Class 10 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Polynomials - Mathematics (Maths) Class 10 in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup