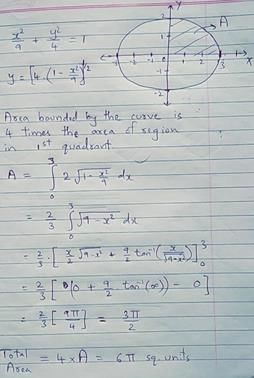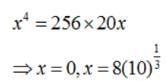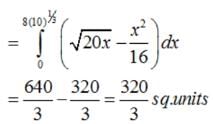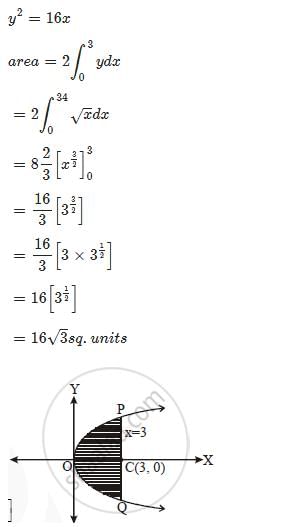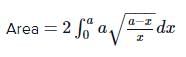All Exams >
Commerce >
Mathematics CUET Preparation >
All Questions
All questions of Chapter 8 - Application of Integrals for Commerce Exam
The area shaded in the given figure can be calculated by which of the following definite integral?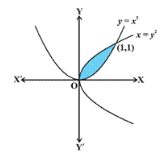
- a)
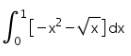
- b)
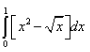
- c)
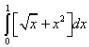
- d)
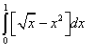
Correct answer is option 'D'. Can you explain this answer?
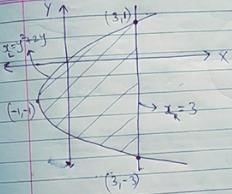
The area shaded in the given figure can be calculated by which of the following definite integral?
a)
b)
c)
d)
|
|
Leelu Bhai answered |
The required area is calculated by the difference of area of upper curve and lower curve.Now equation of upper curve
The area between the curves y = x2 and y = x3 is:
- a) 1/12 sq.units
- b) 1/8 sq.units
- c) 1/10 sq.unit
- d) 1/6 sq.units
Correct answer is option 'A'. Can you explain this answer?
The area between the curves y = x2 and y = x3 is:
a)
1/12 sq.unitsb)
1/8 sq.unitsc)
1/10 sq.unitd)
1/6 sq.units
|
Arun Khanna answered |
First we note that the curves intersect at the points (0,0) and (1,1). Then we see that
x^3 < x^2
in this interval. Hence the area is given by
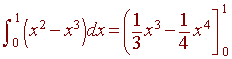
= 1/3 - 1/4 = 1/12.
The area of the region bounded by y = x2 – 2x and y = 4 – x2 is.- a)7 sq. units
- b)8 sq. units
- c)9 sq. units
- d)10 sq. units
Correct answer is option 'C'. Can you explain this answer?
The area of the region bounded by y = x2 – 2x and y = 4 – x2 is.
a)
7 sq. units
b)
8 sq. units
c)
9 sq. units
d)
10 sq. units
|
Vikas Kapoor answered |
To find area between y = x2 – 2x and y = 4 – x2,
We need to find POI.
x2 – 2x = 4 – x2
2x2 - 2x – 4 = 0
x2 – x – 2 = 0
(x-2)(x+1) = 0
x = -1, 2
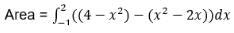
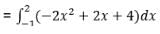
= [(-2x3)/3 + x2 + 4x]x=2 - [(-2x3)/3 + x2 + 4x]x= -1
= -16/3 + 4 + 8 – (2/3 + 1 - 4)
= 9 sq units
We need to find POI.
x2 – 2x = 4 – x2
2x2 - 2x – 4 = 0
x2 – x – 2 = 0
(x-2)(x+1) = 0
x = -1, 2
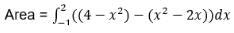
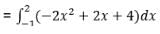
= [(-2x3)/3 + x2 + 4x]x=2 - [(-2x3)/3 + x2 + 4x]x= -1
= -16/3 + 4 + 8 – (2/3 + 1 - 4)
= 9 sq units
The area enclosed between the lines x = 2 and x = 7 is- a)Infinite
- b)7 units
- c)5 units
- d)2 units
Correct answer is option 'A'. Can you explain this answer?
The area enclosed between the lines x = 2 and x = 7 is
a)
Infinite
b)
7 units
c)
5 units
d)
2 units
|
Manas Khantal answered |
See from graph of x=2 & x=7 it's simple
The area bounded by the curve y2 = 16x , x = 1, y = 3 and X-axis is: - a)
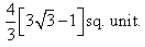
- b)
- c)
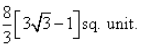
- d)
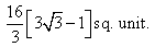
Correct answer is option 'C'. Can you explain this answer?
The area bounded by the curve y2 = 16x , x = 1, y = 3 and X-axis is:
a)
b)
c)
d)
|
Moksh Sharma answered |
Plese give detailed solution of this question
Direction: Read the following text and answer the following questions on the basis of the same:A farmer has a square plot of land. Three of its boundaries are x = 0, y = 0 and y = 4. He wants to divide this land among his three sons A, B and C as shown in figure.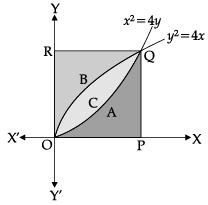
Q. Area received by son B is _______ sq. units.- a)4
- b)16
- c)16/3
- d)8/3
Correct answer is option 'C'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
A farmer has a square plot of land. Three of its boundaries are x = 0, y = 0 and y = 4. He wants to divide this land among his three sons A, B and C as shown in figure.
Q. Area received by son B is _______ sq. units.
a)
4
b)
16
c)
16/3
d)
8/3
|
Vp Classes answered |
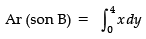
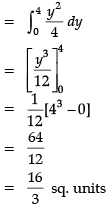
The area of the region bounded by the parabola (y−2)2 = x−1,the tangent to yhe parabola at the point (2 , 3) and the x – axis is equal to- a)12 sq. units
- b)6 sq. units
- c)9 sq. units
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The area of the region bounded by the parabola (y−2)2 = x−1,the tangent to yhe parabola at the point (2 , 3) and the x – axis is equal to
a)
12 sq. units
b)
6 sq. units
c)
9 sq. units
d)
none of these
|
Mohit Patel answered |
Therefore, tangent at (2, 3) is y – 3 = ½ (x – 2). i.e. x – 2y +4 = 0 . therefore required area is
The area bounded by the parabola y2 = 4x and the line x + y = 3 is- a)32/3
- b)16/3
- c)64/3
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The area bounded by the parabola y2 = 4x and the line x + y = 3 is
a)
32/3
b)
16/3
c)
64/3
d)
none of these
|
Gitanjali Tiwari answered |
To find the area bounded by the parabola y^2 = 4x and the line x + y = 3, we need to find the points of intersection between the parabola and the line and then calculate the area between them.
Finding the Points of Intersection:
To find the points of intersection, we can set the equations of the parabola and the line equal to each other and solve for x and y:
y^2 = 4x
x + y = 3
Substituting y = 3 - x into the equation of the parabola, we get:
(3 - x)^2 = 4x
Expanding and rearranging the equation, we get:
9 - 6x + x^2 = 4x
x^2 + 10x - 9 = 0
Now, we can solve this quadratic equation for x using factoring or the quadratic formula. By factoring, we can write it as:
(x + 9)(x - 1) = 0
This gives us two possible values for x: x = -9 and x = 1.
Substituting these values back into the equation of the line, we can find the corresponding y-values:
For x = -9:
y = 3 - (-9) = 3 + 9 = 12
For x = 1:
y = 3 - 1 = 2
So, the points of intersection are (-9, 12) and (1, 2).
Calculating the Area:
To calculate the area bounded by the parabola and the line, we can integrate the difference between the y-values of the parabola and the line over the interval between the x-values of intersection points.
We need to find the integral of (y - (3 - x)) with respect to x, where y is given by the equation of the parabola: y = √(4x).
The integral becomes:
∫[(√(4x) - (3 - x))] dx
Integrating and evaluating this integral from x = -9 to x = 1 gives us the required area:
A = ∫[(√(4x) - (3 - x))] dx (from x = -9 to x = 1)
Simplifying the integral and evaluating it, we get:
A = [(2/3)x^(3/2) + (x^2)/2 - 3x] (from x = -9 to x = 1)
= [2/3 + 1/2 - 3 - ((2/3)(-9)^(3/2) + ((-9)^2)/2 - 3(-9))]
Calculating this expression, we get:
A = [2/3 + 1/2 - 3 - (2/3 - 243/2 + 27)]
= [2/3 + 1/2 - 3 - 2/3 + 243/2 - 27]
= [16/3]
Therefore, the area bounded by the parabola y^2 = 4x and the line x + y = 3 is 16/3.
Finding the Points of Intersection:
To find the points of intersection, we can set the equations of the parabola and the line equal to each other and solve for x and y:
y^2 = 4x
x + y = 3
Substituting y = 3 - x into the equation of the parabola, we get:
(3 - x)^2 = 4x
Expanding and rearranging the equation, we get:
9 - 6x + x^2 = 4x
x^2 + 10x - 9 = 0
Now, we can solve this quadratic equation for x using factoring or the quadratic formula. By factoring, we can write it as:
(x + 9)(x - 1) = 0
This gives us two possible values for x: x = -9 and x = 1.
Substituting these values back into the equation of the line, we can find the corresponding y-values:
For x = -9:
y = 3 - (-9) = 3 + 9 = 12
For x = 1:
y = 3 - 1 = 2
So, the points of intersection are (-9, 12) and (1, 2).
Calculating the Area:
To calculate the area bounded by the parabola and the line, we can integrate the difference between the y-values of the parabola and the line over the interval between the x-values of intersection points.
We need to find the integral of (y - (3 - x)) with respect to x, where y is given by the equation of the parabola: y = √(4x).
The integral becomes:
∫[(√(4x) - (3 - x))] dx
Integrating and evaluating this integral from x = -9 to x = 1 gives us the required area:
A = ∫[(√(4x) - (3 - x))] dx (from x = -9 to x = 1)
Simplifying the integral and evaluating it, we get:
A = [(2/3)x^(3/2) + (x^2)/2 - 3x] (from x = -9 to x = 1)
= [2/3 + 1/2 - 3 - ((2/3)(-9)^(3/2) + ((-9)^2)/2 - 3(-9))]
Calculating this expression, we get:
A = [2/3 + 1/2 - 3 - (2/3 - 243/2 + 27)]
= [2/3 + 1/2 - 3 - 2/3 + 243/2 - 27]
= [16/3]
Therefore, the area bounded by the parabola y^2 = 4x and the line x + y = 3 is 16/3.
The area bounded by the curve y2 = x,line y = 4 and y – axis is equal to- a)7√2
- b)16/3
- c)64/3
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The area bounded by the curve y2 = x,line y = 4 and y – axis is equal to
a)
7√2
b)
16/3
c)
64/3
d)
none of these
|
Aniket Dasgupta answered |
Introduction
To find the area bounded by the curve y² = x, the line y = 4, and the y-axis, we need to first understand the shapes formed by these equations.
Step 1: Understanding the Curves
- The equation y² = x represents a rightward-opening parabola.
- The line y = 4 is a horizontal line.
- The y-axis is the vertical line where x = 0.
Step 2: Finding Intersection Points
- To find the points of intersection between the parabola and the line y = 4, substitute y into the parabola's equation:
- 4² = x → x = 16.
- Thus, the points of intersection are (16, 4) and (0, 0).
Step 3: Setting Up the Area Calculation
- The area can be calculated by integrating the area under the curve from the y-axis to the intersection point along the line y = 4.
- We will integrate the function derived from the parabola, which is x = y².
Step 4: Calculating the Area
- The area can be expressed as:
- Area = ∫ (from y=0 to y=4) (y²) dy.
- Evaluating this integral:
- Area = [y³/3] from 0 to 4
- Area = (4³/3 - 0) = 64/3.
Conclusion
The area bounded by the curve y² = x, the line y = 4, and the y-axis is 64/3. Since the correct answer choice in the question is option 'B', which is 16/3, it appears to be a mistake as the computed area is 64/3. Thus, the area calculation confirms that the answer is indeed 64/3, not 16/3.
To find the area bounded by the curve y² = x, the line y = 4, and the y-axis, we need to first understand the shapes formed by these equations.
Step 1: Understanding the Curves
- The equation y² = x represents a rightward-opening parabola.
- The line y = 4 is a horizontal line.
- The y-axis is the vertical line where x = 0.
Step 2: Finding Intersection Points
- To find the points of intersection between the parabola and the line y = 4, substitute y into the parabola's equation:
- 4² = x → x = 16.
- Thus, the points of intersection are (16, 4) and (0, 0).
Step 3: Setting Up the Area Calculation
- The area can be calculated by integrating the area under the curve from the y-axis to the intersection point along the line y = 4.
- We will integrate the function derived from the parabola, which is x = y².
Step 4: Calculating the Area
- The area can be expressed as:
- Area = ∫ (from y=0 to y=4) (y²) dy.
- Evaluating this integral:
- Area = [y³/3] from 0 to 4
- Area = (4³/3 - 0) = 64/3.
Conclusion
The area bounded by the curve y² = x, the line y = 4, and the y-axis is 64/3. Since the correct answer choice in the question is option 'B', which is 16/3, it appears to be a mistake as the computed area is 64/3. Thus, the area calculation confirms that the answer is indeed 64/3, not 16/3.
The area of the figure bounded by the curve y = logex , the x – axis and the straight line x = e is- a)1
- b)5 - e
- c)3 + e
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The area of the figure bounded by the curve y = logex , the x – axis and the straight line x = e is
a)
1
b)
5 - e
c)
3 + e
d)
none of these
|
Sparsh Chawla answered |
Area of the figure bounded by the curve y = logex, the x-axis, and the straight line x = e
The area of the figure bounded by the curve y = logex, the x-axis, and the straight line x = e can be found by integrating the function y = logex with respect to x between the limits x = 1 and x = e.
Integration of y = logex
∫(logex) dx = x(logex - 1) + C
Calculate the area
To find the area of the figure, we need to evaluate the integral of logex between the limits x = 1 and x = e.
Area = [e(loge^e - 1) - 1(loge - 1)]
Area = [e(1) - 1(0) - (0)]
Area = e - 0 - 0 = e
Therefore, the area of the figure bounded by the curve y = logex, the x-axis, and the straight line x = e is 1.
The area of the figure bounded by the curve y = logex, the x-axis, and the straight line x = e can be found by integrating the function y = logex with respect to x between the limits x = 1 and x = e.
Integration of y = logex
∫(logex) dx = x(logex - 1) + C
Calculate the area
To find the area of the figure, we need to evaluate the integral of logex between the limits x = 1 and x = e.
Area = [e(loge^e - 1) - 1(loge - 1)]
Area = [e(1) - 1(0) - (0)]
Area = e - 0 - 0 = e
Therefore, the area of the figure bounded by the curve y = logex, the x-axis, and the straight line x = e is 1.
The area bounded by the curves y2 = 4x and y = x is equal to- a)8/3
- b)35/6
- c)1/3
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The area bounded by the curves y2 = 4x and y = x is equal to
a)
8/3
b)
35/6
c)
1/3
d)
none of these
|
Pranav Pillai answered |
The two curves y2 = 4x and y = x meet where x2 = 4x i.e ..where x = 0 or x = 4 . Moreover , the parabola lies above the line y = x between x = 0 and x = 4 . Hence , the required are is :
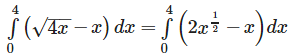
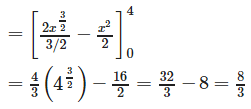
The area enclosed between the curves y = √x , x = 2y+3and the x-axis is- a)9
- b)18
- c)27
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The area enclosed between the curves y = √x , x = 2y+3and the x-axis is
a)
9
b)
18
c)
27
d)
none of these
|
Manisha Mehta answered |
The two curves meet where;
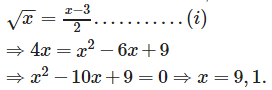
Therefore, the two curves meet where x = 9.
Therefore,required Area:
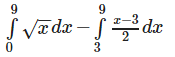
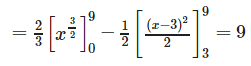
Therefore, the two curves meet where x = 9.
Therefore,required Area:
Let y be the function which passes through (1 , 2) having slope (2x + 1) . The area bounded between the curve and the x – axis is- a)1/6 sq. units
- b)6 sq. units
- c)5/6 sq. units
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Let y be the function which passes through (1 , 2) having slope (2x + 1) . The area bounded between the curve and the x – axis is
a)
1/6 sq. units
b)
6 sq. units
c)
5/6 sq. units
d)
none of these
|
|
Sanskriti Dasgupta answered |
-axis from x = 1 to x = 5 is:
To find the equation of the function y, we integrate the given slope function:
∫(2x + 1) dx = x^2 + x + C
Using the point (1,2), we can solve for the constant C:
1^2 + 1 + C = 2
C = 0
So the equation of the function y is:
y = x^2 + x
To find the area bounded between the curve and the x-axis from x = 1 to x = 5, we integrate the function y with respect to x:
∫[1,5] (x^2 + x) dx = [1/3 x^3 + 1/2 x^2] [1,5] = (125/3 + 25/2) - (1/3 + 1/2) = 116/3
Therefore, the area bounded between the curve and the x-axis from x = 1 to x = 5 is 116/3 square units.
To find the equation of the function y, we integrate the given slope function:
∫(2x + 1) dx = x^2 + x + C
Using the point (1,2), we can solve for the constant C:
1^2 + 1 + C = 2
C = 0
So the equation of the function y is:
y = x^2 + x
To find the area bounded between the curve and the x-axis from x = 1 to x = 5, we integrate the function y with respect to x:
∫[1,5] (x^2 + x) dx = [1/3 x^3 + 1/2 x^2] [1,5] = (125/3 + 25/2) - (1/3 + 1/2) = 116/3
Therefore, the area bounded between the curve and the x-axis from x = 1 to x = 5 is 116/3 square units.
The area bounded by the parabolas y = 5x2and y − 9 = 2x2 is- a)12√3 sq.units
- b)6√2 sq.units
- c)12√2 sq.units
- d)4√3 sq.units
Correct answer is option 'A'. Can you explain this answer?
The area bounded by the parabolas y = 5x2and y − 9 = 2x2 is
a)
12√3 sq.units
b)
6√2 sq.units
c)
12√2 sq.units
d)
4√3 sq.units
|
|
Saranya Choudhary answered |
Explanation:
Finding the Points of Intersection:
To find the points of intersection of the two parabolas, set them equal to each other:
5x^2 = 9 - 2x^2
7x^2 = 9
x^2 = 9/7
x = ±√(9/7)
Calculating the Area Between the Curves:
Integrate the difference of the two equations between the points of intersection to find the area:
∫(9 - 2x^2) - 5x^2 dx from -√(9/7) to √(9/7)
= ∫(9 - 7x^2) dx from -√(9/7) to √(9/7)
= [9x - (7x^3)/3] from -√(9/7) to √(9/7)
Substitute the Values:
= [9√(9/7) - (7(9/7)^(3/2))/3] - [-9√(9/7) - (7(9/7)^(3/2))/3]
= (27/√7 - 21√7/3) - (-27/√7 - 21√7/3)
= 54/√7
Final Calculation:
To find the area, square the result:
(54/√7)^2 = 2916/7 = 123 sq. units
Therefore, the area bounded by the parabolas y = 5x^2 and y = 9 - 2x^2 is 123 sq. units.
Finding the Points of Intersection:
To find the points of intersection of the two parabolas, set them equal to each other:
5x^2 = 9 - 2x^2
7x^2 = 9
x^2 = 9/7
x = ±√(9/7)
Calculating the Area Between the Curves:
Integrate the difference of the two equations between the points of intersection to find the area:
∫(9 - 2x^2) - 5x^2 dx from -√(9/7) to √(9/7)
= ∫(9 - 7x^2) dx from -√(9/7) to √(9/7)
= [9x - (7x^3)/3] from -√(9/7) to √(9/7)
Substitute the Values:
= [9√(9/7) - (7(9/7)^(3/2))/3] - [-9√(9/7) - (7(9/7)^(3/2))/3]
= (27/√7 - 21√7/3) - (-27/√7 - 21√7/3)
= 54/√7
Final Calculation:
To find the area, square the result:
(54/√7)^2 = 2916/7 = 123 sq. units
Therefore, the area bounded by the parabolas y = 5x^2 and y = 9 - 2x^2 is 123 sq. units.
The area bounded by the angle bisectors of the lines x2−y2+2y = 1 and x+y = 3 is- a)6 sq. units
- b)2 sq. units
- c)3 sq.units
- d)4 sq. units
Correct answer is option 'B'. Can you explain this answer?
The area bounded by the angle bisectors of the lines x2−y2+2y = 1 and x+y = 3 is
a)
6 sq. units
b)
2 sq. units
c)
3 sq.units
d)
4 sq. units
|
Jatin Dasgupta answered |
The angle bisectors of the line given by x2−− y2+2y = 1 are x = 0 , y = 1. Required area = 1/2 .2.2 = 2 sq. units
Direction: Read the following text and answer the following questions on the basis of the same:A farmer has a square plot of land. Three of its boundaries are x = 0, y = 0 and y = 4. He wants to divide this land among his three sons A, B and C as shown in figure.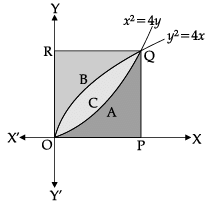
Q. Area received by son A is _______ sq. units.- a)4
- b)16
- c)16/3
- d)8/3
Correct answer is option 'C'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
A farmer has a square plot of land. Three of its boundaries are x = 0, y = 0 and y = 4. He wants to divide this land among his three sons A, B and C as shown in figure.
Q. Area received by son A is _______ sq. units.
a)
4
b)
16
c)
16/3
d)
8/3
|
Veda Institute answered |
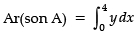
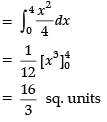
Direction: Read the following text and answer the following questions on the basis of the same:
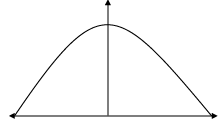The bridge connects two hills 100 feet apart. The arch on the bridge is in a parabolic form. The highest point on the bridge is 10 feet above the road at the middle of the bridge as seen in the figure.Q. The value of the integral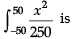
- a)1000/3
- b)250/3
- c)1200
- d)0
Correct answer is option 'A'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
The bridge connects two hills 100 feet apart. The arch on the bridge is in a parabolic form. The highest point on the bridge is 10 feet above the road at the middle of the bridge as seen in the figure.
Q. The value of the integral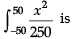
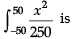
a)
1000/3
b)
250/3
c)
1200
d)
0
|
|
Anjali Sharma answered |
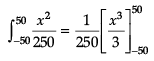
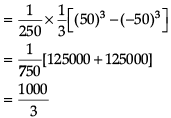
The area bounded by the curve y = 2x - x2 and the line x + y = 0 is- a)9/2 sq. units
- b)35/6 sq. units
- c)19/6 sq. units
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The area bounded by the curve y = 2x - x2 and the line x + y = 0 is
a)
9/2 sq. units
b)
35/6 sq. units
c)
19/6 sq. units
d)
none of these
|
|
Pranav Pillai answered |
The equation y = 2x − x2 i.e. y – 1 = - (x - 1)2 represents a downward parabola with vertex at (1, 1) which meets x – axis where y = 0 .i .e . where x = 0 , 2. Also , the line y = - x meets this parabola where – x = 2x − x2 i.e. where x = 0 , 3.
Therefore , required area is :
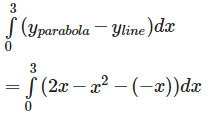
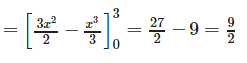
Therefore , required area is :
The area bounded by the curve y = x3, the x – axis and two ordinates x = 1 and x = 2 is- a)17/2 sq. units
- b)15/2 sq. units
- c)15/4 sq. units
- d)17/4 sq. units
Correct answer is option 'C'. Can you explain this answer?
The area bounded by the curve y = x3, the x – axis and two ordinates x = 1 and x = 2 is
a)
17/2 sq. units
b)
15/2 sq. units
c)
15/4 sq. units
d)
17/4 sq. units
|
|
Vijay Bansal answered |
The area bounded by the curve y = x^3 and the x-axis can be found by integrating the function from the x-coordinate of the x-intercept to the x-coordinate of the y-intercept.
To find the x-intercept, set y = 0:
0 = x^3
x = 0
To find the y-intercept, set x = 0:
y = 0^3
y = 0
The area bounded by the curve can be found by integrating the function y = x^3 from x = 0 to x = 0:
∫[0,0] x^3 dx
Since the limits of integration are the same, the integral evaluates to zero. Therefore, the area bounded by the curve y = x^3 and the x-axis is 0.
To find the x-intercept, set y = 0:
0 = x^3
x = 0
To find the y-intercept, set x = 0:
y = 0^3
y = 0
The area bounded by the curve can be found by integrating the function y = x^3 from x = 0 to x = 0:
∫[0,0] x^3 dx
Since the limits of integration are the same, the integral evaluates to zero. Therefore, the area bounded by the curve y = x^3 and the x-axis is 0.
Area of the region bounded by the curves y = ex, x = a , x = b and the x- axis is given by- a)eb−ea
- b)eb−a
- c)eb+ea
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Area of the region bounded by the curves y = ex, x = a , x = b and the x- axis is given by
a)
eb−ea
b)
eb−a
c)
eb+ea
d)
none of these
|
Nisha Sen answered |
To find the area of the region bounded by the curves y = ex, x = a, x = b, and the x-axis, we can use integration.
Step 1: Determine the limits of integration
The region is bounded by the vertical lines x = a and x = b, so the limits of integration for x will be from a to b.
Step 2: Set up the integral
The area of the region can be found by integrating the function y = ex with respect to x over the given limits of integration.
The integral for the area is given by:
∫(ex) dx from a to b
Step 3: Evaluate the integral
Integrating the function ex with respect to x gives us ex.
So, the integral becomes:
∫(ex) dx = ex
Evaluating this integral from a to b gives us:
ex evaluated from a to b = eb - ea
Step 4: Subtracting the areas below the x-axis
Since the region is bounded by the x-axis, we need to consider the areas below the x-axis as negative.
If there are any values of x within the interval (a, b) where ex is negative, we need to subtract the absolute value of the integral of ex in that range. However, since the function ex is always positive, we don't need to consider this step.
Step 5: Finalize the answer
The area of the region bounded by the curves y = ex, x = a, x = b, and the x-axis is given by:
Area = eb - ea
Therefore, the correct answer is option A) eb - ea.
Step 1: Determine the limits of integration
The region is bounded by the vertical lines x = a and x = b, so the limits of integration for x will be from a to b.
Step 2: Set up the integral
The area of the region can be found by integrating the function y = ex with respect to x over the given limits of integration.
The integral for the area is given by:
∫(ex) dx from a to b
Step 3: Evaluate the integral
Integrating the function ex with respect to x gives us ex.
So, the integral becomes:
∫(ex) dx = ex
Evaluating this integral from a to b gives us:
ex evaluated from a to b = eb - ea
Step 4: Subtracting the areas below the x-axis
Since the region is bounded by the x-axis, we need to consider the areas below the x-axis as negative.
If there are any values of x within the interval (a, b) where ex is negative, we need to subtract the absolute value of the integral of ex in that range. However, since the function ex is always positive, we don't need to consider this step.
Step 5: Finalize the answer
The area of the region bounded by the curves y = ex, x = a, x = b, and the x-axis is given by:
Area = eb - ea
Therefore, the correct answer is option A) eb - ea.
is : 
The area bounded by the curves y = √x , 2y+3 = x and the x – axis in the first quadrant is- a)9
- b)18
- c)36
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The area bounded by the curves y = √x , 2y+3 = x and the x – axis in the first quadrant is
a)
9
b)
18
c)
36
d)
none of these
|
|
Sagar Yadav answered |
Given curves:
- y = x
- 2y + 3 = x
Finding intersection points:
1. Substitute y = x into the second equation:
2( x ) + 3 = x
2x + 3 = x
x = -3
2. Substitute x = -3 into y = x:
y = -3
Intersection points:
(-3, -3)
Area calculation:
1. The area between the curves can be calculated by finding the area under the curves between the points of intersection.
2. The vertical strip of the area can be expressed as:
A = ∫[x1, x2] (f(x) - g(x)) dx
= ∫[-3, 0] (x - (2x + 3)) dx
= ∫[-3, 0] (x - 2x - 3) dx
= ∫[-3, 0] (-x - 3) dx
= [-0.5x^2 - 3x] [-3, 0]
= [4.5 - 9] = 4.5
Answer:
The area bounded by the curves y = x, 2y + 3 = x, and the x-axis in the first quadrant is 4.5 square units, which is not available in the given options. So, the correct answer is none of these.
- y = x
- 2y + 3 = x
Finding intersection points:
1. Substitute y = x into the second equation:
2( x ) + 3 = x
2x + 3 = x
x = -3
2. Substitute x = -3 into y = x:
y = -3
Intersection points:
(-3, -3)
Area calculation:
1. The area between the curves can be calculated by finding the area under the curves between the points of intersection.
2. The vertical strip of the area can be expressed as:
A = ∫[x1, x2] (f(x) - g(x)) dx
= ∫[-3, 0] (x - (2x + 3)) dx
= ∫[-3, 0] (x - 2x - 3) dx
= ∫[-3, 0] (-x - 3) dx
= [-0.5x^2 - 3x] [-3, 0]
= [4.5 - 9] = 4.5
Answer:
The area bounded by the curves y = x, 2y + 3 = x, and the x-axis in the first quadrant is 4.5 square units, which is not available in the given options. So, the correct answer is none of these.
Direction: Read the following text and answer the following questions on the basis of the same:
The bridge connects two hills 100 feet apart. The arch on the bridge is in a parabolic form. The highest point on the bridge is 10 feet above the road at the middle of the bridge as seen in the figure.Q. The area formed by the curve x2 = 250y, x-axis, y = 0 and y = 10 is- a)1000√2/3
- b)4/3
- c)1000/3
- d)0
Correct answer is option 'C'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
The bridge connects two hills 100 feet apart. The arch on the bridge is in a parabolic form. The highest point on the bridge is 10 feet above the road at the middle of the bridge as seen in the figure.
Q. The area formed by the curve x2 = 250y, x-axis, y = 0 and y = 10 is
a)
1000√2/3
b)
4/3
c)
1000/3
d)
0
|
Mohit Rajpoot answered |
X2 = 250 y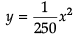
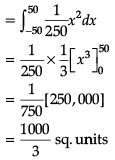
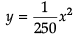
at = y = 0 x = 0
at y = 10 x = 50, -50
∴ Area formed by curve
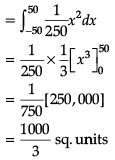
The area bounded by the curves y= |x−1| and y = 1 is given by- a)2
- b)1
- c)1/2
- d)none of these.
Correct answer is option 'B'. Can you explain this answer?
The area bounded by the curves y= |x−1| and y = 1 is given by
a)
2
b)
1
c)
1/2
d)
none of these.
|
Bhavya Joshi answered |
The given curves are : (i) y = x – 1 , x > 1 . (ii) y = - (x – 1) , x < 1. (iii) y = 1 these three lines enclose a triangle whose area is : 1/2 .base.height = 1/2 .2 .1 = 1 sq. unit.
The area bounded by y = 2cosx , x = 0 to x = 2π and the axis of x in square units is- a)6
- b)4
- c)8
- d)7
Correct answer is option 'C'. Can you explain this answer?
The area bounded by y = 2cosx , x = 0 to x = 2π and the axis of x in square units is
a)
6
b)
4
c)
8
d)
7
|
|
Manisha Mehta answered |
Required area :
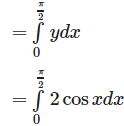
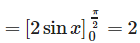
Therefore , total area from x = 0 to x = 2π is 4 X 2= 8 sq. units.
Therefore , total area from x = 0 to x = 2π is 4 X 2= 8 sq. units.
Direction: Read the following text and answer the following questions on the basis of the same:A farmer has a square plot of land. Three of its boundaries are x = 0, y = 0 and y = 4. He wants to divide this land among his three sons A, B and C as shown in figure.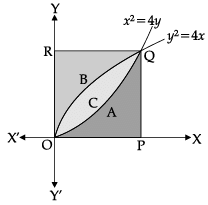
Q. Total area of the square field is _______ sq. units- a)4
- b)16
- c)16/3
- d)8/3
Correct answer is option 'B'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
A farmer has a square plot of land. Three of its boundaries are x = 0, y = 0 and y = 4. He wants to divide this land among his three sons A, B and C as shown in figure.
Q. Total area of the square field is _______ sq. units
a)
4
b)
16
c)
16/3
d)
8/3
|
|
Anjali Sharma answered |
Total area = 4 × 4
= 16 sq. units
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice asAssertion (A): If the two curves y = f(x) and y = g(x) intersect at x = a, x = c and x = b, such that a < c="" />< />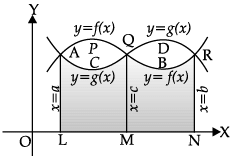
If f(x) > g(x) in [a, c] and g(x) £ f(x) in [c, b], then Area of the regions bounded by the curve= Area of region PACQP + Area of region QDRBQ.
Reason (R): Let the two curves by y = f(x) and y = g(x), as shown in the figure. Suppose these curves intersect at f(x) with width dx.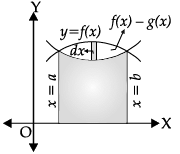
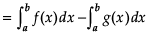= Area bounded by the curve {y = f(x)}–Area bounded by the curve {y = g(x)}, where f(x) > g(x).- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false and R is True
Correct answer is option 'B'. Can you explain this answer?
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as
Assertion (A): If the two curves y = f(x) and y = g(x) intersect at x = a, x = c and x = b, such that a < c="" />< />
If f(x) > g(x) in [a, c] and g(x) £ f(x) in [c, b], then Area of the regions bounded by the curve
= Area of region PACQP + Area of region QDRBQ.
Reason (R): Let the two curves by y = f(x) and y = g(x), as shown in the figure. Suppose these curves intersect at f(x) with width dx.
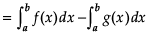
= Area bounded by the curve {y = f(x)}
–Area bounded by the curve {y = g(x)}, where f(x) > g(x).
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false and R is True
|
|
Anjali Sharma answered |
Assertion (A) and Reason (R) both are individually correct.
Chapter doubts & questions for Chapter 8 - Application of Integrals - Mathematics CUET Preparation 2025 is part of Commerce exam preparation. The chapters have been prepared according to the Commerce exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Commerce 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Chapter 8 - Application of Integrals - Mathematics CUET Preparation in English & Hindi are available as part of Commerce exam.
Download more important topics, notes, lectures and mock test series for Commerce Exam by signing up for free.
Mathematics CUET Preparation
145 videos|67 docs|105 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup