All Exams >
SSC MTS / SSC GD >
Quantitative Aptitude for Competitive Exams >
All Questions
All questions of Height & Distance for SSC MTS / SSC GD Exam
A man standing at a point P is watching the top of a tower, which makes an angle of elevation of 30º with the man's eye. The man walks some distance towards the tower to watch its top and the angle of the elevation becomes 60º. What is the distance between the base of the tower and the point P?- a)4√3 units
- b)8 units
- c)12 units
- d)Data inadequate
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
A man standing at a point P is watching the top of a tower, which makes an angle of elevation of 30º with the man's eye. The man walks some distance towards the tower to watch its top and the angle of the elevation becomes 60º. What is the distance between the base of the tower and the point P?
a)
4√3 units
b)
8 units
c)
12 units
d)
Data inadequate
e)
None of these
|
Kalyan Mukherjee answered |
A vertical stick 12 cm long casts a shadow 8 cm long on the ground. At the same time, a tower casts a shadow 40 m long on the ground. The height of the tower is- a)72 m
- b)60 m
- c)65 m
- d)70 m
Correct answer is option 'B'. Can you explain this answer?
A vertical stick 12 cm long casts a shadow 8 cm long on the ground. At the same time, a tower casts a shadow 40 m long on the ground. The height of the tower is
a)
72 m
b)
60 m
c)
65 m
d)
70 m
|
EduRev SSC CGL answered |
We can solve it through ratio proportion rule,
let the tower is x m long, then
12 cm stick casts → 8 cm shadow
x m tower casts → 40 m shadow
On cross multiplying, we get
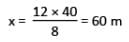
Hence, option B is correct.
let the tower is x m long, then
12 cm stick casts → 8 cm shadow
x m tower casts → 40 m shadow
On cross multiplying, we get
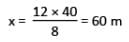
Hence, option B is correct.
Practice Quiz or MCQ (Multiple Choice Questions) with solution are available for Practice, which would help you prepare for "Height and Distance" under Logical Reasoning and Data Interpretative. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations.Q.Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is:- a)173 m
- b)200 m
- c)273 m
- d)300 m
Correct answer is option 'C'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solution are available for Practice, which would help you prepare for "Height and Distance" under Logical Reasoning and Data Interpretative. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations.
Q.
Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is:
a)
173 m
b)
200 m
c)
273 m
d)
300 m
|
Nandini Singh answered |
Let AB be the lighthouse and C and D be the positions of the ships.
A vertical tower stands on ground and is surmounted by a vertical flagpole of height 18 m. At a point on the ground, the angle of elevation of the bottom and the top of the flagpole are 30° and 60° respectively. What is the height of the tower?- a)9 m
- b)10.40 m
- c)15.57 m
- d)12 m
- e)14 m
Correct answer is option 'A'. Can you explain this answer?
A vertical tower stands on ground and is surmounted by a vertical flagpole of height 18 m. At a point on the ground, the angle of elevation of the bottom and the top of the flagpole are 30° and 60° respectively. What is the height of the tower?
a)
9 m
b)
10.40 m
c)
15.57 m
d)
12 m
e)
14 m
|
Talent Skill Learning answered |
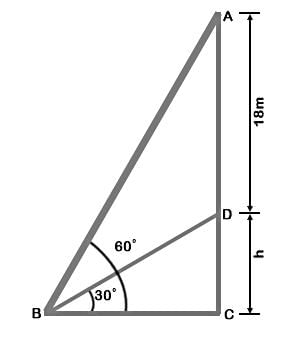
Let DC be the vertical tower and AD be the vertical flagpole. Let B be the point of observation.
Given that AD = 18 m, ∠ ABC = 60°, ∠ DBC = 30°
Let DC be h
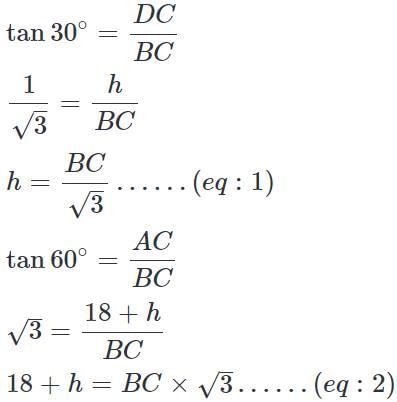
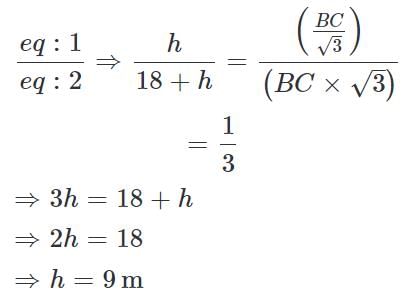
i.e., the height of the tower = 9 m
A man is watching from the top of tower a boat speeding away from the tower. The boat makes an angle of depression of 45° with the man’s eye when at a distance of 60 meters from the tower. After 5 seconds, the angle of depression becomes 30°. What is the approximate speed of the boat, assuming that it is running in still water?- a)32 kmph
- b)36 kmph
- c)38 kmph
- d)40 kmph
- e)42 kmph
Correct answer is option 'A'. Can you explain this answer?
A man is watching from the top of tower a boat speeding away from the tower. The boat makes an angle of depression of 45° with the man’s eye when at a distance of 60 meters from the tower. After 5 seconds, the angle of depression becomes 30°. What is the approximate speed of the boat, assuming that it is running in still water?
a)
32 kmph
b)
36 kmph
c)
38 kmph
d)
40 kmph
e)
42 kmph
|
|
Talent Skill Learning answered |
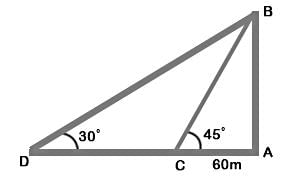
Let AB be the tower and C and D be the two positions of the boats.
Then, ∠ACB = 45∘, ∠ADB = 30∘ and AC = 60 m
Let, AB = h
Then,
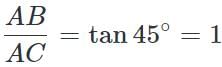
Hence, required speed
Directions: Study the following questions carefully and choose the right answer:A telegraph post gets broken at a point against a storm and its top touches the ground at a distance 20 m from the base of the post making an angle 30° with the ground. What is the height of the post?- a)40/√3 m
- b)20√3 m
- c)40√3 m
- d)30 m
- e)35 m
Correct answer is option 'B'. Can you explain this answer?
Directions: Study the following questions carefully and choose the right answer:
A telegraph post gets broken at a point against a storm and its top touches the ground at a distance 20 m from the base of the post making an angle 30° with the ground. What is the height of the post?
a)
40/√3 m
b)
20√3 m
c)
40√3 m
d)
30 m
e)
35 m
|
|
Talent Skill Learning answered |
Given, BC = 20 m
∠ACB = 30°
Total height of the telegraph post is (AB + CA) = ?
In Δ ABC, tan 30° = AB / BC
1 / √3 = AB / 20
∴ AB = 20 / √3m
Now, cos 30º = BC / AC
√3 / 2 = 20 / AC
∴ AC = 40 /√3 m
So, AB + CA = (20 / √3) + (40 / √3) = (60 / √3)
= 20 √3 m
Hence, option B is correct.
When the sun's altitude changes from 30° to 60°, the length of the shadow of a tower decreases by 70m. What is the height of the tower?- a)35 m
- b)140 m
- c)60.6 m
- d)20.2 m
- e)160 m
Correct answer is option 'C'. Can you explain this answer?
When the sun's altitude changes from 30° to 60°, the length of the shadow of a tower decreases by 70m. What is the height of the tower?
a)
35 m
b)
140 m
c)
60.6 m
d)
20.2 m
e)
160 m
|
|
Talent Skill Learning answered |
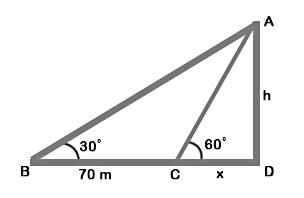
Let AD be the tower, BD be the initial shadow and CD be the final shadow.
Given that BC = 70 m, ∠ ABD = 30°, ∠ ACD = 60°,
Let CD = x, AD = h
From the right ΔCDA
Substituting this value of x in eq : 1, we have
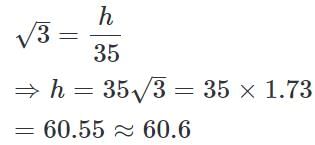
Two houses are in front of each other. Both have chimneys on their top. The line joining the chimneys makes an angle of 45° with the ground. How far are the houses from each other if one house is 25m and other is 10m in height?- a) 18 m
- b) 12 m
- c) 7.5 m
- d) 15 m
- e)None of the above
Correct answer is option 'D'. Can you explain this answer?
Two houses are in front of each other. Both have chimneys on their top. The line joining the chimneys makes an angle of 45° with the ground. How far are the houses from each other if one house is 25m and other is 10m in height?
a)
18 m
b)
12 m
c)
7.5 m
d)
15 m
e)
None of the above
|
|
Talent Skill Learning answered |
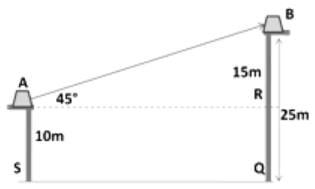
In ΔABR, a ∠ARB = 90° and ∠BAR = 45°
Sum of angles of a triangle = 180°
So ∠ABR = 180-90-90 = 45°
∴ BR = AR
AS = RQ = 10m
Also, BR = BQ-RQ = 25-10 = 15m
∴ AR = 15m = Distance between houses
The angle of elevation of the sun, when the length of the shadow of a tree is equal to the height of the tree, is:- a)30°
- b)60°
- c)45°
- d)50°
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
The angle of elevation of the sun, when the length of the shadow of a tree is equal to the height of the tree, is:
a)
30°
b)
60°
c)
45°
d)
50°
e)
None of these
|
|
Talent Skill Learning answered |
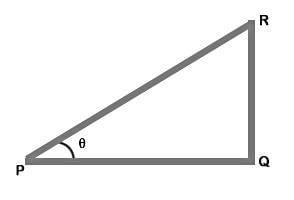
Consider the diagram shown above where QR represents the tree and PQ represents its shadow
We have, QR = PQ
Let ∠QPR = θ
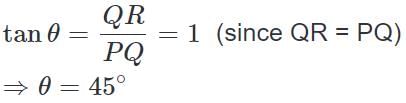
i.e., required angle of elevation = 45°
There is a tree between houses of A and B. If the tree leans on A’s House, the tree top rests on his window which is 12 m from ground. If the tree leans on B’s House, the tree top rests on his window which is 9 m from ground. If the height of the tree is 15 m, what is distance between A’s and B’s house?- a)21 m
- b)25 m
- c)16 m
- d)12 m
- e)17 m
Correct answer is option 'A'. Can you explain this answer?
There is a tree between houses of A and B. If the tree leans on A’s House, the tree top rests on his window which is 12 m from ground. If the tree leans on B’s House, the tree top rests on his window which is 9 m from ground. If the height of the tree is 15 m, what is distance between A’s and B’s house?
a)
21 m
b)
25 m
c)
16 m
d)
12 m
e)
17 m
|
|
Talent Skill Learning answered |
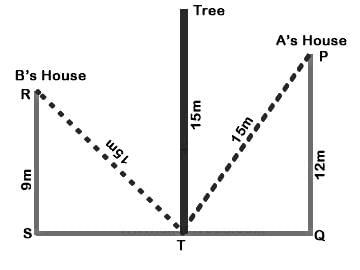
In ΔSTR, by Pythagoras theorem
RT2 = ST2 + RS2
∴ ST2 = 152 − 92 = 144
∴ ST = 12m
In ΔTQP, by Pythagoras theorem
PT2 = TQ2 + PQ2
∴ TQ2 = 152 − 122 = 81
∴ TQ = 9m
Distance between houses
⇒ SQ = ST + TQ
⇒ SQ = 12 + 9
⇒ SQ = 21 m
Directions: Study the following questions carefully and choose the right answer:The shadow of a tower is 15 m when the sun’s elevation is 30°. What is the length of the shadow when the sun’s elevation is 60°?- a)3 m
- b)4 m
- c)5 m
- d)6 m
- e)7 m
Correct answer is option 'C'. Can you explain this answer?
Directions: Study the following questions carefully and choose the right answer:
The shadow of a tower is 15 m when the sun’s elevation is 30°. What is the length of the shadow when the sun’s elevation is 60°?
a)
3 m
b)
4 m
c)
5 m
d)
6 m
e)
7 m
|
|
Talent Skill Learning answered |
Given, ∠ADB = 30° and ∠ ACB = 60°
When the sun's elevation is 30°, the shaadow of tower is "BD = 15 m" and when the sun's elevation is 60°, the shadow of tower is "BC = ?"
Let, BC = x m
In ΔABD, tan 30° = AB/BD
1 / √3 = AB / 15
∴ AB = 15 / √3 ....(i)
In ΔABC, tan 60° = AB/BC
√3 = AB / x
∴ AB = x √3 ...(ii)
From Eqs. (i) and (ii), we get
x√3 = 15 / √3
x = 5 m
Hence, optjon C is correct.
Due to sun, a 6ft man casts a shadow of 4ft, whereas a pole next to the man casts a shadow of 36ft. What is the height of the pole?- a)63 ft
- b)72 ft
- c)54 ft
- d)48 ft
- e)50 ft
Correct answer is option 'C'. Can you explain this answer?
Due to sun, a 6ft man casts a shadow of 4ft, whereas a pole next to the man casts a shadow of 36ft. What is the height of the pole?
a)
63 ft
b)
72 ft
c)
54 ft
d)
48 ft
e)
50 ft
|
|
Talent Skill Learning answered |
Both the man and pole are near each other and are illuminated by same sun from same direction.
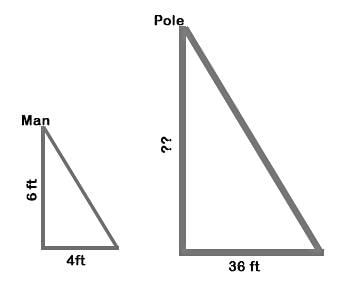
So angle of elevation for sun is same for both.
So ration of object to shadow will be same for all objects. (Proportionality Rule)
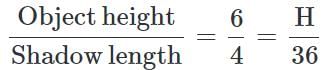
∴ H = 54 ft = Height of pole
So angle of elevation for sun is same for both.
So ration of object to shadow will be same for all objects. (Proportionality Rule)
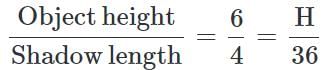
∴ H = 54 ft = Height of pole
The distance between two pillars of length 16 metres and 9 metres is x metres. If two angles of elevation of their respective top from the bottom of the other are complementary to each other, then the value of x (in metres) is- a)15
- b)16
- c)12
- d)9
Correct answer is option 'C'. Can you explain this answer?
The distance between two pillars of length 16 metres and 9 metres is x metres. If two angles of elevation of their respective top from the bottom of the other are complementary to each other, then the value of x (in metres) is
a)
15
b)
16
c)
12
d)
9
|
Ssc Cgl answered |
Given, AB = 16 m, CD = 9 m and BC = x metre
And, ∠ACB and ∠CBD are complementary.
∴ Let, ∠ACB = Θ and ∠CBD = (90° – Θ)
In ΔABC,
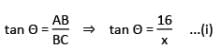
Now, In ΔBCD,
[∵ tan (90° – Θ) = cot Θ]
By multiplying eq. (i) & (ii),
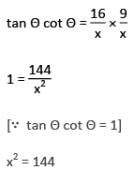
x = 12 m
Hence, option C is correct.
Directions: Study the following questions carefully and choose the right answer:The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 200 m apart, find the height of the light house.- a)100 m
- b)173 m
- c)200 m
- d)273 m
- e)274 m
Correct answer is option 'D'. Can you explain this answer?
Directions: Study the following questions carefully and choose the right answer:
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 200 m apart, find the height of the light house.
a)
100 m
b)
173 m
c)
200 m
d)
273 m
e)
274 m
|
|
Talent Skill Learning answered |
Given,
∠ ACB = 45°
∠ ADB = 30°
and distance between two ships, i.e.,
CD = 200 m
Then, AB = ?
Let BC = x m
In ΔABC,
tan 45º = AB /BC
(∵ tan 45° = 1)
1 = AB / x
∴ AB = x m ....(i)
In ΔABD, tan30º = AB / BD
∴ 1 / √3 = AB / (x + 200)
(∵ tan 30° = 1/√3 )
x = √3, AB – 200 ....(ii)
From Eqs. (i) and (ii),
AB = √3AB – 200
√3 AB – AB = 200
0.732 AB = 200
(∵ √3 = 1.732)
AB = 200 / 0.732 = 273 .22
= 273 m
Hence, option D is correct.
The angle of depression of a car, standing on the ground, from the top of a 75 m tower, is 30°. The distance of the car from the base of the tower (in metres) is- a)25 √3
- b)50 √3
- c)75 √3
- d)150
- e)100
Correct answer is option 'C'. Can you explain this answer?
The angle of depression of a car, standing on the ground, from the top of a 75 m tower, is 30°. The distance of the car from the base of the tower (in metres) is
a)
25 √3
b)
50 √3
c)
75 √3
d)
150
e)
100
|
|
Talent Skill Learning answered |
AB is a tower and AB = 75 m
From A, the angle of depression of a car C
on the ground is 30°
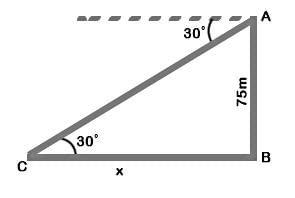
Let distance BC = x
Now in right ΔACB,
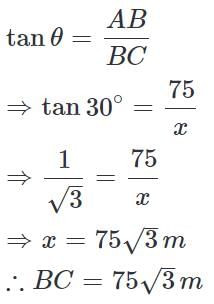
From A, the angle of depression of a car C
on the ground is 30°
Let distance BC = x
Now in right ΔACB,
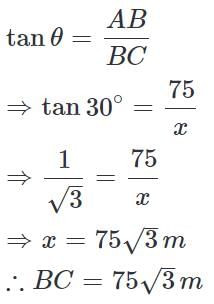
The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 40 m towards the tower, the angle of elevation of the top of the tower increases by 15°. The height of the tower is:- a)64.2 m
- b)62.2 m
- c)52.2 m
- d)54.6 m
- e)55.6 m
Correct answer is option 'D'. Can you explain this answer?
The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 40 m towards the tower, the angle of elevation of the top of the tower increases by 15°. The height of the tower is:
a)
64.2 m
b)
62.2 m
c)
52.2 m
d)
54.6 m
e)
55.6 m
|
|
Talent Skill Learning answered |
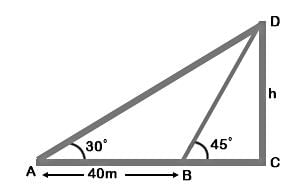
Let DC be the tower and A and B be the positions of the observer such that AB = 40 m
We have ∠DAC = 30°, ∠DBC = 45°
Let DC = h
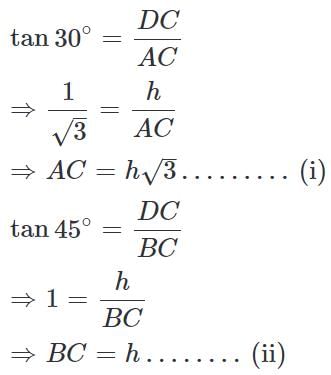
We know that,
AB = (AC − BC)
⇒ 40 = (AC − BC)
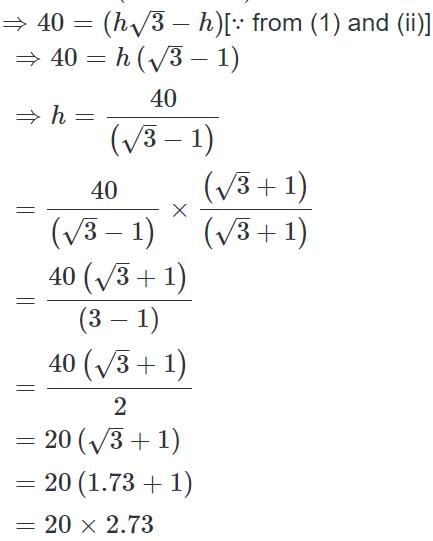
= 54.6 m
The angles of depression and elevation of the top of a wall 11 m high from top and bottom of a tree are 60° and 30° respectively. What is the height of the tree?- a)22 m
- b)44 m
- c)33 m
- d)35 m
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The angles of depression and elevation of the top of a wall 11 m high from top and bottom of a tree are 60° and 30° respectively. What is the height of the tree?
a)
22 m
b)
44 m
c)
33 m
d)
35 m
e)
None of these
|
|
Talent Skill Learning answered |
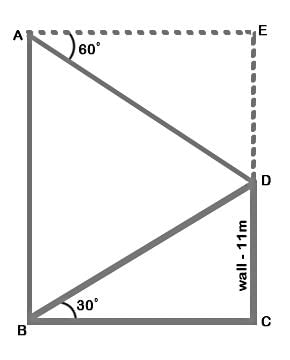
Let DC be the wall, AB be the tree.
Given that ∠DBC = 30°, ∠DAE = 60°, DC = 11 m
On the same side of a tower, two objects are located. Observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 600 m, the distance between the objects is approximately equal to:- a)272 m
- b)284 m
- c)288 m
- d)254 m
- e)260 m
Correct answer is option 'D'. Can you explain this answer?
On the same side of a tower, two objects are located. Observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 600 m, the distance between the objects is approximately equal to:
a)
272 m
b)
284 m
c)
288 m
d)
254 m
e)
260 m
|
|
Talent Skill Learning answered |
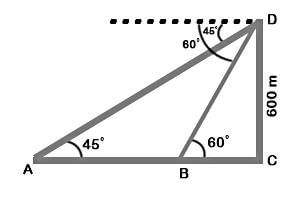
Let DC be the tower and A and B be the objects as shown above.
Given that DC = 600 m, ∠DAC = 45°, ∠DBC = 60°
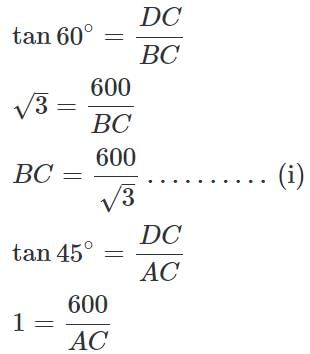
AC = 600.............................(ii)
Distance between the objects
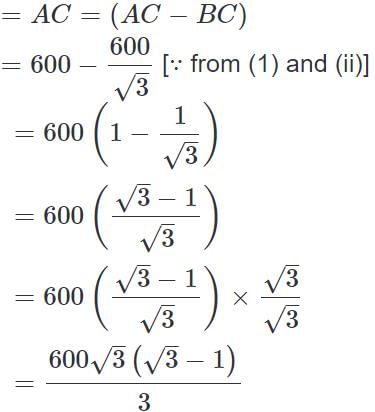
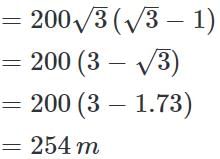
A tree is cut partially and made to fall on ground. The tree however does not fall completely and is still attached to its cut part. The tree top touches the ground at a point 10m from foot of the tree making an angle of 30°. What is the length of the tree?- a)10√3 m
- b)10/√3 m
- c)(√2 - 1)/10 m
- d)10/√2 m
- e)None of the above.
Correct answer is option 'A'. Can you explain this answer?
A tree is cut partially and made to fall on ground. The tree however does not fall completely and is still attached to its cut part. The tree top touches the ground at a point 10m from foot of the tree making an angle of 30°. What is the length of the tree?
a)
10√3 m
b)
10/√3 m
c)
(√2 - 1)/10 m
d)
10/√2 m
e)
None of the above.
|
|
Talent Skill Learning answered |
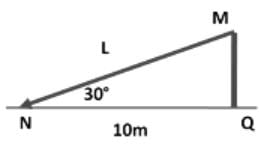
In ΔMNQ, Tan 30° = MQ/NQ
∴ 1/√3 = MQ/10
∴ MQ = 10/√3
Also, By Pythagoras theorem,
MN2 = MQ2 + NQ2
∴ L2 = 100/3 + 100
∴ L = 20/√3
∴ Height of tree = L + MQ
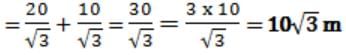
The angle of elevation of a ladder leaning against a wall is 60º and the foot of the ladder is 4.6 m away from the wall. The length of the ladder is:- a)2.3 m
- b)4.6 m
- c)7.8 m
- d)9.2 m
- e)10.2 m
Correct answer is option 'D'. Can you explain this answer?
The angle of elevation of a ladder leaning against a wall is 60º and the foot of the ladder is 4.6 m away from the wall. The length of the ladder is:
a)
2.3 m
b)
4.6 m
c)
7.8 m
d)
9.2 m
e)
10.2 m
|
|
Talent Skill Learning answered |
Let AB be the wall and BC be the ladder.
Then, ∠ACB = 60° = AC = 4.6m
AC/BC = cos 60° = 1/2
⇒ BC = 2 × AC = 2 × 4.6 = 9.2m
Then, ∠ACB = 60° = AC = 4.6m
AC/BC = cos 60° = 1/2
⇒ BC = 2 × AC = 2 × 4.6 = 9.2m
If a 1.5 m tall girl stands at a distance of 3 m from a lamp-post and casts a shadow of length 4.5 m on the ground, then the height of the lamp-post is- a)1.5 m
- b)2 m
- c)2.5 m
- d)2.8 m
- e)3.8 m
Correct answer is option 'C'. Can you explain this answer?
If a 1.5 m tall girl stands at a distance of 3 m from a lamp-post and casts a shadow of length 4.5 m on the ground, then the height of the lamp-post is
a)
1.5 m
b)
2 m
c)
2.5 m
d)
2.8 m
e)
3.8 m
|
|
Talent Skill Learning answered |
Let AB is girls and CD is lamp-post AB = 1.5
which casts her shadow EB
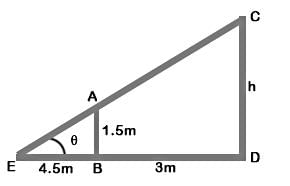
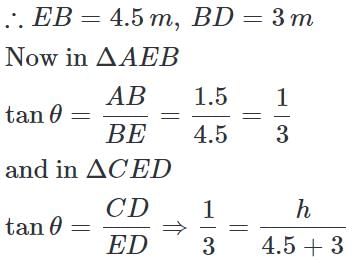
which casts her shadow EB
A poster is on top of a building. Rajesh is standing on the ground at a distance of 50 m from the building. The angles of elevation to the top of the poster and bottom of the poster are 45° and 30° respectively. What is the height of the poster?- a)50(√3 - 1)/ √3 m
- b)50√3 m
- c)25/√3 m
- d)25(√3 - 1)/ √3 m
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A poster is on top of a building. Rajesh is standing on the ground at a distance of 50 m from the building. The angles of elevation to the top of the poster and bottom of the poster are 45° and 30° respectively. What is the height of the poster?
a)
50(√3 - 1)/ √3 m
b)
50√3 m
c)
25/√3 m
d)
25(√3 - 1)/ √3 m
e)
None of these
|
|
Talent Skill Learning answered |
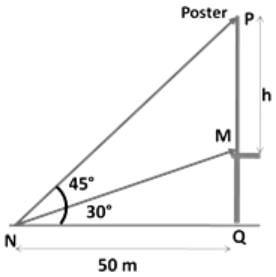
In ΔPNQ, Tan 45° = PQ/NQ
∴ PQ = NQ = 50m
In ΔMNQ, Tan 30° = MQ/NQ
∴ h = PM = PQ - MQ = 50 - 50/√3 = 50/√3 (√3 - 1) = Poster height
From a point P on a level ground, the angle of elevation of the top tower is 30º. If the tower is 100 m high, the distance of point P from the foot of the tower is:- a)149 m
- b)156 m
- c)173 m
- d)200 m
- e)208 m
Correct answer is option 'C'. Can you explain this answer?
From a point P on a level ground, the angle of elevation of the top tower is 30º. If the tower is 100 m high, the distance of point P from the foot of the tower is:
a)
149 m
b)
156 m
c)
173 m
d)
200 m
e)
208 m
|
|
Talent Skill Learning answered |
Let AB be the tower.
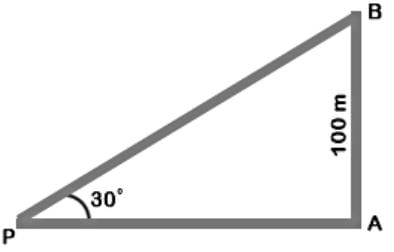
Then, ∠APB = 30° and AB = 100m
AB/AP = tan 30° = 1/√3
⇒ AP = AB × √3 = 100 × √3
⇒ AP = 100 × 1.73 = 173m
Then, ∠APB = 30° and AB = 100m
AB/AP = tan 30° = 1/√3
⇒ AP = AB × √3 = 100 × √3
⇒ AP = 100 × 1.73 = 173m
The length of shadow of a tower on the plane ground is √3 times the height of the tower. The angle of elevation of sun is- a)45°
- b)30°
- c)60°
- d)90°
- e)100°
Correct answer is option 'B'. Can you explain this answer?
The length of shadow of a tower on the plane ground is √3 times the height of the tower. The angle of elevation of sun is
a)
45°
b)
30°
c)
60°
d)
90°
e)
100°
|
|
Talent Skill Learning answered |
Let AB be tower and BC be its shadow
∴ Let AB = x
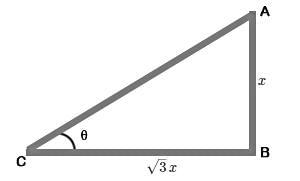
∴ Angle of elevation of the sun = 30∘
∴ Let AB = x
∴ Angle of elevation of the sun = 30∘
A man is watching from the top of a tower a boat speeding away from the tower. The boat makes an angle of depression of 45° with the man's eye when at a distance of 100 metres from the tower. After 10 seconds, the angle of depression becomes 30°. What is the approximate speed of the boat, assuming that it is running in still water?- a)26.28 km/hr
- b)32.42 km/hr
- c)24.22 km/hr
- d)31.25 km/hr
- e)33.20 km/hr
Correct answer is option 'A'. Can you explain this answer?
A man is watching from the top of a tower a boat speeding away from the tower. The boat makes an angle of depression of 45° with the man's eye when at a distance of 100 metres from the tower. After 10 seconds, the angle of depression becomes 30°. What is the approximate speed of the boat, assuming that it is running in still water?
a)
26.28 km/hr
b)
32.42 km/hr
c)
24.22 km/hr
d)
31.25 km/hr
e)
33.20 km/hr
|
|
Talent Skill Learning answered |
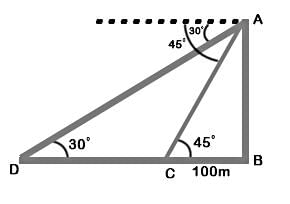
Consider the diagram shown above.
Let AB be the tower. Let C and D be the positions of the boat
Then, ∠ ACB = 45°, ∠ ADC = 30°, BC = 100 m
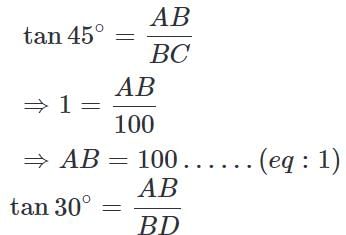
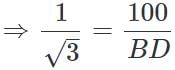(∵ Substituted the value of AB from equation 1)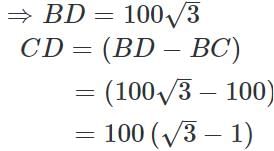
It is given that the distance CD is covered in 10 seconds.
i.e., the distance 100 (√3 - 1) is covered in 10 seconds.
Required speed
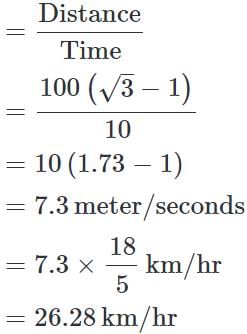
Directions: Study the following questions carefully and choose the right answer:From the top of a cliff 90 m high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°, respectively. What is the height of the tower?- a)30 m
- b)45 m
- c)60 m
- d)75 m
- e)80 m
Correct answer is option 'C'. Can you explain this answer?
Directions: Study the following questions carefully and choose the right answer:
From the top of a cliff 90 m high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°, respectively. What is the height of the tower?
a)
30 m
b)
45 m
c)
60 m
d)
75 m
e)
80 m
|
|
Talent Skill Learning answered |
Given, AB = 90 m
∠ADE = 30°
And ∠ACB = 60°
Then, DC = ?
Ratio of angles,
tan 30º / tan 60º = (AE / ED) / (AB / BC)
[∵ ED = BC]
(1 / √3) / √3 = AE / 90
1 / 3 = AE / 90
AE = 30 m
Now, DC = EB
= AB – AE
= 90 – 30 = 60 m
Hence, option C is correct.
From a tower of 80 m high, the angle of depression of a bus is 30°. How far is the bus from the tower?- a)40 m
- b)138.4 m
- c)46.24 m
- d)160 m
- e)180 m
Correct answer is option 'B'. Can you explain this answer?
From a tower of 80 m high, the angle of depression of a bus is 30°. How far is the bus from the tower?
a)
40 m
b)
138.4 m
c)
46.24 m
d)
160 m
e)
180 m
|
|
Talent Skill Learning answered |
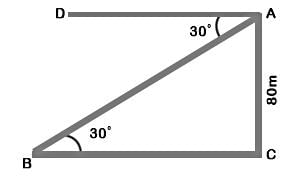
Let AC be the tower and B be the position of the bus.
Then BC = the distance of the bus from the foot of the tower.
Given that height of the tower, AC = 80 m and the angle of depression, ∠DAB = 30°
∠ABC = ∠DAB = 30° (because DA || BC)
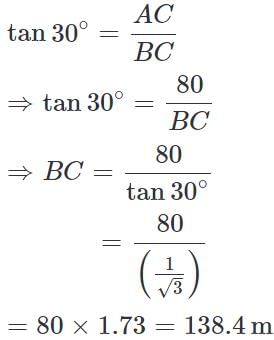
i.e., Distance of the bus from the foot of the tower = 138.4 m
The angle of elevation of the top of a lighthouse 60 m high, from two points on the ground on its opposite sides are 45° and 60°. What is the distance between these two points?- a)45 m
- b)30 m
- c)103.8 m
- d)94.6 m
- e)100 m
Correct answer is option 'D'. Can you explain this answer?
The angle of elevation of the top of a lighthouse 60 m high, from two points on the ground on its opposite sides are 45° and 60°. What is the distance between these two points?
a)
45 m
b)
30 m
c)
103.8 m
d)
94.6 m
e)
100 m
|
|
Talent Skill Learning answered |
Let BD be the lighthouse and A and C be the two points on ground.
Then, BD, the height of the lighthouse = 60 m
∠BAD = 45°, ∠BCD = 60°
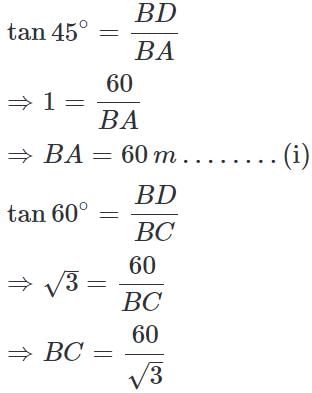
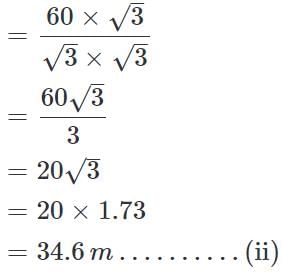
Distance between the two points A and C
= AC = BA + BC
= 60 + 34.6 [∵ Substituted value of BA and BC from (i) and (ii)]
= 94.6 m
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is- a)12 m
- b)10 m
- c)8 m
- d)6 m
- e)7 m
Correct answer is option 'A'. Can you explain this answer?
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
a)
12 m
b)
10 m
c)
8 m
d)
6 m
e)
7 m
|
|
Talent Skill Learning answered |
Let AB and CD be two poles
AB = 20 m, CD = 14 m
A and C are joined by a wire
CE || DB and angle of elevation of A is 30°
Let CE = DB = x and AC = L
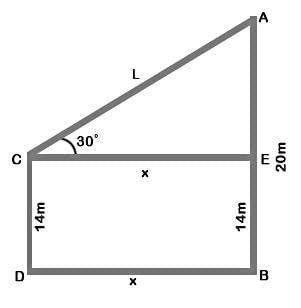
Now AE = AB - EB = AB - CD = 20 - 14 = 6 m
Now in right ΔACE,
AB = 20 m, CD = 14 m
A and C are joined by a wire
CE || DB and angle of elevation of A is 30°
Let CE = DB = x and AC = L
Now AE = AB - EB = AB - CD = 20 - 14 = 6 m
Now in right ΔACE,
Two poles of heights 6 m and 11 m stand vertically upright on a plane ground. If the distance between their feet is 12 m, what is the distance between their tops?- a)11 m
- b)12 m
- c)13 m
- d)14 m
Correct answer is option 'C'. Can you explain this answer?
Two poles of heights 6 m and 11 m stand vertically upright on a plane ground. If the distance between their feet is 12 m, what is the distance between their tops?
a)
11 m
b)
12 m
c)
13 m
d)
14 m
|
Iq Funda answered |
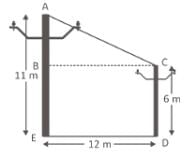
Given that ther are two poles
AE = 11 m and, CD = 6 m
∴ BE = 6 m
[∵CD = BE]
∴ AB = AE – BE = 11 – 6 = 5m
distance between their feet
ED = 12 m
∴ BC = 12 m [∵ED = BC] Now, AC = ?
In ΔABC,
From Pythagorus theorum,
AC2 = AB2 + BC2
AC2 = 52 + 122
AC2 = 25 + 144 = 169
AC = √169
AC = 13
Hence, option C is correct.
A telegraph post is bent at a point above the ground due to storm. Its top just meets the ground at a distance of 8√3 meters from its foot and makes an angle of 30°, then the height of the post is :- a)16 metres
- b)23 metres
- c)24 metres
- d)10 metres
Correct answer is option 'C'. Can you explain this answer?
A telegraph post is bent at a point above the ground due to storm. Its top just meets the ground at a distance of 8√3 meters from its foot and makes an angle of 30°, then the height of the post is :
a)
16 metres
b)
23 metres
c)
24 metres
d)
10 metres
|
T.S Academy answered |
Given, BC = 8 √ m
In ΔABC,
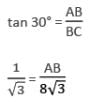
AB = 8 m
Again, sin 30° = AB/AC
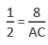
AC = 16 m
∴ The height of the post = AC + AB = 16 + 8 = 24 m.
Hence, option C is correct.
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 200 m apart, find the height of the light house.- a)100 m
- b)173 m
- c)200 m
- d)273 m
Correct answer is option 'D'. Can you explain this answer?
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 200 m apart, find the height of the light house.
a)
100 m
b)
173 m
c)
200 m
d)
273 m
|
|
T.S Academy answered |
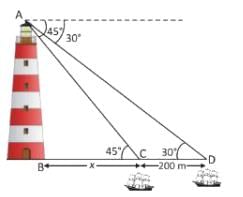
Given, ∠ ACB = 45°
∠ ADB = 30°
and distance between two ships, i.e.,
CD = 200 m
Then, AB = ?
Let BC = x m
In ΔABC, tan 45° = AB/BC
(∵ tan 45° = 1)
1 = AB/x
∴ AB = x m ....(i)
In ΔABD, tan30° = AB/BD
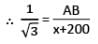
(∵ tan 30° = 1/√3 )
x = √ AB – 200 ...(ii)
From Eqs. (i) and (ii),
AB = √ AB – 200
√ AB – AB = 200
0.732 AB = 200
(∵√ = 1.732)
= 273 m
Hence, option D is correct.
A tree breaks and falls to the ground such that its upper part is still partially attached to its stem. At what height did it break, if the original height of the tree was 24 cm and it makes an angle of 30° with the ground?- a)12 cm
- b)8 cm
- c)9.5 cm
- d)7.5 cm
- e)8.5 cm
Correct answer is option 'B'. Can you explain this answer?
A tree breaks and falls to the ground such that its upper part is still partially attached to its stem. At what height did it break, if the original height of the tree was 24 cm and it makes an angle of 30° with the ground?
a)
12 cm
b)
8 cm
c)
9.5 cm
d)
7.5 cm
e)
8.5 cm
|
|
Talent Skill Learning answered |
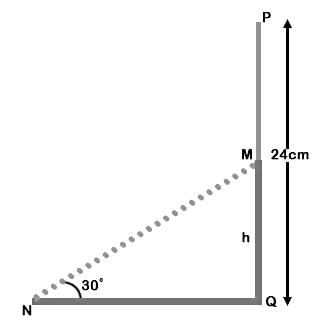
Let the tree break at height h cm from ground at point M.
The broken part makes angle of 30°
∴ Broken Part MP = MN = 24 - h
in ΔMCQ
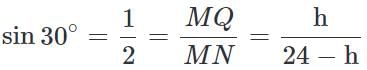
∴ 24 - h = 2h
∴ h = 8 cm = Tree breaks at this height
At an instant, the length of the shadow of a pole is square root of 3 times the height of the pole. Find the angle of elevation of the turn.- a)30°
- b)45°
- c)60°
- d)75°
Correct answer is option 'A'. Can you explain this answer?
At an instant, the length of the shadow of a pole is square root of 3 times the height of the pole. Find the angle of elevation of the turn.
a)
30°
b)
45°
c)
60°
d)
75°
|
|
Iq Funda answered |
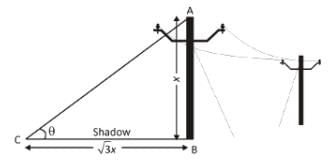
Let AB = x
Then, BC = √ x
and θ = ?
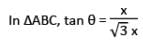
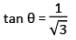
tan θ = tan 30°
[∵ tan 30° = 1/√3]
∴ θ = 30°
Hence, option A is correct.
The shadow of a tower is 15 m when the sun’s elevation is 30°. What is the length of the shadow when the sun’s elevation is 60°?- a)3 m
- b)4 m
- c)5 m
- d)6 m
Correct answer is option 'C'. Can you explain this answer?
The shadow of a tower is 15 m when the sun’s elevation is 30°. What is the length of the shadow when the sun’s elevation is 60°?
a)
3 m
b)
4 m
c)
5 m
d)
6 m
|
|
EduRev SSC CGL answered |
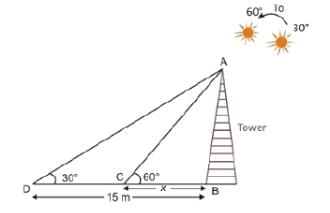
Given, ∠ADB = 30° and ∠ ACB = 60°
When the sun's elevation is 30°, the shadow of tower is "BD = 15 m" and when the sun's elevation is 60°, the shadow of tower is "BC = ?"
Let, BC = x m In ΔABD, tan 30° = AB/BD
In ΔABC, tan 60° = AB/BC
√3 = AB/x
∴ AB = x √3 ...(ii)
From Eqs. (i) and (ii), we get
x √3 = 15/√3
x = 5 m
Hence, option C is correct.
A telegraph post gets broken at a point against a storm and its top touches the ground at a distance 20 m from the base of the post making an angle 30° with the ground. What is the height of the post?- a)
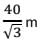
- b)
- c)20
- d)40 √3 m
Correct answer is option 'B'. Can you explain this answer?
A telegraph post gets broken at a point against a storm and its top touches the ground at a distance 20 m from the base of the post making an angle 30° with the ground. What is the height of the post?
a)
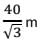
b)
c)
20
d)
40 √3 m
|
|
EduRev SSC CGL answered |
Hence, option B is correct.
The angle of elevation of the top of a building from the top and bottom of a tree are x and y respectively. If the height of the tree is h metre, then (in metre) the height of the building is- a)
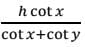
- b)
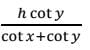
- c)
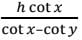
- d)
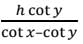
Correct answer is option 'C'. Can you explain this answer?
The angle of elevation of the top of a building from the top and bottom of a tree are x and y respectively. If the height of the tree is h metre, then (in metre) the height of the building is
a)
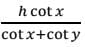
b)
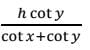
c)
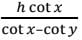
d)
|
|
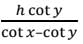
EduRev SSC CGL answered |
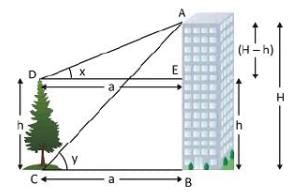
Given, the height of the tree, CD = h metre
Let, the height of the building, AB = H metre
And, BC = a metre
∴ AE = AB – EB = (H – h) metre [∵ CD = BE]
In ΔABC,
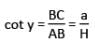
a = H cot y ...(i)
Now, in ΔADE,
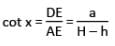
a = (H – h) cot x ...(ii)
From equations (i) and (ii),
H cot y = (H – h) cot x = H cot x – h cot x
H(cot x – cot y) = h cot x
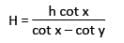
∴ The height of the building
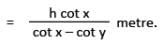
Hence, option C is correct.
The angle of elevation of the top of a tower from a point A on the ground is 30°. On moving a distance of 20 metres towards the foot of the tower to a point B, the angle of elevation increases to 60°. The height of the tower is- a)√3 m
- b)5√3 m
- c)10√3 m
- d)20√3 m
Correct answer is option 'C'. Can you explain this answer?
The angle of elevation of the top of a tower from a point A on the ground is 30°. On moving a distance of 20 metres towards the foot of the tower to a point B, the angle of elevation increases to 60°. The height of the tower is
a)
√3 m
b)
5√3 m
c)
10√3 m
d)
20√3 m
|
Target Study Academy answered |
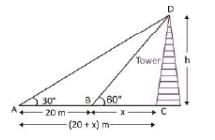
Given, AB = 20 m
Let, the height of the tower = h metre
And, BC = x metre
∴ AC = AB + BC = (20 + x) m
In ΔACD,
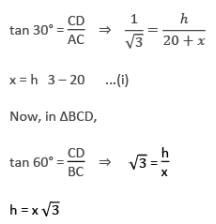
h = (h √3 – 20) √3 [From eq. (i)]
h = 3h – 20 √3
2h = 20 √3
h = 10 √3
∴ The height of the tower is 10 √3 meter.
Hence, option C is correct.
A pole stands vertically, inside a saclene triangular park ABC, if the angle of elevation of the top of the pole from each corner of the park is same, then in ΔABC, the foot of the pole is at the- a)centroid
- b)circumcentre
- c)incentre
- d)orthocenter
Correct answer is option 'B'. Can you explain this answer?
A pole stands vertically, inside a saclene triangular park ABC, if the angle of elevation of the top of the pole from each corner of the park is same, then in ΔABC, the foot of the pole is at the
a)
centroid
b)
circumcentre
c)
incentre
d)
orthocenter
|
|
Iq Funda answered |
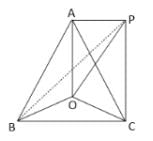
AP = CP = BP
It is possible only when OA = OB = OC i.e. radii of circum circle.
Hence, option B is correct.
If the height of a vertical pole is √3 times the length of its shadow on the ground, then the angle of elevation of the sun at that time is- a)30°
- b)60°
- c)45°
- d)75°
- e)80°
Correct answer is option 'B'. Can you explain this answer?
If the height of a vertical pole is √3 times the length of its shadow on the ground, then the angle of elevation of the sun at that time is
a)
30°
b)
60°
c)
45°
d)
75°
e)
80°
|
|
Talent Skill Learning answered |
Let AB be a vertical pole and let its shadow be BC
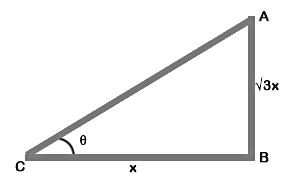
Let BC = x m, then length of pole = √3x,
θ be the angle of elevation
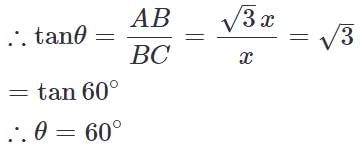
Let BC = x m, then length of pole = √3x,
θ be the angle of elevation
Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is:- a)173 m
- b)200 m
- c)273 m
- d)300 m
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is:
a)
173 m
b)
200 m
c)
273 m
d)
300 m
e)
None of these
|
|
Talent Skill Learning answered |
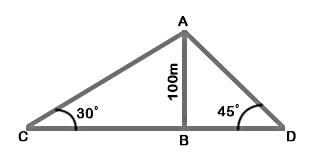
Then, AB = 100m, ∠ACB = 30° and ∠ADB = 45°
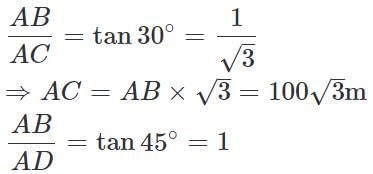
⇒ AD = AB = 100m
∴ CD = (AC+AD) = (100√3 +100)
= 100(√3 +1) = 100(1.73+1) =100 × 2.73 = 273m
⇒ AD = AB = 100m
∴ CD = (AC+AD) = (100√3 +100)
= 100(√3 +1) = 100(1.73+1) =100 × 2.73 = 273m
Two houses are in front of each other. Both have chimneys on their top. The line joining the chimneys makes an angle of 45° with the ground. How far are the houses from each other if one house is 25m and other is 10m in height?- a)18 m
- b)12 m
- c)7.5 m
- d)15 m
- e)17 m
Correct answer is option 'D'. Can you explain this answer?
Two houses are in front of each other. Both have chimneys on their top. The line joining the chimneys makes an angle of 45° with the ground. How far are the houses from each other if one house is 25m and other is 10m in height?
a)
18 m
b)
12 m
c)
7.5 m
d)
15 m
e)
17 m
|
|
Talent Skill Learning answered |
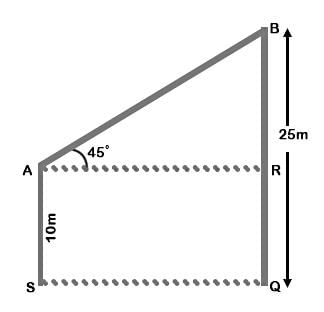
In ∠ABR, ∠ARB = 90° and ∠BAR = 45°
Sum of angles of a triangle = 180°
So ∠ABR = 180 - 90 - 45 = 45°
∴ BR = AR
AS = RQ = 10m
Also, BR = BQ - RQ = 25 - 10 = 15m
∴ AR = 15m = Distance between houses
Directions: Study the following questions carefully and choose the right answer:The angle of elevation of the top of an unfinished pillar at a point 150 m from its base is 30°. If the angle of elevation at the same point is to be 45°, then the pillar has to be raised to a height of how many metres?- a)59.4 m
- b)61.4 m
- c)62.4 m
- d)63.4 m
- e)64.4 m
Correct answer is option 'D'. Can you explain this answer?
Directions: Study the following questions carefully and choose the right answer:
The angle of elevation of the top of an unfinished pillar at a point 150 m from its base is 30°. If the angle of elevation at the same point is to be 45°, then the pillar has to be raised to a height of how many metres?
a)
59.4 m
b)
61.4 m
c)
62.4 m
d)
63.4 m
e)
64.4 m
|
|
Talent Skill Learning answered |
Given, BC = 150 m
∠ACB = 30°
and, ∠DCB = 45°
Then, AD = ?
In ΔABC, tan 30° = AB / BC
1 / √3 = AB / 150
∴ AB = 150 / √3 = 86.6m
In ΔDBC, tan 45° = DB / BC
1 = DB / 150
DB = 150
AD + AB = 150
[∵ DB = AD + AB]
∴ AD = 150 – AB
= 150 – 86.6 = 63.4m
Hence, option D is correct.
Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30º and 45º respectively. If the lighthouse is 200 m high, the distance between the two ships is:- a)600 m
- b)273 m
- c)546 m
- d)446 m
- e)450 m
Correct answer is option 'C'. Can you explain this answer?
Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30º and 45º respectively. If the lighthouse is 200 m high, the distance between the two ships is:
a)
600 m
b)
273 m
c)
546 m
d)
446 m
e)
450 m
|
|
Talent Skill Learning answered |
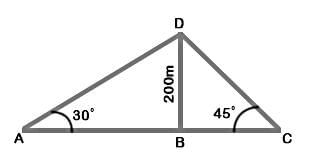
Let BD be the lighthouse and A and C be the positions of the ships.
Then, BD = 200 m, ∠BAD = 30°, ∠BCD = 45°
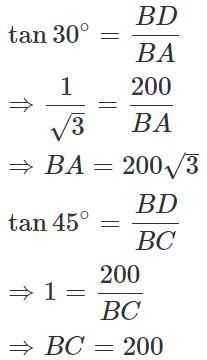
Distance between the two ships
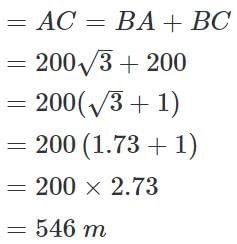
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is- a)25 m
- b)50 m
- c)75 m
- d)100 m
- e)110 m
Correct answer is option 'B'. Can you explain this answer?
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is
a)
25 m
b)
50 m
c)
75 m
d)
100 m
e)
110 m
|
|
Talent Skill Learning answered |
Let AB be the tower and CD be cliff Angle of elevation of A is equal to the angle of depression of B at C
Let angle be Q and CD = 25 m
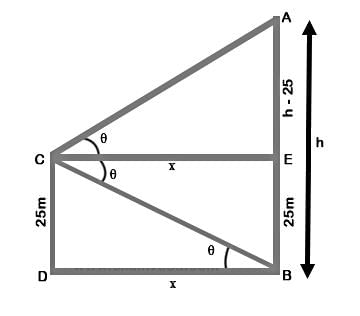
Let AB = h
CE || DB
∴ EC = DB = x (suppose)
EB = CD = 25
∴ AE = h − 25
Now in right ΔCDB,
Let angle be Q and CD = 25 m
Let AB = h
CE || DB
∴ EC = DB = x (suppose)
EB = CD = 25
∴ AE = h − 25
Now in right ΔCDB,
The angle of elevation of the top of a tower from a certain point is 30°. If the observed moves 20 m towards the tower, the angle of elevation the angle of elevation of top of the tower increases by 15°. The height of the tower is- a)17.3 m
- b)21.9 m
- c)27.3 m
- d)30 m
- e)40 m
Correct answer is option 'C'. Can you explain this answer?
The angle of elevation of the top of a tower from a certain point is 30°. If the observed moves 20 m towards the tower, the angle of elevation the angle of elevation of top of the tower increases by 15°. The height of the tower is
a)
17.3 m
b)
21.9 m
c)
27.3 m
d)
30 m
e)
40 m
|
|
Talent Skill Learning answered |
Let AB be the tower and C and D be the points of observation.
Then, ∠ACB = 30°, ∠ADB = 45° and CD = 20m
Let AB = h then,
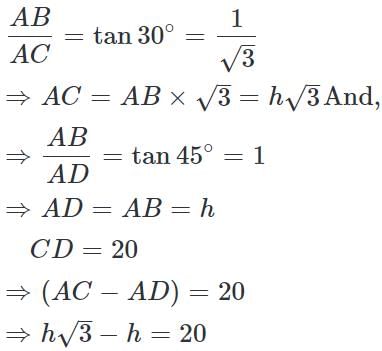
Chapter doubts & questions for Height & Distance - Quantitative Aptitude for Competitive Exams 2025 is part of SSC MTS / SSC GD exam preparation. The chapters have been prepared according to the SSC MTS / SSC GD exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for SSC MTS / SSC GD 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Height & Distance - Quantitative Aptitude for Competitive Exams in English & Hindi are available as part of SSC MTS / SSC GD exam.
Download more important topics, notes, lectures and mock test series for SSC MTS / SSC GD Exam by signing up for free.
Quantitative Aptitude for Competitive Exams
203 videos|110 docs|114 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily