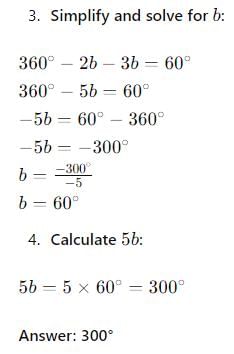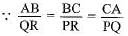All Exams >
BMAT >
Mathematics for BMAT (Section 2) >
All Questions
All questions of Geometry for BMAT Exam
The degree measure of a semi-circle is- a)0°
- b)90°
- c)360°
- d)180°
Correct answer is option 'D'. Can you explain this answer?
The degree measure of a semi-circle is
a)
0°
b)
90°
c)
360°
d)
180°
|
Vikas Kapoor answered |
One circle measures 360 degrees. The half of the circle is called a semi-circle.
Thus, the measure of semi-circle
= 360/2 = 180 degree.
Thus, the measure of semi-circle
= 360/2 = 180 degree.
In the adjoining figure, AB ║ CD and AB ║ EF. The value of x is :-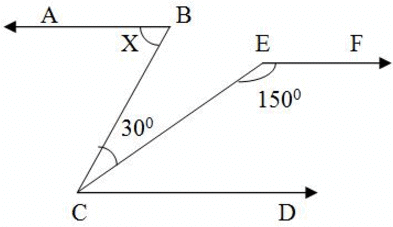
- a)400
- b)600
- c)700
- d)500
Correct answer is option 'B'. Can you explain this answer?
In the adjoining figure, AB ║ CD and AB ║ EF. The value of x is :-
a)
400
b)
600
c)
700
d)
500
|
|
Vivek Rana answered |
Given, AB ║ CD and AB ║ EF
so CD || EF
which means ∠ECD + ∠CEF = 1800 (corresponding angles)
∠ECD = 180 - 150 = 300
since AB || CD so
∠ABC= ∠BCD (alternate interior angles)
∠ABC = 30 + ∠ECD = 30 + 30 = 600
Circles having the same centre and different radii are called- a)Equal circles
- b)Concentric circles
- c)Semi-circles
- d)Congruent circles
Correct answer is option 'B'. Can you explain this answer?
Circles having the same centre and different radii are called
a)
Equal circles
b)
Concentric circles
c)
Semi-circles
d)
Congruent circles
|
Hansa Sharma answered |
Concentric circles are circles with a common center. The region between two concentric circles of different radii is called an annulus.
Any two circles can be made concentric by inversion by picking the inversion center as one of the limiting points.
In the figure, if O is the centre of the circle and ∠BOA = 120°, then the value of x is
- a)90°
- b)60°
- c)120°
- d)30°
Correct answer is option 'B'. Can you explain this answer?
In the figure, if O is the centre of the circle and ∠BOA = 120°, then the value of x is
a)
90°
b)
60°
c)
120°
d)
30°
|
Mohit Rajpoot answered |
∠BOA = 120° (Given)
∠AOC = 60° (Linear Pair)
∠AOC = 60° (Linear Pair)
In triangle OAC,
OA = OC (Radii of same circle)
∠OAC = ∠ OCA = x (angle opposite to equal sides are equal)
∵ ∠A + ∠C +∠O = 180°
⇒ x + x + 60 = 180°
⇒ 2x = 120°
⇒ x =60o
OA = OC (Radii of same circle)
∠OAC = ∠ OCA = x (angle opposite to equal sides are equal)
∵ ∠A + ∠C +∠O = 180°
⇒ x + x + 60 = 180°
⇒ 2x = 120°
⇒ x =60o
A circle divides the plane in which it lies into- a)4 parts
- b)5 parts
- c)3 parts
- d)2 parts
Correct answer is option 'C'. Can you explain this answer?
A circle divides the plane in which it lies into
a)
4 parts
b)
5 parts
c)
3 parts
d)
2 parts
|
|
Vikram Khanna answered |
A circle divides a plane into three parts: the points INSIDE the circle. the points OUTSIDE the circle. and the points ON the circle.
If two parallel lines are intersected by a transversal then the bisectors of the interior angles form a :- a)rhombus
- b)parallogram
- c)Square
- d)Rectangle
Correct answer is option 'D'. Can you explain this answer?
If two parallel lines are intersected by a transversal then the bisectors of the interior angles form a :
a)
rhombus
b)
parallogram
c)
Square
d)
Rectangle
|
Arya Roy answered |
if two parallel lines are intersected by a transversal then prove that bisectors of the interior angles form a triangle.if two parallel lines are intersected by a transversal then prove that bisectors of the interior angles form a rectangle.
In the given figure, if ∠OAB = 40o then ∠ACB is equal to:
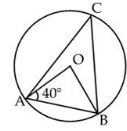
- a)60°
- b)50°
- c)40°
- d)70°
Correct answer is option 'B'. Can you explain this answer?
In the given figure, if ∠OAB = 40o then ∠ACB is equal to:
a)
60°
b)
50°
c)
40°
d)
70°
|
Let's Tute answered |
In triangle OAB
OA = OB (radius of a circle)
∠OAB = ∠OBA
∠OBA = 40º (angles opposite to equal sides are equal)
Using the angle sum property
∠AOB + ∠OBA + ∠BAO = 180º
Substituting the values
∠AOB + 40º + 40º = 180º
By further calculation
∠AOB + 80º = 180º
∠AOB = 180º - 80º
∠AOB = 100º
As the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle
∠AOB = 2 ∠ACB
Substituting the values
100º = 2 ∠ACB
Dividing both sides by 2
∠ACB = 50º
Therefore, ∠ACB is equal to 50º.
In the figure, if O is the centre of a circle, then the measure of ∠ACB is: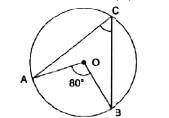
- a)180°
- b)60°
- c)40º
- d)45°
Correct answer is option 'C'. Can you explain this answer?
In the figure, if O is the centre of a circle, then the measure of ∠ACB is:
a)
180°
b)
60°
c)
40º
d)
45°
|
Ishan Choudhury answered |
The angle subtented by the arc at the centre is double the angle subtented by it at any point on the circle.
In ΔABC fig., ∠x + ∠y + ∠z is equal to: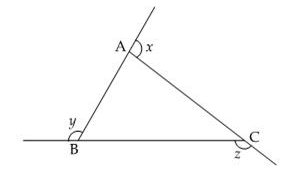
- a)360°
- b)120°
- c)240°
- d)180°
Correct answer is option 'A'. Can you explain this answer?
In ΔABC fig., ∠x + ∠y + ∠z is equal to:
a)
360°
b)
120°
c)
240°
d)
180°
|
|
Himaja Ammu answered |
Sum of exterior angles of a triangle is always 360
In the adjoining figure, if m ║ n, then ∠4 + ∠7 is equal to –
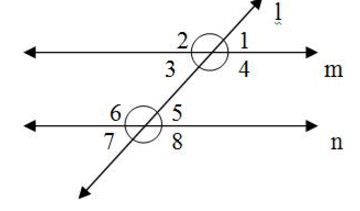
- a)1800
- b)1200
- c)1500
- d)900
Correct answer is option 'A'. Can you explain this answer?
In the adjoining figure, if m ║ n, then ∠4 + ∠7 is equal to –
a)
1800
b)
1200
c)
1500
d)
900
|
Imk Pathshala answered |
∠4 = ∠8 [ corresponding angles are equal]
∠7 + ∠8 = 180 [replacinig ∠8 by ∠4 ]
∠7 + ∠4 = 180
∠7 + ∠8 = 180 [replacinig ∠8 by ∠4 ]
∠7 + ∠4 = 180
Which pair of the given quadrilaterals is similar?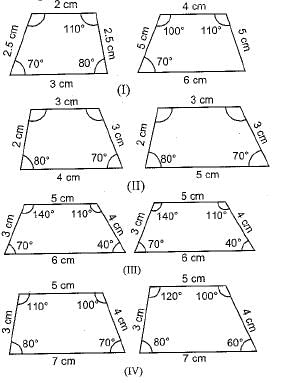
a)I only
b)III onlyc)I and IIId)IVCorrect answer is option 'C'. Can you explain this answer?
|
Naina Sharma answered |
Quadrilaterals are similar if their angles are equal and corresponding sides are proportional.
A line that intersects a circle in two distinct points is a- a)Secant
- b)Chord
- c)Radius
- d)Diameter
Correct answer is option 'A'. Can you explain this answer?
A line that intersects a circle in two distinct points is a
a)
Secant
b)
Chord
c)
Radius
d)
Diameter
|
|
Vikram Khanna answered |
SECANT
In geometry, a secant of a curve is a line that intersects the curve in at least two (distinct) points.The word secant comes from the Latin word secare, meaning to cut. In the case of a circle, a secant will intersect the circle in exactly two points and a chord is the line segment determined by these two points, that is the interval on a secant whose endpoints are these points.
In geometry, a secant of a curve is a line that intersects the curve in at least two (distinct) points.The word secant comes from the Latin word secare, meaning to cut. In the case of a circle, a secant will intersect the circle in exactly two points and a chord is the line segment determined by these two points, that is the interval on a secant whose endpoints are these points.
If two angles are complementary of each other, then each angle is :
- a)An Obtuse angle
- b)A Right angle
- c)An Acute angle
- d)A supplementary angle
Correct answer is option 'C'. Can you explain this answer?
If two angles are complementary of each other, then each angle is :
a)
An Obtuse angle
b)
A Right angle
c)
An Acute angle
d)
A supplementary angle
|
Rachit Agrah.ari answered |
C is correct...If angles are complementary or of 90 degrees then each angle is acute angle because acute angles are those angles whose measure is less than 90 degree... ...Each angle will not be obtuse,right and not supplementary...
The region between an arc and the two radii joining the centre of the end points of the arc is called:a) A Segmentb) A Semicirclec) A Minor arcd) A SectorCorrect answer is option 'D'. Can you explain this answer?
|
Ananya Das answered |
The sector is the region between an arc and two radii joining the center to the endpoints of the arc.
Example: In the given figure, OAB is the sector of the circle.
In the given figure, straight lines PQ and RS intersect at O. If the magnitude of θ is 3 times that of ϕ, then (∠ϕ) is equal to :
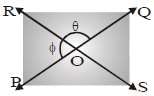
- a)30°
- b)40°
- c)45°
- d)60°
Correct answer is option 'C'. Can you explain this answer?
In the given figure, straight lines PQ and RS intersect at O. If the magnitude of θ is 3 times that of ϕ, then (∠ϕ) is equal to :
a)
30°
b)
40°
c)
45°
d)
60°
|
Arizona Academy answered |
Correct option is C
In the above figure straight lines PQ and RS intersect at O.
It is given that θ=3ϕ .....(1)
∠POR and ∠QOR form linear pair of angles
Also ∠POR=ϕ and ∠QOR=θ
∠POR+∠QOR=180
ϕ+θ=180
ϕ+3ϕ=180 .....(From 1)
4ϕ=180
ϕ= 180/4 =45
Hence, ∠ϕ=45.
In the above figure straight lines PQ and RS intersect at O.
It is given that θ=3ϕ .....(1)
∠POR and ∠QOR form linear pair of angles
Also ∠POR=ϕ and ∠QOR=θ
∠POR+∠QOR=180
ϕ+θ=180
ϕ+3ϕ=180 .....(From 1)
4ϕ=180
ϕ= 180/4 =45
Hence, ∠ϕ=45.
The measure of angle a in the figure below is :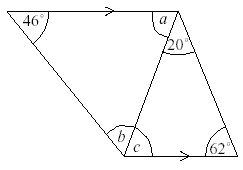
- a)98°
- b)78°
- c)62°
- d)80°
Correct answer is option 'A'. Can you explain this answer?
The measure of angle a in the figure below is :
a)
98°
b)
78°
c)
62°
d)
80°
|
Aarav Love answered |
Ad first u denote the name of figure like A B C then i explain it deplyyyy
If the arms of one angle are respectively parallel to the arms of another angle, then the two angles are :- a)Neither equal nor supplementary
- b)Not equal but supplementary
- c)Equal but not supplementary
- d)Either equal or supplementary
Correct answer is option 'D'. Can you explain this answer?
If the arms of one angle are respectively parallel to the arms of another angle, then the two angles are :
a)
Neither equal nor supplementary
b)
Not equal but supplementary
c)
Equal but not supplementary
d)
Either equal or supplementary
|
|
Imk Pathshala answered |
- Option A: "Neither equal nor supplementary"
This is incorrect because the angles will either be equal or supplementary. - Option B: "Not equal but supplementary"
This is partially correct but does not include the case when the angles are equal. - Option C: "Equal but not supplementary"
This is also partially correct but does not include the case when the angles are supplementary. - Option D: "Either equal or supplementary"
This is correct as it covers both possibilities.
The given figure shows two intersecting circles. If ∠ABC = 75o, then the measure of ∠PAD is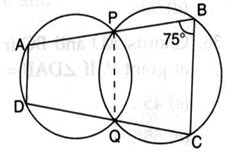
- a)75o
- b)125o
- c)105o
- d)150o
Correct answer is option 'C'. Can you explain this answer?
The given figure shows two intersecting circles. If ∠ABC = 75o, then the measure of ∠PAD is
a)
75o
b)
125o
c)
105o
d)
150o
|
Zachary Foster answered |
In the given figure, the points A, B, C, and D form a cyclic quadrilateral because they lie on the circumferences of the two intersecting circles.
The opposite angles of a cyclic quadrilateral are supplementary, i.e.,
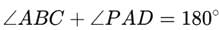
It is given that ∠ABC=75∘
Using the property of cyclic quadrilaterals:
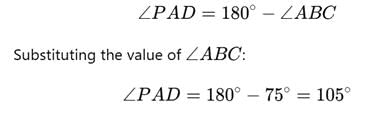
An exterior angle of triangle is 80° and the interior opposite angles are in the ratio 1:3. Measure of each interior opposite angle is:
- a)30°, 60°
- b)30°, 90°
- c)40°, 120°
- d)20°, 60°
Correct answer is option 'D'. Can you explain this answer?
An exterior angle of triangle is 80° and the interior opposite angles are in the ratio 1:3. Measure of each interior opposite angle is:
a)
30°, 60°
b)
30°, 90°
c)
40°, 120°
d)
20°, 60°
|
|
Ananya shah answered |
so interior angle corresponding to 80° will be 100°
let there ratio be x so angles would be x and 3x
x + 3x + 100° = 180°
4x = 80°
x = 20°
so x and 3x will be 20° and 60° respectively
let there ratio be x so angles would be x and 3x
x + 3x + 100° = 180°
4x = 80°
x = 20°
so x and 3x will be 20° and 60° respectively
The longest chord of the circle is the- a)secant
- b)perpendicular
- c)diameter
- d)radius
Correct answer is option 'C'. Can you explain this answer?
The longest chord of the circle is the
a)
secant
b)
perpendicular
c)
diameter
d)
radius
|
Rachit Agrah.ari answered |
Diameter is the Longest Chord of the Circle...So, 'C' is correct..
XY and PQ are two parallel chords of a circle on opposite side of the centre O and radius of circle is 13 cm. if PQ = 10 cm and XY = 24 cm, find the distance between PQ and XY.- a)17 cm
- b)14 cm
- c)25 cm
- d)21 cm
Correct answer is option 'A'. Can you explain this answer?
XY and PQ are two parallel chords of a circle on opposite side of the centre O and radius of circle is 13 cm. if PQ = 10 cm and XY = 24 cm, find the distance between PQ and XY.
a)
17 cm
b)
14 cm
c)
25 cm
d)
21 cm
|
Ashish Menon answered |
Given, PQ = 10 cm, XY = 24 cm and radius of circle = 13 cm
We need to find the distance between PQ and XY.
Let AB be the diameter of the circle passing through O.
Then, OB = OA = AB/2 = 13 cm
Let M be the midpoint of PQ and N be the midpoint of XY.
Then, OM is perpendicular to PQ and ON is perpendicular to XY.
Also, OM = ON = OB = 13 cm (radii of the same circle).
Now, consider the right-angled triangles OMP and ONX.
We have, OP = OX = PQ/2 = 5 cm and OY = OQ = XY/2 = 12 cm.
Using Pythagoras theorem, we can find MP and NX as:
MP = sqrt(OP^2 - OM^2) = sqrt(5^2 - 13^2) = sqrt(144) = 12 cm
NX = sqrt(OX^2 - ON^2) = sqrt(12^2 - 13^2) = sqrt(23) cm
Therefore, the distance between PQ and XY is MN = MP + NX = 12 + sqrt(23) cm
Hence, option (A) 17 cm is the correct answer.
We need to find the distance between PQ and XY.
Let AB be the diameter of the circle passing through O.
Then, OB = OA = AB/2 = 13 cm
Let M be the midpoint of PQ and N be the midpoint of XY.
Then, OM is perpendicular to PQ and ON is perpendicular to XY.
Also, OM = ON = OB = 13 cm (radii of the same circle).
Now, consider the right-angled triangles OMP and ONX.
We have, OP = OX = PQ/2 = 5 cm and OY = OQ = XY/2 = 12 cm.
Using Pythagoras theorem, we can find MP and NX as:
MP = sqrt(OP^2 - OM^2) = sqrt(5^2 - 13^2) = sqrt(144) = 12 cm
NX = sqrt(OX^2 - ON^2) = sqrt(12^2 - 13^2) = sqrt(23) cm
Therefore, the distance between PQ and XY is MN = MP + NX = 12 + sqrt(23) cm
Hence, option (A) 17 cm is the correct answer.
If a chord of a circle is equal to its radius, then the angle subtended by this chord in major segment is- a)45o
- b)30o
- c)60o
- d)90o
Correct answer is option 'B'. Can you explain this answer?
If a chord of a circle is equal to its radius, then the angle subtended by this chord in major segment is
a)
45o
b)
30o
c)
60o
d)
90o
|
|
Zachary Foster answered |
Let AB be the chord of the circle with center O
.
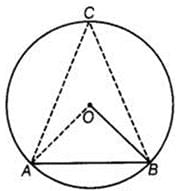
Given that AB = Radius of the circle.
Also, AO = BO = Radius
∴ ΔOAB is an equilateral triangle.
Thus, ∠AOB = ∠OBA = ∠OAB = 60°
Also, angle subtended by an arc at the center of the circle is twice the angle subtended by it at any other point in the remaining part of the circle.
∴ ∠AOB = 2∠ACB
⇒ ∠ACB = 1/2 (∠AOB)
⇒ ∠ACB = 1/2 (60°) = 30°
If ΔABC ~ ΔEDF then which of the following is not true?
- a)BC . EF = AC . FD
- b)AB . EF = AC . DE
- c)BC . DE = AB . EF
- d)BC . DE = AB . FD
Correct answer is option 'C'. Can you explain this answer?
If ΔABC ~ ΔEDF then which of the following is not true?
a)
BC . EF = AC . FD
b)
AB . EF = AC . DE
c)
BC . DE = AB . EF
d)
BC . DE = AB . FD
|
|
Anita Menon answered |
Since △ABC~△EDF
Then, AB/ED = BC/DF = AC/EF
A) BC/DF = AC/EF
⇒BC.EF=AC.FD
So, A) is true
B) AB/ED = AC/EF
⇒AB.EF=AC.DE
So,B) is true
D) AB/ED = BC/DF
BC.DE=AB.EF
So, D) is not true
Therefore, Option C is not true
Find the angle which is four times its compliment is 10° less than twice its complement. - a)15°
- b)10°
- c)25°
- d)5°
Correct answer is option 'D'. Can you explain this answer?
Find the angle which is four times its compliment is 10° less than twice its complement.
a)
15°
b)
10°
c)
25°
d)
5°
|
Sounak Sengupta answered |
If we call the angle a, then...
4(90 - a) = 2(180 - a) - 10
360 - 4a = 360 - 2a - 10
2a = 10
a = 5 deg
If two parallel lines are cut by a transversal, then the pairs of ___________ angles are congruent.
- a)Equal
- b)Complementary
- c)Supplementary
- d)corresponding
Correct answer is option 'D'. Can you explain this answer?
If two parallel lines are cut by a transversal, then the pairs of ___________ angles are congruent.
a)
Equal
b)
Complementary
c)
Supplementary
d)
corresponding
|
|
Vivek Rana answered |
If two parallel lines are cut by a transversal, the corresponding angles are congruent. If two lines are cut by a transversal and the corresponding angles are congruent, the lines are parallel.
In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are- a)congruent but not similar
- b)similar but not congruent
- c)neither congruent nor similar
- d)congruent as well as similar
Correct answer is option 'B'. Can you explain this answer?
In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are
a)
congruent but not similar
b)
similar but not congruent
c)
neither congruent nor similar
d)
congruent as well as similar
|
Kiran Mehta answered |
to be congruent, the conditions are
S S S - three sides
S A S - two sides and the included angle
A S A - two angles and one side
R H S - R H S - Right angle, Hypotenuse and one side
But to be similar,
A A A means 3 angles
A A means only two angles ....
in both triangles should be equal.
In the problem, equality of two angles is given, but equality of sides is not given.
So, given triangles are not congruent.
But they are similar.
S S S - three sides
S A S - two sides and the included angle
A S A - two angles and one side
R H S - R H S - Right angle, Hypotenuse and one side
But to be similar,
A A A means 3 angles
A A means only two angles ....
in both triangles should be equal.
In the problem, equality of two angles is given, but equality of sides is not given.
So, given triangles are not congruent.
But they are similar.
In the given figure, AD/BD = AE/EC and ∠ADE = 70°, ∠BAC = 50°, then angle ∠BCA =
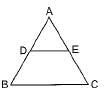
- a)70°
- b)50°
- c)80°
- d)60°
Correct answer is option 'D'. Can you explain this answer?
In the given figure, AD/BD = AE/EC and ∠ADE = 70°, ∠BAC = 50°, then angle ∠BCA =
a)
70°
b)
50°
c)
80°
d)
60°
|
|
Trisha sharma answered |
Explanation: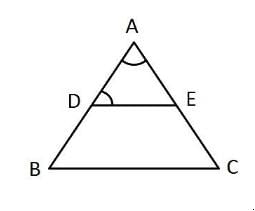
By converse of Thale’s theorem DE II BC
∠ADE = ∠ABC = 70 degree
Given ∠BAC = 50 degree
You can read Important Definitions & Formulas related to Triangles through the document:
In the given figure, the value of x which makes POQ a straight line is :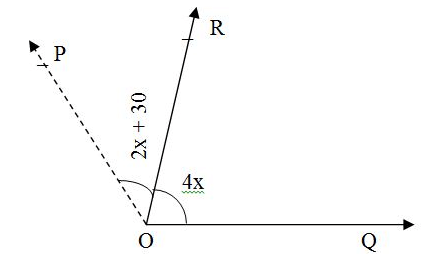
- a)40
- b)30
- c)35
- d)25
Correct answer is option 'D'. Can you explain this answer?
In the given figure, the value of x which makes POQ a straight line is :
a)
40
b)
30
c)
35
d)
25
|
|
Arizona Academy answered |
For POQ=straight line →∠ POQ=180o
2x+30+4x=180
6x+30=180
6x=150
x=25o.
Segment of a circle is the region between an arc and ………..of the circle.- a)perpendicular
- b)radius
- c)chord
- d)secant
Correct answer is option 'C'. Can you explain this answer?
Segment of a circle is the region between an arc and ………..of the circle.
a)
perpendicular
b)
radius
c)
chord
d)
secant
|
|
Ananya Sharma answered |
A sector is the part of a circle enclosed by two radii of a circle and their intercepted arc. A pie-shaped part of a circle. A segment is the region between a chord of a circle and its associated arc. A tangent is a line that touches a circle at only one point.
In a triangle ABC if ∠A = 53° and ∠C = 44° then the value of ∠B is:- a)46°
- b)83°
- c)93°
- d)73°
Correct answer is option 'B'. Can you explain this answer?
In a triangle ABC if ∠A = 53° and ∠C = 44° then the value of ∠B is:
a)
46°
b)
83°
c)
93°
d)
73°
|
Ashish Sen answered |
Solution:
Given, A = 53 and C = 44
We know that sum of angles of a triangle is 180°.
So, A + B + C = 180°
Substituting the given values, we get:
53 + B + 44 = 180
97 + B = 180
B = 180 - 97
B = 83
Therefore, the value of B is 83.
Hence, option B is the correct answer.
Given, A = 53 and C = 44
We know that sum of angles of a triangle is 180°.
So, A + B + C = 180°
Substituting the given values, we get:
53 + B + 44 = 180
97 + B = 180
B = 180 - 97
B = 83
Therefore, the value of B is 83.
Hence, option B is the correct answer.
D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 3 cm, BD = 5 cm, BC = 12.8 cm and DE || BC. Then length of DE (in cm) is- a)4.8 cm
- b)7.6 cm
- c)19.2 cm
- d)2.5 cm
Correct answer is option 'A'. Can you explain this answer?
D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 3 cm, BD = 5 cm, BC = 12.8 cm and DE || BC. Then length of DE (in cm) is
a)
4.8 cm
b)
7.6 cm
c)
19.2 cm
d)
2.5 cm
|
Meera Rana answered |
GIVEN: In Δ ABC, D and E are points on AB and AC , DE || BC and AD = 2.4 cm, AE = 3.2 cm, DE = 2 cm and BE = 5 cm.
In Δ ADE and Δ ABC,
∠ADE =∠ABC (corresponding angles)
[DE || BC, AB is transversal]
∠AED =∠ACB (corresponding angles)
[DE || BC, AC is transversal]
So, Δ ADE ~ Δ ABC (AA similarity)
Therefore, AD/AB = AE/AC = DE/BC
[In similar triangles corresponding sides are proportional]
AD/AB = DE/BC
2.4/(2.4+DB) = 2/5
2.4 × 5 = 2(2.4+ DB)
12 = 4.8 + 2DB
12 - 4.8 = 2DB
7.2 = 2DB
DB = 7.2/2
DB = 3.6 cm
Similarly, AE/AC = DE/BC
3.2/(3.2+EC) = 2/5
3.2 × 5 = 2(3.2+EC)
16 = 6.4 + 2EC
16 - 6.4 = 2EC
9.6 = 2EC
EC = 9.6/2
EC = 4.8 cm
Hence,BD = 3.6 cm and CE = 4.8 cm.
In Δ ADE and Δ ABC,
∠ADE =∠ABC (corresponding angles)
[DE || BC, AB is transversal]
∠AED =∠ACB (corresponding angles)
[DE || BC, AC is transversal]
So, Δ ADE ~ Δ ABC (AA similarity)
Therefore, AD/AB = AE/AC = DE/BC
[In similar triangles corresponding sides are proportional]
AD/AB = DE/BC
2.4/(2.4+DB) = 2/5
2.4 × 5 = 2(2.4+ DB)
12 = 4.8 + 2DB
12 - 4.8 = 2DB
7.2 = 2DB
DB = 7.2/2
DB = 3.6 cm
Similarly, AE/AC = DE/BC
3.2/(3.2+EC) = 2/5
3.2 × 5 = 2(3.2+EC)
16 = 6.4 + 2EC
16 - 6.4 = 2EC
9.6 = 2EC
EC = 9.6/2
EC = 4.8 cm
Hence,BD = 3.6 cm and CE = 4.8 cm.
Two parallel lines have:- a)A common point
- b)Two common points
- c)No common point
- d)Infinite common points
Correct answer is option 'C'. Can you explain this answer?
Two parallel lines have:
a)
A common point
b)
Two common points
c)
No common point
d)
Infinite common points
|
|
Sara Nair answered |
Explanation:
In geometry, two lines are parallel if they never intersect each other. Therefore, they cannot have any common points.
Definition of Parallel Lines:
Parallel lines are two lines that are always the same distance apart and never intersect.
Visual Representation:
We can visualize two parallel lines as two train tracks that run side by side. They never cross each other, and they remain at a constant distance apart.
Common Points:
If two lines have a common point, then they are not parallel. Instead, they are intersecting lines.
Two Common Points:
If two lines have two common points, then they are not parallel. Instead, they are coincident lines. In other words, they are the same line.
Infinite Common Points:
If two lines are the same line, then they have infinite common points. However, this is not the same as having parallel lines with infinite common points. Parallel lines cannot have any common points, whether finite or infinite.
In geometry, two lines are parallel if they never intersect each other. Therefore, they cannot have any common points.
Definition of Parallel Lines:
Parallel lines are two lines that are always the same distance apart and never intersect.
Visual Representation:
We can visualize two parallel lines as two train tracks that run side by side. They never cross each other, and they remain at a constant distance apart.
Common Points:
If two lines have a common point, then they are not parallel. Instead, they are intersecting lines.
Two Common Points:
If two lines have two common points, then they are not parallel. Instead, they are coincident lines. In other words, they are the same line.
Infinite Common Points:
If two lines are the same line, then they have infinite common points. However, this is not the same as having parallel lines with infinite common points. Parallel lines cannot have any common points, whether finite or infinite.
Which one of the following is not correct?
- a)If two lines are intersected by a transversal, then alternate angles are equal.
- b)If two lines are intersected by a transversal then sum of the interior angles on the same side of transversal is 180°.
- c)If two lines are intersected by a transversal then corresponding angles are equal.
- d)none of these.
Correct answer is option 'D'. Can you explain this answer?
Which one of the following is not correct?
a)
If two lines are intersected by a transversal, then alternate angles are equal.
b)
If two lines are intersected by a transversal then sum of the interior angles on the same side of transversal is 180°.
c)
If two lines are intersected by a transversal then corresponding angles are equal.
d)
none of these.
|
|
Tushar Dasgupta answered |
B)If two lines are intersected by a transversal then sum of the interior angles on the same side of transversal is 180 is not correct. The sum of the interior angles on the same side of the transversal is always equal to 180 degrees for any pair of parallel lines intersected by the transversal.
In triangle MNS, A and B are points on the sides MN, NS respectively.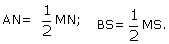 
Then AB is …………………. to NS :- a)Not Perpendicular
- b)Parallel
- c)Perpendicular
- d)Not Parallel
Correct answer is option 'B'. Can you explain this answer?
In triangle MNS, A and B are points on the sides MN, NS respectively. 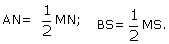Then AB is …………………. to NS :
Then AB is …………………. to NS :a)
Not Perpendicular
b)
Parallel
c)
Perpendicular
d)
Not Parallel
|
|
Anita Menon answered |
In ∆MNS we have,
→ AN = 1/2(MN)
→ AN = (1/2)(MA + AN)
→ AN = (1/2)MA + (1/2)AN
→ AN - (1/2)AN = (1/2)MA
→ AN[1 - (1/2)] = (1/2)MA
→ (1/2)AN = (1/2)MA
→ AN = MA
so, A is mid point of MN .
→ AN = (1/2)(MA + AN)
→ AN = (1/2)MA + (1/2)AN
→ AN - (1/2)AN = (1/2)MA
→ AN[1 - (1/2)] = (1/2)MA
→ (1/2)AN = (1/2)MA
→ AN = MA
so, A is mid point of MN .
similarly,
→ BS = (1/2)(MS)
→ BS = (1/2)(MS)
so, B is mid point of MS .
since AB is a line segment joining the mid points of two sides of ∆MNS .
therefore, → AB || NS { According to Mid point theorem the line segment joining the mid points of two sides of a triangle is parallel to the third side . }
In the given figure, O is the centre of the circle ABE is a straight line,. If ∠DBE = 95o then ∠AOD is equal to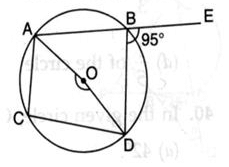
- a)190o
- b)170o
- c)180o
- d)175o
Correct answer is option 'B'. Can you explain this answer?
In the given figure, O is the centre of the circle ABE is a straight line,. If ∠DBE = 95o then ∠AOD is equal to
a)
190o
b)
170o
c)
180o
d)
175o
|
|
Zachary Foster answered |
AE is a straight line so,
angle ABD + angle EBD = 180°
angle ABD + 95° = 180°
angle ABD = 180° - 95°
angle ABD = 85°
so, it is interior angle of circle
So, angle AOD is double of angle suspended on the circle
angle AOD = 2ABD
angle AOD = 2(85°)
angle AOD = 170°
An angle is 14° more than its complementary angle, then angle is :- a)38°
- b)52°
- c)50°
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
An angle is 14° more than its complementary angle, then angle is :
a)
38°
b)
52°
c)
50°
d)
None of these
|
|
Hansa Sharma answered |
Let the angle be x
Then the complement angle will be 90∘ −x
Then the complement angle will be 90∘ −x
Given x is 14∘ more than 90∘ −x
⟹ x = 14∘ + 90∘ −x
⟹ 2x = 104∘
⟹ x = 52∘
The measure of the angle is 52∘
⟹ x = 14∘ + 90∘ −x
⟹ 2x = 104∘
⟹ x = 52∘
The measure of the angle is 52∘
In the given figure PQ = QR = RS and ∠PTS = 75o then the measure of ∠QOR is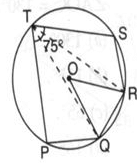
- a)25o
- b)20o
- c)50o
- d)75o
Correct answer is option 'C'. Can you explain this answer?
In the given figure PQ = QR = RS and ∠PTS = 75o then the measure of ∠QOR is
a)
25o
b)
20o
c)
50o
d)
75o
|
Kyojuro Rengoku answered |
PQ=QR=RS
PTR= 75
POS=2×75(centroid angle is double the angle suspended by any arc on remaining part of circle)
POS=150
AS PQ=QR=RS
QOR=150÷3
=50
PTR= 75
POS=2×75(centroid angle is double the angle suspended by any arc on remaining part of circle)
POS=150
AS PQ=QR=RS
QOR=150÷3
=50
In the figure, if AB is the diameter of the circle, then the value of x is: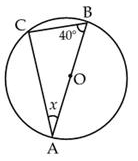
- a)40°
- b)80°
- c)90°
- d)50°
Correct answer is option 'D'. Can you explain this answer?
In the figure, if AB is the diameter of the circle, then the value of x is:
a)
40°
b)
80°
c)
90°
d)
50°
|
|
Sarita Verma answered |
The correct answer is d) 50degree.
In the given figure, AB is a diameter of the circle and it bisects the angle formed by two chords CD and CE. This means that angle x is half of the central angle formed by CD and CE, which is 180
degree. So, x = 180
degree / 2 = 90
degree/ 2 = 50
degree.
In fig., in ΔABC, AB = AC. The value of x is:
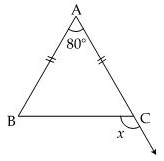
- a)80°
- b)100°
- c)130°
- d)120°
Correct answer is option 'C'. Can you explain this answer?
In fig., in ΔABC, AB = AC. The value of x is:
a)
80°
b)
100°
c)
130°
d)
120°
|
Trisha Vashisht answered |
Solution:
- Given that in triangle ABC, AB = AC
- We know that in an isosceles triangle, the base angles are equal
- So, angle B = angle C
- Let the value of angle B be r
- Therefore, angle C = r
- From angle sum property of a triangle, we have: A + B + C = 180°
- Substituting the values, we get: A + r + r = 180°
- Simplifying, we get: A + 2r = 180°
- 80° +2r =180°
- 2r = 100°
- r = 50°
so x + r = 180°
x + 50° = 180°
x = 130°
- Given that in triangle ABC, AB = AC
- We know that in an isosceles triangle, the base angles are equal
- So, angle B = angle C
- Let the value of angle B be r
- Therefore, angle C = r
- From angle sum property of a triangle, we have: A + B + C = 180°
- Substituting the values, we get: A + r + r = 180°
- Simplifying, we get: A + 2r = 180°
- 80° +2r =180°
- 2r = 100°
- r = 50°
so x + r = 180°
x + 50° = 180°
x = 130°
Chapter doubts & questions for Geometry - Mathematics for BMAT (Section 2) 2025 is part of BMAT exam preparation. The chapters have been prepared according to the BMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for BMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Geometry - Mathematics for BMAT (Section 2) in English & Hindi are available as part of BMAT exam.
Download more important topics, notes, lectures and mock test series for BMAT Exam by signing up for free.
Mathematics for BMAT (Section 2)
52 videos|41 docs|34 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup