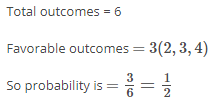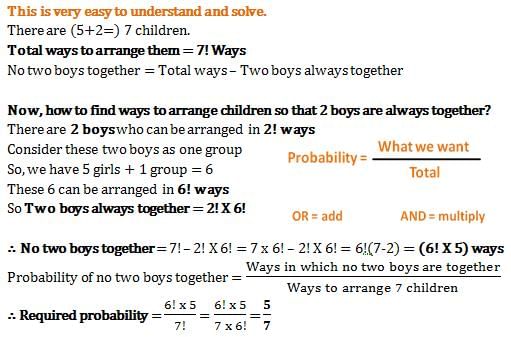All Exams >
BMAT >
Mathematics for BMAT (Section 2) >
All Questions
All questions of Probability for BMAT Exam
The probability of getting an even number, when a die is thrown once, is:- a)1/6
- b)1/2
- c)1/3
- d)5/6
Correct answer is option 'B'. Can you explain this answer?
The probability of getting an even number, when a die is thrown once, is:
a)
1/6
b)
1/2
c)
1/3
d)
5/6
|
|
Pooja Shah answered |
If we throw a die once, then possible outcomes (s), are
S = { 1, 2, 3, 4, 5, 6 }
⇒ n(E) = 6
(i) Let E be the favourable outcomes of getting an even number, then
E = { 2, 4, 6 }
⇒ n(S) = 3
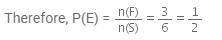
S = { 1, 2, 3, 4, 5, 6 }
⇒ n(E) = 6
(i) Let E be the favourable outcomes of getting an even number, then
E = { 2, 4, 6 }
⇒ n(S) = 3
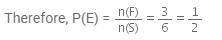
Two coins are tossed together. The probability of getting head on both the coins is- a)1/4
- b)3/4
- c)0
- d)1/2
Correct answer is option 'A'. Can you explain this answer?
Two coins are tossed together. The probability of getting head on both the coins is
a)
1/4
b)
3/4
c)
0
d)
1/2
|
|
Krishna Iyer answered |
The sample space for the event is : (H,H) (T,H) (H,T) (T,T)
Therefore total outcomes= 4
Therefore total outcomes= 4
Probability = 1/4
If a digit is chosen at random from the digits 1, 2, 3, 4, 5, 6, 7, 8, 9 then the probability that it is odd is
- a) 1/9
- b) 5/9
- c) 4/9
- d) 2/3
Correct answer is option 'B'. Can you explain this answer?
If a digit is chosen at random from the digits 1, 2, 3, 4, 5, 6, 7, 8, 9 then the probability that it is odd is
a)
1/9b)
5/9c)
4/9d)
2/3|
|
Nisha Choudhury answered |
The even numbers out of these are= 2, 4, 6, 8
No. of even numbers = 4
Total numbers = 9
So probability of choosing an odd number will be
= No. of odd numbers/Total numbers
= 5 / 9
Similarly probability of choosing an even number will be
= No. of even numbers/Total numbers
= 4 / 9
If a letter of English alphabet is chosen at random, then the probability that the letter is a consonant is:- a)11/13
- b)5/26
- c)10/13
- d)21/26
Correct answer is option 'D'. Can you explain this answer?
If a letter of English alphabet is chosen at random, then the probability that the letter is a consonant is:
a)
11/13
b)
5/26
c)
10/13
d)
21/26
|
|
Naina Sharma answered |
The probability that the letter is a consonant = (26 - 5)/26 = 21/26.
Cards each marked with one of the numbers 4, 5, 6,...., 20 are placed in a box and mixed thoroughly. Onecard is drawn at random from the box. Then, the probability of getting an even prime number is- a)o
- b)1
- c)1/2
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Cards each marked with one of the numbers 4, 5, 6,...., 20 are placed in a box and mixed thoroughly. One
card is drawn at random from the box. Then, the probability of getting an even prime number is
a)
o
b)
1
c)
1/2
d)
None of these
|
|
Pooja Shah answered |
We have one and only even prime number which is 2. So no. of favourable outcomes= 0 and total no. of outcomes=17
Probability of getting 2 =0 this means that 2 cannot occur .
Probability of getting 2 =0 this means that 2 cannot occur .
A card is drawn from a well-shuffled deck of 52 playing cards. The probability that the card will not be an ace card is
a)12/13b)1/4c)3/4d)1/13Correct answer is option 'A'. Can you explain this answer?
|
|
Ananya Das answered |
Total no. of outcomes=52
No. of ace cards=4
No. of non-ace cards=48
Probability of getting a non-ace card = No. of favourable outcomes / total no. of outcomes
=48/52=12/13
No. of ace cards=4
No. of non-ace cards=48
Probability of getting a non-ace card = No. of favourable outcomes / total no. of outcomes
=48/52=12/13
The probability of getting a number between 1 and ... more6 is
a) 1/6
b) 2/6
c) 3/4
d) 2/3
Correct answer is option 'D'. Can you explain this answer?
|
|
Gaurav Kumar answered |
Between 1 and 6, meaning not 1 or 6, then we have four favorable choices (2, 3, 4, 5) out of six possible outcomes (1, 2, 3, 4, 5, 6). Therefore your probability is 4/6 = 2/3.
The probability of an event that is certain to happen is- a)2
- b)1
- c)0
- d)-1
Correct answer is option 'B'. Can you explain this answer?
The probability of an event that is certain to happen is
a)
2
b)
1
c)
0
d)
-1
|
|
Ananya Das answered |
The probability of an event is a number describing the chance that the event will happen. An event that is certain to happen has a probability of 1. An event that cannot possibly happen has a probability of zero. If there is a chance that an event will happen, then its probability is between zero and 1.
Examples of Events:
- tossing a coin and it landing on heads
- tossing a coin and it landing on tails
- rolling a '3' on a die
- rolling a number > 4 on a die
- it rains two days in a row
- drawing a card from the suit of clubs
- guessing a certain number between 000 and 999 (lottery)
If the probability of winning a game is 0.995, then the probability of losing is- a)0.05
- b)1
- c)0.005
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
If the probability of winning a game is 0.995, then the probability of losing is
a)
0.05
b)
1
c)
0.005
d)
None of the above

|
Sun Ray Institute answered |
Let P(winning the game)=0.995
Since the probability of two complimentary event sums to 1 so-
P(not winning the game) + P(winning the game )=1
=P(losing it )=1-P(winning the game )
=1-0.995=0.005
Which of the following cannot be the probability of an event?- a)0.7
- b)15%
- c)2/3
- d)-1.5
Correct answer is option 'D'. Can you explain this answer?
Which of the following cannot be the probability of an event?
a)
0.7
b)
15%
c)
2/3
d)
-1.5
|
|
Rohan Kapoor answered |
D cannot be a probability as it has negative value
The probability of getting a prime number in single throw of a dice is:- a)Zero
- b)1/2
- c)1/4
- d)1/3
Correct answer is option 'B'. Can you explain this answer?
The probability of getting a prime number in single throw of a dice is:
a)
Zero
b)
1/2
c)
1/4
d)
1/3
|
|
Krishna Iyer answered |
Given, A dice is thrown once. So,
Total number of outcomes (n) = 6
Number of prime numbers = {2, 3,5}
So, Favorable number of outcomes (m) = 3
Thus, probability of getting a prime number = m/n = 3/6 = 1/2
The probability that a leap year has 53 Sundays is- a)3/7
- b)2/7
- c)4/7
- d)1/7
Correct answer is option 'B'. Can you explain this answer?
The probability that a leap year has 53 Sundays is
a)
3/7
b)
2/7
c)
4/7
d)
1/7
|
|
Ananya Das answered |
There are 366 days in a leap year, i.e, 1 more than a normal year.
Now, 52 weeks make up 344 days (52 x 7 = 344)
That means that we already have 52 sundays for sure.
That means that we already have 52 sundays for sure.
Then, we are left with 2 days. Now, these days can be any from a pair of- mon-tues,tues-wed,wed-thurs,thurs-fri,fri-sat,sat-sun,sun-mon. Here favourable cases are sat-sun and sun-mon i.e, 2 cases and total number of cases is 7.
So, Probability=number of favourable cases/Total number of cases.
Therefore, Probability= 2/7.
The probability of getting one head is- a)1/2
- b)1/4
- c)3/4
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The probability of getting one head is
a)
1/2
b)
1/4
c)
3/4
d)
None of these
|
|
Pooja Shah answered |
Assume that is an equal chance of the coin landing on heads or tail (the coin is fair, not biased).
Probability of coin landing on head and then on tails=1/2 x 1/2=1/4
Probability of coin landing on tails and then on heads= 1/2 x 1/2 =1/4
Therefore, probability of getting one head and one tail in two coin tosses=1/4+1/4=1/2
If the probability of winning a game is 0.3, then the probability of losing it is:- a)0.3
- b)0.7
- c)0.2
- d)0.5
Correct answer is option 'B'. Can you explain this answer?
If the probability of winning a game is 0.3, then the probability of losing it is:
a)
0.3
b)
0.7
c)
0.2
d)
0.5
|
|
Amit Sharma answered |
Let the probability of losing the game be x
We know that sum of the the sum of probabilities is equal to 1
So
0.3+x=1
x=0.7
We know that sum of the the sum of probabilities is equal to 1
So
0.3+x=1
x=0.7
The probability that a randomly chosen number from one to twelve is a divisor of twelve is- a)1/6
- b)1/12
- c)1/2
- d)1/4
Correct answer is option 'D'. Can you explain this answer?
The probability that a randomly chosen number from one to twelve is a divisor of twelve is
a)
1/6
b)
1/12
c)
1/2
d)
1/4

|
Coachify answered |
We have the numbers from 1 to 12. Total possible outcomes = 12 Now, divisors of 12 : 1, 2, 3, 4, 6 and 12 Number of divisors of 12 = 6 Number of favourable outcomes = 6
Required probability
Required probability

Which one of the following cannot be the probability of an event?- a)1.1
- b)0.1
- c)0.9
- d)5%
Correct answer is option 'A'. Can you explain this answer?
Which one of the following cannot be the probability of an event?
a)
1.1
b)
0.1
c)
0.9
d)
5%
|
|
Krishna Iyer answered |
If the probability is in percentage we divide it by 100
So d) option is 0.05.And we know If an event is impossible its probability is zero. Similarly, if an event is certain to occur, its probability is one. The probability of any event lies in between these values. It is called the range of probability and is denoted as 0 ≤ P (E) ≤ 1.And probability more than one means that favourable outcomes are more than total outcomes which is wrong.
So d) option is 0.05.And we know If an event is impossible its probability is zero. Similarly, if an event is certain to occur, its probability is one. The probability of any event lies in between these values. It is called the range of probability and is denoted as 0 ≤ P (E) ≤ 1.And probability more than one means that favourable outcomes are more than total outcomes which is wrong.
Cards each marked with one of the numbers 4, 5, 6 …20 are put in a box and mixed thoroughly. One card is drawn at random from the box. The probability of getting an even prime number is- a)0
- b)1/20
- c)1
- d)1/2
Correct answer is option 'A'. Can you explain this answer?
Cards each marked with one of the numbers 4, 5, 6 …20 are put in a box and mixed thoroughly. One card is drawn at random from the box. The probability of getting an even prime number is
a)
0
b)
1/20
c)
1
d)
1/2
|
|
Neha Patel answered |
Number of Favourable outcomes= 0
Total outcomes=17
Probability=0/17
Or probability=0
A bag contains cards which are numbered from 2 to 90. A card is drawn at random from the bag. The probability that it bears a two digit number is:- a)88/90
- b)88/92
- c)81/89
- d)89/90
Correct answer is option 'C'. Can you explain this answer?
A bag contains cards which are numbered from 2 to 90. A card is drawn at random from the bag. The probability that it bears a two digit number is:
a)
88/90
b)
88/92
c)
81/89
d)
89/90
|
|
Pooja Shah answered |
Total number of outcomes=90-1=89
No. of favourable outcomes = Total outcomes - One digit number =89-8=81
Probability of having a two digit number=Total number of outcomes/No. of favourable outcomes=81/89
No. of favourable outcomes = Total outcomes - One digit number =89-8=81
Probability of having a two digit number=Total number of outcomes/No. of favourable outcomes=81/89
An urn contains lottery tickets numbered from 1 to 100. If a ticket is selected at random, then the probability that it is a perfect square is- a)0.1
- b)0.08
- c)0.09
- d)0.01
Correct answer is option 'A'. Can you explain this answer?
An urn contains lottery tickets numbered from 1 to 100. If a ticket is selected at random, then the probability that it is a perfect square is
a)
0.1
b)
0.08
c)
0.09
d)
0.01

|
Ujjwal Kumar answered |
Dude see....from 1 to 100...there is 10 perfect square number.
so, ur fav. number of out comes = 10.
nd number of total outcome = 100.
so....probability will be...no. of fav outcomes divided by number of total outcomes.
i.e., 10/100 => 1/10 => 0.1.
hope uh got it.
so, ur fav. number of out comes = 10.
nd number of total outcome = 100.
so....probability will be...no. of fav outcomes divided by number of total outcomes.
i.e., 10/100 => 1/10 => 0.1.
hope uh got it.
In a simultaneous throw of two coins the probability of getting at least one head is
a)1/2b)1/4c)3/4d)None of theseCorrect answer is option 'C'. Can you explain this answer?
|
|
Pooja Shah answered |
Two coins are simultaneously tossed.
So sample space={HH,HT,TH,TT}
No. of favourable outcomes=getting at least one head={HH,HT,TH}
=3
Total number of outcomes=4
Probability of getting at least one head=No. of favourable outcomes/Total number of outcomes
=3/4
So sample space={HH,HT,TH,TT}
No. of favourable outcomes=getting at least one head={HH,HT,TH}
=3
Total number of outcomes=4
Probability of getting at least one head=No. of favourable outcomes/Total number of outcomes
=3/4
The probability of getting a red and a king card is- a)5/26
- b)1/13
- c)7/26
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
The probability of getting a red and a king card is
a)
5/26
b)
1/13
c)
7/26
d)
None of these
|
|
Amit Kumar answered |
Let D be the favourable outcomes of getting red and a king, then n(D)=2 Therefore,
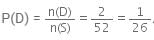
A bag contains 4 red balls and 3 green balls. A ball is drawn at random. The probability of drawing a green ball is- a)1/7
- b)2/7
- c)3/7
- d)4/7
Correct answer is option 'D'. Can you explain this answer?
A bag contains 4 red balls and 3 green balls. A ball is drawn at random. The probability of drawing a green ball is
a)
1/7
b)
2/7
c)
3/7
d)
4/7
|
|
Gaurav Kumar answered |
Total number of outcomes=7
No. of favourable outcomes=3 (no. Of green balls)
Probability of getting a green ball=No. Of favourable outcomes/Total no. of outcomes=3/7
No. of favourable outcomes=3 (no. Of green balls)
Probability of getting a green ball=No. Of favourable outcomes/Total no. of outcomes=3/7
A card is drawn at random from a pack of 52 playing cards. The probability of getting a face card is- a)1/4
- b)4/13
- c)3/13
- d)5/13
Correct answer is option 'C'. Can you explain this answer?
A card is drawn at random from a pack of 52 playing cards. The probability of getting a face card is
a)
1/4
b)
4/13
c)
3/13
d)
5/13
|
|
Anjana Khatri answered |
Clearly, there are 52 cards, out of which there are 12 face cards.
P (getting a face card) = 12/52=3/13.
The probability that a non-leap year selected at random will have 53 Mondays is- a)1/7
- b)7/52
- c)52/365
- d)45/52
Correct answer is option 'A'. Can you explain this answer?
The probability that a non-leap year selected at random will have 53 Mondays is
a)
1/7
b)
7/52
c)
52/365
d)
45/52
|
|
Anjana Khatri answered |
We know that there are 52 weeks in a year.
There are 7 days in a week
52 weeks will be to 7*52 = 364 days.
The remaining 1 day can be any day among Monday, Tuesday,..., Sunday.
Sample space has seven days as options.
So probability of getting 53 Sundays in a non-leap year is 1/7
Harmeet tosses two coins simultaneously. The probability of getting at least one head is- a)1/2
- b)3/4
- c)2/3
- d)1/3
Correct answer is option 'B'. Can you explain this answer?
Harmeet tosses two coins simultaneously. The probability of getting at least one head is
a)
1/2
b)
3/4
c)
2/3
d)
1/3

|
Sneha Khroad2209 answered |
At least means minimum and that is 3/4
A bag has 9 red, 7 green and 4 blue balls. A student randomly selects a ball from the bag. The probability of not getting a blue ball is- a)4/5
- b)7/20
- c)1/5
- d)9/20
Correct answer is option 'A'. Can you explain this answer?
A bag has 9 red, 7 green and 4 blue balls. A student randomly selects a ball from the bag. The probability of not getting a blue ball is
a)
4/5
b)
7/20
c)
1/5
d)
9/20
|
|
Vikram Kapoor answered |
Total number of balls in the bag=9+4+7=20 balls
No. of favourable outcomes=not getting blue ball= getting either the red ball or green ball=9+7=16
Probability of not getting blue ball = no. of favourable outcomes/total number of outcomes=16/20=4/5
No. of favourable outcomes=not getting blue ball= getting either the red ball or green ball=9+7=16
Probability of not getting blue ball = no. of favourable outcomes/total number of outcomes=16/20=4/5
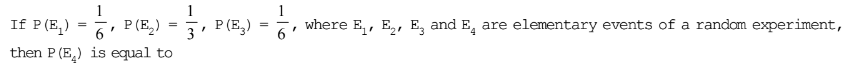
- a)1/2
- b)2/3
- c)1/3
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
a)
1/2
b)
2/3
c)
1/3
d)
None of these
|
|
Aryan Gupta. answered |
Baby Q 👆👆👆👆👆👆👆
nahi dekh rhaa... ... sorry bahenaa. wali baby.😎😎😎😎😎😉😉😉
What is the probability of getting no head when two coins are tossed?a)1/4b)3/4c)1/2d)None of theseCorrect answer is 'A'. Can you explain this answer?
|
|
Amit Sharma answered |
Two coins are tossed simultaneously, so there are four possible outcomes ie, HH,HT,TT,TH
Total number of outcomes=4
Probability of getting no head=no. of favourable outcomes/ total no. of outcomes
=1/4
Total number of outcomes=4
Probability of getting no head=no. of favourable outcomes/ total no. of outcomes
=1/4
Two fair coins are tossed simultaneously. Find the probability of Getting only one head- a)1/2
- b)1/3
- c)2/3
- d)1/4
Correct answer is option 'A'. Can you explain this answer?
Two fair coins are tossed simultaneously. Find the probability of Getting only one head
a)
1/2
b)
1/3
c)
2/3
d)
1/4
|
|
Arun Sharma answered |
When two coins are tossed, the sample space of possible outcomes would be the set
S = {HH, HT, TH, TT}
where H: the outcome is a “Head” and T: the outcome is a “Tail” and the probabilities associated with each of these outcomes are equal assuming the coins are fair.
When we say at most 1 “Head” outcome, it means that only 1 of the two coins show up a head or that the no “Head” outcome shows up.
If A is the event obtaining only 1 “Head” outcome, then the set of outcomes that makes up event A is
A = {(HT), (TH)}
Hence, the probability of event A is
P(A) = 2/4
In a single throw of a die, the probability of getting a multiple of 3 is
- A:
1/6
- B:
1/3
- C:
3/6
- D:
4/6
The answer is B.
1/6
1/3
3/6
4/6

|
Harshitha Das answered |
Given : A die is thrown once .
A die has 6 faces marked as 1, 2, 3, 4, 5 and 6.
If we throw one die then there possible outcomes are as follows: 1, 2, 3, 4, 5 and 6
Number of possible outcomes are = 6
Let E = Event of getting a getting a multiple of 3
Multiples of 3 are = 3, 6
Number of outcome favourable to E = 2
Probability (E) = Number of favourable outcomes / Total number of outcomes
P(E) = 2/6 = 1/3
Hence, the probability of getting a multiple of 3, P(E) = 1/3
The probability that a consonant is selected from the English alphabet is
- a)21/26
- b)1/26
- c)1/2
- d)5/26
Correct answer is option 'A'. Can you explain this answer?
The probability that a consonant is selected from the English alphabet is
a)
21/26
b)
1/26
c)
1/2
d)
5/26

|
Ruminating Friend answered |
Consonants are those English alphabets that are non-vowels. So there are 5 vowels out of 26 alphabets. Thus there are (26-5)= 21 consonants.
So correct probability will be
P(getting a consoant) = ²¹/₂₅.
This is why A is the correct option.
So correct probability will be
P(getting a consoant) = ²¹/₂₅.
This is why A is the correct option.
A die is thrown once. Find the probability of getting a number that is either composite or prime.- a)4/6
- b)3/6
- c)6/6
- d)5/6
Correct answer is option 'D'. Can you explain this answer?
A die is thrown once. Find the probability of getting a number that is either composite or prime.
a)
4/6
b)
3/6
c)
6/6
d)
5/6
|
|
Vikas Kumar answered |
The possible outcomes when a dice is thrown = {1, 2, 3, 4, 5, 6}
Number of possible outcomes of a dice = 6
Prime numbers on a dice are 2, 3, and 5.
Composite numbers on dice = 4, 6
Total prime numbers on a dice = 3
Total composite numbers on a dice = 2
So, total (prime + composite) = 5
Probability of getting a number that is either prime or composite = 5/6
Find the probability of getting a number greater than 2 when a die is thrown- a)1/6
- b)2/6
- c)4/6
- d)2/3
Correct answer is option 'D'. Can you explain this answer?
Find the probability of getting a number greater than 2 when a die is thrown
a)
1/6
b)
2/6
c)
4/6
d)
2/3
|
|
Pooja Shah answered |
Probability of getting a number greater than 2 is
number greater than 2 = 4
total outcomes = 6
so, 4/6
=2/3
number greater than 2 = 4
total outcomes = 6
so, 4/6
=2/3
A fair die is cast in the game of ‘Ludo’. The probability of getting a score greater than 6 is- a)1
- b)1/6
- c)zero
- d)2/3
Correct answer is option 'C'. Can you explain this answer?
A fair die is cast in the game of ‘Ludo’. The probability of getting a score greater than 6 is
a)
1
b)
1/6
c)
zero
d)
2/3
|
|
Ananya Das answered |
A fair dice has number 1,2,3,4,5,6 only . So there are no number greater than 6
No. of favourable outcomes=0
Total no. of outcomes=6
Probability of getting no. higher than 6=No. of favourable outcomes/Total no. of outcomes=0/6=0
No. of favourable outcomes=0
Total no. of outcomes=6
Probability of getting no. higher than 6=No. of favourable outcomes/Total no. of outcomes=0/6=0
The probability of getting a '10' of black suit is- a)1/26
- b)1/13
- c)3/26
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The probability of getting a '10' of black suit is
a)
1/26
b)
1/13
c)
3/26
d)
None of these
|
|
Gaurav Kumar answered |
Let G be the favourable outcomes of getting 10 of black suit then
⇒ n(G) = 2
Therefore, P(G)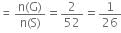
Therefore, P(G)
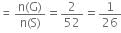
The probability of getting a jack card is- a)1/13
- b)2/13
- c)3/13
- d)4/13
Correct answer is option 'A'. Can you explain this answer?
The probability of getting a jack card is
a)
1/13
b)
2/13
c)
3/13
d)
4/13
|
|
Krishna Iyer answered |
Total number of outcomes = 52
Favourable outcomes = four cards are of Jack.
Total number of favourable outcomes = 4
Favourable outcomes = four cards are of Jack.
Total number of favourable outcomes = 4
Probability = Number of favourable outcomes/ Total number of outcomes.
Required probability = P(jack) = 4/52= 1/13.
Hence, the probability of getting Jack is 1/13.
Practice Test/Quiz or MCQ (Multiple Choice Questions) with Solutions of Chapter "Probability" are available for CBSE Class 10 Mathematics (Maths) and have been compiled as per the syllabus of CBSE Class 10 Mathematics (Maths) Q. If A be the event such that P(A) =2/5, then P(not A) is equal to- a)3/5
- b)4/5
- c)1/5
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Practice Test/Quiz or MCQ (Multiple Choice Questions) with Solutions of Chapter "Probability" are available for CBSE Class 10 Mathematics (Maths) and have been compiled as per the syllabus of CBSE Class 10 Mathematics (Maths)
Q. If A be the event such that P(A) =2/5, then P(not A) is equal to
a)
3/5
b)
4/5
c)
1/5
d)
None of these
|
|
Pooja Shah answered |
We know Probability law which is law of complement
Which is P(not A)=1-P(A)
Where P(A)=⅖
P(not A)=1-⅖=3/5
Which is P(not A)=1-P(A)
Where P(A)=⅖
P(not A)=1-⅖=3/5
From a well-shuffled pack of 52 cards, a card is drawn at random. The probability that it is a face card is:- a)2/13
- b)1/13
- c)4/13
- d)3/13
Correct answer is option 'D'. Can you explain this answer?
From a well-shuffled pack of 52 cards, a card is drawn at random. The probability that it is a face card is:
a)
2/13
b)
1/13
c)
4/13
d)
3/13

|
卩尺乇乇ㄒ卂爪 卩ㄚ卂尺乇 answered |
P(getting face card)
=(Total no.of face cards)/(Total no. of cards of shuffled deck i.e.52)
=12/52
=3/13.. (D)
What is the probability of a sure event?- a)greater than 1
- b)Between 0 and 1
- c)0
- d)1
Correct answer is option 'D'. Can you explain this answer?
What is the probability of a sure event?
a)
greater than 1
b)
Between 0 and 1
c)
0
d)
1
|
|
Nisha Choudhury answered |
The probability of an impossible event has the value of 0. A sure event is an event, which always happens. For example, it's a sure event to obtain a number between “1” and “6” when rolling an ordinary die. The probability of a sure event has the value of 1.
Which one of the following cannot be the probability of an event
- a)2/7
- b)0
- c)13/29
- d)5/2
Correct answer is option 'D'. Can you explain this answer?
Which one of the following cannot be the probability of an event
a)
2/7
b)
0
c)
13/29
d)
5/2
|
|
Krishna Iyer answered |
Probability of an event can only be a proper fraction and not an improper fraction.i.e.the numerator cannot be greater than the denominator.
P(E)=Number of outcomes favourable to E/Number of all possible outcomes of the experiment.
P(E)=Number of outcomes favourable to E/Number of all possible outcomes of the experiment.
The probability of getting a number less than 5 in a single throw of dice is- a)1/2
- b)2/3
- c)5/6
- d)1/3
Correct answer is option 'B'. Can you explain this answer?
The probability of getting a number less than 5 in a single throw of dice is
a)
1/2
b)
2/3
c)
5/6
d)
1/3
|
|
Beauty Dubey answered |
Number less than five in a dice is 1,2,3,4
P(E) = Number of favourable outcomes / Total number of possible outcomes.
= 4/6 =2/3.
P(E) = Number of favourable outcomes / Total number of possible outcomes.
= 4/6 =2/3.
In a throw of a die, the probability of getting a prime number is- a)1/2
- b)6
- c)3/4
- d)3/2
Correct answer is option 'A'. Can you explain this answer?
In a throw of a die, the probability of getting a prime number is
a)
1/2
b)
6
c)
3/4
d)
3/2
|
|
Anjana Khatri answered |
The possible outcomes when a dice is thrown = {1, 2, 3, 4, 5, 6}
Number of possible outcomes of a dice = 6
(i) Prime numbers on a dice are 2, 3, and 5.
Total prime numbers on a dice = 3
Probability of getting a prime number = 3/6 = 1/2
One card is drawn from a deck of 52 cards. The probability of drawing a black card is- a)1/52
- b)1/2
- c)1/4
- d)1/3
Correct answer is option 'B'. Can you explain this answer?
One card is drawn from a deck of 52 cards. The probability of drawing a black card is
a)
1/52
b)
1/2
c)
1/4
d)
1/3
|
|
shubham answered |
There are total 52 cards which consist of 13 suits each of club,spade, diamond and heart.Out of these club and spades are black card and, heart are dimond are red cards.
So there are total 26 black card and hence the probability of getting a black card from the deck of 52 card is 26/52=1/2
What is the probability of getting two heads when a coin is tossed twice?- a)1/2
- b)3/8
- c)1/4
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
What is the probability of getting two heads when a coin is tossed twice?
a)
1/2
b)
3/8
c)
1/4
d)
None of these
|
|
Sarita Pandey answered |
SS= {HH,HT,TH,TT}
n(SS)= 4
P(Two Heads)= 1/4
n(SS)= 4
P(Two Heads)= 1/4
A bag contains 3 white and 5 red balls. If a ball is drawn at random, the probability that the drawn ball is red is- a)3/8
- b)5/15
- c)3/15
- d)5/8
Correct answer is option 'D'. Can you explain this answer?
A bag contains 3 white and 5 red balls. If a ball is drawn at random, the probability that the drawn ball is red is
a)
3/8
b)
5/15
c)
3/15
d)
5/8

|
Nk Classes answered |
Explanation: Total number of balls = 3 white + 5 red = 8 balls.
The number of red balls = 5.
Probability = (Number of red balls) / (Total number of balls) = 5/8.
So, the correct answer is Option D.
Out of a day’s production, which is 1000 machine parts, 100 were found to be sub-standard. The probability that a part selected at random being up to the standard is- a)1/10
- b)7/10
- c)9/10
- d)2/10
Correct answer is option 'C'. Can you explain this answer?
Out of a day’s production, which is 1000 machine parts, 100 were found to be sub-standard. The probability that a part selected at random being up to the standard is
a)
1/10
b)
7/10
c)
9/10
d)
2/10

|
Sudhanshu Shukla answered |
Standard=1000-100=900
probaility=900/1000
=9/10
Three unbiased coins are tossed. What is the probability of getting at most two heads?- a)7/8
- b)3/8
- c)1/4
- d)3/7
Correct answer is option 'A'. Can you explain this answer?
Three unbiased coins are tossed. What is the probability of getting at most two heads?
a)
7/8
b)
3/8
c)
1/4
d)
3/7

|
Gowri Mehta answered |
Understanding the Problem
When three unbiased coins are tossed, each coin can land on either heads (H) or tails (T). We want to find the probability of getting at most two heads.
Total Outcomes
- The total number of outcomes when tossing three coins can be calculated as follows:
- Each coin has 2 possible outcomes (H or T).
- Thus, for three coins: 2 * 2 * 2 = 8 total outcomes.
Possible Outcomes
- The possible outcomes when tossing three coins are:
1. HHH
2. HHT
3. HTH
4. THH
5. HTT
6. THT
7. TTH
8. TTT
Counting Favorable Outcomes
- We need to count the outcomes with at most two heads:
- 0 heads: TTT (1 outcome)
- 1 head: HTT, THT, TTH (3 outcomes)
- 2 heads: HHT, HTH, THH (3 outcomes)
- Total favorable outcomes for at most two heads:
- 1 (0 heads) + 3 (1 head) + 3 (2 heads) = 7 outcomes
Calculating the Probability
- The probability of an event is given by the formula:
Probability = (Number of favorable outcomes) / (Total outcomes)
- In this case:
Probability = 7 / 8
Conclusion
- The probability of getting at most two heads when tossing three unbiased coins is 7/8. Therefore, the correct answer is option 'A'.
When three unbiased coins are tossed, each coin can land on either heads (H) or tails (T). We want to find the probability of getting at most two heads.
Total Outcomes
- The total number of outcomes when tossing three coins can be calculated as follows:
- Each coin has 2 possible outcomes (H or T).
- Thus, for three coins: 2 * 2 * 2 = 8 total outcomes.
Possible Outcomes
- The possible outcomes when tossing three coins are:
1. HHH
2. HHT
3. HTH
4. THH
5. HTT
6. THT
7. TTH
8. TTT
Counting Favorable Outcomes
- We need to count the outcomes with at most two heads:
- 0 heads: TTT (1 outcome)
- 1 head: HTT, THT, TTH (3 outcomes)
- 2 heads: HHT, HTH, THH (3 outcomes)
- Total favorable outcomes for at most two heads:
- 1 (0 heads) + 3 (1 head) + 3 (2 heads) = 7 outcomes
Calculating the Probability
- The probability of an event is given by the formula:
Probability = (Number of favorable outcomes) / (Total outcomes)
- In this case:
Probability = 7 / 8
Conclusion
- The probability of getting at most two heads when tossing three unbiased coins is 7/8. Therefore, the correct answer is option 'A'.
Chapter doubts & questions for Probability - Mathematics for BMAT (Section 2) 2025 is part of BMAT exam preparation. The chapters have been prepared according to the BMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for BMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Probability - Mathematics for BMAT (Section 2) in English & Hindi are available as part of BMAT exam.
Download more important topics, notes, lectures and mock test series for BMAT Exam by signing up for free.
Mathematics for BMAT (Section 2)
52 videos|41 docs|34 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup