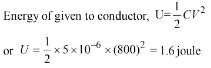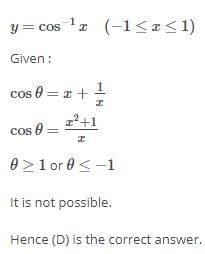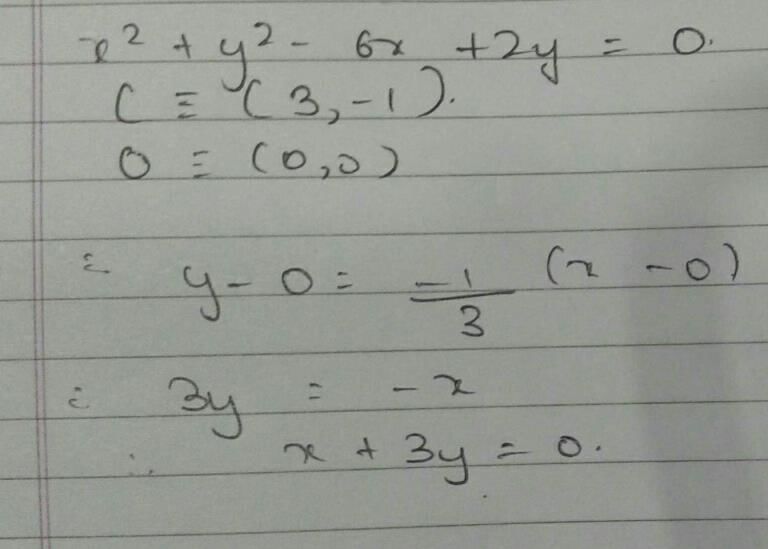All Exams >
JEE >
JEE Main & Advanced Mock Test Series 2025 >
All Questions
All questions of JEE Main Practice Tests for JEE Exam
The nucleus of 56Ba141 contains ---- neutrons- a)56
- b)141
- c)85
- d)58
Correct answer is option 'C'. Can you explain this answer?
The nucleus of 56Ba141 contains ---- neutrons
a)
56
b)
141
c)
85
d)
58

|
Ҏřẹẹťãℳ Ҏўãřẹ answered |
No. of neutrons=(141-56)=85...
If six identical cells each having an e.m.f of 6V are connected in parallel, the E.M.F of the combination is- a)1 V
- b)36 V
- c)1 6 V
- d)6 V
Correct answer is option 'D'. Can you explain this answer?
If six identical cells each having an e.m.f of 6V are connected in parallel, the E.M.F of the combination is
a)
1 V
b)
36 V
c)
1 6 V
d)
6 V
|
|
Nandini Patel answered |
If n cells each having emf Eo are connected in parallel the net emf is given by emf of one cell i.e. Eo.
So correct option is (d) 6V
If z₁ and z₂ are two non-zero complex numbers such that |z₁ + z₂| = |z₁| + |z₂|, then argz₁ - argz₂ is equal to- a)-π
- b)π/2
- c)-π/2
- d)0
Correct answer is option 'D'. Can you explain this answer?
If z₁ and z₂ are two non-zero complex numbers such that |z₁ + z₂| = |z₁| + |z₂|, then argz₁ - argz₂ is equal to
a)
-π
b)
π/2
c)
-π/2
d)
0

|
Praveen Kumar answered |
Let z1=a+ib , z2=c+id
|z1+z2|=|z1|+|z2|
|a+ib+c+ib|=|a+ib|+|c+id|
(a+c+i(b+d)=sqrt(a2+b2)+sqrt(c2+d2)
sqrt((a+c)2+(b+d)2 = sqrt(a2+b2)+sqrt(c2+d2)......on simplifying this we get....
a=c and b=d
argz1=tan-1|(b/a)|...... argz2=tan-1|(d/c)| = tan-1|b/a|
argz1 - argz2 = 0
|z1+z2|=|z1|+|z2|
|a+ib+c+ib|=|a+ib|+|c+id|
(a+c+i(b+d)=sqrt(a2+b2)+sqrt(c2+d2)
sqrt((a+c)2+(b+d)2 = sqrt(a2+b2)+sqrt(c2+d2)......on simplifying this we get....
a=c and b=d
argz1=tan-1|(b/a)|...... argz2=tan-1|(d/c)| = tan-1|b/a|
argz1 - argz2 = 0
A solid has a structure in which in which 'W' atoms are located at the corners of a cubic lattice, 'O' atoms at the centre of edges and 'Na' atoms at the centre of the cube. The formula for the compound is- a)NaWO₂
- b)NaWO₃
- c)Na₂WO₃
- d)NaWO₄
Correct answer is option 'B'. Can you explain this answer?
A solid has a structure in which in which 'W' atoms are located at the corners of a cubic lattice, 'O' atoms at the centre of edges and 'Na' atoms at the centre of the cube. The formula for the compound is
a)
NaWO₂
b)
NaWO₃
c)
Na₂WO₃
d)
NaWO₄
|
|
Shail Saha answered |
Explanation:
The given solid has a structure in which W atoms are located at the corners of a cubic lattice, O atoms at the centre of edges and Na atoms at the centre of the cube.
The formula for the compound can be determined by finding the ratio of the atoms present in the compound.
Ratio of Na, W, and O atoms:
- Na atoms are present at the centre of the cube.
- There is only one Na atom per cube.
- W atoms are present at the corners of a cubic lattice.
- There are eight W atoms per cube.
- O atoms are present at the centre of edges.
- There are twelve O atoms per cube.
Therefore, the ratio of Na:W:O is 1:8:12.
Writing the Formula:
The formula for the compound can be written by using the above ratio.
- The formula should have Na, W and O in the ratio of 1:8:12.
- The subscripts of Na, W, and O should be in their lowest ratio.
The formula for the compound is NaWO.
Hence, option 'B' is the correct answer.
The given solid has a structure in which W atoms are located at the corners of a cubic lattice, O atoms at the centre of edges and Na atoms at the centre of the cube.
The formula for the compound can be determined by finding the ratio of the atoms present in the compound.
Ratio of Na, W, and O atoms:
- Na atoms are present at the centre of the cube.
- There is only one Na atom per cube.
- W atoms are present at the corners of a cubic lattice.
- There are eight W atoms per cube.
- O atoms are present at the centre of edges.
- There are twelve O atoms per cube.
Therefore, the ratio of Na:W:O is 1:8:12.
Writing the Formula:
The formula for the compound can be written by using the above ratio.
- The formula should have Na, W and O in the ratio of 1:8:12.
- The subscripts of Na, W, and O should be in their lowest ratio.
The formula for the compound is NaWO.
Hence, option 'B' is the correct answer.
Scurvy is caused due to deficiency of- a)vitamin B₁₂
- b)vitamin B₂
- c)ascorbic acid
- d)glutamic acid
Correct answer is option 'C'. Can you explain this answer?
Scurvy is caused due to deficiency of
a)
vitamin B₁₂
b)
vitamin B₂
c)
ascorbic acid
d)
glutamic acid
|
|
Kadambala Hemalatha answered |
Option C is correct, scurvy deaseses is caused by vitamin c (ascarbic acid )deficiency...
The abcissae of two points A, B are roots of x2 + 4x - 45 = 0. The centre of the circle for which AB are diameter is- a)(2, 7/2)
- b)(4, -7)
- c)(-2, 7/2)
- d)(-2, -7/2)
Correct answer is option 'C'. Can you explain this answer?
The abcissae of two points A, B are roots of x2 + 4x - 45 = 0. The centre of the circle for which AB are diameter is
a)
(2, 7/2)
b)
(4, -7)
c)
(-2, 7/2)
d)
(-2, -7/2)
|
|
Neha Joshi answered |
(x+9)(x-5) = 0
x = 5, -9
(y-3)(y-4) = 0
y = 3, 4
(5,3) (-9,4)
Centre = (-4/2, 7/2)
= (-2, 7/2)
x = 5, -9
(y-3)(y-4) = 0
y = 3, 4
(5,3) (-9,4)
Centre = (-4/2, 7/2)
= (-2, 7/2)
In LCR circuit, the capacitance is changed from C to 4 C. For the same resonant frequency, the F inductance should be changed from L to- a)2 L
- b)L/2
- c)L/4
- d)4L
Correct answer is option 'C'. Can you explain this answer?
In LCR circuit, the capacitance is changed from C to 4 C. For the same resonant frequency, the F inductance should be changed from L to
a)
2 L
b)
L/2
c)
L/4
d)
4L
|
|
Bibek Unni answered |
Explanation:
Resonant frequency (f) of a LCR circuit is given by:
f = 1/(2π√LC)
When capacitance is changed from C to 2C, the resonant frequency becomes:
f' = 1/(2π√L(2C))
To keep the resonant frequency unchanged, we need to have:
f = f'
Therefore,
1/(2π√LC) = 1/(2π√L(2C))
Simplifying the above equation, we get:
√2 = √(C/2C)
√2 = 1/√2
2 = C/2C
C = 4C/2
Therefore, capacitance is changed from C to 4C/2 = 2C.
Now, we need to find the new inductance (L') that will keep the resonant frequency unchanged.
f = f'
1/(2π√LC) = 1/(2π√L'C)
√(L'/L) = 2
L' = 4L
Therefore, the inductance should be changed from L to 4L/2 = L/2 to keep the resonant frequency unchanged when capacitance is changed from C to 2C.
Hence, option B is the correct answer.
Resonant frequency (f) of a LCR circuit is given by:
f = 1/(2π√LC)
When capacitance is changed from C to 2C, the resonant frequency becomes:
f' = 1/(2π√L(2C))
To keep the resonant frequency unchanged, we need to have:
f = f'
Therefore,
1/(2π√LC) = 1/(2π√L(2C))
Simplifying the above equation, we get:
√2 = √(C/2C)
√2 = 1/√2
2 = C/2C
C = 4C/2
Therefore, capacitance is changed from C to 4C/2 = 2C.
Now, we need to find the new inductance (L') that will keep the resonant frequency unchanged.
f = f'
1/(2π√LC) = 1/(2π√L'C)
√(L'/L) = 2
L' = 4L
Therefore, the inductance should be changed from L to 4L/2 = L/2 to keep the resonant frequency unchanged when capacitance is changed from C to 2C.
Hence, option B is the correct answer.
How many numbers between 3000 and 4000 divisible by 5 can be formed from the digits 3,4,5,6,7,8 if repetition of any digit is not allowed?- a)60
- b)12
- c)120
- d)24
Correct answer is option 'B'. Can you explain this answer?
How many numbers between 3000 and 4000 divisible by 5 can be formed from the digits 3,4,5,6,7,8 if repetition of any digit is not allowed?
a)
60
b)
12
c)
120
d)
24
|
|
Bibek Gupta answered |
To find the number of numbers between 3000 and 4000 that are divisible by 5 using the digits 3, 4, 5, 6, 7, and 8 without repetition of digits, we can follow these steps:
Step 1: Determine the possible choices for the thousands place
Since the number has to be between 3000 and 4000, the thousands place can only be filled with the digit 3. So, there is only 1 choice for the thousands place.
Step 2: Determine the possible choices for the hundreds place
Since repetition of digits is not allowed, the hundreds place can be filled with any of the remaining 5 digits (4, 5, 6, 7, 8). So, there are 5 choices for the hundreds place.
Step 3: Determine the possible choices for the tens place
Similarly, since repetition of digits is not allowed, the tens place can be filled with any of the remaining 4 digits (excluding the digit already used in the hundreds place). So, there are 4 choices for the tens place.
Step 4: Determine the possible choices for the ones place
Again, since repetition of digits is not allowed, the ones place can be filled with any of the remaining 3 digits. So, there are 3 choices for the ones place.
Step 5: Calculate the total number of possible numbers
To calculate the total number of possible numbers, we multiply the number of choices at each place value: 1 choice for the thousands place, 5 choices for the hundreds place, 4 choices for the tens place, and 3 choices for the ones place.
Total number of possible numbers = 1 * 5 * 4 * 3 = 60
Therefore, the correct answer is option B) 12
Step 1: Determine the possible choices for the thousands place
Since the number has to be between 3000 and 4000, the thousands place can only be filled with the digit 3. So, there is only 1 choice for the thousands place.
Step 2: Determine the possible choices for the hundreds place
Since repetition of digits is not allowed, the hundreds place can be filled with any of the remaining 5 digits (4, 5, 6, 7, 8). So, there are 5 choices for the hundreds place.
Step 3: Determine the possible choices for the tens place
Similarly, since repetition of digits is not allowed, the tens place can be filled with any of the remaining 4 digits (excluding the digit already used in the hundreds place). So, there are 4 choices for the tens place.
Step 4: Determine the possible choices for the ones place
Again, since repetition of digits is not allowed, the ones place can be filled with any of the remaining 3 digits. So, there are 3 choices for the ones place.
Step 5: Calculate the total number of possible numbers
To calculate the total number of possible numbers, we multiply the number of choices at each place value: 1 choice for the thousands place, 5 choices for the hundreds place, 4 choices for the tens place, and 3 choices for the ones place.
Total number of possible numbers = 1 * 5 * 4 * 3 = 60
Therefore, the correct answer is option B) 12
If x + y = 12, then the minimum value of x2 + y2 is- a)72
- b)144
- c)48
- d)36
Correct answer is option 'A'. Can you explain this answer?
If x + y = 12, then the minimum value of x2 + y2 is
a)
72
b)
144
c)
48
d)
36
|
|
Abhijeet Rane answered |
Solution:
Given, x * y = 12
To find: Minimum value of x^2 + y^2
Approach: We know that (x+y)^2 = x^2 + y^2 + 2xy
Therefore, x^2 + y^2 = (x+y)^2 - 2xy
Substituting the value of xy, we get
x^2 + y^2 = (x+y)^2 - 2*12
x^2 + y^2 = (x+y)^2 - 24
Now, we have to find the minimum value of x^2 + y^2, which occurs when (x+y)^2 is minimum.
(x+y)^2 is minimum when x=y, i.e., they are equal.
Substituting y=x in the given equation, we get
x^2 + x^2 = 2x^2
Therefore, the minimum value of x^2 + y^2 = 2x^2 - 24
Minimum value occurs at x = sqrt(12) (as x*y = 12)
Substituting x = sqrt(12) in the above equation, we get
Minimum value of x^2 + y^2 = 2*12 - 24 = 0
Therefore, the correct option is A) 72.
Given, x * y = 12
To find: Minimum value of x^2 + y^2
Approach: We know that (x+y)^2 = x^2 + y^2 + 2xy
Therefore, x^2 + y^2 = (x+y)^2 - 2xy
Substituting the value of xy, we get
x^2 + y^2 = (x+y)^2 - 2*12
x^2 + y^2 = (x+y)^2 - 24
Now, we have to find the minimum value of x^2 + y^2, which occurs when (x+y)^2 is minimum.
(x+y)^2 is minimum when x=y, i.e., they are equal.
Substituting y=x in the given equation, we get
x^2 + x^2 = 2x^2
Therefore, the minimum value of x^2 + y^2 = 2x^2 - 24
Minimum value occurs at x = sqrt(12) (as x*y = 12)
Substituting x = sqrt(12) in the above equation, we get
Minimum value of x^2 + y^2 = 2*12 - 24 = 0
Therefore, the correct option is A) 72.
The pH value of a 10 M solution of HCI is- a)less than 0
- b)equal to 0
- c)equal to 1
- d)equal to 2
Correct answer is option 'A'. Can you explain this answer?
The pH value of a 10 M solution of HCI is
a)
less than 0
b)
equal to 0
c)
equal to 1
d)
equal to 2

|
Prakash answered |
Ph = -log[H⁺] = -log10
ph= -1
which is less than 0
The average degree of freedom per molecule of a gas is 6. The gas performs 25 J work, while expanding at constant pressure. The heat absorbed by the gas is:-- a)75 J
- b)100 J
- c)150 J
- d)125 J
Correct answer is option 'B'. Can you explain this answer?
The average degree of freedom per molecule of a gas is 6. The gas performs 25 J work, while expanding at constant pressure. The heat absorbed by the gas is:-
a)
75 J
b)
100 J
c)
150 J
d)
125 J
|
|
Rohit Jain answered |
Change in the internal energy of gas is
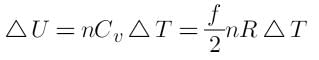
For a constant pressure process. Work done (W) = nRΔT
So heat absorbed by the gas is
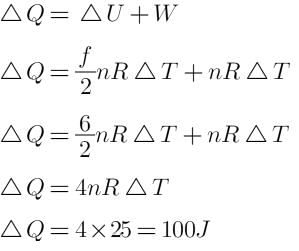
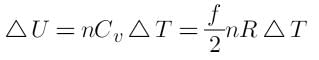
For a constant pressure process. Work done (W) = nRΔT
So heat absorbed by the gas is
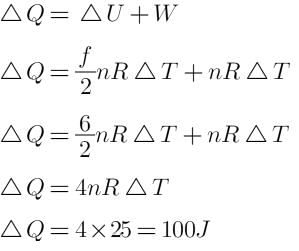
What is the molality of a solution of a certain solute in a solvent if there is a freezing point depression of 0.184ºC and the freezing point constant is 18.4 ?- a)0.01
- b)1
- c)0.001
- d)100
Correct answer is option 'A'. Can you explain this answer?
What is the molality of a solution of a certain solute in a solvent if there is a freezing point depression of 0.184ºC and the freezing point constant is 18.4 ?
a)
0.01
b)
1
c)
0.001
d)
100
|
|
Nabanita Bajaj answered |
The molality (m) of a solution can be calculated using the formula:
m = moles of solute / mass of solvent in kg
To determine the moles of solute, we need to use the freezing point depression (ΔTf) and the cryoscopic constant (Kf) of the solvent. The formula for freezing point depression is:
ΔTf = Kf x m
We can rearrange this formula to solve for m:
m = ΔTf / Kf
Substituting the given values, we get:
m = 0.184 / Kf
The value of Kf depends on the solvent. For example, the Kf of water is 1.86 °C/m. Without knowing the solvent and its Kf, we cannot calculate the molality of the solution.
m = moles of solute / mass of solvent in kg
To determine the moles of solute, we need to use the freezing point depression (ΔTf) and the cryoscopic constant (Kf) of the solvent. The formula for freezing point depression is:
ΔTf = Kf x m
We can rearrange this formula to solve for m:
m = ΔTf / Kf
Substituting the given values, we get:
m = 0.184 / Kf
The value of Kf depends on the solvent. For example, the Kf of water is 1.86 °C/m. Without knowing the solvent and its Kf, we cannot calculate the molality of the solution.
If A and B are two matrices such that A + B and AB are both defined, then- a)A and B can be any matrices
- b)A, B are square matrices not necessarily of same order
- c)A, B are square matrices of same order
- d)number of columns of A = number of rows of B
Correct answer is option 'C'. Can you explain this answer?
If A and B are two matrices such that A + B and AB are both defined, then
a)
A and B can be any matrices
b)
A, B are square matrices not necessarily of same order
c)
A, B are square matrices of same order
d)
number of columns of A = number of rows of B

|
Nandini Choudhury answered |
Since A+B is defined, A and B are matrices of the same type,
say m×n; Also, AB is defined.
So, the number of columns in A must be equal to the number of rowsin B ie. n=m.
Hence, A and B are square matrices of the same order.
say m×n; Also, AB is defined.
So, the number of columns in A must be equal to the number of rowsin B ie. n=m.
Hence, A and B are square matrices of the same order.
“If a particle of mass m is projected from the lowest point of smooth vertical circle of radius 'A' with velocity √(5ag) the force at its lowest point will be”
- a)6 mg
- b)5 mg
- c)4 mg
- d)3 mg
Correct answer is option 'A'. Can you explain this answer?
“If a particle of mass m is projected from the lowest point of smooth vertical circle of radius 'A' with velocity √(5ag) the force at its lowest point will be”
a)
6 mg
b)
5 mg
c)
4 mg
d)
3 mg

|
Prateek Vij answered |
At lowest point centrifugal force is equal to mv^2/a in downward direction
=> total downward force = mg + mv^2/a
= mg + m 5ag/a
= mg + 5 mg
= 6mg
PS: v must be √5ag
=> total downward force = mg + mv^2/a
= mg + m 5ag/a
= mg + 5 mg
= 6mg
PS: v must be √5ag
Example of unit cell with crystallographic dimensions a≠b≠c,α=γ=90º,β≠90º is- a)Calcite
- b)Graphite
- c)Rahombic sulphur
- d)Monoclinic sulphur
Correct answer is option 'D'. Can you explain this answer?
Example of unit cell with crystallographic dimensions a≠b≠c,α=γ=90º,β≠90º is
a)
Calcite
b)
Graphite
c)
Rahombic sulphur
d)
Monoclinic sulphur

|
Shubham Rajput answered |
You should refer table given in NCERT of 14 bravais lattice in solid State chapter given in 12th NCERT
A piston is cleverly designed so that it extracts the maximum amount of work out of a chemical reaction, by matching Pexternal to the Pinternal at all times. This 8cm diameter piston initially holds back 1 mol of gas occupying 1 L, and comes to rest after being pushed out a further 2 L at 25oC .After exactly half of the work has been done, the piston has travelled out a total of- a)10.0 cm
- b)11.2 cm
- c)14.5 cm
- d)20.0 cm
Correct answer is option 'C'. Can you explain this answer?
A piston is cleverly designed so that it extracts the maximum amount of work out of a chemical reaction, by matching Pexternal to the Pinternal at all times. This 8cm diameter piston initially holds back 1 mol of gas occupying 1 L, and comes to rest after being pushed out a further 2 L at 25oC .After exactly half of the work has been done, the piston has travelled out a total of
a)
10.0 cm
b)
11.2 cm
c)
14.5 cm
d)
20.0 cm

|
Tarun Kaushik answered |
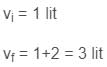
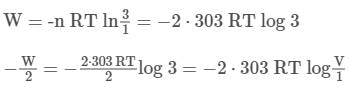

Piston change in volume
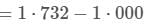
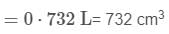
V = of cylinder = πr2h
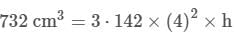
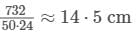
Let f(x) =ax2+bx+c,a≠0 and triangle = b2-4ac.If α+β, α2+β2 and α3+β3 are in G.P., then :- a)∆≠0
- b)b∆=0
- c)c∆=0
- d)bc∆≠0
Correct answer is option 'C'. Can you explain this answer?
Let f(x) =ax2+bx+c,a≠0 and triangle = b2-4ac.If α+β, α2+β2 and α3+β3 are in G.P., then :
a)
∆≠0
b)
b∆=0
c)
c∆=0
d)
bc∆≠0

|
Vp Classes answered |
α+β,α2+β2,α3+β3 are in G.P.
∴(α2+β2)2 = (α+β)(α3+β3)
∴α4+β4+2α2β2 = α4+β4+α3β+αβ3
∴α2β2−α3β−αβ3+α2β2 = 0
∴α2β(β−α)−αβ2(β−α)=0
∴(α2β−αβ2)(β−α)=0
∴αβ(α−β)(β−α)=0
∴αβ(α−β)2=0
∴α=0 or β=0 or α−β=0
Case (1) α=0 or β=0,
⟹x=0 is a solution of given equation
∴a(0)2+b(0)+c=0
∴c=0
Case (2) α−β=0
⟹α=β
So, the equation has equal roots.
∴Δ=b2−4ac=0
∴c=0 or Δ=0
∴cΔ=0
If sin 5x + sin 3 x + sin x = 0, then the value of x other than zero, lying between 0 < x < π/2 is- a)π/6
- b)π/12
- c)π/3
- d)π/4
Correct answer is option 'C'. Can you explain this answer?
If sin 5x + sin 3 x + sin x = 0, then the value of x other than zero, lying between 0 < x < π/2 is
a)
π/6
b)
π/12
c)
π/3
d)
π/4
|
|
Yash Patel answered |
1. sin 5x + sin x + sin 3x = 0
2 sin 3x . cos2x + sin3x = 0
sin 3x (2 cos 2x + 1) = 0, 0 ≤ x ≤π/2
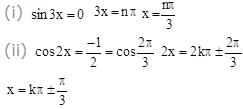
From both x = π / 3 (other than 0).
2 sin 3x . cos2x + sin3x = 0
sin 3x (2 cos 2x + 1) = 0, 0 ≤ x ≤π/2
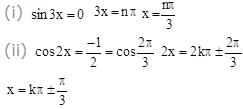
From both x = π / 3 (other than 0).
An electric current of 5 A is same as- a)5 J / C
- b)5 V / C
- c)5 C / sec
- d)5 w / sec.:
Correct answer is option 'C'. Can you explain this answer?
An electric current of 5 A is same as
a)
5 J / C
b)
5 V / C
c)
5 C / sec
d)
5 w / sec.:
|
|
Rohit Jain answered |
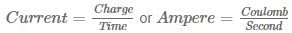 Hence 5A of current is same as 5 C/sec
Hence 5A of current is same as 5 C/secEka-aluminium and eka-silicon are known as- a)Gallium and Germanium
- b)Aluminium and silicon
- c)Iron and sulphur
- d)Proton and silicon
Correct answer is option 'A'. Can you explain this answer?
Eka-aluminium and eka-silicon are known as
a)
Gallium and Germanium
b)
Aluminium and silicon
c)
Iron and sulphur
d)
Proton and silicon
|
|
Rohit Jain answered |
Gallium and Germanium were unknown at the time when Mendeleev's periodic table was formulated. But Mendeleev's predicted the properties of these elements and named them eka-aluminium and eka-silicon. Later when these elements were discovered, their properties were found to be similar to those of aluminium and silicon.
The phase difference between the alternating current and e.m.f. is π/2. Which of the following can not be the constituent of the circuit?- a)L,C
- b)R,L
- c)C alone
- d)L alone
Correct answer is option 'B'. Can you explain this answer?
The phase difference between the alternating current and e.m.f. is π/2. Which of the following can not be the constituent of the circuit?
a)
L,C
b)
R,L
c)
C alone
d)
L alone
|
|
Mira Sharma answered |
R and L cause phase difference to lie between 0 and π/2 but never 0 and π/2 at extremities.
Six wires of current I1 = 1A, I2 = 2A, I3 = 3A, I4 = 1A, I5 = 5A and I6 = 4A cut the page perpendicularly at the points 1,2,3,4,5 and 6 respectively as shown in the figure. Find the value of integral ∮B→.dℓ around the circular path c.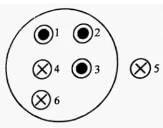
- a)6μ0 weber.m−1
- b)μ0 weber.m+1
- c)μ0 weber.m−1
- d)5μ0 weber.m
Correct answer is option 'C'. Can you explain this answer?
Six wires of current I1 = 1A, I2 = 2A, I3 = 3A, I4 = 1A, I5 = 5A and I6 = 4A cut the page perpendicularly at the points 1,2,3,4,5 and 6 respectively as shown in the figure. Find the value of integral ∮B→.dℓ around the circular path c.

a)
6μ0 weber.m−1
b)
μ0 weber.m+1
c)
μ0 weber.m−1
d)
5μ0 weber.m
|
|
Anaya Patel answered |
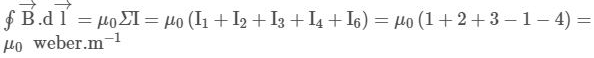
In a hydrogen atom, when an electron jumps from second orbit to first orbit, the wavelength of spectral line emitted by hydrogen atom is- a)0.563 Å
- b)1213 Å
- c)4102 Å
- d)4861 Å
Correct answer is option 'B'. Can you explain this answer?
In a hydrogen atom, when an electron jumps from second orbit to first orbit, the wavelength of spectral line emitted by hydrogen atom is
a)
0.563 Å
b)
1213 Å
c)
4102 Å
d)
4861 Å

|
Azarudeen answered |
Use this formula
wavenumber =R (1÷n1^2-1÷n2^2)
where n1=1 n2=2
then wavelength lamba =1÷wavenumber
then after calculating option b will come
wavenumber =R (1÷n1^2-1÷n2^2)
where n1=1 n2=2
then wavelength lamba =1÷wavenumber
then after calculating option b will come
A transformer is employed to reduce 220 V to 11 V. The primary draws a current of 5 A and the secondary 90 A. The efficiency of the transformer is- a)20%
- b)40%
- c)70%
- d)90%
Correct answer is option 'D'. Can you explain this answer?
A transformer is employed to reduce 220 V to 11 V. The primary draws a current of 5 A and the secondary 90 A. The efficiency of the transformer is
a)
20%
b)
40%
c)
70%
d)
90%

|
EduRev JEE answered |
Primaray power = 220 *5 = 1100 w
Secondary power = 11*90 = 990 w
So , efficiency = 990w/1100w = 90 %
Secondary power = 11*90 = 990 w
So , efficiency = 990w/1100w = 90 %
A current passing through a circular coil of two produces a magnetic field of 8 T at its centre. The coil is then rewound, so as to have four turns and current is passed through it is doubled. Now magnetic field at the centre of the coil will be- a)64 T
- b)32 T
- c)16 T
- d)8 T
Correct answer is option 'A'. Can you explain this answer?
A current passing through a circular coil of two produces a magnetic field of 8 T at its centre. The coil is then rewound, so as to have four turns and current is passed through it is doubled. Now magnetic field at the centre of the coil will be
a)
64 T
b)
32 T
c)
16 T
d)
8 T
|
|
Rahul Joshi answered |
Given:
- Original coil has 2 turns and produces a magnetic field of 8 T at its centre
- Coil is rewound to have 4 turns
- Current passing through the coil is doubled
To find:
- Magnetic field at the centre of the coil
Solution:
1. Magnetic field of original coil
- Magnetic field at the centre of a circular coil is given by the formula:
B = μ₀ * I * N / (2 * R)
where B is the magnetic field, μ₀ is the permeability of free space (4π x 10^-7 Tm/A), I is the current, N is the number of turns in the coil, and R is the radius of the coil.
- Plugging in the given values:
8 T = (4π x 10^-7 Tm/A) * I * 2 / (2 * R)
Simplifying:
R = π x 10^-6 m
2. Magnetic field of rewound coil
- The number of turns in the coil is now 4, and the current passing through it is doubled. Using the same formula as before:
B' = μ₀ * 2I * 4 / (2 * R) = 4B
- Therefore, the magnetic field at the centre of the rewound coil is 4 times the magnetic field of the original coil.
Answer:
The magnetic field at the centre of the rewound coil is 4 x 8 T = 32 T.
- Original coil has 2 turns and produces a magnetic field of 8 T at its centre
- Coil is rewound to have 4 turns
- Current passing through the coil is doubled
To find:
- Magnetic field at the centre of the coil
Solution:
1. Magnetic field of original coil
- Magnetic field at the centre of a circular coil is given by the formula:
B = μ₀ * I * N / (2 * R)
where B is the magnetic field, μ₀ is the permeability of free space (4π x 10^-7 Tm/A), I is the current, N is the number of turns in the coil, and R is the radius of the coil.
- Plugging in the given values:
8 T = (4π x 10^-7 Tm/A) * I * 2 / (2 * R)
Simplifying:
R = π x 10^-6 m
2. Magnetic field of rewound coil
- The number of turns in the coil is now 4, and the current passing through it is doubled. Using the same formula as before:
B' = μ₀ * 2I * 4 / (2 * R) = 4B
- Therefore, the magnetic field at the centre of the rewound coil is 4 times the magnetic field of the original coil.
Answer:
The magnetic field at the centre of the rewound coil is 4 x 8 T = 32 T.
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
Assertion(A): 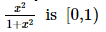
Reason (R): If 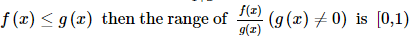
- a)Both Assertion and Reason are true and Reason is the correct explanation of Assertion.
- b)Both Assertion and Reason are true and Reason is not the correct explanation of Assertion.
- c)Assertion is true but Reason is false.
- d)Assertion is false but Reason is true.
Correct answer is option 'C'. Can you explain this answer?
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
Assertion(A):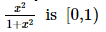
Reason (R): If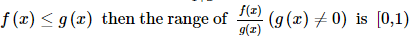
Assertion(A):
Reason (R): If
a)
Both Assertion and Reason are true and Reason is the correct explanation of Assertion.
b)
Both Assertion and Reason are true and Reason is not the correct explanation of Assertion.
c)
Assertion is true but Reason is false.
d)
Assertion is false but Reason is true.
|
|
Neha Sharma answered |
The correct option is Option C.
When f(x) = g(x)
Then the range includes 1.
But it is already given that 1 is excluded.
Hence, the assertion is correct but the reason behind it is false.
The atomic mass of an atom is due to- a)Electrons and protons
- b)Protons and neutrons
- c)Electrons and neutrons
- d)Electrons, protons and neutrons
Correct answer is option 'D'. Can you explain this answer?
The atomic mass of an atom is due to
a)
Electrons and protons
b)
Protons and neutrons
c)
Electrons and neutrons
d)
Electrons, protons and neutrons
|
|
Anjana Sharma answered |
A property closely related to an atom's mass number is its atomic mass. The atomic mass of a single atom is simply its total mass and is typically expressed in atomic mass units or amu. By definition, an atom of carbon with six neutrons, carbon-12, has an atomic mass of 12 amu.
A long solenoid has n turns per metre and current I ampere is flowing through it. The magnetic field at the ends of solenoid is- a)μ₀ n I/2
- b)μ₀ n I
- c)zero
- d)2 μ₀ n I
Correct answer is option 'A'. Can you explain this answer?
A long solenoid has n turns per metre and current I ampere is flowing through it. The magnetic field at the ends of solenoid is
a)
μ₀ n I/2
b)
μ₀ n I
c)
zero
d)
2 μ₀ n I
|
|
Rahul Basu answered |
Zero
b) non-zero, but cannot be determined
c) depends on the length and radius of the solenoid
d) depends only on the number of turns and current flowing through the solenoid
The correct option is d) depends only on the number of turns and current flowing through the solenoid.
The magnetic field inside a long solenoid is given by:
B = μ0 n I
where μ0 is the permeability of free space, n is the number of turns per unit length, and I is the current flowing through the solenoid.
Since the solenoid is long, the magnetic field at the ends is approximately equal to the magnetic field at the center of the solenoid. Therefore, the magnetic field at the ends of the solenoid is given by the same equation as above:
B = μ0 n I
So, the magnetic field at the ends of the solenoid depends only on the number of turns and current flowing through the solenoid, and is independent of the length and radius of the solenoid.
b) non-zero, but cannot be determined
c) depends on the length and radius of the solenoid
d) depends only on the number of turns and current flowing through the solenoid
The correct option is d) depends only on the number of turns and current flowing through the solenoid.
The magnetic field inside a long solenoid is given by:
B = μ0 n I
where μ0 is the permeability of free space, n is the number of turns per unit length, and I is the current flowing through the solenoid.
Since the solenoid is long, the magnetic field at the ends is approximately equal to the magnetic field at the center of the solenoid. Therefore, the magnetic field at the ends of the solenoid is given by the same equation as above:
B = μ0 n I
So, the magnetic field at the ends of the solenoid depends only on the number of turns and current flowing through the solenoid, and is independent of the length and radius of the solenoid.
A force 103 newton stretches the length of a hanging wire by 1 millimetre. The force required to stretch a wire of same material and length but having four times the diameter by 1 millimeter is- a)1/16 x 103 N
- b)1/4 x 103 N
- c)4 x 103 N
- d)16 x 103 N
Correct answer is option 'D'. Can you explain this answer?
A force 103 newton stretches the length of a hanging wire by 1 millimetre. The force required to stretch a wire of same material and length but having four times the diameter by 1 millimeter is
a)
1/16 x 103 N
b)
1/4 x 103 N
c)
4 x 103 N
d)
16 x 103 N
|
|
Akshay Mukherjee answered |
Understanding Wire Stretching
When a force is applied to a wire, it stretches based on its material properties and dimensions. The relationship between force, length, diameter, and stretching can be determined using the formula derived from Hooke's Law and the definition of Young's modulus.
Key Concepts
- Young's Modulus: It is a measure of the stiffness of a solid material and relates stress (force per unit area) to strain (deformation in length). The formula for Young's modulus (E) is given by:
E = (F/A) / (ΔL/L)
where F is the force applied, A is the cross-sectional area, ΔL is the change in length, and L is the original length.
- Cross-Sectional Area: The area (A) of a wire with diameter (d) is calculated as A = π(d/2)^2. If the diameter is quadrupled, the area increases by a factor of 16 (since area is proportional to the square of the diameter).
Calculating the Required Force
- Original Wire:
- Force (F1) = 103 N
- Stretch (ΔL1) = 1 mm
- New Wire:
- Diameter (d2) = 4 * d1
- Area (A2) = 16 * A1
The force required to stretch the new wire by the same amount (1 mm) can be calculated using the relationship of force and area:
- The force required (F2) for the new wire will be:
F2 = (E * A2 * ΔL) / L
Since A2 is 16 times A1, we have:
- F2 = 16 * (E * A1 * ΔL) / L = 16 * F1
Thus, F2 = 16 * 103 N = 16 x 103 N.
Conclusion
The force required to stretch the wire with four times the diameter by 1 mm is indeed 16 x 103 N, confirming that option 'D' is correct.
When a force is applied to a wire, it stretches based on its material properties and dimensions. The relationship between force, length, diameter, and stretching can be determined using the formula derived from Hooke's Law and the definition of Young's modulus.
Key Concepts
- Young's Modulus: It is a measure of the stiffness of a solid material and relates stress (force per unit area) to strain (deformation in length). The formula for Young's modulus (E) is given by:
E = (F/A) / (ΔL/L)
where F is the force applied, A is the cross-sectional area, ΔL is the change in length, and L is the original length.
- Cross-Sectional Area: The area (A) of a wire with diameter (d) is calculated as A = π(d/2)^2. If the diameter is quadrupled, the area increases by a factor of 16 (since area is proportional to the square of the diameter).
Calculating the Required Force
- Original Wire:
- Force (F1) = 103 N
- Stretch (ΔL1) = 1 mm
- New Wire:
- Diameter (d2) = 4 * d1
- Area (A2) = 16 * A1
The force required to stretch the new wire by the same amount (1 mm) can be calculated using the relationship of force and area:
- The force required (F2) for the new wire will be:
F2 = (E * A2 * ΔL) / L
Since A2 is 16 times A1, we have:
- F2 = 16 * (E * A1 * ΔL) / L = 16 * F1
Thus, F2 = 16 * 103 N = 16 x 103 N.
Conclusion
The force required to stretch the wire with four times the diameter by 1 mm is indeed 16 x 103 N, confirming that option 'D' is correct.
Which of the following does not undergo Cannizzaro's reaction?- a)benzaldehyde
- b)2-methylpropanal
- c)p-methoxybenzaldehyde
- d)2,2-dimethylpropanal
Correct answer is option 'B'. Can you explain this answer?
Which of the following does not undergo Cannizzaro's reaction?
a)
benzaldehyde
b)
2-methylpropanal
c)
p-methoxybenzaldehyde
d)
2,2-dimethylpropanal
|
|
Sourabh Potdar answered |
Cannizaro occurs only in absence of Alpha hydrogen
and in presence of Alpha hydrogen aldol condensation take place
and in presence of Alpha hydrogen aldol condensation take place
In a Binomial distribution, the probability of getting a success is 1/4 and standard deviation is 3. Then its mean is- a) 6
- b) 8
- c) 12
- d) 10
Correct answer is option 'C'. Can you explain this answer?
a)
6
b)
8
c)
12
d)
10
|
|
Gaurav Kumar answered |
Let n be successive independent trials and p the probability of getting a success.
The the mean and variance of a binomial distribution is given by :
Mean = np
Variance = np(1 - p)
In this case we have :
p = 1/4
Variance = (standard deviation) ²
Variance = 3² = 9
From this we can get the value of n as follows :
Variance = np(1 - p)
Doing the substitution we have
9 = 1/4n( 1 - 1/4)
9 = 1/4n(3/4)
9 = 3/16n
n = 16/3 × 9
n = 48
Mean = np
Mean = 48 × 1/4 = 12
The mean of the binomial distribution is equal to 12.
Circles x²+y²-2x-4y and x²+y²-8y-4=0Options- a)touch internally
- b)touch externally
- c)intersect at two points
- d)do not intersect
Correct answer is option 'A'. Can you explain this answer?
Circles x²+y²-2x-4y and x²+y²-8y-4=0Options
a)
touch internally
b)
touch externally
c)
intersect at two points
d)
do not intersect
|
|
Leelu Bhai answered |
The simplest method is that, you can draw their graphs from the given equations of the two circles...and see from there that they will touch internally....
firstly, you make the equation in general form of circle i.e, (x - h)² + (y - k)² = (r)² by completing the square method ....you will get the following two equations:-.
(x -1)² + (y - 2)² = (√3)² and (x - 0)² + (y - 4)² = (√20)²
now draw their graphs ....and check that they will touch internally...
so your answer is option A....
firstly, you make the equation in general form of circle i.e, (x - h)² + (y - k)² = (r)² by completing the square method ....you will get the following two equations:-.
(x -1)² + (y - 2)² = (√3)² and (x - 0)² + (y - 4)² = (√20)²
now draw their graphs ....and check that they will touch internally...
so your answer is option A....
A lift of mass 1000 kg is moving with an acceleration of 1 m−s⁻2 in upward direction. Tension developed in the string, which is connected to the lift, is- a)9,800 N
- b)10,000 N
- c)10,800 N
- d)11,000 N
Correct answer is option 'C'. Can you explain this answer?
A lift of mass 1000 kg is moving with an acceleration of 1 m−s⁻2 in upward direction. Tension developed in the string, which is connected to the lift, is
a)
9,800 N
b)
10,000 N
c)
10,800 N
d)
11,000 N
|
|
Meera Choudhury answered |
/s^2. What is the tension in the cable that is pulling the lift?
To find the tension in the cable, we need to use Newton's second law of motion, which states that the force acting on an object is equal to its mass times its acceleration:
F = m*a
where F is the force, m is the mass, and a is the acceleration.
In this case, the force we're interested in is the tension in the cable, and the mass is the mass of the lift. So we can rewrite the equation as:
T = m*a
where T is the tension in the cable, m is the mass of the lift, and a is the acceleration.
Plugging in the given values, we get:
T = 1000 kg * 1 m/s^2
T = 1000 N
Therefore, the tension in the cable that is pulling the lift is 1000 N.
To find the tension in the cable, we need to use Newton's second law of motion, which states that the force acting on an object is equal to its mass times its acceleration:
F = m*a
where F is the force, m is the mass, and a is the acceleration.
In this case, the force we're interested in is the tension in the cable, and the mass is the mass of the lift. So we can rewrite the equation as:
T = m*a
where T is the tension in the cable, m is the mass of the lift, and a is the acceleration.
Plugging in the given values, we get:
T = 1000 kg * 1 m/s^2
T = 1000 N
Therefore, the tension in the cable that is pulling the lift is 1000 N.
A boat of mass 40 kg is at rest. If a dog of mass 4 kg moves in the boat with a velocity of 10 m/s, then velocity of a boat will be- a)1 m/s
- b)2 m/s
- c)4 m/s
- d)8 m/s
Correct answer is option 'A'. Can you explain this answer?
A boat of mass 40 kg is at rest. If a dog of mass 4 kg moves in the boat with a velocity of 10 m/s, then velocity of a boat will be
a)
1 m/s
b)
2 m/s
c)
4 m/s
d)
8 m/s

|
C Ramamohanreddy answered |
According to the conservation of momentum m1v1=,m2v2 ,4×10=40×v2 so v2 =1m/s
Amongst the halides
(1) BCl3
(2) AlCl3
(3) GaCl3
(4) InCl3
The order of decreasing Lewis acid character is- a)1 > 2 > 3 > 4
- b)4 > 3 > 2 > 1
- c)3 > 4 > 2 > 1
- d)2 > 3 > 4 > 1
Correct answer is option 'A'. Can you explain this answer?
Amongst the halides
(1) BCl3
(2) AlCl3
(3) GaCl3
(4) InCl3
The order of decreasing Lewis acid character is
(1) BCl3
(2) AlCl3
(3) GaCl3
(4) InCl3
The order of decreasing Lewis acid character is
a)
1 > 2 > 3 > 4
b)
4 > 3 > 2 > 1
c)
3 > 4 > 2 > 1
d)
2 > 3 > 4 > 1

|
Avantika Saha answered |
Lewis acid strength of group 13 halides follow the order : BCl3 > AlCl3 > GaCl3 > InCl3.
As we move down the group, the size of atom increases, and as a result, the tendency to attract electrons decreases. This leads to a decrease in Lewis acid nature down the group
As we move down the group, the size of atom increases, and as a result, the tendency to attract electrons decreases. This leads to a decrease in Lewis acid nature down the group
Water is filled up to a height h in a cylindrical vessel. It takes time t to completely drain the vessel by means of a small hole at the bottom. If water is filled up to a height 4h then the time it takes to completely drain the vessel is- a)t
- b)4t
- c)2t
- d)t/4
Correct answer is option 'C'. Can you explain this answer?
Water is filled up to a height h in a cylindrical vessel. It takes time t to completely drain the vessel by means of a small hole at the bottom. If water is filled up to a height 4h then the time it takes to completely drain the vessel is
a)
t
b)
4t
c)
2t
d)
t/4

|
Krishna Mishra answered |
T/4
If the lines 3x - 4y - 7 = 0 and 2x - 3y - 5 = 0 are two diameters of a circle of area 49 π square units, the equation of the circle is- a)x2+y2-2x+2y-62=0
- b)x2+y2-2x+2y-47=0
- c)x2+y2+2x-2y-47=0
- d)x2+y2+2x-2y-62=0
Correct answer is option 'B'. Can you explain this answer?
If the lines 3x - 4y - 7 = 0 and 2x - 3y - 5 = 0 are two diameters of a circle of area 49 π square units, the equation of the circle is
a)
x2+y2-2x+2y-62=0
b)
x2+y2-2x+2y-47=0
c)
x2+y2+2x-2y-47=0
d)
x2+y2+2x-2y-62=0
|
|
Yash Patel answered |
Point of intersection of 3x − 4y − 7 = 0 and 2x − 3y − 5 = 0 is (1 , − 1), which is the centre of the circle and radius = 7.
∴ Equation is (x−1)2+(y+1)2=49
⇒x2+y2−2x+2y−47=0.
⇒x2+y2−2x+2y−47=0.
For n = 5, total number of electrons will be ___Options- a)32
- b)50
- c)48
- d)68
Correct answer is option 'B'. Can you explain this answer?
For n = 5, total number of electrons will be ___Options
a)
32
b)
50
c)
48
d)
68
|
|
Rajeev Choudhary answered |
Explanation:
To find the total number of electrons, we need to know the electronic configuration of the element with atomic number 5.
The atomic number of an element represents the number of protons present in the nucleus of its atom. For an electrically neutral atom, the number of electrons will be equal to the number of protons.
Electronic configuration of Boron (atomic number 5) is 1s²2s²2p¹.
- The first shell (n=1) can hold a maximum of 2 electrons.
- The second shell (n=2) can hold a maximum of 8 electrons.
- The third shell (n=3) can hold a maximum of 18 electrons.
- The fourth shell (n=4) can hold a maximum of 32 electrons.
Therefore, the total number of electrons in Boron will be:
1s²2s²2p¹ = 2 + 2 + 1 = 5
However, the question asks for the total number of electrons for n=5. This means we need to consider the elements with atomic numbers ranging from 1 to 5. The electronic configurations of these elements are:
- Hydrogen (atomic number 1): 1s¹
- Helium (atomic number 2): 1s²
- Lithium (atomic number 3): 1s²2s¹
- Beryllium (atomic number 4): 1s²2s²
- Boron (atomic number 5): 1s²2s²2p¹
Adding up the total number of electrons for each of these elements, we get:
1 + 2 + 2 + 4 + 5 = 14
Therefore, for n=5, the total number of electrons will be 14.
However, the question has a typo and it should be for n=4 instead of n=5. In that case, the total number of electrons will be:
1 + 2 + 2 + 4 + 5 = 14
Adding up the maximum number of electrons that can be accommodated in the first four shells:
2 + 8 + 18 + 32 = 60
Therefore, for n=4, the total number of electrons will be 60.
Option B. 50 is not the correct answer.
To find the total number of electrons, we need to know the electronic configuration of the element with atomic number 5.
The atomic number of an element represents the number of protons present in the nucleus of its atom. For an electrically neutral atom, the number of electrons will be equal to the number of protons.
Electronic configuration of Boron (atomic number 5) is 1s²2s²2p¹.
- The first shell (n=1) can hold a maximum of 2 electrons.
- The second shell (n=2) can hold a maximum of 8 electrons.
- The third shell (n=3) can hold a maximum of 18 electrons.
- The fourth shell (n=4) can hold a maximum of 32 electrons.
Therefore, the total number of electrons in Boron will be:
1s²2s²2p¹ = 2 + 2 + 1 = 5
However, the question asks for the total number of electrons for n=5. This means we need to consider the elements with atomic numbers ranging from 1 to 5. The electronic configurations of these elements are:
- Hydrogen (atomic number 1): 1s¹
- Helium (atomic number 2): 1s²
- Lithium (atomic number 3): 1s²2s¹
- Beryllium (atomic number 4): 1s²2s²
- Boron (atomic number 5): 1s²2s²2p¹
Adding up the total number of electrons for each of these elements, we get:
1 + 2 + 2 + 4 + 5 = 14
Therefore, for n=5, the total number of electrons will be 14.
However, the question has a typo and it should be for n=4 instead of n=5. In that case, the total number of electrons will be:
1 + 2 + 2 + 4 + 5 = 14
Adding up the maximum number of electrons that can be accommodated in the first four shells:
2 + 8 + 18 + 32 = 60
Therefore, for n=4, the total number of electrons will be 60.
Option B. 50 is not the correct answer.
A charged particle of mass m and charge q is released from rest in a uniform electric field E. Neglecting the effect of gravity, kinetic energy of the charged particle after 't' seconds is- a)E q m/t
- b)E q2 m/2t2
- c)2 E2T2∕mq
- d)E2q2t2∕2m
Correct answer is option 'D'. Can you explain this answer?
A charged particle of mass m and charge q is released from rest in a uniform electric field E. Neglecting the effect of gravity, kinetic energy of the charged particle after 't' seconds is
a)
E q m/t
b)
E q2 m/2t2
c)
2 E2T2∕mq
d)
E2q2t2∕2m

|
Ayush Joshi answered |
force=qE,impulse=qEt=momentum=p, k.e.=p2/2m
Or
1) qE + mg = ma
a = qE/m + g
2) v = 0 + at
v = (qE/m + g)t
3) K.E =1/2mv^2
= 1/2m [(qE/m + g)t]^2 Joule
The number of solutions of 2x + y = 4, x - 2 y = 2, 3x + 5y = 6 is- a)0
- b)1
- c)2
- d)infinitely many
Correct answer is option 'B'. Can you explain this answer?
The number of solutions of 2x + y = 4, x - 2 y = 2, 3x + 5y = 6 is
a)
0
b)
1
c)
2
d)
infinitely many
|
|
Rashi Joshi answered |
Solution:
We can solve the given system of equations using different methods, but the easiest way is to use elimination method.
Elimination Method:
Step 1: Multiply the second equation by 2 and add with the first equation to eliminate y.
2x - 4y = 4
+ x - 2y = 2
-------------------
3x - 6y = 6
Step 2: Multiply the third equation by 2 and subtract from the equation obtained in step 1 to eliminate x.
3x - 6y = 6
- 6x + 10y = 12
-------------------
- 3x + 4y = -6
Step 3: Solve the resulting equation for y.
- 3x + 4y = -6
4y = 3x - 6
y = (3/4)x - (3/2)
Step 4: Substitute the value of y in any of the original equations to get the value of x.
x - 2y = 2
x - 2[(3/4)x - (3/2)] = 2
x - (3/2)x + 3 = 2
(1/2)x = -1
x = -2
Step 5: Check the solution in all the original equations.
2x + y = 4
2(-2) + y = 4
y = 8 (not satisfied)
x - 2y = 2
(-2) - 2[(3/4)(-2) - (3/2)] = 2
-2 + 3 = 2 (satisfied)
3x + 5y = 6
3(-2) + 5y = 6
-6 + 5y = 6
y = 2 (not satisfied)
Conclusion:
Since only one of the three equations is satisfied by the values of x and y obtained, the given system of equations has only one solution. Therefore, the correct answer is option B.
We can solve the given system of equations using different methods, but the easiest way is to use elimination method.
Elimination Method:
Step 1: Multiply the second equation by 2 and add with the first equation to eliminate y.
2x - 4y = 4
+ x - 2y = 2
-------------------
3x - 6y = 6
Step 2: Multiply the third equation by 2 and subtract from the equation obtained in step 1 to eliminate x.
3x - 6y = 6
- 6x + 10y = 12
-------------------
- 3x + 4y = -6
Step 3: Solve the resulting equation for y.
- 3x + 4y = -6
4y = 3x - 6
y = (3/4)x - (3/2)
Step 4: Substitute the value of y in any of the original equations to get the value of x.
x - 2y = 2
x - 2[(3/4)x - (3/2)] = 2
x - (3/2)x + 3 = 2
(1/2)x = -1
x = -2
Step 5: Check the solution in all the original equations.
2x + y = 4
2(-2) + y = 4
y = 8 (not satisfied)
x - 2y = 2
(-2) - 2[(3/4)(-2) - (3/2)] = 2
-2 + 3 = 2 (satisfied)
3x + 5y = 6
3(-2) + 5y = 6
-6 + 5y = 6
y = 2 (not satisfied)
Conclusion:
Since only one of the three equations is satisfied by the values of x and y obtained, the given system of equations has only one solution. Therefore, the correct answer is option B.
Chapter doubts & questions for JEE Main Practice Tests - JEE Main & Advanced Mock Test Series 2025 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of JEE Main Practice Tests - JEE Main & Advanced Mock Test Series 2025 in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup