All Exams >
CLAT >
Quantitative Techniques for CLAT >
All Questions
All questions of Average for CLAT Exam
David obtained 76, 65, 82, 67 and 85 marks (out of 100) in English, Mathematics,Physics, Chemistry and Biology What are his average marks ?- a)75
- b)68
- c)65
- d)60
- e)None
Correct answer is option 'A'. Can you explain this answer?
David obtained 76, 65, 82, 67 and 85 marks (out of 100) in English, Mathematics,Physics, Chemistry and Biology What are his average marks ?
a)
75
b)
68
c)
65
d)
60
e)
None
|
|
Aarav Sharma answered |
Average = (76 + 65 + 82 + 67 + 85 )/ 5 = 375/5 = 75.
The average of 5 consecutive even numbers A, B, C, D and E is 52. What is the product of B and E?
- a)2916
- b)2988
- c)3000
- d)2800
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
The average of 5 consecutive even numbers A, B, C, D and E is 52. What is the product of B and E?
a)
2916
b)
2988
c)
3000
d)
2800
e)
None of these

|
Target Study Academy answered |
Let the five consecutive even numbers be x,
x + 2, x + 4, x + 6 and x + 8 respectively.
According to the question,
x + x + 2 + x + 4 + x + 6 + x + 8 = 5 × 52

B = x + 2 = 48 + 2 = 50 and E = x + 8 = 48 + 8 = 56
B × E = 50 × 56 = 2800
x + 2, x + 4, x + 6 and x + 8 respectively.
According to the question,
x + x + 2 + x + 4 + x + 6 + x + 8 = 5 × 52

B = x + 2 = 48 + 2 = 50 and E = x + 8 = 48 + 8 = 56
B × E = 50 × 56 = 2800
So, the correct option is 'D'
The sum of seven consecutive numbers is 175. What is the sum of the first and the last number- a)58
- b)48
- c)60
- d)50
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
The sum of seven consecutive numbers is 175. What is the sum of the first and the last number
a)
58
b)
48
c)
60
d)
50
e)
None of these

|
Bank Exams India answered |
Sum of seven consecutive numbers x+(x+1)+(x+2)+(x+3)+(x+4)+(x+5)+(x+6)=175 7x+21=175
7x=154
x=22
First number will be 22 and consecutive series is 22, 23, 24, 25, 26, 27, 28
7x=154
x=22
First number will be 22 and consecutive series is 22, 23, 24, 25, 26, 27, 28
Sum of first and last number =22+28=50
So, the correct option is 'D'
Find the average of first 10 even numbers
- a)11
- b)12
- c)18
- d)9
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
Find the average of first 10 even numbers
a)
11
b)
12
c)
18
d)
9
e)
None of these

|
Future Foundation Institute answered |
2+4+6+8+10+12+14+16+18+20/10 = 110/10
=11
=11
So, the correct option is 'A'
Average age of 54 girls in a class was found to be 10 years. It was later on realised that the actual age of one of the girls in the class was 8 years but it was wrongly taken as 18. The actual average age of the girls in the class is- a)9.11
- b)9.81
- c)10.11
- d)10.81
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Average age of 54 girls in a class was found to be 10 years. It was later on realised that the actual age of one of the girls in the class was 8 years but it was wrongly taken as 18. The actual average age of the girls in the class is
a)
9.11
b)
9.81
c)
10.11
d)
10.81
e)
None of these

|
Divey Sethi answered |
Summation of ages of 54 girls= 54*10= 540 since 18 is mistakely taken in place of 8 so total summation of ages of girls after correction= 540-18+8= 530 Now the actual average age of the girls = 530/54 =9.81
So,the correct option is 'B'
The average weight of 21 boys was recorded as 64 kg. If the weight of the teacher was added, the average increased by one kg. What was the teacher's weight?
- a)82 kg
- b)85 kg
- c)86 kg
- d)90 kg
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
The average weight of 21 boys was recorded as 64 kg. If the weight of the teacher was added, the average increased by one kg. What was the teacher's weight?
a)
82 kg
b)
85 kg
c)
86 kg
d)
90 kg
e)
None of these

|
Divey Sethi answered |
Here, n = 21, a = 64, b = 65
Weight of teacher = n (b - a) + b
= 21 (65 - 64) + 65 = 21 + 65 = 86 kg
Weight of teacher = n (b - a) + b
= 21 (65 - 64) + 65 = 21 + 65 = 86 kg
So, the correct option is 'C'
The average age of a group of 10 students was 20. The average age increased by 2 years when two new students joined the group. What is the average age of the two new students who joined the group?- a)32 years
- b)49 years
- c)50 years
- d)46 years
- e)None
Correct answer is option 'A'. Can you explain this answer?
The average age of a group of 10 students was 20. The average age increased by 2 years when two new students joined the group. What is the average age of the two new students who joined the group?
a)
32 years
b)
49 years
c)
50 years
d)
46 years
e)
None

|
Kavya Sharma answered |
The average age of a group of 10 students = 20 years
Sum of the ages of these 10 students = 10 * 20 = 200 years.
when 2 new students joined the average age is increased by = 2 years
Hence the average age becomes 22 years and total students become 12.
Therefore, the sum of the ages of the 12 students = 12 * 22 = 264 years
So, the difference between the sum of the ages of 12 students and 10 students = 264 - 200 = 64 years.
Sum of the ages of the 2 new students = 64 years.
Average age of the 2 new students = 64/2
= 32 years.
The average weight of 20 girls was recorded as 54 kgm. If the weight of teacher is added, the average increased by 1 kg. The teachers weight is- a)72 kg
- b)73 kg
- c)74 kg
- d)75 kg
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
The average weight of 20 girls was recorded as 54 kgm. If the weight of teacher is added, the average increased by 1 kg. The teachers weight is
a)
72 kg
b)
73 kg
c)
74 kg
d)
75 kg
e)
None of these
|
|
Aisha Gupta answered |
Given that average is 54 kg for 15 girls.
(Sum of weight of 15 girls) / 15 = 54
Sum of weight of 15 girls = 15 x 54 = 810
Now weight of teacher is also added so the average becomes 54 + 1 kg = 55 kg
(Sum of weight of 15 girls + Weight of teacher ) / (15 girls + 1 teacher) = New average = 55 (Given)
(810 + Weight of teacher ) / (16) = 55 + 1
810 + Weight of teacher = 16 (56)
Weight of teacher = 896 - 810 = 86 kg
Average age of girls in a class is 16 years. If the average of the boys in class is also added, the average becomes 15.5 years. If there were 20 boys in the class with average age 15 years, how many girls were there in the class?- a)15
- b)40
- c)20
- d)25
- e)30
Correct answer is option 'C'. Can you explain this answer?
Average age of girls in a class is 16 years. If the average of the boys in class is also added, the average becomes 15.5 years. If there were 20 boys in the class with average age 15 years, how many girls were there in the class?
a)
15
b)
40
c)
20
d)
25
e)
30
|
|
Aisha Gupta answered |
C) 20
Explanation: Let x girls in the class, so 16x + 20*15 = 15.5 (x+20)
Explanation: Let x girls in the class, so 16x + 20*15 = 15.5 (x+20)
The average weight of 8 persons increases by 2.5 kg when a new person comes in place of one of them weighing 65 kg. What might be the weight of the new person ?
- a)76 kg
- b)76.5 kg
- c)85 kg
- d)Data inadequate
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
The average weight of 8 persons increases by 2.5 kg when a new person comes in place of one of them weighing 65 kg. What might be the weight of the new person ?
a)
76 kg
b)
76.5 kg
c)
85 kg
d)
Data inadequate
e)
None of these
|
|
Preeti Khanna answered |
Total weight increased = (8 x 2.5) kg = 20 kg.
Weight of new person = (65 + 20) kg = 85 kg.
So, the correct option is 'C'
Can you explain the answer of this question below:The average age of 24 boys and their teacher is 15 years. When the teacher’s age is excluded, the average age decreases by one year. The age of the teacher is
- A:
40 years
- B:
38 years
- C:
39 years
- D:
41 years
- E:
None of these
The answer is c.
The average age of 24 boys and their teacher is 15 years. When the teacher’s age is excluded, the average age decreases by one year. The age of the teacher is
40 years
38 years
39 years
41 years
None of these

|
Gowri Chakraborty answered |
Age of the teacher = (25x15−24x14)years
(375 − 336) years = 39years
Average score of Rahul, Manish & Suresh is 63. Rahul's score is 15 less than Ajay and 10 more than Manish. If Ajay scored 30 marks more than the average score of Rahul, Manish & Suresh, what is the sum of Manish's and Suresh's score?
- a)120
- b)111
- c)117
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Average score of Rahul, Manish & Suresh is 63. Rahul's score is 15 less than Ajay and 10 more than Manish. If Ajay scored 30 marks more than the average score of Rahul, Manish & Suresh, what is the sum of Manish's and Suresh's score?
a)
120
b)
111
c)
117
d)
None of these

|
Sajad Ahmad answered |
Let the score of Rahul Manish andSurash be r m s.
now total score of these boys is=3*63=189
so r+m+s=189 (1)
as ajay scored 30 more than tha average score of Rahul'Manish'Surash.
then
score of Ajay =63+30=93
as in guestion Rahuls score is 15 less then Ajay =93-15=78
so r=78
put this value in eq (1)
78+m+s=189
so m+s=189 - 78=111Ans
now total score of these boys is=3*63=189
so r+m+s=189 (1)
as ajay scored 30 more than tha average score of Rahul'Manish'Surash.
then
score of Ajay =63+30=93
as in guestion Rahuls score is 15 less then Ajay =93-15=78
so r=78
put this value in eq (1)
78+m+s=189
so m+s=189 - 78=111Ans
Sum of the ages of a father and son is 45 years. Five years, ago product of their ages was 4 times the father’s age at that time. Present ages of father and his son, respectively are:- a)25,10
- b)36,9
- c)39,6
- d)20,5
- e)None
Correct answer is option 'B'. Can you explain this answer?
Sum of the ages of a father and son is 45 years. Five years, ago product of their ages was 4 times the father’s age at that time. Present ages of father and his son, respectively are:
a)
25,10
b)
36,9
c)
39,6
d)
20,5
e)
None

|
Arya Roy answered |
Let sons age = x years. Then fathers age = (45 - x)years.
(x—5)(45—x—5) = 4(45- x - 5) hence (x—5) = 4 so x = 9
Their ages are 36 years and 9 years.
The average of four consecutive odd numbers is 24. Find the largest number.- a)25
- b)27
- c)29
- d)31
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The average of four consecutive odd numbers is 24. Find the largest number.
a)
25
b)
27
c)
29
d)
31
e)
None of these

|
Cstoppers Instructors answered |
Let the numbers are x, x+2, x+4, x+6, then
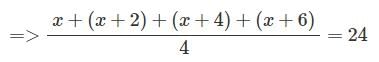
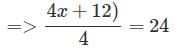
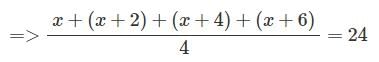
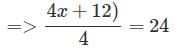
=>x+3=24=>x=21
So largest number is 21 + 6 = 27
So largest number is 21 + 6 = 27
So, the correct option is 'B'
Can you explain the answer of this question below:The average of 7 consecutive numbers is 20. The largest of these numbers is :- A:21
- B:22
- C:23
- D:24
- E:None of these
The answer is c.
The average of 7 consecutive numbers is 20. The largest of these numbers is :
A:
21
B:
22
C:
23
D:
24
E:
None of these
|
|
Wahid Khan answered |
Let the numbers be x, x + 1, x + 2, x + 3, x + 4, x + 5 and x + 6,
Then (x + (x + 1) + (x + 2) + (x + 3) + (x + 4) + (x + 5) + (x + 6)) / 7 = 20.
or 7x + 21 = 140 or 7x = 119 or x =17.
Latest number = x + 6 = 23.
Then (x + (x + 1) + (x + 2) + (x + 3) + (x + 4) + (x + 5) + (x + 6)) / 7 = 20.
or 7x + 21 = 140 or 7x = 119 or x =17.
Latest number = x + 6 = 23.
Can you explain the answer of this question below:The average of four consecutive odd numbers is 24. Find the largest number.
- A:
25
- B:
27
- C:
29
- D:
31
- E:
None of these
The answer is b.
The average of four consecutive odd numbers is 24. Find the largest number.
25
27
29
31
None of these

|
Gowri Chakraborty answered |
Let the numbers are x, x+2, x+4, x+6, then
=>x+(x+2)+(x+4)+(x+6) / 4 =24
=>4x+12) / 4 =24
=>x+3=24=>x=21
So largest number is 21 + 6 = 27
The average of 10 reading is 25.5. In this the average of first three is 20 and the next four is 26. If the eight reading is 5 less than the night one and also 8 less than the tenth one, then find the eight reading?- a)22
- b)24
- c)26
- d)28
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
The average of 10 reading is 25.5. In this the average of first three is 20 and the next four is 26. If the eight reading is 5 less than the night one and also 8 less than the tenth one, then find the eight reading?
a)
22
b)
24
c)
26
d)
28
e)
None of these

|
Cstoppers Instructors answered |
Answer – 3.26 Explanation : sum of all ten reading = 255 sum of first three = 60 and sum of next 4 = 104.
Sum of 8th , 9th and 10th reading = 91 = 3*x + 13 X = 26
Sum of 8th , 9th and 10th reading = 91 = 3*x + 13 X = 26
There are total 600 students in a school. Average age of boys is 12 years and of girls is 11 years while average age of all students is 11 yrs. And 9 months. Find the number of girls in the school. - a)130
- b)140
- c)150
- d)160
- e)120
Correct answer is option 'C'. Can you explain this answer?
There are total 600 students in a school. Average age of boys is 12 years and of girls is 11 years while average age of all students is 11 yrs. And 9 months. Find the number of girls in the school.
a)
130
b)
140
c)
150
d)
160
e)
120
|
|
Nikita Singh answered |
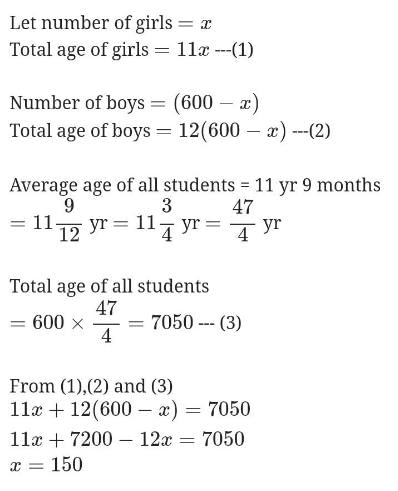
The average of five positive numbers is 308. The average of first two numbers is 482.5 and the average of last two numbers is 258.5. What is the third number.
- a)224
- b)121
- c)58
- d)Cannot be determined
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
The average of five positive numbers is 308. The average of first two numbers is 482.5 and the average of last two numbers is 258.5. What is the third number.
a)
224
b)
121
c)
58
d)
Cannot be determined
e)
None of these

|
Avantika Chakraborty answered |
Let the numbers be A1, A2 , A3 , A4 , A5
► Average of 5 numbers = (A1 + A2 + A3 + A4 + A5) / 5 = 308
► Now A1 + A2 + A3 + A4 + A5 = 308 x 5 = 1540
► Also,A1 + A2 = 482.5 x 2 = 965
and A4 + A5 = 258.5 x 2 = 517
► A3 = 1540 − 965 − 517 = 58
So, the correct option is 'C'
The average of five positive numbers is 213. The average of the first two numbers is 233.5 and the average of last two numbers is 271. What is the third number?- a)64
- b)56
- c)106
- d)Cannot be determined
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The average of five positive numbers is 213. The average of the first two numbers is 233.5 and the average of last two numbers is 271. What is the third number?
a)
64
b)
56
c)
106
d)
Cannot be determined
e)
None of these

|
Ishani Rane answered |
The sum of the five numbers = 5 * 213 =1065
The sum of the first two numbers = 2 * 233.5 = 467
The sum of the last two numbers = 542
Then the sum of the four numbers = 467 + 542 =1009
So, the third number will be = 1065 – 1009
= 56
Suman got married 6 years ago. Today her age is 1(1/4) times her age at the time of marriage. Her son’s age is 1/10 times her age. Her son’s age is:- a)2 yrs.
- b)3 yrs.
- c)4 yrs.
- d)5 yrs.
- e)6 yrs
Correct answer is option 'D'. Can you explain this answer?
Suman got married 6 years ago. Today her age is 1(1/4) times her age at the time of marriage. Her son’s age is 1/10 times her age. Her son’s age is:
a)
2 yrs.
b)
3 yrs.
c)
4 yrs.
d)
5 yrs.
e)
6 yrs

|
Ishani Rane answered |
The answer is b.
Age of Kamla x
Age of Kamla x
Age after six years x+6
x+6 = (5/4)x
4x+24=5x
x=24
Present age = 24+6
=30
Present age of son = (1/10)*30
= 3 years
The average weight of 8 men is increased by 1.5 kg when one of them whose weight is 65 kg is replaced by a new man. The weight of the new man is- a)72 kg
- b)70 kg
- c)74 kg
- d)77 kg
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
The average weight of 8 men is increased by 1.5 kg when one of them whose weight is 65 kg is replaced by a new man. The weight of the new man is
a)
72 kg
b)
70 kg
c)
74 kg
d)
77 kg
e)
None of these
|
|
Nikita Singh answered |
Total weight increased = (8 * 1.5) kg = 12 kg.
Weight of new man = 65 + 12 = 77 kg
Weight of new man = 65 + 12 = 77 kg
The age of father is 5 times that of his son. 3 years ago, the age of father was 8 times that of his son. Find the present age of father.
- a)35
- b)45
- c)55
- d)46
- e)None
Correct answer is option 'A'. Can you explain this answer?
The age of father is 5 times that of his son. 3 years ago, the age of father was 8 times that of his son. Find the present age of father.
a)
35
b)
45
c)
55
d)
46
e)
None

|
Bank Exams India answered |
Given:
Present age
Age of father = 5 × Age of Son
3 years ago,
Age of father = 8 × Age of son
Calculation:
Let the age of father and son be F and S.
According to the question,
F = 5S ----(1)
Again according to the question,
⇒ (F - 3) = 8(S - 3) ----(2)
After equating the equation (1) and equation (2)
⇒ 5S - 3 = 8S - 24
⇒ -3S = -21
⇒ S = 7 years
From equation (1)
⇒ F = 5 × 7
⇒ F = 35 years
∴ The present age of the father is 35 years.
So, the correct option is A .
The average age of 5 children of a family is 10 years but if we include the age of father and mother then the average age becomes 22 years. It is given that father age is 6 years more than the mother so what will be the age of mother at present.- a)47
- b)48
- c)49
- d)50
Correct answer is option 'C'. Can you explain this answer?
The average age of 5 children of a family is 10 years but if we include the age of father and mother then the average age becomes 22 years. It is given that father age is 6 years more than the mother so what will be the age of mother at present.
a)
47
b)
48
c)
49
d)
50
|
|
Aisha Gupta answered |
Answer – c) 49 Explanation : sum of age of children = 50 50 + M+ F = 22*7 = 154.
M+F = 104 and F= M+6 . So, M = 49
M+F = 104 and F= M+6 . So, M = 49
Find the average of first 15 odd numbers- a)18
- b)14
- c)20
- d)15
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
Find the average of first 15 odd numbers
a)
18
b)
14
c)
20
d)
15
e)
None of these

|
Pallabi Deshpande answered |
The first 15 odd numbers are 1,3,5,7,9,11,13,15,17,19,21,23,25,27,29
The sum of first 15 odd numbers are 225
Therefore mean is equal to 225/15=15
Median =Middle value=15
The ratio of Vipan’s age & Sonia’s age is 3:5 and the sum of their age is 80 years. The ratio of their ages after 10 years will be.- a)2:3
- b)1:2
- c)3:2
- d)3:5
- e)None
Correct answer is option 'A'. Can you explain this answer?
The ratio of Vipan’s age & Sonia’s age is 3:5 and the sum of their age is 80 years. The ratio of their ages after 10 years will be.
a)
2:3
b)
1:2
c)
3:2
d)
3:5
e)
None
|
|
Sagar Sharma answered |
Understanding the Problem
To solve the problem, we need to determine the current ages of Vipans and Sonia based on the given ratio and sum of their ages.
Given Information
- The ratio of Vipans' age to Sonia's age is 3:5.
- The sum of their ages is 80 years.
Setting Up the Equations
1. Let Vipans' age be 3x and Sonia's age be 5x.
2. According to the problem:
- 3x + 5x = 80
3. Simplifying this gives:
- 8x = 80
4. Solving for x:
- x = 10
Calculating Current Ages
- Vipans' age = 3x = 3 * 10 = 30 years
- Sonia's age = 5x = 5 * 10 = 50 years
Finding Ages After 10 Years
1. After 10 years:
- Vipans' age = 30 + 10 = 40 years
- Sonia's age = 50 + 10 = 60 years
Calculating the New Ratio
1. The new ratio of their ages will be:
- Vipans' age : Sonia's age = 40 : 60
2. Simplifying this ratio:
- 40/20 : 60/20 = 2 : 3
Conclusion
Thus, the ratio of Vipans' age to Sonia's age after 10 years is 2:3, which corresponds to option 'A'.
To solve the problem, we need to determine the current ages of Vipans and Sonia based on the given ratio and sum of their ages.
Given Information
- The ratio of Vipans' age to Sonia's age is 3:5.
- The sum of their ages is 80 years.
Setting Up the Equations
1. Let Vipans' age be 3x and Sonia's age be 5x.
2. According to the problem:
- 3x + 5x = 80
3. Simplifying this gives:
- 8x = 80
4. Solving for x:
- x = 10
Calculating Current Ages
- Vipans' age = 3x = 3 * 10 = 30 years
- Sonia's age = 5x = 5 * 10 = 50 years
Finding Ages After 10 Years
1. After 10 years:
- Vipans' age = 30 + 10 = 40 years
- Sonia's age = 50 + 10 = 60 years
Calculating the New Ratio
1. The new ratio of their ages will be:
- Vipans' age : Sonia's age = 40 : 60
2. Simplifying this ratio:
- 40/20 : 60/20 = 2 : 3
Conclusion
Thus, the ratio of Vipans' age to Sonia's age after 10 years is 2:3, which corresponds to option 'A'.
The ratio of father’s age to the son’s age is 4:1 the product of their ages is 196. What will be the ratio of their ages after 5 years?- a)12:4
- b)4:11
- c)11:4
- d)5 : 6
- e)None
Correct answer is option 'C'. Can you explain this answer?
The ratio of father’s age to the son’s age is 4:1 the product of their ages is 196. What will be the ratio of their ages after 5 years?
a)
12:4
b)
4:11
c)
11:4
d)
5 : 6
e)
None

|
Dhruv Mehra answered |
Let father's age be 4T and son's age T years.
∵ 4T * T = 196
⇒ T2 = 49
∴ T = 7
Father's age after 5 years = (4T + 5) = 33 years
Son's age after 5 years = (T + 5) = 12 years
∴ Ratio of their ages after 5 years = 33 : 12 = 11 : 4
While calculating the weight of a group of men, the weight of 63 kg of one of the member was mistakenly written as 83 kg. Due to this the average of the weights increased by half kg. What is the number of men in the group?- a)25
- b)20
- c)40
- d)60
- e)24
Correct answer is option 'C'. Can you explain this answer?
While calculating the weight of a group of men, the weight of 63 kg of one of the member was mistakenly written as 83 kg. Due to this the average of the weights increased by half kg. What is the number of men in the group?
a)
25
b)
20
c)
40
d)
60
e)
24

|
Naroj Boda answered |
C) 40
Explanation: Increase in marks lead to increase in average by ½ So (83-63) = x/2 x = 40
Explanation: Increase in marks lead to increase in average by ½ So (83-63) = x/2 x = 40
The average marks of nine students in a group is 63. Three of them scored 78, 69 and 48 marks. What are the average marks of remaining six students?- a)63.5
- b)64
- c)63
- d)62.5
- e)None of these
Correct answer is option 'E'. Can you explain this answer?
The average marks of nine students in a group is 63. Three of them scored 78, 69 and 48 marks. What are the average marks of remaining six students?
a)
63.5
b)
64
c)
63
d)
62.5
e)
None of these

|
Sounak Malik answered |
The total marks of nine students = 9 x 63 = 567
Sum of the marks of three students = 78 + 69 + 48 = 195
Therefore, the sum of marks of the remaining six students= 567 – 195 = 372
Average marks of remaining six students = 372/6 = 62. Ans.e is correct.
What will be the average of even numbers between 11 to 63- a)37.5
- b)47
- c)42
- d)37
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
What will be the average of even numbers between 11 to 63
a)
37.5
b)
47
c)
42
d)
37
e)
None of these

|
Raghavendra Sharma answered |
Even numbers between 11 to 63
= 12,14,16,18,20,62.
Clearly, this is a series of consecutive even number
According to the formula
Average of consecutive even numbers = (First number + Last number)/2
= (12 + 62)/2
= 74/2
= 37
The average age of a class is 19 years. While the average age of boys is 20 and the average age of girls is 17. If the number of boys is 20 then find the number of girls in the class- a)10
- b)15
- c)16
- d)18
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
The average age of a class is 19 years. While the average age of boys is 20 and the average age of girls is 17. If the number of boys is 20 then find the number of girls in the class
a)
10
b)
15
c)
16
d)
18
e)
None of these

|
Bhoomi Jain answered |
let number of girls be g
sum of boy's ages= 20*20=400sum of girl's ages= 17*g=17g
19 = 400 +17g / 20+g
380+19g= 400+17g
g=10
Ratio between present ages of A, B and C is 5:4:6. Total of the ages of A and C after 5 years will be 54 years. What will be the ratio of ages of B and C after 4 years?- a)5:4
- b)5:7
- c)4:5
- d)Data inadequate
- e)None
Correct answer is option 'B'. Can you explain this answer?
Ratio between present ages of A, B and C is 5:4:6. Total of the ages of A and C after 5 years will be 54 years. What will be the ratio of ages of B and C after 4 years?
a)
5:4
b)
5:7
c)
4:5
d)
Data inadequate
e)
None

|
Target Study Academy answered |
Option (2) 5:7 is correct✅answer.
Explanation:-
Let age of A = 5 x
B= 4x
C = 6x
Then, according to the question;
( 5x+5) + (6x+5) = 54
11x + 10 = 54
=> 11x = 54-10
=> 11x = 44
=> x = 4
B's age after 4 years;
= 4x +4
=> 4*4+4
=> 20 years.
C's age after 4 years ;
= 6x+4
=>6*4+4
= 28 years
Therefore, ratio = 20/28
=> ratio = 5:7
In a hostel there are 30 students and if the number of students increased by 5 then the expense is increased by 40 per day. But the average expenditure diminishes by 3. Find the original expenditure.- a)810
- b)870
- c)910
- d)950
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
In a hostel there are 30 students and if the number of students increased by 5 then the expense is increased by 40 per day. But the average expenditure diminishes by 3. Find the original expenditure.
a)
810
b)
870
c)
910
d)
950
e)
None of these
|
|
Kavya Saxena answered |
Answer – 2.870 Explanation : Let average expenditure be P. (30*P + 40)/35 = P-3
P = 29. So expenditure = 29*30 = 870
P = 29. So expenditure = 29*30 = 870
In a group of 8 boys, 2 men aged at 21 and 23 were replaced two new boys.Due to this the average cost of the group increased by 2 years. What is the average age of the 2 new boys?- a)17
- b)30
- c)28
- d)23
- e)18
Correct answer is option 'B'. Can you explain this answer?
In a group of 8 boys, 2 men aged at 21 and 23 were replaced two new boys.Due to this the average cost of the group increased by 2 years. What is the average age of the 2 new boys?
a)
17
b)
30
c)
28
d)
23
e)
18
|
|
Preeti Khanna answered |
B) 30
Explanation: Average of 8 boys increased by 2, this means the total age of boys increased by 8*2 = 16 yrs So sum of ages of two new boys = 21+23+16 = 60 Average of these = 60/2
Explanation: Average of 8 boys increased by 2, this means the total age of boys increased by 8*2 = 16 yrs So sum of ages of two new boys = 21+23+16 = 60 Average of these = 60/2
The average of 5 consecutive even numbers A, B, C, D and E is 52. What is the product of B and E? - a)2916
- b)2988
- c)3000
- d)2800
- e)None of these
Correct answer is 'D'. Can you explain this answer?
The average of 5 consecutive even numbers A, B, C, D and E is 52. What is the product of B and E?
a)
2916
b)
2988
c)
3000
d)
2800
e)
None of these

|
Divya Goyal answered |
Answer is 2800 5 consecutive even so series should be 48 50 52 54 56 so product of 50*56 = 2800
If a man spends 1000rs for the first five months, 2000rs for the next four months and 3000rs for the next 3 months and he saves 2000rs in the whole year then his average monthly salary will be ?- a)1000
- b)2000
- c)3000
- d)4000
Correct answer is option 'B'. Can you explain this answer?
If a man spends 1000rs for the first five months, 2000rs for the next four months and 3000rs for the next 3 months and he saves 2000rs in the whole year then his average monthly salary will be ?
a)
1000
b)
2000
c)
3000
d)
4000
|
|
Preeti Khanna answered |
Answer – b) 2000 Explanation : 1000*5 + 2000*4 + 3000*3 + 2000 = 24000
24000/12 = 2000
24000/12 = 2000
Mr. Ravi’s family has 10 males and a few females, the average monthly consumption of rice per head is 8 kg. If the average monthly consumption of rice per head be 10 kg in the case of males and 6 kg in the case of females, find the number of females in Ravi’s family?
- a)2
- b)4
- c)6
- d)10
- e)8
Correct answer is option 'D'. Can you explain this answer?
Mr. Ravi’s family has 10 males and a few females, the average monthly consumption of rice per head is 8 kg. If the average monthly consumption of rice per head be 10 kg in the case of males and 6 kg in the case of females, find the number of females in Ravi’s family?
a)
2
b)
4
c)
6
d)
10
e)
8
|
|
Aisha Gupta answered |

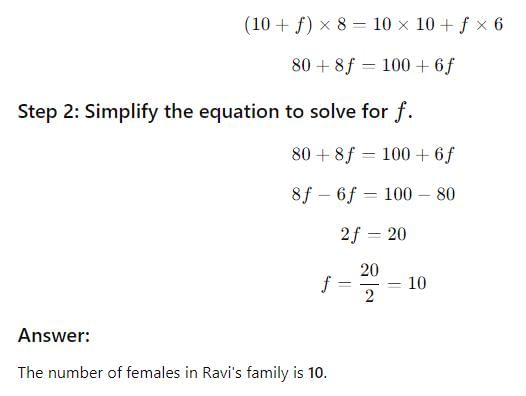
Nine students of a class contribute a certain sum. Seven of them give Rs. 5 each and the other two give Rs. 5 & 9 more then the average contribution of all the 9 students. The average contribution of the class of 9 students is.- a)Rs.10
- b)Rs14
- c)Rs 7
- d)Rs12
- e)None
Correct answer is option 'C'. Can you explain this answer?
Nine students of a class contribute a certain sum. Seven of them give Rs. 5 each and the other two give Rs. 5 & 9 more then the average contribution of all the 9 students. The average contribution of the class of 9 students is.
a)
Rs.10
b)
Rs14
c)
Rs 7
d)
Rs12
e)
None

|
Manoj Ghosh answered |
Average = sum/n
Average of 9 students = x
n = 9
x = sum/9
Seven of them give Rs. 5 = 7 * 5 = 35
35+(5+x)+(9+x) ∴ other two give Rs. 5 and Rs. 9 more than the average contribution
x = 35+(5+x)+(9+x)/9
x = 49+2x/9
9x = 49 + 2x
9x - 2x = 49
7x = 49
x = 7
The average ages of 4 member, each having the age difference of 2yrs is 54 yrs.What is the sum of the youngest and oldest family member ?- a)102
- b)105
- c)107
- d)108
Correct answer is option 'D'. Can you explain this answer?
The average ages of 4 member, each having the age difference of 2yrs is 54 yrs.What is the sum of the youngest and oldest family member ?
a)
102
b)
105
c)
107
d)
108
|
|
Mehak Jaju answered |
Let's say ages be x y z and w
y=x-2
z=x-4
w=x-6
now average is
x+x-2-6-4+x+x/4=54
4x-12=216
x=57
w=57-6=51
sum is 57+51=108
y=x-2
z=x-4
w=x-6
now average is
x+x-2-6-4+x+x/4=54
4x-12=216
x=57
w=57-6=51
sum is 57+51=108
The average of 5 consecutive number is 58.Find the first number ?- a)55
- b)56
- c)57
- d)58
Correct answer is option 'B'. Can you explain this answer?
The average of 5 consecutive number is 58.Find the first number ?
a)
55
b)
56
c)
57
d)
58
|
|
Aisha Gupta answered |
Answer – B)56 Explanation : X+x+1+x+2+x+3+x+4 = 58*5 = 290 5x+10 = 290 X = 290 – 10/5 = 280/5 = 56
The average marks secured by 15 students are 70 and later it was found that one entry is wrong and 65 is written instead of 45. Find out he corrected average.- a)67.66
- b)68.66
- c)69.66
- d)70
Correct answer is option 'B'. Can you explain this answer?
The average marks secured by 15 students are 70 and later it was found that one entry is wrong and 65 is written instead of 45. Find out he corrected average.
a)
67.66
b)
68.66
c)
69.66
d)
70
|
|
Anaya Patel answered |
Answer –b) 68.66 Explanation : (15*70-65+45)/15
Mr.Suresh’s average monthly expenditure for the first four months of the year was Rs.260 For the next five months,the average monthly expenditure was Rs.40 more than what it was during the first four months. If he spent Rs.560 in all during the remaining three months of the year, Find what percentage of his annual income of Rs.5000 did he save in the year?- a)42%
- b)48%
- c)38%
- d)24%
- e)28%
Correct answer is option 'C'. Can you explain this answer?
Mr.Suresh’s average monthly expenditure for the first four months of the year was Rs.260 For the next five months,the average monthly expenditure was Rs.40 more than what it was during the first four months. If he spent Rs.560 in all during the remaining three months of the year, Find what percentage of his annual income of Rs.5000 did he save in the year?
a)
42%
b)
48%
c)
38%
d)
24%
e)
28%
|
|
Kavya Saxena answered |
Answer – C. 38% Explanation: Suresh’s average monthly expenditure for the first four months of the year = Rs.260. 260 * 4 = Rs. 1040 For the next five months,the average monthly expenditure was Rs.40 more than what it was during the first four months. He spent 260 + 40 for one month In 5 months he spent 300 * 5 = 1500 He spent Rs.560 in all during the remaining three months of the year.
Total expenditure = 1040 + 1500 + 560 = 3100 Savings = 5000-3100 = 1900 % savings = 1900/5000 * 100 = 38%
Total expenditure = 1040 + 1500 + 560 = 3100 Savings = 5000-3100 = 1900 % savings = 1900/5000 * 100 = 38%
A batsman in his 17th innings makes a score of 85, and thereby increases his average by 3. What is his average after 17 innings?- a)30
- b)37
- c)40
- d)45
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A batsman in his 17th innings makes a score of 85, and thereby increases his average by 3. What is his average after 17 innings?
a)
30
b)
37
c)
40
d)
45
e)
None of these
|
|
Nikita Singh answered |
Answer – B (37) Explanation – Let the average after 16th innings be a, then total score after 17th innings => 16a+85 = 17 (a+3) a = 85-51 = 34 Average after 17 innings = a + 3 = 34 + 3 = 37
The batting average of a batsman for 20 innings is 35 and the difference b/w the runs of best inning and worst inning is 50. If these two innings are not included the average becomes 32 for 18 innings. The best score of the batsman is.- a)91
- b)77
- c)87
- d)82
Correct answer is option 'C'. Can you explain this answer?
The batting average of a batsman for 20 innings is 35 and the difference b/w the runs of best inning and worst inning is 50. If these two innings are not included the average becomes 32 for 18 innings. The best score of the batsman is.
a)
91
b)
77
c)
87
d)
82
|
|
Preeti Khanna answered |
Answer – c) 87 Explanation : 35*20 = 700.
Best(B) – Worst(W) = 50 700 – B – H = 18*32= 576. B+H = 124 and B-H = 50. So B =87
Best(B) – Worst(W) = 50 700 – B – H = 18*32= 576. B+H = 124 and B-H = 50. So B =87
The average temperature in Delhi for the first four days of the month was reported as 580 . It reported as 600 for 2nd, 3rd, 4th and 5th days. The ratio of the temperatures of 1st and 5th day was 7 : 8. Find the temperature on the first day.- a)420
- b)460
- c)630
- d)680
- e)560
Correct answer is option 'E'. Can you explain this answer?
The average temperature in Delhi for the first four days of the month was reported as 580 . It reported as 600 for 2nd, 3rd, 4th and 5th days. The ratio of the temperatures of 1st and 5th day was 7 : 8. Find the temperature on the first day.
a)
420
b)
460
c)
630
d)
680
e)
560
|
|
Nikita Singh answered |
E) 560
Explanation: A+B+C+D = 58*4
B+C+D+E = 60*4
Subtract both, E – A = 8 So 8x – 7x = 8, x = 8 So temperature of A(1st day) = 7x = 7*8
Explanation: A+B+C+D = 58*4
B+C+D+E = 60*4
Subtract both, E – A = 8 So 8x – 7x = 8, x = 8 So temperature of A(1st day) = 7x = 7*8
Sonam calculates average of 10 positive 2 digit integers. By mistake she interchanges the digits of one number while calculating the average. Because of which, the average becomes 2.7 less than the correct answer. What is the difference between the two digits of the number which was reversed while calculating the average?- a)3
- b)7
- c)5
- d)10
Correct answer is option 'A'. Can you explain this answer?
Sonam calculates average of 10 positive 2 digit integers. By mistake she interchanges the digits of one number while calculating the average. Because of which, the average becomes 2.7 less than the correct answer. What is the difference between the two digits of the number which was reversed while calculating the average?
a)
3
b)
7
c)
5
d)
10

|
Sam !!! answered |
I don't understand when the equation is like this:
=10(a+b) + 2.7*10
then the very next step should be like this:
10a+ 10b +27
which is not there instead it's written 9a-9b
how's that relatable I may be absolutely wrong but I need a clarification
=10(a+b) + 2.7*10
then the very next step should be like this:
10a+ 10b +27
which is not there instead it's written 9a-9b
how's that relatable I may be absolutely wrong but I need a clarification
The average salary of all the workers in factory is 7000. The average salary of 9 mechanic is 5000 and for the rest of the workers it 4000. Find the total number of workers in the factory.- a)10
- b)11
- c)12
- d)13
Correct answer is option 'C'. Can you explain this answer?
The average salary of all the workers in factory is 7000. The average salary of 9 mechanic is 5000 and for the rest of the workers it 4000. Find the total number of workers in the factory.
a)
10
b)
11
c)
12
d)
13
|
|
Yash Patel answered |
Answer – c) 12 Explanation : Total workers T, so 7000*T = 9*5000 + (T-9)*4000.
T = 3 so 3+9 =12
T = 3 so 3+9 =12
The average of first and second number is 25 more than the average off the second and third number. Find the difference between the first and the third number- a)20
- b)30
- c)40
- d)50
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
The average of first and second number is 25 more than the average off the second and third number. Find the difference between the first and the third number
a)
20
b)
30
c)
40
d)
50
e)
None of these
|
|
Shalini Robinson answered |
First number is x
second number is y
third number is z
then (x+y)/2 =25+((y+z)/2)
then x +y =50+y+z
x-z = 50
second number is y
third number is z
then (x+y)/2 =25+((y+z)/2)
then x +y =50+y+z
x-z = 50
Chapter doubts & questions for Average - Quantitative Techniques for CLAT 2025 is part of CLAT exam preparation. The chapters have been prepared according to the CLAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CLAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Average - Quantitative Techniques for CLAT in English & Hindi are available as part of CLAT exam.
Download more important topics, notes, lectures and mock test series for CLAT Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup