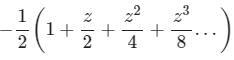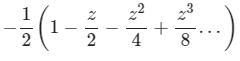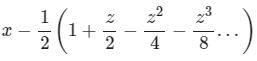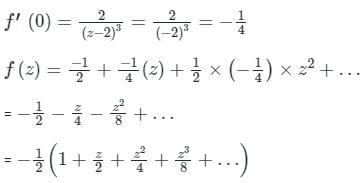All Exams >
Mechanical Engineering >
Engineering Mathematics for Mechanical Engineering >
All Questions
All questions of Complex variables for Mechanical Engineering Exam
The quadratic approximation of (x) = x3 - 3x2 - 5 at the point x = 0 is- a)3x2 − 6x − 5
- b)−3x2 − 5
- c)−3x2 + 6x − 5
- d)3x2 – 5
Correct answer is option 'B'. Can you explain this answer?
The quadratic approximation of (x) = x3 - 3x2 - 5 at the point x = 0 is
a)
3x2 − 6x − 5
b)
−3x2 − 5
c)
−3x2 + 6x − 5
d)
3x2 – 5

|
Gate Funda answered |
Concept:
The Taylor's series expansion of f(x) about origin (i.e x = 0) is given by
f(x) = f(0) + x × f′(0) + x2/2! × f"(0)+.....
The Taylor's series expansion of f(x) about origin (i.e x = 0) is given by
f(x) = f(0) + x × f′(0) + x2/2! × f"(0)+.....
It is also called Maclaurin's series.
Calculation:
Calculation:
f(x) = x3 - 3x2-5
f(0) = 03 - 3 × 02 - 5 = - 5
f'(0) = 3x2 - 6x = 0
f"(0) = 6x - 6 = - 6
The quadratic approximation of f(x) at the point x = 0 is
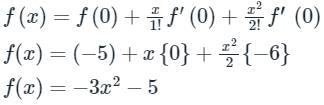
If the principal part of the Laurent’s series vanishes, then the Laurent’s series reduces to- a)Cauchy’s series
- b)Maclaurin’s series
- c)Taylor’s series
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
If the principal part of the Laurent’s series vanishes, then the Laurent’s series reduces to
a)
Cauchy’s series
b)
Maclaurin’s series
c)
Taylor’s series
d)
None of the above
|
|
Sanya Agarwal answered |
Taylor Series:
If f(z) is analytic inside a circle 'C', centre at z = a, and radius 'r', then for all z inside 'C'; the Taylor series is given by-
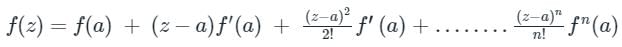
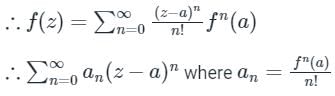
Laurent Series:
If f(z) is analytic at every point inside and on the boundary of a ring shaped region 'R' bounded by two concentric circle C1 and C2 having centre at 'a' & respective radii r1 and r2 (r1 > r2).
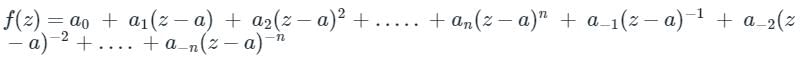
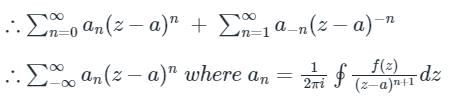
The negative part of Laurent's series i.e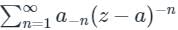 is called the singular part, and if that vanishes the terms that remain will be
is called the singular part, and if that vanishes the terms that remain will be 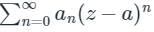 , which is nothing but Taylor series.
, which is nothing but Taylor series.
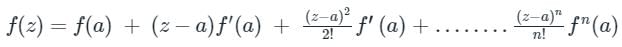
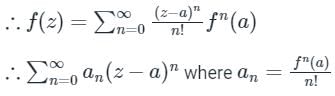
Laurent Series:
If f(z) is analytic at every point inside and on the boundary of a ring shaped region 'R' bounded by two concentric circle C1 and C2 having centre at 'a' & respective radii r1 and r2 (r1 > r2).
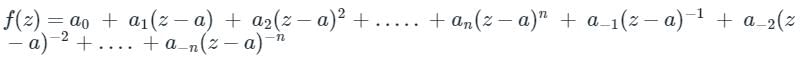
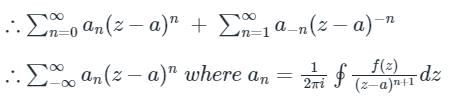
The negative part of Laurent's series i.e
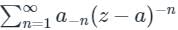 is called the singular part, and if that vanishes the terms that remain will be
is called the singular part, and if that vanishes the terms that remain will be 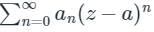 , which is nothing but Taylor series.
, which is nothing but Taylor series.Let f(z) = 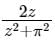 if C is a counter clock wise path in the z plane such that |z - i| = 2, then the value of
if C is a counter clock wise path in the z plane such that |z - i| = 2, then the value of 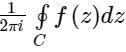 is____
is____- a)0
- b)1
- c)π/2
- d)-π
Correct answer is option 'A'. Can you explain this answer?
Let f(z) = 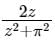 if C is a counter clock wise path in the z plane such that |z - i| = 2, then the value of
if C is a counter clock wise path in the z plane such that |z - i| = 2, then the value of 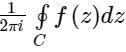 is____
is____
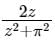 if C is a counter clock wise path in the z plane such that |z - i| = 2, then the value of
if C is a counter clock wise path in the z plane such that |z - i| = 2, then the value of 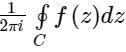 is____
is____a)
0
b)
1
c)
π/2
d)
-π
|
|
Sanya Agarwal answered |
Concept:
Cauchy’s Theorem:
If f(z) is an analytic function and f’(z) is continuous at each point within and on a closed curve C, then
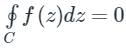
Calculation:
Given:
C: |z - i| = 2
The above path is a circle with a radius of 2 and center as (0, 1). The graph of the circle is given below,

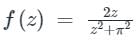
⇒ After putting the denominator as zero, the poles will be 'z = ± πi '. These pole points A and B are outside of the given circle as shown above. So, the complex function f(z) will be an analytic function for all points inside the circle.

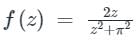
⇒ After putting the denominator as zero, the poles will be 'z = ± πi '. These pole points A and B are outside of the given circle as shown above. So, the complex function f(z) will be an analytic function for all points inside the circle.
By Cauchy’s Theorem (Using equation (1))
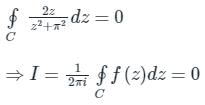
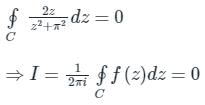
The Laurent series expansion of the function 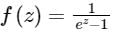 valid in the region 0 < |z| < 2, is given by
valid in the region 0 < |z| < 2, is given by- a)

- b)
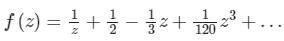
- c)
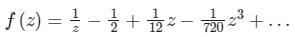
- d)
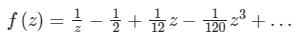
Correct answer is option 'C'. Can you explain this answer?
The Laurent series expansion of the function 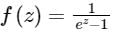 valid in the region 0 < |z| < 2, is given by
valid in the region 0 < |z| < 2, is given by
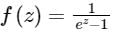 valid in the region 0 < |z| < 2, is given by
valid in the region 0 < |z| < 2, is given bya)

b)
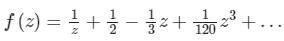
c)
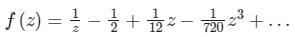
d)
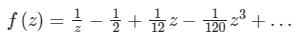

|
Gate Gurus answered |
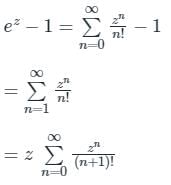
ex – 1 has a zero at ‘0’ of multiplicity one and hence f(z) has pole at 0 of order 1. So, the Laurent series f(z) is given by
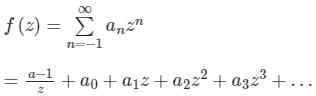
Since (ez – 1) f(z) = 1
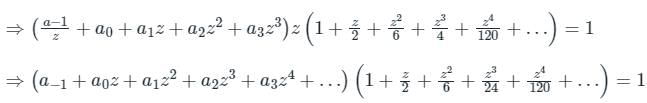
By comparing both the sides,
a-1 = 1
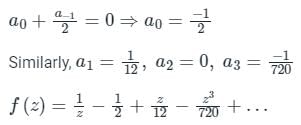
The function f(z) of complex variable z = x + iy, where i = √−1, is given as f(z) = (x3 – 3xy2) + i v(x,y). For this function to be analytic, v(x,y) should be- a)(3xy2 – y3) + constant
- b)(3x2y2 – y3) + constant
- c)(x3 – 3x2y) + constant
- d)(3x2y – y3) + constant
Correct answer is option 'D'. Can you explain this answer?
The function f(z) of complex variable z = x + iy, where i = √−1, is given as f(z) = (x3 – 3xy2) + i v(x,y). For this function to be analytic, v(x,y) should be
a)
(3xy2 – y3) + constant
b)
(3x2y2 – y3) + constant
c)
(x3 – 3x2y) + constant
d)
(3x2y – y3) + constant
|
|
Sanvi Kapoor answered |
Concept:
f(z) = u + iv
u = real part
v = imaginary part
f(z) = u + iv
u = real part
v = imaginary part
If f(z) is an analytic function
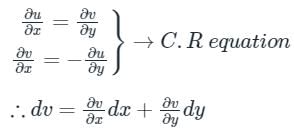
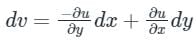
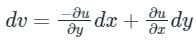 (This is an exact differential equation)
(This is an exact differential equation)
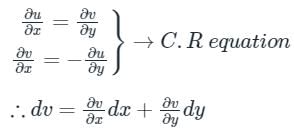
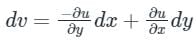
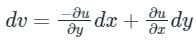 (This is an exact differential equation)
(This is an exact differential equation)Calculation:
Given,
u = x3 – 3xy2
∂u/∂x = 3x2 − 3y2
∂u/∂y = −6xy
Given,
u = x3 – 3xy2
∂u/∂x = 3x2 − 3y2
∂u/∂y = −6xy
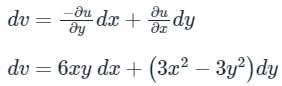
It is an exact differential equation the solution is obtained by treating y as constant in the first term and in the second term only that part is integrated which is not containing x.
Integrating the above equation
v = 3x2y − y3 + constant
v = 3x2y − y3 + constant
If f(z) = u + iv is an analytic function of z = x + iy and u – v = ex (cosy - siny), then f(z) in terms of z is- a)e−z2 + (1 + i)c
- b)e- z + (1 + i)c
- c)ez + (1 + i)c
- d)e- 2z + (1 + i)c
Correct answer is option 'C'. Can you explain this answer?
If f(z) = u + iv is an analytic function of z = x + iy and u – v = ex (cosy - siny), then f(z) in terms of z is
a)
e−z2 + (1 + i)c
b)
e- z + (1 + i)c
c)
ez + (1 + i)c
d)
e- 2z + (1 + i)c

|
Pranavi Gupta answered |
And v are real-valued functions, then the Cauchy-Riemann equations must hold:
∂u/∂x = ∂v/∂y
and
∂u/∂y = -∂v/∂x
Conversely, if these equations hold for a given function f(z), then it is analytic.
∂u/∂x = ∂v/∂y
and
∂u/∂y = -∂v/∂x
Conversely, if these equations hold for a given function f(z), then it is analytic.
C is a closed path in the z-plane given by |z| = 3. The value of the integral 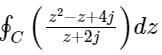 is
is- a)-4π (1 + j2)
- b)4π (3 – j2)
- c)-4π (3 + j2)
- d)4π (1 – j2)
Correct answer is option 'C'. Can you explain this answer?
C is a closed path in the z-plane given by |z| = 3. The value of the integral 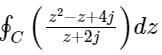 is
is
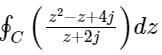 is
isa)
-4π (1 + j2)
b)
4π (3 – j2)
c)
-4π (3 + j2)
d)
4π (1 – j2)
|
|
Sanya Agarwal answered |
Concept:
If f(z) is analytic within and on a closed curve, and if ‘a’ is any point within C then according to Cauchy Integral formula:
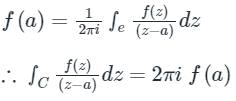
Application:
|z| = 3
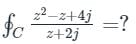
Pole z = -2j, which lies Inside the given C i.e. |z| = 3
∴ Using the Cauchy Integral formula, we get:
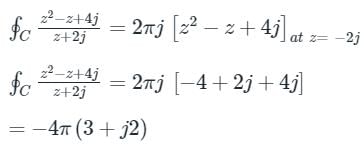
If f(z) is analytic within and on a closed curve, and if ‘a’ is any point within C then according to Cauchy Integral formula:
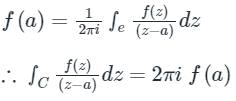
Application:
|z| = 3
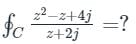
Pole z = -2j, which lies Inside the given C i.e. |z| = 3
∴ Using the Cauchy Integral formula, we get:
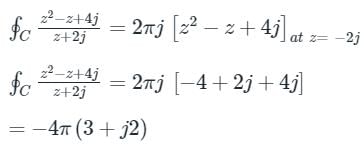
A harmonic function is analytic if it satisfies the Laplace equation. If u(x, y) = 2x2 − 2y2 + 4xy is a harmonic function, then its conjugate harmonic function v(x, y) is- a)4xy − 2x2 + 2y2 + constant
- b)4y2 − 4xy + constant
- c)2x2 − 2y2 + xy + constant
- d)−4xy + 2y2 − 2x2 + constant
Correct answer is option 'A'. Can you explain this answer?
A harmonic function is analytic if it satisfies the Laplace equation. If u(x, y) = 2x2 − 2y2 + 4xy is a harmonic function, then its conjugate harmonic function v(x, y) is
a)
4xy − 2x2 + 2y2 + constant
b)
4y2 − 4xy + constant
c)
2x2 − 2y2 + xy + constant
d)
−4xy + 2y2 − 2x2 + constant

|
Sharmila Gupta answered |
To determine if the function u(x, y) = 2x^2 satisfies the Laplace equation and is therefore analytic, we need to calculate its Laplacian.
The Laplacian of a function u(x, y) is given by the second partial derivatives with respect to x and y:
∇²u = ∂²u/∂x² + ∂²u/∂y²
Let's calculate the partial derivatives of u(x, y):
∂u/∂x = 4x
∂²u/∂x² = 4
∂u/∂y = 0
∂²u/∂y² = 0
Now, let's calculate the Laplacian:
∇²u = ∂²u/∂x² + ∂²u/∂y² = 4 + 0 = 4
Since the Laplacian of u(x, y) = 2x^2 is equal to 4 and not zero, it does not satisfy the Laplace equation. Therefore, u(x, y) = 2x^2 is not analytic.
The Laplacian of a function u(x, y) is given by the second partial derivatives with respect to x and y:
∇²u = ∂²u/∂x² + ∂²u/∂y²
Let's calculate the partial derivatives of u(x, y):
∂u/∂x = 4x
∂²u/∂x² = 4
∂u/∂y = 0
∂²u/∂y² = 0
Now, let's calculate the Laplacian:
∇²u = ∂²u/∂x² + ∂²u/∂y² = 4 + 0 = 4
Since the Laplacian of u(x, y) = 2x^2 is equal to 4 and not zero, it does not satisfy the Laplace equation. Therefore, u(x, y) = 2x^2 is not analytic.
A function f of the complex variable z = x + i y, is given as f(x, y) = u(x, y) + i v(x, y), where u(x, y) = 2kxy and v(x, y) = x2 – y2. The value of k, for which the function is analytic is _____
Correct answer is between '-1.1,-0.9'. Can you explain this answer?
A function f of the complex variable z = x + i y, is given as f(x, y) = u(x, y) + i v(x, y), where u(x, y) = 2kxy and v(x, y) = x2 – y2. The value of k, for which the function is analytic is _____
|
|
Sanya Agarwal answered |
Given u = 2kxy & V = x2 – y2
Concept:
For function to be analytic:
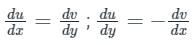
∴ Apply any of the above condition to get the answer.
By first condition:
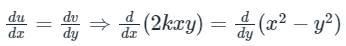 2ky = -2y ⇒ k = -1
2ky = -2y ⇒ k = -1
Concept:
For function to be analytic:
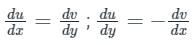
∴ Apply any of the above condition to get the answer.
By first condition:
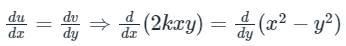 2ky = -2y ⇒ k = -1
2ky = -2y ⇒ k = -1f(z) = u(x, y) + iv(x, y) is an analytic function of complex variable z = x + iy. If v = xy then u(x, y) equals- a)x2 + y2
- b)x2 – y2
- c)
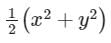
- d)
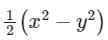
Correct answer is option 'D'. Can you explain this answer?
f(z) = u(x, y) + iv(x, y) is an analytic function of complex variable z = x + iy. If v = xy then u(x, y) equals
a)
x2 + y2
b)
x2 – y2
c)
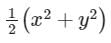
d)
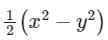

|
Pioneer Academy answered |
Concept:
if f(z) = u(x, y) + iv(x, y) is an analytic function then Cauchy-Riemann condition will be satisfied.

Calculation:
Given:
v = xy

du = xdx - ydy
Integrating both sides

Calculation:
Given:
v = xy

du = xdx - ydy
Integrating both sides
∫du = ∫ (x)dx − ∫ ydy
u = 1/2(x2−y2)
u = 1/2(x2−y2)
Expand the function 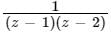 in Laurent’s series for 1 < |z| < 2
in Laurent’s series for 1 < |z| < 2- a)

- b)
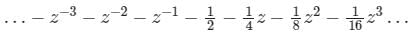
- c)
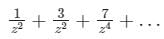
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
Expand the function 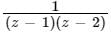 in Laurent’s series for 1 < |z| < 2
in Laurent’s series for 1 < |z| < 2
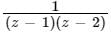 in Laurent’s series for 1 < |z| < 2
in Laurent’s series for 1 < |z| < 2a)

b)
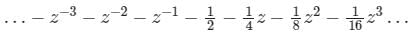
c)
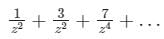
d)
None of the above
|
|
Sanya Agarwal answered |
Concept:
Laurent Series:
If f(z) is analytic at every point inside and on the boundary of a ring-shaped region 'R' bounded by two concentric circle C1 and C2 having centre at 'a' & respective radii r1 and r2 (r1 > r2).
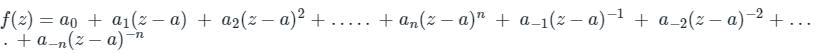
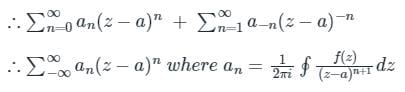
Calculation:
Laurent Series:
If f(z) is analytic at every point inside and on the boundary of a ring-shaped region 'R' bounded by two concentric circle C1 and C2 having centre at 'a' & respective radii r1 and r2 (r1 > r2).
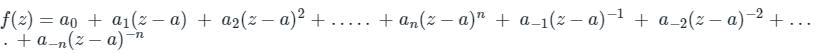
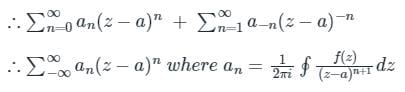
Calculation:
Given:
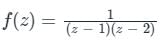 and 1 < |z| < 2
and 1 < |z| < 2Here region of convergence is 1 < |z| and |z| < 2

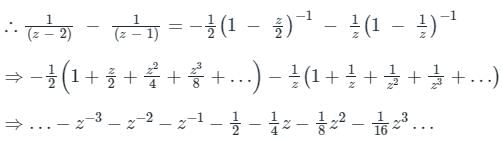
The closed loop line integral 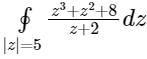 evaluated counter-clockwise, is
evaluated counter-clockwise, is- a)+8jπ
- b)-8jπ
- c)-4jπ
- d)+4jπ
Correct answer is option 'A'. Can you explain this answer?
The closed loop line integral 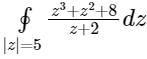 evaluated counter-clockwise, is
evaluated counter-clockwise, is
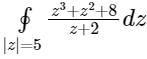 evaluated counter-clockwise, is
evaluated counter-clockwise, isa)
+8jπ
b)
-8jπ
c)
-4jπ
d)
+4jπ

|
Gate Funda answered |
Concept:
Residue Theorem:
If f(z) is analytic in a closed curve C except at a finite number of singular points within C, then
Residue Theorem:
If f(z) is analytic in a closed curve C except at a finite number of singular points within C, then
∫cf(z) dz = 2πj × [sum of residues at the singular points within C]
Formula to find residue:
1. If f(z) has a simple pole at z = a, then
Resf(α) = 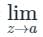 a[(z−α)f(z)]
a[(z−α)f(z)]
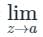 a[(z−α)f(z)]
a[(z−α)f(z)]2. If f(z) has a pole of order n at z = a, then
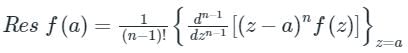
Calculation:
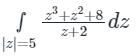
z + 2 = 0 z = -2 |z| = 2 < 5
f(x) is not analytic at z = -2
By Cauchy’s residue theorem
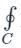 f(x) dz = 2πi × (sum of residues)
f(x) dz = 2πi × (sum of residues)At z = -2
Residue of f(x) = 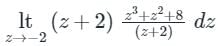
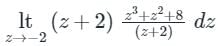
= -8 + 4 + 8 = 4
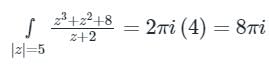
What is the expansion of y = sin-1 x?- a)
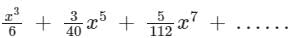
- b)
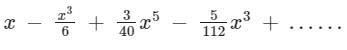
- c)
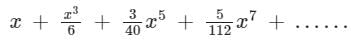
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
What is the expansion of y = sin-1 x?
a)
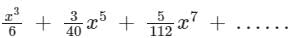
b)
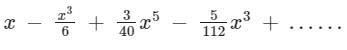
c)
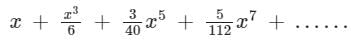
d)
None of the above
|
|
Sanya Agarwal answered |
Concept:
Binomial expansion of (1 - x)-n is given by
(1 - x)-n = 1 + nx +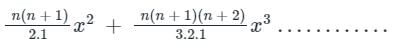
Formula used:
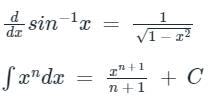
Calculation:
Given,
y = sin-1 x
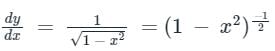 ....(1)
....(1)
Using the above binomial expansion formula

Integrating both sides with respect to x,
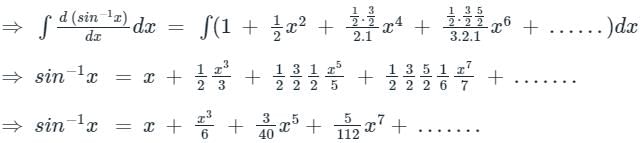
Hence, option c is the correct answer.
(1 - x)-n = 1 + nx +
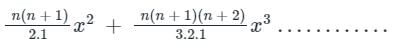
Formula used:
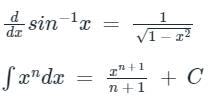
Calculation:
Given,
y = sin-1 x
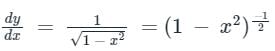 ....(1)
....(1)Using the above binomial expansion formula

Integrating both sides with respect to x,
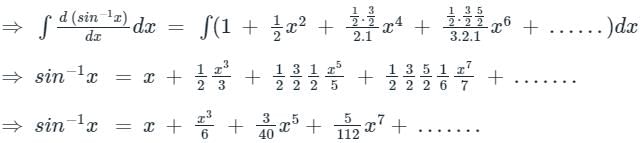
Hence, option c is the correct answer.
The number of integral solutions of  is
is- a)4
- b)5
- c)3
- d)6
Correct answer is option 'B'. Can you explain this answer?
The number of integral solutions of  is
is
 is
isa)
4
b)
5
c)
3
d)
6
|
|
Sanya Agarwal answered |
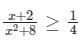
4x + 8 ≥ x2 + 8
∴ x2 – 4x ≤ 0
x(x – 4) ≤ 0 → (1)
Clearly the integral solution of (1) are 0, 1, 2, 3 and 4
∴ Total 5 values of x satisfies (1)
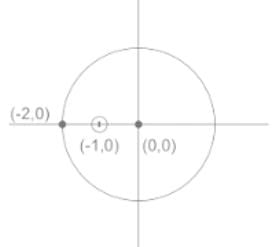
The value of 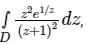 where contour D is |z| = 2
where contour D is |z| = 2- a)
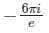
- b)
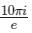
- c)
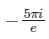
- d)0
Correct answer is option 'A'. Can you explain this answer?
The value of 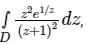 where contour D is |z| = 2
where contour D is |z| = 2
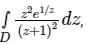 where contour D is |z| = 2
where contour D is |z| = 2a)
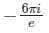
b)
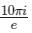
c)
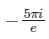
d)
0

|
Gate Gurus answered |
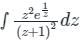 has its poles at z = -1
has its poles at z = -1and contour |z| = 2 is a circle of radius 2, centre (0, 0)
So
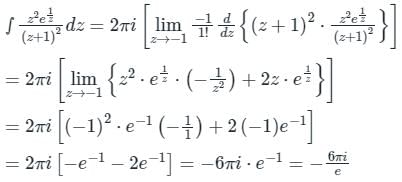
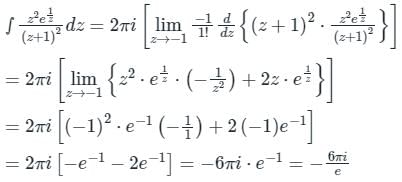
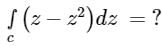 where c is the upper half of the circle |z| = 1.
where c is the upper half of the circle |z| = 1.- a)-2/3
- b)2/3
- c)3/2
- d)-3/2
Correct answer is option 'B'. Can you explain this answer?
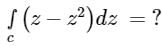 where c is the upper half of the circle |z| = 1.
where c is the upper half of the circle |z| = 1.a)
-2/3
b)
2/3
c)
3/2
d)
-3/2

|
Gate Gurus answered |
Given counter c is the circle, |z| = 1
⇒ z = eiθ ⇒ dz = ieiθdθ
Now, for upper half of the circle, 0 ≤ θ ≤ π
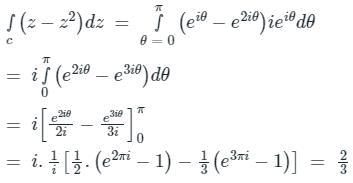
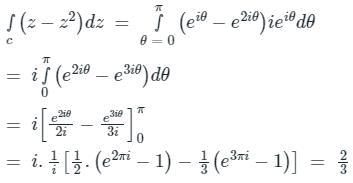
The value of the contour integral in the complex plane
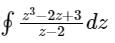
along the contour |z| = 3, taken counterclockwise is- a)-18πi
- b)0
- c)14πi
- d)48πi
Correct answer is option 'C'. Can you explain this answer?
The value of the contour integral in the complex plane
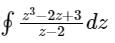
along the contour |z| = 3, taken counterclockwise is
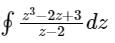
along the contour |z| = 3, taken counterclockwise is
a)
-18πi
b)
0
c)
14πi
d)
48πi

|
Pioneer Academy answered |
Concept:
For a given complex function with poles, the complex integral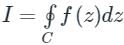 is given by
is given by
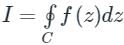 is given by
is given byResidue theorem as;
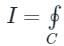 Cf(z)dz = 2π i × {Sum of residue of poles in side or onC}
Cf(z)dz = 2π i × {Sum of residue of poles in side or onC}
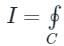 Cf(z)dz = 2π i × {Sum of residue of poles in side or onC}
Cf(z)dz = 2π i × {Sum of residue of poles in side or onC}Calculation:
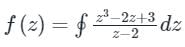
Contour: |z|= 3
Simple pole, z = 2 and it is lies inside the contour.
Residue of f(z) at z = 2 is,
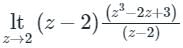 = 23 − 2(2) + 3 = 7
= 23 − 2(2) + 3 = 7
f(z) = 2πi(7) = 14πi
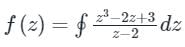
Contour: |z|= 3
Simple pole, z = 2 and it is lies inside the contour.
Residue of f(z) at z = 2 is,
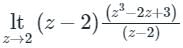 = 23 − 2(2) + 3 = 7
= 23 − 2(2) + 3 = 7f(z) = 2πi(7) = 14πi
The real part of an analytic function f(z) where z = x + iy is given by e-y cos (x). The imaginary part of f(z) is- a)ey cos (x)
- b)e-y sin (x)
- c)-ey sin (x)
- d)-e-y sin (x)
Correct answer is option 'B'. Can you explain this answer?
The real part of an analytic function f(z) where z = x + iy is given by e-y cos (x). The imaginary part of f(z) is
a)
ey cos (x)
b)
e-y sin (x)
c)
-ey sin (x)
d)
-e-y sin (x)

|
Raghavendra Sengupta answered |
The real part of an analytic function f(z) is given by e^(-y) * cos(x). We are required to find the imaginary part of f(z).
To find the imaginary part of f(z), we can make use of the Cauchy-Riemann equations. According to these equations, if f(z) is an analytic function, then it satisfies the following conditions:
∂u/∂x = ∂v/∂y (1)
∂u/∂y = -∂v/∂x (2)
where u(x, y) is the real part of f(z) and v(x, y) is the imaginary part of f(z).
Let's differentiate the given real part of f(z) with respect to x and y:
∂u/∂x = -e^(-y) * sin(x) (3)
∂u/∂y = -e^(-y) * cos(x) (4)
Comparing equations (1) and (3), we can see that:
∂v/∂y = -e^(-y) * sin(x) (5)
Comparing equations (2) and (4), we can see that:
∂v/∂x = e^(-y) * cos(x) (6)
Now, integrating equation (5) with respect to y, we get:
v(x, y) = -e^(-y) * sin(x) + g(x) (7)
where g(x) is an arbitrary function of x.
Next, substituting equation (7) into equation (6), we can solve for g(x):
∂v/∂x = e^(-y) * cos(x) (6)
e^(-y) * cos(x) = e^(-y) * cos(x) + g'(x) (8)
g'(x) = 0 (9)
Since g'(x) = 0, it implies that g(x) is a constant.
Therefore, the imaginary part of f(z) is given by:
v(x, y) = -e^(-y) * sin(x) + C (10)
where C is a constant.
Comparing equation (10) with the given options, we can see that the correct answer is option B, i.e., e^(-y) * sin(x).
To find the imaginary part of f(z), we can make use of the Cauchy-Riemann equations. According to these equations, if f(z) is an analytic function, then it satisfies the following conditions:
∂u/∂x = ∂v/∂y (1)
∂u/∂y = -∂v/∂x (2)
where u(x, y) is the real part of f(z) and v(x, y) is the imaginary part of f(z).
Let's differentiate the given real part of f(z) with respect to x and y:
∂u/∂x = -e^(-y) * sin(x) (3)
∂u/∂y = -e^(-y) * cos(x) (4)
Comparing equations (1) and (3), we can see that:
∂v/∂y = -e^(-y) * sin(x) (5)
Comparing equations (2) and (4), we can see that:
∂v/∂x = e^(-y) * cos(x) (6)
Now, integrating equation (5) with respect to y, we get:
v(x, y) = -e^(-y) * sin(x) + g(x) (7)
where g(x) is an arbitrary function of x.
Next, substituting equation (7) into equation (6), we can solve for g(x):
∂v/∂x = e^(-y) * cos(x) (6)
e^(-y) * cos(x) = e^(-y) * cos(x) + g'(x) (8)
g'(x) = 0 (9)
Since g'(x) = 0, it implies that g(x) is a constant.
Therefore, the imaginary part of f(z) is given by:
v(x, y) = -e^(-y) * sin(x) + C (10)
where C is a constant.
Comparing equation (10) with the given options, we can see that the correct answer is option B, i.e., e^(-y) * sin(x).
Find the Laurent expansion of f(z) = 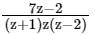 in the region 1 < z + 1 < 3
in the region 1 < z + 1 < 3- a)
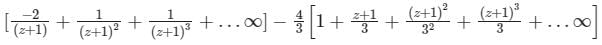
- b)

- c)
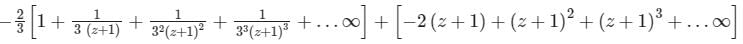
- d)
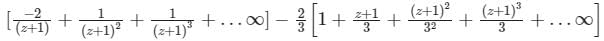
Correct answer is option 'D'. Can you explain this answer?
Find the Laurent expansion of f(z) = 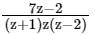 in the region 1 < z + 1 < 3
in the region 1 < z + 1 < 3
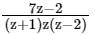 in the region 1 < z + 1 < 3
in the region 1 < z + 1 < 3a)
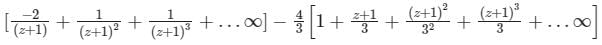
b)

c)
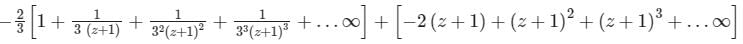
d)
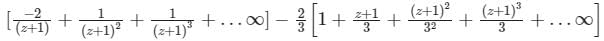

|
Gate Gurus answered |
Calculation:
Let z +1 = u ⇒ z = u – 1
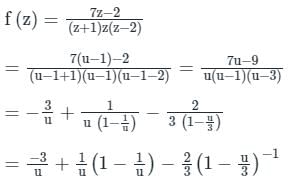
Given 1 < z + 1 < 3
⇒ 1 < u < 3
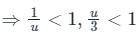
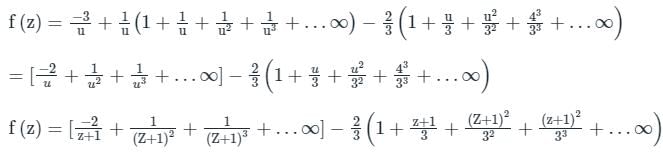
Let z +1 = u ⇒ z = u – 1
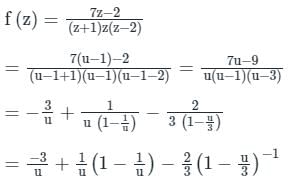
Given 1 < z + 1 < 3
⇒ 1 < u < 3
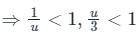
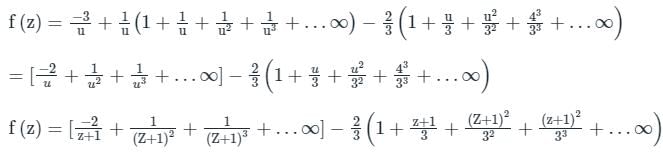
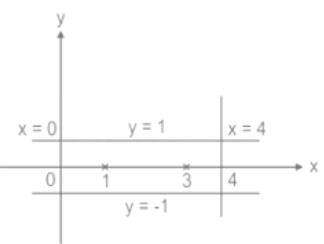
Evaluate 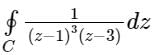 where C is the rectangular region defined by x = 0, x = 4, y = -1 and y = 1
where C is the rectangular region defined by x = 0, x = 4, y = -1 and y = 1- a)1
- b)0
- c)
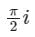
- d)π (3 + 2i)
Correct answer is option 'B'. Can you explain this answer?
Evaluate 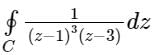 where C is the rectangular region defined by x = 0, x = 4, y = -1 and y = 1
where C is the rectangular region defined by x = 0, x = 4, y = -1 and y = 1
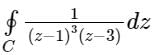 where C is the rectangular region defined by x = 0, x = 4, y = -1 and y = 1
where C is the rectangular region defined by x = 0, x = 4, y = -1 and y = 1a)
1
b)
0
c)
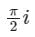
d)
π (3 + 2i)
|
|
Sanvi Kapoor answered |
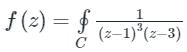
(z - 1)3 (z - 3) = 0
⇒ z = 1, z = 3
The function has a simple pole at z = 3 and has a multiple pole at z = 1
Both z = 1, and z = 3 are inside the region C
According to Cauchy’s Residue theorem
 f (z)dz = 2πi [sum of the residues at the poles in side ′C′]
f (z)dz = 2πi [sum of the residues at the poles in side ′C′]
If z = a is a pole of order ‘m’, then residue of f(z) at z = a is,
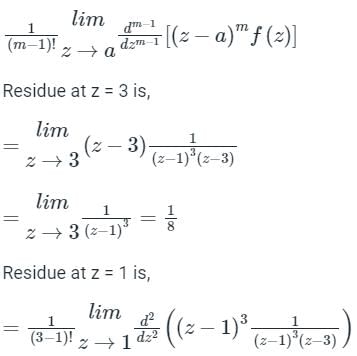
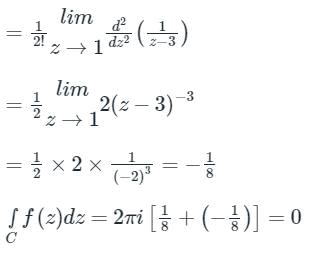
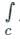 f (z)dz = 2πi [sum of the residues at the poles in side ′C′]
f (z)dz = 2πi [sum of the residues at the poles in side ′C′]If z = a is a pole of order ‘m’, then residue of f(z) at z = a is,
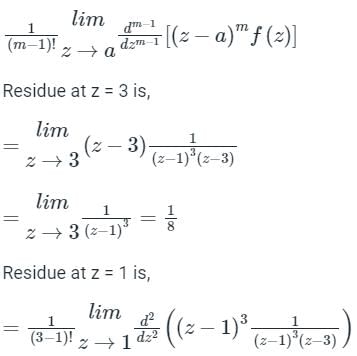
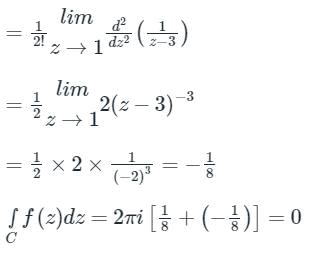
Which of the following function f(z), of the complex variable z, is NOT analytic at all the points of the complex plane?- a)f(z) = z2
- b)f(z) = ez
- c)f(z) = sin z
- d)f(z) = log z
Correct answer is option 'D'. Can you explain this answer?
Which of the following function f(z), of the complex variable z, is NOT analytic at all the points of the complex plane?
a)
f(z) = z2
b)
f(z) = ez
c)
f(z) = sin z
d)
f(z) = log z

|
Sneha Nair answered |
Analytic Functions in Complex Analysis
An analytic function is a complex function that is differentiable at every point in its domain.
If a function is analytic at all the points in the complex plane, then it is called an entire function.
If a function is not analytic at any point in its domain, then it is called a non-analytic function.
Out of the given options, the function f(z) = log z is not analytic at all the points in the complex plane.
Explanation
The function f(z) = log z is not analytic at z = 0 and any other point where z is negative or zero.
The reason for this is that the complex logarithm is a multivalued function. For any non-zero complex number z, there are infinitely many complex numbers w such that ez = w. So, we define the complex logarithm as follows:
log z = ln |z| + i arg(z)
where arg(z) is any angle whose tangent is the imaginary part divided by the real part of z.
However, when z is negative or zero, arg(z) is not well-defined, and so log z is not analytic at these points.
Hence, the function f(z) = log z is not analytic at all the points in the complex plane.
An analytic function is a complex function that is differentiable at every point in its domain.
If a function is analytic at all the points in the complex plane, then it is called an entire function.
If a function is not analytic at any point in its domain, then it is called a non-analytic function.
Out of the given options, the function f(z) = log z is not analytic at all the points in the complex plane.
Explanation
The function f(z) = log z is not analytic at z = 0 and any other point where z is negative or zero.
The reason for this is that the complex logarithm is a multivalued function. For any non-zero complex number z, there are infinitely many complex numbers w such that ez = w. So, we define the complex logarithm as follows:
log z = ln |z| + i arg(z)
where arg(z) is any angle whose tangent is the imaginary part divided by the real part of z.
However, when z is negative or zero, arg(z) is not well-defined, and so log z is not analytic at these points.
Hence, the function f(z) = log z is not analytic at all the points in the complex plane.
The value of the integral 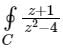 dz in counter clockwise direction around a circle C of radius 1 with center at the point z = −2 is
dz in counter clockwise direction around a circle C of radius 1 with center at the point z = −2 is- a)πi/2
- b)2πi
- c)
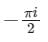
- d)– 2πi
Correct answer is option 'A'. Can you explain this answer?
The value of the integral 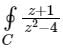 dz in counter clockwise direction around a circle C of radius 1 with center at the point z = −2 is
dz in counter clockwise direction around a circle C of radius 1 with center at the point z = −2 is
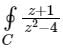 dz in counter clockwise direction around a circle C of radius 1 with center at the point z = −2 is
dz in counter clockwise direction around a circle C of radius 1 with center at the point z = −2 isa)
πi/2
b)
2πi
c)
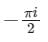
d)
– 2πi

|
Pioneer Academy answered |
Given that,
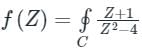
C : |Z – (-2)| = 1
⇒ C : |Z + 2| = 1
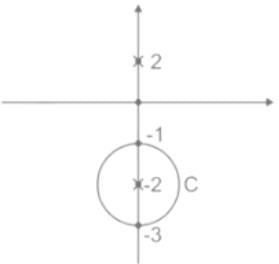
poles of f(Z) are z2 – 4 = 0
⇒ Z = ±2
Z = 2 is lies outside the curve C.
f(Z) = 2πi [residue at Z = -2]
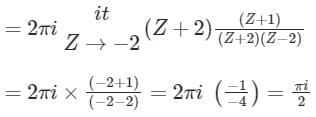
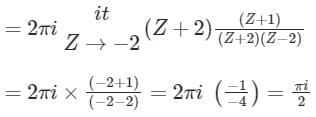
The series expansion of sinx/x near origin is- a)
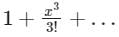
- b)
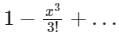
- c)
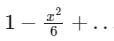
- d)
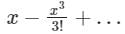
Correct answer is option 'C'. Can you explain this answer?
The series expansion of sinx/x near origin is
a)
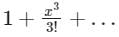
b)
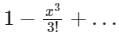
c)
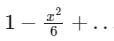
d)
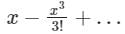

|
Engineers Adda answered |
Concept:
Taylor series:
The Taylor series of a real or complex-valued function f (x) that is infinitely differentiable at a real or complex number ‘a’ is the power series.
Expression of Taylor series is:
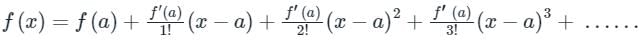
Calculation:
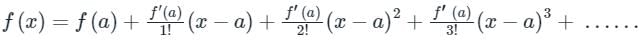
Calculation:
Given:
We have to find the series expansion of sinx/x near origin, or a = 0.
Let f(x) = sin x
f(0) = sin (0) = 0,
f'(0) = cos (0) = 1,
f''(0) = -sin(0) = 0,
f'''(0) = -1 .... so on
Putting all the values in Taylor series expansion, we get:
Series expansion of sin x will be:
sinx = x − x3/3!+…
Therefore the series expansion of sin x/x near origin will be:
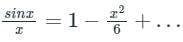
sinx = x − x3/3!+…
Therefore the series expansion of sin x/x near origin will be:
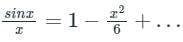
The Maclaurin's series expansion of esin x is- a)
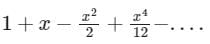
- b)
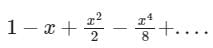
- c)
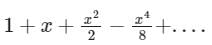
- d)
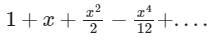
Correct answer is option 'C'. Can you explain this answer?
The Maclaurin's series expansion of esin x is
a)
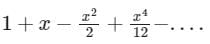
b)
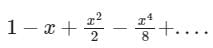
c)
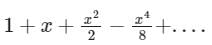
d)
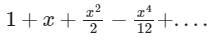
|
|
Sanya Agarwal answered |
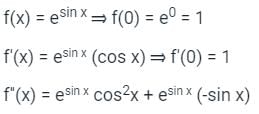
f''(0) = 1
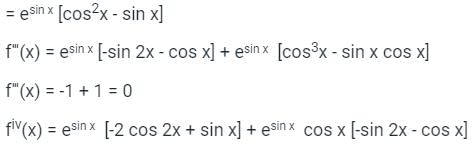
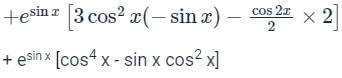
fiv(0) = -2 -1 -1 + 1 = -3
Substitue in Maclaurin Series

Evaluate the line integral  (x + 4iy2)dz where c is the line x = 2y and x varies from 0 to 1 and z = x + iy
(x + 4iy2)dz where c is the line x = 2y and x varies from 0 to 1 and z = x + iy- a)
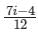
- b)

- c)
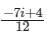
- d)
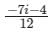
Correct answer is option 'B'. Can you explain this answer?
Evaluate the line integral  (x + 4iy2)dz where c is the line x = 2y and x varies from 0 to 1 and z = x + iy
(x + 4iy2)dz where c is the line x = 2y and x varies from 0 to 1 and z = x + iy
 (x + 4iy2)dz where c is the line x = 2y and x varies from 0 to 1 and z = x + iy
(x + 4iy2)dz where c is the line x = 2y and x varies from 0 to 1 and z = x + iya)
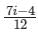
b)

c)
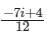
d)
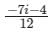
|
|
Sanya Agarwal answered |
Calculation:
z = x + iy ⇒ dz = dx + i dy
given line is x = 2y ⇒ dy/dx = 1/2
lets substitute y in terms of x
I = ∫ x + i x2 (dx + i/2 dx)
I = ∫ x dx + i/2 x dx + i x2 dx - x2/2 dx
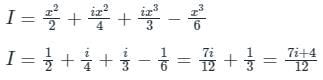
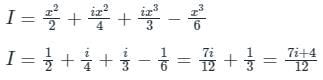
Which of the following statements is FALSE?- a)If a sequence X of real numbers converges to a real number and has two convergent subsequences X' and X" whose limits are not equal, then X is divergent.
- b)A Cauchy sequence of real numbers is unbounded.
- c)If a sequence (xn) of real number converges to a real number x, then any subsequence (xnK) of (xn) also converges to x.
- d)A bounded sequence of real numbers has a convergent subsequence.
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements is FALSE?
a)
If a sequence X of real numbers converges to a real number and has two convergent subsequences X' and X" whose limits are not equal, then X is divergent.
b)
A Cauchy sequence of real numbers is unbounded.
c)
If a sequence (xn) of real number converges to a real number x, then any subsequence (xnK) of (xn) also converges to x.
d)
A bounded sequence of real numbers has a convergent subsequence.
|
|
Sanya Agarwal answered |
All the statements given are verified by different theorems,
Theorem: If a sequence converges then all subsequences converge and all convergent subsequences converge to the same limit (Option 3)
Theorem: Every bounded sequence has a convergent subsequence (Option 4)
Theorem: If {an}n∈N is a sequence that either has a subsequence that diverges or two convergent subsequences with different limits then {an}n∈N is divergent (Option 1)
Theorem:
1) A sequence {an} of real numbers is called a Cauchy sequence if for each ϵ > 0 there is a number N ∈ N so that if m, n > N then |an − am| < ϵ.
2) If a real sequence {an} converges, then for every ε > 0, there exists N ∈ N such that |an − am| < ε ∀ n,m ≥ N
3) Convergent sequences are Cauchy sequences.
A Cauchy sequence of real numbers is bounded (Option 2 is false)
A sequence is a convergent sequence if and only if it is a Cauchy sequence.
In the Laurent series expression of 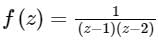 valid for 0 < |z - 1|< 1, the co-efficient of 1/(z−1)is
valid for 0 < |z - 1|< 1, the co-efficient of 1/(z−1)is- a)-2
- b)-1
- c)0
- d)1
Correct answer is option 'B'. Can you explain this answer?
In the Laurent series expression of 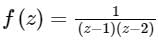 valid for 0 < |z - 1|< 1, the co-efficient of 1/(z−1)is
valid for 0 < |z - 1|< 1, the co-efficient of 1/(z−1)is
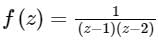 valid for 0 < |z - 1|< 1, the co-efficient of 1/(z−1)is
valid for 0 < |z - 1|< 1, the co-efficient of 1/(z−1)isa)
-2
b)
-1
c)
0
d)
1

|
Gate Gurus answered |
Concept:
Laurentz Series is obtained by the arrangement and manipulation of standard series or expansions, i.e.
(1 - x)-1 = 1 + x + x2 + x3 + …… |x| < 1
(1 + x)-1 = 1 – x + x2 – x3 + ….. |x| < 1
(1 - x)-2 = 1 + 2x + 3x2 + ….. |x| < 1
(1 + x)-2 1 – 2x + 3x2 – 4x2 + …. |x| < 1
Observe that in all the expansions; |x| should be less than 1.
∴ We need to manipulate the variable to satisfy the above condition.
Calculation:
Given:
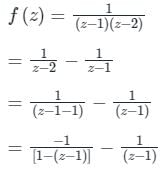
= -1 [1 - (z - 1)]-1 - [z - 1]-1
= -[z - 1]-1 - [1 + (z - 1) + (z - 1)2 + (z - 1)3 +…]
Co-efficient of 1z−1 is -1
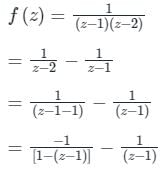
= -1 [1 - (z - 1)]-1 - [z - 1]-1
= -[z - 1]-1 - [1 + (z - 1) + (z - 1)2 + (z - 1)3 +…]
Co-efficient of 1z−1 is -1
Given z = x +iy, i = √-1 C is a circle of radius 2 with the centre at the origin. If the contour C is traversed anticlockwise, then the value of the integral  is ________ (round off to one decimal place.)
is ________ (round off to one decimal place.)
Correct answer is '0.2'. Can you explain this answer?
Given z = x +iy, i = √-1 C is a circle of radius 2 with the centre at the origin. If the contour C is traversed anticlockwise, then the value of the integral  is ________ (round off to one decimal place.)
is ________ (round off to one decimal place.)
 is ________ (round off to one decimal place.)
is ________ (round off to one decimal place.)

|
Pioneer Academy answered |
Concept:
if f(z) is analytic in closed curve C except at a finite number of singular points within C then
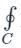 f(Z)dz = 2πi × [sum of residues at singular points within C]
f(Z)dz = 2πi × [sum of residues at singular points within C]Calculation:
Given:


Singular points: z = i, -4i
C is a circle of radius 2, only z = i will lie inside the circle
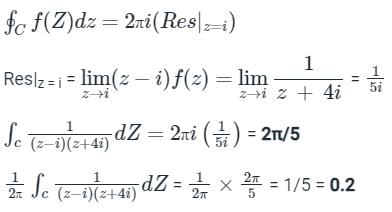
If f(z) is analytic in a simply connected domain D, then for every closed path C and D- a)
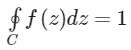
- b)
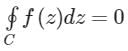
- c)
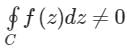
- d)
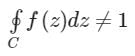
Correct answer is option 'B'. Can you explain this answer?
If f(z) is analytic in a simply connected domain D, then for every closed path C and D
a)
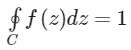
b)
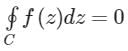
c)
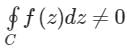
d)
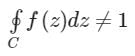

|
Pioneer Academy answered |
Cauchy's Theorem:
If f(z) is single-valued and an analytic function of z and f'(z) is continuous at each point within and on the closed curve c, then according to the theorem, 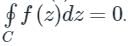
Cauchy's Integral Formula:
For Simple Pole:
If f(z) is analytic within and on a closed curve c and if a (simple pole) is any point within c, then
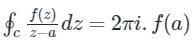
For Multiple Pole:
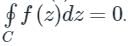
Cauchy's Integral Formula:
For Simple Pole:
If f(z) is analytic within and on a closed curve c and if a (simple pole) is any point within c, then
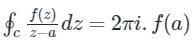
For Multiple Pole:
If f(z) is analytic within and on a closed curve c, and if a (multiple poles) are points within c, then
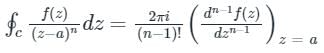
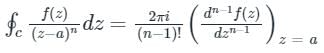
Which one of the following functions is analytic in the region |z| ≤ 1?- a)
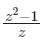
- b)
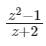
- c)
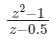
- d)
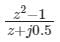
Correct answer is option 'B'. Can you explain this answer?
Which one of the following functions is analytic in the region |z| ≤ 1?
a)
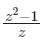
b)
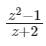
c)
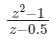
d)
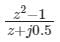
|
|
Sanvi Kapoor answered |
Given region |z|≤ 1
a) 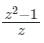
z = 0 |z| = 0 ≤ 1
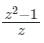
z = 0 |z| = 0 ≤ 1
The pole is lies inside the given region.
Hence, the function is not analytic.
b) 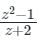
z + 2 = 0 → z = -2 |z| = 2 ≥ 1
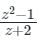
z + 2 = 0 → z = -2 |z| = 2 ≥ 1
the pole is lies outside the given region.
Hence, the function is analytic.
c) 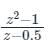
z – 0.5 = 0 z = 0.5 |z| = 0.5 ≤ 1
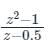
z – 0.5 = 0 z = 0.5 |z| = 0.5 ≤ 1
The pole is lies inside the given region.
Hence, the function is not analytic.
d) 
z + j 0.5 = 0 ⇒ z = -j 0.5 ⇒ |z| = 0.5 ≤ 1

z + j 0.5 = 0 ⇒ z = -j 0.5 ⇒ |z| = 0.5 ≤ 1
The pole is lies inside the given region.
Hence, the function is not analytic.
The value of the integral

evaluated using contour integration and the residue theorem is- a)-π sin (1)/e
- b)-π cos (1)/e
- c)sin (1)/e
- d)cos (1)/e
Correct answer is option 'A'. Can you explain this answer?
The value of the integral

evaluated using contour integration and the residue theorem is

evaluated using contour integration and the residue theorem is
a)
-π sin (1)/e
b)
-π cos (1)/e
c)
sin (1)/e
d)
cos (1)/e

|
Naroj Boda answered |
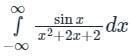
Concept:
Cauchy Integral Theorem:
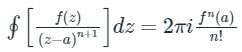
Where z = a be any point inside the close region.
Cauchy’s Residue Theorem:
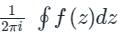 = Sum of Residue at Pole or singularity with in the region
= Sum of Residue at Pole or singularity with in the region
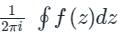 = Sum of Residue at Pole or singularity with in the region
= Sum of Residue at Pole or singularity with in the regionRes at z = a
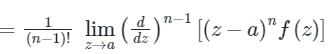
Calculation:
We know that eix = cos x + i sin x
Let x replace by z.
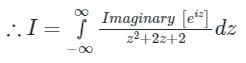
Now, z2 + 2z + 2 = 0 then roots of z are:
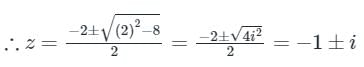
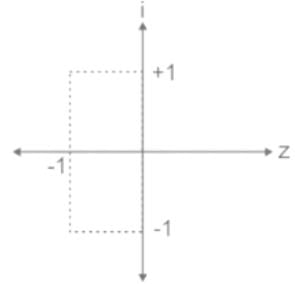
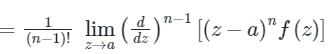
Calculation:
We know that eix = cos x + i sin x
Let x replace by z.
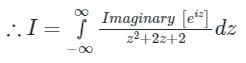
Now, z2 + 2z + 2 = 0 then roots of z are:
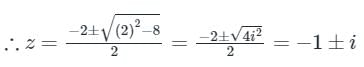

z = -1 ± i is the only pole lying in f(z) > 0
Here n = 1
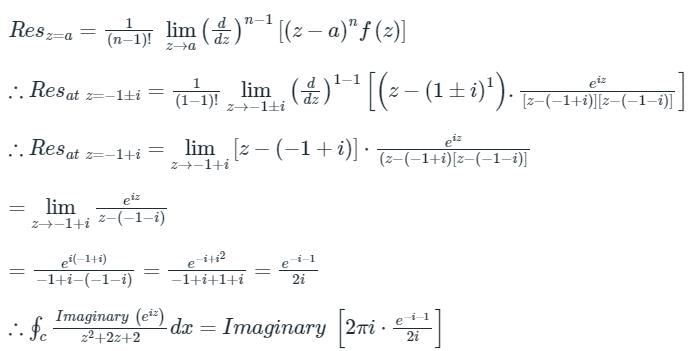
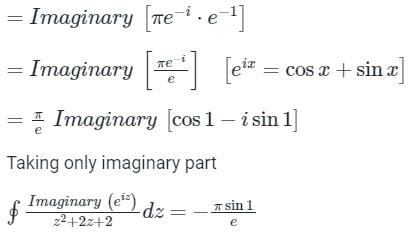
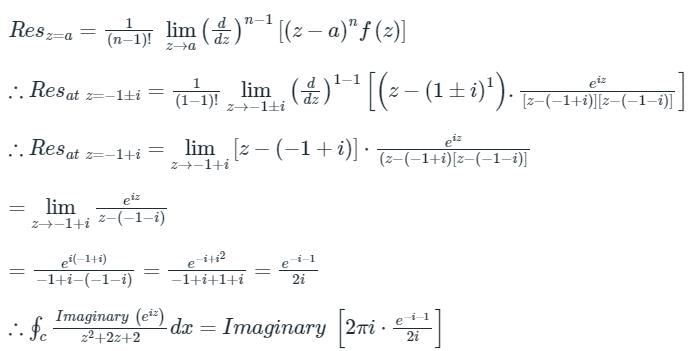
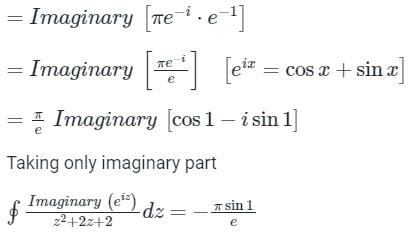
Evaluate 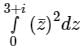 along the straight line joining the points (0, 0) and (3, 1)
along the straight line joining the points (0, 0) and (3, 1)- a)
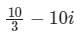
- b)
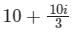
- c)
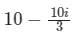
- d)
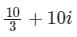
Correct answer is option 'C'. Can you explain this answer?
Evaluate 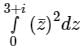 along the straight line joining the points (0, 0) and (3, 1)
along the straight line joining the points (0, 0) and (3, 1)
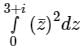 along the straight line joining the points (0, 0) and (3, 1)
along the straight line joining the points (0, 0) and (3, 1)a)
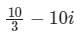
b)
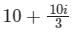
c)
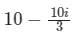
d)
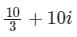
|
|
Sanya Agarwal answered |
Concept:
Integral of a complex function f(z) is given
∫ f(z) dz = ∫ (udx -vdy) + i ∫ (vdx + udy)
Noting f(z) = u(x, y) + i v(x, y) and dz = dx + i dy;
Calculation:
Given Along the straight line joining the points (0, 0) and (3, 1);
The equation of straight line will be x = 3y
⇒ dx = 3 dy ⇒ dz = (3 + i) dy;
Along the line x = 3y, the complex number z will be
z = x + iy = 3y + iy = (3 + i) y
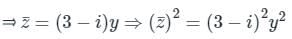
Substituting both in the integral,
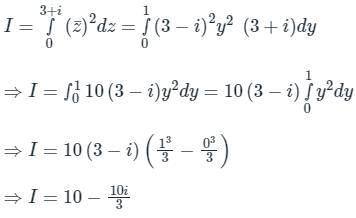
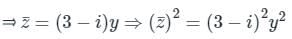
Substituting both in the integral,
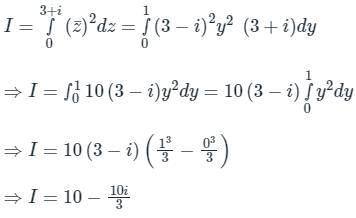
If f (z) = u + iv is an analytic function, then- a)u is harmonic function
- b)v is harmonic function
- c)Both u and v are harmonic functions
- d)Both u and v are not harmonic functions
Correct answer is option 'C'. Can you explain this answer?
If f (z) = u + iv is an analytic function, then
a)
u is harmonic function
b)
v is harmonic function
c)
Both u and v are harmonic functions
d)
Both u and v are not harmonic functions
|
|
Sanya Agarwal answered |
Concept:
If a function f satisfies Laplace's equation ∇2f = 0, then f is said to be a harmonic function.
Calculation:
If f (z) = u + iv is an analytic function, then
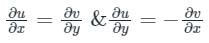
Now
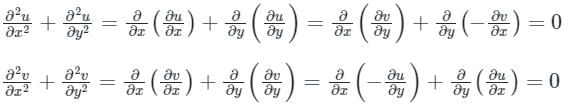
Both u and v are satisfying Laplace’s equation (∇2f = 0).
∴ Both u and v are harmonic functions.
If a function f satisfies Laplace's equation ∇2f = 0, then f is said to be a harmonic function.
Calculation:
If f (z) = u + iv is an analytic function, then
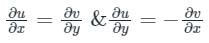
Now
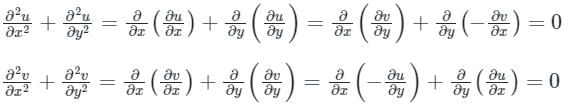
Both u and v are satisfying Laplace’s equation (∇2f = 0).
∴ Both u and v are harmonic functions.
If u = x2 – y2, then the conjugate harmonic function is- a)2xy
- b)x2 + y2
- c)y2 – x2
- d)-x2 – y2
Correct answer is option 'A'. Can you explain this answer?
If u = x2 – y2, then the conjugate harmonic function is
a)
2xy
b)
x2 + y2
c)
y2 – x2
d)
-x2 – y2
|
|
Sanya Agarwal answered |
Concept:
If two functions u and v satisfy Cauchy-Riemann equations, then they are said to be harmonic conjugates with respect to each other.
Cauchy-Riemann equations are
vy = ux
vx = - uy
vy = ux
vx = - uy
Calculation:
Given u = x2 – y2, let v be the harmonic conjugate.
By Cauchy-Riemann equations,
vy = ux = 2x; vx = - uy = - (-2y) = 2y;
We have dv = vx dx + vy dy
⇒ dv = 2y dx + 2x dy = d(2xy)
⇒ v = 2xy + k or v = 2xy
∴ The conjugate harmonic function is 2xy
∴ The conjugate harmonic function is 2xy
The Cauchy Riemann equations for f(z) = u(x, y) + iv(x, y) to be analytic are:- a)
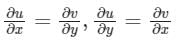
- b)
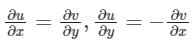
- c)
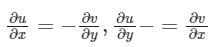
- d)
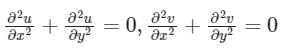
Correct answer is option 'B'. Can you explain this answer?
The Cauchy Riemann equations for f(z) = u(x, y) + iv(x, y) to be analytic are:
a)
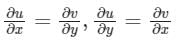
b)
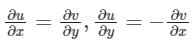
c)
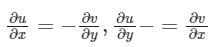
d)
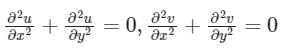
|
|
Sanvi Kapoor answered |
Concept:
Cauchy-Riemann equations:
Rectangular form:
f(z) = u(x, y) + f v(x, y)
f(z) to be analytic it needs to satisfy Cauchy Riemann equations
ux = vy, uy = -vx
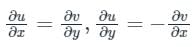
Polar form:
f(z) = u(r, θ) + f v(r, θ)
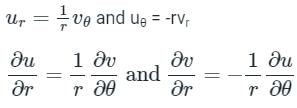
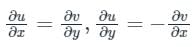
Polar form:
f(z) = u(r, θ) + f v(r, θ)
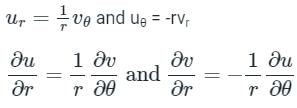
The integration of f (z) = x2 + ixy from A(1, 1) to B(2, 4) along the straight line AB joining the two points is- a)

- b)
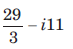
- c)
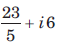
- d)
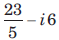
Correct answer is 'A'. Can you explain this answer?
The integration of f (z) = x2 + ixy from A(1, 1) to B(2, 4) along the straight line AB joining the two points is
a)
b)
c)
d)

|
Prakhar Goyal answered |
Find the slope of the line joining A and B then convert whole to *x* form or *y* form including dz=dx+idy then integrate from the upper limit and lower limit of the variable which you have converted to.
The value of the integral
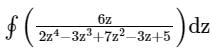
evaluated over a counter-clockwise circular contour in the complex plane enclosing only the pole z = i, where i is the imaginary unit, is- a)(-1 + i) π
- b)(1 + i) π
- c)2(1 - i) π
- d)(2 + i) π
Correct answer is option 'A'. Can you explain this answer?
The value of the integral
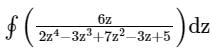
evaluated over a counter-clockwise circular contour in the complex plane enclosing only the pole z = i, where i is the imaginary unit, is
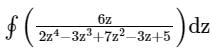
evaluated over a counter-clockwise circular contour in the complex plane enclosing only the pole z = i, where i is the imaginary unit, is
a)
(-1 + i) π
b)
(1 + i) π
c)
2(1 - i) π
d)
(2 + i) π

|
Gate Funda answered |
Concept:
Residue theorem: if f(z) is an analytic function in a closed curve C except at a finite number of singular points within C then
∮cf(z)dz = 2πi × (sum of the residues at the singular point within curve C)
Residue for simple pole z = a:
Res f(a) =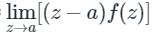
Calculation:
Residue theorem: if f(z) is an analytic function in a closed curve C except at a finite number of singular points within C then
∮cf(z)dz = 2πi × (sum of the residues at the singular point within curve C)
Residue for simple pole z = a:
Res f(a) =
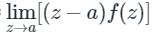
Calculation:
Given:
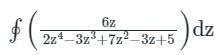
pole z = i
Check for singularity at pole z = i
f(z) = 2z4 - 3z3 + 7z2 - 3z + 5
f(i) = 2(i)4 - 3(i)3 + 7(i)2 - 3i + 5
f(i) = 2 ×1 - 3(-i) - 7 - 3i + 5 = 0
since, f(i) = 0 ⇒ z = i is a singular point
From Residue theorem:
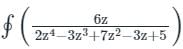 dz = 2πi (Residue at z = i )
dz = 2πi (Residue at z = i )
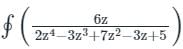 dz = 2πi (Residue at z = i )
dz = 2πi (Residue at z = i )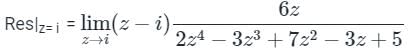
at z = i , Res = 0/0 form, applying L'hospital rule
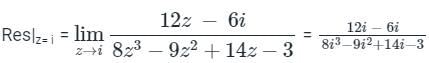
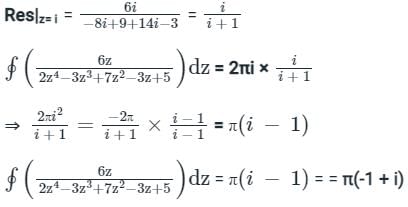
The value of the following complex integral, with C representing the unit circle centered at origin in the counterclockwise sense, is: 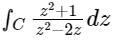
- a)8πi
- b)-8πi
- c)-πi
- d)πi
Correct answer is option 'C'. Can you explain this answer?
The value of the following complex integral, with C representing the unit circle centered at origin in the counterclockwise sense, is: 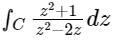
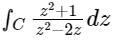
a)
8πi
b)
-8πi
c)
-πi
d)
πi

|
Pioneer Academy answered |
Concept:
Cauchy’s Theorem:
If f(z) is an analytic function and f’(z) is continuous at each point within and on a closed curve C, then
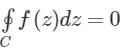
Cauchy’s Integral Formula:
If f(z) is an analytic function within a closed curve and if a is any point within C, then
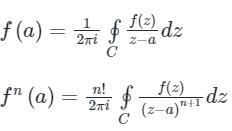
Residue Theorem:
If f(z) is analytic in a closed curve C except at a finite number of singular points within C, then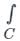 f(z)dz = 2πi × [sum of residues at the singualr points with in C]
f(z)dz = 2πi × [sum of residues at the singualr points with in C]
Cauchy’s Integral Formula:
If f(z) is an analytic function within a closed curve and if a is any point within C, then
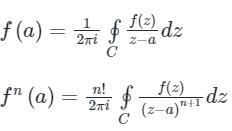
Residue Theorem:
If f(z) is analytic in a closed curve C except at a finite number of singular points within C, then
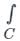 f(z)dz = 2πi × [sum of residues at the singualr points with in C]
f(z)dz = 2πi × [sum of residues at the singualr points with in C]Formula to find residue:
1. If f(z) has a simple pole at z = a, then
 2. If f(z) has a pole of order n at z = a, then
2. If f(z) has a pole of order n at z = a, then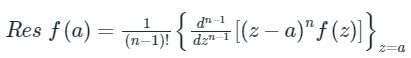
Application:
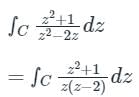
The simple poles are: z = 0, 2
The given region is a unit circle.
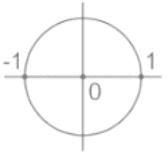
The residue at z = 2 is zero as it lies outside the given region.
The reside at z = 0, is given by
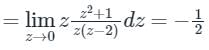
The value of the given integral =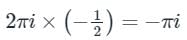
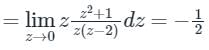
The value of the given integral =
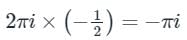
If f (z) is an analytic function whose modulus is constant, then f (z) is a- a)Function of z
- b)Constant
- c)Function whose only imaginary part is constant
- d)Function whose only real part is constant
Correct answer is option 'B'. Can you explain this answer?
If f (z) is an analytic function whose modulus is constant, then f (z) is a
a)
Function of z
b)
Constant
c)
Function whose only imaginary part is constant
d)
Function whose only real part is constant
|
|
Sanvi Kapoor answered |
Concept:
Let f(z) = u + iv be the analytic function,
then According to Cauchy-Riemann Equations
ux = vy & uy = - vx
Calculation:
Given:
modulus is constant
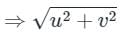 = k ⇒ u2 + v2 = k
= k ⇒ u2 + v2 = k
Now differentiating both sides w.r.t x and y, we get
2uux + 2vvx = 0 ⇒ 2uux = -2vvx --- (1)
2uuy + 2vvy = 0 ⇒ 2uuy = -2vvy --- (2)
Now applying Cauchy-Riemann Equations ux = vy & uy = - vx
2uux – 2vuy = 0 ⇒ 2uux = 2vuy --- (3)
2uuy + 2vux = 0 ⇒ 2uuy = -2vux --- (4)
Now dividing equations 3 and 4, we get
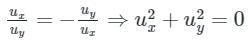
⇒ ux = uy = 0 ⇒ u is a constant function.
Similarly, we will get v is a constant function.
∴ f(z) is a constant function.
Let f(z) = u + iv be the analytic function,
then According to Cauchy-Riemann Equations
ux = vy & uy = - vx
Calculation:
Given:
modulus is constant
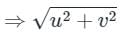 = k ⇒ u2 + v2 = k
= k ⇒ u2 + v2 = kNow differentiating both sides w.r.t x and y, we get
2uux + 2vvx = 0 ⇒ 2uux = -2vvx --- (1)
2uuy + 2vvy = 0 ⇒ 2uuy = -2vvy --- (2)
Now applying Cauchy-Riemann Equations ux = vy & uy = - vx
2uux – 2vuy = 0 ⇒ 2uux = 2vuy --- (3)
2uuy + 2vux = 0 ⇒ 2uuy = -2vux --- (4)
Now dividing equations 3 and 4, we get
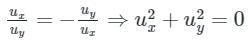
⇒ ux = uy = 0 ⇒ u is a constant function.
Similarly, we will get v is a constant function.
∴ f(z) is a constant function.
In the Laurent expansion of f(z) =  valid in the region 1 < |z| < 2, the co-efficient of 1/z2 is
valid in the region 1 < |z| < 2, the co-efficient of 1/z2 is- a)0
- b)1/2
- c)1
- d)-1
Correct answer is option 'D'. Can you explain this answer?
In the Laurent expansion of f(z) =  valid in the region 1 < |z| < 2, the co-efficient of 1/z2 is
valid in the region 1 < |z| < 2, the co-efficient of 1/z2 is
 valid in the region 1 < |z| < 2, the co-efficient of 1/z2 is
valid in the region 1 < |z| < 2, the co-efficient of 1/z2 isa)
0
b)
1/2
c)
1
d)
-1
|
|
Sanya Agarwal answered |
Concept:
Laurent series of f(z) is given by:
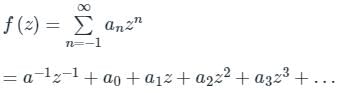
Calculation:
Given:
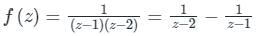
The given region is 1 < |z| < 2
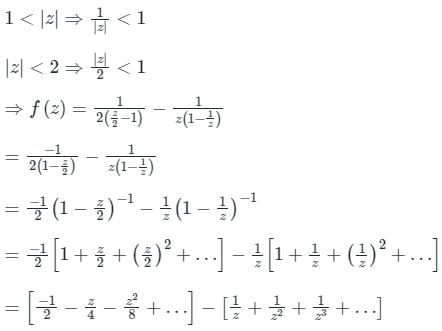
Co-efficient of 1/z2 is -1
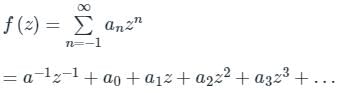
Calculation:
Given:
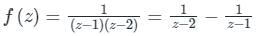
The given region is 1 < |z| < 2
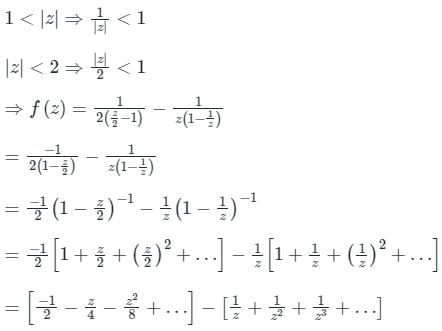
Co-efficient of 1/z2 is -1
Let f (x) = 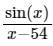 . Then f(100)(54) is given by
. Then f(100)(54) is given by- a)Undefined
- b)100
- c)10
- d)0
Correct answer is option 'A'. Can you explain this answer?
Let f (x) = 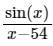 . Then f(100)(54) is given by
. Then f(100)(54) is given by
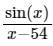 . Then f(100)(54) is given by
. Then f(100)(54) is given bya)
Undefined
b)
100
c)
10
d)
0
|
|
Sanya Agarwal answered |
Concept:
Taylor’s series method:
The Taylor series can be used to calculate the value of an entire function at every point, if the value of the function, and all of its derivatives, are known at a single point.
Taylor's series expansion for f (x + h) is
f(x+h) = f(x) + hf′(x) + h2/2!f″(x) + h3/3! + f‴(x)+…∞
f(x) = f(a) + (x−α)f′(x) +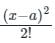 (x) +........∞
(x) +........∞
f(x+h) = f(x) + hf′(x) + h2/2!f″(x) + h3/3! + f‴(x)+…∞
f(x) = f(a) + (x−α)f′(x) +
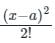 (x) +........∞
(x) +........∞Calculation:
Given:
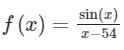
f(100)(54) = ?
Using Taylor series expansion for Sin x at a = 54
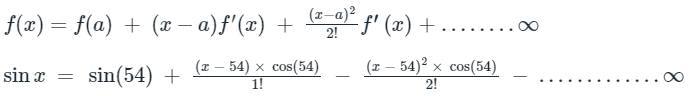
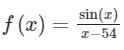
f(100)(54) = ?
Using Taylor series expansion for Sin x at a = 54
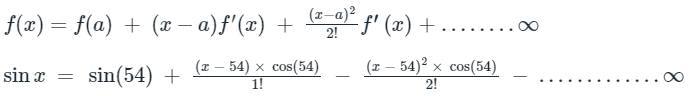
Now the function transforms into:
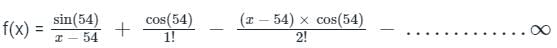
After Observing carefully the first term in the above infinite series, the (x - 54) term is always in the denominator, which will become zero when we put x = 54.
Every derivative will also have the same term till infinite.
So, every term will have zero in its denominator after putting x = 54.
⇒ f(100)(54) is Undefined.
Which of the following is not true?- a)log(1 + z) = z −
 …..about z = 0
…..about z = 0 - b)
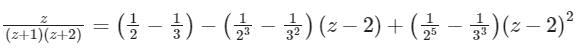 +……about z = 2
+……about z = 2 - c)
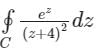 =0 where C is the circle |z-1| = 2
=0 where C is the circle |z-1| = 2 - d)
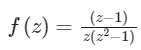 has no singularity
has no singularity
Correct answer is option 'D'. Can you explain this answer?
Which of the following is not true?
a)
log(1 + z) = z − …..about z = 0
…..about z = 0
 …..about z = 0
…..about z = 0b)
 +……about z = 2
+……about z = 2c)
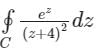 =0 where C is the circle |z-1| = 2
=0 where C is the circle |z-1| = 2d)
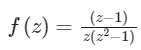 has no singularity
has no singularity|
|
Sanya Agarwal answered |
Concept:
Taylor series expansion
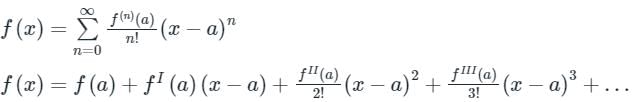
Option 1:
The standard expansion of log(1 + z) is given as
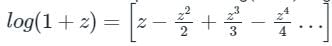
Hence, Option 1 is true
Option 2:
Given complex function is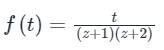
→ Let’s Resolve f(z) into partial fractions
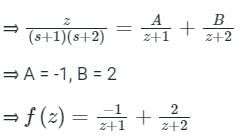
For expanding about z = 2, let z – 2 = t ⇒ z = 2 + t
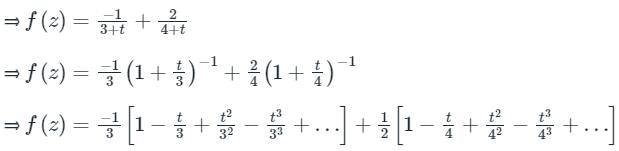
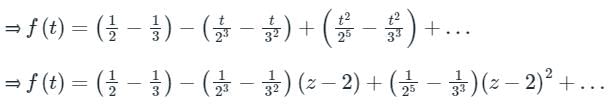
Option 3:
Cauchy’s Integral Formula:
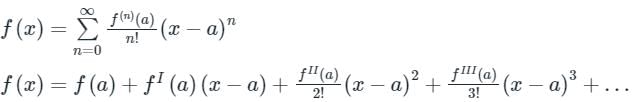
Option 1:
The standard expansion of log(1 + z) is given as
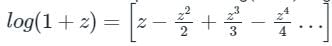
Hence, Option 1 is true
Option 2:
Given complex function is
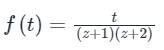
→ Let’s Resolve f(z) into partial fractions
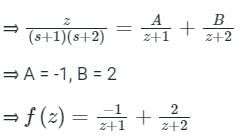
For expanding about z = 2, let z – 2 = t ⇒ z = 2 + t
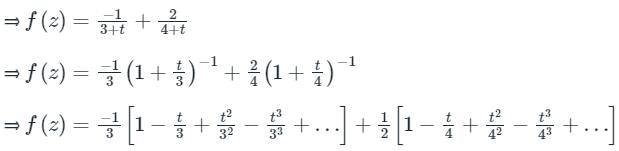
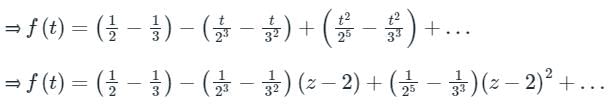
Option 3:
Cauchy’s Integral Formula:
If f(z) is an analytic function within a closed curve and if a is any point within C, then

Residue Theorem:

Residue Theorem:
If f(z) is analytic in a closed curve C except at a finite number of singular points within C, then
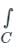 f(z)dz = 2πi × [sum of residues at the singualr points with in C]
f(z)dz = 2πi × [sum of residues at the singualr points with in C]Formula to find residue:
1. If f(z) has a simple pole at z = a, then
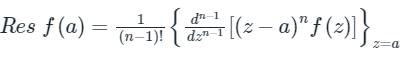
2. If f(z) has a pole of order n at z = a, then
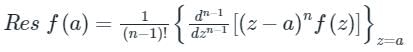
Given complex integral is
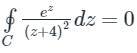 where Cis the circle |z-1| = 2;
where Cis the circle |z-1| = 2;
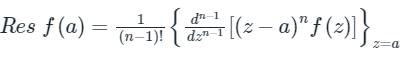
2. If f(z) has a pole of order n at z = a, then
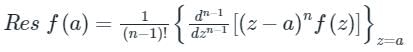
Given complex integral is
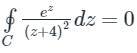 where Cis the circle |z-1| = 2;
where Cis the circle |z-1| = 2;Now for the given complex function, the pole is -4 with order 2;
The pole - 4 lies outside the given circle C;
Therefore, no residue inside the circle, hence integration will be zero.
Option 3 is also correct
Option 4:
The given complex function is f(z) = 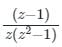
In this function, the singularities are z = 0, +i, -i;
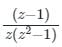
In this function, the singularities are z = 0, +i, -i;
Therefore, the given function has 3 singularities...
Option 4 is incorrect
The value of 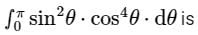
- a)π
- b)2π
- c)π2/32
- d)π/16
Correct answer is option 'D'. Can you explain this answer?
The value of 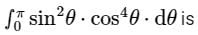
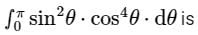
a)
π
b)
2π
c)
π2/32
d)
π/16
|
|
Sanya Agarwal answered |
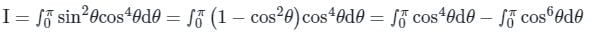
Now it is known that
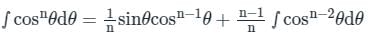
Applying this result to the second term
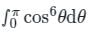 ( n = 6) of the expression of I we get,
( n = 6) of the expression of I we get,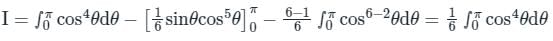
Again, applying this result to the term
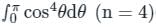 of the expression of I we get,
of the expression of I we get,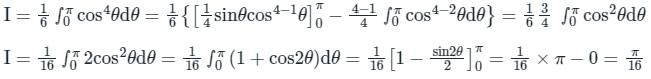
The coefficient of z2 in the expansion of 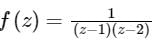 in the region 1 < |z| < 2
in the region 1 < |z| < 2- a)- 1/4
- b)1/4
- c)- 1/8
- d)1/8
Correct answer is option 'C'. Can you explain this answer?
The coefficient of z2 in the expansion of 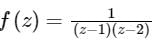 in the region 1 < |z| < 2
in the region 1 < |z| < 2
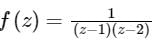 in the region 1 < |z| < 2
in the region 1 < |z| < 2a)
- 1/4
b)
1/4
c)
- 1/8
d)
1/8
|
|
Sanya Agarwal answered |
Concept:
The given region is a ring-shaped region bounded by two concentric circles with center at origin.
The expansion will be Laurent's series.
Calculation:
Given function is 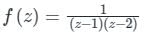
By partial fractions,
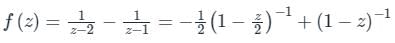
Now using standard expansions,
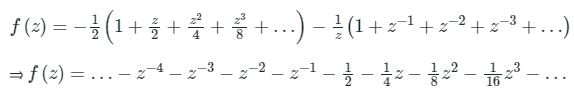
∴ the coefficient of z2 is – 1/8
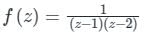
By partial fractions,
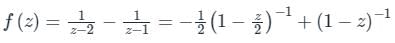
Now using standard expansions,
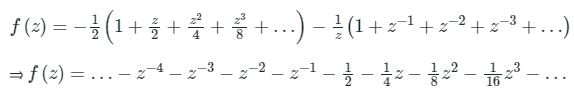
∴ the coefficient of z2 is – 1/8
Let f(Z) = u(x, y) + i(v(x, y)) be an analytical function. If u = 5x + 2xy then v is equal to _________, where c is a constant.- a)x2 + y2 - 5x + c
- b)x2 - y2 - 5xy + c
- c)x2 + y2 + 5xy + c
- d)y2 - x2 + 5y + c
Correct answer is option 'D'. Can you explain this answer?
Let f(Z) = u(x, y) + i(v(x, y)) be an analytical function. If u = 5x + 2xy then v is equal to _________, where c is a constant.
a)
x2 + y2 - 5x + c
b)
x2 - y2 - 5xy + c
c)
x2 + y2 + 5xy + c
d)
y2 - x2 + 5y + c

|
Sreemoyee Deshpande answered |
Understanding the Analytical Function
Given the function f(Z) = u(x, y) + i(v(x, y)), where u = 5x + 2xy, we need to find the corresponding v using the Cauchy-Riemann equations.
Cauchy-Riemann Equations
The Cauchy-Riemann equations state:
1. ∂u/∂x = ∂v/∂y
2. ∂u/∂y = -∂v/∂x
Calculate the Partial Derivatives of u
- ∂u/∂x = ∂(5x + 2xy)/∂x = 5 + 2y
- ∂u/∂y = ∂(5x + 2xy)/∂y = 2x
Apply the Cauchy-Riemann Equations
Using the first Cauchy-Riemann equation:
- ∂v/∂y = 5 + 2y
Using the second Cauchy-Riemann equation:
- -∂v/∂x = 2x → ∂v/∂x = -2x
Integrate to Find v
Now we integrate to find v:
1. Integrate ∂v/∂y with respect to y:
- v = (5y + y^2) + g(x), where g(x) is a function of x.
2. Differentiate the result with respect to x:
- ∂v/∂x = g'(x) → set it equal to -2x.
- g'(x) = -2x → Integrating gives g(x) = -x^2 + C, where C is a constant.
Final Expression for v
Thus, substituting g(x) back into the equation for v:
v = 5y + y^2 - x^2 + C
To match the format of the options provided and rearranging, we have:
v = -x^2 + y^2 + 5y + C
Hence, the correct answer is option 'D': y^2 - x^2 + 5y + c.
Given the function f(Z) = u(x, y) + i(v(x, y)), where u = 5x + 2xy, we need to find the corresponding v using the Cauchy-Riemann equations.
Cauchy-Riemann Equations
The Cauchy-Riemann equations state:
1. ∂u/∂x = ∂v/∂y
2. ∂u/∂y = -∂v/∂x
Calculate the Partial Derivatives of u
- ∂u/∂x = ∂(5x + 2xy)/∂x = 5 + 2y
- ∂u/∂y = ∂(5x + 2xy)/∂y = 2x
Apply the Cauchy-Riemann Equations
Using the first Cauchy-Riemann equation:
- ∂v/∂y = 5 + 2y
Using the second Cauchy-Riemann equation:
- -∂v/∂x = 2x → ∂v/∂x = -2x
Integrate to Find v
Now we integrate to find v:
1. Integrate ∂v/∂y with respect to y:
- v = (5y + y^2) + g(x), where g(x) is a function of x.
2. Differentiate the result with respect to x:
- ∂v/∂x = g'(x) → set it equal to -2x.
- g'(x) = -2x → Integrating gives g(x) = -x^2 + C, where C is a constant.
Final Expression for v
Thus, substituting g(x) back into the equation for v:
v = 5y + y^2 - x^2 + C
To match the format of the options provided and rearranging, we have:
v = -x^2 + y^2 + 5y + C
Hence, the correct answer is option 'D': y^2 - x^2 + 5y + c.
The function f(x, y) satisfies the Laplace equation
∇2f(x,y)=0
on a circular domain of radius r = 1 with its center at point P with coordinates x = 0, y = 0. The value of this function on the circular boundary of this domain is equal to 3.
The numerical value of f(0, 0) is:- a)0
- b)2
- c)3
- d)1
Correct answer is option 'C'. Can you explain this answer?
The function f(x, y) satisfies the Laplace equation
∇2f(x,y)=0
on a circular domain of radius r = 1 with its center at point P with coordinates x = 0, y = 0. The value of this function on the circular boundary of this domain is equal to 3.
The numerical value of f(0, 0) is:
∇2f(x,y)=0
on a circular domain of radius r = 1 with its center at point P with coordinates x = 0, y = 0. The value of this function on the circular boundary of this domain is equal to 3.
The numerical value of f(0, 0) is:
a)
0
b)
2
c)
3
d)
1
|
|
Sanya Agarwal answered |
Given that,
The function f(x, y) satisfies the Laplace equation ∇2f(x,y)=0
on a circular domain of radius r = 1 with its center at point P with coordinates x = 0, y = 0.
The value of this function on the circular boundary of this domain is equal to 3.
Here it is given that the value of the function is 3 for its domain, which signifies that it is a constant function whose value is 3.
So the value of the function at (0, 0) is 3.
Consider the integral
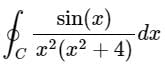
Where C is a counter-clockwise oriented circle defined as |x - i| = 2. The value of the integral is- a)
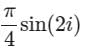
- b)
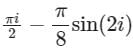
- c)
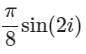
- d)
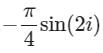
Correct answer is option 'B'. Can you explain this answer?
Consider the integral
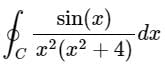
Where C is a counter-clockwise oriented circle defined as |x - i| = 2. The value of the integral is
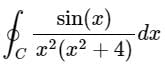
Where C is a counter-clockwise oriented circle defined as |x - i| = 2. The value of the integral is
a)
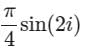
b)
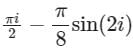
c)
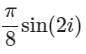
d)
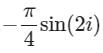
|
|
Sanya Agarwal answered |
Concept:
Residue Theorem:
If f(z) is analytic inside and on a closed curve ‘C’ except at a finite number of singularities inside ‘C’
Residue Theorem:
If f(z) is analytic inside and on a closed curve ‘C’ except at a finite number of singularities inside ‘C’
Then:
∮f(z) dz = 2πi (sum of residues)
Singularity: A point where the function f(z) fails to be analytic
Analysis:
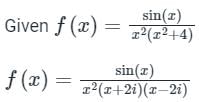
x = 0 pole of order 2
x = 2i, -2i
Given curve or region is |x - i| = 2
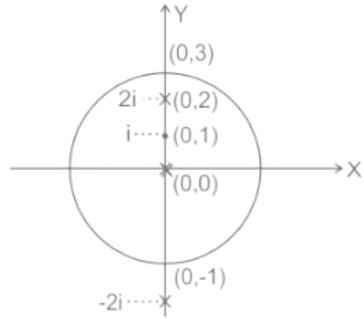
x = -2i lies outside |x - i| = 2
So the singular points are x = 0 & x = 2i
Residue at x = 0
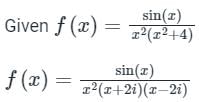
x = 0 pole of order 2
x = 2i, -2i
Given curve or region is |x - i| = 2

x = -2i lies outside |x - i| = 2
So the singular points are x = 0 & x = 2i
Residue at x = 0

Residue at x = 2i
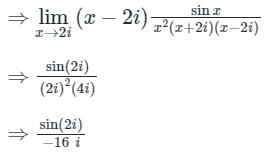
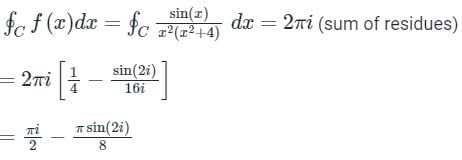
Chapter doubts & questions for Complex variables - Engineering Mathematics for Mechanical Engineering 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Complex variables - Engineering Mathematics for Mechanical Engineering in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Engineering Mathematics for Mechanical Engineering
53 videos|124 docs|63 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily

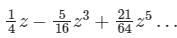
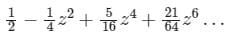
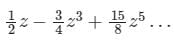
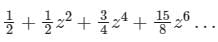
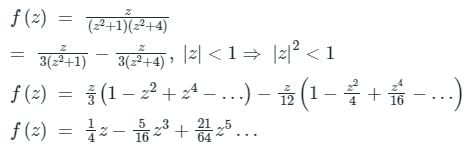
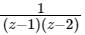 in the region 1 ≤ |z| ≤ 2 and around z = 1 is
in the region 1 ≤ |z| ≤ 2 and around z = 1 is 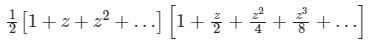
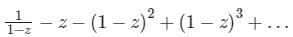
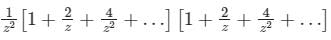
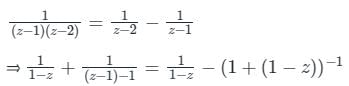
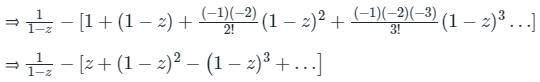
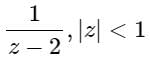 is
is