All Exams >
Mechanical Engineering >
Engineering Mechanics for Mechanical Engineering >
All Questions
All questions of Work & Energy for Mechanical Engineering Exam
For what angle between Force and Displacement will the work done be positive?- a)

- b)
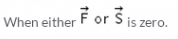
- c)

- d)

Correct answer is option 'C'. Can you explain this answer?
For what angle between Force and Displacement will the work done be positive?
a)
b)
c)
d)
|
|
Om Desai answered |
- If a force acting on a body has a component in the opposite direction of displacement, the work done is negative.
- So when a body slides against a rough horizontal surface, its displacement is opposite to that of the force of friction. The work done by the friction is negative.
Time rate at which work is done by a force is- a)Power
- b)Torque
- c)Centrifugal Force
- d)Acceleration
Correct answer is option 'A'. Can you explain this answer?
Time rate at which work is done by a force is
a)
Power
b)
Torque
c)
Centrifugal Force
d)
Acceleration
|
|
Gaurav Kumar answered |
We know that Work done, W = F.s
where F is force and s is displacement due to that force.
Thus rate of work done is:
where F is force and s is displacement due to that force.
Thus rate of work done is:
dW/dt = d(F.s)/dt
So as F is constant we get,
dW/dt = F.d(s)/dt = F.v = P (Power)
dW/dt = F.d(s)/dt = F.v = P (Power)
There are two bodies X and Y with equal kinetic energy but different masses m and 4m respectively. The ratio of their linear momentum is-- a)1:2
- b)4:1
- c)1:√2
- d)1:4
Correct answer is option 'A'. Can you explain this answer?
There are two bodies X and Y with equal kinetic energy but different masses m and 4m respectively. The ratio of their linear momentum is-
a)
1:2
b)
4:1
c)
1:√2
d)
1:4
|
|
Suresh Iyer answered |
X and Y have equal kinetic energy but their masses are m and 4m respectively.
► 1/2 m1v12 = 1/2 m2v22
► mv12 = 4m * v22
► v1 : v2 = 2 : 1
Hence the ratio of their linear momentum is:
m1v1 : m2v2 = m * 2v : 4m * v = 1 : 2
► 1/2 m1v12 = 1/2 m2v22
► mv12 = 4m * v22
► v1 : v2 = 2 : 1
Hence the ratio of their linear momentum is:
m1v1 : m2v2 = m * 2v : 4m * v = 1 : 2
By how much does kinetic energy increase if the momentum is increased by 20%?- a)55 %
- b)20 %
- c)44 %
- d)60 %
Correct answer is option 'C'. Can you explain this answer?
By how much does kinetic energy increase if the momentum is increased by 20%?
a)
55 %
b)
20 %
c)
44 %
d)
60 %
|
|
Hansa Sharma answered |
The kinetic energy is given by:
KE= p2/2m
So, ΔKE = 2pΔp / 2m = pΔp / m
ΔKE / KE = (pΔp/m) * (2m/p2) = 2Δp / p
Since the momentum p increases by 20%, so the final momentum becomes 1.2p.
Hence, KEfinal = (1.2p)2 / 2m = 1.44p2 / 2m = 1.44KE
So, % change in KE = 44%
ΔKE / KE = (pΔp/m) * (2m/p2) = 2Δp / p
Since the momentum p increases by 20%, so the final momentum becomes 1.2p.
Hence, KEfinal = (1.2p)2 / 2m = 1.44p2 / 2m = 1.44KE
So, % change in KE = 44%
Output of a truck is 4500 J and its efficiency is 50%, the input energy provided to the truck is- a)5000 J
- b)900 J
- c)9000 J
- d)500 J
Correct answer is option 'C'. Can you explain this answer?
Output of a truck is 4500 J and its efficiency is 50%, the input energy provided to the truck is
a)
5000 J
b)
900 J
c)
9000 J
d)
500 J
|
|
Naina Sharma answered |
► η = work output / heat input
► η = 50% = 50/100 = 1/2
► 1/2 = 4500 / Heat input
► Heat input = 9000 J
► η = 50% = 50/100 = 1/2
► 1/2 = 4500 / Heat input
► Heat input = 9000 J
A machine gun fires 60 bullets per minute, with a velocity of 700 m/s. If each bullet has a mass of 50g, find the power developed by the gun.
- a)1225 W
- b)12250 W
- c)122.5 W
- d)122 W
Correct answer is option 'B'. Can you explain this answer?
A machine gun fires 60 bullets per minute, with a velocity of 700 m/s. If each bullet has a mass of 50g, find the power developed by the gun.
a)
1225 W
b)
12250 W
c)
122.5 W
d)
122 W
|
|
Tejas Verma answered |
Each bullet will have KE = 1/2 * 0.05 * 700 * 700 = 12250 J
So for 60 bullets the energy given by machine in 60 second = 60 x 12250 J
Hence power developed = Energy / time =60 x12250/60 =12250W
Or power = 12.250 kW.
So for 60 bullets the energy given by machine in 60 second = 60 x 12250 J
Hence power developed = Energy / time =60 x12250/60 =12250W
Or power = 12.250 kW.
Which of the following is not a unit of energy?- a)newton meter
- b)electron volt
- c)joule/meter
- d)kilowatt hour
Correct answer is option 'C'. Can you explain this answer?
Which of the following is not a unit of energy?
a)
newton meter
b)
electron volt
c)
joule/meter
d)
kilowatt hour

|
Gargey Dudhe answered |
C is correct option because energy The joule ( symbol: J) is a derived unit of energy in the International System of Units. It is equal to the energy transferred to (or work done on) an object when a force of one newton acts on that object in the direction of its motion through a distance of one metre (1 newton metreor N⋅m). pls upvote and follow me.
Which of the following statements is false:- a)kinetic energy is positiv
- b)potential energy is positive
- c)kinetic energy is negative
- d)potential energy is negative
Correct answer is option 'C'. Can you explain this answer?
Which of the following statements is false:
a)
kinetic energy is positiv
b)
potential energy is positive
c)
kinetic energy is negative
d)
potential energy is negative

|
Aiims answered |
K.E never negative as velocity negative then its square becomes it positive.
If a force acts perpendicular to the direction of motion of a body, what is the amount of work done?- a)Infinity
- b)Constant
- c)Zero
- d)sinθ
Correct answer is option 'C'. Can you explain this answer?
If a force acts perpendicular to the direction of motion of a body, what is the amount of work done?
a)
Infinity
b)
Constant
c)
Zero
d)
sinθ
|
|
Anjali Sharma answered |
If a force acts perpendicular to the direction of a body, the amount of work done is zero because there is no displacement in the direction of a force.
Which of the following needs to zero for the perfect equilibrium for the calculation of the work?- a)∑F=0, ∑M=0 and ∑θ = 0
- b)∑F=0, ∑M≠0 and ∑θ = 0
- c)∑F≠0, ∑M=0 and ∑θ = 0
- d)∑F=0, ∑M=0 and ∑θ≠0
Correct answer is option 'D'. Can you explain this answer?
Which of the following needs to zero for the perfect equilibrium for the calculation of the work?
a)
∑F=0, ∑M=0 and ∑θ = 0
b)
∑F=0, ∑M≠0 and ∑θ = 0
c)
∑F≠0, ∑M=0 and ∑θ = 0
d)
∑F=0, ∑M=0 and ∑θ≠0
|
|
Bhargavi Chauhan answered |
The summation of the forces needs to be zero. So does the summation of the moments need to zero. But talking about the angles, they not needed to zero. But the forces which are acting at particular angles, must needed to be equal to zero. The basic need of the forces to make the body in equilibrium.
∑Fx=0, ∑Fy=0 and ∑Fz=0 are vector equations for the three dimensions. They are satisfied when the body is achieved it state of equilibrium and the net work done is zero.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
∑Fx=0, ∑Fy=0 and ∑Fz=0 are vector equations for the three dimensions. They are satisfied when the body is achieved it state of equilibrium and the net work done is zero.
a)
True
b)
False
|
|
Divya Banerjee answered |
The answer is false as the equations asked are scalars. As we make the net sum of the forces along the axis equal to zero. Of course this equation comes from the solving the vector forms, but still the result is a scalar, hence the equations are scalar.
The supports in the 3D are having more than three reaction forces. Because they are having three axis on which the components of the work needs to be zero.- a)The first part of the statement is false and other part is true
- b)The first part of the statement is false and other part is false too
- c)The first part of the statement is true and other part is false
- d)The first part of the statement is true and other part is true too
Correct answer is option 'D'. Can you explain this answer?
The supports in the 3D are having more than three reaction forces. Because they are having three axis on which the components of the work needs to be zero.
a)
The first part of the statement is false and other part is true
b)
The first part of the statement is false and other part is false too
c)
The first part of the statement is true and other part is false
d)
The first part of the statement is true and other part is true too
|
|
Sagnik Choudhary answered |
Explanation:
Statement Analysis:
The statement claims that supports in 3D have more than three reaction forces because they have three axes on which the components of the work need to be zero.
Supports in 3D:
In 3D structures, supports can have up to six reaction forces. These forces can be categorized into three translational forces (forces acting along the x, y, and z axes) and three rotational forces (moments or torques acting about the x, y, and z axes).
Components of Work:
The statement mentions that the components of the work need to be zero on three axes. This is incorrect. The components of the work are not associated with the reaction forces on the supports. The work done by a force is given by the dot product of the force and the displacement. The components of the work depend on the direction of the force and the direction of the displacement, not the reaction forces on the supports.
Correct Answer:
The correct answer is option 'D' - The first part of the statement is true and the other part is also true.
Explanation:
The first part of the statement is true because supports in 3D can have more than three reaction forces. As mentioned earlier, supports in 3D structures can have up to six reaction forces - three translational forces and three rotational forces.
The second part of the statement is also true because the components of the work are not related to the reaction forces on the supports. The work done by a force depends on the force's direction and the displacement's direction, not the reaction forces on the supports.
To summarize, supports in 3D can have more than three reaction forces, and the components of the work are not associated with the reaction forces on the supports.
Statement Analysis:
The statement claims that supports in 3D have more than three reaction forces because they have three axes on which the components of the work need to be zero.
Supports in 3D:
In 3D structures, supports can have up to six reaction forces. These forces can be categorized into three translational forces (forces acting along the x, y, and z axes) and three rotational forces (moments or torques acting about the x, y, and z axes).
Components of Work:
The statement mentions that the components of the work need to be zero on three axes. This is incorrect. The components of the work are not associated with the reaction forces on the supports. The work done by a force is given by the dot product of the force and the displacement. The components of the work depend on the direction of the force and the direction of the displacement, not the reaction forces on the supports.
Correct Answer:
The correct answer is option 'D' - The first part of the statement is true and the other part is also true.
Explanation:
The first part of the statement is true because supports in 3D can have more than three reaction forces. As mentioned earlier, supports in 3D structures can have up to six reaction forces - three translational forces and three rotational forces.
The second part of the statement is also true because the components of the work are not related to the reaction forces on the supports. The work done by a force depends on the force's direction and the displacement's direction, not the reaction forces on the supports.
To summarize, supports in 3D can have more than three reaction forces, and the components of the work are not associated with the reaction forces on the supports.
Work done is best given by _____________- a)dU = F.dr
- b)dU = Fdrsinθ
- c)dU = F.drcotθ
- d)dU = Fxdrdθ
Correct answer is option 'A'. Can you explain this answer?
Work done is best given by _____________
a)
dU = F.dr
b)
dU = Fdrsinθ
c)
dU = F.drcotθ
d)
dU = Fxdrdθ
|
|
Keerthana Joshi answered |
The work is defined as the dot product of the force and the distance. This means that the work done does depends upon the angle of the force. That is the angle which is being made by the force vector to the surface of action of the force.
Which statement is right for conservative force vector F = Ai + Bj + Ck?- a)In rectangular components representation of any vector we have vector F = Ai + Bj + Ck
- b)In rectangular components representation of any vector we have vector F = Ax + By + Cz
- c)In rectangular components representation of any vector we have vector F = Fx + Fy + Fz
- d)In rectangular components representation of any vector we have vector F = Fi + Fj + Fk
Correct answer is option 'C'. Can you explain this answer?
Which statement is right for conservative force vector F = Ai + Bj + Ck?
a)
In rectangular components representation of any vector we have vector F = Ai + Bj + Ck
b)
In rectangular components representation of any vector we have vector F = Ax + By + Cz
c)
In rectangular components representation of any vector we have vector F = Fx + Fy + Fz
d)
In rectangular components representation of any vector we have vector F = Fi + Fj + Fk
|
|
Gaurav Kapoor answered |
As given the vector is F = Ai + Bj + Ck, this implies that the x ,y and z-axis components of this vector is A, B and C respectively. But, in rectangular components representation of any vector, the vector is written as F = Fx + Fy + Fz.
What is the sum of squares of the cosine angles made by the conservative force vector with the coordinate axis?- a)1
- b)½
- c)2
- d)3
Correct answer is option 'A'. Can you explain this answer?
What is the sum of squares of the cosine angles made by the conservative force vector with the coordinate axis?
a)
1
b)
½
c)
2
d)
3
|
|
Mahi Kaur answered |
The sum of the squares of the cosines of the vector will give you the squares of the components in the numerator, and the vector’s magnitude’s square in the denominator. But the numerator sum is equal to the vector’s magnitude’s square. Thus, the answer = 1.
Principle of virtual work done is having condition___________- a)δU = 0
- b)δU = δF
- c)δU = δM
- d)δU = δD
Correct answer is option 'A'. Can you explain this answer?
Principle of virtual work done is having condition___________
a)
δU = 0
b)
δU = δF
c)
δU = δM
d)
δU = δD
|
|
Aditya Chavan answered |
The virtual work done is working on the equation: δU = 0. This means that the body must be in the equilibrium and the net work done must be zero. Thus the unknown forces are being determined by the same technique.
Find the potential energy stored in a ball of mass 5 kg placed at a height of 3 m above the ground.- a)121.20 J
- b)227.31 J
- c)147.15 J
- d)182.21 J
Correct answer is option 'C'. Can you explain this answer?
Find the potential energy stored in a ball of mass 5 kg placed at a height of 3 m above the ground.
a)
121.20 J
b)
227.31 J
c)
147.15 J
d)
182.21 J
|
|
Aarya Das answered |
To find the potential energy stored in the ball, we can use the formula:
Potential Energy = mass * gravity * height
Given:
mass = 5 kg
height = 3 m
gravity = 9.8 m/s^2 (acceleration due to gravity)
Substituting the given values into the formula, we get:
Potential Energy = 5 kg * 9.8 m/s^2 * 3 m
Calculating the expression, we have:
Potential Energy = 147 J
Therefore, the potential energy stored in the ball is 147 J.
Hence, the correct answer is option C) 147.15 J.
Potential Energy = mass * gravity * height
Given:
mass = 5 kg
height = 3 m
gravity = 9.8 m/s^2 (acceleration due to gravity)
Substituting the given values into the formula, we get:
Potential Energy = 5 kg * 9.8 m/s^2 * 3 m
Calculating the expression, we have:
Potential Energy = 147 J
Therefore, the potential energy stored in the ball is 147 J.
Hence, the correct answer is option C) 147.15 J.
The conservative frictional force always acts ____________ to the surface of the application of the friction.- a)Tangential
- b)Perpendicular
- c)Parallel
- d)Normal
Correct answer is option 'A'. Can you explain this answer?
The conservative frictional force always acts ____________ to the surface of the application of the friction.
a)
Tangential
b)
Perpendicular
c)
Parallel
d)
Normal
|
|
Sagarika Mukherjee answered |
The friction is the phenomena that defines that there is a resistance which is present there between the two surfaces. This friction is applied tangentially to the surfaces in contact. Thus the main thing is that the forces on both of the surfaces act tangential to each other.
For equilibrium the net moment acting on the body by various conservative forces is zero.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
For equilibrium the net moment acting on the body by various conservative forces is zero.
a)
True
b)
False
|
|
Dhruv Dasgupta answered |
The equilibrium is only attained if the net moment on the body tends to be equal to zero. Thus the moments caused by different forces cancels out. If this happens there is no motion of the body along any direction and hence the body is said to be in equilibrium. The body here is a rigid body.
At time t = 0 s particle starts moving along the x-axis. If its kinetic energy increases uniformly with time ‘t’, the net force acting on it must be proportional to- a) √t
- b) 1/√t
- c)constant
- d)t
Correct answer is option 'B'. Can you explain this answer?
At time t = 0 s particle starts moving along the x-axis. If its kinetic energy increases uniformly with time ‘t’, the net force acting on it must be proportional to
a)
√t
b)
1/√t
c)
constant
d)
t
|
|
Sinjini Choudhury answered |
, then its acceleration is also constant. We can use the following kinematic equation to relate the acceleration, time, initial velocity, and displacement:
x = x0 + v0*t + (1/2)*a*t^2
where x is the displacement, x0 is the initial position (assumed to be zero), v0 is the initial velocity, t is the time, and a is the acceleration.
Since the kinetic energy increases uniformly with time, we can assume that the acceleration is also constant. Let's call this acceleration a. Then, the velocity at time t is:
v(t) = v0 + a*t
The kinetic energy is given by:
KE = (1/2)*m*v^2
where m is the mass of the particle.
Since the kinetic energy increases uniformly with time, we can write:
dKE/dt = constant
Taking the derivative with respect to time, we get:
dKE/dt = m*v*(dv/dt)
Substituting v(t) and dv/dt = a, we get:
dKE/dt = m*(v0 + a*t)*a
Since dKE/dt is constant, we can write:
dKE/dt = m*a*(v0 + a*t) = constant
Solving for a, we get:
a = constant/dt
where dt is a small time interval.
Now, we can use the kinematic equation to find the displacement x at time t:
x = (1/2)*a*t^2 + v0*t
Substituting a = constant/dt and v0 = 0, we get:
x = (1/2)*(constant/dt)*t^2
Simplifying, we get:
x = (constant/2)*t
Therefore, the particle moves with a constant velocity given by:
v = dx/dt = constant/2
This means that the velocity increases linearly with time, and the displacement increases quadratically with time.
x = x0 + v0*t + (1/2)*a*t^2
where x is the displacement, x0 is the initial position (assumed to be zero), v0 is the initial velocity, t is the time, and a is the acceleration.
Since the kinetic energy increases uniformly with time, we can assume that the acceleration is also constant. Let's call this acceleration a. Then, the velocity at time t is:
v(t) = v0 + a*t
The kinetic energy is given by:
KE = (1/2)*m*v^2
where m is the mass of the particle.
Since the kinetic energy increases uniformly with time, we can write:
dKE/dt = constant
Taking the derivative with respect to time, we get:
dKE/dt = m*v*(dv/dt)
Substituting v(t) and dv/dt = a, we get:
dKE/dt = m*(v0 + a*t)*a
Since dKE/dt is constant, we can write:
dKE/dt = m*a*(v0 + a*t) = constant
Solving for a, we get:
a = constant/dt
where dt is a small time interval.
Now, we can use the kinematic equation to find the displacement x at time t:
x = (1/2)*a*t^2 + v0*t
Substituting a = constant/dt and v0 = 0, we get:
x = (1/2)*(constant/dt)*t^2
Simplifying, we get:
x = (constant/2)*t
Therefore, the particle moves with a constant velocity given by:
v = dx/dt = constant/2
This means that the velocity increases linearly with time, and the displacement increases quadratically with time.
What does the Newton’s third law states for the conservative forces?- a)The rate of change of momentum is equal to the force applied
- b)For every reaction there is an opposite reaction
- c)The body is tend to be rotated if the force is applied tangentially
- d)The body is rest until a force is applied
Correct answer is option 'B'. Can you explain this answer?
What does the Newton’s third law states for the conservative forces?
a)
The rate of change of momentum is equal to the force applied
b)
For every reaction there is an opposite reaction
c)
The body is tend to be rotated if the force is applied tangentially
d)
The body is rest until a force is applied
|
|
Ashutosh Sharma answered |
The requirement of the third law is important in the equilibrium of the body. Specially the rigid bodies. The rigid body particles are in the equilibrium and are thus facing the forces and to be in the equilibrium they also react and apply the opposite force and thus the third law of newton.It is same for all the methods.
The principle of work was proposed by________________- a)Mathematician Jean Bernoulli
- b)Physios Jean Bernoulli
- c)Chemist Jean Bernoulli
- d)John Jean Bernoulli
Correct answer is option 'A'. Can you explain this answer?
The principle of work was proposed by________________
a)
Mathematician Jean Bernoulli
b)
Physios Jean Bernoulli
c)
Chemist Jean Bernoulli
d)
John Jean Bernoulli
|
|
Rashi Chauhan answered |
The concept of work was proposed by Jean Bernoulli. He was a mathematician. It was proposed in 18th century. It gave us various alternative methods to calculate the work done. Thus the answer.
Which of the following is an example of zero work?- a)The work done by the tension in the string, when a body tied with the string move along a circular path
- b)When a person holds some amount of load but, does not move from his position.
- c)The work done by a coolie when he travels on a horizontal platform, with a load on his head.
- d)When a horse pulls a cart on a level road.
Correct answer is option 'B'. Can you explain this answer?
Which of the following is an example of zero work?
a)
The work done by the tension in the string, when a body tied with the string move along a circular path
b)
When a person holds some amount of load but, does not move from his position.
c)
The work done by a coolie when he travels on a horizontal platform, with a load on his head.
d)
When a horse pulls a cart on a level road.
|
|
Megha Desai answered |
Work done, W = Force x Δdisplacement
So, when a person holds some amount of load but does not move from his position, the displacement is 0. Hence, W done = 0.
Work done by the couple is best given by___________- a)dU = Mdθ
- b)dU = M.dθ
- c)dU = Mxdθ
- d)dU = Mθ
Correct answer is option 'A'. Can you explain this answer?
Work done by the couple is best given by___________
a)
dU = Mdθ
b)
dU = M.dθ
c)
dU = Mxdθ
d)
dU = Mθ
|
|
Bhargavi Chauhan answered |
The work done by the couple is defined as the product of the moment and the del angle. This means that the work done does depends upon the angle of the moment. That is the angle which is being made by the moment vector to the surface of action of the moment.
____________ is the phenomena that resist the movement of the two surfaces in contact. This phenomena is also having its scope in the work and the conservative nature of the force.- a)Friction
- b)Motion
- c)Circular movement
- d)Rotation
Correct answer is option 'A'. Can you explain this answer?
____________ is the phenomena that resist the movement of the two surfaces in contact. This phenomena is also having its scope in the work and the conservative nature of the force.
a)
Friction
b)
Motion
c)
Circular movement
d)
Rotation
|
|
Ayush Chawla answered |
The friction is the phenomena that defines that there is a resistance which is present there between the two surfaces. The two surfaces are in contact and the friction applies at that surface only, resisting the motion of the surface.
For the conditions of the equilibrium of the body, i.e. the rigid body only the external conservative forces defines the equilibrium. Because the internal conservative forces cancels out so not to be considered.- a)The first part of the statement is false and other part is true
- b)The first part of the statement is false and other part is false too
- c)The first part of the statement is true and other part is false
- d)The first part of the statement is true and other part is true too
Correct answer is option 'C'. Can you explain this answer?
For the conditions of the equilibrium of the body, i.e. the rigid body only the external conservative forces defines the equilibrium. Because the internal conservative forces cancels out so not to be considered.
a)
The first part of the statement is false and other part is true
b)
The first part of the statement is false and other part is false too
c)
The first part of the statement is true and other part is false
d)
The first part of the statement is true and other part is true too
|
|
Nitin Joshi answered |
The application of the internal forces does affect the conditions of the equilibrium of the body. Not only the external but the internal forces that are developed by the sake of external forces does develop a tending effect on the equilibrium of the body. Thus the internal forces doesn’t cancels out.
If solving the question in 3D calculations is difficult, then use the 2D system and then equate the total work done to zero.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
If solving the question in 3D calculations is difficult, then use the 2D system and then equate the total work done to zero.
a)
True
b)
False
|
|
Isha Nambiar answered |
The answer is obviously yes. If we are having any difficulty in making the vector components, then we can go in 2D. As if the particle is in equilibrium, the net force will be zero. No matter where you see first. Net work done is zero.
In the explanation of the theory of friction over which conservative forces were acted upon, the block used have an assumption. That is the upper portion of the block is considered to be rigid.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
In the explanation of the theory of friction over which conservative forces were acted upon, the block used have an assumption. That is the upper portion of the block is considered to be rigid.
a)
True
b)
False
|
|
Nitin Joshi answered |
The block used to explain the theory of friction is placed on a deformable surface. As we know that the theory of friction says that when there is no lubricating fluid present between the surfaces in contact, the dry friction occurs. Thus to show the same, experiments are done over a non-rigid/deformable surface which is having a rigid shape.
What is not the condition for the equilibrium in three dimensional system of axis so as to calculate the unknown forces acting on the body?- a)∑Fx=0
- b)∑Fy=0
- c)∑Fz=0
- d)∑F≠0
Correct answer is option 'D'. Can you explain this answer?
What is not the condition for the equilibrium in three dimensional system of axis so as to calculate the unknown forces acting on the body?
a)
∑Fx=0
b)
∑Fy=0
c)
∑Fz=0
d)
∑F≠0
|
|
Stuti Bajaj answered |
For the equilibrium in the three dimensional system of axis we have all the conditions true as, ∑Fx=0, ∑Fy=0 and ∑Fz=0. Also we have the summation of the forces equal to zero. Which is not a non-zero value.
We use sometimes the measures to know the direction of moment in the calculations of the moments caused by the conservative forces. Which one is right about it(consider the mentioned axis to be positive)?- a)Thumb is z-axis, fingers curled from x-axis to y-axis
- b)Thumb is x-axis, fingers curled from z-axis to y-axis
- c)Thumb is y-axis, fingers curled from x-axis to z-axis
- d)Thumb is z-axis, fingers curled from y-axis to x-axis
Correct answer is option 'A'. Can you explain this answer?
We use sometimes the measures to know the direction of moment in the calculations of the moments caused by the conservative forces. Which one is right about it(consider the mentioned axis to be positive)?
a)
Thumb is z-axis, fingers curled from x-axis to y-axis
b)
Thumb is x-axis, fingers curled from z-axis to y-axis
c)
Thumb is y-axis, fingers curled from x-axis to z-axis
d)
Thumb is z-axis, fingers curled from y-axis to x-axis
|
|
Pritam Das answered |
As right handed coordinate system means that you are curling your fingers from positive x-axis towards y-axis and the thumb which is projected is pointed to the positive z-axis. Thus visualizing the same and knowing the basic members of axis will not create much problem.
Determine the horizontal force acting in the given figure.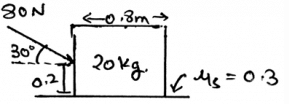
- a)80cos30
- b)60cos30
- c)40cos30
- d)8cos30
Correct answer is option 'A'. Can you explain this answer?
Determine the horizontal force acting in the given figure.
a)
80cos30
b)
60cos30
c)
40cos30
d)
8cos30

|
Janhavi Datta answered |
The net forces acting on the body is shown by the help of the resultant forces. There are two types, first the frictional and the second is the normal. This is because the resultant forces have the sum of all the forces which are acting on the direction which is same.
Find the tension in the cable AC.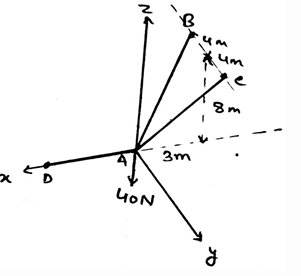
- a)23.6N
- b)55N
- c)89N
- d)-29N
Correct answer is option 'A'. Can you explain this answer?
Find the tension in the cable AC.
a)
23.6N
b)
55N
c)
89N
d)
-29N
|
|
Shruti Bose answered |
First represent the forces in their vector form. Then equate the net sum of the forces in the x, y and z directions to be zero. You will get FB = FC and 2(.848) = 40N. This gives the answer as 23.6N.
What does the Newton’s third law states for the work done?- a)The rate of change of momentum is equal to the force applied
- b)For every reaction there is an opposite reaction
- c)The body is tend to be rotated if the force is applied tangentially
- d)The body is rest until a force is applied
Correct answer is option 'B'. Can you explain this answer?
What does the Newton’s third law states for the work done?
a)
The rate of change of momentum is equal to the force applied
b)
For every reaction there is an opposite reaction
c)
The body is tend to be rotated if the force is applied tangentially
d)
The body is rest until a force is applied
|
|
Gayatri Dasgupta answered |
The requirement of the third law is important in the equilibrium of the body. Specially the rigid bodies. The rigid body particles are in the equilibrium and are thus facing the forces and to be in the equilibrium they also react and apply the opposite force and thus the third law of newton.
Virtual Work done is best given by_______________- a)δU = Fδrcosθ
- b)δU = Fδrsinθ
- c)δU = Fδrcotθ
- d)δU = Fδrδθ
Correct answer is option 'A'. Can you explain this answer?
Virtual Work done is best given by_______________
a)
δU = Fδrcosθ
b)
δU = Fδrsinθ
c)
δU = Fδrcotθ
d)
δU = Fδrδθ
|
|
Kiran Basu answered |
The work is defined as the dot product of the δ force and the δ distance. This means that the work done does depends upon the angle of the force. That is the angle which is being made by the force vector to the surface of action of the force.
If a block moves from a height h above the ground then the work done is given by_______- a)
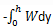
- b)
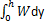
- c)
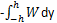
- d)
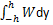
Correct answer is option 'A'. Can you explain this answer?
If a block moves from a height h above the ground then the work done is given by_______
a)
b)
c)
d)

|
Sahil Chawla answered |
The potential energy is converted into the work done. Thus is the block moves from the height h to the ground, the work done is given by
Negative because the work done is in the opposite direction of the motion of the body.
Determine the vertical force acting in the given figure.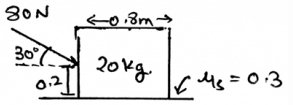
- a)236N
- b)600n
- c)403N
- d)830N
Correct answer is option 'A'. Can you explain this answer?
Determine the vertical force acting in the given figure.
a)
236N
b)
600n
c)
403N
d)
830N
|
|
Ashish Pillai answered |
The net forces acting on the body is shown by the help of the resultant forces. There are two types, first the frictional and the second is the normal. This is because the resultant forces have the sum of all the forces which are acting on the direction which is same.
The net moment of the body is zero that means the work done by the force and the rotational axis is zero.- a)The first part of the statement is false and other part is true
- b)The first part of the statement is false and other part is false too
- c)The first part of the statement is true and other part is false
- d)The first part of the statement is true and other part is true too
Correct answer is option 'B'. Can you explain this answer?
The net moment of the body is zero that means the work done by the force and the rotational axis is zero.
a)
The first part of the statement is false and other part is true
b)
The first part of the statement is false and other part is false too
c)
The first part of the statement is true and other part is false
d)
The first part of the statement is true and other part is true too
|
|
Athul Kumar answered |
The net moment of the body is zero that doesn’t means that the work done by the force and the rotational axis is zero. Work done is something different. It does not depend on the rotational axis. It only depends on the distance. And the forces.
We first make equilibrium equations of the body by considering all the three dimensional forces and then the free body diagram is made and solved.- a)The first part of the statement is false and other part is true
- b)The first part of the statement is false and other part is false too
- c)The first part of the statement is true and other part is false
- d)The first part of the statement is true and other part is true too
Correct answer is option 'D'. Can you explain this answer?
We first make equilibrium equations of the body by considering all the three dimensional forces and then the free body diagram is made and solved.
a)
The first part of the statement is false and other part is true
b)
The first part of the statement is false and other part is false too
c)
The first part of the statement is true and other part is false
d)
The first part of the statement is true and other part is true too
|
|
Athul Kumar answered |
We first make the free body diagram and then we make the equilibrium equations to satisfy the given conditions. This helps us to solve the question easily. As this reduces the part of imagination and increases accuracy too.
If five forces are acting on the single particle and having an angle of 72˚ between each and are collinear, then_____________- a)The net force acting on the body is zero and the net work done is also zero
- b)The net force acting on the body is horizontal
- c)The net force acting on the body is vertical but net work done is non-zero
- d)The net force acting on the body is at an angle of 45
Correct answer is option 'A'. Can you explain this answer?
If five forces are acting on the single particle and having an angle of 72˚ between each and are collinear, then_____________
a)
The net force acting on the body is zero and the net work done is also zero
b)
The net force acting on the body is horizontal
c)
The net force acting on the body is vertical but net work done is non-zero
d)
The net force acting on the body is at an angle of 45
|
|
Kiran Basu answered |
The net force acting on the body is zero. This means that the forces cancel out. This means that the body is in equilibrium and doesn’t need any of the external force to make itself in the equilibrium.
Ram and sham together can complete a vocation in 8 days. Ram can do likewise work all alone in 12 days. To what extent will sham take to carry out the occupation without anyone else's input?- a)16 days
- b)24 days
- c)20 days
- d)30 days
Correct answer is option 'B'. Can you explain this answer?
Ram and sham together can complete a vocation in 8 days. Ram can do likewise work all alone in 12 days. To what extent will sham take to carry out the occupation without anyone else's input?
a)
16 days
b)
24 days
c)
20 days
d)
30 days
|
|
Rajesh Gupta answered |
(Ram + sham)'s 1 day work = 1 / 8,
Ram 1 day work = 1 / 12
Sham 1 day work = (1 / 8 - 1 / 12) = 1 / 24
∴ Sham alone can finish the work in 24 days.
Ram 1 day work = 1 / 12
Sham 1 day work = (1 / 8 - 1 / 12) = 1 / 24
∴ Sham alone can finish the work in 24 days.
Work done by a spring to a body from moving it from x1 to x2 distance is given by _________- a)
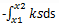
- b)
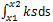
- c)
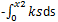
- d)
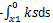
Correct answer is option 'A'. Can you explain this answer?
Work done by a spring to a body from moving it from x1 to x2 distance is given by _________
a)
b)
c)
d)
|
|
Sagarika Mukherjee answered |
The potential energy is converted into the work done. Thus is the block moves from the distance x2 to x1, the work done is given by
. Negative because the work done is in the opposite direction of the motion of the body.
If the body is in equilibrium, but it having a rotational curled ray shown in the free body diagram then:- a)The diagram is wrong
- b)Such rotations can’t be shown in the fbds(free body diagrams)
- c)The ray shown may be correct, but the body is not said to be in equilibrium
- d)The body is said to be in equilibrium only, as the other forces will cancel out that rotation and the net work done will be zero
Correct answer is option 'D'. Can you explain this answer?
If the body is in equilibrium, but it having a rotational curled ray shown in the free body diagram then:
a)
The diagram is wrong
b)
Such rotations can’t be shown in the fbds(free body diagrams)
c)
The ray shown may be correct, but the body is not said to be in equilibrium
d)
The body is said to be in equilibrium only, as the other forces will cancel out that rotation and the net work done will be zero
|
|
Debolina Menon answered |
The body having equilibrium will not rotate at any cost. Yes, the diagram may contain the rotational array showing the couple being acted over the structure. But the thing is that the forces, i.e. the other forces which are outside the dependency of this rotation will cancel out this rotation and thus the body is in equilibrium.
Which statement is correct about the vector F in the showing the conservative nature of the forces?- a)F= Fcos β + Fcos α + Fcosγ
- b)F= Fsin β + Fcos α + Fcosγ
- c)F= Fcos β + Fsin α + Fcosγ
- d)F= Fcos β + Fcos α + Fsinγ
Correct answer is option 'A'. Can you explain this answer?
Which statement is correct about the vector F in the showing the conservative nature of the forces?
a)
F= Fcos β + Fcos α + Fcosγ
b)
F= Fsin β + Fcos α + Fcosγ
c)
F= Fcos β + Fsin α + Fcosγ
d)
F= Fcos β + Fcos α + Fsinγ
|
|
Gaurav Kapoor answered |
As we know the α, β and γ are the angles made by the x, y and z-axis respectively. Thus, is the magnitude of the vector is F, the F= Fcos β + Fcos α + Fcosγ. Which means the force is the resultant of all its axis’ components.
Determine the horizontal components of the reaction on the beam caused by the pin at Q. The force 60N is multiplied by 10 and then is applied.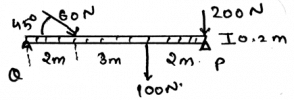
- a)0N
- b)445N
- c)45N
- d)40N
Correct answer is option 'A'. Can you explain this answer?
Determine the horizontal components of the reaction on the beam caused by the pin at Q. The force 60N is multiplied by 10 and then is applied.
a)
0N
b)
445N
c)
45N
d)
40N
|
|
Shruti Bose answered |
The summation of the forces needs to be zero. So does the summation of the moments need to zero. But talking about the angles, they not needed to zero. But the forces which are acting at particular angles, must needed to.
Which of the following is correct?- a)Work done is of one type only
- b)Work done is of two type only
- c)Work done is of three type only
- d)Work done is of infinite type
Correct answer is option 'D'. Can you explain this answer?
Which of the following is correct?
a)
Work done is of one type only
b)
Work done is of two type only
c)
Work done is of three type only
d)
Work done is of infinite type
|
|
Sanskriti Chakraborty answered |
The work done is of many types. They are countless. For example the work can be done by moving, pushing or pulling. Or can be done by car, bus, truck or any other vehicle. Thus work can be done in many ways.
Virtual work done by the couple is best given by_____________- a)δU = Mδθ
- b)δU = M.δθ
- c)δU = Mxδθ
- d)δU = Mθ
Correct answer is option 'A'. Can you explain this answer?
Virtual work done by the couple is best given by_____________
a)
δU = Mδθ
b)
δU = M.δθ
c)
δU = Mxδθ
d)
δU = Mθ
|
|
Akshat Mehta answered |
The work done by the couple is defined as the product of the δ moment and the δ angle. This means that the work done does depends upon the angle of the moment. That is the angle which is being made by the moment vector to the surface of action of the moment.
We first make equilibrium equations of the body by considering all the three dimensional forces and then the free body diagram is made and solved.- a)The first part of the statement is false and other part is true
- b)The first part of the statement is false and other part is false too
- c)The first part of the statement is true and other part is false
- d)The first part of the statement is true and other part is true too
Correct answer is option 'D'. Can you explain this answer?
We first make equilibrium equations of the body by considering all the three dimensional forces and then the free body diagram is made and solved.
a)
The first part of the statement is false and other part is true
b)
The first part of the statement is false and other part is false too
c)
The first part of the statement is true and other part is false
d)
The first part of the statement is true and other part is true too
|
|
Hrishikesh Chakraborty answered |
We first make the free body diagram and then we make the equilibrium equations to satisfy the given conditions. This helps us to solve the question easily. As this reduces the part of imagination and increases accuracy too.
Calculate the Normal force developed between the body and the surface due to the work done by the force.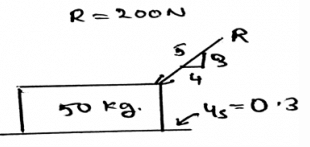
- a)611N
- b)116N
- c)100N
- d)180N
Correct answer is option 'A'. Can you explain this answer?
Calculate the Normal force developed between the body and the surface due to the work done by the force.
a)
611N
b)
116N
c)
100N
d)
180N

|
Anisha Chakraborty answered |
The net forces acting on the body is shown by the help of the resultant forces. There are two types, first the frictional and the second is the normal. This is because the resultant forces have the sum of all the forces which are acting on the direction which is same.
Chapter doubts & questions for Work & Energy - Engineering Mechanics for Mechanical Engineering 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Work & Energy - Engineering Mechanics for Mechanical Engineering in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Engineering Mechanics for Mechanical Engineering
33 videos|78 docs|44 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily










