All Exams >
Mechanical Engineering >
Engineering Mechanics for Mechanical Engineering >
All Questions
All questions of Moment of Inertia (MOI) for Mechanical Engineering Exam
What is the mass MOI of a rectangular plate about y-axis passing through the C.G of the plate if the y-axis is parallel to d and perpendicular to b?- a)Mb2/12
- b)Md2/12
- c)Md2/6
- d)Mb2/6
Correct answer is option 'A'. Can you explain this answer?
What is the mass MOI of a rectangular plate about y-axis passing through the C.G of the plate if the y-axis is parallel to d and perpendicular to b?
a)
Mb2/12
b)
Md2/12
c)
Md2/6
d)
Mb2/6

|
Diya Chopra answered |
Mass Moment of Inertia (MOI) is a measure of an object's resistance to changes in rotational motion. It depends on the mass distribution of the object and the axis of rotation.
To determine the mass MOI of a rectangular plate about the y-axis passing through the center of gravity (C.G) of the plate, we need to consider the dimensions of the plate and its mass distribution.
Given:
- The y-axis is parallel to d and perpendicular to b.
To calculate the mass MOI of the rectangular plate, we can use the parallel axis theorem. This theorem states that the MOI about an axis parallel to and a distance 'd' away from an axis passing through the center of mass is equal to the MOI about the center of mass plus the product of the mass and the square of the distance 'd'.
Let's break down the solution into steps:
Step 1: Determine the MOI of the plate about its center of mass
- The MOI of a rectangular plate about an axis passing through its center of mass and perpendicular to its plane can be calculated using the formula: I_cm = (m * (b^2 + d^2)) / 12, where 'm' is the mass of the plate, 'b' is the length of the plate along the y-axis, and 'd' is the width of the plate along the x-axis.
Step 2: Calculate the distance of the parallel axis from the center of mass
- Since the parallel axis passing through the center of gravity is parallel to the y-axis and a distance 'd' away from the center of mass, the distance is equal to 'd'.
Step 3: Apply the parallel axis theorem
- According to the parallel axis theorem, the mass MOI about the parallel axis is given by I_parallel = I_cm + (m * d^2)
Step 4: Simplify the equation
- Substitute the value of I_cm from Step 1 into the equation from Step 3:
I_parallel = ((m * (b^2 + d^2)) / 12) + (m * d^2)
Simplifying further, we get: I_parallel = (m * (b^2 + 3d^2)) / 12
Comparing this result with the given options, we can see that the correct answer is option A) Mb^2/12, as it matches the derived equation (m * (b^2 + 3d^2)) / 12.
Hence, the mass MOI of the rectangular plate about the y-axis passing through the center of gravity of the plate is Mb^2/12.
To determine the mass MOI of a rectangular plate about the y-axis passing through the center of gravity (C.G) of the plate, we need to consider the dimensions of the plate and its mass distribution.
Given:
- The y-axis is parallel to d and perpendicular to b.
To calculate the mass MOI of the rectangular plate, we can use the parallel axis theorem. This theorem states that the MOI about an axis parallel to and a distance 'd' away from an axis passing through the center of mass is equal to the MOI about the center of mass plus the product of the mass and the square of the distance 'd'.
Let's break down the solution into steps:
Step 1: Determine the MOI of the plate about its center of mass
- The MOI of a rectangular plate about an axis passing through its center of mass and perpendicular to its plane can be calculated using the formula: I_cm = (m * (b^2 + d^2)) / 12, where 'm' is the mass of the plate, 'b' is the length of the plate along the y-axis, and 'd' is the width of the plate along the x-axis.
Step 2: Calculate the distance of the parallel axis from the center of mass
- Since the parallel axis passing through the center of gravity is parallel to the y-axis and a distance 'd' away from the center of mass, the distance is equal to 'd'.
Step 3: Apply the parallel axis theorem
- According to the parallel axis theorem, the mass MOI about the parallel axis is given by I_parallel = I_cm + (m * d^2)
Step 4: Simplify the equation
- Substitute the value of I_cm from Step 1 into the equation from Step 3:
I_parallel = ((m * (b^2 + d^2)) / 12) + (m * d^2)
Simplifying further, we get: I_parallel = (m * (b^2 + 3d^2)) / 12
Comparing this result with the given options, we can see that the correct answer is option A) Mb^2/12, as it matches the derived equation (m * (b^2 + 3d^2)) / 12.
Hence, the mass MOI of the rectangular plate about the y-axis passing through the center of gravity of the plate is Mb^2/12.
Moment of inertia of a square of side 'b' about an axis through its centre of gravity is- a)b3/3
- b)b4/3
- c)b4/12
- d)b4/8
Correct answer is option 'C'. Can you explain this answer?
Moment of inertia of a square of side 'b' about an axis through its centre of gravity is
a)
b3/3
b)
b4/3
c)
b4/12
d)
b4/8
|
|
Neha Joshi answered |
Moment of inertia of an area or Second moment of area (MI):
- MI of a body about any axis is defined as the summation of the second moment of all elementary areas about the axis.
- I = Σ(A × d2)
Unit: m4 or mm4 or cm4
For a square of side a or b:

Moment of inertia is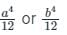
For a square of side a or b:

Moment of inertia is
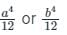
What is the product of the mass and the square of the distance of the center of gravity of the mass from an axis?- a)Moment of inertia
- b)Mass moment of inertia
- c)Center of gravity
- d)Product of inertia
Correct answer is option 'B'. Can you explain this answer?
What is the product of the mass and the square of the distance of the center of gravity of the mass from an axis?
a)
Moment of inertia
b)
Mass moment of inertia
c)
Center of gravity
d)
Product of inertia
|
|
Kritika Joshi answered |
Mass Moment of Inertia
The product of the mass and the square of the distance of the center of gravity of the mass from an axis is known as the mass moment of inertia. It is represented by the symbol 'I'. The mass moment of inertia is an important parameter in rotational dynamics and is used to determine how difficult it is to change the rotational motion of an object.
Mathematical Representation
The mass moment of inertia is mathematically represented as follows:
I = m * r^2
where I is the mass moment of inertia, m is the mass of the object, and r is the distance of the center of gravity of the mass from the axis of rotation.
Units of Mass Moment of Inertia
The SI unit of mass moment of inertia is kilogram-meter square (kg-m^2). However, it can also be expressed in other units such as gram-centimeter square (g-cm^2) or pound-foot square (lb-ft^2) depending on the system of measurement used.
Importance of Mass Moment of Inertia
The mass moment of inertia is an important parameter in rotational dynamics as it determines the torque required to change the rotational motion of an object. Objects with a larger mass moment of inertia require more torque to change their rotational motion, while objects with a smaller mass moment of inertia require less torque. The mass moment of inertia is also used to determine the stability of an object in rotational motion. Objects with a larger mass moment of inertia are generally more stable than objects with a smaller mass moment of inertia.
Conclusion
In conclusion, the mass moment of inertia is the product of the mass and the square of the distance of the center of gravity of the mass from an axis. It is an important parameter in rotational dynamics and is used to determine the torque required to change the rotational motion of an object.
The product of the mass and the square of the distance of the center of gravity of the mass from an axis is known as the mass moment of inertia. It is represented by the symbol 'I'. The mass moment of inertia is an important parameter in rotational dynamics and is used to determine how difficult it is to change the rotational motion of an object.
Mathematical Representation
The mass moment of inertia is mathematically represented as follows:
I = m * r^2
where I is the mass moment of inertia, m is the mass of the object, and r is the distance of the center of gravity of the mass from the axis of rotation.
Units of Mass Moment of Inertia
The SI unit of mass moment of inertia is kilogram-meter square (kg-m^2). However, it can also be expressed in other units such as gram-centimeter square (g-cm^2) or pound-foot square (lb-ft^2) depending on the system of measurement used.
Importance of Mass Moment of Inertia
The mass moment of inertia is an important parameter in rotational dynamics as it determines the torque required to change the rotational motion of an object. Objects with a larger mass moment of inertia require more torque to change their rotational motion, while objects with a smaller mass moment of inertia require less torque. The mass moment of inertia is also used to determine the stability of an object in rotational motion. Objects with a larger mass moment of inertia are generally more stable than objects with a smaller mass moment of inertia.
Conclusion
In conclusion, the mass moment of inertia is the product of the mass and the square of the distance of the center of gravity of the mass from an axis. It is an important parameter in rotational dynamics and is used to determine the torque required to change the rotational motion of an object.
What will be the the radius of gyration of a circular plate of diameter 10cm?- a)1.5cm
- b)2.0cm
- c)2.5cm
- d)3cm
Correct answer is option 'C'. Can you explain this answer?
What will be the the radius of gyration of a circular plate of diameter 10cm?
a)
1.5cm
b)
2.0cm
c)
2.5cm
d)
3cm
|
|
Neha Joshi answered |
The moment of inertia of a circle, I = πD4/64 = 491.07 cm4
The area of circle = 78.57 cm,
Radius of gyration = (I/A)1/2 = 2.5 cm.
The area of circle = 78.57 cm,
Radius of gyration = (I/A)1/2 = 2.5 cm.
Point, where the total volume of the body is assumed to be concentrated is ____________- a)Center of area
- b)Centroid of volume
- c)Centroid of mass
- d)All of the mentioned
Correct answer is option 'B'. Can you explain this answer?
Point, where the total volume of the body is assumed to be concentrated is ____________
a)
Center of area
b)
Centroid of volume
c)
Centroid of mass
d)
All of the mentioned

|
Athul Das answered |
The centroid of volume is the point within a solid body where the total volume of the body is assumed to be concentrated. It is an important concept in mechanics and engineering, as it helps in determining the stability, balance, and behavior of objects under various conditions.
The centroid of volume is analogous to the centroid of an area or the center of mass. However, while the centroid of an area represents the point where the area is balanced, the centroid of volume represents the point where the volume is balanced.
Why is the centroid of volume important?
The centroid of volume is used in various engineering applications, including structural analysis, fluid mechanics, and material science. Here are a few reasons why it is important:
- Stability: The centroid of volume helps in determining the stability of an object. For example, in structures, the centroid of volume is used to calculate the stability and balance of the structure under different loads and forces.
- Structural Analysis: The centroid of volume is used in structural analysis to determine the distribution of forces within a solid body. This information is crucial for designing structures that can withstand different loads and forces.
- Fluid Mechanics: In fluid mechanics, the centroid of volume is used to calculate the center of pressure and center of buoyancy. These parameters are essential for understanding the behavior of fluids and designing systems that involve fluid flow.
- Material Science: The centroid of volume is used to determine the properties of composite materials. By knowing the position of the centroid of volume, engineers can predict the behavior of composite materials under different loading conditions.
How is the centroid of volume calculated?
The centroid of volume can be calculated using mathematical formulas or by applying integration techniques. The method used depends on the shape and complexity of the object. For simple shapes like cubes, spheres, and cylinders, the centroid of volume can be easily determined using geometric formulas. However, for irregular shapes, numerical methods or computer simulations may be required.
In conclusion, the centroid of volume is an important concept in engineering and mechanics. It represents the point within a solid body where the total volume is assumed to be concentrated. Understanding the centroid of volume helps engineers in designing stable structures, analyzing the behavior of objects under different conditions, and predicting the properties of materials.
The centroid of volume is analogous to the centroid of an area or the center of mass. However, while the centroid of an area represents the point where the area is balanced, the centroid of volume represents the point where the volume is balanced.
Why is the centroid of volume important?
The centroid of volume is used in various engineering applications, including structural analysis, fluid mechanics, and material science. Here are a few reasons why it is important:
- Stability: The centroid of volume helps in determining the stability of an object. For example, in structures, the centroid of volume is used to calculate the stability and balance of the structure under different loads and forces.
- Structural Analysis: The centroid of volume is used in structural analysis to determine the distribution of forces within a solid body. This information is crucial for designing structures that can withstand different loads and forces.
- Fluid Mechanics: In fluid mechanics, the centroid of volume is used to calculate the center of pressure and center of buoyancy. These parameters are essential for understanding the behavior of fluids and designing systems that involve fluid flow.
- Material Science: The centroid of volume is used to determine the properties of composite materials. By knowing the position of the centroid of volume, engineers can predict the behavior of composite materials under different loading conditions.
How is the centroid of volume calculated?
The centroid of volume can be calculated using mathematical formulas or by applying integration techniques. The method used depends on the shape and complexity of the object. For simple shapes like cubes, spheres, and cylinders, the centroid of volume can be easily determined using geometric formulas. However, for irregular shapes, numerical methods or computer simulations may be required.
In conclusion, the centroid of volume is an important concept in engineering and mechanics. It represents the point within a solid body where the total volume is assumed to be concentrated. Understanding the centroid of volume helps engineers in designing stable structures, analyzing the behavior of objects under different conditions, and predicting the properties of materials.
What is mass moment of inertia of circular plate?- a)Md2/3
- b)Md2/12
- c)Mr2/4
- d)Mr2/3
Correct answer is option 'C'. Can you explain this answer?
What is mass moment of inertia of circular plate?
a)
Md2/3
b)
Md2/12
c)
Mr2/4
d)
Mr2/3
|
|
Suyash Patel answered |
Mass moment of inertia of circular plate
Definition:
Mass moment of inertia is the resistance of an object to rotational motion around an axis.
Formula:
The mass moment of inertia of a circular plate with mass 'M' and radius 'r' is given by the formula:
I = (Mr²)/4
Explanation:
The circular plate can be considered as a 2D object with uniform mass distribution. The mass moment of inertia of a 2D object is given by the formula:
I = ∫r²dm
where 'r' is the distance of a small element of mass 'dm' from the axis of rotation.
For a circular plate, the mass distribution is uniform and the distance of each small element of mass from the axis of rotation is equal to the radius 'r'. Therefore, we can replace 'r' with 'R' which is the radius of the circular plate.
The mass of the circular plate is given by 'M' and the area is given by 'πR²'. Therefore, the mass per unit area is given by 'M/πR²'. Using this, we can express 'dm' in terms of 'dA' which is a small area element.
dm = (M/πR²)dA
Substituting this in the equation for mass moment of inertia, we get:
I = ∫R²(M/πR²)dA
I = (M/π)∫R²dA
I = (M/π)πR²
I = (Mr²)/4
Therefore, the mass moment of inertia of a circular plate with mass 'M' and radius 'r' is given by the formula:
I = (Mr²)/4
Answer:
Hence, option 'C' is the correct answer which is (Mr²)/4.
Definition:
Mass moment of inertia is the resistance of an object to rotational motion around an axis.
Formula:
The mass moment of inertia of a circular plate with mass 'M' and radius 'r' is given by the formula:
I = (Mr²)/4
Explanation:
The circular plate can be considered as a 2D object with uniform mass distribution. The mass moment of inertia of a 2D object is given by the formula:
I = ∫r²dm
where 'r' is the distance of a small element of mass 'dm' from the axis of rotation.
For a circular plate, the mass distribution is uniform and the distance of each small element of mass from the axis of rotation is equal to the radius 'r'. Therefore, we can replace 'r' with 'R' which is the radius of the circular plate.
The mass of the circular plate is given by 'M' and the area is given by 'πR²'. Therefore, the mass per unit area is given by 'M/πR²'. Using this, we can express 'dm' in terms of 'dA' which is a small area element.
dm = (M/πR²)dA
Substituting this in the equation for mass moment of inertia, we get:
I = ∫R²(M/πR²)dA
I = (M/π)∫R²dA
I = (M/π)πR²
I = (Mr²)/4
Therefore, the mass moment of inertia of a circular plate with mass 'M' and radius 'r' is given by the formula:
I = (Mr²)/4
Answer:
Hence, option 'C' is the correct answer which is (Mr²)/4.
The axis about which moment of area is taken is known as ____________- a)Axis of area
- b)Axis of moment
- c)Axis of reference
- d)Axis of rotation
Correct answer is option 'C'. Can you explain this answer?
The axis about which moment of area is taken is known as ____________
a)
Axis of area
b)
Axis of moment
c)
Axis of reference
d)
Axis of rotation
|
|
Kirti Bose answered |
Understanding the Moment of Area
The moment of area, also known as the area moment of inertia, is a crucial concept in mechanical engineering, particularly in structural analysis and design. It measures how the area of a shape is distributed relative to a specific axis.
Axis of Reference
The term "axis of reference" pertains to the axis about which this moment of area is calculated. It serves as the baseline for evaluating the "resistance" of a shape to bending or flexural stress.
Importance of the Axis of Reference
- Bending Resistance: The moment of area directly influences how a beam or structural member will respond to applied loads.
- Design Optimization: Engineers use the axis of reference to optimize the cross-sectional shape of beams for maximum strength and minimum weight.
Why Option C is Correct
- Definition Clarity: The axis of reference provides a defined point around which the distribution of area is analyzed.
- Conceptual Foundation: Understanding the moment of area in relation to this axis is fundamental for calculations involving bending moments and shear stresses.
Conclusion
In summary, the axis about which the moment of area is computed is indeed referred to as the axis of reference. This term highlights its role as the critical point of evaluation for calculating how structural elements will perform under various loads. Understanding this concept is essential for any mechanical engineer engaged in design and analysis tasks.
The moment of area, also known as the area moment of inertia, is a crucial concept in mechanical engineering, particularly in structural analysis and design. It measures how the area of a shape is distributed relative to a specific axis.
Axis of Reference
The term "axis of reference" pertains to the axis about which this moment of area is calculated. It serves as the baseline for evaluating the "resistance" of a shape to bending or flexural stress.
Importance of the Axis of Reference
- Bending Resistance: The moment of area directly influences how a beam or structural member will respond to applied loads.
- Design Optimization: Engineers use the axis of reference to optimize the cross-sectional shape of beams for maximum strength and minimum weight.
Why Option C is Correct
- Definition Clarity: The axis of reference provides a defined point around which the distribution of area is analyzed.
- Conceptual Foundation: Understanding the moment of area in relation to this axis is fundamental for calculations involving bending moments and shear stresses.
Conclusion
In summary, the axis about which the moment of area is computed is indeed referred to as the axis of reference. This term highlights its role as the critical point of evaluation for calculating how structural elements will perform under various loads. Understanding this concept is essential for any mechanical engineer engaged in design and analysis tasks.
Moment of inertia of a square of side 'b' about an axis through its centre of gravity is- a)b3/3
- b)b4/3
- c)b4/12
- d)b4/8
Correct answer is option 'C'. Can you explain this answer?
Moment of inertia of a square of side 'b' about an axis through its centre of gravity is
a)
b3/3
b)
b4/3
c)
b4/12
d)
b4/8
|
|
Bibek Das answered |
Calculation of Moment of Inertia of a Square
Moment of inertia is the measure of resistance of a body to rotational motion. The moment of inertia of a square of side b about an axis through its centre of gravity can be calculated as follows:
- Consider a square of side b with its centre of gravity at the intersection of its diagonals.
- Divide the square into four equal parts by drawing two perpendicular lines passing through the centre of the square.
- Consider one of the parts of the square. Its moment of inertia about an axis passing through its centre of gravity and perpendicular to its plane can be calculated as I = (1/12)mb^2, where m is the mass of the part.
- The moment of inertia of the entire square about the same axis can be calculated as I = 4I = 4(1/12)mb^2 = (1/3)mb^2.
- Therefore, the moment of inertia of a square of side b about an axis passing through its centre of gravity and perpendicular to its plane is (1/3)mb^2.
The correct answer is option C, which provides the formula for the moment of inertia of a square of side b about an axis through its centre of gravity.
Moment of inertia is the measure of resistance of a body to rotational motion. The moment of inertia of a square of side b about an axis through its centre of gravity can be calculated as follows:
- Consider a square of side b with its centre of gravity at the intersection of its diagonals.
- Divide the square into four equal parts by drawing two perpendicular lines passing through the centre of the square.
- Consider one of the parts of the square. Its moment of inertia about an axis passing through its centre of gravity and perpendicular to its plane can be calculated as I = (1/12)mb^2, where m is the mass of the part.
- The moment of inertia of the entire square about the same axis can be calculated as I = 4I = 4(1/12)mb^2 = (1/3)mb^2.
- Therefore, the moment of inertia of a square of side b about an axis passing through its centre of gravity and perpendicular to its plane is (1/3)mb^2.
The correct answer is option C, which provides the formula for the moment of inertia of a square of side b about an axis through its centre of gravity.
What is the mass MOI of right circular cone of radius R and height H about its axis?- a)4MR2/10
- b)MR2/10
- c)3MR2/10
- d)MR2/12
Correct answer is option 'C'. Can you explain this answer?
What is the mass MOI of right circular cone of radius R and height H about its axis?
a)
4MR2/10
b)
MR2/10
c)
3MR2/10
d)
MR2/12

|
Navya Sarkar answered |
Understanding the Mass Moment of Inertia (MOI)
The mass moment of inertia (MOI) of an object quantifies its resistance to rotational motion about an axis. For a right circular cone with height H and radius R, we need to derive the MOI about its central axis.
Mass Distribution of a Cone
- A right circular cone can be visualized as a collection of infinitesimally thin discs stacked along its height.
- The mass (M) of the cone is uniformly distributed, and the volume (V) can be calculated as V = (1/3)πR²H.
Deriving the MOI for the Cone
1. Elemental Disc: Consider a thin disc at a height 'z' from the base with thickness 'dz'. Its radius can be expressed as (R/H)z.
2. Volume of the Disc: The volume of this elemental disc is dV = π[(R/H)z]²dz = (πR²z²/H²)dz.
3. Mass of the Disc: The mass of the elemental disc is dm = (M/V)dV = (3M/(πR²H))(πR²z²/H²)dz = (3Mz²/(H³))dz.
4. MOI Contribution: The contribution to the MOI from this disc is dI = (1/2)r²dm = (1/2)((R/H)z)²(3Mz²/(H³))dz.
5. Integrating: The total MOI I is found by integrating from z=0 to z=H.
6. Final Result: After performing the integration, we obtain I = (3/10)MR².
Conclusion
Thus, the mass moment of inertia of a right circular cone about its axis is:
- I = (3/10)MR²
The correct answer is option 'C' - 3MR²/10.
The mass moment of inertia (MOI) of an object quantifies its resistance to rotational motion about an axis. For a right circular cone with height H and radius R, we need to derive the MOI about its central axis.
Mass Distribution of a Cone
- A right circular cone can be visualized as a collection of infinitesimally thin discs stacked along its height.
- The mass (M) of the cone is uniformly distributed, and the volume (V) can be calculated as V = (1/3)πR²H.
Deriving the MOI for the Cone
1. Elemental Disc: Consider a thin disc at a height 'z' from the base with thickness 'dz'. Its radius can be expressed as (R/H)z.
2. Volume of the Disc: The volume of this elemental disc is dV = π[(R/H)z]²dz = (πR²z²/H²)dz.
3. Mass of the Disc: The mass of the elemental disc is dm = (M/V)dV = (3M/(πR²H))(πR²z²/H²)dz = (3Mz²/(H³))dz.
4. MOI Contribution: The contribution to the MOI from this disc is dI = (1/2)r²dm = (1/2)((R/H)z)²(3Mz²/(H³))dz.
5. Integrating: The total MOI I is found by integrating from z=0 to z=H.
6. Final Result: After performing the integration, we obtain I = (3/10)MR².
Conclusion
Thus, the mass moment of inertia of a right circular cone about its axis is:
- I = (3/10)MR²
The correct answer is option 'C' - 3MR²/10.
What is the mass MOI of a rectangular plate about x-axis passing through the C.G of the plate if the y-axis is parallel to d and perpendicular to b?- a)Mb2/12
- b)Md2/12
- c)Md2/6
- d)Mb2/6
Correct answer is option 'B'. Can you explain this answer?
What is the mass MOI of a rectangular plate about x-axis passing through the C.G of the plate if the y-axis is parallel to d and perpendicular to b?
a)
Mb2/12
b)
Md2/12
c)
Md2/6
d)
Mb2/6
|
|
Mansi Rane answered |
Mass Moment of Inertia (MOI) is a measure of an object's resistance to rotational motion. It depends on the mass distribution of the object and the axis of rotation. In this case, we are given a rectangular plate and asked to find its MOI about the x-axis passing through the center of gravity (C.G) of the plate.
Since the y-axis is parallel to d and perpendicular to b, we can assume that the dimensions of the rectangular plate are b (width) and d (height). The plate's center of gravity is located at the midpoint of the plate, which is also the intersection point of the x and y axes.
To find the MOI of the rectangular plate about the x-axis passing through the C.G, we can use the parallel axis theorem. According to this theorem, the MOI about any axis parallel to an axis passing through the center of gravity can be found by adding the MOI about the center of gravity to the product of the mass and the distance squared between the two axes.
Let's calculate the MOI using the parallel axis theorem:
1. MOI about the center of gravity:
The MOI of a rectangular plate about an axis passing through its center of gravity and perpendicular to the plane of the plate can be calculated using the formula:
Ic.g = (m * (b^2 + d^2)) / 12
Here, m represents the mass of the plate.
2. Distance squared between the two axes:
The distance between the x-axis passing through the C.G and the center of gravity is zero since the C.G is located on the x-axis.
3. MOI about the x-axis passing through the C.G:
Using the parallel axis theorem, we can calculate the MOI about the x-axis passing through the C.G as:
Ix = Ic.g + (m * (0^2))
Simplifying the equation:
Ix = Ic.g = (m * (b^2 + d^2)) / 12
Comparing the equation with the given options, we can see that the correct answer is option B:
Mass MOI of a rectangular plate about x-axis passing through the C.G = Md^2/12
Since the y-axis is parallel to d and perpendicular to b, we can assume that the dimensions of the rectangular plate are b (width) and d (height). The plate's center of gravity is located at the midpoint of the plate, which is also the intersection point of the x and y axes.
To find the MOI of the rectangular plate about the x-axis passing through the C.G, we can use the parallel axis theorem. According to this theorem, the MOI about any axis parallel to an axis passing through the center of gravity can be found by adding the MOI about the center of gravity to the product of the mass and the distance squared between the two axes.
Let's calculate the MOI using the parallel axis theorem:
1. MOI about the center of gravity:
The MOI of a rectangular plate about an axis passing through its center of gravity and perpendicular to the plane of the plate can be calculated using the formula:
Ic.g = (m * (b^2 + d^2)) / 12
Here, m represents the mass of the plate.
2. Distance squared between the two axes:
The distance between the x-axis passing through the C.G and the center of gravity is zero since the C.G is located on the x-axis.
3. MOI about the x-axis passing through the C.G:
Using the parallel axis theorem, we can calculate the MOI about the x-axis passing through the C.G as:
Ix = Ic.g + (m * (0^2))
Simplifying the equation:
Ix = Ic.g = (m * (b^2 + d^2)) / 12
Comparing the equation with the given options, we can see that the correct answer is option B:
Mass MOI of a rectangular plate about x-axis passing through the C.G = Md^2/12
What is the formula of radius of gyration?- a)k2 = I/A
- b)k2 = I2/A
- c)k2 = I2/A2
- d)k2 = (I/A)1/2
Correct answer is option 'A'. Can you explain this answer?
What is the formula of radius of gyration?
a)
k2 = I/A
b)
k2 = I2/A
c)
k2 = I2/A2
d)
k2 = (I/A)1/2
|
|
Neha Joshi answered |
The radius of gyration of a body about an axis is a distance such that its square multiplied by the area gives moment of inertia of the area about the given axis. The formula of radius of gyration is given as k2 = I/A.
What is the formula of theorem of parallel axis?- a)IAD = IG + Ah
- b)IAB = Ah2 + IG
- c)IAB = IG – Ah2
- d)IAB = IG + Ixx
Correct answer is option 'B'. Can you explain this answer?
What is the formula of theorem of parallel axis?
a)
IAD = IG + Ah
b)
IAB = Ah2 + IG
c)
IAB = IG – Ah2
d)
IAB = IG + Ixx
|
|
Siddharth Menon answered |
Formula of Theorem of Parallel Axis:
The formula of the theorem of parallel axis is given by:
IAB = IG + A*h2
where:
- IAB is the moment of inertia of an object about an axis parallel to the center of mass.
- IG is the moment of inertia of the object about its center of mass.
- A is the mass of the object.
- h is the distance between the parallel axis and the center of mass.
Explanation:
- The theorem of parallel axis states that the moment of inertia of a rigid body about any axis parallel to an axis passing through the center of mass is equal to the sum of the moment of inertia about the center of mass and the product of the mass of the object and the square of the distance between the two axes.
- This theorem is useful in calculating the moment of inertia of complex objects that cannot be easily calculated using simple geometric shapes.
- By using this formula, engineers and physicists can determine the distribution of mass in an object and predict its rotational behavior accurately.
In conclusion, the formula of the theorem of parallel axis is a crucial tool in the study of rotational motion and mechanics, allowing for the calculation of moment of inertia about parallel axes.
What is the unit of radius of gyration?- a)m4
- b)m
- c)N
- d)m2
Correct answer is option 'B'. Can you explain this answer?
What is the unit of radius of gyration?
a)
m4
b)
m
c)
N
d)
m2
|
|
Neha Joshi answered |
The radius of gyration = (length4/length2)1/2 = length
So its unit will be m.
So its unit will be m.
The ratio of the moment of inertia of a circular plate of diameter same as that of a side of a square plate is - a)less than one
- b)more than one
- c)equal to one
- d)equal to 3π /16
Correct answer is option 'D'. Can you explain this answer?
The ratio of the moment of inertia of a circular plate of diameter same as that of a side of a square plate is
a)
less than one
b)
more than one
c)
equal to one
d)
equal to 3π /16
|
|
Neha Joshi answered |
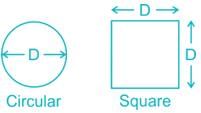
The moment of inertia (I1) of a circular plate of diameter “D” is given by:
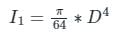
The moment of inertia (I2) of the square plate of side equal to the diameter “D” of the circular plate is given by:
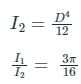
The ratio of the moment of inertia of a circular plate of diameter same as that of a side of a square plate is - a)less than one
- b)more than one
- c)equal to one
- d)equal to 3π /16
Correct answer is option 'D'. Can you explain this answer?
The ratio of the moment of inertia of a circular plate of diameter same as that of a side of a square plate is
a)
less than one
b)
more than one
c)
equal to one
d)
equal to 3π /16
|
|
Neha Joshi answered |
The moment of inertia (I1) of a circular plate of diameter “D” is given by:

The moment of inertia (I2) of the square plate of side equal to the diameter “D” of the circular plate is given by:
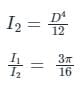
The polar moment of inertia of a hollow circular shaft of outer diameter (D) and inner diameter (d) is- a)

- b)
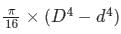
- c)
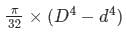
- d)
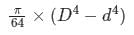
Correct answer is option 'C'. Can you explain this answer?
The polar moment of inertia of a hollow circular shaft of outer diameter (D) and inner diameter (d) is
a)

b)
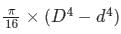
c)
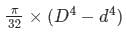
d)
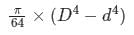
|
|
Neha Joshi answered |
Polar moment of inertia of Solid cylinder:
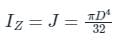
Polar moment of inertia of Hollow Cylinder:
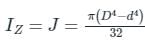
where outer diameter = D and inner diameter = d
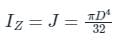
Polar moment of inertia of Hollow Cylinder:
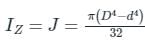
where outer diameter = D and inner diameter = d
Chapter doubts & questions for Moment of Inertia (MOI) - Engineering Mechanics for Mechanical Engineering 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Moment of Inertia (MOI) - Engineering Mechanics for Mechanical Engineering in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Engineering Mechanics for Mechanical Engineering
33 videos|78 docs|44 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup











