NEET Exam > NEET Questions > A source of sound has a noise level of 20 dB....
Start Learning for Free
A source of sound has a noise level of 20 dB. if the intensity of sound produced by the source increases by 100 times, the noise level become?
Most Upvoted Answer
A source of sound has a noise level of 20 dB. if the intensity of soun...
Introduction:
Noise level is a measure of the loudness of a sound and is typically expressed in decibels (dB). The decibel scale is logarithmic, meaning that an increase of 10 dB represents a tenfold increase in sound intensity. In this scenario, we are given that the noise level of a source is 20 dB and we need to determine the new noise level when the intensity of the sound produced by the source increases by 100 times.
Understanding the decibel scale:
Before we proceed, it is important to understand the decibel scale and how it relates to sound intensity. The decibel scale is logarithmic because the human ear perceives sound intensity logarithmically. Each 10 dB increase represents a tenfold increase in sound intensity, while a 20 dB increase represents a hundredfold increase in intensity.
Calculating the new noise level:
To calculate the new noise level, we can use the formula:
Noise Level (dB) = 10 * log10(Intensity2/Intensity1)
In this case, the intensity increases by 100 times, so the ratio of Intensity2 to Intensity1 is 100. Applying this to the formula, we get:
Noise Level (dB) = 10 * log10(100)
Solving the equation:
Now, let's solve the equation to find the new noise level.
Noise Level (dB) = 10 * log10(100)
= 10 * log10(10^2) [since 100 = 10^2]
= 10 * 2 [using the logarithmic property log10(x^y) = y * log10(x)]
= 20 dB
Conclusion:
The new noise level, when the intensity of sound produced by the source increases by 100 times, is 20 dB. This means that despite the increase in sound intensity, the noise level remains the same. The decibel scale takes into account the logarithmic perception of sound by the human ear, allowing us to quantify and compare different sound intensities accurately.
Noise level is a measure of the loudness of a sound and is typically expressed in decibels (dB). The decibel scale is logarithmic, meaning that an increase of 10 dB represents a tenfold increase in sound intensity. In this scenario, we are given that the noise level of a source is 20 dB and we need to determine the new noise level when the intensity of the sound produced by the source increases by 100 times.
Understanding the decibel scale:
Before we proceed, it is important to understand the decibel scale and how it relates to sound intensity. The decibel scale is logarithmic because the human ear perceives sound intensity logarithmically. Each 10 dB increase represents a tenfold increase in sound intensity, while a 20 dB increase represents a hundredfold increase in intensity.
Calculating the new noise level:
To calculate the new noise level, we can use the formula:
Noise Level (dB) = 10 * log10(Intensity2/Intensity1)
In this case, the intensity increases by 100 times, so the ratio of Intensity2 to Intensity1 is 100. Applying this to the formula, we get:
Noise Level (dB) = 10 * log10(100)
Solving the equation:
Now, let's solve the equation to find the new noise level.
Noise Level (dB) = 10 * log10(100)
= 10 * log10(10^2) [since 100 = 10^2]
= 10 * 2 [using the logarithmic property log10(x^y) = y * log10(x)]
= 20 dB
Conclusion:
The new noise level, when the intensity of sound produced by the source increases by 100 times, is 20 dB. This means that despite the increase in sound intensity, the noise level remains the same. The decibel scale takes into account the logarithmic perception of sound by the human ear, allowing us to quantify and compare different sound intensities accurately.
Community Answer
A source of sound has a noise level of 20 dB. if the intensity of soun...
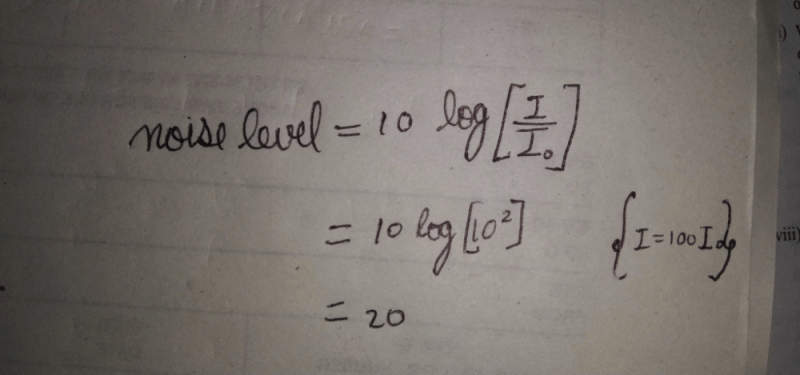

|
Explore Courses for NEET exam
|

|
Question Description
A source of sound has a noise level of 20 dB. if the intensity of sound produced by the source increases by 100 times, the noise level become? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about A source of sound has a noise level of 20 dB. if the intensity of sound produced by the source increases by 100 times, the noise level become? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A source of sound has a noise level of 20 dB. if the intensity of sound produced by the source increases by 100 times, the noise level become?.
A source of sound has a noise level of 20 dB. if the intensity of sound produced by the source increases by 100 times, the noise level become? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about A source of sound has a noise level of 20 dB. if the intensity of sound produced by the source increases by 100 times, the noise level become? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A source of sound has a noise level of 20 dB. if the intensity of sound produced by the source increases by 100 times, the noise level become?.
Solutions for A source of sound has a noise level of 20 dB. if the intensity of sound produced by the source increases by 100 times, the noise level become? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of A source of sound has a noise level of 20 dB. if the intensity of sound produced by the source increases by 100 times, the noise level become? defined & explained in the simplest way possible. Besides giving the explanation of
A source of sound has a noise level of 20 dB. if the intensity of sound produced by the source increases by 100 times, the noise level become?, a detailed solution for A source of sound has a noise level of 20 dB. if the intensity of sound produced by the source increases by 100 times, the noise level become? has been provided alongside types of A source of sound has a noise level of 20 dB. if the intensity of sound produced by the source increases by 100 times, the noise level become? theory, EduRev gives you an
ample number of questions to practice A source of sound has a noise level of 20 dB. if the intensity of sound produced by the source increases by 100 times, the noise level become? tests, examples and also practice NEET tests.

|
Explore Courses for NEET exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























