Electronics and Communication Engineering (ECE) Exam > Electronics and Communication Engineering (ECE) Questions > Two RC coupled amplifiers are connected to fo...
Start Learning for Free
Two RC coupled amplifiers are connected to form a 2-stage amplifier. If the lower and upper cut off frequencies of each individual amplifiers is 100 Hz and 20 kHz. Then the 3-dB bandwidth of the two-state amplifier is ____ Hz.
Correct answer is between '12700,12720'. Can you explain this answer?
Verified Answer
Two RC coupled amplifiers are connected to form a 2-stage amplifier. I...
Concept:
For multistage amplifier consisting of n identical amplifying states, the lower cut off fL (multi) is expressed as
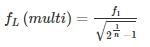
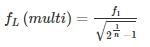
Where f1 = lower cut off frequency of individual state.
Upper cut off frequency is given by:
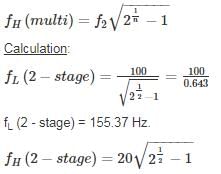
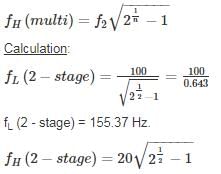
= 20 × 0.643
= 12.87 kHz
Bandwidth =
= 12714.6 Hz.
Most Upvoted Answer
Two RC coupled amplifiers are connected to form a 2-stage amplifier. I...
To determine the 3-dB bandwidth of the two-stage amplifier, we need to consider the frequency response of each individual amplifier and the overall frequency response of the two-stage amplifier.
Frequency Response of Individual Amplifiers:
The lower and upper cutoff frequencies of each individual amplifier are given as 100 Hz and 20 kHz. This means that the gain of each amplifier starts to decrease below 100 Hz and above 20 kHz.
Overall Frequency Response of the Two-Stage Amplifier:
When two amplifiers are connected in series, the overall frequency response is determined by the product of the individual frequency responses. In this case, the two amplifiers are connected in a "RC coupled" configuration, which means the output of the first amplifier is connected to the input of the second amplifier through a coupling capacitor.
The coupling capacitor acts as a high-pass filter, allowing only frequencies above its cutoff frequency to pass through. The cutoff frequency of the coupling capacitor can be calculated using the formula:
fc = 1 / (2πRC)
where fc is the cutoff frequency and R and C are the resistance and capacitance values of the coupling capacitor.
Since the two amplifiers are connected in series, the overall cutoff frequency of the two-stage amplifier is determined by the lowest cutoff frequency of the two amplifiers. In this case, the lowest cutoff frequency is 100 Hz.
Calculating the 3-dB Bandwidth:
The 3-dB bandwidth is the range of frequencies over which the gain of the amplifier is within 3 dB of its maximum value. In other words, it is the range of frequencies over which the gain is not significantly attenuated.
To calculate the 3-dB bandwidth, we need to determine the upper and lower frequencies at which the gain is reduced by 3 dB from its maximum value.
Since the lower cutoff frequency of the two-stage amplifier is 100 Hz, we can assume that the gain is reduced by 3 dB at this frequency.
To determine the upper frequency, we can use the upper cutoff frequency of the individual amplifiers, which is 20 kHz. However, since the two amplifiers are connected in series, the gain will also start to decrease before the upper cutoff frequency of the second amplifier is reached.
Therefore, we can estimate the upper frequency at which the gain is reduced by 3 dB by finding the geometric mean of the upper cutoff frequencies of the two amplifiers.
Geometric Mean = √(f1 * f2)
where f1 and f2 are the upper cutoff frequencies of the individual amplifiers.
Using the given upper cutoff frequencies of 20 kHz, the geometric mean is:
√(20,000 * 20,000) = 20,000 Hz
Therefore, the estimated upper frequency at which the gain is reduced by 3 dB is 20,000 Hz.
Thus, the 3-dB bandwidth of the two-stage amplifier is the difference between the upper and lower frequencies at which the gain is reduced by 3 dB:
3-dB Bandwidth = Upper Frequency - Lower Frequency
= 20,000 Hz - 100 Hz
= 19,900 Hz
Therefore, the 3-dB bandwidth of the two-stage amplifier is approximately 19,900 Hz, which is between the given range of 12,700 Hz and 12,720 Hz.
Frequency Response of Individual Amplifiers:
The lower and upper cutoff frequencies of each individual amplifier are given as 100 Hz and 20 kHz. This means that the gain of each amplifier starts to decrease below 100 Hz and above 20 kHz.
Overall Frequency Response of the Two-Stage Amplifier:
When two amplifiers are connected in series, the overall frequency response is determined by the product of the individual frequency responses. In this case, the two amplifiers are connected in a "RC coupled" configuration, which means the output of the first amplifier is connected to the input of the second amplifier through a coupling capacitor.
The coupling capacitor acts as a high-pass filter, allowing only frequencies above its cutoff frequency to pass through. The cutoff frequency of the coupling capacitor can be calculated using the formula:
fc = 1 / (2πRC)
where fc is the cutoff frequency and R and C are the resistance and capacitance values of the coupling capacitor.
Since the two amplifiers are connected in series, the overall cutoff frequency of the two-stage amplifier is determined by the lowest cutoff frequency of the two amplifiers. In this case, the lowest cutoff frequency is 100 Hz.
Calculating the 3-dB Bandwidth:
The 3-dB bandwidth is the range of frequencies over which the gain of the amplifier is within 3 dB of its maximum value. In other words, it is the range of frequencies over which the gain is not significantly attenuated.
To calculate the 3-dB bandwidth, we need to determine the upper and lower frequencies at which the gain is reduced by 3 dB from its maximum value.
Since the lower cutoff frequency of the two-stage amplifier is 100 Hz, we can assume that the gain is reduced by 3 dB at this frequency.
To determine the upper frequency, we can use the upper cutoff frequency of the individual amplifiers, which is 20 kHz. However, since the two amplifiers are connected in series, the gain will also start to decrease before the upper cutoff frequency of the second amplifier is reached.
Therefore, we can estimate the upper frequency at which the gain is reduced by 3 dB by finding the geometric mean of the upper cutoff frequencies of the two amplifiers.
Geometric Mean = √(f1 * f2)
where f1 and f2 are the upper cutoff frequencies of the individual amplifiers.
Using the given upper cutoff frequencies of 20 kHz, the geometric mean is:
√(20,000 * 20,000) = 20,000 Hz
Therefore, the estimated upper frequency at which the gain is reduced by 3 dB is 20,000 Hz.
Thus, the 3-dB bandwidth of the two-stage amplifier is the difference between the upper and lower frequencies at which the gain is reduced by 3 dB:
3-dB Bandwidth = Upper Frequency - Lower Frequency
= 20,000 Hz - 100 Hz
= 19,900 Hz
Therefore, the 3-dB bandwidth of the two-stage amplifier is approximately 19,900 Hz, which is between the given range of 12,700 Hz and 12,720 Hz.

|
Explore Courses for Electronics and Communication Engineering (ECE) exam
|

|
Similar Electronics and Communication Engineering (ECE) Doubts
Question Description
Two RC coupled amplifiers are connected to form a 2-stage amplifier. If the lower and upper cut off frequencies of each individual amplifiers is 100 Hz and 20 kHz. Then the 3-dB bandwidth of the two-state amplifier is ____ Hz.Correct answer is between '12700,12720'. Can you explain this answer? for Electronics and Communication Engineering (ECE) 2025 is part of Electronics and Communication Engineering (ECE) preparation. The Question and answers have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. Information about Two RC coupled amplifiers are connected to form a 2-stage amplifier. If the lower and upper cut off frequencies of each individual amplifiers is 100 Hz and 20 kHz. Then the 3-dB bandwidth of the two-state amplifier is ____ Hz.Correct answer is between '12700,12720'. Can you explain this answer? covers all topics & solutions for Electronics and Communication Engineering (ECE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two RC coupled amplifiers are connected to form a 2-stage amplifier. If the lower and upper cut off frequencies of each individual amplifiers is 100 Hz and 20 kHz. Then the 3-dB bandwidth of the two-state amplifier is ____ Hz.Correct answer is between '12700,12720'. Can you explain this answer?.
Two RC coupled amplifiers are connected to form a 2-stage amplifier. If the lower and upper cut off frequencies of each individual amplifiers is 100 Hz and 20 kHz. Then the 3-dB bandwidth of the two-state amplifier is ____ Hz.Correct answer is between '12700,12720'. Can you explain this answer? for Electronics and Communication Engineering (ECE) 2025 is part of Electronics and Communication Engineering (ECE) preparation. The Question and answers have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. Information about Two RC coupled amplifiers are connected to form a 2-stage amplifier. If the lower and upper cut off frequencies of each individual amplifiers is 100 Hz and 20 kHz. Then the 3-dB bandwidth of the two-state amplifier is ____ Hz.Correct answer is between '12700,12720'. Can you explain this answer? covers all topics & solutions for Electronics and Communication Engineering (ECE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two RC coupled amplifiers are connected to form a 2-stage amplifier. If the lower and upper cut off frequencies of each individual amplifiers is 100 Hz and 20 kHz. Then the 3-dB bandwidth of the two-state amplifier is ____ Hz.Correct answer is between '12700,12720'. Can you explain this answer?.
Solutions for Two RC coupled amplifiers are connected to form a 2-stage amplifier. If the lower and upper cut off frequencies of each individual amplifiers is 100 Hz and 20 kHz. Then the 3-dB bandwidth of the two-state amplifier is ____ Hz.Correct answer is between '12700,12720'. Can you explain this answer? in English & in Hindi are available as part of our courses for Electronics and Communication Engineering (ECE).
Download more important topics, notes, lectures and mock test series for Electronics and Communication Engineering (ECE) Exam by signing up for free.
Here you can find the meaning of Two RC coupled amplifiers are connected to form a 2-stage amplifier. If the lower and upper cut off frequencies of each individual amplifiers is 100 Hz and 20 kHz. Then the 3-dB bandwidth of the two-state amplifier is ____ Hz.Correct answer is between '12700,12720'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Two RC coupled amplifiers are connected to form a 2-stage amplifier. If the lower and upper cut off frequencies of each individual amplifiers is 100 Hz and 20 kHz. Then the 3-dB bandwidth of the two-state amplifier is ____ Hz.Correct answer is between '12700,12720'. Can you explain this answer?, a detailed solution for Two RC coupled amplifiers are connected to form a 2-stage amplifier. If the lower and upper cut off frequencies of each individual amplifiers is 100 Hz and 20 kHz. Then the 3-dB bandwidth of the two-state amplifier is ____ Hz.Correct answer is between '12700,12720'. Can you explain this answer? has been provided alongside types of Two RC coupled amplifiers are connected to form a 2-stage amplifier. If the lower and upper cut off frequencies of each individual amplifiers is 100 Hz and 20 kHz. Then the 3-dB bandwidth of the two-state amplifier is ____ Hz.Correct answer is between '12700,12720'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Two RC coupled amplifiers are connected to form a 2-stage amplifier. If the lower and upper cut off frequencies of each individual amplifiers is 100 Hz and 20 kHz. Then the 3-dB bandwidth of the two-state amplifier is ____ Hz.Correct answer is between '12700,12720'. Can you explain this answer? tests, examples and also practice Electronics and Communication Engineering (ECE) tests.

|
Explore Courses for Electronics and Communication Engineering (ECE) exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



























