LR Exam > LR Questions > Rasik walked 20 m towards north. Then he turn...
Start Learning for Free
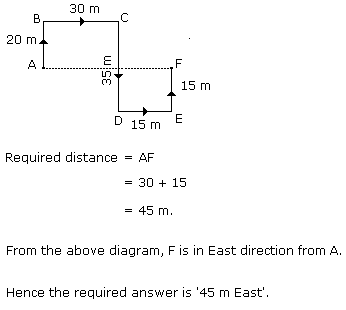
Rasik walked 20 m towards north. Then he turned right and walks 30 m. Then he turns right and walks 35 m. Then he turns left and walks 15 m. Finally he turns left and walks 15 m. In which direction and how many metres is he from the starting position?
- a)15 m West
- b)30 m East
- c)30 m West
- d)45 m East
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Rasik walked 20 m towards north. Then he turned right and walks 30 m. ...
Most Upvoted Answer
Rasik walked 20 m towards north. Then he turned right and walks 30 m. ...
Rasik's movements can be traced as follows:
1. Rasik walks 20 m towards north: This means that Rasik moves in the direction directly opposite to the gravitational force, also known as "up" on a map.
2. Rasik turns right and walks 30 m: After turning right, Rasik is facing east and walks 30 m in that direction.
3. Rasik turns right again and walks 35 m: Following the previous movement, Rasik is now facing south and walks 35 m in that direction.
4. Rasik turns left and walks 15 m: After turning left, Rasik is facing east again and walks 15 m in that direction.
5. Rasik turns left once more and walks 15 m: Following the previous movement, Rasik is now facing north and walks 15 m in that direction.
To determine Rasik's final position, we can calculate the net displacement in the north-south and east-west directions.
Net displacement in the north-south direction:
Rasik initially moves 20 m towards the north and then walks 15 m towards the north, resulting in a net displacement of 20 m + 15 m = 35 m towards the north.
Net displacement in the east-west direction:
Rasik walks 30 m towards the east, then turns left and walks 15 m towards the west. The net displacement in the east-west direction is 30 m - 15 m = 15 m towards the east.
Therefore, Rasik's final position is 35 m towards the north and 15 m towards the east from the starting position. This can be represented as a vector with magnitude and direction, where the magnitude is the distance and the direction is the angle measured from the north direction. In this case, the magnitude is √(35^2 + 15^2) = √(1225 + 225) = √1450 ≈ 38.08 m and the direction is arctan(15/35) ≈ 22.62 degrees east of north.
To summarize, Rasik is approximately 38.08 m away from the starting position in the direction that is 22.62 degrees east of north. Therefore, the correct answer is option D: 45 m east.
1. Rasik walks 20 m towards north: This means that Rasik moves in the direction directly opposite to the gravitational force, also known as "up" on a map.
2. Rasik turns right and walks 30 m: After turning right, Rasik is facing east and walks 30 m in that direction.
3. Rasik turns right again and walks 35 m: Following the previous movement, Rasik is now facing south and walks 35 m in that direction.
4. Rasik turns left and walks 15 m: After turning left, Rasik is facing east again and walks 15 m in that direction.
5. Rasik turns left once more and walks 15 m: Following the previous movement, Rasik is now facing north and walks 15 m in that direction.
To determine Rasik's final position, we can calculate the net displacement in the north-south and east-west directions.
Net displacement in the north-south direction:
Rasik initially moves 20 m towards the north and then walks 15 m towards the north, resulting in a net displacement of 20 m + 15 m = 35 m towards the north.
Net displacement in the east-west direction:
Rasik walks 30 m towards the east, then turns left and walks 15 m towards the west. The net displacement in the east-west direction is 30 m - 15 m = 15 m towards the east.
Therefore, Rasik's final position is 35 m towards the north and 15 m towards the east from the starting position. This can be represented as a vector with magnitude and direction, where the magnitude is the distance and the direction is the angle measured from the north direction. In this case, the magnitude is √(35^2 + 15^2) = √(1225 + 225) = √1450 ≈ 38.08 m and the direction is arctan(15/35) ≈ 22.62 degrees east of north.
To summarize, Rasik is approximately 38.08 m away from the starting position in the direction that is 22.62 degrees east of north. Therefore, the correct answer is option D: 45 m east.

|
Explore Courses for LR exam
|

|
Similar LR Doubts
Rasik walked 20 m towards north. Then he turned right and walks 30 m. Then he turns right and walks 35 m. Then he turns left and walks 15 m. Finally he turns left and walks 15 m. In which direction and how many metres is he from the starting position?a)15 m Westb)30 m Eastc)30 m Westd)45 m EastCorrect answer is option 'D'. Can you explain this answer?
Question Description
Rasik walked 20 m towards north. Then he turned right and walks 30 m. Then he turns right and walks 35 m. Then he turns left and walks 15 m. Finally he turns left and walks 15 m. In which direction and how many metres is he from the starting position?a)15 m Westb)30 m Eastc)30 m Westd)45 m EastCorrect answer is option 'D'. Can you explain this answer? for LR 2024 is part of LR preparation. The Question and answers have been prepared according to the LR exam syllabus. Information about Rasik walked 20 m towards north. Then he turned right and walks 30 m. Then he turns right and walks 35 m. Then he turns left and walks 15 m. Finally he turns left and walks 15 m. In which direction and how many metres is he from the starting position?a)15 m Westb)30 m Eastc)30 m Westd)45 m EastCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for LR 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Rasik walked 20 m towards north. Then he turned right and walks 30 m. Then he turns right and walks 35 m. Then he turns left and walks 15 m. Finally he turns left and walks 15 m. In which direction and how many metres is he from the starting position?a)15 m Westb)30 m Eastc)30 m Westd)45 m EastCorrect answer is option 'D'. Can you explain this answer?.
Rasik walked 20 m towards north. Then he turned right and walks 30 m. Then he turns right and walks 35 m. Then he turns left and walks 15 m. Finally he turns left and walks 15 m. In which direction and how many metres is he from the starting position?a)15 m Westb)30 m Eastc)30 m Westd)45 m EastCorrect answer is option 'D'. Can you explain this answer? for LR 2024 is part of LR preparation. The Question and answers have been prepared according to the LR exam syllabus. Information about Rasik walked 20 m towards north. Then he turned right and walks 30 m. Then he turns right and walks 35 m. Then he turns left and walks 15 m. Finally he turns left and walks 15 m. In which direction and how many metres is he from the starting position?a)15 m Westb)30 m Eastc)30 m Westd)45 m EastCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for LR 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Rasik walked 20 m towards north. Then he turned right and walks 30 m. Then he turns right and walks 35 m. Then he turns left and walks 15 m. Finally he turns left and walks 15 m. In which direction and how many metres is he from the starting position?a)15 m Westb)30 m Eastc)30 m Westd)45 m EastCorrect answer is option 'D'. Can you explain this answer?.
Solutions for Rasik walked 20 m towards north. Then he turned right and walks 30 m. Then he turns right and walks 35 m. Then he turns left and walks 15 m. Finally he turns left and walks 15 m. In which direction and how many metres is he from the starting position?a)15 m Westb)30 m Eastc)30 m Westd)45 m EastCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for LR.
Download more important topics, notes, lectures and mock test series for LR Exam by signing up for free.
Here you can find the meaning of Rasik walked 20 m towards north. Then he turned right and walks 30 m. Then he turns right and walks 35 m. Then he turns left and walks 15 m. Finally he turns left and walks 15 m. In which direction and how many metres is he from the starting position?a)15 m Westb)30 m Eastc)30 m Westd)45 m EastCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Rasik walked 20 m towards north. Then he turned right and walks 30 m. Then he turns right and walks 35 m. Then he turns left and walks 15 m. Finally he turns left and walks 15 m. In which direction and how many metres is he from the starting position?a)15 m Westb)30 m Eastc)30 m Westd)45 m EastCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for Rasik walked 20 m towards north. Then he turned right and walks 30 m. Then he turns right and walks 35 m. Then he turns left and walks 15 m. Finally he turns left and walks 15 m. In which direction and how many metres is he from the starting position?a)15 m Westb)30 m Eastc)30 m Westd)45 m EastCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of Rasik walked 20 m towards north. Then he turned right and walks 30 m. Then he turns right and walks 35 m. Then he turns left and walks 15 m. Finally he turns left and walks 15 m. In which direction and how many metres is he from the starting position?a)15 m Westb)30 m Eastc)30 m Westd)45 m EastCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Rasik walked 20 m towards north. Then he turned right and walks 30 m. Then he turns right and walks 35 m. Then he turns left and walks 15 m. Finally he turns left and walks 15 m. In which direction and how many metres is he from the starting position?a)15 m Westb)30 m Eastc)30 m Westd)45 m EastCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice LR tests.

|
Explore Courses for LR exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















