NEET Exam > NEET Questions > A car is moving in a circular horizontal trac...
Start Learning for Free
A car is moving in a circular horizontal track of radius 10 m with a constant speed of 10 m/s. A bob is suspended from the roof of the car by a light wire of length 1.0 m. The angle made by the wire with the vertical is [NEET Kar. 2013]
- a)0°
- b)
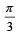
- c)
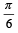
- d)
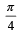
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
A car is moving in a circular horizontal track of radius 10 m with a c...
Given; speed = 10 m/s; radius r = 10 m
Angle made by the wire with the vertical
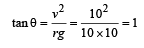
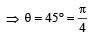
Most Upvoted Answer
A car is moving in a circular horizontal track of radius 10 m with a c...
Since the car is moving in a circular track at a constant speed, the bob is also moving in a circle with the same speed. The force acting on the bob is tension in the wire and its weight. At any point on its path, the force acting on the bob is towards the center of the circle, which is the car. Therefore, the wire makes an angle with the vertical, which is equal to the angle between the tension in the wire and the weight of the bob.
The tension in the wire is equal to the weight of the bob, which is given by:
weight = mass x gravity
where mass is the mass of the bob and gravity is the acceleration due to gravity. Since the wire is light, its mass can be neglected. Therefore,
weight = mg
where g = 9.8 m/s^2 is the acceleration due to gravity and m is the mass of the bob. Since the mass of the bob is not given, we cannot determine its weight or the tension in the wire.
However, we can determine the angle between the tension in the wire and the weight of the bob. Let θ be this angle, as shown in the figure below.
[asy]
unitsize(1cm);
draw((0,0)--(10,0));
draw((5,0)--(5,5));
draw((5,5)--(5.5,5));
draw((4.5,5)--(5,5));
draw((5,5)--(5,0),dashed);
label("$r = 10\,\mathrm{m}$",(5,-0.5));
label("$\theta$",(5.25,4.75));
label("$l = 1.0\,\mathrm{m}$",(5,2.5),rotate(90));
dot((5,5));
[/asy]
Since the length of the wire is 1.0 m, the component of the tension in the wire along the vertical direction is l cosθ. The weight of the bob is mg, which is also the component of the weight along the vertical direction. Therefore, we have:
l cosθ = mg
Dividing both sides by l and substituting g = 9.8 m/s^2, we get:
cosθ = g/l
Substituting l = 1.0 m, we get:
cosθ = 9.8/1.0 = 9.8
This is not possible, since the cosine of an angle is always between -1 and 1. Therefore, there is no real angle θ that satisfies the given conditions. The answer is (d) None of the above.
The tension in the wire is equal to the weight of the bob, which is given by:
weight = mass x gravity
where mass is the mass of the bob and gravity is the acceleration due to gravity. Since the wire is light, its mass can be neglected. Therefore,
weight = mg
where g = 9.8 m/s^2 is the acceleration due to gravity and m is the mass of the bob. Since the mass of the bob is not given, we cannot determine its weight or the tension in the wire.
However, we can determine the angle between the tension in the wire and the weight of the bob. Let θ be this angle, as shown in the figure below.
[asy]
unitsize(1cm);
draw((0,0)--(10,0));
draw((5,0)--(5,5));
draw((5,5)--(5.5,5));
draw((4.5,5)--(5,5));
draw((5,5)--(5,0),dashed);
label("$r = 10\,\mathrm{m}$",(5,-0.5));
label("$\theta$",(5.25,4.75));
label("$l = 1.0\,\mathrm{m}$",(5,2.5),rotate(90));
dot((5,5));
[/asy]
Since the length of the wire is 1.0 m, the component of the tension in the wire along the vertical direction is l cosθ. The weight of the bob is mg, which is also the component of the weight along the vertical direction. Therefore, we have:
l cosθ = mg
Dividing both sides by l and substituting g = 9.8 m/s^2, we get:
cosθ = g/l
Substituting l = 1.0 m, we get:
cosθ = 9.8/1.0 = 9.8
This is not possible, since the cosine of an angle is always between -1 and 1. Therefore, there is no real angle θ that satisfies the given conditions. The answer is (d) None of the above.
Free Test
FREE
| Start Free Test |
Community Answer
A car is moving in a circular horizontal track of radius 10 m with a c...
Tan theta =(velocity)square/Rg where R is radius and g is acceleration due to gravity.So acc to question v=10 m/sec.g=10m/sec square.and R=10m hence tan theta =1,so theta =45 so pie/4

|
Explore Courses for NEET exam
|

|
Question Description
A car is moving in a circular horizontal track of radius 10 m with a constant speed of 10 m/s. A bob is suspended from the roof of the car by a light wire of length 1.0 m. The angle made by the wire with the vertical is [NEET Kar. 2013]a)0°b)c)d)Correct answer is option 'D'. Can you explain this answer? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about A car is moving in a circular horizontal track of radius 10 m with a constant speed of 10 m/s. A bob is suspended from the roof of the car by a light wire of length 1.0 m. The angle made by the wire with the vertical is [NEET Kar. 2013]a)0°b)c)d)Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A car is moving in a circular horizontal track of radius 10 m with a constant speed of 10 m/s. A bob is suspended from the roof of the car by a light wire of length 1.0 m. The angle made by the wire with the vertical is [NEET Kar. 2013]a)0°b)c)d)Correct answer is option 'D'. Can you explain this answer?.
A car is moving in a circular horizontal track of radius 10 m with a constant speed of 10 m/s. A bob is suspended from the roof of the car by a light wire of length 1.0 m. The angle made by the wire with the vertical is [NEET Kar. 2013]a)0°b)c)d)Correct answer is option 'D'. Can you explain this answer? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about A car is moving in a circular horizontal track of radius 10 m with a constant speed of 10 m/s. A bob is suspended from the roof of the car by a light wire of length 1.0 m. The angle made by the wire with the vertical is [NEET Kar. 2013]a)0°b)c)d)Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A car is moving in a circular horizontal track of radius 10 m with a constant speed of 10 m/s. A bob is suspended from the roof of the car by a light wire of length 1.0 m. The angle made by the wire with the vertical is [NEET Kar. 2013]a)0°b)c)d)Correct answer is option 'D'. Can you explain this answer?.
Solutions for A car is moving in a circular horizontal track of radius 10 m with a constant speed of 10 m/s. A bob is suspended from the roof of the car by a light wire of length 1.0 m. The angle made by the wire with the vertical is [NEET Kar. 2013]a)0°b)c)d)Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of A car is moving in a circular horizontal track of radius 10 m with a constant speed of 10 m/s. A bob is suspended from the roof of the car by a light wire of length 1.0 m. The angle made by the wire with the vertical is [NEET Kar. 2013]a)0°b)c)d)Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A car is moving in a circular horizontal track of radius 10 m with a constant speed of 10 m/s. A bob is suspended from the roof of the car by a light wire of length 1.0 m. The angle made by the wire with the vertical is [NEET Kar. 2013]a)0°b)c)d)Correct answer is option 'D'. Can you explain this answer?, a detailed solution for A car is moving in a circular horizontal track of radius 10 m with a constant speed of 10 m/s. A bob is suspended from the roof of the car by a light wire of length 1.0 m. The angle made by the wire with the vertical is [NEET Kar. 2013]a)0°b)c)d)Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of A car is moving in a circular horizontal track of radius 10 m with a constant speed of 10 m/s. A bob is suspended from the roof of the car by a light wire of length 1.0 m. The angle made by the wire with the vertical is [NEET Kar. 2013]a)0°b)c)d)Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A car is moving in a circular horizontal track of radius 10 m with a constant speed of 10 m/s. A bob is suspended from the roof of the car by a light wire of length 1.0 m. The angle made by the wire with the vertical is [NEET Kar. 2013]a)0°b)c)d)Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice NEET tests.

|
Explore Courses for NEET exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















