NEET Exam > NEET Questions > Masses MA and MB hanging from the ends of str...
Start Learning for Free
Masses MA and MB hanging from the ends of strings of lengths LA and LB are executing simple harmonic motions. If their frequencies are fA = 2fB, then [2000]
- a)LA = 2LB and MA = MB/2
- b)LA = 4LB regardless of masses
- c)LA = LB/4 regardless of masses
- d)LA = 2LB and MA = 2MB
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
Masses MA and MB hanging from the ends of strings of lengths LA and LB...
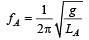
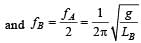
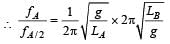
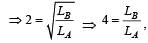
regardless of mass.
Most Upvoted Answer
Masses MA and MB hanging from the ends of strings of lengths LA and LB...
To understand why the correct answer is option 'C', let's break down the given information and analyze the relationship between the frequencies and lengths of the strings.
Given:
- Masses MA and MB are hanging from strings of lengths LA and LB, respectively.
- The masses are executing simple harmonic motions.
- The frequency of MA, fA, is twice the frequency of MB, fB.
Frequency of Simple Harmonic Motion:
The frequency of an object executing simple harmonic motion is given by the formula:
f = 1/2π * √(k/m)
where f is the frequency, k is the spring constant, and m is the mass of the object.
Analyzing the Given Information:
1. Frequency Relationship:
Since fA = 2fB, we can write the equation as:
1/2π * √(kA/MA) = 2 * (1/2π * √(kB/MB))
Simplifying this equation, we get:
√(kA/MA) = 2 * √(kB/MB)
Squaring both sides of the equation, we have:
kA/MA = 4 * (kB/MB)
2. Length Relationship:
The length of a simple pendulum affects its frequency. The formula for the frequency of a simple pendulum is:
f = 1/2π * √(g/L)
where g is the acceleration due to gravity and L is the length of the pendulum.
Since the lengths of the strings are LA and LB, we can write the equation as:
1/2π * √(g/LA) = 2 * (1/2π * √(g/LB))
Simplifying this equation, we get:
√(g/LA) = 2 * √(g/LB)
Squaring both sides of the equation, we have:
g/LA = 4 * (g/LB)
Simplifying further, we can cancel out g from both sides:
1/LA = 4 * (1/LB)
LA = LB/4
Conclusion:
From the analysis above, we can conclude that the correct answer is option 'C':
LA = LB/4, regardless of the masses.
This means that the length of the string for mass A is four times smaller than the length of the string for mass B, irrespective of the masses of the objects.
Given:
- Masses MA and MB are hanging from strings of lengths LA and LB, respectively.
- The masses are executing simple harmonic motions.
- The frequency of MA, fA, is twice the frequency of MB, fB.
Frequency of Simple Harmonic Motion:
The frequency of an object executing simple harmonic motion is given by the formula:
f = 1/2π * √(k/m)
where f is the frequency, k is the spring constant, and m is the mass of the object.
Analyzing the Given Information:
1. Frequency Relationship:
Since fA = 2fB, we can write the equation as:
1/2π * √(kA/MA) = 2 * (1/2π * √(kB/MB))
Simplifying this equation, we get:
√(kA/MA) = 2 * √(kB/MB)
Squaring both sides of the equation, we have:
kA/MA = 4 * (kB/MB)
2. Length Relationship:
The length of a simple pendulum affects its frequency. The formula for the frequency of a simple pendulum is:
f = 1/2π * √(g/L)
where g is the acceleration due to gravity and L is the length of the pendulum.
Since the lengths of the strings are LA and LB, we can write the equation as:
1/2π * √(g/LA) = 2 * (1/2π * √(g/LB))
Simplifying this equation, we get:
√(g/LA) = 2 * √(g/LB)
Squaring both sides of the equation, we have:
g/LA = 4 * (g/LB)
Simplifying further, we can cancel out g from both sides:
1/LA = 4 * (1/LB)
LA = LB/4
Conclusion:
From the analysis above, we can conclude that the correct answer is option 'C':
LA = LB/4, regardless of the masses.
This means that the length of the string for mass A is four times smaller than the length of the string for mass B, irrespective of the masses of the objects.

|
Explore Courses for NEET exam
|

|
Question Description
Masses MA and MB hanging from the ends of strings of lengths LA and LB are executing simple harmonic motions. If their frequencies are fA = 2fB, then [2000]a)LA = 2LB and MA = MB/2b)LA = 4LB regardless of massesc)LA = LB/4 regardless of massesd)LA = 2LB and MA = 2MBCorrect answer is option 'C'. Can you explain this answer? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about Masses MA and MB hanging from the ends of strings of lengths LA and LB are executing simple harmonic motions. If their frequencies are fA = 2fB, then [2000]a)LA = 2LB and MA = MB/2b)LA = 4LB regardless of massesc)LA = LB/4 regardless of massesd)LA = 2LB and MA = 2MBCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Masses MA and MB hanging from the ends of strings of lengths LA and LB are executing simple harmonic motions. If their frequencies are fA = 2fB, then [2000]a)LA = 2LB and MA = MB/2b)LA = 4LB regardless of massesc)LA = LB/4 regardless of massesd)LA = 2LB and MA = 2MBCorrect answer is option 'C'. Can you explain this answer?.
Masses MA and MB hanging from the ends of strings of lengths LA and LB are executing simple harmonic motions. If their frequencies are fA = 2fB, then [2000]a)LA = 2LB and MA = MB/2b)LA = 4LB regardless of massesc)LA = LB/4 regardless of massesd)LA = 2LB and MA = 2MBCorrect answer is option 'C'. Can you explain this answer? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about Masses MA and MB hanging from the ends of strings of lengths LA and LB are executing simple harmonic motions. If their frequencies are fA = 2fB, then [2000]a)LA = 2LB and MA = MB/2b)LA = 4LB regardless of massesc)LA = LB/4 regardless of massesd)LA = 2LB and MA = 2MBCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Masses MA and MB hanging from the ends of strings of lengths LA and LB are executing simple harmonic motions. If their frequencies are fA = 2fB, then [2000]a)LA = 2LB and MA = MB/2b)LA = 4LB regardless of massesc)LA = LB/4 regardless of massesd)LA = 2LB and MA = 2MBCorrect answer is option 'C'. Can you explain this answer?.
Solutions for Masses MA and MB hanging from the ends of strings of lengths LA and LB are executing simple harmonic motions. If their frequencies are fA = 2fB, then [2000]a)LA = 2LB and MA = MB/2b)LA = 4LB regardless of massesc)LA = LB/4 regardless of massesd)LA = 2LB and MA = 2MBCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of Masses MA and MB hanging from the ends of strings of lengths LA and LB are executing simple harmonic motions. If their frequencies are fA = 2fB, then [2000]a)LA = 2LB and MA = MB/2b)LA = 4LB regardless of massesc)LA = LB/4 regardless of massesd)LA = 2LB and MA = 2MBCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Masses MA and MB hanging from the ends of strings of lengths LA and LB are executing simple harmonic motions. If their frequencies are fA = 2fB, then [2000]a)LA = 2LB and MA = MB/2b)LA = 4LB regardless of massesc)LA = LB/4 regardless of massesd)LA = 2LB and MA = 2MBCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for Masses MA and MB hanging from the ends of strings of lengths LA and LB are executing simple harmonic motions. If their frequencies are fA = 2fB, then [2000]a)LA = 2LB and MA = MB/2b)LA = 4LB regardless of massesc)LA = LB/4 regardless of massesd)LA = 2LB and MA = 2MBCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of Masses MA and MB hanging from the ends of strings of lengths LA and LB are executing simple harmonic motions. If their frequencies are fA = 2fB, then [2000]a)LA = 2LB and MA = MB/2b)LA = 4LB regardless of massesc)LA = LB/4 regardless of massesd)LA = 2LB and MA = 2MBCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Masses MA and MB hanging from the ends of strings of lengths LA and LB are executing simple harmonic motions. If their frequencies are fA = 2fB, then [2000]a)LA = 2LB and MA = MB/2b)LA = 4LB regardless of massesc)LA = LB/4 regardless of massesd)LA = 2LB and MA = 2MBCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice NEET tests.

|
Explore Courses for NEET exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















