NEET Exam > NEET Questions > A 600 kg rocket is set for a vertical firing....
Start Learning for Free
A 600 kg rocket is set for a vertical firing. If the exhaust speed is 1000 ms–1 , the mass of the gas ejected per second to supply the thrust needed to overcome the weight of rocket is [1990]
- a)117.6 kg s–1
- b)58.6 kg s–1
- c)6 kg s–1
- d)76.4 kg s–1
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
A 600 kg rocket is set for a vertical firing. If the exhaust speed is ...
Thrust 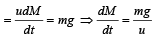
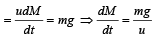

Most Upvoted Answer
A 600 kg rocket is set for a vertical firing. If the exhaust speed is ...
In this question if we substitute the value of 'g' as 9.8m/s we get 5.88 which is near to the 2nd option. It should have be mentioned that take g=10m/s unless otherwise stated the value of 'g' must be taken as 9.8m/s. So I think 2nd option is correct
Free Test
FREE
| Start Free Test |
Community Answer
A 600 kg rocket is set for a vertical firing. If the exhaust speed is ...
To solve this problem, we can use the concept of conservation of momentum.
Let's assume that the rocket initially has a velocity of 0 m/s and is at rest. When the rocket fires, it expels exhaust with a speed of 1000 m/s. According to the conservation of momentum, the total momentum before and after the firing should be equal.
The momentum of an object is given by the product of its mass and velocity. So, the initial momentum of the system (rocket + exhaust) is 0 kg*m/s (since both the mass and velocity are 0).
After the rocket fires, the mass of the rocket decreases due to the expulsion of exhaust. Let's assume that the mass of the rocket decreases by 'm' kg. So, the mass of the rocket after firing is (600 - m) kg.
The velocity of the rocket after firing is 'v' m/s. Since the rocket is moving upwards, the velocity is positive.
The momentum of the rocket after firing is given by (600 - m) * v kg*m/s.
According to the conservation of momentum, the initial momentum is equal to the final momentum:
0 = (600 - m) * v
Simplifying the equation:
600 - m = 0
m = 600 kg
Therefore, the mass of the exhaust expelled is 600 kg.
Note: In this problem, we assumed that the mass of the exhaust is equal to the change in mass of the rocket. This is a simplification, and in reality, the exhaust mass may be different due to various factors such as fuel consumption rate and combustion efficiency.
Let's assume that the rocket initially has a velocity of 0 m/s and is at rest. When the rocket fires, it expels exhaust with a speed of 1000 m/s. According to the conservation of momentum, the total momentum before and after the firing should be equal.
The momentum of an object is given by the product of its mass and velocity. So, the initial momentum of the system (rocket + exhaust) is 0 kg*m/s (since both the mass and velocity are 0).
After the rocket fires, the mass of the rocket decreases due to the expulsion of exhaust. Let's assume that the mass of the rocket decreases by 'm' kg. So, the mass of the rocket after firing is (600 - m) kg.
The velocity of the rocket after firing is 'v' m/s. Since the rocket is moving upwards, the velocity is positive.
The momentum of the rocket after firing is given by (600 - m) * v kg*m/s.
According to the conservation of momentum, the initial momentum is equal to the final momentum:
0 = (600 - m) * v
Simplifying the equation:
600 - m = 0
m = 600 kg
Therefore, the mass of the exhaust expelled is 600 kg.
Note: In this problem, we assumed that the mass of the exhaust is equal to the change in mass of the rocket. This is a simplification, and in reality, the exhaust mass may be different due to various factors such as fuel consumption rate and combustion efficiency.

|
Explore Courses for NEET exam
|

|
Question Description
A 600 kg rocket is set for a vertical firing. If the exhaust speed is 1000 ms–1 , the mass of the gas ejected per second to supply the thrust needed to overcome the weight of rocket is [1990]a)117.6 kg s–1b)58.6 kg s–1c)6 kg s–1d)76.4 kg s–1Correct answer is option 'C'. Can you explain this answer? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about A 600 kg rocket is set for a vertical firing. If the exhaust speed is 1000 ms–1 , the mass of the gas ejected per second to supply the thrust needed to overcome the weight of rocket is [1990]a)117.6 kg s–1b)58.6 kg s–1c)6 kg s–1d)76.4 kg s–1Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A 600 kg rocket is set for a vertical firing. If the exhaust speed is 1000 ms–1 , the mass of the gas ejected per second to supply the thrust needed to overcome the weight of rocket is [1990]a)117.6 kg s–1b)58.6 kg s–1c)6 kg s–1d)76.4 kg s–1Correct answer is option 'C'. Can you explain this answer?.
A 600 kg rocket is set for a vertical firing. If the exhaust speed is 1000 ms–1 , the mass of the gas ejected per second to supply the thrust needed to overcome the weight of rocket is [1990]a)117.6 kg s–1b)58.6 kg s–1c)6 kg s–1d)76.4 kg s–1Correct answer is option 'C'. Can you explain this answer? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about A 600 kg rocket is set for a vertical firing. If the exhaust speed is 1000 ms–1 , the mass of the gas ejected per second to supply the thrust needed to overcome the weight of rocket is [1990]a)117.6 kg s–1b)58.6 kg s–1c)6 kg s–1d)76.4 kg s–1Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A 600 kg rocket is set for a vertical firing. If the exhaust speed is 1000 ms–1 , the mass of the gas ejected per second to supply the thrust needed to overcome the weight of rocket is [1990]a)117.6 kg s–1b)58.6 kg s–1c)6 kg s–1d)76.4 kg s–1Correct answer is option 'C'. Can you explain this answer?.
Solutions for A 600 kg rocket is set for a vertical firing. If the exhaust speed is 1000 ms–1 , the mass of the gas ejected per second to supply the thrust needed to overcome the weight of rocket is [1990]a)117.6 kg s–1b)58.6 kg s–1c)6 kg s–1d)76.4 kg s–1Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of A 600 kg rocket is set for a vertical firing. If the exhaust speed is 1000 ms–1 , the mass of the gas ejected per second to supply the thrust needed to overcome the weight of rocket is [1990]a)117.6 kg s–1b)58.6 kg s–1c)6 kg s–1d)76.4 kg s–1Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A 600 kg rocket is set for a vertical firing. If the exhaust speed is 1000 ms–1 , the mass of the gas ejected per second to supply the thrust needed to overcome the weight of rocket is [1990]a)117.6 kg s–1b)58.6 kg s–1c)6 kg s–1d)76.4 kg s–1Correct answer is option 'C'. Can you explain this answer?, a detailed solution for A 600 kg rocket is set for a vertical firing. If the exhaust speed is 1000 ms–1 , the mass of the gas ejected per second to supply the thrust needed to overcome the weight of rocket is [1990]a)117.6 kg s–1b)58.6 kg s–1c)6 kg s–1d)76.4 kg s–1Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of A 600 kg rocket is set for a vertical firing. If the exhaust speed is 1000 ms–1 , the mass of the gas ejected per second to supply the thrust needed to overcome the weight of rocket is [1990]a)117.6 kg s–1b)58.6 kg s–1c)6 kg s–1d)76.4 kg s–1Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A 600 kg rocket is set for a vertical firing. If the exhaust speed is 1000 ms–1 , the mass of the gas ejected per second to supply the thrust needed to overcome the weight of rocket is [1990]a)117.6 kg s–1b)58.6 kg s–1c)6 kg s–1d)76.4 kg s–1Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice NEET tests.

|
Explore Courses for NEET exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















