GMAT Exam > GMAT Questions > Bill and Jane pl ay a simple game involving t...
Start Learning for Free
Bill and Jane pl ay a simple game involving two fair dice, each of which has six sides numbered from 1 to 6 (with an equal chance of landing on any side). Bill rolls the dice and his score is the total of the two dice. Jane then rolls the dice and her score is the total of her two dice. If Jane’s score is higher than Bill’s, she wins the game. What is the probability the Jane will win the game?
- a)15/36
- b)175/432
- c)575/1296
- d)583/1296
- e)1/2
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
Bill and Jane pl ay a simple game involving two fair dice, each of whi...
Since each die has 6 possible outcomes, there are 6 × 6 = 36 different ways that Bill can roll two dice. Similarly there are 6 × 6 = 36 different ways for Jane to roll the dice. Hence, there are a total of 36 × 36 = 1296 different possible ways the game can be played.
One way to approach this problem (the hard way) is to consider, in turn, the number of ways that Bill can get each possible score, compute the number of ways that Jane can beat him for each score, and then divide by 1296. The number of ways to make each score is: 1 way to make a 2 (1 and 1), 2 ways to make a 3 (1 and 2, or 2 and 1), 3 ways to make a 4 (1 and 3, 2 and 2, 3 and 1), 4 ways to make a 5 (use similar reasoning…), 5 ways to make a 6, 6 ways to make a 7, 5 ways to make an 8, 4 ways to make a 9, 3 ways to make a 10, 2 ways to make an 11, and 1 way to make a 12. We can see that there is only 1 way for Bill to score a 2 (1 and 1). Since there are 36 total ways to roll two dice, there are 35 ways for Jane to beat Bob's 2.
Next, there are 2 ways that Bob can score a 3 (1 and 2, 2 and 1). There are only three ways in which Jane would not beat Bob: if she scores a 2 (1 and 1), she would lose to Bob or if she scores a 3 (1 and 2, 2 and 1), she would tie Bob. Since there are 36 total ways to roll the dice, Jane has 33 ways to beat Bob.
Using similar logic, we can quickly create the following table:
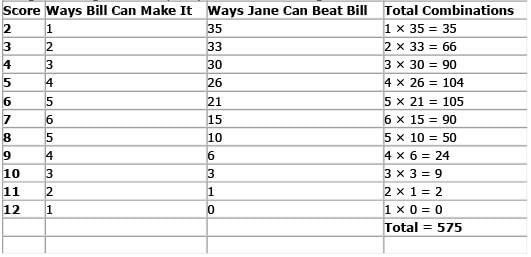
Out of the 1296 possible ways the game can be played, 575 of them result in Jane winning the game. Hence, the probability the Jane will win is 575/1296 and the correct answer is C.
There is a much easier way to compute this probability. Observe that this is a “symmetric” game in that neither Bill nor Jane has an advantage over the other. That is, each has an equal change of winning. Hence, we can determine the number of ways each can win by subtracting out the ways they can tie and then dividing the remaining possibilities by 2.
Note that for each score, the number of ways that Jane will tie Bill is equal to the number of ways that Bill can make that score (i.e., both have an equal number of ways to make a particular score). Thus, referring again to the table above, the total number of ways to ti e are: 12 + 22 + 32 + 42 +52 +62 + 52 + 42 + 32 + 22 + 12 = 146. Therefore, there are 1296 – 146 = 1150 non-ties. Since this is a symmetric problem, Jane will win 1150/2 or 575 times out of the 1296 possible games. Hence, the probability that she will win is 575/1296.
One way to approach this problem (the hard way) is to consider, in turn, the number of ways that Bill can get each possible score, compute the number of ways that Jane can beat him for each score, and then divide by 1296. The number of ways to make each score is: 1 way to make a 2 (1 and 1), 2 ways to make a 3 (1 and 2, or 2 and 1), 3 ways to make a 4 (1 and 3, 2 and 2, 3 and 1), 4 ways to make a 5 (use similar reasoning…), 5 ways to make a 6, 6 ways to make a 7, 5 ways to make an 8, 4 ways to make a 9, 3 ways to make a 10, 2 ways to make an 11, and 1 way to make a 12. We can see that there is only 1 way for Bill to score a 2 (1 and 1). Since there are 36 total ways to roll two dice, there are 35 ways for Jane to beat Bob's 2.
Next, there are 2 ways that Bob can score a 3 (1 and 2, 2 and 1). There are only three ways in which Jane would not beat Bob: if she scores a 2 (1 and 1), she would lose to Bob or if she scores a 3 (1 and 2, 2 and 1), she would tie Bob. Since there are 36 total ways to roll the dice, Jane has 33 ways to beat Bob.
Using similar logic, we can quickly create the following table:

Out of the 1296 possible ways the game can be played, 575 of them result in Jane winning the game. Hence, the probability the Jane will win is 575/1296 and the correct answer is C.
There is a much easier way to compute this probability. Observe that this is a “symmetric” game in that neither Bill nor Jane has an advantage over the other. That is, each has an equal change of winning. Hence, we can determine the number of ways each can win by subtracting out the ways they can tie and then dividing the remaining possibilities by 2.
Note that for each score, the number of ways that Jane will tie Bill is equal to the number of ways that Bill can make that score (i.e., both have an equal number of ways to make a particular score). Thus, referring again to the table above, the total number of ways to ti e are: 12 + 22 + 32 + 42 +52 +62 + 52 + 42 + 32 + 22 + 12 = 146. Therefore, there are 1296 – 146 = 1150 non-ties. Since this is a symmetric problem, Jane will win 1150/2 or 575 times out of the 1296 possible games. Hence, the probability that she will win is 575/1296.
Most Upvoted Answer
Bill and Jane pl ay a simple game involving two fair dice, each of whi...
Rolls a higher score than Bill, she wins. If Bill rolls a higher score than Jane, he wins. If they both roll the same score, it is a tie.
To determine the probability of each outcome, we can use a probability distribution table.
First, let's list all the possible outcomes for Bill's roll:
Bill's Roll: | 1 | 2 | 3 | 4 | 5 | 6 |
Probability: | 1/6| 1/6| 1/6| 1/6| 1/6| 1/6|
Now, let's list all the possible outcomes for Jane's roll:
Jane's Roll: | 1 | 2 | 3 | 4 | 5 | 6 |
Probability: | 1/36| 2/36| 3/36| 4/36| 5/36| 6/36|
Note that the probability of each outcome for Jane's roll is calculated by multiplying the probability of each individual roll. For example, the probability of rolling a 2 is 1/6 * 1/6 = 1/36.
To determine the probability of each outcome, we need to calculate the sum of the probabilities for each combination of Bill's roll and Jane's roll.
Here is the probability distribution table:
Bill's Roll: | 1 | 2 | 3 | 4 | 5 | 6 |
Jane's Roll: | | | | | | |
Probability: | | | | | | |
We can fill in the table by multiplying the probability of each combination of rolls. For example, the probability of Bill rolling a 1 and Jane rolling a 2 is 1/6 * 1/36 = 1/216.
Bill's Roll: | 1 | 2 | 3 | 4 | 5 | 6 |
Jane's Roll: | | | | | | |
Probability: | 1/216| 1/108| 1/72| 1/54| 1/43.2| 1/36|
Now, we can calculate the probability of each outcome:
- If Jane rolls a higher score than Bill (Jane wins), we sum the probabilities of all combinations where Jane's roll is greater than Bill's roll:
P(Jane wins) = P(Jane rolls 2 and Bill rolls 1) + P(Jane rolls 3 and Bill rolls 1 or 2) + P(Jane rolls 4 and Bill rolls 1, 2, or 3) + P(Jane rolls 5 and Bill rolls 1, 2, 3, or 4) + P(Jane rolls 6 and Bill rolls 1, 2, 3, 4, or 5)
= 1/216 + (1/108 + 1/216) + (1/72 + 1/108 + 1/216) + (1/54 + 1/72 + 1/108 + 1/216) + (1/43.2 + 1/54 +
To determine the probability of each outcome, we can use a probability distribution table.
First, let's list all the possible outcomes for Bill's roll:
Bill's Roll: | 1 | 2 | 3 | 4 | 5 | 6 |
Probability: | 1/6| 1/6| 1/6| 1/6| 1/6| 1/6|
Now, let's list all the possible outcomes for Jane's roll:
Jane's Roll: | 1 | 2 | 3 | 4 | 5 | 6 |
Probability: | 1/36| 2/36| 3/36| 4/36| 5/36| 6/36|
Note that the probability of each outcome for Jane's roll is calculated by multiplying the probability of each individual roll. For example, the probability of rolling a 2 is 1/6 * 1/6 = 1/36.
To determine the probability of each outcome, we need to calculate the sum of the probabilities for each combination of Bill's roll and Jane's roll.
Here is the probability distribution table:
Bill's Roll: | 1 | 2 | 3 | 4 | 5 | 6 |
Jane's Roll: | | | | | | |
Probability: | | | | | | |
We can fill in the table by multiplying the probability of each combination of rolls. For example, the probability of Bill rolling a 1 and Jane rolling a 2 is 1/6 * 1/36 = 1/216.
Bill's Roll: | 1 | 2 | 3 | 4 | 5 | 6 |
Jane's Roll: | | | | | | |
Probability: | 1/216| 1/108| 1/72| 1/54| 1/43.2| 1/36|
Now, we can calculate the probability of each outcome:
- If Jane rolls a higher score than Bill (Jane wins), we sum the probabilities of all combinations where Jane's roll is greater than Bill's roll:
P(Jane wins) = P(Jane rolls 2 and Bill rolls 1) + P(Jane rolls 3 and Bill rolls 1 or 2) + P(Jane rolls 4 and Bill rolls 1, 2, or 3) + P(Jane rolls 5 and Bill rolls 1, 2, 3, or 4) + P(Jane rolls 6 and Bill rolls 1, 2, 3, 4, or 5)
= 1/216 + (1/108 + 1/216) + (1/72 + 1/108 + 1/216) + (1/54 + 1/72 + 1/108 + 1/216) + (1/43.2 + 1/54 +

|
Explore Courses for GMAT exam
|

|
Question Description
Bill and Jane pl ay a simple game involving two fair dice, each of which has six sides numbered from 1 to 6 (with an equal chance of landing on any side). Bill rolls the dice and his score is the total of the two dice. Jane then rolls the dice and her score is the total of her two dice. If Jane’s score is higher than Bill’s, she wins the game. What is the probability the Jane will win the game?a)15/36b)175/432c)575/1296d)583/1296e)1/2Correct answer is option 'C'. Can you explain this answer? for GMAT 2025 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about Bill and Jane pl ay a simple game involving two fair dice, each of which has six sides numbered from 1 to 6 (with an equal chance of landing on any side). Bill rolls the dice and his score is the total of the two dice. Jane then rolls the dice and her score is the total of her two dice. If Jane’s score is higher than Bill’s, she wins the game. What is the probability the Jane will win the game?a)15/36b)175/432c)575/1296d)583/1296e)1/2Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for GMAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Bill and Jane pl ay a simple game involving two fair dice, each of which has six sides numbered from 1 to 6 (with an equal chance of landing on any side). Bill rolls the dice and his score is the total of the two dice. Jane then rolls the dice and her score is the total of her two dice. If Jane’s score is higher than Bill’s, she wins the game. What is the probability the Jane will win the game?a)15/36b)175/432c)575/1296d)583/1296e)1/2Correct answer is option 'C'. Can you explain this answer?.
Bill and Jane pl ay a simple game involving two fair dice, each of which has six sides numbered from 1 to 6 (with an equal chance of landing on any side). Bill rolls the dice and his score is the total of the two dice. Jane then rolls the dice and her score is the total of her two dice. If Jane’s score is higher than Bill’s, she wins the game. What is the probability the Jane will win the game?a)15/36b)175/432c)575/1296d)583/1296e)1/2Correct answer is option 'C'. Can you explain this answer? for GMAT 2025 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about Bill and Jane pl ay a simple game involving two fair dice, each of which has six sides numbered from 1 to 6 (with an equal chance of landing on any side). Bill rolls the dice and his score is the total of the two dice. Jane then rolls the dice and her score is the total of her two dice. If Jane’s score is higher than Bill’s, she wins the game. What is the probability the Jane will win the game?a)15/36b)175/432c)575/1296d)583/1296e)1/2Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for GMAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Bill and Jane pl ay a simple game involving two fair dice, each of which has six sides numbered from 1 to 6 (with an equal chance of landing on any side). Bill rolls the dice and his score is the total of the two dice. Jane then rolls the dice and her score is the total of her two dice. If Jane’s score is higher than Bill’s, she wins the game. What is the probability the Jane will win the game?a)15/36b)175/432c)575/1296d)583/1296e)1/2Correct answer is option 'C'. Can you explain this answer?.
Solutions for Bill and Jane pl ay a simple game involving two fair dice, each of which has six sides numbered from 1 to 6 (with an equal chance of landing on any side). Bill rolls the dice and his score is the total of the two dice. Jane then rolls the dice and her score is the total of her two dice. If Jane’s score is higher than Bill’s, she wins the game. What is the probability the Jane will win the game?a)15/36b)175/432c)575/1296d)583/1296e)1/2Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for GMAT.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
Here you can find the meaning of Bill and Jane pl ay a simple game involving two fair dice, each of which has six sides numbered from 1 to 6 (with an equal chance of landing on any side). Bill rolls the dice and his score is the total of the two dice. Jane then rolls the dice and her score is the total of her two dice. If Jane’s score is higher than Bill’s, she wins the game. What is the probability the Jane will win the game?a)15/36b)175/432c)575/1296d)583/1296e)1/2Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Bill and Jane pl ay a simple game involving two fair dice, each of which has six sides numbered from 1 to 6 (with an equal chance of landing on any side). Bill rolls the dice and his score is the total of the two dice. Jane then rolls the dice and her score is the total of her two dice. If Jane’s score is higher than Bill’s, she wins the game. What is the probability the Jane will win the game?a)15/36b)175/432c)575/1296d)583/1296e)1/2Correct answer is option 'C'. Can you explain this answer?, a detailed solution for Bill and Jane pl ay a simple game involving two fair dice, each of which has six sides numbered from 1 to 6 (with an equal chance of landing on any side). Bill rolls the dice and his score is the total of the two dice. Jane then rolls the dice and her score is the total of her two dice. If Jane’s score is higher than Bill’s, she wins the game. What is the probability the Jane will win the game?a)15/36b)175/432c)575/1296d)583/1296e)1/2Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of Bill and Jane pl ay a simple game involving two fair dice, each of which has six sides numbered from 1 to 6 (with an equal chance of landing on any side). Bill rolls the dice and his score is the total of the two dice. Jane then rolls the dice and her score is the total of her two dice. If Jane’s score is higher than Bill’s, she wins the game. What is the probability the Jane will win the game?a)15/36b)175/432c)575/1296d)583/1296e)1/2Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Bill and Jane pl ay a simple game involving two fair dice, each of which has six sides numbered from 1 to 6 (with an equal chance of landing on any side). Bill rolls the dice and his score is the total of the two dice. Jane then rolls the dice and her score is the total of her two dice. If Jane’s score is higher than Bill’s, she wins the game. What is the probability the Jane will win the game?a)15/36b)175/432c)575/1296d)583/1296e)1/2Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice GMAT tests.

|
Explore Courses for GMAT exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















