Physics Exam > Physics Questions > A calcite plate 0.0031 mm thick is cut and po...
Start Learning for Free
A calcite plate 0.0031 mm thick is cut and polished such that its optic axis is parallel to the surface. A plane polarized white light from a polariser is incident normally on the plate. Estimate the phase difference if the emergent beam for wavelengths is 7068 A, and μO = 1.6521 μe = 1.4811.
- a)3π/2
- b)π
- c)5π/2
- d)π/2
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A calcite plate 0.0031 mm thick is cut and polished such that its opti...
For a negative uniaxial crystal like calcite ,μO > μe. Therefore, the path difference between O and E-rays for calcite plate of thickness t is, Δ = ( μO- μe ) t and corresponding phase difference,
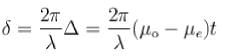
Here t= 0.00031 cm
For λ = 70684,
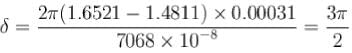
As the phase difference between O and E-rays is add multiple of π/2 therefore plane 2
polarized beam is converted into elliptically polarized light in general and circularly polarized light, if the vibration in the incident plane polarised light makes an angle of 45° with the optic axis of plate.
The correct answer is: 3π/2
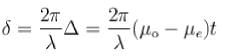
Here t= 0.00031 cm
For λ = 70684,
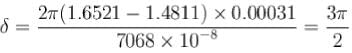
As the phase difference between O and E-rays is add multiple of π/2 therefore plane 2
polarized beam is converted into elliptically polarized light in general and circularly polarized light, if the vibration in the incident plane polarised light makes an angle of 45° with the optic axis of plate.
The correct answer is: 3π/2
Most Upvoted Answer
A calcite plate 0.0031 mm thick is cut and polished such that its opti...
To estimate the phase difference, we need to consider the birefringence of calcite. Calcite is a birefringent material, meaning it has two different indices of refraction for different polarizations of light. The phase difference between these two polarizations can be calculated using the equation:
Δφ = 2π * d * (n_e - n_o) / λ
Where:
Δφ is the phase difference
d is the thickness of the calcite plate (0.0031 mm)
n_e is the refractive index for the extraordinary ray
n_o is the refractive index for the ordinary ray
λ is the wavelength of the incident light (7068 Ångstroms)
To find the refractive indices for the extraordinary and ordinary rays, we need to know the birefringence of calcite. The birefringence (Δn) of calcite is typically around 0.172.
n_e = n_o + Δn/2
n_o = n_o - Δn/2
Substituting these values into the equation, we can calculate the phase difference:
n_e = n_o + Δn/2 = n_o + 0.172/2 = n_o + 0.086
n_o = n_o - Δn/2 = n_o - 0.172/2 = n_o - 0.086
Δφ = 2π * d * (n_e - n_o) / λ
Δφ = 2π * 0.0031 mm * (n_o + 0.086 - n_o + 0.086) / 7068 Ångstroms
Simplifying the equation:
Δφ = 2π * 0.0031 mm * 0.172 / 7068 Ångstroms
Converting the units to a common base:
1 mm = 10,000 Ångstroms
Δφ = 2π * (0.0031 mm * 10,000 Ångstroms/mm) * 0.172 / (7068 Ångstroms)
Δφ = 2π * 0.031 * 0.172 / 7068
Δφ ≈ 0.00148 radians
Therefore, the estimated phase difference is approximately 0.00148 radians.
Δφ = 2π * d * (n_e - n_o) / λ
Where:
Δφ is the phase difference
d is the thickness of the calcite plate (0.0031 mm)
n_e is the refractive index for the extraordinary ray
n_o is the refractive index for the ordinary ray
λ is the wavelength of the incident light (7068 Ångstroms)
To find the refractive indices for the extraordinary and ordinary rays, we need to know the birefringence of calcite. The birefringence (Δn) of calcite is typically around 0.172.
n_e = n_o + Δn/2
n_o = n_o - Δn/2
Substituting these values into the equation, we can calculate the phase difference:
n_e = n_o + Δn/2 = n_o + 0.172/2 = n_o + 0.086
n_o = n_o - Δn/2 = n_o - 0.172/2 = n_o - 0.086
Δφ = 2π * d * (n_e - n_o) / λ
Δφ = 2π * 0.0031 mm * (n_o + 0.086 - n_o + 0.086) / 7068 Ångstroms
Simplifying the equation:
Δφ = 2π * 0.0031 mm * 0.172 / 7068 Ångstroms
Converting the units to a common base:
1 mm = 10,000 Ångstroms
Δφ = 2π * (0.0031 mm * 10,000 Ångstroms/mm) * 0.172 / (7068 Ångstroms)
Δφ = 2π * 0.031 * 0.172 / 7068
Δφ ≈ 0.00148 radians
Therefore, the estimated phase difference is approximately 0.00148 radians.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
A calcite plate 0.0031 mm thick is cut and polished such that its optic axis is parallel to the surface. A plane polarized white light from a polariser is incident normally on the plate. Estimate the phase difference if the emergent beam for wavelengths is 7068A, andμO =1.6521μe = 1.4811.a)3π/2b)πc)5π/2d)π/2Correct answer is option 'A'. Can you explain this answer?
Question Description
A calcite plate 0.0031 mm thick is cut and polished such that its optic axis is parallel to the surface. A plane polarized white light from a polariser is incident normally on the plate. Estimate the phase difference if the emergent beam for wavelengths is 7068A, andμO =1.6521μe = 1.4811.a)3π/2b)πc)5π/2d)π/2Correct answer is option 'A'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A calcite plate 0.0031 mm thick is cut and polished such that its optic axis is parallel to the surface. A plane polarized white light from a polariser is incident normally on the plate. Estimate the phase difference if the emergent beam for wavelengths is 7068A, andμO =1.6521μe = 1.4811.a)3π/2b)πc)5π/2d)π/2Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A calcite plate 0.0031 mm thick is cut and polished such that its optic axis is parallel to the surface. A plane polarized white light from a polariser is incident normally on the plate. Estimate the phase difference if the emergent beam for wavelengths is 7068A, andμO =1.6521μe = 1.4811.a)3π/2b)πc)5π/2d)π/2Correct answer is option 'A'. Can you explain this answer?.
A calcite plate 0.0031 mm thick is cut and polished such that its optic axis is parallel to the surface. A plane polarized white light from a polariser is incident normally on the plate. Estimate the phase difference if the emergent beam for wavelengths is 7068A, andμO =1.6521μe = 1.4811.a)3π/2b)πc)5π/2d)π/2Correct answer is option 'A'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A calcite plate 0.0031 mm thick is cut and polished such that its optic axis is parallel to the surface. A plane polarized white light from a polariser is incident normally on the plate. Estimate the phase difference if the emergent beam for wavelengths is 7068A, andμO =1.6521μe = 1.4811.a)3π/2b)πc)5π/2d)π/2Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A calcite plate 0.0031 mm thick is cut and polished such that its optic axis is parallel to the surface. A plane polarized white light from a polariser is incident normally on the plate. Estimate the phase difference if the emergent beam for wavelengths is 7068A, andμO =1.6521μe = 1.4811.a)3π/2b)πc)5π/2d)π/2Correct answer is option 'A'. Can you explain this answer?.
Solutions for A calcite plate 0.0031 mm thick is cut and polished such that its optic axis is parallel to the surface. A plane polarized white light from a polariser is incident normally on the plate. Estimate the phase difference if the emergent beam for wavelengths is 7068A, andμO =1.6521μe = 1.4811.a)3π/2b)πc)5π/2d)π/2Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of A calcite plate 0.0031 mm thick is cut and polished such that its optic axis is parallel to the surface. A plane polarized white light from a polariser is incident normally on the plate. Estimate the phase difference if the emergent beam for wavelengths is 7068A, andμO =1.6521μe = 1.4811.a)3π/2b)πc)5π/2d)π/2Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A calcite plate 0.0031 mm thick is cut and polished such that its optic axis is parallel to the surface. A plane polarized white light from a polariser is incident normally on the plate. Estimate the phase difference if the emergent beam for wavelengths is 7068A, andμO =1.6521μe = 1.4811.a)3π/2b)πc)5π/2d)π/2Correct answer is option 'A'. Can you explain this answer?, a detailed solution for A calcite plate 0.0031 mm thick is cut and polished such that its optic axis is parallel to the surface. A plane polarized white light from a polariser is incident normally on the plate. Estimate the phase difference if the emergent beam for wavelengths is 7068A, andμO =1.6521μe = 1.4811.a)3π/2b)πc)5π/2d)π/2Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of A calcite plate 0.0031 mm thick is cut and polished such that its optic axis is parallel to the surface. A plane polarized white light from a polariser is incident normally on the plate. Estimate the phase difference if the emergent beam for wavelengths is 7068A, andμO =1.6521μe = 1.4811.a)3π/2b)πc)5π/2d)π/2Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A calcite plate 0.0031 mm thick is cut and polished such that its optic axis is parallel to the surface. A plane polarized white light from a polariser is incident normally on the plate. Estimate the phase difference if the emergent beam for wavelengths is 7068A, andμO =1.6521μe = 1.4811.a)3π/2b)πc)5π/2d)π/2Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















