Physics Exam > Physics Questions > Consider two horizontal glass plates with a t...
Start Learning for Free
Consider two horizontal glass plates with a thin film of air between them. Find the minimum value of the thickness of the film in nm of air for which the film as seen by the reflected light will appear bright if it is illuminated normally from above by blue light of wavelength 485 nm?
Correct answer is '122'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Consider two horizontal glass plates with a thin film of air between t...
For a thin film of thickness t, one can easily find the condition for interference phenomenon. Since the light has to travel approximately 2t to get back to the original incidence interface, one has 2t = mλ. However, since the light changes phase at the interface between air & glass, the condition for constructive interference becomes,
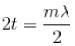
Minimum thickness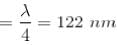
The correct answer is: 122
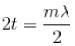
Minimum thickness
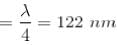
The correct answer is: 122
Most Upvoted Answer
Consider two horizontal glass plates with a thin film of air between t...
Introduction:
The phenomenon of interference occurs when two or more waves superpose to form a resultant wave. In thin film interference, light waves reflecting from the upper and lower surfaces of a thin film interfere with each other. This interference can be constructive or destructive, resulting in the appearance of bright or dark fringes, respectively.
Given:
- The incident light has a wavelength of 485 nm (blue light).
- The film is between two glass plates.
Approach:
To find the minimum thickness of the film for which it appears bright, we need to consider constructive interference between the reflected waves. Constructive interference occurs when the path difference between the two reflected waves is an integer multiple of the wavelength.
Path Difference:
The path difference between the two waves can be calculated using the formula:
Path Difference = 2 * (thickness of the film) * refractive index of the film
Constructive Interference Condition:
For constructive interference, the path difference should be equal to an integer multiple of the wavelength of the incident light:
Path Difference = m * wavelength
where m is an integer.
Calculation:
Let's substitute the given values into the equations and solve for the minimum thickness of the film.
Path Difference = 2 * (thickness of the film) * refractive index of the film
Path Difference = m * wavelength
For constructive interference, the path difference should be equal to an integer multiple of the wavelength:
2 * (thickness of the film) * refractive index of the film = m * wavelength
Since the film is surrounded by air on both sides, the refractive index of the film is approximately 1.
2 * (thickness of the film) = m * wavelength
Substituting the values:
2 * (thickness of the film) = 1 * 485 nm
Simplifying the equation:
thickness of the film = 485 nm / 2
thickness of the film = 242.5 nm
Therefore, the minimum thickness of the film for which it appears bright is 242.5 nm. Rounding it to the nearest whole number, the answer is 243 nm.
The phenomenon of interference occurs when two or more waves superpose to form a resultant wave. In thin film interference, light waves reflecting from the upper and lower surfaces of a thin film interfere with each other. This interference can be constructive or destructive, resulting in the appearance of bright or dark fringes, respectively.
Given:
- The incident light has a wavelength of 485 nm (blue light).
- The film is between two glass plates.
Approach:
To find the minimum thickness of the film for which it appears bright, we need to consider constructive interference between the reflected waves. Constructive interference occurs when the path difference between the two reflected waves is an integer multiple of the wavelength.
Path Difference:
The path difference between the two waves can be calculated using the formula:
Path Difference = 2 * (thickness of the film) * refractive index of the film
Constructive Interference Condition:
For constructive interference, the path difference should be equal to an integer multiple of the wavelength of the incident light:
Path Difference = m * wavelength
where m is an integer.
Calculation:
Let's substitute the given values into the equations and solve for the minimum thickness of the film.
Path Difference = 2 * (thickness of the film) * refractive index of the film
Path Difference = m * wavelength
For constructive interference, the path difference should be equal to an integer multiple of the wavelength:
2 * (thickness of the film) * refractive index of the film = m * wavelength
Since the film is surrounded by air on both sides, the refractive index of the film is approximately 1.
2 * (thickness of the film) = m * wavelength
Substituting the values:
2 * (thickness of the film) = 1 * 485 nm
Simplifying the equation:
thickness of the film = 485 nm / 2
thickness of the film = 242.5 nm
Therefore, the minimum thickness of the film for which it appears bright is 242.5 nm. Rounding it to the nearest whole number, the answer is 243 nm.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
Consider two horizontal glass plates with a thin film of air between them. Find the minimum value of the thickness of the film in nm of air for which the film as seen by the reflected light will appear bright if it is illuminated normally from above by blue light of wavelength 485 nm?Correct answer is '122'. Can you explain this answer?
Question Description
Consider two horizontal glass plates with a thin film of air between them. Find the minimum value of the thickness of the film in nm of air for which the film as seen by the reflected light will appear bright if it is illuminated normally from above by blue light of wavelength 485 nm?Correct answer is '122'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Consider two horizontal glass plates with a thin film of air between them. Find the minimum value of the thickness of the film in nm of air for which the film as seen by the reflected light will appear bright if it is illuminated normally from above by blue light of wavelength 485 nm?Correct answer is '122'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider two horizontal glass plates with a thin film of air between them. Find the minimum value of the thickness of the film in nm of air for which the film as seen by the reflected light will appear bright if it is illuminated normally from above by blue light of wavelength 485 nm?Correct answer is '122'. Can you explain this answer?.
Consider two horizontal glass plates with a thin film of air between them. Find the minimum value of the thickness of the film in nm of air for which the film as seen by the reflected light will appear bright if it is illuminated normally from above by blue light of wavelength 485 nm?Correct answer is '122'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Consider two horizontal glass plates with a thin film of air between them. Find the minimum value of the thickness of the film in nm of air for which the film as seen by the reflected light will appear bright if it is illuminated normally from above by blue light of wavelength 485 nm?Correct answer is '122'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider two horizontal glass plates with a thin film of air between them. Find the minimum value of the thickness of the film in nm of air for which the film as seen by the reflected light will appear bright if it is illuminated normally from above by blue light of wavelength 485 nm?Correct answer is '122'. Can you explain this answer?.
Solutions for Consider two horizontal glass plates with a thin film of air between them. Find the minimum value of the thickness of the film in nm of air for which the film as seen by the reflected light will appear bright if it is illuminated normally from above by blue light of wavelength 485 nm?Correct answer is '122'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of Consider two horizontal glass plates with a thin film of air between them. Find the minimum value of the thickness of the film in nm of air for which the film as seen by the reflected light will appear bright if it is illuminated normally from above by blue light of wavelength 485 nm?Correct answer is '122'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Consider two horizontal glass plates with a thin film of air between them. Find the minimum value of the thickness of the film in nm of air for which the film as seen by the reflected light will appear bright if it is illuminated normally from above by blue light of wavelength 485 nm?Correct answer is '122'. Can you explain this answer?, a detailed solution for Consider two horizontal glass plates with a thin film of air between them. Find the minimum value of the thickness of the film in nm of air for which the film as seen by the reflected light will appear bright if it is illuminated normally from above by blue light of wavelength 485 nm?Correct answer is '122'. Can you explain this answer? has been provided alongside types of Consider two horizontal glass plates with a thin film of air between them. Find the minimum value of the thickness of the film in nm of air for which the film as seen by the reflected light will appear bright if it is illuminated normally from above by blue light of wavelength 485 nm?Correct answer is '122'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Consider two horizontal glass plates with a thin film of air between them. Find the minimum value of the thickness of the film in nm of air for which the film as seen by the reflected light will appear bright if it is illuminated normally from above by blue light of wavelength 485 nm?Correct answer is '122'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















