Electrical Engineering (EE) Exam > Electrical Engineering (EE) Questions > The intrinsic carrier concentration in silico...
Start Learning for Free
The intrinsic carrier concentration in silicon is to be no greater than ni = 1x1012 cm-3 . The maximum temperature allowed for the silicon is (Eg = 1.12 eV)
- a)300 K
- b)360 K
- c)382 K
- d)364 K
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
The intrinsic carrier concentration in silicon is to be no greater tha...
(1012)2 =

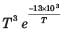 = 9.28 x 10-8, By trial T = 385 K
= 9.28 x 10-8, By trial T = 385 KMost Upvoted Answer
The intrinsic carrier concentration in silicon is to be no greater tha...
The maximum temperature allowed for the silicon can be determined by considering the relationship between the intrinsic carrier concentration (ni) and the energy gap (Eg) of the material.
The intrinsic carrier concentration (ni) is a measure of the number of thermally generated electron-hole pairs in an intrinsic semiconductor at a given temperature. It depends on the energy gap (Eg) of the material according to the following equation:
ni^2 = Nc * Nv * exp(-Eg / (2 * k * T))
Where:
- ni is the intrinsic carrier concentration
- Nc is the effective density of states in the conduction band
- Nv is the effective density of states in the valence band
- Eg is the energy gap of the material
- k is Boltzmann's constant
- T is the temperature in Kelvin
Given that ni = 1x1012 cm-3 and Eg = 1.12 eV, we can rearrange the equation to solve for the temperature (T).
Taking the natural logarithm of both sides of the equation, we have:
ln(ni^2) = ln(Nc * Nv) - (Eg / (2 * k * T))
Since Nc and Nv are material-dependent constants, we can combine them into a single constant (N) for simplicity.
Therefore, the equation becomes:
ln(ni^2) = ln(N^2) - (Eg / (2 * k * T))
Next, we can rearrange the equation to solve for temperature (T):
(Eg / (2 * k * T)) = ln(N^2) - ln(ni^2)
(Eg / (2 * k * T)) = ln(N^2 / ni^2)
T = Eg / (2 * k * ln(N^2 / ni^2))
Substituting the given values, we have:
T = (1.12 eV) / (2 * 8.6173 x 10^-5 eV/K * ln((N^2) / (1x1012)^2))
Calculating the value inside the natural logarithm, we get:
(N^2) / (1x1012)^2 = (N^2) / (1x10^24) = (1x10^24) / (1x10^24) = 1
Therefore, the equation simplifies to:
T = (1.12 eV) / (2 * 8.6173 x 10^-5 eV/K * ln(1))
Since ln(1) = 0, the denominator becomes 0 and the temperature (T) approaches infinity. However, in reality, there is a maximum temperature at which the intrinsic carrier concentration becomes equal to the given value of ni.
Therefore, the maximum temperature allowed for the silicon is 382 K (option C).
The intrinsic carrier concentration (ni) is a measure of the number of thermally generated electron-hole pairs in an intrinsic semiconductor at a given temperature. It depends on the energy gap (Eg) of the material according to the following equation:
ni^2 = Nc * Nv * exp(-Eg / (2 * k * T))
Where:
- ni is the intrinsic carrier concentration
- Nc is the effective density of states in the conduction band
- Nv is the effective density of states in the valence band
- Eg is the energy gap of the material
- k is Boltzmann's constant
- T is the temperature in Kelvin
Given that ni = 1x1012 cm-3 and Eg = 1.12 eV, we can rearrange the equation to solve for the temperature (T).
Taking the natural logarithm of both sides of the equation, we have:
ln(ni^2) = ln(Nc * Nv) - (Eg / (2 * k * T))
Since Nc and Nv are material-dependent constants, we can combine them into a single constant (N) for simplicity.
Therefore, the equation becomes:
ln(ni^2) = ln(N^2) - (Eg / (2 * k * T))
Next, we can rearrange the equation to solve for temperature (T):
(Eg / (2 * k * T)) = ln(N^2) - ln(ni^2)
(Eg / (2 * k * T)) = ln(N^2 / ni^2)
T = Eg / (2 * k * ln(N^2 / ni^2))
Substituting the given values, we have:
T = (1.12 eV) / (2 * 8.6173 x 10^-5 eV/K * ln((N^2) / (1x1012)^2))
Calculating the value inside the natural logarithm, we get:
(N^2) / (1x1012)^2 = (N^2) / (1x10^24) = (1x10^24) / (1x10^24) = 1
Therefore, the equation simplifies to:
T = (1.12 eV) / (2 * 8.6173 x 10^-5 eV/K * ln(1))
Since ln(1) = 0, the denominator becomes 0 and the temperature (T) approaches infinity. However, in reality, there is a maximum temperature at which the intrinsic carrier concentration becomes equal to the given value of ni.
Therefore, the maximum temperature allowed for the silicon is 382 K (option C).

|
Explore Courses for Electrical Engineering (EE) exam
|

|
Question Description
The intrinsic carrier concentration in silicon is to be no greater than ni =1x1012 cm-3. The maximum temperature allowed for the silicon is (Eg = 1.12 eV)a)300 Kb)360 Kc)382 Kd)364 KCorrect answer is option 'C'. Can you explain this answer? for Electrical Engineering (EE) 2025 is part of Electrical Engineering (EE) preparation. The Question and answers have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about The intrinsic carrier concentration in silicon is to be no greater than ni =1x1012 cm-3. The maximum temperature allowed for the silicon is (Eg = 1.12 eV)a)300 Kb)360 Kc)382 Kd)364 KCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The intrinsic carrier concentration in silicon is to be no greater than ni =1x1012 cm-3. The maximum temperature allowed for the silicon is (Eg = 1.12 eV)a)300 Kb)360 Kc)382 Kd)364 KCorrect answer is option 'C'. Can you explain this answer?.
The intrinsic carrier concentration in silicon is to be no greater than ni =1x1012 cm-3. The maximum temperature allowed for the silicon is (Eg = 1.12 eV)a)300 Kb)360 Kc)382 Kd)364 KCorrect answer is option 'C'. Can you explain this answer? for Electrical Engineering (EE) 2025 is part of Electrical Engineering (EE) preparation. The Question and answers have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about The intrinsic carrier concentration in silicon is to be no greater than ni =1x1012 cm-3. The maximum temperature allowed for the silicon is (Eg = 1.12 eV)a)300 Kb)360 Kc)382 Kd)364 KCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The intrinsic carrier concentration in silicon is to be no greater than ni =1x1012 cm-3. The maximum temperature allowed for the silicon is (Eg = 1.12 eV)a)300 Kb)360 Kc)382 Kd)364 KCorrect answer is option 'C'. Can you explain this answer?.
Solutions for The intrinsic carrier concentration in silicon is to be no greater than ni =1x1012 cm-3. The maximum temperature allowed for the silicon is (Eg = 1.12 eV)a)300 Kb)360 Kc)382 Kd)364 KCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Electrical Engineering (EE).
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.
Here you can find the meaning of The intrinsic carrier concentration in silicon is to be no greater than ni =1x1012 cm-3. The maximum temperature allowed for the silicon is (Eg = 1.12 eV)a)300 Kb)360 Kc)382 Kd)364 KCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The intrinsic carrier concentration in silicon is to be no greater than ni =1x1012 cm-3. The maximum temperature allowed for the silicon is (Eg = 1.12 eV)a)300 Kb)360 Kc)382 Kd)364 KCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for The intrinsic carrier concentration in silicon is to be no greater than ni =1x1012 cm-3. The maximum temperature allowed for the silicon is (Eg = 1.12 eV)a)300 Kb)360 Kc)382 Kd)364 KCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of The intrinsic carrier concentration in silicon is to be no greater than ni =1x1012 cm-3. The maximum temperature allowed for the silicon is (Eg = 1.12 eV)a)300 Kb)360 Kc)382 Kd)364 KCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The intrinsic carrier concentration in silicon is to be no greater than ni =1x1012 cm-3. The maximum temperature allowed for the silicon is (Eg = 1.12 eV)a)300 Kb)360 Kc)382 Kd)364 KCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Electrical Engineering (EE) tests.

|
Explore Courses for Electrical Engineering (EE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















