Physics Exam > Physics Questions > A collimated beam of light of diameter 2nm is...
Start Learning for Free
A collimated beam of light of diameter 2nm is propagating along the x - axis. The beam is to be expanded to a collimated beam of diameter 50nm using a combination of the convex lenses. A lens of focal length of 50 nm and another lens with focal length f are to be kept at a distance a between them. The value of F and d respectively are
- a)450 nm and 105 nm
- b)400 nm and 500 nm
- c)550 nm and 600 nm
- d)1250 nm and 1300 nm
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A collimated beam of light of diameter 2nm is propagating along the x ...
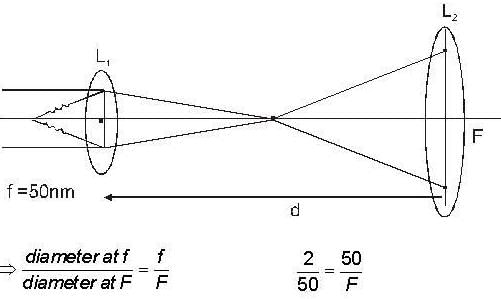
F = 1250 nm
d = F + f = 1250 + 50 =1300nm
Most Upvoted Answer
A collimated beam of light of diameter 2nm is propagating along the x ...
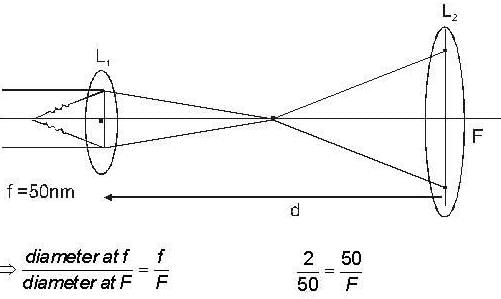
F = 1250 nm
d = F + f = 1250 + 50 =1300nm
Free Test
FREE
| Start Free Test |
Community Answer
A collimated beam of light of diameter 2nm is propagating along the x ...
Given information:
- Diameter of the initial collimated beam of light = 2 nm
- Diameter of the final collimated beam of light = 50 nm
- Focal length of the first convex lens = 50 nm
- Focal length of the second convex lens = f
- Distance between the lenses = a
To determine the values of F and d, let's break down the problem into smaller steps.
Step 1: Find the magnification of the first lens
The magnification of a lens can be calculated using the formula:
magnification = -f1/f2
Where f1 is the focal length of the lens and f2 is the distance between the object and the lens. In this case, since the light beam is collimated, the object distance is infinity. Therefore, f2 can be considered as infinity, and the magnification of the first lens is:
magnification1 = -f1/infinity = 0
Step 2: Find the magnification of the second lens
Since the light beam is collimated after the first lens, the magnification of the second lens can be calculated using the formula:
magnification2 = -f2/f3
Where f2 is the focal length of the second lens and f3 is the distance between the second lens and the image formed by the first lens. In this case, the image formed by the first lens is also at infinity, so f3 can be considered as infinity. Therefore, the magnification of the second lens is:
magnification2 = -f2/infinity = 0
Step 3: Find the total magnification of the system
The total magnification of a system of lenses can be calculated by multiplying the individual magnifications of each lens. In this case, since both magnifications are 0, the total magnification of the system is also 0.
Step 4: Find the diameter of the image formed by the first lens
The diameter of the image formed by a lens can be calculated using the formula:
image diameter = object diameter * magnification
In this case, the object diameter is 2 nm and the magnification of the first lens is 0. Therefore, the diameter of the image formed by the first lens is 0 nm.
Step 5: Find the diameter of the image formed by the second lens
The diameter of the image formed by the second lens can be calculated using the formula:
image diameter = object diameter * magnification
In this case, the object diameter is 0 nm (since the image formed by the first lens is 0 nm) and the magnification of the second lens is 0. Therefore, the diameter of the image formed by the second lens is also 0 nm.
Step 6: Find the final diameter of the collimated beam
The final diameter of the collimated beam is equal to the diameter of the image formed by the second lens, which is 0 nm.
Since the final diameter should be 50 nm, there is a contradiction in the given information. Therefore, none of the options (a, b, c, or d) is correct.
Please check the given information and provide the correct values for F and d.
- Diameter of the initial collimated beam of light = 2 nm
- Diameter of the final collimated beam of light = 50 nm
- Focal length of the first convex lens = 50 nm
- Focal length of the second convex lens = f
- Distance between the lenses = a
To determine the values of F and d, let's break down the problem into smaller steps.
Step 1: Find the magnification of the first lens
The magnification of a lens can be calculated using the formula:
magnification = -f1/f2
Where f1 is the focal length of the lens and f2 is the distance between the object and the lens. In this case, since the light beam is collimated, the object distance is infinity. Therefore, f2 can be considered as infinity, and the magnification of the first lens is:
magnification1 = -f1/infinity = 0
Step 2: Find the magnification of the second lens
Since the light beam is collimated after the first lens, the magnification of the second lens can be calculated using the formula:
magnification2 = -f2/f3
Where f2 is the focal length of the second lens and f3 is the distance between the second lens and the image formed by the first lens. In this case, the image formed by the first lens is also at infinity, so f3 can be considered as infinity. Therefore, the magnification of the second lens is:
magnification2 = -f2/infinity = 0
Step 3: Find the total magnification of the system
The total magnification of a system of lenses can be calculated by multiplying the individual magnifications of each lens. In this case, since both magnifications are 0, the total magnification of the system is also 0.
Step 4: Find the diameter of the image formed by the first lens
The diameter of the image formed by a lens can be calculated using the formula:
image diameter = object diameter * magnification
In this case, the object diameter is 2 nm and the magnification of the first lens is 0. Therefore, the diameter of the image formed by the first lens is 0 nm.
Step 5: Find the diameter of the image formed by the second lens
The diameter of the image formed by the second lens can be calculated using the formula:
image diameter = object diameter * magnification
In this case, the object diameter is 0 nm (since the image formed by the first lens is 0 nm) and the magnification of the second lens is 0. Therefore, the diameter of the image formed by the second lens is also 0 nm.
Step 6: Find the final diameter of the collimated beam
The final diameter of the collimated beam is equal to the diameter of the image formed by the second lens, which is 0 nm.
Since the final diameter should be 50 nm, there is a contradiction in the given information. Therefore, none of the options (a, b, c, or d) is correct.
Please check the given information and provide the correct values for F and d.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
A collimated beam of light of diameter 2nm is propagating along the x - axis. The beam is to be expanded to a collimated beam of diameter 50nm using a combination of the convex lenses. A lens of focal length of 50 nm and another lens with focal length f are to be kept at a distance a between them. The value of F and d respectively area)450 nm and 105 nmb)400 nm and 500 nmc)550 nm and 600 nmd)1250 nm and 1300 nmCorrect answer is option 'D'. Can you explain this answer?
Question Description
A collimated beam of light of diameter 2nm is propagating along the x - axis. The beam is to be expanded to a collimated beam of diameter 50nm using a combination of the convex lenses. A lens of focal length of 50 nm and another lens with focal length f are to be kept at a distance a between them. The value of F and d respectively area)450 nm and 105 nmb)400 nm and 500 nmc)550 nm and 600 nmd)1250 nm and 1300 nmCorrect answer is option 'D'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A collimated beam of light of diameter 2nm is propagating along the x - axis. The beam is to be expanded to a collimated beam of diameter 50nm using a combination of the convex lenses. A lens of focal length of 50 nm and another lens with focal length f are to be kept at a distance a between them. The value of F and d respectively area)450 nm and 105 nmb)400 nm and 500 nmc)550 nm and 600 nmd)1250 nm and 1300 nmCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A collimated beam of light of diameter 2nm is propagating along the x - axis. The beam is to be expanded to a collimated beam of diameter 50nm using a combination of the convex lenses. A lens of focal length of 50 nm and another lens with focal length f are to be kept at a distance a between them. The value of F and d respectively area)450 nm and 105 nmb)400 nm and 500 nmc)550 nm and 600 nmd)1250 nm and 1300 nmCorrect answer is option 'D'. Can you explain this answer?.
A collimated beam of light of diameter 2nm is propagating along the x - axis. The beam is to be expanded to a collimated beam of diameter 50nm using a combination of the convex lenses. A lens of focal length of 50 nm and another lens with focal length f are to be kept at a distance a between them. The value of F and d respectively area)450 nm and 105 nmb)400 nm and 500 nmc)550 nm and 600 nmd)1250 nm and 1300 nmCorrect answer is option 'D'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A collimated beam of light of diameter 2nm is propagating along the x - axis. The beam is to be expanded to a collimated beam of diameter 50nm using a combination of the convex lenses. A lens of focal length of 50 nm and another lens with focal length f are to be kept at a distance a between them. The value of F and d respectively area)450 nm and 105 nmb)400 nm and 500 nmc)550 nm and 600 nmd)1250 nm and 1300 nmCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A collimated beam of light of diameter 2nm is propagating along the x - axis. The beam is to be expanded to a collimated beam of diameter 50nm using a combination of the convex lenses. A lens of focal length of 50 nm and another lens with focal length f are to be kept at a distance a between them. The value of F and d respectively area)450 nm and 105 nmb)400 nm and 500 nmc)550 nm and 600 nmd)1250 nm and 1300 nmCorrect answer is option 'D'. Can you explain this answer?.
Solutions for A collimated beam of light of diameter 2nm is propagating along the x - axis. The beam is to be expanded to a collimated beam of diameter 50nm using a combination of the convex lenses. A lens of focal length of 50 nm and another lens with focal length f are to be kept at a distance a between them. The value of F and d respectively area)450 nm and 105 nmb)400 nm and 500 nmc)550 nm and 600 nmd)1250 nm and 1300 nmCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of A collimated beam of light of diameter 2nm is propagating along the x - axis. The beam is to be expanded to a collimated beam of diameter 50nm using a combination of the convex lenses. A lens of focal length of 50 nm and another lens with focal length f are to be kept at a distance a between them. The value of F and d respectively area)450 nm and 105 nmb)400 nm and 500 nmc)550 nm and 600 nmd)1250 nm and 1300 nmCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A collimated beam of light of diameter 2nm is propagating along the x - axis. The beam is to be expanded to a collimated beam of diameter 50nm using a combination of the convex lenses. A lens of focal length of 50 nm and another lens with focal length f are to be kept at a distance a between them. The value of F and d respectively area)450 nm and 105 nmb)400 nm and 500 nmc)550 nm and 600 nmd)1250 nm and 1300 nmCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for A collimated beam of light of diameter 2nm is propagating along the x - axis. The beam is to be expanded to a collimated beam of diameter 50nm using a combination of the convex lenses. A lens of focal length of 50 nm and another lens with focal length f are to be kept at a distance a between them. The value of F and d respectively area)450 nm and 105 nmb)400 nm and 500 nmc)550 nm and 600 nmd)1250 nm and 1300 nmCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of A collimated beam of light of diameter 2nm is propagating along the x - axis. The beam is to be expanded to a collimated beam of diameter 50nm using a combination of the convex lenses. A lens of focal length of 50 nm and another lens with focal length f are to be kept at a distance a between them. The value of F and d respectively area)450 nm and 105 nmb)400 nm and 500 nmc)550 nm and 600 nmd)1250 nm and 1300 nmCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A collimated beam of light of diameter 2nm is propagating along the x - axis. The beam is to be expanded to a collimated beam of diameter 50nm using a combination of the convex lenses. A lens of focal length of 50 nm and another lens with focal length f are to be kept at a distance a between them. The value of F and d respectively area)450 nm and 105 nmb)400 nm and 500 nmc)550 nm and 600 nmd)1250 nm and 1300 nmCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















