Computer Science Engineering (CSE) Exam > Computer Science Engineering (CSE) Questions > Let a = (aij) be an n-rowed square matrix and...
Start Learning for Free
Let a = (aij) be an n-rowed square matrix and I12 be the matrix obtained by interchanging the first and second rows of the n-rowed Identity matrix. Then AI12 is such that its first
- a)Row the same as its second row
- b)Row is the same as the second row of A
- c)Column is the same as the second column A
- d)Row is all zero
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Let a = (aij) be an n-rowed square matrix and I12 be the matrix obtain...
Let, 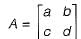
I12 is the matrix obtained by inter-changing the first and second row of the identity Matrix I.
So

AI12 is the matrix having first column same as the second column of A.
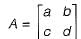
I12 is the matrix obtained by inter-changing the first and second row of the identity Matrix I.
So

AI12 is the matrix having first column same as the second column of A.
Most Upvoted Answer
Let a = (aij) be an n-rowed square matrix and I12 be the matrix obtain...
Question Analysis:
We are given a square matrix 'A' and we need to find the matrix 'AI12', obtained by interchanging the first and second rows of the n-rowed Identity matrix. We need to determine the properties of the resulting matrix 'AI12'.
Solution:
To solve this problem, let's break it down into steps:
Step 1: Write the given information:
- 'A' is an n-rowed square matrix.
- 'I12' is the matrix obtained by interchanging the first and second rows of the n-rowed Identity matrix.
Step 2: Understand the properties of the Identity matrix:
- The Identity matrix is a square matrix with ones on the diagonal and zeros elsewhere.
- It is denoted by 'I'.
- For example, if n = 3, then the Identity matrix is:
I = |1 0 0|
|0 1 0|
|0 0 1|
Step 3: Understand the operation of interchanging rows:
- Interchanging rows means swapping the elements of one row with the elements of another row.
- In this case, we are interchanging the first and second rows of the Identity matrix 'I' to obtain 'I12'.
Step 4: Calculate 'AI12':
- 'AI12' is the matrix obtained by multiplying 'A' with 'I12'.
- To calculate 'AI12', we need to multiply each element of 'A' with the corresponding element of 'I12'.
- Since 'I12' is obtained by interchanging the first and second rows of 'I', the resulting matrix will have the same elements as 'A', but with the first and second rows interchanged.
- Therefore, the resulting matrix 'AI12' will have the same elements as 'A', but with the second row as the first row and the first row as the second row.
Step 5: Determine the properties of 'AI12':
- From the above explanation, we can conclude that the resulting matrix 'AI12' will have its:
- First row the same as the second row of 'A'.
- Second row the same as the first row of 'A'.
- Third row (if applicable) the same as the third row of 'A'.
- And so on, for all the rows of 'A'.
Conclusion:
The correct answer is option 'C', which states that the column of 'AI12' is the same as the second column of 'A'. This is the correct interpretation of the properties of 'AI12' based on the given information and matrix operations.
We are given a square matrix 'A' and we need to find the matrix 'AI12', obtained by interchanging the first and second rows of the n-rowed Identity matrix. We need to determine the properties of the resulting matrix 'AI12'.
Solution:
To solve this problem, let's break it down into steps:
Step 1: Write the given information:
- 'A' is an n-rowed square matrix.
- 'I12' is the matrix obtained by interchanging the first and second rows of the n-rowed Identity matrix.
Step 2: Understand the properties of the Identity matrix:
- The Identity matrix is a square matrix with ones on the diagonal and zeros elsewhere.
- It is denoted by 'I'.
- For example, if n = 3, then the Identity matrix is:
I = |1 0 0|
|0 1 0|
|0 0 1|
Step 3: Understand the operation of interchanging rows:
- Interchanging rows means swapping the elements of one row with the elements of another row.
- In this case, we are interchanging the first and second rows of the Identity matrix 'I' to obtain 'I12'.
Step 4: Calculate 'AI12':
- 'AI12' is the matrix obtained by multiplying 'A' with 'I12'.
- To calculate 'AI12', we need to multiply each element of 'A' with the corresponding element of 'I12'.
- Since 'I12' is obtained by interchanging the first and second rows of 'I', the resulting matrix will have the same elements as 'A', but with the first and second rows interchanged.
- Therefore, the resulting matrix 'AI12' will have the same elements as 'A', but with the second row as the first row and the first row as the second row.
Step 5: Determine the properties of 'AI12':
- From the above explanation, we can conclude that the resulting matrix 'AI12' will have its:
- First row the same as the second row of 'A'.
- Second row the same as the first row of 'A'.
- Third row (if applicable) the same as the third row of 'A'.
- And so on, for all the rows of 'A'.
Conclusion:
The correct answer is option 'C', which states that the column of 'AI12' is the same as the second column of 'A'. This is the correct interpretation of the properties of 'AI12' based on the given information and matrix operations.
Attention Computer Science Engineering (CSE) Students!
To make sure you are not studying endlessly, EduRev has designed Computer Science Engineering (CSE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Computer Science Engineering (CSE).

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Similar Computer Science Engineering (CSE) Doubts
Let a = (aij) be an n-rowed square matrix and I12 be the matrix obtained by interchanging the first and second rows of the n-rowed Identity matrix. Then AI12 is such that its firsta)Row the same as its second rowb)Row is the same as the second row of Ac)Column is the same as the second column Ad)Row is all zeroCorrect answer is option 'C'. Can you explain this answer?
Question Description
Let a = (aij) be an n-rowed square matrix and I12 be the matrix obtained by interchanging the first and second rows of the n-rowed Identity matrix. Then AI12 is such that its firsta)Row the same as its second rowb)Row is the same as the second row of Ac)Column is the same as the second column Ad)Row is all zeroCorrect answer is option 'C'. Can you explain this answer? for Computer Science Engineering (CSE) 2024 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Let a = (aij) be an n-rowed square matrix and I12 be the matrix obtained by interchanging the first and second rows of the n-rowed Identity matrix. Then AI12 is such that its firsta)Row the same as its second rowb)Row is the same as the second row of Ac)Column is the same as the second column Ad)Row is all zeroCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Let a = (aij) be an n-rowed square matrix and I12 be the matrix obtained by interchanging the first and second rows of the n-rowed Identity matrix. Then AI12 is such that its firsta)Row the same as its second rowb)Row is the same as the second row of Ac)Column is the same as the second column Ad)Row is all zeroCorrect answer is option 'C'. Can you explain this answer?.
Let a = (aij) be an n-rowed square matrix and I12 be the matrix obtained by interchanging the first and second rows of the n-rowed Identity matrix. Then AI12 is such that its firsta)Row the same as its second rowb)Row is the same as the second row of Ac)Column is the same as the second column Ad)Row is all zeroCorrect answer is option 'C'. Can you explain this answer? for Computer Science Engineering (CSE) 2024 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Let a = (aij) be an n-rowed square matrix and I12 be the matrix obtained by interchanging the first and second rows of the n-rowed Identity matrix. Then AI12 is such that its firsta)Row the same as its second rowb)Row is the same as the second row of Ac)Column is the same as the second column Ad)Row is all zeroCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Let a = (aij) be an n-rowed square matrix and I12 be the matrix obtained by interchanging the first and second rows of the n-rowed Identity matrix. Then AI12 is such that its firsta)Row the same as its second rowb)Row is the same as the second row of Ac)Column is the same as the second column Ad)Row is all zeroCorrect answer is option 'C'. Can you explain this answer?.
Solutions for Let a = (aij) be an n-rowed square matrix and I12 be the matrix obtained by interchanging the first and second rows of the n-rowed Identity matrix. Then AI12 is such that its firsta)Row the same as its second rowb)Row is the same as the second row of Ac)Column is the same as the second column Ad)Row is all zeroCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Computer Science Engineering (CSE).
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Here you can find the meaning of Let a = (aij) be an n-rowed square matrix and I12 be the matrix obtained by interchanging the first and second rows of the n-rowed Identity matrix. Then AI12 is such that its firsta)Row the same as its second rowb)Row is the same as the second row of Ac)Column is the same as the second column Ad)Row is all zeroCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Let a = (aij) be an n-rowed square matrix and I12 be the matrix obtained by interchanging the first and second rows of the n-rowed Identity matrix. Then AI12 is such that its firsta)Row the same as its second rowb)Row is the same as the second row of Ac)Column is the same as the second column Ad)Row is all zeroCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for Let a = (aij) be an n-rowed square matrix and I12 be the matrix obtained by interchanging the first and second rows of the n-rowed Identity matrix. Then AI12 is such that its firsta)Row the same as its second rowb)Row is the same as the second row of Ac)Column is the same as the second column Ad)Row is all zeroCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of Let a = (aij) be an n-rowed square matrix and I12 be the matrix obtained by interchanging the first and second rows of the n-rowed Identity matrix. Then AI12 is such that its firsta)Row the same as its second rowb)Row is the same as the second row of Ac)Column is the same as the second column Ad)Row is all zeroCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Let a = (aij) be an n-rowed square matrix and I12 be the matrix obtained by interchanging the first and second rows of the n-rowed Identity matrix. Then AI12 is such that its firsta)Row the same as its second rowb)Row is the same as the second row of Ac)Column is the same as the second column Ad)Row is all zeroCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Computer Science Engineering (CSE) tests.

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























