Physics Exam > Physics Questions > A horizontal platform executes up and clown S...
Start Learning for Free
A horizontal platform executes up and clown S.H.M. about a mean position. Its period is 2π sec. A mass m is resting on the platform. The greatest value of amplitude (in m) so that the mass ‘m' may not leave the platform i s _________ .
Correct answer is '9.8'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A horizontal platform executes up and clown S.H.M. about a mean positi...
Here if R = normal reaction then R-mg
= -mg
or R = mg-ma = m(g-a)
Also Max. acceleration a= Aω2
∴ R = mg - mAω2
For object, not to leave the platform R = 0
∴ mg = - mAω2
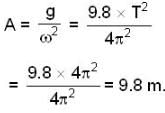
= -mg
or R = mg-ma = m(g-a)
Also Max. acceleration a= Aω2
∴ R = mg - mAω2
For object, not to leave the platform R = 0
∴ mg = - mAω2
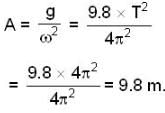
Most Upvoted Answer
A horizontal platform executes up and clown S.H.M. about a mean positi...
Here if R = normal reaction then R-mg
= -mg
or R = mg-ma = m(g-a)
Also Max. acceleration a= Aω2
∴ R = mg - mAω2
For object, not to leave the platform R = 0
∴ mg = - mAω2
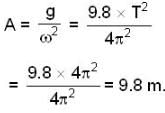
= -mg
or R = mg-ma = m(g-a)
Also Max. acceleration a= Aω2
∴ R = mg - mAω2
For object, not to leave the platform R = 0
∴ mg = - mAω2
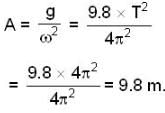
Free Test
FREE
| Start Free Test |
Community Answer
A horizontal platform executes up and clown S.H.M. about a mean positi...
The period of a simple harmonic motion (SHM) is the time taken for one complete cycle of the motion. In this case, the period of the horizontal platform executing SHM is given as 2 units of time.
This means that it takes 2 units of time for the platform to go through one complete cycle of oscillation. In other words, it takes 2 units of time for the platform to move from its initial position, reach its maximum displacement in one direction, return to its initial position, reach its maximum displacement in the opposite direction, and finally return to its initial position again.
During this period of 2 units of time, the platform will go through all the phases of SHM, including moving away from the mean position, reaching the maximum displacement, moving back towards the mean position, passing through the mean position, moving away from the mean position in the opposite direction, reaching the maximum displacement in the opposite direction, moving back towards the mean position again, and finally passing through the mean position to complete one cycle.
The frequency of the SHM can be calculated by taking the reciprocal of the period. In this case, the frequency would be 1/2 units of time, which means that the platform completes one cycle of oscillation every 1/2 unit of time.
It's important to note that in SHM, the mean position refers to the equilibrium position of the platform, where the net force acting on it is zero.
This means that it takes 2 units of time for the platform to go through one complete cycle of oscillation. In other words, it takes 2 units of time for the platform to move from its initial position, reach its maximum displacement in one direction, return to its initial position, reach its maximum displacement in the opposite direction, and finally return to its initial position again.
During this period of 2 units of time, the platform will go through all the phases of SHM, including moving away from the mean position, reaching the maximum displacement, moving back towards the mean position, passing through the mean position, moving away from the mean position in the opposite direction, reaching the maximum displacement in the opposite direction, moving back towards the mean position again, and finally passing through the mean position to complete one cycle.
The frequency of the SHM can be calculated by taking the reciprocal of the period. In this case, the frequency would be 1/2 units of time, which means that the platform completes one cycle of oscillation every 1/2 unit of time.
It's important to note that in SHM, the mean position refers to the equilibrium position of the platform, where the net force acting on it is zero.
|
Explore Courses for Physics exam
|
|
Similar Physics Doubts
A horizontal platform executes up and clown S.H.M. about a mean position. Its period is 2π sec. A mass m is resting on the platform. The greatest value of amplitude (in m) so that the mass ‘m may not leave the platform i s _________ .Correct answer is '9.8'. Can you explain this answer?
Question Description
A horizontal platform executes up and clown S.H.M. about a mean position. Its period is 2π sec. A mass m is resting on the platform. The greatest value of amplitude (in m) so that the mass ‘m may not leave the platform i s _________ .Correct answer is '9.8'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A horizontal platform executes up and clown S.H.M. about a mean position. Its period is 2π sec. A mass m is resting on the platform. The greatest value of amplitude (in m) so that the mass ‘m may not leave the platform i s _________ .Correct answer is '9.8'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A horizontal platform executes up and clown S.H.M. about a mean position. Its period is 2π sec. A mass m is resting on the platform. The greatest value of amplitude (in m) so that the mass ‘m may not leave the platform i s _________ .Correct answer is '9.8'. Can you explain this answer?.
A horizontal platform executes up and clown S.H.M. about a mean position. Its period is 2π sec. A mass m is resting on the platform. The greatest value of amplitude (in m) so that the mass ‘m may not leave the platform i s _________ .Correct answer is '9.8'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A horizontal platform executes up and clown S.H.M. about a mean position. Its period is 2π sec. A mass m is resting on the platform. The greatest value of amplitude (in m) so that the mass ‘m may not leave the platform i s _________ .Correct answer is '9.8'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A horizontal platform executes up and clown S.H.M. about a mean position. Its period is 2π sec. A mass m is resting on the platform. The greatest value of amplitude (in m) so that the mass ‘m may not leave the platform i s _________ .Correct answer is '9.8'. Can you explain this answer?.
Solutions for A horizontal platform executes up and clown S.H.M. about a mean position. Its period is 2π sec. A mass m is resting on the platform. The greatest value of amplitude (in m) so that the mass ‘m may not leave the platform i s _________ .Correct answer is '9.8'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of A horizontal platform executes up and clown S.H.M. about a mean position. Its period is 2π sec. A mass m is resting on the platform. The greatest value of amplitude (in m) so that the mass ‘m may not leave the platform i s _________ .Correct answer is '9.8'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A horizontal platform executes up and clown S.H.M. about a mean position. Its period is 2π sec. A mass m is resting on the platform. The greatest value of amplitude (in m) so that the mass ‘m may not leave the platform i s _________ .Correct answer is '9.8'. Can you explain this answer?, a detailed solution for A horizontal platform executes up and clown S.H.M. about a mean position. Its period is 2π sec. A mass m is resting on the platform. The greatest value of amplitude (in m) so that the mass ‘m may not leave the platform i s _________ .Correct answer is '9.8'. Can you explain this answer? has been provided alongside types of A horizontal platform executes up and clown S.H.M. about a mean position. Its period is 2π sec. A mass m is resting on the platform. The greatest value of amplitude (in m) so that the mass ‘m may not leave the platform i s _________ .Correct answer is '9.8'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A horizontal platform executes up and clown S.H.M. about a mean position. Its period is 2π sec. A mass m is resting on the platform. The greatest value of amplitude (in m) so that the mass ‘m may not leave the platform i s _________ .Correct answer is '9.8'. Can you explain this answer? tests, examples and also practice Physics tests.
|
|
Explore Courses for Physics exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup