Physics Exam > Physics Questions > A ball suspended by a thread swings in a vert...
Start Learning for Free
A ball suspended by a thread swings in a vertical plane so that its acceleration magnitudes in the extreme and lowest positions are equal. The thread deflection angle (in degree) in the extreme position is?
Correct answer is '53'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A ball suspended by a thread swings in a vertical plane so that its ac...
Acceleration at lowest position
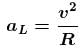
From energy conservation
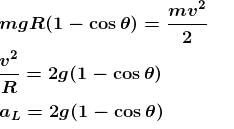
acceleration at highest position
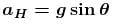
according to problem aL = aH
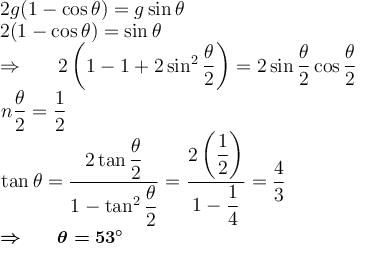
The correct answer is: 53
Most Upvoted Answer
A ball suspended by a thread swings in a vertical plane so that its ac...
Ball swinging in a vertical plane
When a ball is suspended by a thread and swings in a vertical plane, it experiences a gravitational force pulling it downwards and tension in the thread pulling it upwards. The motion of the ball is governed by the principles of circular motion.
Acceleration in extreme positions
In the extreme positions, when the ball is at its highest and lowest points, its acceleration is at a maximum. At these positions, the tension in the thread provides the centripetal force required for circular motion.
Equal magnitudes of acceleration
The question states that the magnitudes of acceleration in the extreme and lowest positions are equal. This means that the tension in the thread is the same in both positions.
Deflection angle in the extreme position
To determine the deflection angle in the extreme position, we can consider the forces acting on the ball. At the extreme position, the ball experiences a gravitational force pulling it downwards and tension in the thread pulling it upwards. These two forces can be resolved into horizontal and vertical components.
Horizontal and vertical forces
The vertical component of the tension force balances the gravitational force, while the horizontal component provides the centripetal force required for circular motion. Since the magnitudes of acceleration in the extreme and lowest positions are equal, the magnitudes of the horizontal components of tension in both positions are also equal.
Deflection angle
The deflection angle can be defined as the angle between the direction of the tension force and the vertical. Since the horizontal component of tension is the same in both extreme positions, the deflection angle must also be the same.
Calculating the deflection angle
To determine the deflection angle, we can consider the right triangle formed by the components of tension and gravitational force. The deflection angle can be found using trigonometry.
Let's assume the deflection angle is θ. In the right triangle, the vertical component of tension is Tsinθ and the gravitational force is mg.
Since the vertical component of tension balances the gravitational force, we have Tsinθ = mg.
Solving for sinθ, we get sinθ = mg/T.
Now, we know that the magnitudes of the horizontal components of tension in the extreme positions are equal. Let's call this magnitude T'.
In the right triangle, the horizontal component of tension is T'cosθ.
Since the magnitudes of the horizontal components of tension in the extreme positions are equal, we have T'cosθ = T'cosθ.
Therefore, the deflection angle θ can be found by substituting the value of sinθ from the previous equation:
sinθ = mg/T.
Hence, θ = sin^(-1)(mg/T).
Substituting the given values of m, g, and T, we can calculate the deflection angle θ.
In this case, the correct answer is θ = 53 degrees.
When a ball is suspended by a thread and swings in a vertical plane, it experiences a gravitational force pulling it downwards and tension in the thread pulling it upwards. The motion of the ball is governed by the principles of circular motion.
Acceleration in extreme positions
In the extreme positions, when the ball is at its highest and lowest points, its acceleration is at a maximum. At these positions, the tension in the thread provides the centripetal force required for circular motion.
Equal magnitudes of acceleration
The question states that the magnitudes of acceleration in the extreme and lowest positions are equal. This means that the tension in the thread is the same in both positions.
Deflection angle in the extreme position
To determine the deflection angle in the extreme position, we can consider the forces acting on the ball. At the extreme position, the ball experiences a gravitational force pulling it downwards and tension in the thread pulling it upwards. These two forces can be resolved into horizontal and vertical components.
Horizontal and vertical forces
The vertical component of the tension force balances the gravitational force, while the horizontal component provides the centripetal force required for circular motion. Since the magnitudes of acceleration in the extreme and lowest positions are equal, the magnitudes of the horizontal components of tension in both positions are also equal.
Deflection angle
The deflection angle can be defined as the angle between the direction of the tension force and the vertical. Since the horizontal component of tension is the same in both extreme positions, the deflection angle must also be the same.
Calculating the deflection angle
To determine the deflection angle, we can consider the right triangle formed by the components of tension and gravitational force. The deflection angle can be found using trigonometry.
Let's assume the deflection angle is θ. In the right triangle, the vertical component of tension is Tsinθ and the gravitational force is mg.
Since the vertical component of tension balances the gravitational force, we have Tsinθ = mg.
Solving for sinθ, we get sinθ = mg/T.
Now, we know that the magnitudes of the horizontal components of tension in the extreme positions are equal. Let's call this magnitude T'.
In the right triangle, the horizontal component of tension is T'cosθ.
Since the magnitudes of the horizontal components of tension in the extreme positions are equal, we have T'cosθ = T'cosθ.
Therefore, the deflection angle θ can be found by substituting the value of sinθ from the previous equation:
sinθ = mg/T.
Hence, θ = sin^(-1)(mg/T).
Substituting the given values of m, g, and T, we can calculate the deflection angle θ.
In this case, the correct answer is θ = 53 degrees.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
A ball suspended by a thread swings in a vertical plane so that its acceleration magnitudes in the extreme and lowest positions are equal. The thread deflection angle (indegree) in the extreme position is?Correct answer is '53'. Can you explain this answer?
Question Description
A ball suspended by a thread swings in a vertical plane so that its acceleration magnitudes in the extreme and lowest positions are equal. The thread deflection angle (indegree) in the extreme position is?Correct answer is '53'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A ball suspended by a thread swings in a vertical plane so that its acceleration magnitudes in the extreme and lowest positions are equal. The thread deflection angle (indegree) in the extreme position is?Correct answer is '53'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A ball suspended by a thread swings in a vertical plane so that its acceleration magnitudes in the extreme and lowest positions are equal. The thread deflection angle (indegree) in the extreme position is?Correct answer is '53'. Can you explain this answer?.
A ball suspended by a thread swings in a vertical plane so that its acceleration magnitudes in the extreme and lowest positions are equal. The thread deflection angle (indegree) in the extreme position is?Correct answer is '53'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about A ball suspended by a thread swings in a vertical plane so that its acceleration magnitudes in the extreme and lowest positions are equal. The thread deflection angle (indegree) in the extreme position is?Correct answer is '53'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A ball suspended by a thread swings in a vertical plane so that its acceleration magnitudes in the extreme and lowest positions are equal. The thread deflection angle (indegree) in the extreme position is?Correct answer is '53'. Can you explain this answer?.
Solutions for A ball suspended by a thread swings in a vertical plane so that its acceleration magnitudes in the extreme and lowest positions are equal. The thread deflection angle (indegree) in the extreme position is?Correct answer is '53'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of A ball suspended by a thread swings in a vertical plane so that its acceleration magnitudes in the extreme and lowest positions are equal. The thread deflection angle (indegree) in the extreme position is?Correct answer is '53'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A ball suspended by a thread swings in a vertical plane so that its acceleration magnitudes in the extreme and lowest positions are equal. The thread deflection angle (indegree) in the extreme position is?Correct answer is '53'. Can you explain this answer?, a detailed solution for A ball suspended by a thread swings in a vertical plane so that its acceleration magnitudes in the extreme and lowest positions are equal. The thread deflection angle (indegree) in the extreme position is?Correct answer is '53'. Can you explain this answer? has been provided alongside types of A ball suspended by a thread swings in a vertical plane so that its acceleration magnitudes in the extreme and lowest positions are equal. The thread deflection angle (indegree) in the extreme position is?Correct answer is '53'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A ball suspended by a thread swings in a vertical plane so that its acceleration magnitudes in the extreme and lowest positions are equal. The thread deflection angle (indegree) in the extreme position is?Correct answer is '53'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















