NEET Exam > NEET Questions > If a man goes 10 m toward north and 20 m towa...
Start Learning for Free
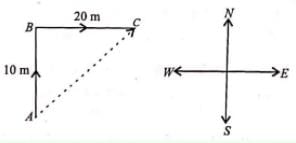
If a man goes 10 m toward north and 20 m toward east, then his displacement is
- a)22.5 m
- b)32 m
- c)29 m
- d)30 m
Correct answer is option 'A'. Can you explain this answer?
Most Upvoted Answer
If a man goes 10 m toward north and 20 m toward east, then his displac...
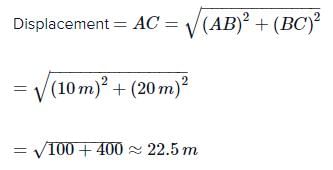
Free Test
FREE
| Start Free Test |
Community Answer
If a man goes 10 m toward north and 20 m toward east, then his displac...
**Displacement** is the shortest distance between the initial and final positions of an object. It is a vector quantity, meaning it has both magnitude and direction.
In this case, the man moves 10 m toward the north and 20 m toward the east. To find the displacement, we can use the Pythagorean theorem.
**Using the Pythagorean theorem:**
The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
Let's consider the displacement as the hypotenuse of a right-angled triangle. The northward movement can be considered as the vertical side, and the eastward movement can be considered as the horizontal side.
**Applying the Pythagorean theorem:**
Using the Pythagorean theorem, we can calculate the displacement as follows:
Displacement = √(vertical^2 + horizontal^2)
Given that the man moves 10 m toward the north and 20 m toward the east, we can substitute these values into the formula:
Displacement = √(10^2 + 20^2)
= √(100 + 400)
= √500
≈ 22.36 m
**Rounding the answer:**
Since the options provided are in whole numbers, we need to round our answer. The closest whole number to 22.36 is 22. Therefore, the correct answer is option 'A' - 22.5 m.
**Explanation:**
The displacement is the straight-line distance between the initial and final positions of an object. In this case, the man moves 10 m toward the north and 20 m toward the east. By using the Pythagorean theorem, we can find the displacement to be approximately 22.36 m. Rounding this value gives us the closest whole number, which is 22. Therefore, the correct answer is option 'A' - 22.5 m.
In this case, the man moves 10 m toward the north and 20 m toward the east. To find the displacement, we can use the Pythagorean theorem.
**Using the Pythagorean theorem:**
The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
Let's consider the displacement as the hypotenuse of a right-angled triangle. The northward movement can be considered as the vertical side, and the eastward movement can be considered as the horizontal side.
**Applying the Pythagorean theorem:**
Using the Pythagorean theorem, we can calculate the displacement as follows:
Displacement = √(vertical^2 + horizontal^2)
Given that the man moves 10 m toward the north and 20 m toward the east, we can substitute these values into the formula:
Displacement = √(10^2 + 20^2)
= √(100 + 400)
= √500
≈ 22.36 m
**Rounding the answer:**
Since the options provided are in whole numbers, we need to round our answer. The closest whole number to 22.36 is 22. Therefore, the correct answer is option 'A' - 22.5 m.
**Explanation:**
The displacement is the straight-line distance between the initial and final positions of an object. In this case, the man moves 10 m toward the north and 20 m toward the east. By using the Pythagorean theorem, we can find the displacement to be approximately 22.36 m. Rounding this value gives us the closest whole number, which is 22. Therefore, the correct answer is option 'A' - 22.5 m.
|
Explore Courses for NEET exam
|
|
Top Courses for NEETView all
Question Description
If a man goes 10 m toward north and 20 m toward east, then his displacement isa)22.5 mb)32 mc)29 md)30 mCorrect answer is option 'A'. Can you explain this answer? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about If a man goes 10 m toward north and 20 m toward east, then his displacement isa)22.5 mb)32 mc)29 md)30 mCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If a man goes 10 m toward north and 20 m toward east, then his displacement isa)22.5 mb)32 mc)29 md)30 mCorrect answer is option 'A'. Can you explain this answer?.
If a man goes 10 m toward north and 20 m toward east, then his displacement isa)22.5 mb)32 mc)29 md)30 mCorrect answer is option 'A'. Can you explain this answer? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about If a man goes 10 m toward north and 20 m toward east, then his displacement isa)22.5 mb)32 mc)29 md)30 mCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If a man goes 10 m toward north and 20 m toward east, then his displacement isa)22.5 mb)32 mc)29 md)30 mCorrect answer is option 'A'. Can you explain this answer?.
Solutions for If a man goes 10 m toward north and 20 m toward east, then his displacement isa)22.5 mb)32 mc)29 md)30 mCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of If a man goes 10 m toward north and 20 m toward east, then his displacement isa)22.5 mb)32 mc)29 md)30 mCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
If a man goes 10 m toward north and 20 m toward east, then his displacement isa)22.5 mb)32 mc)29 md)30 mCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for If a man goes 10 m toward north and 20 m toward east, then his displacement isa)22.5 mb)32 mc)29 md)30 mCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of If a man goes 10 m toward north and 20 m toward east, then his displacement isa)22.5 mb)32 mc)29 md)30 mCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice If a man goes 10 m toward north and 20 m toward east, then his displacement isa)22.5 mb)32 mc)29 md)30 mCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice NEET tests.
|
|
Explore Courses for NEET exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup