CLAT Exam > CLAT Questions > Directions: Study the given information and ...
Start Learning for Free
Directions: Study the given information and answer the following question.
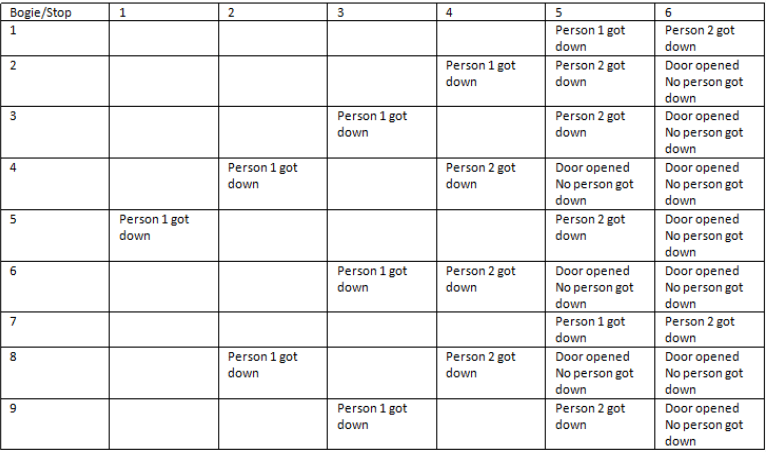
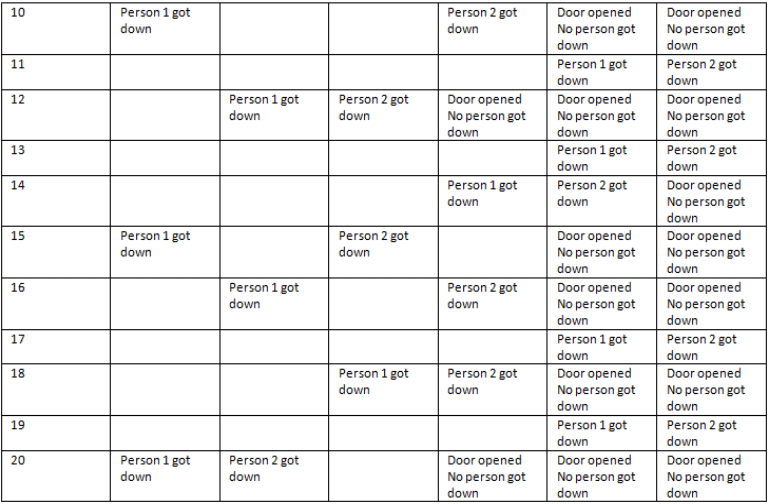
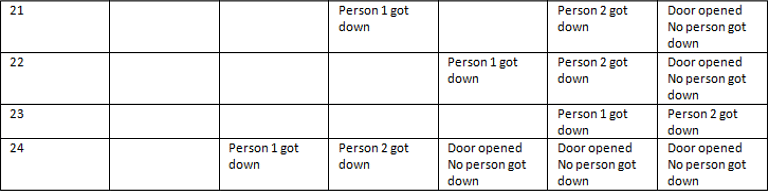
In an exhibition, there is a train with 24 bogies numbered 1 to 24. Each bogie has 2 seats only. It moves all over the exhibition in a circular path and reaches to the same point. It stops at 5 places before coming to the starting point, i.e. it stops at the same place 6th time.
The following information is given about stops:
(i) The stops were considered as stop 1, stop 2, ……… and stop 6 (the starting point).
(ii) At nth stop, only the doors of bogies whose numbers are multiples of (6 – n) will be opened, i.e. at stop 1, the doors whose numbers are multiples of (6 – 1) = 5 will be opened.
(iii) At stop 6, all the doors will be opened.
(iv) Assume that all the bogies are full of passengers and the two persons in the same bogie should not get down together at the same stop, but if the door of any bogie is opened at any stop and if there is a person in that bogie, he has to get down at that stop.
How many person got down at stop 6?
- a)6
- b)7
- c)8
- d)9
Correct answer is option 'B'. Can you explain this answer?
Most Upvoted Answer
Directions: Study the given information and answer the following ques...
Free Test
FREE
| Start Free Test |
Community Answer
Directions: Study the given information and answer the following ques...
Understanding the Scenario
In the exhibition train with 24 bogies, each bogie is numbered from 1 to 24 and has 2 seats. The train makes 6 stops, and at each stop, only certain bogies have their doors opened based on the rule provided.
Stop Rules
- Stop 1: Doors of bogies that are multiples of (6 - 1) = 5 will open.
- Open bogies: 5, 10, 15, 20.
- Stop 2: Doors of bogies that are multiples of (6 - 2) = 4 will open.
- Open bogies: 4, 8, 12, 16, 20, 24.
- Stop 3: Doors of bogies that are multiples of (6 - 3) = 3 will open.
- Open bogies: 3, 6, 9, 12, 15, 18, 21.
- Stop 4: Doors of bogies that are multiples of (6 - 4) = 2 will open.
- Open bogies: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24.
- Stop 5: Doors of bogies that are multiples of (6 - 5) = 1 will open.
- All bogies (1 to 24) will have their doors opened.
- Stop 6: All doors will be opened, allowing all passengers to get down.
Calculating Passengers Getting Down
- At each stop, the passengers in the opened bogies must get down individually. Since no two passengers in the same bogie can get down at the same stop, only one passenger from each opened bogie can exit.
- The total number of unique bogies that had their doors opened at the previous stops is important for stop 6.
Unique Bogies with Opened Doors
1. From Stop 1: 5, 10, 15, 20 (4 bogies)
2. From Stop 2: 4, 8, 12, 16, 20, 24 (6 bogies, but 20 is a repeat)
3. From Stop 3: 3, 6, 9, 12, 15, 18, 21 (7 bogies, but 12, 15 are repeats)
4. From Stop 4: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24 (12 bogies, with many repeats)
5. From Stop 5: All (24 bogies)
By analyzing, it is found that 7 unique bogies had their doors opened at previous stops which can have passengers getting down at Stop 6.
Conclusion
Thus, the total number of persons who got down at Stop 6 is 7. Hence, the correct answer is option B.
In the exhibition train with 24 bogies, each bogie is numbered from 1 to 24 and has 2 seats. The train makes 6 stops, and at each stop, only certain bogies have their doors opened based on the rule provided.
Stop Rules
- Stop 1: Doors of bogies that are multiples of (6 - 1) = 5 will open.
- Open bogies: 5, 10, 15, 20.
- Stop 2: Doors of bogies that are multiples of (6 - 2) = 4 will open.
- Open bogies: 4, 8, 12, 16, 20, 24.
- Stop 3: Doors of bogies that are multiples of (6 - 3) = 3 will open.
- Open bogies: 3, 6, 9, 12, 15, 18, 21.
- Stop 4: Doors of bogies that are multiples of (6 - 4) = 2 will open.
- Open bogies: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24.
- Stop 5: Doors of bogies that are multiples of (6 - 5) = 1 will open.
- All bogies (1 to 24) will have their doors opened.
- Stop 6: All doors will be opened, allowing all passengers to get down.
Calculating Passengers Getting Down
- At each stop, the passengers in the opened bogies must get down individually. Since no two passengers in the same bogie can get down at the same stop, only one passenger from each opened bogie can exit.
- The total number of unique bogies that had their doors opened at the previous stops is important for stop 6.
Unique Bogies with Opened Doors
1. From Stop 1: 5, 10, 15, 20 (4 bogies)
2. From Stop 2: 4, 8, 12, 16, 20, 24 (6 bogies, but 20 is a repeat)
3. From Stop 3: 3, 6, 9, 12, 15, 18, 21 (7 bogies, but 12, 15 are repeats)
4. From Stop 4: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24 (12 bogies, with many repeats)
5. From Stop 5: All (24 bogies)
By analyzing, it is found that 7 unique bogies had their doors opened at previous stops which can have passengers getting down at Stop 6.
Conclusion
Thus, the total number of persons who got down at Stop 6 is 7. Hence, the correct answer is option B.

|
Explore Courses for CLAT exam
|

|
Similar CLAT Doubts
Directions: Study the given information and answer the following question.In an exhibition, there is a train with 24 bogies numbered 1 to 24. Each bogie has 2 seats only. It moves all over the exhibition in a circular path and reaches to the same point. It stops at 5 places before coming to the starting point, i.e. it stops at the same place 6th time.The following information is given about stops:(i) The stops were considered as stop 1, stop 2, ……… and stop 6 (the starting point).(ii) At nth stop, only the doors of bogies whose numbers are multiples of (6 – n) will be opened, i.e. at stop 1, the doors whose numbers are multiples of (6 – 1) = 5 will be opened.(iii) At stop 6, all the doors will be opened.(iv) Assume that all the bogies are full of passengers and the two persons in the same bogie should not get down together at the same stop, but if the door of any bogie is opened at any stop and if there is a person in that bogie, he has to get down at that stop.How many person got down at stop 6?a)6b)7c)8d)9Correct answer is option 'B'. Can you explain this answer?
Question Description
Directions: Study the given information and answer the following question.In an exhibition, there is a train with 24 bogies numbered 1 to 24. Each bogie has 2 seats only. It moves all over the exhibition in a circular path and reaches to the same point. It stops at 5 places before coming to the starting point, i.e. it stops at the same place 6th time.The following information is given about stops:(i) The stops were considered as stop 1, stop 2, ……… and stop 6 (the starting point).(ii) At nth stop, only the doors of bogies whose numbers are multiples of (6 – n) will be opened, i.e. at stop 1, the doors whose numbers are multiples of (6 – 1) = 5 will be opened.(iii) At stop 6, all the doors will be opened.(iv) Assume that all the bogies are full of passengers and the two persons in the same bogie should not get down together at the same stop, but if the door of any bogie is opened at any stop and if there is a person in that bogie, he has to get down at that stop.How many person got down at stop 6?a)6b)7c)8d)9Correct answer is option 'B'. Can you explain this answer? for CLAT 2025 is part of CLAT preparation. The Question and answers have been prepared according to the CLAT exam syllabus. Information about Directions: Study the given information and answer the following question.In an exhibition, there is a train with 24 bogies numbered 1 to 24. Each bogie has 2 seats only. It moves all over the exhibition in a circular path and reaches to the same point. It stops at 5 places before coming to the starting point, i.e. it stops at the same place 6th time.The following information is given about stops:(i) The stops were considered as stop 1, stop 2, ……… and stop 6 (the starting point).(ii) At nth stop, only the doors of bogies whose numbers are multiples of (6 – n) will be opened, i.e. at stop 1, the doors whose numbers are multiples of (6 – 1) = 5 will be opened.(iii) At stop 6, all the doors will be opened.(iv) Assume that all the bogies are full of passengers and the two persons in the same bogie should not get down together at the same stop, but if the door of any bogie is opened at any stop and if there is a person in that bogie, he has to get down at that stop.How many person got down at stop 6?a)6b)7c)8d)9Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for CLAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Directions: Study the given information and answer the following question.In an exhibition, there is a train with 24 bogies numbered 1 to 24. Each bogie has 2 seats only. It moves all over the exhibition in a circular path and reaches to the same point. It stops at 5 places before coming to the starting point, i.e. it stops at the same place 6th time.The following information is given about stops:(i) The stops were considered as stop 1, stop 2, ……… and stop 6 (the starting point).(ii) At nth stop, only the doors of bogies whose numbers are multiples of (6 – n) will be opened, i.e. at stop 1, the doors whose numbers are multiples of (6 – 1) = 5 will be opened.(iii) At stop 6, all the doors will be opened.(iv) Assume that all the bogies are full of passengers and the two persons in the same bogie should not get down together at the same stop, but if the door of any bogie is opened at any stop and if there is a person in that bogie, he has to get down at that stop.How many person got down at stop 6?a)6b)7c)8d)9Correct answer is option 'B'. Can you explain this answer?.
Directions: Study the given information and answer the following question.In an exhibition, there is a train with 24 bogies numbered 1 to 24. Each bogie has 2 seats only. It moves all over the exhibition in a circular path and reaches to the same point. It stops at 5 places before coming to the starting point, i.e. it stops at the same place 6th time.The following information is given about stops:(i) The stops were considered as stop 1, stop 2, ……… and stop 6 (the starting point).(ii) At nth stop, only the doors of bogies whose numbers are multiples of (6 – n) will be opened, i.e. at stop 1, the doors whose numbers are multiples of (6 – 1) = 5 will be opened.(iii) At stop 6, all the doors will be opened.(iv) Assume that all the bogies are full of passengers and the two persons in the same bogie should not get down together at the same stop, but if the door of any bogie is opened at any stop and if there is a person in that bogie, he has to get down at that stop.How many person got down at stop 6?a)6b)7c)8d)9Correct answer is option 'B'. Can you explain this answer? for CLAT 2025 is part of CLAT preparation. The Question and answers have been prepared according to the CLAT exam syllabus. Information about Directions: Study the given information and answer the following question.In an exhibition, there is a train with 24 bogies numbered 1 to 24. Each bogie has 2 seats only. It moves all over the exhibition in a circular path and reaches to the same point. It stops at 5 places before coming to the starting point, i.e. it stops at the same place 6th time.The following information is given about stops:(i) The stops were considered as stop 1, stop 2, ……… and stop 6 (the starting point).(ii) At nth stop, only the doors of bogies whose numbers are multiples of (6 – n) will be opened, i.e. at stop 1, the doors whose numbers are multiples of (6 – 1) = 5 will be opened.(iii) At stop 6, all the doors will be opened.(iv) Assume that all the bogies are full of passengers and the two persons in the same bogie should not get down together at the same stop, but if the door of any bogie is opened at any stop and if there is a person in that bogie, he has to get down at that stop.How many person got down at stop 6?a)6b)7c)8d)9Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for CLAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Directions: Study the given information and answer the following question.In an exhibition, there is a train with 24 bogies numbered 1 to 24. Each bogie has 2 seats only. It moves all over the exhibition in a circular path and reaches to the same point. It stops at 5 places before coming to the starting point, i.e. it stops at the same place 6th time.The following information is given about stops:(i) The stops were considered as stop 1, stop 2, ……… and stop 6 (the starting point).(ii) At nth stop, only the doors of bogies whose numbers are multiples of (6 – n) will be opened, i.e. at stop 1, the doors whose numbers are multiples of (6 – 1) = 5 will be opened.(iii) At stop 6, all the doors will be opened.(iv) Assume that all the bogies are full of passengers and the two persons in the same bogie should not get down together at the same stop, but if the door of any bogie is opened at any stop and if there is a person in that bogie, he has to get down at that stop.How many person got down at stop 6?a)6b)7c)8d)9Correct answer is option 'B'. Can you explain this answer?.
Solutions for Directions: Study the given information and answer the following question.In an exhibition, there is a train with 24 bogies numbered 1 to 24. Each bogie has 2 seats only. It moves all over the exhibition in a circular path and reaches to the same point. It stops at 5 places before coming to the starting point, i.e. it stops at the same place 6th time.The following information is given about stops:(i) The stops were considered as stop 1, stop 2, ……… and stop 6 (the starting point).(ii) At nth stop, only the doors of bogies whose numbers are multiples of (6 – n) will be opened, i.e. at stop 1, the doors whose numbers are multiples of (6 – 1) = 5 will be opened.(iii) At stop 6, all the doors will be opened.(iv) Assume that all the bogies are full of passengers and the two persons in the same bogie should not get down together at the same stop, but if the door of any bogie is opened at any stop and if there is a person in that bogie, he has to get down at that stop.How many person got down at stop 6?a)6b)7c)8d)9Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for CLAT.
Download more important topics, notes, lectures and mock test series for CLAT Exam by signing up for free.
Here you can find the meaning of Directions: Study the given information and answer the following question.In an exhibition, there is a train with 24 bogies numbered 1 to 24. Each bogie has 2 seats only. It moves all over the exhibition in a circular path and reaches to the same point. It stops at 5 places before coming to the starting point, i.e. it stops at the same place 6th time.The following information is given about stops:(i) The stops were considered as stop 1, stop 2, ……… and stop 6 (the starting point).(ii) At nth stop, only the doors of bogies whose numbers are multiples of (6 – n) will be opened, i.e. at stop 1, the doors whose numbers are multiples of (6 – 1) = 5 will be opened.(iii) At stop 6, all the doors will be opened.(iv) Assume that all the bogies are full of passengers and the two persons in the same bogie should not get down together at the same stop, but if the door of any bogie is opened at any stop and if there is a person in that bogie, he has to get down at that stop.How many person got down at stop 6?a)6b)7c)8d)9Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Directions: Study the given information and answer the following question.In an exhibition, there is a train with 24 bogies numbered 1 to 24. Each bogie has 2 seats only. It moves all over the exhibition in a circular path and reaches to the same point. It stops at 5 places before coming to the starting point, i.e. it stops at the same place 6th time.The following information is given about stops:(i) The stops were considered as stop 1, stop 2, ……… and stop 6 (the starting point).(ii) At nth stop, only the doors of bogies whose numbers are multiples of (6 – n) will be opened, i.e. at stop 1, the doors whose numbers are multiples of (6 – 1) = 5 will be opened.(iii) At stop 6, all the doors will be opened.(iv) Assume that all the bogies are full of passengers and the two persons in the same bogie should not get down together at the same stop, but if the door of any bogie is opened at any stop and if there is a person in that bogie, he has to get down at that stop.How many person got down at stop 6?a)6b)7c)8d)9Correct answer is option 'B'. Can you explain this answer?, a detailed solution for Directions: Study the given information and answer the following question.In an exhibition, there is a train with 24 bogies numbered 1 to 24. Each bogie has 2 seats only. It moves all over the exhibition in a circular path and reaches to the same point. It stops at 5 places before coming to the starting point, i.e. it stops at the same place 6th time.The following information is given about stops:(i) The stops were considered as stop 1, stop 2, ……… and stop 6 (the starting point).(ii) At nth stop, only the doors of bogies whose numbers are multiples of (6 – n) will be opened, i.e. at stop 1, the doors whose numbers are multiples of (6 – 1) = 5 will be opened.(iii) At stop 6, all the doors will be opened.(iv) Assume that all the bogies are full of passengers and the two persons in the same bogie should not get down together at the same stop, but if the door of any bogie is opened at any stop and if there is a person in that bogie, he has to get down at that stop.How many person got down at stop 6?a)6b)7c)8d)9Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of Directions: Study the given information and answer the following question.In an exhibition, there is a train with 24 bogies numbered 1 to 24. Each bogie has 2 seats only. It moves all over the exhibition in a circular path and reaches to the same point. It stops at 5 places before coming to the starting point, i.e. it stops at the same place 6th time.The following information is given about stops:(i) The stops were considered as stop 1, stop 2, ……… and stop 6 (the starting point).(ii) At nth stop, only the doors of bogies whose numbers are multiples of (6 – n) will be opened, i.e. at stop 1, the doors whose numbers are multiples of (6 – 1) = 5 will be opened.(iii) At stop 6, all the doors will be opened.(iv) Assume that all the bogies are full of passengers and the two persons in the same bogie should not get down together at the same stop, but if the door of any bogie is opened at any stop and if there is a person in that bogie, he has to get down at that stop.How many person got down at stop 6?a)6b)7c)8d)9Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Directions: Study the given information and answer the following question.In an exhibition, there is a train with 24 bogies numbered 1 to 24. Each bogie has 2 seats only. It moves all over the exhibition in a circular path and reaches to the same point. It stops at 5 places before coming to the starting point, i.e. it stops at the same place 6th time.The following information is given about stops:(i) The stops were considered as stop 1, stop 2, ……… and stop 6 (the starting point).(ii) At nth stop, only the doors of bogies whose numbers are multiples of (6 – n) will be opened, i.e. at stop 1, the doors whose numbers are multiples of (6 – 1) = 5 will be opened.(iii) At stop 6, all the doors will be opened.(iv) Assume that all the bogies are full of passengers and the two persons in the same bogie should not get down together at the same stop, but if the door of any bogie is opened at any stop and if there is a person in that bogie, he has to get down at that stop.How many person got down at stop 6?a)6b)7c)8d)9Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice CLAT tests.

|
Explore Courses for CLAT exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























