Class 10 Exam > Class 10 Questions > Make a project of mathematical designs and pa...
Start Learning for Free
Make a project of mathematical designs and patterns using arithmetic progression
Verified Answer
Make a project of mathematical designs and patterns using arithmetic p...
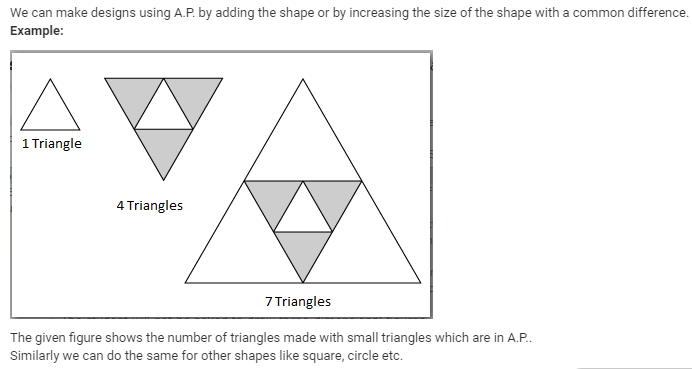
 This question is part of UPSC exam. View all Class 10 courses
This question is part of UPSC exam. View all Class 10 courses
Most Upvoted Answer
Make a project of mathematical designs and patterns using arithmetic p...
Introduction:
Arithmetic progression (AP) is a sequence of numbers in which the difference between any two consecutive terms is constant. These progressions are widely used in mathematics and have various applications in real-life scenarios. In this project, we will explore mathematical designs and patterns created using arithmetic progressions.
Creating Patterns:
Arithmetic progressions can be used to create visually appealing patterns by plotting the terms on a graph or arranging them in specific formations. Let's consider an example of an arithmetic progression with a common difference of 3:
1, 4, 7, 10, 13, 16, ...
Graphical Patterns:
One way to represent an arithmetic progression is by plotting the terms on a graph. We can graphically represent the above arithmetic progression as follows:
- Plotting the terms on the x-axis:
- (1, 1), (2, 4), (3, 7), (4, 10), (5, 13), (6, 16), ...
- Joining the points consecutively:
(1, 1) --- (2, 4) --- (3, 7) --- (4, 10) --- (5, 13) --- (6, 16)
- Analyzing the pattern:
By connecting the points, we can observe a straight line with a positive slope. Each point on the line corresponds to a term in the arithmetic progression.
Geometric Patterns:
Arithmetic progressions can also be used to create geometric patterns by arranging the terms in specific formations. Let's consider the same arithmetic progression as before:
1, 4, 7, 10, 13, 16, ...
- Circle Pattern:
Arrange the terms in a circular formation, starting from the center and moving outward. The terms will be placed equidistantly on the circumference of the circle.
7
4 10
1 13
16 7
10
- Triangle Pattern:
Arrange the terms in a triangular formation, starting from the top and moving downward. Each row will have one more term than the previous row.
1
4 7
10 13 16
Conclusion:
Arithmetic progressions offer a wide range of possibilities for creating mathematical designs and patterns. By graphing the terms or arranging them in specific formations, we can observe visually appealing patterns. These patterns can be further explored and analyzed to understand the properties and characteristics of arithmetic progressions. By experimenting with different common differences and initial terms, we can create an infinite variety of patterns using arithmetic progressions.
Arithmetic progression (AP) is a sequence of numbers in which the difference between any two consecutive terms is constant. These progressions are widely used in mathematics and have various applications in real-life scenarios. In this project, we will explore mathematical designs and patterns created using arithmetic progressions.
Creating Patterns:
Arithmetic progressions can be used to create visually appealing patterns by plotting the terms on a graph or arranging them in specific formations. Let's consider an example of an arithmetic progression with a common difference of 3:
1, 4, 7, 10, 13, 16, ...
Graphical Patterns:
One way to represent an arithmetic progression is by plotting the terms on a graph. We can graphically represent the above arithmetic progression as follows:
- Plotting the terms on the x-axis:
- (1, 1), (2, 4), (3, 7), (4, 10), (5, 13), (6, 16), ...
- Joining the points consecutively:
(1, 1) --- (2, 4) --- (3, 7) --- (4, 10) --- (5, 13) --- (6, 16)
- Analyzing the pattern:
By connecting the points, we can observe a straight line with a positive slope. Each point on the line corresponds to a term in the arithmetic progression.
Geometric Patterns:
Arithmetic progressions can also be used to create geometric patterns by arranging the terms in specific formations. Let's consider the same arithmetic progression as before:
1, 4, 7, 10, 13, 16, ...
- Circle Pattern:
Arrange the terms in a circular formation, starting from the center and moving outward. The terms will be placed equidistantly on the circumference of the circle.
7
4 10
1 13
16 7
10
- Triangle Pattern:
Arrange the terms in a triangular formation, starting from the top and moving downward. Each row will have one more term than the previous row.
1
4 7
10 13 16
Conclusion:
Arithmetic progressions offer a wide range of possibilities for creating mathematical designs and patterns. By graphing the terms or arranging them in specific formations, we can observe visually appealing patterns. These patterns can be further explored and analyzed to understand the properties and characteristics of arithmetic progressions. By experimenting with different common differences and initial terms, we can create an infinite variety of patterns using arithmetic progressions.
Community Answer
Make a project of mathematical designs and patterns using arithmetic p...
Five mathematical design and patterns

|
Explore Courses for Class 10 exam
|

|
Similar Class 10 Doubts
Make a project of mathematical designs and patterns using arithmetic progression
Question Description
Make a project of mathematical designs and patterns using arithmetic progression for Class 10 2025 is part of Class 10 preparation. The Question and answers have been prepared according to the Class 10 exam syllabus. Information about Make a project of mathematical designs and patterns using arithmetic progression covers all topics & solutions for Class 10 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Make a project of mathematical designs and patterns using arithmetic progression.
Make a project of mathematical designs and patterns using arithmetic progression for Class 10 2025 is part of Class 10 preparation. The Question and answers have been prepared according to the Class 10 exam syllabus. Information about Make a project of mathematical designs and patterns using arithmetic progression covers all topics & solutions for Class 10 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Make a project of mathematical designs and patterns using arithmetic progression.
Solutions for Make a project of mathematical designs and patterns using arithmetic progression in English & in Hindi are available as part of our courses for Class 10.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Here you can find the meaning of Make a project of mathematical designs and patterns using arithmetic progression defined & explained in the simplest way possible. Besides giving the explanation of
Make a project of mathematical designs and patterns using arithmetic progression, a detailed solution for Make a project of mathematical designs and patterns using arithmetic progression has been provided alongside types of Make a project of mathematical designs and patterns using arithmetic progression theory, EduRev gives you an
ample number of questions to practice Make a project of mathematical designs and patterns using arithmetic progression tests, examples and also practice Class 10 tests.

|
Explore Courses for Class 10 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























