NEET Exam > NEET Questions > The upper half of an inclined plane with inc...
Start Learning for Free
The upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is
- a)tan ϕ
- b)2 tan ϕ
- c)2 cos ϕ
- d)2 sin ϕ
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
The upper half of an inclined plane with inclination ϕ is perfectly s...
Analysis:
To understand why the correct answer is option 'B', let's analyze the motion of the body on the inclined plane.
1. Motion on the Upper Half:
Since the upper half of the inclined plane is perfectly smooth, there is no friction acting on the body. Therefore, the body will slide down the incline without any hindrance. Let's denote the acceleration of the body on the upper half as 'a'.
2. Motion on the Lower Half:
On the lower half of the inclined plane, the surface is rough, and there is friction acting on the body. Let's denote the coefficient of friction as 'μ'. The body will experience a frictional force in the opposite direction to its motion.
3. Equations of Motion:
To determine the condition for the body to come to rest at the bottom, we can use the equations of motion.
On the upper half:
- Distance traveled, d₁ = h/2
- Initial velocity, u = 0
- Final velocity, v = ?
- Acceleration, a = ?
Using the equation v² = u² + 2as, we can find the acceleration on the upper half:
v² = 0 + 2a(h/2)
v² = ah
On the lower half:
- Distance traveled, d₂ = h/2
- Initial velocity, u = ?
- Final velocity, v = 0
- Acceleration, a = ?
Since the body comes to rest at the bottom, we can use the equation v² = u² + 2as to find the acceleration on the lower half:
0 = u² + 2a(h/2)
u² = -ah
4. Condition for Rest:
For the body to come to rest at the bottom, the velocity on the lower half should be zero. Therefore, we can equate the final velocity on the upper half to the initial velocity on the lower half:
v² = u²
Substituting the values of v² and u² from the equations of motion:
ah = -ah
2ah = 0
ah = 0
5. Coefficient of Friction:
The frictional force acting on the lower half of the inclined plane is given by f = μN, where N is the normal force. The normal force N is equal to the weight of the body, which is mg.
Since the body is not accelerating on the lower half (ah = 0), the net force acting on it is zero. Therefore, the frictional force must be equal to the component of the weight along the incline.
Using trigonometry, we can write:
mg sin ϕ = μmg cos ϕ
sin ϕ = μ cos ϕ
μ = tan ϕ
The coefficient of friction μ is equal to tan ϕ.
6. Conclusion:
From the above analysis, we can conclude that the coefficient of friction for the lower half of the inclined plane is equal to tan ϕ. Therefore, the correct answer is option 'B' - 2 tan ϕ.
To understand why the correct answer is option 'B', let's analyze the motion of the body on the inclined plane.
1. Motion on the Upper Half:
Since the upper half of the inclined plane is perfectly smooth, there is no friction acting on the body. Therefore, the body will slide down the incline without any hindrance. Let's denote the acceleration of the body on the upper half as 'a'.
2. Motion on the Lower Half:
On the lower half of the inclined plane, the surface is rough, and there is friction acting on the body. Let's denote the coefficient of friction as 'μ'. The body will experience a frictional force in the opposite direction to its motion.
3. Equations of Motion:
To determine the condition for the body to come to rest at the bottom, we can use the equations of motion.
On the upper half:
- Distance traveled, d₁ = h/2
- Initial velocity, u = 0
- Final velocity, v = ?
- Acceleration, a = ?
Using the equation v² = u² + 2as, we can find the acceleration on the upper half:
v² = 0 + 2a(h/2)
v² = ah
On the lower half:
- Distance traveled, d₂ = h/2
- Initial velocity, u = ?
- Final velocity, v = 0
- Acceleration, a = ?
Since the body comes to rest at the bottom, we can use the equation v² = u² + 2as to find the acceleration on the lower half:
0 = u² + 2a(h/2)
u² = -ah
4. Condition for Rest:
For the body to come to rest at the bottom, the velocity on the lower half should be zero. Therefore, we can equate the final velocity on the upper half to the initial velocity on the lower half:
v² = u²
Substituting the values of v² and u² from the equations of motion:
ah = -ah
2ah = 0
ah = 0
5. Coefficient of Friction:
The frictional force acting on the lower half of the inclined plane is given by f = μN, where N is the normal force. The normal force N is equal to the weight of the body, which is mg.
Since the body is not accelerating on the lower half (ah = 0), the net force acting on it is zero. Therefore, the frictional force must be equal to the component of the weight along the incline.
Using trigonometry, we can write:
mg sin ϕ = μmg cos ϕ
sin ϕ = μ cos ϕ
μ = tan ϕ
The coefficient of friction μ is equal to tan ϕ.
6. Conclusion:
From the above analysis, we can conclude that the coefficient of friction for the lower half of the inclined plane is equal to tan ϕ. Therefore, the correct answer is option 'B' - 2 tan ϕ.
Free Test
FREE
| Start Free Test |
Community Answer
The upper half of an inclined plane with inclination ϕ is perfectly s...
For the smooth upper half, using v2 − u2 = 2as, we get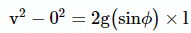
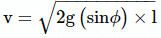
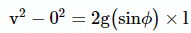
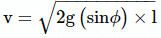
For the lower half, using v2 − u2 = 2as, we get
02 − 2g sin ϕ × l = −2 (μk cosϕ − sinϕ)g × l
or sinϕ = μk cosϕ − sinϕ
μk cosϕ = 2sinϕ
or μk = 2tanϕ
Attention NEET Students!
To make sure you are not studying endlessly, EduRev has designed NEET study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in NEET.
|
Explore Courses for NEET exam
|
|
Top Courses for NEETView all
The upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half isa)tan ϕb)2 tan ϕc)2 cos ϕd)2 sin ϕCorrect answer is option 'B'. Can you explain this answer?
Question Description
The upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half isa)tan ϕb)2 tan ϕc)2 cos ϕd)2 sin ϕCorrect answer is option 'B'. Can you explain this answer? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about The upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half isa)tan ϕb)2 tan ϕc)2 cos ϕd)2 sin ϕCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half isa)tan ϕb)2 tan ϕc)2 cos ϕd)2 sin ϕCorrect answer is option 'B'. Can you explain this answer?.
The upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half isa)tan ϕb)2 tan ϕc)2 cos ϕd)2 sin ϕCorrect answer is option 'B'. Can you explain this answer? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about The upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half isa)tan ϕb)2 tan ϕc)2 cos ϕd)2 sin ϕCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half isa)tan ϕb)2 tan ϕc)2 cos ϕd)2 sin ϕCorrect answer is option 'B'. Can you explain this answer?.
Solutions for The upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half isa)tan ϕb)2 tan ϕc)2 cos ϕd)2 sin ϕCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of The upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half isa)tan ϕb)2 tan ϕc)2 cos ϕd)2 sin ϕCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half isa)tan ϕb)2 tan ϕc)2 cos ϕd)2 sin ϕCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for The upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half isa)tan ϕb)2 tan ϕc)2 cos ϕd)2 sin ϕCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of The upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half isa)tan ϕb)2 tan ϕc)2 cos ϕd)2 sin ϕCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half isa)tan ϕb)2 tan ϕc)2 cos ϕd)2 sin ϕCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice NEET tests.
|
|
Explore Courses for NEET exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup