Electronics and Communication Engineering (ECE) Exam > Electronics and Communication Engineering (ECE) Questions > Consider a long rectangular bar of direct ba...
Start Learning for Free
Consider a long rectangular bar of direct bandgap p-type semiconductor. The equilibrium hole density is 1017 cm-3 the intrinsic carrier concentration is 1010 cm-3 . Electron and hole diffusion lengths are 2μm and 1μm , respectively. The left side of the bar ( x = 0) is uniformly illuminated with a laser having photon energy greater than the bandgap of the semiconductor. Excess electron-hole pairs are generated ONLY at x = 0 because of the laser. The steady state electron density at x = 0 is 1014 cm-3 due to laser illumination. Under these conditions and ignoring electric field, the closest approximation (among the given options) of the steady state electron density at x = 2μm , is
- a)0.63 x 1013 cm-3
- b)3.7 x 1014 cm-3
- c)0.37 x 1014 cm-3
- d)103 cm-3
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
Consider a long rectangular bar of direct bandgap p-type semiconducto...
Given parameters:
- Direct bandgap p-type semiconductor
- Equilibrium hole density = 1017 cm-3
- Intrinsic carrier concentration = 1010 cm-3
- Electron diffusion length = 2 μm
- Hole diffusion length = 1 μm
- Laser illumination generates excess electron-hole pairs only at x = 0
- Steady state electron density at x = 0 due to laser illumination = 1014 cm-3
- Find the steady state electron density at x = 2 μm
Approach:
- Calculate excess hole density at x = 0 due to laser illumination
- Calculate excess electron density at x = 0 due to laser illumination
- Find the distance over which excess electron-hole pairs diffuse before recombination
- Calculate the steady state electron density at x = 2 μm
Calculation:
- Excess hole density at x = 0 due to laser illumination:
- As excess electron-hole pairs are generated only at x = 0, the excess hole density at x = 0 will be equal to the excess electron density at x = 0.
- Excess electron density at x = 0 due to laser illumination = 1014 cm-3
- Therefore, excess hole density at x = 0 due to laser illumination = 1014 cm-3
- Distance over which excess electron-hole pairs diffuse before recombination:
- As electron diffusion length is greater than hole diffusion length, excess electron-hole pairs will diffuse over a distance of 1 μm before recombination.
- Therefore, excess electron-hole pairs will recombine within a distance of 1 μm from x = 0.
- Steady state electron density at x = 2 μm:
- As excess electron-hole pairs recombine within a distance of 1 μm from x = 0, the steady state electron density at x = 2 μm will be equal to the equilibrium electron density at x = 2 μm plus the excess electron density that has diffused from x = 0 to x = 2 μm.
- Equilibrium electron density at x = 2 μm = intrinsic carrier concentration + excess hole density at x = 0 = 1010 + 1014 = 1014 cm-3
- Excess electron density that has diffused from x = 0 to x = 2 μm:
- As electron diffusion length is 2 μm, excess electron density that has diffused from x = 0 to x = 2 μm will be equal to the excess electron density at x = 0 minus the excess electron density that has recombined within a distance of 1 μm from x = 0.
- Excess electron density that has recombined within a distance of 1 μm from x = 0 = excess electron density at x = 0 - steady state electron density at x = 0 due to laser illumination = 1014 - 1014 = 0 cm-3
- Therefore, excess electron density that has diffused from x = 0 to x = 2 μm = 1014 cm-3
- Steady state electron density at x = 2 μm = equilibrium electron density at x = 2 μm + excess electron density that has diffused from x = 0 to x = 2 μ
- Direct bandgap p-type semiconductor
- Equilibrium hole density = 1017 cm-3
- Intrinsic carrier concentration = 1010 cm-3
- Electron diffusion length = 2 μm
- Hole diffusion length = 1 μm
- Laser illumination generates excess electron-hole pairs only at x = 0
- Steady state electron density at x = 0 due to laser illumination = 1014 cm-3
- Find the steady state electron density at x = 2 μm
Approach:
- Calculate excess hole density at x = 0 due to laser illumination
- Calculate excess electron density at x = 0 due to laser illumination
- Find the distance over which excess electron-hole pairs diffuse before recombination
- Calculate the steady state electron density at x = 2 μm
Calculation:
- Excess hole density at x = 0 due to laser illumination:
- As excess electron-hole pairs are generated only at x = 0, the excess hole density at x = 0 will be equal to the excess electron density at x = 0.
- Excess electron density at x = 0 due to laser illumination = 1014 cm-3
- Therefore, excess hole density at x = 0 due to laser illumination = 1014 cm-3
- Distance over which excess electron-hole pairs diffuse before recombination:
- As electron diffusion length is greater than hole diffusion length, excess electron-hole pairs will diffuse over a distance of 1 μm before recombination.
- Therefore, excess electron-hole pairs will recombine within a distance of 1 μm from x = 0.
- Steady state electron density at x = 2 μm:
- As excess electron-hole pairs recombine within a distance of 1 μm from x = 0, the steady state electron density at x = 2 μm will be equal to the equilibrium electron density at x = 2 μm plus the excess electron density that has diffused from x = 0 to x = 2 μm.
- Equilibrium electron density at x = 2 μm = intrinsic carrier concentration + excess hole density at x = 0 = 1010 + 1014 = 1014 cm-3
- Excess electron density that has diffused from x = 0 to x = 2 μm:
- As electron diffusion length is 2 μm, excess electron density that has diffused from x = 0 to x = 2 μm will be equal to the excess electron density at x = 0 minus the excess electron density that has recombined within a distance of 1 μm from x = 0.
- Excess electron density that has recombined within a distance of 1 μm from x = 0 = excess electron density at x = 0 - steady state electron density at x = 0 due to laser illumination = 1014 - 1014 = 0 cm-3
- Therefore, excess electron density that has diffused from x = 0 to x = 2 μm = 1014 cm-3
- Steady state electron density at x = 2 μm = equilibrium electron density at x = 2 μm + excess electron density that has diffused from x = 0 to x = 2 μ
Free Test
FREE
| Start Free Test |
Community Answer
Consider a long rectangular bar of direct bandgap p-type semiconducto...
Given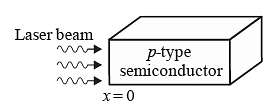
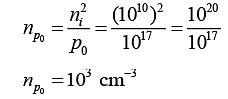

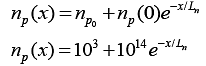
(i) p-type semiconductor
(ii) Equilibrium hole density, p0 = 1017 cm-3
(iii) Intrinsic carrier concentration, ni = 1010 cm-3
(iv) Electron diffusion length, Ln = 2μm
(v) Hole diffusion length, Lp = 1μm
(vi) Excess electron density at x = 0 , np (0) = 1014 cm-3
Consider a bar of direct bandgap p-type semiconductor with light is illuminated at left side of the bar at x = 0 .

From Mass action law, np = ni2 Electron or minority carrier concentration is given by,
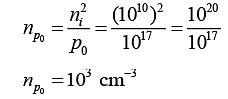

Electron concentration at any distance ' x' is given by,
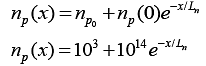
Electron concentration (density) at x = 2μm is,
np (x = 2) = 103 +1014 e-2/2
np (x = 2) = 103 +1014 e-1
np (x = 2) = 103 + 1014 x 0.37
np (x = 2) ≅ 0.37 x 1014 cm-3
Hence, the correct option is (C).
Attention Electronics and Communication Engineering (ECE) Students!
To make sure you are not studying endlessly, EduRev has designed Electronics and Communication Engineering (ECE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Electronics and Communication Engineering (ECE).

|
Explore Courses for Electronics and Communication Engineering (ECE) exam
|

|
Similar Electronics and Communication Engineering (ECE) Doubts
Consider a long rectangular bar of direct bandgap p-type semiconductor. The equilibrium hole density is 1017 cm-3 the intrinsic carrier concentration is 1010 cm-3 . Electron and hole diffusion lengths are 2μm and 1μm , respectively. The left side of the bar ( x = 0) is uniformly illuminated with a laser having photon energy greater than the bandgap of the semiconductor. Excess electron-hole pairs are generated ONLY at x = 0 because of the laser. The steady state electron density at x = 0 is 1014 cm-3 due to laser illumination. Under these conditions and ignoring electric field, the closest approximation (among the given options) of the steady state electron density at x = 2μm , isa)0.63 x 1013 cm-3b)3.7 x 1014 cm-3c)0.37 x 1014 cm-3d)103 cm-3Correct answer is option 'C'. Can you explain this answer?
Question Description
Consider a long rectangular bar of direct bandgap p-type semiconductor. The equilibrium hole density is 1017 cm-3 the intrinsic carrier concentration is 1010 cm-3 . Electron and hole diffusion lengths are 2μm and 1μm , respectively. The left side of the bar ( x = 0) is uniformly illuminated with a laser having photon energy greater than the bandgap of the semiconductor. Excess electron-hole pairs are generated ONLY at x = 0 because of the laser. The steady state electron density at x = 0 is 1014 cm-3 due to laser illumination. Under these conditions and ignoring electric field, the closest approximation (among the given options) of the steady state electron density at x = 2μm , isa)0.63 x 1013 cm-3b)3.7 x 1014 cm-3c)0.37 x 1014 cm-3d)103 cm-3Correct answer is option 'C'. Can you explain this answer? for Electronics and Communication Engineering (ECE) 2024 is part of Electronics and Communication Engineering (ECE) preparation. The Question and answers have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. Information about Consider a long rectangular bar of direct bandgap p-type semiconductor. The equilibrium hole density is 1017 cm-3 the intrinsic carrier concentration is 1010 cm-3 . Electron and hole diffusion lengths are 2μm and 1μm , respectively. The left side of the bar ( x = 0) is uniformly illuminated with a laser having photon energy greater than the bandgap of the semiconductor. Excess electron-hole pairs are generated ONLY at x = 0 because of the laser. The steady state electron density at x = 0 is 1014 cm-3 due to laser illumination. Under these conditions and ignoring electric field, the closest approximation (among the given options) of the steady state electron density at x = 2μm , isa)0.63 x 1013 cm-3b)3.7 x 1014 cm-3c)0.37 x 1014 cm-3d)103 cm-3Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Electronics and Communication Engineering (ECE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider a long rectangular bar of direct bandgap p-type semiconductor. The equilibrium hole density is 1017 cm-3 the intrinsic carrier concentration is 1010 cm-3 . Electron and hole diffusion lengths are 2μm and 1μm , respectively. The left side of the bar ( x = 0) is uniformly illuminated with a laser having photon energy greater than the bandgap of the semiconductor. Excess electron-hole pairs are generated ONLY at x = 0 because of the laser. The steady state electron density at x = 0 is 1014 cm-3 due to laser illumination. Under these conditions and ignoring electric field, the closest approximation (among the given options) of the steady state electron density at x = 2μm , isa)0.63 x 1013 cm-3b)3.7 x 1014 cm-3c)0.37 x 1014 cm-3d)103 cm-3Correct answer is option 'C'. Can you explain this answer?.
Consider a long rectangular bar of direct bandgap p-type semiconductor. The equilibrium hole density is 1017 cm-3 the intrinsic carrier concentration is 1010 cm-3 . Electron and hole diffusion lengths are 2μm and 1μm , respectively. The left side of the bar ( x = 0) is uniformly illuminated with a laser having photon energy greater than the bandgap of the semiconductor. Excess electron-hole pairs are generated ONLY at x = 0 because of the laser. The steady state electron density at x = 0 is 1014 cm-3 due to laser illumination. Under these conditions and ignoring electric field, the closest approximation (among the given options) of the steady state electron density at x = 2μm , isa)0.63 x 1013 cm-3b)3.7 x 1014 cm-3c)0.37 x 1014 cm-3d)103 cm-3Correct answer is option 'C'. Can you explain this answer? for Electronics and Communication Engineering (ECE) 2024 is part of Electronics and Communication Engineering (ECE) preparation. The Question and answers have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. Information about Consider a long rectangular bar of direct bandgap p-type semiconductor. The equilibrium hole density is 1017 cm-3 the intrinsic carrier concentration is 1010 cm-3 . Electron and hole diffusion lengths are 2μm and 1μm , respectively. The left side of the bar ( x = 0) is uniformly illuminated with a laser having photon energy greater than the bandgap of the semiconductor. Excess electron-hole pairs are generated ONLY at x = 0 because of the laser. The steady state electron density at x = 0 is 1014 cm-3 due to laser illumination. Under these conditions and ignoring electric field, the closest approximation (among the given options) of the steady state electron density at x = 2μm , isa)0.63 x 1013 cm-3b)3.7 x 1014 cm-3c)0.37 x 1014 cm-3d)103 cm-3Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Electronics and Communication Engineering (ECE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider a long rectangular bar of direct bandgap p-type semiconductor. The equilibrium hole density is 1017 cm-3 the intrinsic carrier concentration is 1010 cm-3 . Electron and hole diffusion lengths are 2μm and 1μm , respectively. The left side of the bar ( x = 0) is uniformly illuminated with a laser having photon energy greater than the bandgap of the semiconductor. Excess electron-hole pairs are generated ONLY at x = 0 because of the laser. The steady state electron density at x = 0 is 1014 cm-3 due to laser illumination. Under these conditions and ignoring electric field, the closest approximation (among the given options) of the steady state electron density at x = 2μm , isa)0.63 x 1013 cm-3b)3.7 x 1014 cm-3c)0.37 x 1014 cm-3d)103 cm-3Correct answer is option 'C'. Can you explain this answer?.
Solutions for Consider a long rectangular bar of direct bandgap p-type semiconductor. The equilibrium hole density is 1017 cm-3 the intrinsic carrier concentration is 1010 cm-3 . Electron and hole diffusion lengths are 2μm and 1μm , respectively. The left side of the bar ( x = 0) is uniformly illuminated with a laser having photon energy greater than the bandgap of the semiconductor. Excess electron-hole pairs are generated ONLY at x = 0 because of the laser. The steady state electron density at x = 0 is 1014 cm-3 due to laser illumination. Under these conditions and ignoring electric field, the closest approximation (among the given options) of the steady state electron density at x = 2μm , isa)0.63 x 1013 cm-3b)3.7 x 1014 cm-3c)0.37 x 1014 cm-3d)103 cm-3Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Electronics and Communication Engineering (ECE).
Download more important topics, notes, lectures and mock test series for Electronics and Communication Engineering (ECE) Exam by signing up for free.
Here you can find the meaning of Consider a long rectangular bar of direct bandgap p-type semiconductor. The equilibrium hole density is 1017 cm-3 the intrinsic carrier concentration is 1010 cm-3 . Electron and hole diffusion lengths are 2μm and 1μm , respectively. The left side of the bar ( x = 0) is uniformly illuminated with a laser having photon energy greater than the bandgap of the semiconductor. Excess electron-hole pairs are generated ONLY at x = 0 because of the laser. The steady state electron density at x = 0 is 1014 cm-3 due to laser illumination. Under these conditions and ignoring electric field, the closest approximation (among the given options) of the steady state electron density at x = 2μm , isa)0.63 x 1013 cm-3b)3.7 x 1014 cm-3c)0.37 x 1014 cm-3d)103 cm-3Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Consider a long rectangular bar of direct bandgap p-type semiconductor. The equilibrium hole density is 1017 cm-3 the intrinsic carrier concentration is 1010 cm-3 . Electron and hole diffusion lengths are 2μm and 1μm , respectively. The left side of the bar ( x = 0) is uniformly illuminated with a laser having photon energy greater than the bandgap of the semiconductor. Excess electron-hole pairs are generated ONLY at x = 0 because of the laser. The steady state electron density at x = 0 is 1014 cm-3 due to laser illumination. Under these conditions and ignoring electric field, the closest approximation (among the given options) of the steady state electron density at x = 2μm , isa)0.63 x 1013 cm-3b)3.7 x 1014 cm-3c)0.37 x 1014 cm-3d)103 cm-3Correct answer is option 'C'. Can you explain this answer?, a detailed solution for Consider a long rectangular bar of direct bandgap p-type semiconductor. The equilibrium hole density is 1017 cm-3 the intrinsic carrier concentration is 1010 cm-3 . Electron and hole diffusion lengths are 2μm and 1μm , respectively. The left side of the bar ( x = 0) is uniformly illuminated with a laser having photon energy greater than the bandgap of the semiconductor. Excess electron-hole pairs are generated ONLY at x = 0 because of the laser. The steady state electron density at x = 0 is 1014 cm-3 due to laser illumination. Under these conditions and ignoring electric field, the closest approximation (among the given options) of the steady state electron density at x = 2μm , isa)0.63 x 1013 cm-3b)3.7 x 1014 cm-3c)0.37 x 1014 cm-3d)103 cm-3Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of Consider a long rectangular bar of direct bandgap p-type semiconductor. The equilibrium hole density is 1017 cm-3 the intrinsic carrier concentration is 1010 cm-3 . Electron and hole diffusion lengths are 2μm and 1μm , respectively. The left side of the bar ( x = 0) is uniformly illuminated with a laser having photon energy greater than the bandgap of the semiconductor. Excess electron-hole pairs are generated ONLY at x = 0 because of the laser. The steady state electron density at x = 0 is 1014 cm-3 due to laser illumination. Under these conditions and ignoring electric field, the closest approximation (among the given options) of the steady state electron density at x = 2μm , isa)0.63 x 1013 cm-3b)3.7 x 1014 cm-3c)0.37 x 1014 cm-3d)103 cm-3Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Consider a long rectangular bar of direct bandgap p-type semiconductor. The equilibrium hole density is 1017 cm-3 the intrinsic carrier concentration is 1010 cm-3 . Electron and hole diffusion lengths are 2μm and 1μm , respectively. The left side of the bar ( x = 0) is uniformly illuminated with a laser having photon energy greater than the bandgap of the semiconductor. Excess electron-hole pairs are generated ONLY at x = 0 because of the laser. The steady state electron density at x = 0 is 1014 cm-3 due to laser illumination. Under these conditions and ignoring electric field, the closest approximation (among the given options) of the steady state electron density at x = 2μm , isa)0.63 x 1013 cm-3b)3.7 x 1014 cm-3c)0.37 x 1014 cm-3d)103 cm-3Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice Electronics and Communication Engineering (ECE) tests.

|
Explore Courses for Electronics and Communication Engineering (ECE) exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























