Humanities/Arts Exam > Humanities/Arts Questions > Convert the following infix expression to pos...
Start Learning for Free
Convert the following infix expression to postfix expression using stack:
(A+B*(C-D)^E+(F/G)^H-I)
- a)ABCD-E^*+FG/H^+I-
- b)ABCD-E^*+FG/H^I-+
- c)AB+CD-E^*FG/H^+I-
- d)AB+CD-E^*FG/H^I-+
Correct answer is option 'A'. Can you explain this answer?
Most Upvoted Answer
Convert the following infix expression to postfix expression using sta...
The conversion using stack is as follows:
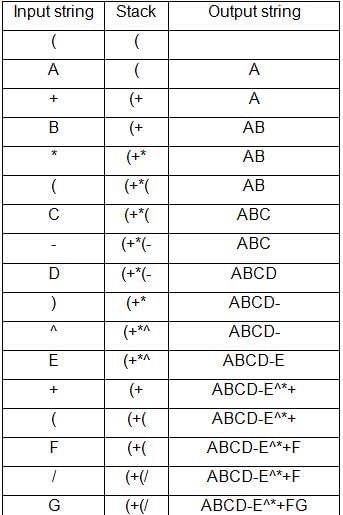
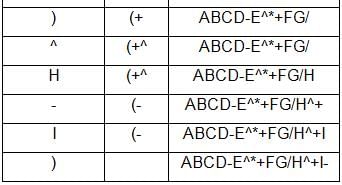
Free Test
FREE
| Start Free Test |
Community Answer
Convert the following infix expression to postfix expression using sta...
Converting Infix Expression to Postfix Expression using Stack
To convert an infix expression to a postfix expression, we need to follow the rules of the operator precedence and the use of parentheses. We will use a stack to help us in the conversion process.
Given Infix Expression:
A B*(C-D)^E (F/G)^H-I
Steps to Convert:
1. Initialize an empty stack to hold the operators temporarily.
2. Scan the infix expression from left to right and perform the following steps for each element:
a. If the element is an operand (A-Z), append it directly to the postfix expression.
b. If the element is an opening parenthesis "(", push it onto the stack.
c. If the element is a closing parenthesis ")", pop all operators from the stack and append them to the postfix expression until an opening parenthesis is encountered. Discard the opening parenthesis.
d. If the element is an operator (+-*/^), check the operator precedence and associativity rules:
i. If the stack is empty or contains an opening parenthesis, push the operator onto the stack.
ii. If the operator has higher precedence than the top of the stack, push it onto the stack.
iii. If the operator has lower precedence than or equal precedence to the top of the stack, pop operators from the stack and append them to the postfix expression until a lower precedence operator is encountered or the stack becomes empty. Then push the current operator onto the stack.
3. After scanning the entire infix expression, pop any remaining operators from the stack and append them to the postfix expression.
Conversion Process:
Let's follow the above steps to convert the given infix expression to postfix expression:
Step 1: Initialize an empty stack.
Step 2: Scan the infix expression from left to right.
Element: A
Stack:
Postfix: A
Element:
Stack:
Postfix: A
Element: B
Stack:
Postfix: AB
Element: *
Stack: *
Postfix: AB
Element: (
Stack: *, (
Postfix: AB
Element: C
Stack: *, (
Postfix: ABC
Element: -
Stack: *, (
Postfix: ABC-
Element: D
Stack: *, (
Postfix: ABC-D
Element: )
Stack: *
Postfix: ABC-D*
Element: ^
Stack: ^, *
Postfix: ABC-D*
Element: E
Stack: ^, *
Postfix: ABC-D*E
Element:
Stack:
Postfix: ABC-D*E^
Element: (
Stack: (
Postfix: ABC-D*E^
Element: F
Stack: (
Postfix: ABC-D*E^F
Element: /
Stack: /, (
Postfix: ABC-D*E^F/
Element: G
Stack: /, (
Postfix: ABC-D*E^FG/
Element: )
Stack:
Postfix: ABC-D*E^FG/
Element: ^
Stack: ^
Post
To convert an infix expression to a postfix expression, we need to follow the rules of the operator precedence and the use of parentheses. We will use a stack to help us in the conversion process.
Given Infix Expression:
A B*(C-D)^E (F/G)^H-I
Steps to Convert:
1. Initialize an empty stack to hold the operators temporarily.
2. Scan the infix expression from left to right and perform the following steps for each element:
a. If the element is an operand (A-Z), append it directly to the postfix expression.
b. If the element is an opening parenthesis "(", push it onto the stack.
c. If the element is a closing parenthesis ")", pop all operators from the stack and append them to the postfix expression until an opening parenthesis is encountered. Discard the opening parenthesis.
d. If the element is an operator (+-*/^), check the operator precedence and associativity rules:
i. If the stack is empty or contains an opening parenthesis, push the operator onto the stack.
ii. If the operator has higher precedence than the top of the stack, push it onto the stack.
iii. If the operator has lower precedence than or equal precedence to the top of the stack, pop operators from the stack and append them to the postfix expression until a lower precedence operator is encountered or the stack becomes empty. Then push the current operator onto the stack.
3. After scanning the entire infix expression, pop any remaining operators from the stack and append them to the postfix expression.
Conversion Process:
Let's follow the above steps to convert the given infix expression to postfix expression:
Step 1: Initialize an empty stack.
Step 2: Scan the infix expression from left to right.
Element: A
Stack:
Postfix: A
Element:
Stack:
Postfix: A
Element: B
Stack:
Postfix: AB
Element: *
Stack: *
Postfix: AB
Element: (
Stack: *, (
Postfix: AB
Element: C
Stack: *, (
Postfix: ABC
Element: -
Stack: *, (
Postfix: ABC-
Element: D
Stack: *, (
Postfix: ABC-D
Element: )
Stack: *
Postfix: ABC-D*
Element: ^
Stack: ^, *
Postfix: ABC-D*
Element: E
Stack: ^, *
Postfix: ABC-D*E
Element:
Stack:
Postfix: ABC-D*E^
Element: (
Stack: (
Postfix: ABC-D*E^
Element: F
Stack: (
Postfix: ABC-D*E^F
Element: /
Stack: /, (
Postfix: ABC-D*E^F/
Element: G
Stack: /, (
Postfix: ABC-D*E^FG/
Element: )
Stack:
Postfix: ABC-D*E^FG/
Element: ^
Stack: ^
Post
|
Explore Courses for Humanities/Arts exam
|
|
Top Courses for Humanities/ArtsView all
Question Description
Convert the following infix expression to postfix expression using stack:(A+B*(C-D)^E+(F/G)^H-I)a)ABCD-E^*+FG/H^+I-b)ABCD-E^*+FG/H^I-+c)AB+CD-E^*FG/H^+I-d)AB+CD-E^*FG/H^I-+Correct answer is option 'A'. Can you explain this answer? for Humanities/Arts 2025 is part of Humanities/Arts preparation. The Question and answers have been prepared according to the Humanities/Arts exam syllabus. Information about Convert the following infix expression to postfix expression using stack:(A+B*(C-D)^E+(F/G)^H-I)a)ABCD-E^*+FG/H^+I-b)ABCD-E^*+FG/H^I-+c)AB+CD-E^*FG/H^+I-d)AB+CD-E^*FG/H^I-+Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for Humanities/Arts 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Convert the following infix expression to postfix expression using stack:(A+B*(C-D)^E+(F/G)^H-I)a)ABCD-E^*+FG/H^+I-b)ABCD-E^*+FG/H^I-+c)AB+CD-E^*FG/H^+I-d)AB+CD-E^*FG/H^I-+Correct answer is option 'A'. Can you explain this answer?.
Convert the following infix expression to postfix expression using stack:(A+B*(C-D)^E+(F/G)^H-I)a)ABCD-E^*+FG/H^+I-b)ABCD-E^*+FG/H^I-+c)AB+CD-E^*FG/H^+I-d)AB+CD-E^*FG/H^I-+Correct answer is option 'A'. Can you explain this answer? for Humanities/Arts 2025 is part of Humanities/Arts preparation. The Question and answers have been prepared according to the Humanities/Arts exam syllabus. Information about Convert the following infix expression to postfix expression using stack:(A+B*(C-D)^E+(F/G)^H-I)a)ABCD-E^*+FG/H^+I-b)ABCD-E^*+FG/H^I-+c)AB+CD-E^*FG/H^+I-d)AB+CD-E^*FG/H^I-+Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for Humanities/Arts 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Convert the following infix expression to postfix expression using stack:(A+B*(C-D)^E+(F/G)^H-I)a)ABCD-E^*+FG/H^+I-b)ABCD-E^*+FG/H^I-+c)AB+CD-E^*FG/H^+I-d)AB+CD-E^*FG/H^I-+Correct answer is option 'A'. Can you explain this answer?.
Solutions for Convert the following infix expression to postfix expression using stack:(A+B*(C-D)^E+(F/G)^H-I)a)ABCD-E^*+FG/H^+I-b)ABCD-E^*+FG/H^I-+c)AB+CD-E^*FG/H^+I-d)AB+CD-E^*FG/H^I-+Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Humanities/Arts.
Download more important topics, notes, lectures and mock test series for Humanities/Arts Exam by signing up for free.
Here you can find the meaning of Convert the following infix expression to postfix expression using stack:(A+B*(C-D)^E+(F/G)^H-I)a)ABCD-E^*+FG/H^+I-b)ABCD-E^*+FG/H^I-+c)AB+CD-E^*FG/H^+I-d)AB+CD-E^*FG/H^I-+Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Convert the following infix expression to postfix expression using stack:(A+B*(C-D)^E+(F/G)^H-I)a)ABCD-E^*+FG/H^+I-b)ABCD-E^*+FG/H^I-+c)AB+CD-E^*FG/H^+I-d)AB+CD-E^*FG/H^I-+Correct answer is option 'A'. Can you explain this answer?, a detailed solution for Convert the following infix expression to postfix expression using stack:(A+B*(C-D)^E+(F/G)^H-I)a)ABCD-E^*+FG/H^+I-b)ABCD-E^*+FG/H^I-+c)AB+CD-E^*FG/H^+I-d)AB+CD-E^*FG/H^I-+Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of Convert the following infix expression to postfix expression using stack:(A+B*(C-D)^E+(F/G)^H-I)a)ABCD-E^*+FG/H^+I-b)ABCD-E^*+FG/H^I-+c)AB+CD-E^*FG/H^+I-d)AB+CD-E^*FG/H^I-+Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Convert the following infix expression to postfix expression using stack:(A+B*(C-D)^E+(F/G)^H-I)a)ABCD-E^*+FG/H^+I-b)ABCD-E^*+FG/H^I-+c)AB+CD-E^*FG/H^+I-d)AB+CD-E^*FG/H^I-+Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice Humanities/Arts tests.
|
|
Explore Courses for Humanities/Arts exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup