Class 10 Exam > Class 10 Questions > A person dressed in a new suit stands in fron...
Start Learning for Free
A person dressed in a new suit stands in front of a plane mirror fixed on a vertical wall. Height of a person is 'H' and that of his eyes from the ground is 'h'. Show that minimum length of the mirror so that the person can have his full view is 'H/2' and that it is independent of the position of eyes. Also determine the position of the mirror relative to ground and show image formation with a ray diagram.?
Verified Answer
A person dressed in a new suit stands in front of a plane mirror fixed...
Your questions is same as this answer it will heplfull for you:
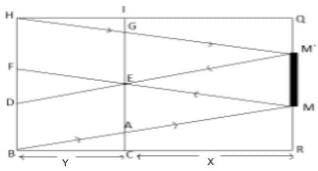
Let HB be the wall with height h and MM' is the mirror. Man standing at distance x from mirror and the wall is at distance y from man.
Let HB be the wall with height h and MM' is the mirror. Man standing at distance x from mirror and the wall is at distance y from man.
Let MM' be r, then,
EA=EG=HF=DB=MM'=r ---(1)
in Triangle RMB, C is midpoint of BA and CA is parallel to RM
A is midpoint of BM.
I is the midpoint of QH, G is midpoint of HM'
in triangle MFB, A is midpoint of BM and AE is parallel to BF.
E is midpoint of MF.
from midpoint theorem,
In triangle M"DH, E is midpoint of M'D
Therefore,
2EA=FB=
and 2GE=HD which meanss HD=FB =2r --(2 eq)
from eq 1 and 2 we get,
HD=HF+HD=r+FD=2r
FD=r
therefore, HD=FD=BD=r
HB=HD+FD+Bd=3r
h=3r
r=h/3
Therefore, to see the complete wall infront of height H in the mirror the person will require plane mirror of 1/3 of height of wall.

 This question is part of UPSC exam. View all Class 10 courses
This question is part of UPSC exam. View all Class 10 courses
Most Upvoted Answer
A person dressed in a new suit stands in front of a plane mirror fixed...
Minimum Length of the Mirror:
To determine the minimum length of the mirror required for a person to have their full view, we can consider the geometry of the situation.
Let's assume the person's height is 'H' and the height of their eyes from the ground is 'h'.
Step 1: Determine the position of the person's image formed in the mirror.
When light from the person falls on the mirror, it reflects back according to the law of reflection. The image of the person is formed behind the mirror at the same distance as the object's distance from the mirror. Since the person is standing in front of the mirror, the image will be formed behind them.
Step 2: Determine the height of the person's image formed in the mirror.
The height of the person's image can be determined using similar triangles. The person's height 'H' and the distance between the mirror and the person's eyes 'h' form a right-angled triangle. The height of the image 'h' and the distance between the mirror and the image 'd' also form a right-angled triangle.
Using the properties of similar triangles, we can establish the following relationship:
H/h = h/d
Simplifying the equation, we get:
d = (h^2) / H
Step 3: Determine the minimum length of the mirror.
The minimum length of the mirror should be such that the person's entire image is visible. This means that the top of the person's image should be at the top edge of the mirror.
Let's assume the length of the mirror is 'L'. The distance between the mirror and the top of the person's image is 'd'. Therefore, the minimum length of the mirror should be:
L = d
Substituting the value of 'd' from step 2, we get:
L = (h^2) / H
Independence of Eye Position:
The minimum length of the mirror, as derived in step 3, is independent of the position of the person's eyes. This is because the length of the mirror depends only on the person's height 'H' and the distance between their eyes and the ground 'h'. The position of the eyes does not affect the geometry of the situation or the relationship between the lengths and distances involved.
Therefore, regardless of the person's eye position, the minimum length of the mirror required for them to have their full view is always 'H/2'.
Position of the Mirror:
The position of the mirror relative to the ground can be determined by considering the height of the person's eyes from the ground 'h' and the minimum length of the mirror 'H/2'.
The mirror should be placed in such a way that the top edge of the mirror is at the same height as the person's eyes. This ensures that the person's entire image is visible in the mirror.
To illustrate the position of the mirror, we can draw a ray diagram. The ray diagram will show the incident rays from the person, the reflected rays, and the position of the person's image formed in the mirror.
(Note: Draw a ray diagram showing the incident rays from the person, the reflected rays, and the position of the person's image formed in the mirror.
Attention Class 10 Students!
To make sure you are not studying endlessly, EduRev has designed Class 10 study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Class 10.

|
Explore Courses for Class 10 exam
|

|
Similar Class 10 Doubts
A person dressed in a new suit stands in front of a plane mirror fixed on a vertical wall. Height of a person is 'H' and that of his eyes from the ground is 'h'. Show that minimum length of the mirror so that the person can have his full view is 'H/2' and that it is independent of the position of eyes. Also determine the position of the mirror relative to ground and show image formation with a ray diagram.?
Question Description
A person dressed in a new suit stands in front of a plane mirror fixed on a vertical wall. Height of a person is 'H' and that of his eyes from the ground is 'h'. Show that minimum length of the mirror so that the person can have his full view is 'H/2' and that it is independent of the position of eyes. Also determine the position of the mirror relative to ground and show image formation with a ray diagram.? for Class 10 2024 is part of Class 10 preparation. The Question and answers have been prepared according to the Class 10 exam syllabus. Information about A person dressed in a new suit stands in front of a plane mirror fixed on a vertical wall. Height of a person is 'H' and that of his eyes from the ground is 'h'. Show that minimum length of the mirror so that the person can have his full view is 'H/2' and that it is independent of the position of eyes. Also determine the position of the mirror relative to ground and show image formation with a ray diagram.? covers all topics & solutions for Class 10 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A person dressed in a new suit stands in front of a plane mirror fixed on a vertical wall. Height of a person is 'H' and that of his eyes from the ground is 'h'. Show that minimum length of the mirror so that the person can have his full view is 'H/2' and that it is independent of the position of eyes. Also determine the position of the mirror relative to ground and show image formation with a ray diagram.?.
A person dressed in a new suit stands in front of a plane mirror fixed on a vertical wall. Height of a person is 'H' and that of his eyes from the ground is 'h'. Show that minimum length of the mirror so that the person can have his full view is 'H/2' and that it is independent of the position of eyes. Also determine the position of the mirror relative to ground and show image formation with a ray diagram.? for Class 10 2024 is part of Class 10 preparation. The Question and answers have been prepared according to the Class 10 exam syllabus. Information about A person dressed in a new suit stands in front of a plane mirror fixed on a vertical wall. Height of a person is 'H' and that of his eyes from the ground is 'h'. Show that minimum length of the mirror so that the person can have his full view is 'H/2' and that it is independent of the position of eyes. Also determine the position of the mirror relative to ground and show image formation with a ray diagram.? covers all topics & solutions for Class 10 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A person dressed in a new suit stands in front of a plane mirror fixed on a vertical wall. Height of a person is 'H' and that of his eyes from the ground is 'h'. Show that minimum length of the mirror so that the person can have his full view is 'H/2' and that it is independent of the position of eyes. Also determine the position of the mirror relative to ground and show image formation with a ray diagram.?.
Solutions for A person dressed in a new suit stands in front of a plane mirror fixed on a vertical wall. Height of a person is 'H' and that of his eyes from the ground is 'h'. Show that minimum length of the mirror so that the person can have his full view is 'H/2' and that it is independent of the position of eyes. Also determine the position of the mirror relative to ground and show image formation with a ray diagram.? in English & in Hindi are available as part of our courses for Class 10.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Here you can find the meaning of A person dressed in a new suit stands in front of a plane mirror fixed on a vertical wall. Height of a person is 'H' and that of his eyes from the ground is 'h'. Show that minimum length of the mirror so that the person can have his full view is 'H/2' and that it is independent of the position of eyes. Also determine the position of the mirror relative to ground and show image formation with a ray diagram.? defined & explained in the simplest way possible. Besides giving the explanation of
A person dressed in a new suit stands in front of a plane mirror fixed on a vertical wall. Height of a person is 'H' and that of his eyes from the ground is 'h'. Show that minimum length of the mirror so that the person can have his full view is 'H/2' and that it is independent of the position of eyes. Also determine the position of the mirror relative to ground and show image formation with a ray diagram.?, a detailed solution for A person dressed in a new suit stands in front of a plane mirror fixed on a vertical wall. Height of a person is 'H' and that of his eyes from the ground is 'h'. Show that minimum length of the mirror so that the person can have his full view is 'H/2' and that it is independent of the position of eyes. Also determine the position of the mirror relative to ground and show image formation with a ray diagram.? has been provided alongside types of A person dressed in a new suit stands in front of a plane mirror fixed on a vertical wall. Height of a person is 'H' and that of his eyes from the ground is 'h'. Show that minimum length of the mirror so that the person can have his full view is 'H/2' and that it is independent of the position of eyes. Also determine the position of the mirror relative to ground and show image formation with a ray diagram.? theory, EduRev gives you an
ample number of questions to practice A person dressed in a new suit stands in front of a plane mirror fixed on a vertical wall. Height of a person is 'H' and that of his eyes from the ground is 'h'. Show that minimum length of the mirror so that the person can have his full view is 'H/2' and that it is independent of the position of eyes. Also determine the position of the mirror relative to ground and show image formation with a ray diagram.? tests, examples and also practice Class 10 tests.

|
Explore Courses for Class 10 exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

























