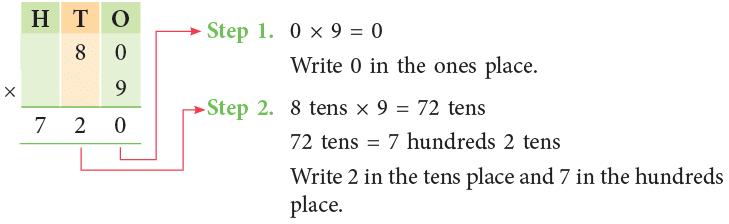Multiplication Class 3 Notes Maths

What is Multiplication?

Multiplication as Repeated Addition

Instead of adding same amount repeatedly to find the sum, we can multiply to find the same result in a much quicker way.
Consider 4 groups of chocolates with 3 chocolates in each group.
How many chocolates are there altogether? You can add and find out.
3 + 3 + 3 + 3 = 12
There are 12 chocolates in all.
In short, we can write this as:
Using multiplication,
4 × 3 = 12 is read as 3 multiplied by 4 is equal to 12 or 4 times 3 is 12 or 4 threes are 12.

2. Terms Related to Multiplication

• The number that is repeated is called the multiplicand.
• A number which expresses how often the multiplicand is repeated is called the multiplier.
• The numbers which are being multiplied are called factors.
• The result obtained after multiplying two numbers is known as the product. 
  In 4 × 3 = 12, 4 is the multiplier, 3 is the multiplicand and 12 is the product.

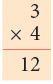
Properties of Multiplication

1. Property of one
Look and understand.
Also, by order property given on next page, 1 × 4 = 4 or

When 1 is a factor, the product is equal to the other factor.

2. Property of zero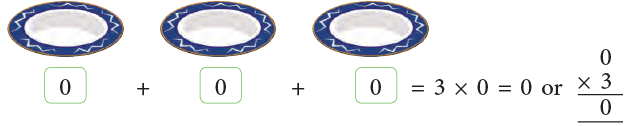

When 0 is a factor, the product is always 0.

Also, 0 × 3 = 3 × 0 = 0 or

3. Order Property
Observe the different ways of arranging the dots as shown below: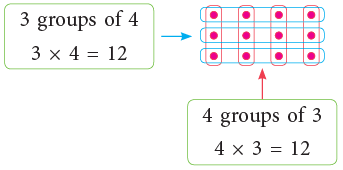
3 × 4 = 4 × 3 = 12
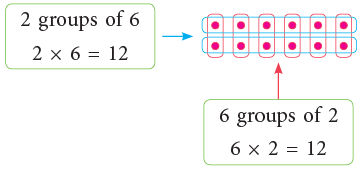2 × 6 = 6 × 2 = 12
We observe that:

Changing the order of the two factors does not change the product.

The above property is called the commutative property of multiplication. We say multiplication is commutative.
We can show the commutative property using a number line as shown below: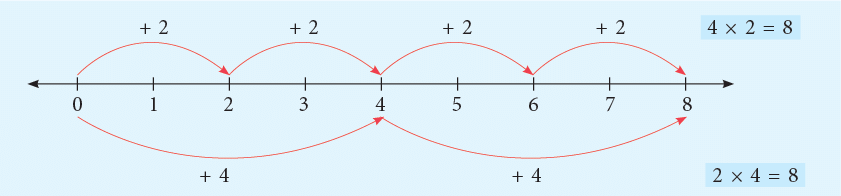

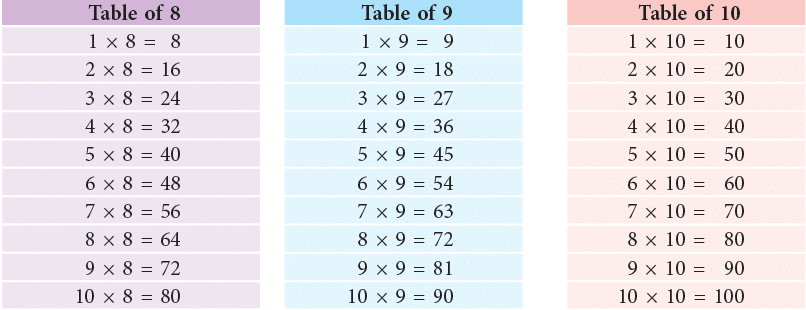
Multiplication Tables

You have learnt the multiplication tables up to 10 in your previous class. They are given here so that you may revise them.

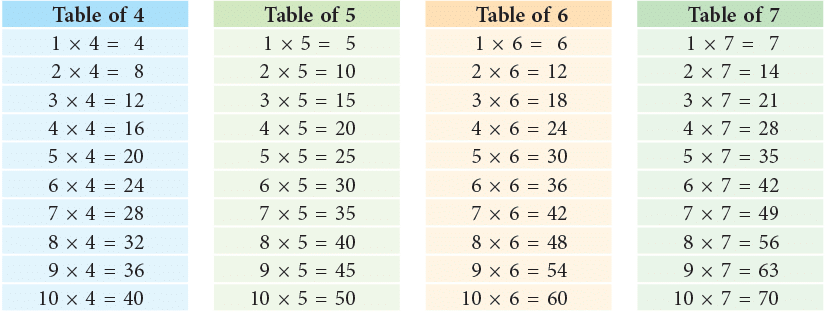
Multiplication Grid

You can find products of 2 numbers with the help of a multiplication grid as shown here. The numbers along the top and side are factors. Suppose, you have to find 2 × 5.
Step 1: Find the row for 2 and the column for 5.
Step 2: Locate the number in the square where the row and column meet. This number which is 10 gives the product of 2 and 5.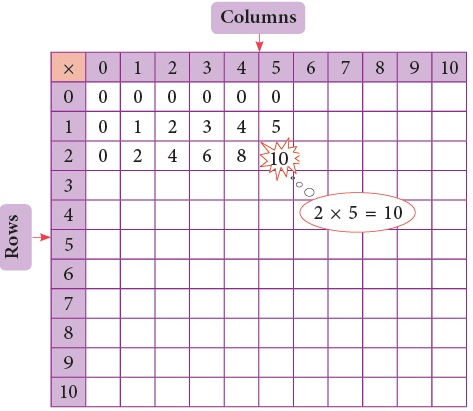

Skip Counting

Counting by 2s up to 20, we have 2, 4, 6, 8, 10, 12, 14, 16, 18, 20.
The counting by 2s means finding the products 2 × 1, 2 × 2, 2 × 3, … 2 × 10.

Multiples

The multiples of any counting number are obtained on multiplying this counting number by the counting numbers 1, 2, 3, 4, …

Thus, the multiples of 3 are 3 × 1, 3 × 2, 3 × 3, 3 × 4, …, that is, 3, 6, 9, 12, …

Multiplication by a Single Digit Number

1. Without Carrying

Example 1: Multiply 43 by 2.

Thus, 43 × 2 = 86.

Example 2: Multiply 80 by 9.

Thus, 80 × 9 = 720.

Example 3: Multiply 123 by 3.

Thus, 123 × 3 = 369.

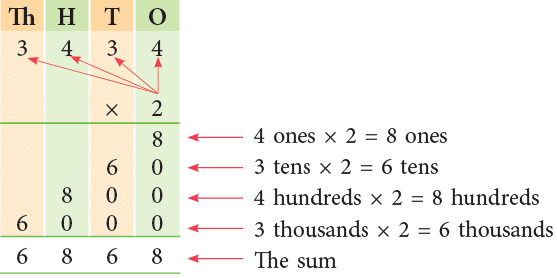
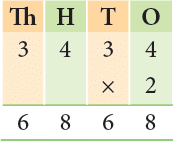
Example 4: Multiply 3434 by 2.

Thus, 3434 × 2 = 6868.
Think:

• 4 ones × 2 = 8 ones. Write 8 at ones place.
• 3 tens × 2  = 6 tens. Write 6 at tens place.
• 4 hundreds × 2  = 8 hundreds. Write 8 at hundreds place.
• 3 thousands × 2 = 6 thousands. Write 6 at thousands place.

Thus, 3434 × 2 = 6868.

2. Multiplication with Carrying
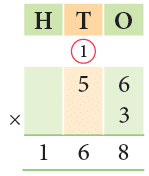
Example 5: Multiply 56 by 3.

Step 1: Multiply 6 ones by 3. 6 ones × 3 = 18 ones
= 1 ten 8 ones. Write 8 in the ones place and carry 1 to the tens place.
Step 2: Multiply 5 tens by 3. 5 tens × 3 = 15 tens
15 tens + 1 ten (carried over) = 16 tens Write 6 at tens place and 1 at hundreds place.

Thus, 56 × 3 = 168.

Example 6: Multiply 126 by 7.

Step 1: 6 ones × 7 = 42 ones = 4 tens 2 ones.
Write 2 in the ones place and carry 4 to the tens place.
Step 2: 2 tens × 7 = 14 tens
14 tens + 4 tens (carried over) = 18 tens
= 1 hundred 8 tens.
Write 8 in the tens place and carry 1 to the hundreds place.
Step 3: 1 hundred × 7 = 7 hundreds
7 hundreds + 1 hundred (carried over)
= 8 hundreds.
Write 8 in the hundreds place.
Thus, 126 × 7 = 882.

Example 7: Multiply 1252 by 6.

2 ones × 6  = 12 ones = 1 ten 2 ones
Write 2 in the ones place and carry 1 ten to the tens place.
5 tens × 6 + 1 ten (carried over) = 31 tens
= 3 hundreds 1 ten
Write 1 in the tens place and carry 3 hundreds to hundreds place.
(2 × 6) hundreds + 3 hundreds (carried over)
= 15 hundreds = 1 thousand 5 hundreds
Write 5 in the hundreds place and carry 1 thousand to the thousands place.
1 thousand × 6 + 1 thousand (carried over) = 7 thousands.
Write 7 in the thousands place.
Thus, 1252 × 6 = 7512.

3. Multiplying by 10, 100, 1000

(i) Look at these.
6 × 10 = 6 tens = 60
61 × 10 = 61 tens = 610
348 × 10 = 348 tens = 3480

Rule: When you multiply a number by 10, you simply write the number and put a zero. That is, you write a 0 after the numeral.

(ii) Look at these.

Rule: When you multiply a number by 100, you write two zeros after the numeral.

(iii) Look at these.

Rule: When you multiply a number by 1000, you write three zeros after the numeral.

4. Multiplying by Multiples of 10, i.e., 20, 30, 300, etc.
Observe the following:
(i) 8 × 20 = 8 × 2 tens
= 16 tens
= 160

Multiply 8 by 2. You get 16. Now write one zero to the right of product 16. You get 160.

(ii) 15 × 300 = 15 × 3 hundreds
= 45 hundreds
= 4500

Multiply 15 by 3. You get 45. Now write two zeros to the right of product 45 You get 4500.

Similarly, 4 × 20 = 80, 7 × 70 = 490, 9 × 600 = 5400, 30 × 300 = 9000.
We observe that,

To multiply a number by a multiple of 10, i.e., 20, 30, … 90, multiply the number by 2, 3, … 9 and put one zero to the right of the product.

Multiplication Tables from 11 to 20 (Memorise)

Memorise the tables of 11 to 20.

Multiplication Grid for Tables of 11–20

Example 8: Find the product of 16 and 8.

Select the row showing 8 and the column showing 16. The product of 16 × 8 is the number at the intersection of this row and column. Thus, the product is 128. Verify the answer from the multiplication table of 16. Memorizing the tables from 1–20 will help you in doing multiplication very fast.

Multiplication by a Two-Digit Number

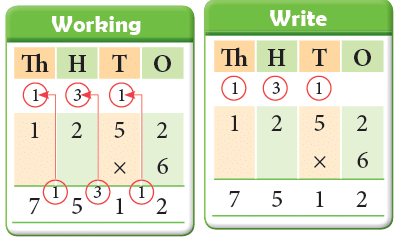
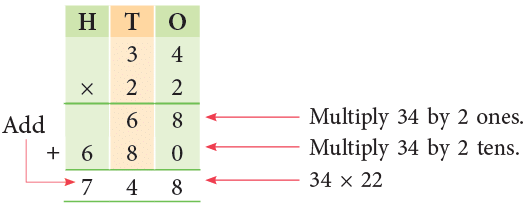
Example 9: There were 34 cartons with 22 apples in each carton. How many apples were there in all?

You have to think of equal groups as being put together, so you multiply 34 by 22.
Using the place value system, this can be done in a short way as under:

34 × 2  = 68
34 × 20 = 680
Thus, there were 748 apples in all.

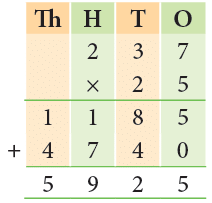
Example 10: Multiply:
(a) 423 by 14
(b) 237 by 25

Thus, 423 × 14 = 5922
(b) Similarly,

Thus, 237 × 25 = 5925.

Problems Based on Real Life Situations

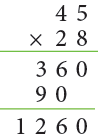
Example 11: Aman's stamp book has 45 pages and each page has 28 stamps. How many stamps does Aman have?

Total number of pages = 45
Number of stamps in each page = 28
Working:

∴ Total number of stamps = 45 × 28 = 1260 stamps.