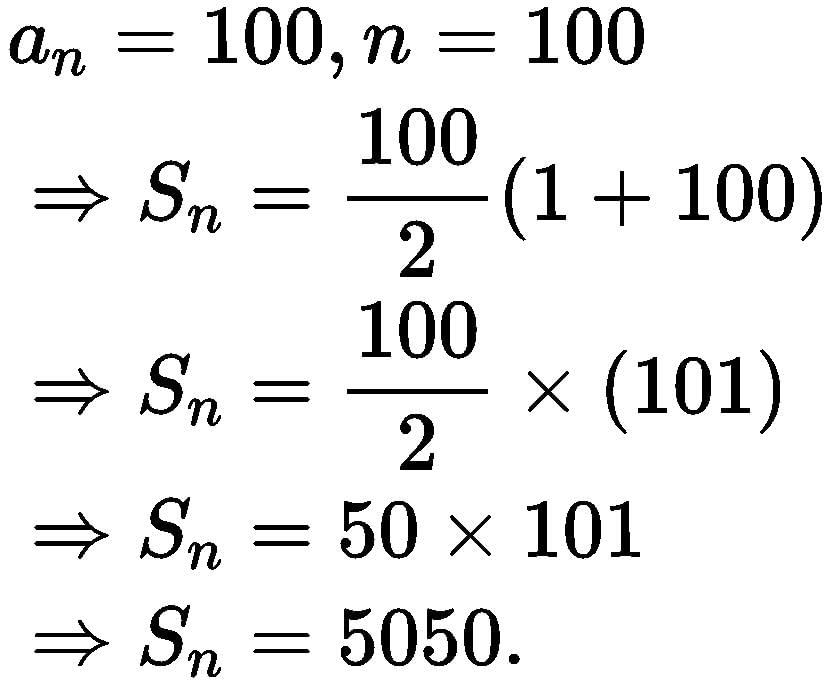Important Formulas: Number System | General Aptitude for GATE - Mechanical Engineering PDF Download
Understanding the number system is crucial for competitive exams like GATE, as it forms the foundation for various quantitative topics. The topic is known for intriguing conceptual problems that test the best brains. Instead of just solving problems, focus on grasping the concepts thoroughly. Explore alternative approaches to solve questions, as it enhances your problem-solving skills and prepares you comprehensively for the exam.

What is Number System?
Number system is a method of representing a number on the number line. Number system is a system of writing or expressing numbers. This Page from here on contains Formulas and definition of Number System.
Here is a list of Important Formulas that candidates need to master to crack the exam successfully.
Important Formulas in Algebra
Algebra is a branch of mathematics that substitutes letters for numbers. An algebraic equation depicts a scale, what is done on one side of the scale with a number is also done to either side of the scale.
- (a + b)(a - b) = (a2 - b2)
- (a + b)2 = (a2 + b2 + 2ab)
- (a - b)2 = (a2 + b2 - 2ab)
- (a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca)
- (a3 + b3) = (a + b)(a2 - ab + b2)
- (a3 - b3) = (a - b)(a2 + ab + b2)
- (a3 + b3 + c3 - 3abc) = (a + b + c)(a2 + b2 + c2 - ab - bc - ac)
⇒ When a + b + c = 0, then a3 + b3 + c3 = 3abc - (a + b)n = an + (nC1)an-1b + (nC2)an-2b² + … + (nCn-1)abn-1 + bn
Visual Representation of Formulas in Algebra
- (a + b)2 = a2 + b2 + 2ab
The (a + b)2 formula is the algebraic identity used to find the square of the sum of two numbers. To find the formula of the binomial in the form (a + b)2, we will just multiply (a + b) (a + b).
(a + b)2 = (a + b)(a + b)
= a2 + ab + ba + b2
= a2 + 2ab + b2
Therefore, (a + b)2 formula is: (a + b)2 = a2 + 2ab + b2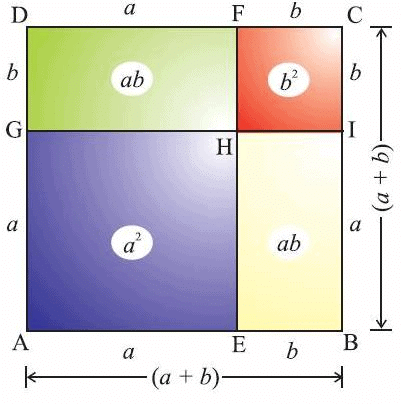
- (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
The (a + b + c)2 formula is used to find the sum of squares of three numbers without actually calculating the squares. (a + b + c)2 formula is one of the major algebraic identities. To derive the expansion of (a + b + c)2 formula we just multiply (a + b + c) by itself to get (a + b + c)2.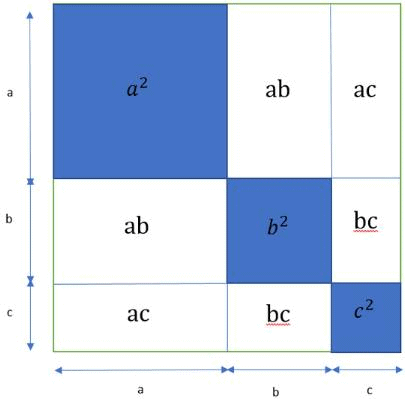
Important Formulas in Number System
- 1 + 2 + 3 + 4 + 5 + … + n = n(n + 1)/2
Example: Find the sum of the first 35 natural numbers.
Solution: Given, n = 35
The sum of natural numbers formula is:
S = [n(n+1)]/2
S = [35(35+1)]/2
S = 630 - (1² + 2² + 3² + ….. + n²) = n ( n + 1 ) (2n + 1) / 6
Example: Find the addition of squares of the first 40 natural numbers.
Solution: The formula of the sum of squared natural numbers is given by:
Σn2 = [n(n+1)(2n+1)]/6
Here, n = 40
Σ40² = (40/6) (40 + 1)(2 x 40 + 1)
Σ40² = (20/3) (41)(81)
Σ40² = (20)(41)(27)
Σ40² = 22140 - (1³ + 2³ + 3³ + ….. + n³) = (n(n + 1)/ 2)²
Example: Find the sum of cubes of natural numbers from 5 to 14.
Solution: To find the sum of cubes of numbers from 5 to 14, we will first find the sum of cubes of the first 14 natural numbers and then we will find the sum of cubes of the first 4 natural numbers. Then we subtract the values obtained to get the answer.
Sum of cubes of n natural numbers = [n² (n + 1)2]/4
Sum of cubes of first 14 natural numbers = 142 × (14+1)2/4
= 142 × 152/4
= 196 × 225/4
= 49 × 225= 11025
Now, the sum of cubes of first 4 natural numbers = 42 × (4+1)2/4
= 42 × 52/4
= 4 × 25
= 100
Therefore, the sum of cubes of natural numbers from 5 to 14 = 11025 - 100 = 10925. - Sum of first n odd numbers = n²
Example: Find the sum of odd numbers 1 to 50.Solution: We know that there are 25 odd numbers between 1 to 50. Thus, by using the sum of n odd numbers formula which is n2, we get, S25 = 252 = 625.
We can alternatively show this using the formula Sn = n/2 × [a + l]. We know that the sum of odd numbers 1 to 50 is represented as Sn = 1 + 3 + ... + 49.Thus, a = 1, l = 49, and n = 25.
S25 = (25/2) × [1 + 49]= (25/2) × 50
= 25 × 25 = 625
Thus, the sum of odd numbers 1 to 50 is equal to 625. - Sum of first n even numbers = n (n + 1)
Example: What is the sum of even numbers from 1 to 50?
Solution: We know that, from 1 to 50, there are 25 even numbers.
Thus, n = 25
By the formula of sum of even numbers we know;
Sn = n(n+1)
Sn = 25(25+1) = 25 x 26 = 650 Highest power of n in m! is [m/n] + [m/n2] + [m/n3] +….. where, [x] is the greatest integer less than or equal to x.
Example: Find the highest power of 7 in 100!.
Highest power of 7 in 100! = [100/7] + [100/49] = 16- To find the number of zeroes in n! find the highest power of 5 in n!
Example : What is the number of trailing zeroes in 23!?[23/5] = 4. It is less than 5, so we stop here. The answer is 4.
If all possible permutations of n distinct digits are added together with the sum
= (n-1)! * (sum of n digits) * (11111… n times)
Example: What would be the sum of all the numbers which can be formed by using the digits 1, 3, 5, 7 all at a time and which have no digits repeated?
Solution: The sum of the numbers formed by taking all the given n digits is (sum of all the n digits) * (n - 1)! * (111…..n times).
Here n = 4, and Sum of 4 digits = 16
The sum of all the numbers which can be formed by using the digits 1, 3, 5, 7= (16) * (4 – 1)! * ( 1111) = 16 * 3! * 1111If the number can be represented as N = ap∗ bq ∗ cr. Then, the number of factors of N is (p+1) * (q+1) * (r+1)
Sum of all factors: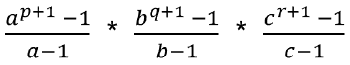
Example: Find the number of factors of 98 and also find the sum and product of all factors.
Solution: First, write the number 98 into prime factorization.
i.e. 98 = 2 × 49 = 2 × 7 × 7 = 21 x 72
Here A = 2, B = 7, p = 1, q = 2
Number of factors for 98 = (p + 1)(q +1) = 2 × 3 = 6
Sum of all factors of 98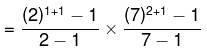 = 3 × 57 = 171
= 3 × 57 = 171
Product of all factors of number 98 = (98)6/2 = 941192If the number of factors is odd, then N is a perfect square.
Example: Find the number of odd, even, perfect square, perfect cube factors of 4500.
4500 = 45 × 100 = 9 × 5 × 10 × 10 = 3 × 3 × 5 × 5 × 2 × 5 × 2 = 22 × 32 × 53
Here, consider A = 2 , B = 3 , C = 5 , p= 2 , q = 2 and r = 3
Here identifying that odd number are 3 and 5.
Numbers of odd factors of number 4500 = (q + 1) (r + 1) = 3 × 4 = 12
∴ Total number of factors = (p + 1)(q +1)(r +1) = 3 × 3 × 4 =36
Numbers of even factors of number = (Total number of factors – Numbers of odd factors) = 36 – 12 = 24
Number of perfect square factors of number 4500 = 2 x 2 x 2 = 8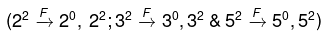
Number of perfect cube factors of number 4500 = 1 x 1 x 2 = 2Suppose a number N and if there are n factors including the number N and 1, then the number of pairs of factors would be n/2. If N is a perfect square, then the number of pairs (including the square root) is (n+1)/2.
Example: In how many ways you can express 36 as the product of two of its factors?
Prime factorization of 36 i.e. we write 36 = 22 × 32
Number of factors of 36 will be (2+1)(2+1) = 9
(i.e. factors are 1, 2,3, 4, 6, 9, 12, 18, 36).
Since we are asked the total number of ways hence we include the square root of 36 i.e. 6 as well.
Thus the number of ways you can express 36 as the product of two of its factors is (9+1)/2 = 5.If the number can be expressed as N = 2p ∗ aq ∗ br . . . where the power of 2 is p and a, b are prime numbers then:
(i) The number of even factors of N = p (1 + q) (1 + r) . . .
(ii) The number of odd factors of N = (1 + q) (1 + r)…When we are asked to calculate how many positive integral solutions are possible for the equation X2– Y2= N, there can be 4 cases.
Let us look at them one by one by solving examples:
Positive Integral Solutions for the equation X2 - Y2 = N?
When we are asked to calculate how many positive integral solutions are possible for the equation X2 - Y2 = N, there can be 4 cases.
Case 1: N is an odd number and not a perfect square
Case 2: N is an odd number and a perfect square
Case 3: N is an even number and not a perfect square
Case 4: N is an even number and a perfect square
Case 1: N is an odd number and not a perfect square
The total number of positive integral solutions will be = (Total number of factors of N)/2
Example: How many positive integral solutions are possible for the equation X2 – Y2 = 135?The total number of factors of 135 = 1, 3, 5, 9, 15, 27, 45 and 135 is 8.
So, total number of positive integral solutions = 8/2 = 4.
Case 2: N is an odd number and a perfect square
The total number of positive integral solutions will be = [(Total number of factors of N) – 1]/ 2
Example: How many positive integral solutions are possible for the equation X2– Y2 = 121?
The total number of factors of 121 = 1, 11 and 121 is 3.
So, the total number of positive integral solutions = (3-1)/2 = 1
Case 3: N is an even number and not a perfect square
The total number of positive integral solutions will be = [Total number of factors of (N/4)] / 2
Example: How many positive integral solutions are possible for the equation X2– Y2 = 160?Total number of factors of 40 = 1, 2, 4, 5, 8, 10, 20 and 40 is 8 (as N = 160 and N/4 = 40)
So, total number of positive integral solutions = 8/2 = 4
Case 4: N is an even number and a perfect square
The total number of positive integral solutions will be = {[Total number of factors of (N/4)] – 1 } / 2
Example: How many positive integral solutions are possible for the equation X2– Y2= 256?
The total number of factors of 64 = 1, 2, 4, 8, 16, 32 and 64 is 7 (as N = 256 and N/4 = 64)
So, (7-1)/2 = 3 positive integral solutions.
EduRev Tip: A number can be written as the sum of two squares while including prime factors of the form 4k + 3 as long as those prime factors are raised to an even power.The number of digits in ab = [b logm(a)] + 1; where m is the base of the number and [.] denotes the greatest integer function.
Even a number that is not a multiple of 4, can never be expressed as a difference of 2 perfect squares.
Basic summation properties:
(i) Sum of first n odd numbers is n2
(ii) Sum of first n even numbers is n(n + 1)
(iii) 1 + 2 + 3 + 4 + 5 + … + n = n(n + 1)/2
(iv) (1² + 2² + 3² + ….. + n²) = n ( n + 1 ) (2n + 1) / 6
(v) (1³ + 2³ + 3³ + ….. + n³) = (n(n + 1)/ 2)²The product of the factors of N is given by Na/2, where 'a' is the number of factors.
The last two digits of a2, (50 – a)2, (50 + a)2, (100 – a)2 . . . . . are same. Every number can be written as (50n ± x), where x is a number from 0 to 25. Hereby 50n, it just means any multiple of 50 i.e. 0, 50, 100, 150, ……
0 to 25 = (0 to 25) itself.
25 to 50 = 50 – (25 to 0)
50 to 75 = 50 + (0 to 25)
75 to 100 = 100 – (25 to 0)
100 to 125 = 100 + (0 to 25)
125 to 150 = 150 – (25 to 0) and so on.But how does this help us in finding the last two digits of any square?
Example: What are the last two digits of 2682?
(50n ± x)2 = 2500n2 ± 100nx + x2
The last two digits of each of 2500n2 and 100nx will be 00. Thus the last two digits of the RHS, and hence of the LHS, will be the last two digits of x2.268 = 50 × 5 + 18.
Example: What are the last two digits of 2782?
Thus, the last two digits of 2682 will be same as the last two digits of 182 i.e. 24.While you can consider 278 = 50 × 5 + 28, it will consider
278 = 50 × 6 – 22, to be x in the range 0 to 25.
Thus, the last two digits of 2782 will be the same as the last two digits of 222 i.e. 84.If the number is written as 210n:
(i) When n is odd, the last 2 digits are 24.
(ii) When n is even, the last 2 digits are 76.
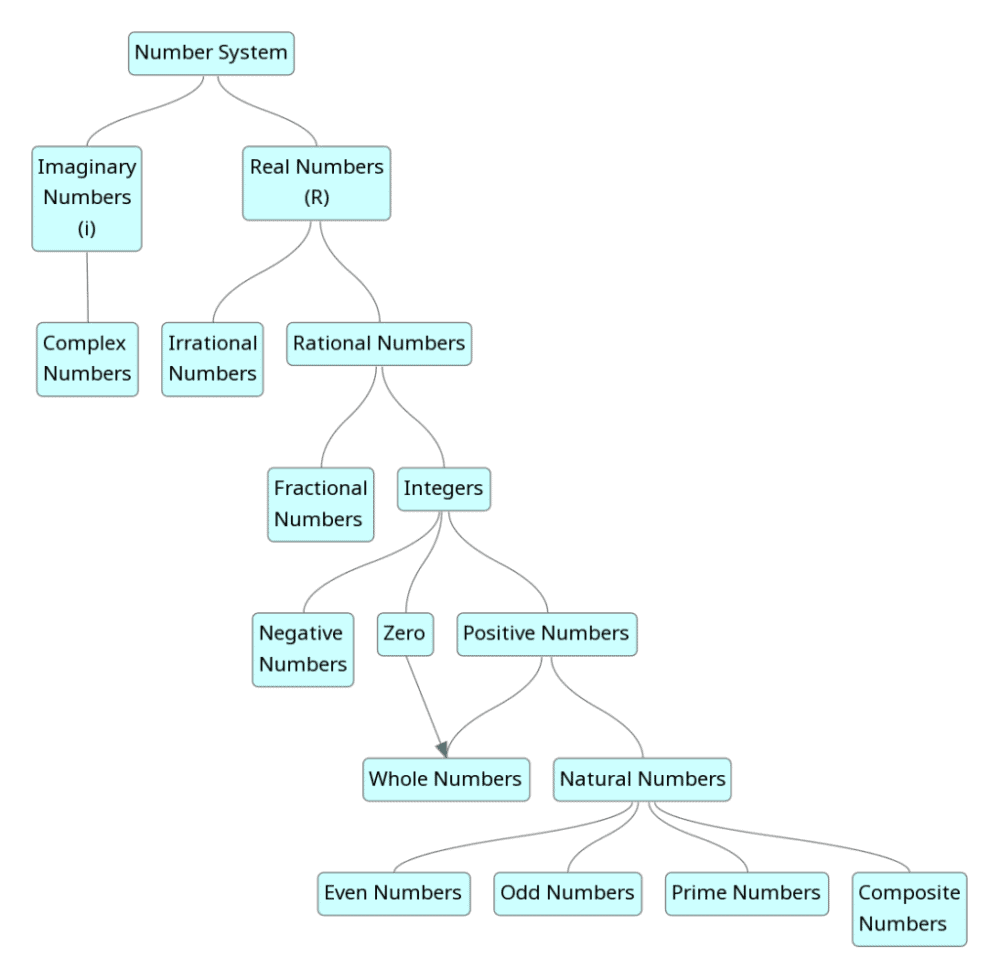
Types of Numbers
- Natural Numbers
All positive integers are called natural numbers. All counting numbers from 1 to infinity are natural numbers.
N = {1, 2, 3, 4, 5, 6……….∞} - Whole Numbers
The set of numbers that includes all natural numbers and the number zero are called whole numbers. They are also called as Non-negative integers.
W = { 0,1,2,3,4,5,6,7,8,…………..∞} - Integers
All numbers that do not have the decimal places in them are called integers.
Z = {∞…….-3, -2, -1, 0, 1, 2, 3………∞}
a. Positive Integers
1, 2, 3, 4….. is the set of all positive integers.
b. Negative Integers
−1, −2, −3….. is the set of all negative integers.
c. Non-Positive and Non-Negative Integers
0 is neither positive nor negative. - Real Numbers
All numbers that can be represented on the number line are called real numbers. - Rational Numbers
A rational number is defined as a number of the form a/b where ‘a’ and ‘b’ are integers and b ≠ 0. The rational numbers that are not integers will have decimal values. These values can be of two types
a. Terminating decimal fractions:
For example: 1551
= 0.5,12544125
= 31.25
b. Non-Terminating decimal fractions:
For example:196619
= 3.1666666, 219921
= 2.33333 - Irrational Numbers
It is a number that cannot be written as a ratio form (or fraction). An Irrational numbers are non-terminating and non-periodic fractions.
For example: 22
= 1.414 - Complex Numbers
The complex numbers are the set {a+bi}, where, a and b are real numbers and ‘i’ is the imaginary unit. - Imaginary Numbers
A number does not exist on the number line is called imaginary number.
For example square root of negative numbers are imaginary numbers. It is denoted by ‘i’ or ‘j. - Even Numbers
A number divisible by 2 is called an even number.
For example: 2, 6, 8, 14, 18, 246, etc. - Odd Numbers
A number not divisible by 2 is called an odd number.
For example: 3, 7, 9, 15, 17, 373, etc. - Prime Numbers
A number greater than 1 is called a prime number, if it has exactly two factors, namely 1 and the number itself.
For example: 2, 3, 5, 7, 11, 13, 17, etc. - Composite Numbers
Numbers greater than 1 which are not prime, are known as composite numbers.
For example: 4, 6, 8, 10, etc.
Divisibility Rules
- Divisibility by 2 → A number that is even or a number whose last digit is an even number i.e. 0, 2, 4, 6, and 8.
- Divisibility by 3 → The sum of all the digits of the number should be divisible by 3.
- Divisibility by 4 → Number formed by the last two digits of the number should be divisible by 4 or should be 00.
- Divisibility by 5 → Numbers having 0 or 5 as their ones place digit.
- Divisibility by 6 → A number that is divisible by both 2 and 3.
- Divisibility by 7 → Subtracting twice the last digit of the number from the remaining digits gives a multiple of 7.
- Divisibility by 8 → Number formed by the last three digits of the number should be divisible by 8 or should be 000.
- Divisibility by 9 → The sum of all the digits of the number should be divisible by 9.
- Divisibility by 10 → Divisibility rule for 10 states that any number whose last digit is 0, is divisible by 10.
- Divisibility by 11 → The difference of the sums of the alternative digits of a number is divisible by 11.
- Divisibility by 12 → A number that is divisible by both 3 and 4.
- Divisibility by 13 → For any given number, to check if it is divisible by 13, we have to add four times of the last digit of the number to the remaining number and repeat the process until you get a two-digit number. Now check if that two-digit number is divisible by 13 or not. If it is divisible, then the given number is divisible by 13.
- Divisibility by 14→ A number divisible by both 2 and 7.
- Divisibility by 16 → Last four-digit divisible by 16
- Divisibility by 27 → Sum of blocks of 3 (taken a right to left) divisible by 27
Solved Examples of Divisibility
Q.1. Is 7248 is divisible (i) by 4, (ii) by 2, and (iii) by 8?
Answer:
(i) The number 7248 has 48 on its extreme right side which is exactly divisible by 4. When we divide 48 by 4 we get 12.
Therefore, 7248 is divisible by 4.
(ii) The number 7248 has 8 on its unit place which is an even number so, 7248 is divisible by 2.
(iii) 7248 is divisible by 8 as 7248 has 248 at its hundred place, tens place and unit place which is exactly divisible by 8.
Q.2. A number is divisible by 4 and 12. Is it necessary that it will be divisible by 48? Give another example in support of your answer.
Answer: 48 = 4 × 12 but 4 and 12 are not co-prime.
Therefore, it is not necessary that the number will be divisible by 48.
Let us consider the number 72 for an example
72 ÷ 4 = 18, so 72 is divisible by 4.
72 ÷ 12 = 6, so 72 is divisible by 12.
But 72 is not divisible by 48.
Q.3. Without actual division, find if 235932 is divisible (i) by 4 and (ii) 8.
Answer:
(i) The number formed by the last two digits on the extreme right side of 235932 is 32
32 ÷ 4 = 8, i.e. 32 is divisible by 4.
Therefore, 235932 is divisible by 4.
(ii) The number formed by the last three digits on the extreme right side of 235932 is 932
But 932 is not divisible by 8.
Therefore, 235932 is not divisible by 8.
Q.4. Check whether 998 is divisible by 9.
Answer:
According to the rule, if the sum of the digits in a number is a multiple of 9, then it is divisible by 9.
Sum of the digits in 998: 9 + 9 + 8 = 26
26 is not a multiple of 9
So, 998 is not divisible by 9.
Q.5. Check whether 1782 is divisible by 11.
Answer:
According to the rule, in a number, if the sum of the digits in odd places and sum of the digits in even places are equal or they differ by a number divisible by 11, then the number is divisible by 11.
In 1782, the sum of the digits in odd places:
1 + 8 = 9
In 1782, the sum of the digits in even places:
7 + 2 = 9
In 1782, the sum of the digits in odd places and sum of the digits in even places are equal.
So, 1782 is divisible by 11.
Cyclicity of Exponents
Cyclicity refers to the repeating pattern in the units digit of a number raised to increasing powers. Understanding cyclicity helps in quickly determining the last digit of large powers without direct computation.
Key Concept
For any integer , the units digit of an (where is a positive integer) follows a repeating cycle. This cycle depends on the units digit of the base .
Examples:
Units digit of 2 raised to various powers:
- =2
- =4
- =8
- 16 (units digit is 6)
- =32 (units digit is 2)
- Pattern:
- Cycle: 4 (2, 4, 8, 6)
Units digit of 3 raised to various powers:
- =3
- 9
- =27 (units digit is 7)
- =81 (units digit is 1)
- =243 (units digit is 3)
- Pattern:
- Cycle: 4 (3, 9, 7, 1)
Units digit of 4 raised to various powers:
- =4
- =16 (units digit is 6)
- =64 (units digit is 4)
- =256 (units digit is 6)
- Pattern:
- Cycle: 2 (4, 6)
Units digit of 7 raised to various powers:
- 7
- =49 (units digit is 9)
- =343 (units digit is 3)
- =2401 (units digit is 1)
- Pattern:
- Cycle: 4 (7, 9, 3, 1)
Units digit of 9 raised to various powers:
- =9
- 81 (units digit is 1)
- =729 (units digit is 9)
- Pattern:
- Cycle: 2 (9, 1)
Finding the Units Digit of Large Powers
- Determine the base's units digit and identify the cycle length.
- Find the effective exponent within the cycle by taking the exponent modulo the cycle length.
Example: Find the units digit of
- Base's units digit: 7
- Cycle of 7: 4 (7, 9, 3, 1)
- Effective exponent: = 3
- Units digit of 73: 3 (from the cycle: 7, 9, 3, 1)
Thus, the units digit of 7^{2023} is 3.
HCF and LCM
- HCF * LCM of two numbers = Product of two numbers.
- The greatest number dividing a, b, and c leaving remainders of x1, x2, and x3 is the HCF of (a - x1), (b - x2), and (c - x3).
- The greatest number dividing a, b, and c (a < b < c) leaving the same remainder each time is the HCF of (c - b), (c - a), (b - a).
- If a number, N, is divisible by X and Y and HCF (X, Y) = 1. Then, N is divisible by X * Y.
Solved Examples of HCF and LCM
Example 1: Find the HCF of 96, 36, and 18.
96 = 2 × 3 × 2 × 2 × 2 × 2
36 = 2 × 3 × 2 × 3
18 = 2 × 3 × 3
Therefore, the HCF of 96, 36 and 18 is the product of the highest number of common factors in the given numbers i.e., 2 × 3 = 6.
In other words, 6 is the largest possible integer, which can divide 96, 36 and 18 without leaving any remainder.
Example 2: Find the HCF of 42 and 70.
42 = 3 × 2 × 7
70 = 5 × 2 × 7
Hence, HCF is 2 x 7 = 14.
Example 3: Find the HCF of numbers 144, 630, and 756.
144 = 24 × 32
630 =2 × 32 × 5 × 7
756 = 22 x 33 x 7
Hence, HCF of 144, 630, 756 = 2 × 32 = 18.
Example 4: Find the LCM of 96, 36, and 18.
96 = 2 × 2 × 2 × 2 × 2 × 3 = 25 × 31
36 = 2 x 2 x 3 x 3 = 22 x 32
18 = 2 x 3 x 3 = 21 x 32
Therefore, LCM of 96, 36 and 18 is the product of the highest powers of all the prime factors, i.e. 25 x 32 = 32 x 9 = 288.
That is, 288 is the smallest integer which is divisible by 96, 36 and 18 without leaving any remainder.
Example 5: Find the LCM of 42 and 70.
42 = 3 × 2 × 7
70 = 5 × 2 × 7
Hence, LCM is 2 × 3 × 5 × 7 = 210.
Apart from the method of prime factorization, there is another method of finding the LCM of given numbers, and the method is known as the long division method. This method is quite helpful in getting LCM quickly if there are three or more than three numbers.
Example 6: Find out the LCM of 48 and 300.
Here, we need to find out the LCM of 48 and 300.
48 = 2 × 2 × 2 × 2 × 3 = 24 × 31
300 = 2 × 2 × 3 × 5 × 5 = 22 × 31 × 52
List all numbers found, as many times as they occur, most often any one given number, and multiply them together to find the LCM.
Thus, 24 × 31 × 52 = 1200
Hence, the LCM of 48 and 300 is 1200.
Example 7: Find the LCM of 12, 18, 30.
Here, we need to find the LCM of 12, 18, 30.
Now, let us find the prime factors of the above three numbers.
12 = 2 × 2 × 3 = 22 × 31
18 = 2 × 3 × 3 = 21 × 32
30 = 2 × 3 × 5 = 21 × 31 × 51
Now, list all the prime numbers found as many times as they occur most often for anyone given number and multiply them together to find the LCM.
So, 2 × 2 × 3 × 3 × 5 = 180
Using exponents instead, multiply together each of the prime numbers with the highest power
Thus, 22 × 32 × 51 = 180
Hence, the LCM of 12, 18, 30 is 180.
EduRev Tip:
HCF of two prime numbers is always 1.
HCF of co-prime numbers is always 1.
Links for other topics of Number System:
Introduction: Number System
Important Concepts: Number System - 1
Important Concepts: Number System - 2
Base Systems
Overview: Number System
Divisibility Rules
Introduction & Concept: HCF & LCM
|
206 videos|190 docs|158 tests
|
FAQs on Important Formulas: Number System - General Aptitude for GATE - Mechanical Engineering
| 1. What are the important formulas in Algebra? |  |
| 2. How can visual representation help in understanding formulas in Algebra? |  |
| 3. What are the important formulas in the Number System? |  |
| 4. What are the different types of numbers in the Number System? |  |
| 5. What are the divisibility rules in the Number System? |  |