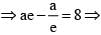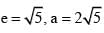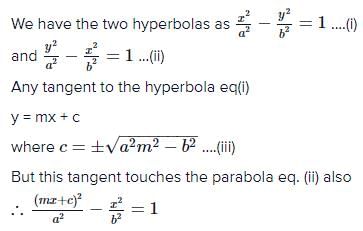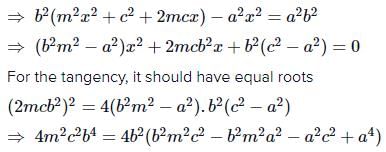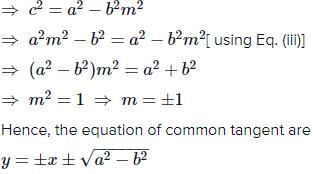All Exams >
JEE >
6 Months Preparation for JEE >
All Questions
All questions of Hyperbola for JEE Exam
The equation of the tangent lines to the hyperbola x2 – 2y2 = 18 which are perpendicular to the line y = x are- a)y = x ± 3
- b)y = –x ± 3
- c)2x + 3y + 4 = 0
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The equation of the tangent lines to the hyperbola x2 – 2y2 = 18 which are perpendicular to the line y = x are
a)
y = x ± 3
b)
y = –x ± 3
c)
2x + 3y + 4 = 0
d)
None of these
|
|
Preeti Khanna answered |
Equation of line perpendicular to x−y=0 is given by
y=−x+c
Also this line is tangent to the hyperbola x2−2y2=18
So we have m=−1, a2=18, b2=9
Thus Using condition of tangency c2 = a2m2−b2
= 18−9=9
⇒ c = ±3
Hence required equation of tangent is x+y = ±3
y=−x+c
Also this line is tangent to the hyperbola x2−2y2=18
So we have m=−1, a2=18, b2=9
Thus Using condition of tangency c2 = a2m2−b2
= 18−9=9
⇒ c = ±3
Hence required equation of tangent is x+y = ±3
Foot of normals drawn from the point p(h,k) to the hyperbola 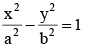 will always lie on the conic
will always lie on the conic- a)
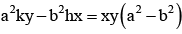
- b)
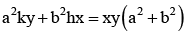
- c)
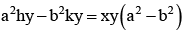
- d)
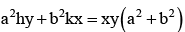
Correct answer is option 'D'. Can you explain this answer?
Foot of normals drawn from the point p(h,k) to the hyperbola 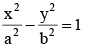 will always lie on the conic
will always lie on the conic
a)
b)
c)
d)
|
|
Vijay Kumar answered |
Equation of normal at any point (x1, y1) is 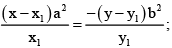 it passes through
it passes through
P (h, k) then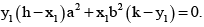 thus (x1, y1) lie on the conic
thus (x1, y1) lie on the conic
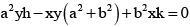
P (h, k) then
The asymptotes of the hyperbola xy–3x–2y = 0 are- a)x – 2 = 0 and y – 3 = 0
- b)x – 3 = 0 and y – 2 = 0
- c)x + 2 = 0 and y + 3 = 0
- d)x +3 = 0 and y + 2 = 0
Correct answer is option 'A'. Can you explain this answer?
The asymptotes of the hyperbola xy–3x–2y = 0 are
a)
x – 2 = 0 and y – 3 = 0
b)
x – 3 = 0 and y – 2 = 0
c)
x + 2 = 0 and y + 3 = 0
d)
x +3 = 0 and y + 2 = 0
|
|
Suresh Reddy answered |
xy - 3x - 2y + λ = 0.
Then abc + 2fgh − af2 − bg2 − ch2 = 0
⇒ 3/2 − λ/4 = 0
⇒ λ = 6
∴ Equation of asymptotes is xy-3x-2y+6=0
⇒ (x-2)(y-3)=0
⇒x - 2 = 0 and y - 3 = 0
Then abc + 2fgh − af2 − bg2 − ch2 = 0
⇒ 3/2 − λ/4 = 0
⇒ λ = 6
∴ Equation of asymptotes is xy-3x-2y+6=0
⇒ (x-2)(y-3)=0
⇒x - 2 = 0 and y - 3 = 0
Equation of the chord of the hyperbola 25x2 – 16y2 = 400 which is bisected at the point (6, 2) is- a)16x – 75y = 418
- b)75x – 16y = 418
- c)25x – 4y = 400
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Equation of the chord of the hyperbola 25x2 – 16y2 = 400 which is bisected at the point (6, 2) is
a)
16x – 75y = 418
b)
75x – 16y = 418
c)
25x – 4y = 400
d)
None of these
|
|
Hansa Sharma answered |
Given hyperbola is 25x2−16y2=400
If (6, 2) is the midpoint of the chord, then equation of chord is T = S1
⇒25(6x)−16(2y)=25(36)−16(4)
⇒75x−16y=450−32
⇒75x−16y=418
If (6, 2) is the midpoint of the chord, then equation of chord is T = S1
⇒25(6x)−16(2y)=25(36)−16(4)
⇒75x−16y=450−32
⇒75x−16y=418
The equation of the hyperbola whose foci are (6, 5), (–4, 5) and eccentricity 5/4 is- a)
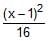 -
- 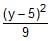 = 1
= 1 - b)
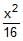 -
- 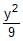 = 1
= 1 - c)
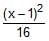 -
- 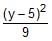 = - 1
= - 1 - d)None of these
Correct answer is option 'A'. Can you explain this answer?
The equation of the hyperbola whose foci are (6, 5), (–4, 5) and eccentricity 5/4 is
a)
b)
c)
d)
None of these
|
|
Om Desai answered |
Let the centre of hyperbola be (α,β)
As y=5 line has the foci, it also has the major axis.
∴ [(x−α)2]/a2 − [(y−β)2]/b2 = 1
Midpoint of foci = centre of hyperbola
∴ α=1,β=5
Given, e= 5/4
We know that foci is given by (α±ae,β)
∴ α+ae=6
⇒1+(5/4a)=6
⇒ a=4
Using b2 = a2(e2 − 1)
⇒ b2=16((25/16)−1)=9
∴ Equation of hyperbola ⇒ [(x−1)2]/16−[(y−5)2]/9=1
As y=5 line has the foci, it also has the major axis.
∴ [(x−α)2]/a2 − [(y−β)2]/b2 = 1
Midpoint of foci = centre of hyperbola
∴ α=1,β=5
Given, e= 5/4
We know that foci is given by (α±ae,β)
∴ α+ae=6
⇒1+(5/4a)=6
⇒ a=4
Using b2 = a2(e2 − 1)
⇒ b2=16((25/16)−1)=9
∴ Equation of hyperbola ⇒ [(x−1)2]/16−[(y−5)2]/9=1
The eccentricity of the hyperbola 4x2–9y2–8x=32 is- a)
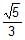
- b)
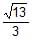
- c)
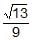
- d)
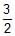
Correct answer is option 'B'. Can you explain this answer?
The eccentricity of the hyperbola 4x2–9y2–8x=32 is
a)
b)
c)
d)

|
Top Rankers answered |
4x2−9y2−8x=32
⇒4(x2−2x)−9y2 = 32
⇒4(x2−2x+1)−9y2 = 32 + 4 = 36
⇒(x−1)2]/9 − [y2]/4 = 1
⇒a2=9, b2=4
∴e=[1+b2/a2]1/2
= [(13)1/2]/3
⇒4(x2−2x)−9y2 = 32
⇒4(x2−2x+1)−9y2 = 32 + 4 = 36
⇒(x−1)2]/9 − [y2]/4 = 1
⇒a2=9, b2=4
∴e=[1+b2/a2]1/2
= [(13)1/2]/3
The equation of the transverse and conjugate axes of a hyperbola are respectively x + 2y – 3 = 0, 2x – y + 4 = 0 and their respective lengths are 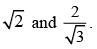 The equation of the hyperbola is
The equation of the hyperbola is- a)
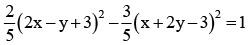
- b)
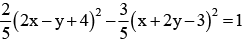
- c)
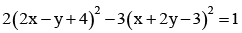
- d)2(x + 2y -3)2 -3 (2x - y + 4)2 = 1
Correct answer is option 'A'. Can you explain this answer?
The equation of the transverse and conjugate axes of a hyperbola are respectively x + 2y – 3 = 0, 2x – y + 4 = 0 and their respective lengths are 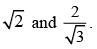 The equation of the hyperbola is
The equation of the hyperbola is
a)
b)
c)
d)
2(x + 2y -3)2 -3 (2x - y + 4)2 = 1
|
|
Vikas Kapoor answered |
Equation of the hyperbola is
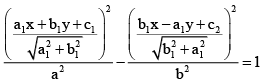
Where a1x + b1y + c1 = 0, b1x - a1y + c2 = 0 are conjugate and transverse axes respectively and a, b are lengths of semitransverse and semiconjugate axes respectively.
Where a1x + b1y + c1 = 0, b1x - a1y + c2 = 0 are conjugate and transverse axes respectively and a, b are lengths of semitransverse and semiconjugate axes respectively.
Area of triangle formed by tangent to the hyperbola xy = 16 at (16, 1) and co-ordinate axes equals- a)8
- b)16
- c)32
- d)64
Correct answer is option 'C'. Can you explain this answer?
Area of triangle formed by tangent to the hyperbola xy = 16 at (16, 1) and co-ordinate axes equals
a)
8
b)
16
c)
32
d)
64
|
|
Riya Banerjee answered |
Differentiating xy=16, (xdy)/x+y=0
⇒ dy/dx=−y/x=−1/16= Slope of tangent
⇒ Its (tangent's) equation : y=−1=−1/16(x−16)
⇒ 16y−16=−x+16 ⇒ 16y=−x−32
⇒ 16y+x+32=0
It will cut x−axis at A(−32, 0)
& y−axis at B(0, −2)
⇒ Area of △OAB= 1/2×2×32
⇒ 32
⇒ dy/dx=−y/x=−1/16= Slope of tangent
⇒ Its (tangent's) equation : y=−1=−1/16(x−16)
⇒ 16y−16=−x+16 ⇒ 16y=−x−32
⇒ 16y+x+32=0
It will cut x−axis at A(−32, 0)
& y−axis at B(0, −2)
⇒ Area of △OAB= 1/2×2×32
⇒ 32
If the latus rectum of an hyperbola be 8 and eccentricity be 3/√5 then the equation of the hyperbola is- a)4x2 – 5y2 = 100
- b)5x2 – 4y2 = 100
- c)4x2 + 5y2 = 100
- d)5x2 + 4y2 = 100
Correct answer is option 'A'. Can you explain this answer?
If the latus rectum of an hyperbola be 8 and eccentricity be 3/√5 then the equation of the hyperbola is
a)
4x2 – 5y2 = 100
b)
5x2 – 4y2 = 100
c)
4x2 + 5y2 = 100
d)
5x2 + 4y2 = 100
|
|
Neha Joshi answered |
Give eccentricity of the hyperbola is, e= 3/(5)1/2
⇒ (b2)/(a2) = 4/5..(1)
And latus rectum is =2(b2)/a=8
⇒ b2/a=4…(2)
By (2)/(1) a=5
∴ b2=20
Hence required hyperbola is, (x2)/25−(y2)/20=1
⇒ 4x2−5y2 =100
⇒ (b2)/(a2) = 4/5..(1)
And latus rectum is =2(b2)/a=8
⇒ b2/a=4…(2)
By (2)/(1) a=5
∴ b2=20
Hence required hyperbola is, (x2)/25−(y2)/20=1
⇒ 4x2−5y2 =100
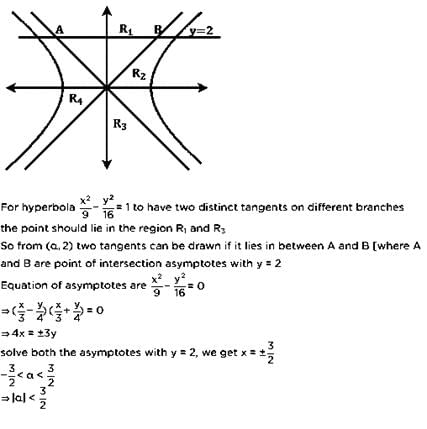
If the product of the perpendicular distances from any point on the hyperbola 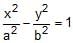 of eccentricity e= on its asymptotes is equal to 6, then the length of the transverse axis of the hyperbola is
of eccentricity e= on its asymptotes is equal to 6, then the length of the transverse axis of the hyperbola is- a)3
- b)6
- c)8
- d)12
Correct answer is option 'B'. Can you explain this answer?
If the product of the perpendicular distances from any point on the hyperbola 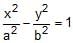 of eccentricity e= on its asymptotes is equal to 6, then the length of the transverse axis of the hyperbola is
of eccentricity e= on its asymptotes is equal to 6, then the length of the transverse axis of the hyperbola is
a)
3
b)
6
c)
8
d)
12

|
New Words answered |
e2 = (a2 / b2) + 1
3 = (a2 / b2) + 1
a2/b2 = 2
a2 = 2b2
Product of perpendicular distance of any point on hyperbola = (a2b2)/a2 + b2
= [2(b2).b2]/(2b2 + b2)
= [2b2]/3 = 6
= 2b2 = 18
=> b2 = 9
=> b = 3
Length (2b) = 2(3)
= 6
3 = (a2 / b2) + 1
a2/b2 = 2
a2 = 2b2
Product of perpendicular distance of any point on hyperbola = (a2b2)/a2 + b2
= [2(b2).b2]/(2b2 + b2)
= [2b2]/3 = 6
= 2b2 = 18
=> b2 = 9
=> b = 3
Length (2b) = 2(3)
= 6
The number of points on X-axis which are at a distance c units (c < 3) from (2, 3) is- a)1
- b)0
- c)3
- d)2
Correct answer is option 'B'. Can you explain this answer?
The number of points on X-axis which are at a distance c units (c < 3) from (2, 3) is
a)
1
b)
0
c)
3
d)
2

|
Mohit Rajpoot answered |
Distance of 'c' units from (2,3)
Let the no: of points be (x,0)
By distance formula
{(2−x)2+(3−0)2}=c
4−4x+x2+9=c
⇒x2−4x+13 = c:c=2,2
There are the points of c,such that when they are applied back to the equations,the number of points will become zero.
Let the no: of points be (x,0)
By distance formula
{(2−x)2+(3−0)2}=c
4−4x+x2+9=c
⇒x2−4x+13 = c:c=2,2
There are the points of c,such that when they are applied back to the equations,the number of points will become zero.
The equation of a line passing through the centre of a rectangular hyperbola is x – y –1 = 0. if one of its asymptote is 3x-4y-6 = 0, then equation of its other asymptote is- a)4x + 3y + 17 = 0
- b)4x + 3y -17 = 0
- c)4x + 3y -15 = 0
- d)4x + 3y + 15 = 0
Correct answer is option 'B'. Can you explain this answer?
The equation of a line passing through the centre of a rectangular hyperbola is x – y –1 = 0. if one of its asymptote is 3x-4y-6 = 0, then equation of its other asymptote is
a)
4x + 3y + 17 = 0
b)
4x + 3y -17 = 0
c)
4x + 3y -15 = 0
d)
4x + 3y + 15 = 0

|
Ishita Reddy answered |
Pt of intersection of x-y-1=0 and 3x-4y-6=0 is (-2,-3) other asymptote will be in the form of 4x + 3y + λ =0 and it should pass through (-2,-3). Thus λ = -17
A tangent to the parabola x2 = 4ay meets the hyperbola x2 - y2 = a2 at two points P and Q, then midpoint of P and Q lies on the curve- a)y3 = x (y- a)
- b)y3 = x2 (y- a)
- c)y2 = x2 (y- a)
- d)y2 = x3 (a- y)
Correct answer is option 'B'. Can you explain this answer?
A tangent to the parabola x2 = 4ay meets the hyperbola x2 - y2 = a2 at two points P and Q, then midpoint of P and Q lies on the curve
a)
y3 = x (y- a)
b)
y3 = x2 (y- a)
c)
y2 = x2 (y- a)
d)
y2 = x3 (a- y)
|
|
Nitya Basak answered |
Equation of tangent to parabola y = mx- am2 .......(1) equation of chord of hyperbola whose midpoint is (h, k) is hx - ky = h2 - k2 ...... (2) form (1) and (2)
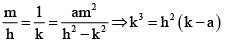
Locus of the middle points of the parallel chords with gradient m of the rectangular hyperbola xy = c2 is- a)y + mx = 0
- b)y – mx = 0
- c)my – mx = 0
- d)my + x = 0
Correct answer is option 'A'. Can you explain this answer?
Locus of the middle points of the parallel chords with gradient m of the rectangular hyperbola xy = c2 is
a)
y + mx = 0
b)
y – mx = 0
c)
my – mx = 0
d)
my + x = 0
|
|
Rohit Shah answered |
Let the mid point of chord be p (h,k) The equation of chord with p as mid point is Kx + hy =2hk The given slope m of the chord is m Hence -k/h =m Therefore required ans is y+mx =0 .
The asymptotes of the curve 2x2 + 5xy + 2y2 + 4x + 5y = 0 are given by- a)2x2 + 5xy + 2y2 + 4x + 5y + 2 = 0
- b)2x2 + 5xy + 2y2 + 4x + 5y - 2 = 0
- c)2x2 + 5xy + 2y2 + 4x + 5y - 4 = 0
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The asymptotes of the curve 2x2 + 5xy + 2y2 + 4x + 5y = 0 are given by
a)
2x2 + 5xy + 2y2 + 4x + 5y + 2 = 0
b)
2x2 + 5xy + 2y2 + 4x + 5y - 2 = 0
c)
2x2 + 5xy + 2y2 + 4x + 5y - 4 = 0
d)
None of these
|
|
Baishali Tiwari answered |
The hyperbola is given by
2x2 + 5xy + 2y2 + 4x + 5y = 0 ............................(i)
Since the equation of hyperbola will differ from equation of asymptote by a constant. So, equation of asymptote is
2x2 + 5xy + 2y3 + 4x + 5y + λ = 0 ......................(ii)
If (ii) represents 2 straight lines, we must have
abc + 2fgh - af2- bg2 - ch2 = 0
or 22λ + 2.5 / 2.4 / 2.5 / 2 - 2.25 / 4 - 2.4 - λ (25 / 4) = 0
or 9λ = 18 ∴ λ = 2
2x2 + 5xy + 2y3 + 4x + 5y + 2 = 0
2x2 + 5xy + 2y2 + 4x + 5y = 0 ............................(i)
Since the equation of hyperbola will differ from equation of asymptote by a constant. So, equation of asymptote is
2x2 + 5xy + 2y3 + 4x + 5y + λ = 0 ......................(ii)
If (ii) represents 2 straight lines, we must have
abc + 2fgh - af2- bg2 - ch2 = 0
or 22λ + 2.5 / 2.4 / 2.5 / 2 - 2.25 / 4 - 2.4 - λ (25 / 4) = 0
or 9λ = 18 ∴ λ = 2
2x2 + 5xy + 2y3 + 4x + 5y + 2 = 0
A hyperbola passing through origin has 3x – 4y – 1 = 0 and 4x – 3y – 6 = 0 as its asymptotes. Then the equation of its transverse axis is- a)x – y – 5 = 0
- b)x + y + 1 = 0
- c)x + y – 5 = 0
- d)x – y – 1 = 0
Correct answer is option 'C'. Can you explain this answer?
A hyperbola passing through origin has 3x – 4y – 1 = 0 and 4x – 3y – 6 = 0 as its asymptotes. Then the equation of its transverse axis is
a)
x – y – 5 = 0
b)
x + y + 1 = 0
c)
x + y – 5 = 0
d)
x – y – 1 = 0
|
|
Hiral Rane answered |
Given Information:
- Equation of one asymptote: 3x - 4y - 1 = 0
- Equation of the other asymptote: 4x - 3y - 6 = 0
Explanation:
Finding the Slope of the Asymptotes:
1. Write the equations of the asymptotes in the form of y = mx + c.
2. Compare the coefficients of x and y to find the slopes of the asymptotes.
- For the first asymptote: slope = 3/4
- For the second asymptote: slope = 4/3
Equation of Transverse Axis:
3. Since the hyperbola passes through the origin, its center is also at the origin.
4. The transverse axis of the hyperbola passes through the center and is parallel to the asymptotes.
5. The equation of the transverse axis in the form of y = mx + c is given by y = x.
6. To find the equation in the form Ax + By + C = 0, we rearrange y = x to get x - y = 0.
7. Therefore, the equation of the transverse axis is x + y = 0, which can be rewritten as x + y - 0 = 0 or x + y = 0.
Conclusion:
The equation of the transverse axis of the hyperbola passing through the origin with asymptotes 3x - 4y - 1 = 0 and 4x - 3y - 6 = 0 is x + y = 0, which is option 'C'.
- Equation of one asymptote: 3x - 4y - 1 = 0
- Equation of the other asymptote: 4x - 3y - 6 = 0
Explanation:
Finding the Slope of the Asymptotes:
1. Write the equations of the asymptotes in the form of y = mx + c.
2. Compare the coefficients of x and y to find the slopes of the asymptotes.
- For the first asymptote: slope = 3/4
- For the second asymptote: slope = 4/3
Equation of Transverse Axis:
3. Since the hyperbola passes through the origin, its center is also at the origin.
4. The transverse axis of the hyperbola passes through the center and is parallel to the asymptotes.
5. The equation of the transverse axis in the form of y = mx + c is given by y = x.
6. To find the equation in the form Ax + By + C = 0, we rearrange y = x to get x - y = 0.
7. Therefore, the equation of the transverse axis is x + y = 0, which can be rewritten as x + y - 0 = 0 or x + y = 0.
Conclusion:
The equation of the transverse axis of the hyperbola passing through the origin with asymptotes 3x - 4y - 1 = 0 and 4x - 3y - 6 = 0 is x + y = 0, which is option 'C'.
The equations x = at2, y = 4at ; t ∈ R represent- a)a parabola
- b)a circle
- c)an ellipse
- d)a hyperbola
Correct answer is option 'A'. Can you explain this answer?
The equations x = at2, y = 4at ; t ∈ R represent
a)
a parabola
b)
a circle
c)
an ellipse
d)
a hyperbola

|
Anjali Mehla answered |
Firstly I think you have to know the equation of a parabola and it's proff
The line y = c is a tangent to the parabola 7/2 if c is equal to- a)a
- b)0
- c)2a
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
The line y = c is a tangent to the parabola 7/2 if c is equal to
a)
a
b)
0
c)
2a
d)
none of these
|
|
Sravya Nair answered |
y = x is tangent to the parabola
y=ax2+c
if a= then c=?
y′ =2ax
y’ = 2(7/2)x =1
x = 1/7
1/7 = 2(1/7)2 + c
c = 1/7 * 2/49
c = 7/2
y=ax2+c
if a= then c=?
y′ =2ax
y’ = 2(7/2)x =1
x = 1/7
1/7 = 2(1/7)2 + c
c = 1/7 * 2/49
c = 7/2
The ellipse 4x2 + 9y2 = 36 and the hyperbola 4x2 – y2 = 4 have the same foci and they intersect at right angles then the equation of the circle through the points of intersection of two conics is- a)x2 + y2 = 5
- b)√5 (x2+y2) – 3x – 4y = 0
- c)√5 (x2+y2)+3x+4y=0
- d)x2 + y2 = 25
Correct answer is option 'A'. Can you explain this answer?
The ellipse 4x2 + 9y2 = 36 and the hyperbola 4x2 – y2 = 4 have the same foci and they intersect at right angles then the equation of the circle through the points of intersection of two conics is
a)
x2 + y2 = 5
b)
√5 (x2+y2) – 3x – 4y = 0
c)
√5 (x2+y2)+3x+4y=0
d)
x2 + y2 = 25
|
|
Rithika Desai answered |

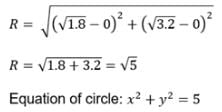
A and B are two distinct points, Locus of a point P satisfying |PA| + |PB| = 2k, a constant is- a)nothing can be said
- b)the line segment [AB]
- c)an ellipse
- d)a hyperbola
Correct answer is option 'A'. Can you explain this answer?
A and B are two distinct points, Locus of a point P satisfying |PA| + |PB| = 2k, a constant is
a)
nothing can be said
b)
the line segment [AB]
c)
an ellipse
d)
a hyperbola
|
|
Ram Mohith answered |
I think the locus of P is an ellipse because if yo... moreu take any point on the ellipse then the sum of distance from focii to that
The asymptotes of the hyperbola hx + ky = xy are- a)x - k = 0, y - h = 0
- b)x + h = 0, y + k = 0
- c)x - h = 0, y - k = 0
- d)x + k = 0, y + k = 0
Correct answer is option 'A'. Can you explain this answer?
The asymptotes of the hyperbola hx + ky = xy are
a)
x - k = 0, y - h = 0
b)
x + h = 0, y + k = 0
c)
x - h = 0, y - k = 0
d)
x + k = 0, y + k = 0

|
Nandini Nair answered |
hx + ky - xy = 0
let asymptotes be hx + ky - xy + c = 0 ; This represents a pair of straight lines if Δ = 0
i.e. c =-hk ∴ asymptotes are xh+yk-xy-hk =0 ⇒ (x - k) (y - h) = 0
let asymptotes be hx + ky - xy + c = 0 ; This represents a pair of straight lines if Δ = 0
i.e. c =-hk ∴ asymptotes are xh+yk-xy-hk =0 ⇒ (x - k) (y - h) = 0
The locus of the point of intersection of tangents drawn at the extremities of normal chords to hyperbola xy = c2- a)(x2 - y2)2 + 4c2xy = 0
- b)(x2 + y2)2 + 4c2xy = 0
- c)(x2 - y2)2 + 4c xy = 0
- d)(x2 + y2)2 + 4cxy = 0
Correct answer is option 'A'. Can you explain this answer?
The locus of the point of intersection of tangents drawn at the extremities of normal chords to hyperbola xy = c2
a)
(x2 - y2)2 + 4c2xy = 0
b)
(x2 + y2)2 + 4c2xy = 0
c)
(x2 - y2)2 + 4c xy = 0
d)
(x2 + y2)2 + 4cxy = 0

|
Sinjini Datta answered |
Method to Solve :
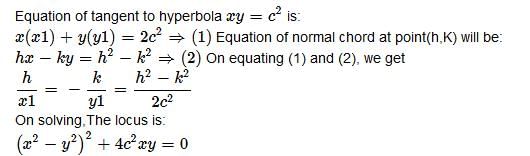
The angle between the tangents drawn from the origin to the circle = (x−7)2+(y+1)2 = 25 is - a)π/8
- b)π/2
- c)π/6
- d)π/3
Correct answer is option 'B'. Can you explain this answer?
The angle between the tangents drawn from the origin to the circle = (x−7)2+(y+1)2 = 25 is
a)
π/8
b)
π/2
c)
π/6
d)
π/3
|
|
Shalini Yadav answered |
Let the equation of tangent drawn from (0,0) to the circle be y=mx. Then, p = a ⇒ 7m+1/(m2+1)1/2= 5
⇒24m2 + 14m−24=0
⇒12m2 + 7m−12=0
⇒m1m2 = −12/12 =−1
∴ Required angle = π/2
⇒24m2 + 14m−24=0
⇒12m2 + 7m−12=0
⇒m1m2 = −12/12 =−1
∴ Required angle = π/2
If the equation 4x2 + ky2 = 18 represents a rectangular hyperbola, then k =- a)4
- b)–4
- c)3
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
If the equation 4x2 + ky2 = 18 represents a rectangular hyperbola, then k =
a)
4
b)
–4
c)
3
d)
none of these

|
Nikhil Sen answered |
We know that the equation
ax2 + by2 + 2hxy + 2gx + 2fy + c = 0
represent a rectangular hyperbola if Δ ≠ 0, h2 > ab and a + b = 0.
∴ The given equation represents a rectangular hyperbola if 4 + k = 0 i.e. k = -4
ax2 + by2 + 2hxy + 2gx + 2fy + c = 0
represent a rectangular hyperbola if Δ ≠ 0, h2 > ab and a + b = 0.
∴ The given equation represents a rectangular hyperbola if 4 + k = 0 i.e. k = -4
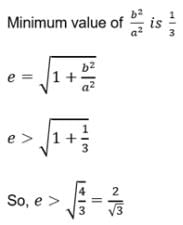
The eccentricity of the conic 9x2 − 16y2 = 144 is- a)4/3
- b)5/4
- c)√7
- d)4/5
Correct answer is option 'B'. Can you explain this answer?
The eccentricity of the conic 9x2 − 16y2 = 144 is
a)
4/3
b)
5/4
c)
√7
d)
4/5
|
|
Mihir Chaudhary answered |
+16y2=144 is:
To find the eccentricity of a conic, we need to first identify the type of conic. We can rewrite the given equation as:
9x^2/144 + 16y^2/144 = 1
Dividing both sides by 144, we get:
x^2/16 + y^2/9 = 1
This is the equation of an ellipse. To find the eccentricity, we need to first find the distance between the center of the ellipse and one of its foci. The center of the ellipse is at the point (0,0). We can find the length of the semi-major axis (a) and the semi-minor axis (b) using the equation:
a^2 = 16, b^2 = 9
a = 4, b = 3
The distance between the center and one of the foci (c) can be found using the equation:
c^2 = a^2 - b^2
c^2 = 16 - 9 = 7
c = sqrt(7)
The eccentricity (e) of the ellipse is given by the equation:
e = c/a
e = sqrt(7)/4
Therefore, the eccentricity of the conic 9x^2+16y^2=144 is sqrt(7)/4.
To find the eccentricity of a conic, we need to first identify the type of conic. We can rewrite the given equation as:
9x^2/144 + 16y^2/144 = 1
Dividing both sides by 144, we get:
x^2/16 + y^2/9 = 1
This is the equation of an ellipse. To find the eccentricity, we need to first find the distance between the center of the ellipse and one of its foci. The center of the ellipse is at the point (0,0). We can find the length of the semi-major axis (a) and the semi-minor axis (b) using the equation:
a^2 = 16, b^2 = 9
a = 4, b = 3
The distance between the center and one of the foci (c) can be found using the equation:
c^2 = a^2 - b^2
c^2 = 16 - 9 = 7
c = sqrt(7)
The eccentricity (e) of the ellipse is given by the equation:
e = c/a
e = sqrt(7)/4
Therefore, the eccentricity of the conic 9x^2+16y^2=144 is sqrt(7)/4.
If x = 9 is the chord of contact of the hyperbola x2 - y2 = 9, then the equation of the tangent at one of the points of contact is - a)
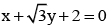
- b)
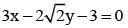
- c)
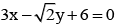
- d)
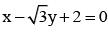
Correct answer is option 'B'. Can you explain this answer?
If x = 9 is the chord of contact of the hyperbola x2 - y2 = 9, then the equation of the tangent at one of the points of contact is
a)
b)
c)
d)

|
Nilesh Goyal answered |
Solve x = 9 and x2 – y2 = 9 equation of tangent at point of contact is S1 = 0
The number of tangents and normals to the hyperbola 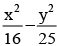 of the slope 1 is
of the slope 1 is- a)2, 2
- b)2, 0
- c)0, 0
- d)0, 2
Correct answer is option 'C'. Can you explain this answer?
The number of tangents and normals to the hyperbola 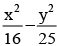 of the slope 1 is
of the slope 1 is
a)
2, 2
b)
2, 0
c)
0, 0
d)
0, 2

|
Pranavi Chavan answered |
Equation of tangents and normal with slope 'm' will be
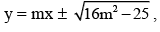
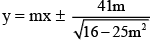
A hyperbola, having the transverse axis of length 2 sin θ, is confocal with the ellipse 3x2 + 4y2 = 12. Then its equation is:- a)x2 cosec2θ - y2 sec2 θ = 1
- b)x2 sec2 θ - y2 cosec2θ = 1
- c)x2 sin2θ - y2 cos2θ = 1
- d)x2 cos2θ - y2 sin2θ = 1
Correct answer is option 'A'. Can you explain this answer?
A hyperbola, having the transverse axis of length 2 sin θ, is confocal with the ellipse 3x2 + 4y2 = 12. Then its equation is:
a)
x2 cosec2θ - y2 sec2 θ = 1
b)
x2 sec2 θ - y2 cosec2θ = 1
c)
x2 sin2θ - y2 cos2θ = 1
d)
x2 cos2θ - y2 sin2θ = 1

|
Ishita Reddy answered |
The given ellipse is 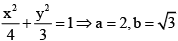
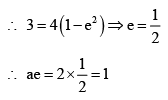
Hence, the eccentricity e1, of the hyperbola is given by
1 = e1 sinθ ⇒ e1 = cosec θ ⇒ b2 = sin2θ (cosec2θ - 1) = cos2θ
Hence, the eccentricity e1, of the hyperbola is given by
1 = e1 sinθ ⇒ e1 = cosec θ ⇒ b2 = sin2θ (cosec2θ - 1) = cos2θ
Let a and b be non–zero real numbers. Then, the equation (ax2 + by2 + (C) (x2 – 5xy + 6y2) = 0 represents - a)four straight lines, when c = 0 and a, b are of the same sign
- b)two straight lines and a circle, when a = b, and c is of sign opposite to that of a
- c)two straight lines and a hyperbola, when a and b are of the same sign and c is of sign opposite to that of a
- d)a circle and an ellipse, when a and b are of the same sign and c is of sign opposite to that of a.
Correct answer is option 'B'. Can you explain this answer?
Let a and b be non–zero real numbers. Then, the equation (ax2 + by2 + (C) (x2 – 5xy + 6y2) = 0 represents
a)
four straight lines, when c = 0 and a, b are of the same sign
b)
two straight lines and a circle, when a = b, and c is of sign opposite to that of a
c)
two straight lines and a hyperbola, when a and b are of the same sign and c is of sign opposite to that of a
d)
a circle and an ellipse, when a and b are of the same sign and c is of sign opposite to that of a.

|
Bhavana Das answered |
x2 – 5xy + 6y2 = 0 represent a pair of lines passing through origin
ax2 + ay2 = - c
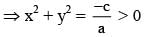
⇒ ax2 + ay2 + c = 0 represent a circle
ax2 + ay2 = - c
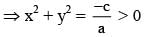
⇒ ax2 + ay2 + c = 0 represent a circle
Tangents are drawn to 3x2 - 2y2 = 6 from a point P. If these tangents intersects the coordinate axes at concyclic points, The locus of P is- a)x2 + y2 = 5
- b)
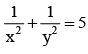
- c)x2 - y2 = 13
- d)
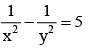
Correct answer is option 'C'. Can you explain this answer?
Tangents are drawn to 3x2 - 2y2 = 6 from a point P. If these tangents intersects the coordinate axes at concyclic points, The locus of P is
a)
x2 + y2 = 5
b)
c)
x2 - y2 = 13
d)
|
|
Mahi Reddy answered |
x2/2 - y2/3 = 1
= [y2 + (3)2]/[x2 - (2)2] = 1
=> [y2 + 9]/[x2 - 4] = 1
=> [y2 + 9] = [x2 - 4]
x2 - y2 = 13
= [y2 + (3)2]/[x2 - (2)2] = 1
=> [y2 + 9]/[x2 - 4] = 1
=> [y2 + 9] = [x2 - 4]
x2 - y2 = 13
The vertex of the parabola y2 = 4a(x−a) is- a)(0, 0)
- b)(a, 0)
- c)(0, a)
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The vertex of the parabola y2 = 4a(x−a) is
a)
(0, 0)
b)
(a, 0)
c)
(0, a)
d)
none of these
|
|
Harshad Das answered |
The vertex of the parabola y^2 = 4a(x) is (0,0).
If the tangent at the point (h, k) on the hyperbola 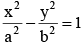 meets the auxiallary circle of the hyperbola in two points whose ordinates y1, y2 then
meets the auxiallary circle of the hyperbola in two points whose ordinates y1, y2 then 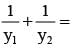
- a)1/k
- b)
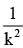
- c)
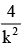
- d)2/k
Correct answer is option 'D'. Can you explain this answer?
If the tangent at the point (h, k) on the hyperbola 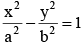 meets the auxiallary circle of the hyperbola in two points whose ordinates y1, y2 then
meets the auxiallary circle of the hyperbola in two points whose ordinates y1, y2 then 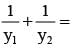
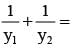
a)
1/k
b)
c)
d)
2/k
|
|
Bibek Khanna answered |
Equation of the tangent at (h, k) is
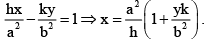
Equation of auxiallary circle x2 + y2 = a2
Equation of auxiallary circle x2 + y2 = a2
Chapter doubts & questions for Hyperbola - 6 Months Preparation for JEE 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Hyperbola - 6 Months Preparation for JEE in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup



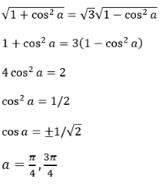
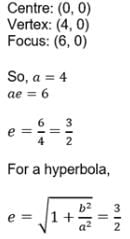
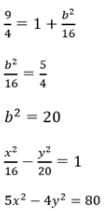
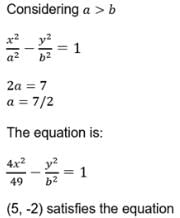
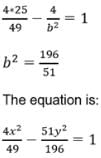




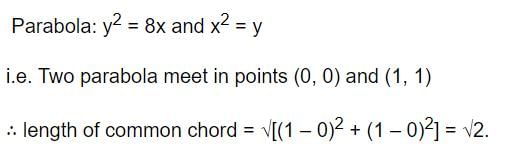

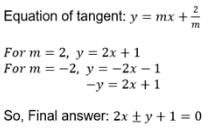
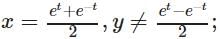 t ∈ R represents
t ∈ R represents


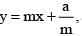 a = 2 and c2 = a2m2 - b2
a = 2 and c2 = a2m2 - b2