All Exams >
GMAT >
35 Days Preparation for GMAT >
All Questions
All questions of Mock Test for GMAT Exam
How many keystrokes are needed to type numbers from 1 to 1000?- a)3001
- b)2893
- c)2704
- d)2890
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
How many keystrokes are needed to type numbers from 1 to 1000?
a)
3001
b)
2893
c)
2704
d)
2890
e)
None of these
|
EduRev GMAT answered |
While typing numbers from 1 to 1000, there are 9 single digit numbers: from 1 to 9.
Each of these numbers requires one keystroke.
That is 9 key strokes.
Each of these numbers requires one keystroke.
That is 9 key strokes.
There are 90 two-digit numbers: from 10 to 99.
Each of these numbers requires 2 keystrokes.
Therefore, 180 keystrokes to type the 2-digit numbers.
Each of these numbers requires 2 keystrokes.
Therefore, 180 keystrokes to type the 2-digit numbers.
There are 900 three-digit numbers: from 100 to 999.
Each of these numbers requires 3 keystrokes.
Therefore, 2700 keystrokes to type the 3-digit numbers.
Each of these numbers requires 3 keystrokes.
Therefore, 2700 keystrokes to type the 3-digit numbers.
1000 is a four-digit number which requires 4 keystrokes.
Totally, therefore, one requires 9 + 180 + 2700 + 4 = 2893 keystrokes.
Choice B is the correct answer.
Choice B is the correct answer.
Watch out for the common mistake that many of us make of counting only 89 2-digit numbers and 899 3-digit numbers. The temptation is to say, 99 - 10 = 89. So, 89 2-digit numbers exist. 99 - 10 means that we are not counting 10 as a 2-digit number. The correct approach is: of the 99 numbers from 1 to 99, we are not counting the first 9 single digit numbers. So, we have 99 - 9 = 90 2-digit numbers. The same logic applies when we count 3-digit numbers.
Peter invested a certain sum of money in a simple interest bond whose value grew to $300 at the end of 3 years and to $ 400 at the end of another 5 years. What was the rate of interest in which he invested his sum?- a)12%
- b)12.5%
- c)6.67%
- d)6.25%
- e)8.33%
Correct answer is option 'E'. Can you explain this answer?
Peter invested a certain sum of money in a simple interest bond whose value grew to $300 at the end of 3 years and to $ 400 at the end of another 5 years. What was the rate of interest in which he invested his sum?
a)
12%
b)
12.5%
c)
6.67%
d)
6.25%
e)
8.33%
|
|
EduRev GMAT answered |
Step 1: Compute principal invested
Concept: Simple interest earned remains same year after year.
Concept: Simple interest earned remains same year after year.
Initial amount invested = P
Value of investment (Amount) at the end of year 3 = $300
Value of investment (Amount) at the end of year 8 (another 5 years) = $400
Therefore, the interest earned for the 5 year period between the 3rd year and 8th year = $400 - $300 = $100.
Value of investment (Amount) at the end of year 3 = $300
Value of investment (Amount) at the end of year 8 (another 5 years) = $400
Therefore, the interest earned for the 5 year period between the 3rd year and 8th year = $400 - $300 = $100.
So, interest earned per year = 100/5 = $20.
Therefore, interest earned for 3 years = 3 × 20 = $60.
Hence, initial amount invested P = Amount after 3 years - interest for 3 years
P = $300 − $60 = $240
Step 2: Find the rate of interest
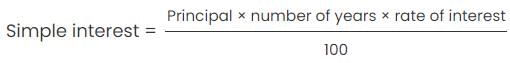
Simple interest = $20, Principal P = $240, n = 1 year.
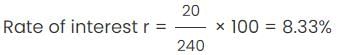
Rate of interest is 8.33%.
Therefore, interest earned for 3 years = 3 × 20 = $60.
Hence, initial amount invested P = Amount after 3 years - interest for 3 years
P = $300 − $60 = $240
Step 2: Find the rate of interest
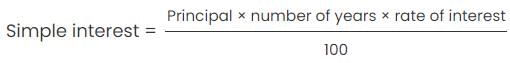
Simple interest = $20, Principal P = $240, n = 1 year.
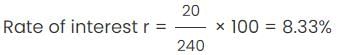
Rate of interest is 8.33%.
How many trailing zeros will be there after the rightmost non-zero digit in the value of 25!?- a)25
- b)8
- c)6
- d)5
- e)2
Correct answer is option 'C'. Can you explain this answer?
How many trailing zeros will be there after the rightmost non-zero digit in the value of 25!?
a)
25
b)
8
c)
6
d)
5
e)
2
|
Amar Chakraborty answered |
Trailing Zeros in Factorials
In order to find the number of trailing zeros in the value of 25!, we need to understand how trailing zeros are formed in factorials.
Formation of Trailing Zeros
- A trailing zero is formed when a multiple of 10 is produced in the factorial.
- Since 10 can be expressed as 2 * 5, we need to find the number of pairs of 2's and 5's in the factorial to determine the number of trailing zeros.
Counting the Number of 5's
- In the factorial of 25!, we need to count the number of multiples of 5 present.
- There are 5 multiples of 5 (5, 10, 15, 20, 25) in 25!.
- However, we need to consider the power of 5 in numbers like 25, where there are two factors of 5.
- So, we count 2 additional 5's from 25, making a total of 7 factors of 5 in 25!.
Number of Trailing Zeros
- Since there will always be more factors of 2 than 5 in factorials, we only need to count the number of factors of 5 to determine the number of trailing zeros.
- Therefore, the number of trailing zeros in 25! will be equal to the number of factors of 5, which is 6.
Therefore, the correct answer is option C) 6.
In order to find the number of trailing zeros in the value of 25!, we need to understand how trailing zeros are formed in factorials.
Formation of Trailing Zeros
- A trailing zero is formed when a multiple of 10 is produced in the factorial.
- Since 10 can be expressed as 2 * 5, we need to find the number of pairs of 2's and 5's in the factorial to determine the number of trailing zeros.
Counting the Number of 5's
- In the factorial of 25!, we need to count the number of multiples of 5 present.
- There are 5 multiples of 5 (5, 10, 15, 20, 25) in 25!.
- However, we need to consider the power of 5 in numbers like 25, where there are two factors of 5.
- So, we count 2 additional 5's from 25, making a total of 7 factors of 5 in 25!.
Number of Trailing Zeros
- Since there will always be more factors of 2 than 5 in factorials, we only need to count the number of factors of 5 to determine the number of trailing zeros.
- Therefore, the number of trailing zeros in 25! will be equal to the number of factors of 5, which is 6.
Therefore, the correct answer is option C) 6.
If "x" is an integer, which of the following inequalities has (have) a finite range of values of "x" satisfying it (them)?- a)x2 + 5x + 6 > 0
- b)|x + 2| > 4
- c)9x - 7 < 3x + 14
- d)x2 - 4x + 3 < 0
- e)(B) and (D)
Correct answer is option 'D'. Can you explain this answer?
If "x" is an integer, which of the following inequalities has (have) a finite range of values of "x" satisfying it (them)?
a)
x2 + 5x + 6 > 0
b)
|x + 2| > 4
c)
9x - 7 < 3x + 14
d)
x2 - 4x + 3 < 0
e)
(B) and (D)
|
|
EduRev GMAT answered |
Step 1: Find the values of "x" that will satisfy the four inequalities
Choice A: x2 + 5x + 6 > 0
Factorize the given expression: x2 + 5x + 6 > 0 = (x + 2)(x + 3) > 0.
This inequality will hold good when both (x + 2) and (x + 3) are simultaneously positive OR are simultaneously negative.
Factorize the given expression: x2 + 5x + 6 > 0 = (x + 2)(x + 3) > 0.
This inequality will hold good when both (x + 2) and (x + 3) are simultaneously positive OR are simultaneously negative.
Possibility 1: Both (x + 2) and (x + 3) are positive.
i.e., x + 2 > 0 AND x + 3 > 0
i.e., x > -2 AND x > -3
Essentially translates to x > -2
i.e., x + 2 > 0 AND x + 3 > 0
i.e., x > -2 AND x > -3
Essentially translates to x > -2
Possibility 2: Both (x + 2) and (x + 3) are negative.
i.e., x + 2 < 0 AND x + 3 < 0
i.e., x < -2 AND x < -3
Essentially translates to x < -3
i.e., x + 2 < 0 AND x + 3 < 0
i.e., x < -2 AND x < -3
Essentially translates to x < -3
Evaluating both the possibilities, we get the range of values of "x" that satisfy this inequality to be x > -2 or x < -3. i.e., "x" does not lie between -3 and -2.
i.e., x takes values lesser than -3 or greater than -2.
The range of values that x takes is infinite.
i.e., x takes values lesser than -3 or greater than -2.
The range of values that x takes is infinite.
Choice B: |x + 2| > 4
|x + 2| > 4 is a modulus function and therefore, has two possibilities
|x + 2| > 4 is a modulus function and therefore, has two possibilities
Possiblity 1: x + 2 > 4
i.e., x > 2
i.e., x > 2
Possiblity 2: (x + 2) < -4.
i.e., x < -6
Evaluating the two options together, we get the values of "x" that satisfy the inequality as x > 2 OR x < -6.
i.e., "x" does not lie between -6 and 2.
An infinite range of values.
i.e., x < -6
Evaluating the two options together, we get the values of "x" that satisfy the inequality as x > 2 OR x < -6.
i.e., "x" does not lie between -6 and 2.
An infinite range of values.
Choice C: 9x - 7 < 3x + 14
Simplifying, we get 6x < 21 or x < 3.5.
An infinite range of values.
Simplifying, we get 6x < 21 or x < 3.5.
An infinite range of values.
Choice D: x2 - 4x + 3 < 0
Factorizing x2 - 4x + 3 < 0 we get, (x - 3)(x - 1) < 0.
This inequality will hold good when one of the terms (x - 3) or (x - 1) is positive and the other is negative.
Factorizing x2 - 4x + 3 < 0 we get, (x - 3)(x - 1) < 0.
This inequality will hold good when one of the terms (x - 3) or (x - 1) is positive and the other is negative.
Possibility 1: (x -3) is positive and (x - 1) is negative.
i.e., x - 3 > 0 AND x -1 < 0
i.e., x > 3 AND x < 1
Such a number DOES NOT exist. It is an infeasible solution.
i.e., x - 3 > 0 AND x -1 < 0
i.e., x > 3 AND x < 1
Such a number DOES NOT exist. It is an infeasible solution.
Possibility 2: (x - 3) is negative and (x - 1) is positive.
i.e., x - 3 < 0 AND x - 1 > 0
i.e., x < 3 AND x > 1
Essentially translates to 1 < x < 3 Finite range of values for "x".
i.e., x - 3 < 0 AND x - 1 > 0
i.e., x < 3 AND x > 1
Essentially translates to 1 < x < 3 Finite range of values for "x".
Choice D is the correct answer.
What is the standard deviation (SD) of the four numbers p, q, r, and s?Statement 1: The sum of p, q, r, and s is 24.
Statement 2: The sum of the squares of p, q, r, and s is 224.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
- c)Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
- d)EACH statement ALONE is sufficient
- e)Statements (1) and (2) TOGETHER are NOT sufficient
Correct answer is option 'C'. Can you explain this answer?
What is the standard deviation (SD) of the four numbers p, q, r, and s?
Statement 1: The sum of p, q, r, and s is 24.
Statement 2: The sum of the squares of p, q, r, and s is 224.
Statement 2: The sum of the squares of p, q, r, and s is 224.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
c)
Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
d)
EACH statement ALONE is sufficient
e)
Statements (1) and (2) TOGETHER are NOT sufficient
|
|
EduRev GMAT answered |
Step 1: Understand the Question Stem
What kind of an answer will the question fetch?
The question is an "What is" question. Answer to the question should be a number that is the standard deviation of p, q, r, and s.
The question is an "What is" question. Answer to the question should be a number that is the standard deviation of p, q, r, and s.
When is the data sufficient?
The data is sufficient if we are able to get a UNIQUE value for the SD of the four numbers from the information given in the statements.
The data is sufficient if we are able to get a UNIQUE value for the SD of the four numbers from the information given in the statements.
How to find the standard deviation of a set of numbers?
Step 2: Evaluating Statement (1) ALONE: The sum of p, q, r, and s is 24.
From the information in statement 1 we can find the mean of the four numbers to be 6 and the square of the mean of the numbers to be 36.
We need additional information to find the SD.
This statement does not provide any information about the mean of the squares of the numbers.
We need additional information to find the SD.
This statement does not provide any information about the mean of the squares of the numbers.
Statement 1 alone is NOT sufficient.
Eliminate choices A and D. Choices narrow down to B, C, or E.
Eliminate choices A and D. Choices narrow down to B, C, or E.
Step 3: Evaluating Statement (2) ALONE: The sum of the squares of p, q, r, and s is 224.
Hence, the mean of the squares of the numbers is 56.
However, this statement does not provide any information about the square of the mean of the numbers.
However, this statement does not provide any information about the square of the mean of the numbers.
Statement 2 alone is NOT sufficient.
Eliminate choice B. Choices narrow down to C and E.
Eliminate choice B. Choices narrow down to C and E.
Step 4: Evaluating the statements together.
From statement 1 we know that the square of the means is 36.
From statement 2 we know that the mean of the squares is 56.
Using the formula,
we can find the SD of the 4 numbers.
From statement 2 we know that the mean of the squares is 56.
Using the formula,
we can find the SD of the 4 numbers.
Statements together are sufficient. Choice C is the answer.
Set A contains all the even numbers between 2 and 50 inclusive. Set B contains all the even numbers between 102 and 150 inclusive. What is the difference between the sum of elements of set B and that of set A?- a)2500
- b)5050
- c)11325
- d)6275
- e)2550
Correct answer is option 'A'. Can you explain this answer?
Set A contains all the even numbers between 2 and 50 inclusive. Set B contains all the even numbers between 102 and 150 inclusive. What is the difference between the sum of elements of set B and that of set A?
a)
2500
b)
5050
c)
11325
d)
6275
e)
2550
|
|
EduRev GMAT answered |
SET A: {2, 4, 6, 8,...., 50}. Set of first 25 consecutive positive even numbers.
SET B: {102, 104, 106,....., 150}. Another set of 25 consecutive even numbers starting from 102.
Difference between 1st term of set A and that of set B is 100. Difference between 2nd term of set A and that of set B is 100.
Each term in set B is 100 more than the corresponding term in set A.
Each term in set B is 100 more than the corresponding term in set A.
So sum of the differences of all the terms is (100 + 100 + 100 + ....) = 25 * 100 = 2500.
Choice A is the correct answer.
In a class 40% of the students enrolled for Math and 70% enrolled for Economics. If 15% of the students enrolled for both Math and Economics, what % of the students of the class did not enroll for either of the two subjects?- a)5%
- b)15%
- c)0%
- d)25%
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
In a class 40% of the students enrolled for Math and 70% enrolled for Economics. If 15% of the students enrolled for both Math and Economics, what % of the students of the class did not enroll for either of the two subjects?
a)
5%
b)
15%
c)
0%
d)
25%
e)
None of these
|
Avantika Dey answered |
Understanding the Problem
To find the percentage of students who did not enroll in either Math or Economics, we can use the principle of inclusion-exclusion.
Given Data
- Percentage of students enrolled in Math = 40%
- Percentage of students enrolled in Economics = 70%
- Percentage of students enrolled in both subjects = 15%
Applying Inclusion-Exclusion Principle
We can calculate the percentage of students enrolled in at least one of the two subjects using the formula:
\[
\text{Percentage enrolled in either Math or Economics} = P(M) + P(E) - P(M \cap E)
\]
Where:
- \( P(M) \) = Percentage enrolled in Math = 40%
- \( P(E) \) = Percentage enrolled in Economics = 70%
- \( P(M \cap E) \) = Percentage enrolled in both = 15%
Calculation
Substituting the values:
\[
P(M \cup E) = 40\% + 70\% - 15\%
\]
\[
P(M \cup E) = 95\%
\]
Finding Students Not Enrolled in Either Subject
To find the percentage of students who did not enroll in either Math or Economics, we subtract the percentage enrolled in at least one subject from 100%:
\[
\text{Percentage not enrolled in either} = 100\% - P(M \cup E)
\]
\[
\text{Percentage not enrolled in either} = 100\% - 95\% = 5\%
\]
Conclusion
Therefore, the percentage of students who did not enroll for either Math or Economics is **5%**, which corresponds to option 'A'.
To find the percentage of students who did not enroll in either Math or Economics, we can use the principle of inclusion-exclusion.
Given Data
- Percentage of students enrolled in Math = 40%
- Percentage of students enrolled in Economics = 70%
- Percentage of students enrolled in both subjects = 15%
Applying Inclusion-Exclusion Principle
We can calculate the percentage of students enrolled in at least one of the two subjects using the formula:
\[
\text{Percentage enrolled in either Math or Economics} = P(M) + P(E) - P(M \cap E)
\]
Where:
- \( P(M) \) = Percentage enrolled in Math = 40%
- \( P(E) \) = Percentage enrolled in Economics = 70%
- \( P(M \cap E) \) = Percentage enrolled in both = 15%
Calculation
Substituting the values:
\[
P(M \cup E) = 40\% + 70\% - 15\%
\]
\[
P(M \cup E) = 95\%
\]
Finding Students Not Enrolled in Either Subject
To find the percentage of students who did not enroll in either Math or Economics, we subtract the percentage enrolled in at least one subject from 100%:
\[
\text{Percentage not enrolled in either} = 100\% - P(M \cup E)
\]
\[
\text{Percentage not enrolled in either} = 100\% - 95\% = 5\%
\]
Conclusion
Therefore, the percentage of students who did not enroll for either Math or Economics is **5%**, which corresponds to option 'A'.
How many integral divisors does the number 120 have?- a)14
- b)16
- c)12
- d)20
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
How many integral divisors does the number 120 have?
a)
14
b)
16
c)
12
d)
20
e)
None of these
|
|
EduRev GMAT answered |
Step 1: Express the number in terms of its prime factors
120 = 23 * 3 * 5.
The three prime factors are 2, 3 and 5.
The powers of these prime factors are 3, 1 and 1 respectively.
The three prime factors are 2, 3 and 5.
The powers of these prime factors are 3, 1 and 1 respectively.
Step 2: Find the number of factors as follows
To find the number of factors / integral divisors that 120 has, increment the powers of each of the prime factors by 1 and then multiply them.
Number of factors = (3 + 1) * (1 + 1) * (1 + 1) = 4 * 2 * 2 =16
Choice B is the correct answer.
Key Takeaway
How to find the number of factors of a number? Method: Prime Factorization
Let the number be 'n'.
Step 1: Prime factorize 'n'. Let n = ap * bq, where 'a' and 'b' are the only prime factors of 'n'.
Step 2: Number of factors equals product of powers of primes incremented by 1.
i.e., number of factors = (p + 1)(q + 1)
How to find the number of factors of a number? Method: Prime Factorization
Let the number be 'n'.
Step 1: Prime factorize 'n'. Let n = ap * bq, where 'a' and 'b' are the only prime factors of 'n'.
Step 2: Number of factors equals product of powers of primes incremented by 1.
i.e., number of factors = (p + 1)(q + 1)
A child learning to play the piano will not succeed unless the child has an instrument at home on which to practice. However, good-quality pianos, whether new or secondhand, are costly. Buying one is justified only if the child has the necessary talent and perseverance, which is precisely what one cannot know in advance. Consequently, parents should buy an inexpensive secondhand instrument at first and upgrade if and when the child's ability and inclination are proven.
Q. Which of the following, if true, casts the most serious doubt on the course of action recommended for parents?
- a)Learners, particularly those with genuine musical talent, are apt to lose interest in the instrument if they have to play on a piano that fails to produce a pleasing sound.
- b)Reputable piano teachers do not accept children as pupils unless they know that the children can practice on a piano at home.
- c)Ideally, the piano on which a child practices at home should be located in a room away from family activities going on at the same time.
- d)Very young beginners often make remarkable progress at playing the piano at first, but then appear to stand still for a considerable period of time.
- e)In some parents, spending increasing amounts of money on having their children learn to play the piano produces increasing anxiety to hear immediate results.
Correct answer is option 'D'. Can you explain this answer?
A child learning to play the piano will not succeed unless the child has an instrument at home on which to practice. However, good-quality pianos, whether new or secondhand, are costly. Buying one is justified only if the child has the necessary talent and perseverance, which is precisely what one cannot know in advance. Consequently, parents should buy an inexpensive secondhand instrument at first and upgrade if and when the child's ability and inclination are proven.
Q. Which of the following, if true, casts the most serious doubt on the course of action recommended for parents?
a)
Learners, particularly those with genuine musical talent, are apt to lose interest in the instrument if they have to play on a piano that fails to produce a pleasing sound.
b)
Reputable piano teachers do not accept children as pupils unless they know that the children can practice on a piano at home.
c)
Ideally, the piano on which a child practices at home should be located in a room away from family activities going on at the same time.
d)
Very young beginners often make remarkable progress at playing the piano at first, but then appear to stand still for a considerable period of time.
e)
In some parents, spending increasing amounts of money on having their children learn to play the piano produces increasing anxiety to hear immediate results.
|
|
EduRev GMAT answered |
The argument talks about 'child' (say 3 - 12 yrs). Option (D) talks about 'very young' which implies a little child (say 3 - 5 yrs). Since very young will be a subset of child, most of my interest in the option is already lost. It is like saying "some children will..." and that is usually irrelevant.
Secondly it uses "beginners" which means the stage at which they have the second hand cheap instrument. They may show promise but will stop suddenly. Well, all the more reason to wait and watch with a temporary instrument. If you begin with an expensive one, it will go waste.
If we know that kids show progress initially and then stand still, we would buy a cheaper instrument and see whether they are showing continuous progress to buy an expensive one later.
Secondly it uses "beginners" which means the stage at which they have the second hand cheap instrument. They may show promise but will stop suddenly. Well, all the more reason to wait and watch with a temporary instrument. If you begin with an expensive one, it will go waste.
If we know that kids show progress initially and then stand still, we would buy a cheaper instrument and see whether they are showing continuous progress to buy an expensive one later.
Direction: Read the following Passage and Answer the following Question.Is there any knowledge in the world which is so certain that no reasonable man could doubt it? This question, which at first sight might not seem difficult, is really one of the most difficult that can be asked. When we have realized the obstacles in the way of a straightforward and confident answer, we shall be well launched on the study of philosophy—for philosophy is merely the attempt to answer such ultimate questions, not carelessly and dogmatically, as we do in ordinary life and even in the sciences, but critically, after exploring all that makes such questions puzzling, and after realizing all the vagueness and confusion that underlie our ordinary ideas.In daily life, we assume as certain many things which, on a closer scrutiny, are found to be so full of apparent contradictions that only a great amount of thought enables us to know what it is that we really may believe. In the search for certainty, it is natural to begin with our present experiences, and in some sense, no doubt, knowledge is to be derived from them. But any statement as to what it is that our immediate experiences make us know is very likely to be wrong. It seems to me that I am now sitting in a chair, at a table of a certain shape, on which I see sheets of paper with writing or print. By turning my head I see out of the window buildings and clouds and the sun. I believe that the sun is about ninety-three million miles from the earth; that it is a hot globe many times bigger than the earth; that, owing to the earth's rotation, it rises every morning, and will continue to do so for an indefinite time in the future. I believe that, if any other normal person comes into my room, he will see the same chairs and tables and books and papers as I see, and that the table which I see is the same as the table which I feel pressing against my arm. All this seems to be so evident as to be hardly worth stating, except in answer to a man who doubts whether I know anything. Yet all this may be reasonably doubted, and all of it requires much careful discussion before we can be sure that we have stated it in a form that is wholly true.Q. Suppose you state that 'you are sitting in a garden observing a yellow butterfly'. According to the passage:- a)Your statement could be doubted
- b)The butterfly may actually be a blue one
- c)The butterfly may not be there at all
- d)You have been dogmatic in making that statement
- e)You are correct in making that statement
Correct answer is option 'A'. Can you explain this answer?
Direction: Read the following Passage and Answer the following Question.
Is there any knowledge in the world which is so certain that no reasonable man could doubt it? This question, which at first sight might not seem difficult, is really one of the most difficult that can be asked. When we have realized the obstacles in the way of a straightforward and confident answer, we shall be well launched on the study of philosophy—for philosophy is merely the attempt to answer such ultimate questions, not carelessly and dogmatically, as we do in ordinary life and even in the sciences, but critically, after exploring all that makes such questions puzzling, and after realizing all the vagueness and confusion that underlie our ordinary ideas.
In daily life, we assume as certain many things which, on a closer scrutiny, are found to be so full of apparent contradictions that only a great amount of thought enables us to know what it is that we really may believe. In the search for certainty, it is natural to begin with our present experiences, and in some sense, no doubt, knowledge is to be derived from them. But any statement as to what it is that our immediate experiences make us know is very likely to be wrong. It seems to me that I am now sitting in a chair, at a table of a certain shape, on which I see sheets of paper with writing or print. By turning my head I see out of the window buildings and clouds and the sun. I believe that the sun is about ninety-three million miles from the earth; that it is a hot globe many times bigger than the earth; that, owing to the earth's rotation, it rises every morning, and will continue to do so for an indefinite time in the future. I believe that, if any other normal person comes into my room, he will see the same chairs and tables and books and papers as I see, and that the table which I see is the same as the table which I feel pressing against my arm. All this seems to be so evident as to be hardly worth stating, except in answer to a man who doubts whether I know anything. Yet all this may be reasonably doubted, and all of it requires much careful discussion before we can be sure that we have stated it in a form that is wholly true.
Q. Suppose you state that 'you are sitting in a garden observing a yellow butterfly'. According to the passage:
a)
Your statement could be doubted
b)
The butterfly may actually be a blue one
c)
The butterfly may not be there at all
d)
You have been dogmatic in making that statement
e)
You are correct in making that statement
|
|
EduRev GMAT answered |
From the last paragraph, it clearly follows that even the most simplistic of our observations can be doubted. Hence the answer has to be (A)
Shawn invested one half of his savings in a bond that paid simple interest for 2 years and received $ 550 as interest. He invested the remaining in a bond that paid compound interest, interest being compounded annually, for the same 2 years at the same rate of interest and received $605 as interest. What was the value of his total savings before investing in these two bonds?- a)$ 5500
- b)$ 11000
- c)$ 22000
- d)$ 2750
- e)$ 44000
Correct answer is option 'D'. Can you explain this answer?
Shawn invested one half of his savings in a bond that paid simple interest for 2 years and received $ 550 as interest. He invested the remaining in a bond that paid compound interest, interest being compounded annually, for the same 2 years at the same rate of interest and received $605 as interest. What was the value of his total savings before investing in these two bonds?
a)
$ 5500
b)
$ 11000
c)
$ 22000
d)
$ 2750
e)
$ 44000
|
|
EduRev GMAT answered |
Step 1: Compute interest for each year for both simple and compound interest
Simple Interest:
Concept: Simple interest earned is same value year on year.
Shawn received $550 as interest for 2 years.
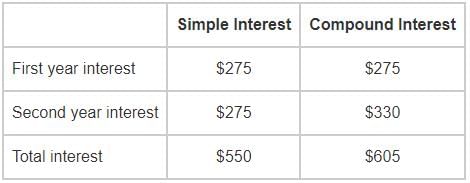
Simple interest earned for first year = 550/2 = $275
The simple interest for second year is also $275.
Concept: Simple interest earned is same value year on year.
Shawn received $550 as interest for 2 years.
Simple interest earned for first year = 550/2 = $275
The simple interest for second year is also $275.
In Compound interest: Shawn received $605 as interest for 2 years.
Concept: Interest earned is same for both simple and compound interest in the first year.
Compund interest earned for first year = $275.
Compund interest earned for second year = 605 − 275 = $330
Extra interest received from compound interest = $55.
Interest for each year
Concept: Interest earned is same for both simple and compound interest in the first year.
Compund interest earned for first year = $275.
Compund interest earned for second year = 605 − 275 = $330
Extra interest received from compound interest = $55.
Interest for each year
Step 2: Find the rate of interest
Concept: In Compound interest, interest earned on first year's interest will get added in second year and contributes to the additional interest when invested in compound interest.
Compound interest for first year = $275.
Therefore, $55 is the interest earned during the second year on $275.
Therefore, the rate of interest =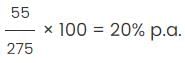
Therefore, $55 is the interest earned during the second year on $275.
Therefore, the rate of interest =
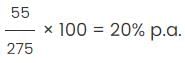
Step 3: Compute the principal invested
At 20% rate of interest, the simple interest earned for 1 year = $275
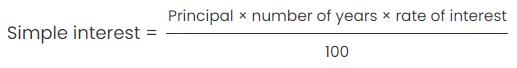
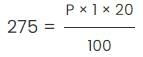
or P = $1375
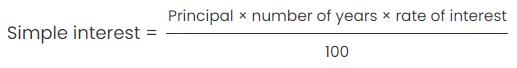
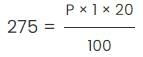
or P = $1375
Shawn had invested equal sums in both the bonds.
His total savings before investing = 2 × 1375 = $2750
Total savings = $2750
His total savings before investing = 2 × 1375 = $2750
Total savings = $2750
Choice D is the correct answer.
When 242 is divided by a certain divisor the remainder obtained is 8. When 698 is divided by the same divisor the remainder obtained is 9. However, when the sum of the two numbers 242 and 698 is divided by the divisor, the remainder obtained is 4. What is the value of the divisor?- a)11
- b)17
- c)13
- d)23
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
When 242 is divided by a certain divisor the remainder obtained is 8. When 698 is divided by the same divisor the remainder obtained is 9. However, when the sum of the two numbers 242 and 698 is divided by the divisor, the remainder obtained is 4. What is the value of the divisor?
a)
11
b)
17
c)
13
d)
23
e)
None of these
|
|
EduRev GMAT answered |
When 242 is divided by a certain divisor the remainder obtained is 8.
Let the divisor be d.
When 242 is divided by d, let the quotient be 'x'. The remainder is 8.
Therefore, 242 = xd + 8
When 242 is divided by d, let the quotient be 'x'. The remainder is 8.
Therefore, 242 = xd + 8
When 698 is divided by the same divisor the remainder obtained is 9.
Let y be the quotient when 698 is divided by d.
Then, 698 = yd + 9.
Then, 698 = yd + 9.
When the sum of the two numbers, 242 and 698, is divided by the divisor, the remainder obtained is 4.
242 + 698 = 940 = xd + yd + 8 + 9
940 = xd + yd + 17
940 = xd + yd + 17
Because xd and yd are divisible by d, the remainder when 940 is divided by d should have been 17.
However, because we know that the remainder is 4, it would be possible only when 17/d leaves a remainder of 4.
If the remainder obtained is 4 when 17 is divided by 'd', then 'd' has to be 13.
Choice C is the correct answer.
Direction: Read the following Passage and Answer the following Question.“Strange Bedfellows!” lamented the title of a recent letter to Museum News, in which a certain Harriet Sherman excoriated the National Gallery of Art in Washington for its handling of tickets to the much-ballyhooed “Van Gogh’s van Goghs” exhibit. A huge proportion of the 200,000 free tickets were snatched up by the opportunists in the dead of winter, who then scalped those tickets at $85 apiece to less hardy connoiseurs.Yet, Sherman’s bedfellows are far from strange. Art, despite its religious and magical origins, very soon became a commercial venture. From bourgeois patrons funding art they barely understood in order to share their protegee’s prestige, to museum curators stage-managing the cult of artists in order to enhance the market value of museum holdings, entrepreneurs have found validation and profit in big-name art. Speculators, thieves, and promoters long ago created and fed a market where cultural icons could be traded like commodities.This trend toward commodification of high-brow art took an ominous, if predictable, turn in the 1980s during the Japanese “bubble economy.” At a time when Japanese share prices more than doubled, individual tycoons and industrial giants alike invested record amounts in some of the West’s greatest masterpieces. Ryoei Saito, for example, purchased van Gogh’s Portrait of Dr. Gachet for a record-breaking $82.5 million. The work, then on loan to the Metropolitan Museum of Modern Art, suddenly vanished from the public domain. Later learning that he owed the Japanese government $24 million in taxes, Saito remarked that he would have the paining cremated with him to spare his heirs the inheritance tax. This statement, which he later dismissed as a joke, alarmed and enraged many. A representative of the Van Gogh museum, conceding that he had no legal redress, made an ethical appeal to Mr. Saito, asserting, “a work of art remains the possession of the world at large.”Ethical appeals notwithstanding, great art will increasingly devolve into big business. Firstly, great art can only be certified by its market value. Moreover, the “world at large” hasn’t the means of acquisition. Only one museum currently has the funding to contend for the best pieces–the J. Paul Getty Museum, founded by the billionaire oilman. The art may disappear into private hands, but its transfer will disseminate once static fortunes into the hands of various investors, collectors, and occasionally the artist.Q. Which of the following would be the most appropriate title for the passage?- a)Art of Art’s Sake: A Japanese Ideal
- b)Van Gogh: Breaking New Ground
- c)Museums and the Press: Strange Bedfellows
- d)Money vs. Art: An Ethical Mismatch
- e)Great Art: Business as Usual
Correct answer is option 'E'. Can you explain this answer?
Direction: Read the following Passage and Answer the following Question.
“Strange Bedfellows!” lamented the title of a recent letter to Museum News, in which a certain Harriet Sherman excoriated the National Gallery of Art in Washington for its handling of tickets to the much-ballyhooed “Van Gogh’s van Goghs” exhibit. A huge proportion of the 200,000 free tickets were snatched up by the opportunists in the dead of winter, who then scalped those tickets at $85 apiece to less hardy connoiseurs.
Yet, Sherman’s bedfellows are far from strange. Art, despite its religious and magical origins, very soon became a commercial venture. From bourgeois patrons funding art they barely understood in order to share their protegee’s prestige, to museum curators stage-managing the cult of artists in order to enhance the market value of museum holdings, entrepreneurs have found validation and profit in big-name art. Speculators, thieves, and promoters long ago created and fed a market where cultural icons could be traded like commodities.
This trend toward commodification of high-brow art took an ominous, if predictable, turn in the 1980s during the Japanese “bubble economy.” At a time when Japanese share prices more than doubled, individual tycoons and industrial giants alike invested record amounts in some of the West’s greatest masterpieces. Ryoei Saito, for example, purchased van Gogh’s Portrait of Dr. Gachet for a record-breaking $82.5 million. The work, then on loan to the Metropolitan Museum of Modern Art, suddenly vanished from the public domain. Later learning that he owed the Japanese government $24 million in taxes, Saito remarked that he would have the paining cremated with him to spare his heirs the inheritance tax. This statement, which he later dismissed as a joke, alarmed and enraged many. A representative of the Van Gogh museum, conceding that he had no legal redress, made an ethical appeal to Mr. Saito, asserting, “a work of art remains the possession of the world at large.”
Ethical appeals notwithstanding, great art will increasingly devolve into big business. Firstly, great art can only be certified by its market value. Moreover, the “world at large” hasn’t the means of acquisition. Only one museum currently has the funding to contend for the best pieces–the J. Paul Getty Museum, founded by the billionaire oilman. The art may disappear into private hands, but its transfer will disseminate once static fortunes into the hands of various investors, collectors, and occasionally the artist.
Q. Which of the following would be the most appropriate title for the passage?
a)
Art of Art’s Sake: A Japanese Ideal
b)
Van Gogh: Breaking New Ground
c)
Museums and the Press: Strange Bedfellows
d)
Money vs. Art: An Ethical Mismatch
e)
Great Art: Business as Usual
|
|
EduRev GMAT answered |
This is a GLOBAL question. A good title should sum up the theme and content of the passage as a whole. If you see a question asking you to choose a title for a passage, you have encountered a Global question and should look at the passage as a whole, using the Topic, Scope, and Purpose that you noted to help find your answer. You are looking for a choice that represents the author’s view that art and business are closely connected.
Choice (A) is a distortion of the topic. The issue of “art of art’s sake” does underlie the passage, and there is some attention to an incident involving a Japanese businessperson, but there is no suggestion that the ideal is particularly Japanese.
Choice (B) focuses on the artist van Gogh, who is mentioned in two paragraphs; however, van Gogh is not the topic of the passage, and there is no discussion of his innovations.
Choice (C) distorts the topic of the first paragraph. In fact, that paragraph discussed a letter published in a magazine, but it did not discuss the press per se. The passage does not actually state who the “strange bedfellows” were, but the implication is that Sherman was referring to either the scalpers and the art aficionados who were vying for tickets, or to art and (illegal) business.
Choice (D) is actually a reversal of the author’s theme, which is that money and are art quite often intimately linked; the first sentence of paragraph 4 dismisses the ethical concerns.
The correct answer is choice (E), which states that art is business.
A number when divided by a divisor leaves a remainder of 24. When twice the original number is divided by the same divisor, the remainder is 11. What is the value of the divisor?- a)13
- b)59
- c)35
- d)37
- e)12
Correct answer is option 'D'. Can you explain this answer?
A number when divided by a divisor leaves a remainder of 24. When twice the original number is divided by the same divisor, the remainder is 11. What is the value of the divisor?
a)
13
b)
59
c)
35
d)
37
e)
12
|
|
EduRev GMAT answered |
Step 1: Decode "A number when divided by a divisor leaves a remainder of 24"
Let the original number be 'a'.
Let the divisor be 'd'.
Let the quotient of dividing 'a' by 'd' be 'x'.
Therefore, we can write the division as a/d = x and the remainder is 24.
i.e., a = dx + 24
Let the divisor be 'd'.
Let the quotient of dividing 'a' by 'd' be 'x'.
Therefore, we can write the division as a/d = x and the remainder is 24.
i.e., a = dx + 24
Step 2: Decode "When twice the original number is divided by the same divisor, the remainder is 11"
Twice the original number is divided by 'd' means 2a is divided by d.
We know from Step 1 that a = dx + 24.
Therefore, 2a = 2(dx + 48) or 2a = 2dx + 48
We know from Step 1 that a = dx + 24.
Therefore, 2a = 2(dx + 48) or 2a = 2dx + 48
When (2dx + 48) is divided by 'd' the remainder is 11.
2dx is divisible by 'd' and will therefore, not leave a remainder.
The remainder of 11 would be the remainder of dividing 48 by d.
2dx is divisible by 'd' and will therefore, not leave a remainder.
The remainder of 11 would be the remainder of dividing 48 by d.
The question essentially becomes "What number will leave a remainder of 11 when it divides 48?"
When 37 divides 48, the remainder is 11.
When 37 divides 48, the remainder is 11.
Hence, the divisor is 37.
Choice D is the correct answer.
Direction: Read the following Passage and Answer the following Question.Is there any knowledge in the world which is so certain that no reasonable man could doubt it? This question, which at first sight might not seem difficult, is really one of the most difficult that can be asked. When we have realized the obstacles in the way of a straightforward and confident answer, we shall be well launched on the study of philosophy—for philosophy is merely the attempt to answer such ultimate questions, not carelessly and dogmatically, as we do in ordinary life and even in the sciences, but critically, after exploring all that makes such questions puzzling, and after realizing all the vagueness and confusion that underlie our ordinary ideas.In daily life, we assume as certain many things which, on a closer scrutiny, are found to be so full of apparent contradictions that only a great amount of thought enables us to know what it is that we really may believe. In the search for certainty, it is natural to begin with our present experiences, and in some sense, no doubt, knowledge is to be derived from them. But any statement as to what it is that our immediate experiences make us know is very likely to be wrong. It seems to me that I am now sitting in a chair, at a table of a certain shape, on which I see sheets of paper with writing or print. By turning my head I see out of the window buildings and clouds and the sun. I believe that the sun is about ninety-three million miles from the earth; that it is a hot globe many times bigger than the earth; that, owing to the earth's rotation, it rises every morning, and will continue to do so for an indefinite time in the future. I believe that, if any other normal person comes into my room, he will see the same chairs and tables and books and papers as I see, and that the table which I see is the same as the table which I feel pressing against my arm. All this seems to be so evident as to be hardly worth stating, except in answer to a man who doubts whether I know anything. Yet all this may be reasonably doubted, and all of it requires much careful discussion before we can be sure that we have stated it in a form that is wholly true.Q. According to the information in the passage, which of the following can be inferred about the manner in which we attempt to answer questions in our day to day life?- a)Some of these questions may not have an answer at all
- b)What we think is the answer to a question may, in fact, not be the answer
- c)Sometimes we allow dogma to affect our thinking while arriving at an answer
- d)We tend to be satisfied with the answers, even if they appear vague and unclear
- e)We always make a lot of assumptions while arriving at an answer
Correct answer is option 'C'. Can you explain this answer?
Direction: Read the following Passage and Answer the following Question.
Is there any knowledge in the world which is so certain that no reasonable man could doubt it? This question, which at first sight might not seem difficult, is really one of the most difficult that can be asked. When we have realized the obstacles in the way of a straightforward and confident answer, we shall be well launched on the study of philosophy—for philosophy is merely the attempt to answer such ultimate questions, not carelessly and dogmatically, as we do in ordinary life and even in the sciences, but critically, after exploring all that makes such questions puzzling, and after realizing all the vagueness and confusion that underlie our ordinary ideas.
In daily life, we assume as certain many things which, on a closer scrutiny, are found to be so full of apparent contradictions that only a great amount of thought enables us to know what it is that we really may believe. In the search for certainty, it is natural to begin with our present experiences, and in some sense, no doubt, knowledge is to be derived from them. But any statement as to what it is that our immediate experiences make us know is very likely to be wrong. It seems to me that I am now sitting in a chair, at a table of a certain shape, on which I see sheets of paper with writing or print. By turning my head I see out of the window buildings and clouds and the sun. I believe that the sun is about ninety-three million miles from the earth; that it is a hot globe many times bigger than the earth; that, owing to the earth's rotation, it rises every morning, and will continue to do so for an indefinite time in the future. I believe that, if any other normal person comes into my room, he will see the same chairs and tables and books and papers as I see, and that the table which I see is the same as the table which I feel pressing against my arm. All this seems to be so evident as to be hardly worth stating, except in answer to a man who doubts whether I know anything. Yet all this may be reasonably doubted, and all of it requires much careful discussion before we can be sure that we have stated it in a form that is wholly true.
Q. According to the information in the passage, which of the following can be inferred about the manner in which we attempt to answer questions in our day to day life?
a)
Some of these questions may not have an answer at all
b)
What we think is the answer to a question may, in fact, not be the answer
c)
Sometimes we allow dogma to affect our thinking while arriving at an answer
d)
We tend to be satisfied with the answers, even if they appear vague and unclear
e)
We always make a lot of assumptions while arriving at an answer
|
|
Sharmila Singh answered |
Understanding the Passage
The passage delves into the complexities of knowledge and certainty, highlighting how our daily assumptions can often be misguided or dogmatic.
Key Insights from the Passage
- The passage suggests that in our daily lives, we often accept answers without rigorous scrutiny.
- It emphasizes that answers to questions can be influenced by preconceptions or dogmas rather than critical thinking.
Why Option C is Correct
- The author points out that people tend to approach questions with a sense of certainty based on their immediate experiences.
- However, these experiences can be misleading and require deeper examination, which implies that our thinking may be clouded by assumptions or dogmatic beliefs.
- The term "dogmatically" is specifically used to contrast the casual acceptance of ideas in everyday life with the critical approach that philosophy advocates.
Supporting Evidence
- The passage states that many assumptions in daily life may hold apparent contradictions and need careful thought to ascertain their truth.
- It indicates that people often take for granted what seems evident, but in reality, these conclusions can be based on unexamined beliefs, hence reflecting a dogmatic approach.
Conclusion
- Overall, the passage illustrates how the acceptance of ideas without critical examination reflects a tendency to allow dogma to influence our understanding of knowledge, making option C the most fitting inference.
The passage delves into the complexities of knowledge and certainty, highlighting how our daily assumptions can often be misguided or dogmatic.
Key Insights from the Passage
- The passage suggests that in our daily lives, we often accept answers without rigorous scrutiny.
- It emphasizes that answers to questions can be influenced by preconceptions or dogmas rather than critical thinking.
Why Option C is Correct
- The author points out that people tend to approach questions with a sense of certainty based on their immediate experiences.
- However, these experiences can be misleading and require deeper examination, which implies that our thinking may be clouded by assumptions or dogmatic beliefs.
- The term "dogmatically" is specifically used to contrast the casual acceptance of ideas in everyday life with the critical approach that philosophy advocates.
Supporting Evidence
- The passage states that many assumptions in daily life may hold apparent contradictions and need careful thought to ascertain their truth.
- It indicates that people often take for granted what seems evident, but in reality, these conclusions can be based on unexamined beliefs, hence reflecting a dogmatic approach.
Conclusion
- Overall, the passage illustrates how the acceptance of ideas without critical examination reflects a tendency to allow dogma to influence our understanding of knowledge, making option C the most fitting inference.
What is the remainder when 1044 × 1047 × 1050 × 1053 is divided by 33?- a)3
- b)27
- c)30
- d)21
- e)18
Correct answer is option 'C'. Can you explain this answer?
What is the remainder when 1044 × 1047 × 1050 × 1053 is divided by 33?
a)
3
b)
27
c)
30
d)
21
e)
18
|
|
EduRev GMAT answered |
Useful result pertaining to remainders
You can solve this problem if you know this rule about remainders.
Let a number x divide the product of A and B.
The remainder will be the product of the remainders when x divides A and when x divides B.
Let a number x divide the product of A and B.
The remainder will be the product of the remainders when x divides A and when x divides B.
Using this rule,
The remainder when 33 divides 1044 is 21.
The remainder when 33 divides 1047 is 24.
The remainder when 33 divides 1050 is 27.
The remainder when 33 divides 1053 is 30.
The remainder when 33 divides 1044 is 21.
The remainder when 33 divides 1047 is 24.
The remainder when 33 divides 1050 is 27.
The remainder when 33 divides 1053 is 30.
∴ the remainder when 33 divides 1044 × 1047 × 1050 × 1053 is 21 × 24 × 27 × 30.
Note: The remainder when a number is divided by a divisor 'd' will take values from 0 to (d - 1). It will not be equal to or more than 'd'
The value of 21 × 24 × 27 × 30 is more than 33.
When the value of the remainder is more than the divisor, the final remainder will be the remainder of dividing the product by the divisor.
i.e., the final remainder is the remainder when 33 divides 21 × 24 × 27 × 30.
When 33 divides 21 × 24 × 27 × 30, the remainder is 30.
When the value of the remainder is more than the divisor, the final remainder will be the remainder of dividing the product by the divisor.
i.e., the final remainder is the remainder when 33 divides 21 × 24 × 27 × 30.
When 33 divides 21 × 24 × 27 × 30, the remainder is 30.
Choice C is the correct answer.
Braun invested a certain sum of money at 8% p.a. simple interest for 'n' years. At the end of 'n' years, Braun got back 4 times his original investment. What is the value of n?- a)50 years
- b)25 years
- c)12 years 6 months
- d)37 years 6 months
- e)40 years
Correct answer is option 'D'. Can you explain this answer?
Braun invested a certain sum of money at 8% p.a. simple interest for 'n' years. At the end of 'n' years, Braun got back 4 times his original investment. What is the value of n?
a)
50 years
b)
25 years
c)
12 years 6 months
d)
37 years 6 months
e)
40 years
|
|
EduRev GMAT answered |
Step 1: Assume initial investment (Principal) and compute final value (amount) after n years
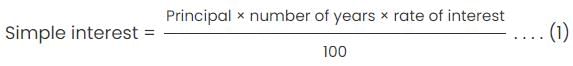
For any assumed principal, the number of years is going to remain the same because the amount is expressed as ‘x’ times the principal i.e., 4 times in this case.
Let us assume the initial investment (principal) by Braun to be $100.
Amount = 4 × Principal = $400
Amount = Principal + Simple Interest
Therefore, the Simple Interest earned = 400 - 100 = $300.
Step 2: Find the number of years n
Substitute assumed value of principal and the corresponding interest earned, and rate of interest in equation 1.
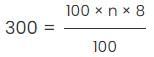
Or 8n = 300
Or n = 37.5 years
Any amount, when invested for 37.5 years at 8% per annum simple interest would become 4 times the initial value.
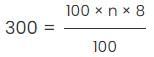
Or 8n = 300
Or n = 37.5 years
Any amount, when invested for 37.5 years at 8% per annum simple interest would become 4 times the initial value.
Alternative Method:
Find the number of years required to double the initial amount (principal).
When the initial investment doubles, the interest earned is the same as the initial investment (principal).
So, if principal = 100, interest earned = 100 and r = 8%.
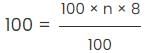
So, n = 100/8 = 12.5 years.
When the initial investment doubles, the interest earned is the same as the initial investment (principal).
So, if principal = 100, interest earned = 100 and r = 8%.
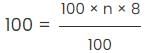
So, n = 100/8 = 12.5 years.
Initial investment of $100 becomes $400 after earning an interest of $300.
To earn $100 interest it took 12.5 years. Hence, it will take 3 × 12.5 = 37.5 years to earn $300 interest.
To earn $100 interest it took 12.5 years. Hence, it will take 3 × 12.5 = 37.5 years to earn $300 interest.
Choice D is the correct answer.
Megalimpet is a nationwide owner of office space. They have major office buildings in the downtowns of several cities in the 48 lower states, and rent this space to individual companies. Megalimpet office spaces vary from small office to large suites, and every space has custom-designed wall-to-wall carpeting. The carpet in several Megalimpet facilities needed replacing. The winning bid for the nationwide carpet replacement was submitted by Bathyderm Carpet Company (BCC). The bid contract involves all delivery costs, all installation, and any ongoing maintenance and upkeep while the carpet is under the three-year warranty. Both BCC executives and independent consultants they hired felt BCC would be able to perform all these services for far less than their bid price; these circumstances would allow BCC to reap a considerable profit.Q. Which of the following, if true, most calls in question the argument that BCC will make a large profit from this contract with Megalimpet?- a)All the carpets will have to be transported by train from BCC factory in Louisville, KY, to Megalimpet's locations from coast to coast.
- b)BCC has already supplied carpets to a number of restaurant chains, and some of those spaces are as large as Megalimpet's largest office spaces.
- c)The carpet installation teams will have to cut different sizes of the carpets for the different size office suites in the Megalimpet buildings.
- d)The material in BCC carpets degrades rapidly when it comes into contact with standard toner, found in most laser printers and photocopiers; the degraded sections are unsightly and smell bad, so they often need to be replaced.
- e)The next competing bid after BCC's was 50% higher than BCC's bid.
Correct answer is option 'D'. Can you explain this answer?
Megalimpet is a nationwide owner of office space. They have major office buildings in the downtowns of several cities in the 48 lower states, and rent this space to individual companies. Megalimpet office spaces vary from small office to large suites, and every space has custom-designed wall-to-wall carpeting. The carpet in several Megalimpet facilities needed replacing. The winning bid for the nationwide carpet replacement was submitted by Bathyderm Carpet Company (BCC). The bid contract involves all delivery costs, all installation, and any ongoing maintenance and upkeep while the carpet is under the three-year warranty. Both BCC executives and independent consultants they hired felt BCC would be able to perform all these services for far less than their bid price; these circumstances would allow BCC to reap a considerable profit.
Q. Which of the following, if true, most calls in question the argument that BCC will make a large profit from this contract with Megalimpet?
a)
All the carpets will have to be transported by train from BCC factory in Louisville, KY, to Megalimpet's locations from coast to coast.
b)
BCC has already supplied carpets to a number of restaurant chains, and some of those spaces are as large as Megalimpet's largest office spaces.
c)
The carpet installation teams will have to cut different sizes of the carpets for the different size office suites in the Megalimpet buildings.
d)
The material in BCC carpets degrades rapidly when it comes into contact with standard toner, found in most laser printers and photocopiers; the degraded sections are unsightly and smell bad, so they often need to be replaced.
e)
The next competing bid after BCC's was 50% higher than BCC's bid.
|
|
Moumita Sen answered |
Analysis:
The argument presented in the passage suggests that BCC will make a significant profit from the contract with Megalimpet due to their ability to perform the services for less than their bid price. However, option D calls this argument into question by introducing a potential issue with the quality of BCC's carpets.
Explanation:
Material Degradation:
- The material in BCC's carpets degrades rapidly when in contact with standard toner, causing unsightly and smelly degraded sections.
- This degradation would likely lead to additional costs for BCC in terms of replacing the degraded sections, potentially cutting into their expected profit margin.
Impact on Profitability:
- The need for frequent replacements due to material degradation could increase BCC's costs and reduce the profitability of the contract with Megalimpet.
- This potential issue with the quality of BCC's carpets casts doubt on their ability to make a large profit as initially suggested in the passage.
In conclusion, option D raises a significant concern about the quality of BCC's carpets and the potential impact on their profitability from the contract with Megalimpet. This information undermines the argument that BCC will make a substantial profit from the deal.
The argument presented in the passage suggests that BCC will make a significant profit from the contract with Megalimpet due to their ability to perform the services for less than their bid price. However, option D calls this argument into question by introducing a potential issue with the quality of BCC's carpets.
Explanation:
Material Degradation:
- The material in BCC's carpets degrades rapidly when in contact with standard toner, causing unsightly and smelly degraded sections.
- This degradation would likely lead to additional costs for BCC in terms of replacing the degraded sections, potentially cutting into their expected profit margin.
Impact on Profitability:
- The need for frequent replacements due to material degradation could increase BCC's costs and reduce the profitability of the contract with Megalimpet.
- This potential issue with the quality of BCC's carpets casts doubt on their ability to make a large profit as initially suggested in the passage.
In conclusion, option D raises a significant concern about the quality of BCC's carpets and the potential impact on their profitability from the contract with Megalimpet. This information undermines the argument that BCC will make a substantial profit from the deal.
Each of the question below consists of a question and two statements numbered I and II are given below it You have to decide whether the data provided in the statements are sufficient to answer the question Read both the statement and answer the following question.Who reached the station first among L, M, J, T and R if no two persons reached together?
I. M reached only after J and T
II. L reached before R- a)If the data in Statement I alone are sufficient to answer the question while the data in Statement II alone are not sufficient to answer the question
- b)If the data in Statement II alone are sufficient to answer the question while the data in Statement I alone are not sufficient to answer the question
- c)If the data in Statement I alone or in Statement II alone are sufficient to answer the question
- d)If the data in both the Statement I and II are not sufficient to answer the question
- e)If the data in both the Statements I and II together are necessary to answer the question
Correct answer is option 'D'. Can you explain this answer?
Each of the question below consists of a question and two statements numbered I and II are given below it You have to decide whether the data provided in the statements are sufficient to answer the question Read both the statement and answer the following question.
Who reached the station first among L, M, J, T and R if no two persons reached together?
I. M reached only after J and T
II. L reached before R
I. M reached only after J and T
II. L reached before R
a)
If the data in Statement I alone are sufficient to answer the question while the data in Statement II alone are not sufficient to answer the question
b)
If the data in Statement II alone are sufficient to answer the question while the data in Statement I alone are not sufficient to answer the question
c)
If the data in Statement I alone or in Statement II alone are sufficient to answer the question
d)
If the data in both the Statement I and II are not sufficient to answer the question
e)
If the data in both the Statements I and II together are necessary to answer the question
|
|
Nikhil Khanna answered |
Understanding the Problem
To determine who reached the station first among L, M, J, T, and R, we analyze the two statements provided.
Statement I Analysis
- M reached only after J and T.
- This indicates that both J and T arrived before M.
- However, it does not provide any information about the arrival times of L and R in relation to J and T.
Statement II Analysis
- L reached before R.
- This tells us about the relative positions of L and R but does not indicate where L, R, or T stands concerning M and J.
Conclusion from Both Statements
- **From Statement I**: We know the order of M, J, and T, but without knowing L and R's positions, we cannot determine who arrived first overall.
- **From Statement II**: We learn about L and R, but this is insufficient to place them relative to J, T, or M.
Final Evaluation
- Neither statement alone is sufficient to determine who reached the station first.
- Combining both statements does not yield enough information either, as we still lack the full order of arrival among all five individuals.
Thus, the correct answer is option **D**: the data in both statements I and II together are not sufficient to answer the question.
To determine who reached the station first among L, M, J, T, and R, we analyze the two statements provided.
Statement I Analysis
- M reached only after J and T.
- This indicates that both J and T arrived before M.
- However, it does not provide any information about the arrival times of L and R in relation to J and T.
Statement II Analysis
- L reached before R.
- This tells us about the relative positions of L and R but does not indicate where L, R, or T stands concerning M and J.
Conclusion from Both Statements
- **From Statement I**: We know the order of M, J, and T, but without knowing L and R's positions, we cannot determine who arrived first overall.
- **From Statement II**: We learn about L and R, but this is insufficient to place them relative to J, T, or M.
Final Evaluation
- Neither statement alone is sufficient to determine who reached the station first.
- Combining both statements does not yield enough information either, as we still lack the full order of arrival among all five individuals.
Thus, the correct answer is option **D**: the data in both statements I and II together are not sufficient to answer the question.
How many real solutions exist for the equation x2 – 11|x| - 60 = 0?- a)3
- b)2
- c)1
- d)4
- e)None
Correct answer is option 'B'. Can you explain this answer?
How many real solutions exist for the equation x2 – 11|x| - 60 = 0?
a)
3
b)
2
c)
1
d)
4
e)
None
|
|
Manasa Kulkarni answered |
Analysis:
To find the number of real solutions for the given equation x^2 - 11|x| - 60 = 0, we need to consider two cases: when x is positive and when x is negative.
Case 1: x is positive
When x is positive, the equation becomes x^2 - 11x - 60 = 0.
Factoring the equation, we get (x - 15)(x + 4) = 0.
This gives us two possible solutions: x = 15 and x = -4.
Case 2: x is negative
When x is negative, the equation becomes x^2 + 11x - 60 = 0.
Factoring the equation, we get (x + 15)(x - 4) = 0.
This gives us two possible solutions: x = -15 and x = 4.
Combining the solutions:
Since we are looking for real solutions, we can see that only x = 4 is a valid solution that satisfies the absolute value requirement. Therefore, there are 2 real solutions for the equation x^2 - 11|x| - 60 = 0.
Therefore, the correct answer is option B) 2.
To find the number of real solutions for the given equation x^2 - 11|x| - 60 = 0, we need to consider two cases: when x is positive and when x is negative.
Case 1: x is positive
When x is positive, the equation becomes x^2 - 11x - 60 = 0.
Factoring the equation, we get (x - 15)(x + 4) = 0.
This gives us two possible solutions: x = 15 and x = -4.
Case 2: x is negative
When x is negative, the equation becomes x^2 + 11x - 60 = 0.
Factoring the equation, we get (x + 15)(x - 4) = 0.
This gives us two possible solutions: x = -15 and x = 4.
Combining the solutions:
Since we are looking for real solutions, we can see that only x = 4 is a valid solution that satisfies the absolute value requirement. Therefore, there are 2 real solutions for the equation x^2 - 11|x| - 60 = 0.
Therefore, the correct answer is option B) 2.
Direction: Read the following Passage and Answer the following Question.In the world of modern technology, the race to develop quantum computers has become the new gold rush. While classical computers have driven the digital age, quantum computers hold the promise of solving problems beyond the reach of classical systems. This race, however, is not just about technological superiority; it's a strategic chess game involving national pride and potential economic supremacy.The United States and China have emerged as the front-runners in this race. The U.S., with its long history of technological innovation, has poured billions into research and development. Silicon Valley giants like Google and IBM are in a fierce competition to build the first fully functional quantum computer. On the other hand, China's ambitious national strategy has led to significant advancements, including the launch of the world's first quantum satellite.At the heart of this competition lies the principle of quantum supremacy - the point at which a quantum computer can perform a calculation that is impossible for a classical computer. Achieving this would not only be a scientific breakthrough but also have profound implications for cybersecurity, as quantum computers can potentially break many of the encryption methods currently in use.Despite the excitement, there are skeptics who question the practicality of quantum computing. They argue that these computers are incredibly sensitive to environmental factors and require extreme conditions to function, such as near-absolute zero temperatures. Moreover, the technology is still in its infancy, and real-world applications are years, if not decades, away.
As the race continues, one thing is certain: the arrival of quantum computing will mark a new era in the technological landscape, reshaping industries and possibly redefining global power dynamics.Q. Based on the passage, which of the following can be inferred about quantum computers compared to classical computers?- a)Quantum computers are more environmentally friendly.
- b)Quantum computers can perform all tasks faster than classical computers.
- c)Quantum computers require specific environmental conditions to operate effectively.
- d)Quantum computers are more practical for everyday use.
- e)Quantum computers are less expensive to produce.
Correct answer is option 'C'. Can you explain this answer?
Direction: Read the following Passage and Answer the following Question.
In the world of modern technology, the race to develop quantum computers has become the new gold rush. While classical computers have driven the digital age, quantum computers hold the promise of solving problems beyond the reach of classical systems. This race, however, is not just about technological superiority; it's a strategic chess game involving national pride and potential economic supremacy.
The United States and China have emerged as the front-runners in this race. The U.S., with its long history of technological innovation, has poured billions into research and development. Silicon Valley giants like Google and IBM are in a fierce competition to build the first fully functional quantum computer. On the other hand, China's ambitious national strategy has led to significant advancements, including the launch of the world's first quantum satellite.
At the heart of this competition lies the principle of quantum supremacy - the point at which a quantum computer can perform a calculation that is impossible for a classical computer. Achieving this would not only be a scientific breakthrough but also have profound implications for cybersecurity, as quantum computers can potentially break many of the encryption methods currently in use.
Despite the excitement, there are skeptics who question the practicality of quantum computing. They argue that these computers are incredibly sensitive to environmental factors and require extreme conditions to function, such as near-absolute zero temperatures. Moreover, the technology is still in its infancy, and real-world applications are years, if not decades, away.
As the race continues, one thing is certain: the arrival of quantum computing will mark a new era in the technological landscape, reshaping industries and possibly redefining global power dynamics.
As the race continues, one thing is certain: the arrival of quantum computing will mark a new era in the technological landscape, reshaping industries and possibly redefining global power dynamics.
Q. Based on the passage, which of the following can be inferred about quantum computers compared to classical computers?
a)
Quantum computers are more environmentally friendly.
b)
Quantum computers can perform all tasks faster than classical computers.
c)
Quantum computers require specific environmental conditions to operate effectively.
d)
Quantum computers are more practical for everyday use.
e)
Quantum computers are less expensive to produce.
|
|
EduRev GMAT answered |
This is an INFERENCE question. The passage mentions that quantum computers are "incredibly sensitive to environmental factors" and require "near-absolute zero temperatures" to function. This information allows us to infer that quantum computers require specific environmental conditions to operate effectively (Choice C). The other choices are either not supported by the passage or are incorrect based on the information provided.
If the curve described by the equation y = x2 + bx + c cuts the x-axis at -4 and y axis at 4, at which other point does it cut the x-axis?- a)-1
- b)4
- c)1
- d)-4
- e)0
Correct answer is option 'A'. Can you explain this answer?
If the curve described by the equation y = x2 + bx + c cuts the x-axis at -4 and y axis at 4, at which other point does it cut the x-axis?
a)
-1
b)
4
c)
1
d)
-4
e)
0
|
|
Athira Choudhury answered |
Analysis:
The curve described by the equation y = x^2 + bx + c cuts the x-axis at -4 and the y-axis at 4. This means that the curve intersects the x-axis at the point (-4, 0) and the y-axis at the point (0, 4).
Using the x-axis intercept to find the third point:
To find the third point at which the curve intersects the x-axis, we can substitute y = 0 into the equation y = x^2 + bx + c and solve for x. This will give us the x-coordinate of the third point of intersection.
Given that the curve intersects the x-axis at -4, we can substitute x = -4 into the equation:
0 = (-4)^2 + b(-4) + c
0 = 16 - 4b + c
Using the y-axis intercept to find the third point:
We know that the curve intersects the y-axis at the point (0, 4). Substituting x = 0 and y = 4 into the equation y = x^2 + bx + c gives:
4 = 0^2 + b(0) + c
4 = c
Substitute c = 4 into the equation:
Now that we have found that c = 4, we can substitute this value back into the equation 0 = 16 - 4b + c:
0 = 16 - 4b + 4
0 = 20 - 4b
4b = 20
b = 5
Find the x-coordinate of the third point:
Substitute b = 5 and c = 4 into the equation 0 = 16 - 4b + c:
0 = 16 - 4(5) + 4
0 = 16 - 20 + 4
0 = 0
Therefore, the curve intersects the x-axis at x = 0. Hence, the correct answer is option 'A' (-1).
The curve described by the equation y = x^2 + bx + c cuts the x-axis at -4 and the y-axis at 4. This means that the curve intersects the x-axis at the point (-4, 0) and the y-axis at the point (0, 4).
Using the x-axis intercept to find the third point:
To find the third point at which the curve intersects the x-axis, we can substitute y = 0 into the equation y = x^2 + bx + c and solve for x. This will give us the x-coordinate of the third point of intersection.
Given that the curve intersects the x-axis at -4, we can substitute x = -4 into the equation:
0 = (-4)^2 + b(-4) + c
0 = 16 - 4b + c
Using the y-axis intercept to find the third point:
We know that the curve intersects the y-axis at the point (0, 4). Substituting x = 0 and y = 4 into the equation y = x^2 + bx + c gives:
4 = 0^2 + b(0) + c
4 = c
Substitute c = 4 into the equation:
Now that we have found that c = 4, we can substitute this value back into the equation 0 = 16 - 4b + c:
0 = 16 - 4b + 4
0 = 20 - 4b
4b = 20
b = 5
Find the x-coordinate of the third point:
Substitute b = 5 and c = 4 into the equation 0 = 16 - 4b + c:
0 = 16 - 4(5) + 4
0 = 16 - 20 + 4
0 = 0
Therefore, the curve intersects the x-axis at x = 0. Hence, the correct answer is option 'A' (-1).
In a few recent cases, some teenagers with advanced programming abilities used a new programming language, FANTOD, to hack into ETS and change their own SAT scores. All of the teenagers convicted of this crime were highly skilled in programming FANTOD. In light of these cases, some colleges have discounted the official SAT scores of applicants with a knowledge of FANTOD, and have required them to take special admission tests in supervised conditions on their own campuses.Q. Which of following conclusions can most properly be drawn from the information above?- a)Most people who learn to program in FANTOD do so to commit some kind of hacking.
- b)Colleges should rely on their own admissions tests instead of the SATs
- c)The college admissions process possibly places some students with a knowledge of FANTOD at a disadvantage.
- d)Students who learn FANTOD tend to have much lower SAT scores than do their peers.
- e)Not all colleges requiring special admissions tests have administered these tests under supervised conditions.
Correct answer is option 'C'. Can you explain this answer?
In a few recent cases, some teenagers with advanced programming abilities used a new programming language, FANTOD, to hack into ETS and change their own SAT scores. All of the teenagers convicted of this crime were highly skilled in programming FANTOD. In light of these cases, some colleges have discounted the official SAT scores of applicants with a knowledge of FANTOD, and have required them to take special admission tests in supervised conditions on their own campuses.
Q. Which of following conclusions can most properly be drawn from the information above?
a)
Most people who learn to program in FANTOD do so to commit some kind of hacking.
b)
Colleges should rely on their own admissions tests instead of the SATs
c)
The college admissions process possibly places some students with a knowledge of FANTOD at a disadvantage.
d)
Students who learn FANTOD tend to have much lower SAT scores than do their peers.
e)
Not all colleges requiring special admissions tests have administered these tests under supervised conditions.
|
|
EduRev GMAT answered |
The evidence says: all the ETS hackers were FANTOD programmers. What the colleges seem to be assuming is the converse: all FANTOD programmers are hackers. Of course, there is no direct evidence for this converse. Presumably there are some students who learn FANTOD in good faith and who are not hackers, but because of the assumption the colleges are making, these students are faced with extra challenges, such as having their justly achieved SAT scores disregarded and being forced to take additional admission tests.
(C) is the credited answer. Since there is no evidence for the converse statement, we have reason to believe there are FANTOD programmers who are entirely innocent of any hacking, yet those very students will have their perfectly valid SAT scores dismissed and will have to take a new test to achieve admission: this certainly would not be fun, would not be fair, and could place them at a disadvantage with respect to all the non-programming students who could just take the ordinary SATs and be done with all testing.
(A) assumes too much based on the information provided in the prompt. Specifically, we only know about a specific group of those with FANTOD knowledge: those who used it to hack into ETS. Therefore, we cannot make any airtight conclusions about "most people". It is very possible that most people who know FANTOD use it for purposes other than hacking.
(B) might be true, but it's much too broad. This is about the much larger issue of what is the best way for colleges to determine who should be admitted. This entire argument is focused quite specifically on the FANTOD programmers and the issues associated with them.
We have absolutely no evidence for (D). All we know is that, whatever scores those hackers achieved on the real SAT, they falsified the records to make them higher. We don't know if those scores were already high, and we certainly can draw no conclusion about all the students who know how to program in FANTOD who are not hackers. In fact, one might suspect the opposite, that folks bright enough to figure out this sophisticated programming language might be more intelligent and more successful on average, but even that we strictly can't assume. Therefore, we can't draw a clear conclusion about this.
(E) is a tricky one. We are told that some colleges took a certain set of special measures. We are given no information on what the other colleges did. Did they take another set of special measures? Did they not address the issue at all? We don't know. Therefore, we can't draw a clear conclusion along these lines.
Studies show that children who listen too much classic music are more likely than others to become silent adults. Shawn, who is a silent adult, must have listened more classic music as a child than I did, since I am not silent.Q. Which of the following most closely parallels the logical structure above?- a)The shoes store in the city must have had a bigger advertisement in the Today paper than the shoes store in the countryside. The shoes store in the city sold twice as many shoes as the shoes store in the countryside did last week, and a Today paper advertisement has been shown to increase the number of shoes sold.
- b)Studies show that fat people live shorter lives, on average, than thin people do. Tom is a fat man and therefore might be expected to live a shorter life than Peter, who is a thin man.
- c)The mayor stated that all meetings would be canceled for the day if rainfall last night were greater than five inches. Therefore, since the rainfall was only four inches, we must be attending the meeting today.
- d)According to research, people with unusual math talent do not achieve their true potential unless they are given formal lessons. Therefore Jeff, who has achieved his full math potential without formal lessons must not have unusual math talent.
- e)People who like dogs also like cats. Karen does not like cats, so she must not like dogs either.
Correct answer is option 'A'. Can you explain this answer?
Studies show that children who listen too much classic music are more likely than others to become silent adults. Shawn, who is a silent adult, must have listened more classic music as a child than I did, since I am not silent.
Q. Which of the following most closely parallels the logical structure above?
a)
The shoes store in the city must have had a bigger advertisement in the Today paper than the shoes store in the countryside. The shoes store in the city sold twice as many shoes as the shoes store in the countryside did last week, and a Today paper advertisement has been shown to increase the number of shoes sold.
b)
Studies show that fat people live shorter lives, on average, than thin people do. Tom is a fat man and therefore might be expected to live a shorter life than Peter, who is a thin man.
c)
The mayor stated that all meetings would be canceled for the day if rainfall last night were greater than five inches. Therefore, since the rainfall was only four inches, we must be attending the meeting today.
d)
According to research, people with unusual math talent do not achieve their true potential unless they are given formal lessons. Therefore Jeff, who has achieved his full math potential without formal lessons must not have unusual math talent.
e)
People who like dogs also like cats. Karen does not like cats, so she must not like dogs either.
|
|
Ankita Chauhan answered |
Analysis:
Similar Logical Structure:
- The given statement presents a logical structure where a correlation between listening to classic music as a child and becoming a silent adult is established.
- It then concludes that since Shawn is a silent adult, he must have listened more to classic music as a child compared to the speaker, who is not silent.
Application to Option A:
- In option A, a similar logical structure is presented where a correlation between advertising in the Today paper and selling more shoes is established.
- It then concludes that since the shoe store in the city sold more shoes than the store in the countryside, the city store must have had a bigger advertisement in the Today paper.
Explanation of Correct Answer:
- The logical structure in option A mirrors the one in the given statement by establishing a correlation between two factors and drawing a conclusion based on that correlation.
- Just like how the speaker in the given statement assumes Shawn listened more to classic music as a child, the conclusion in option A assumes the city store had a bigger advertisement in the Today paper.
- Therefore, option A most closely parallels the logical structure provided in the given statement.
Similar Logical Structure:
- The given statement presents a logical structure where a correlation between listening to classic music as a child and becoming a silent adult is established.
- It then concludes that since Shawn is a silent adult, he must have listened more to classic music as a child compared to the speaker, who is not silent.
Application to Option A:
- In option A, a similar logical structure is presented where a correlation between advertising in the Today paper and selling more shoes is established.
- It then concludes that since the shoe store in the city sold more shoes than the store in the countryside, the city store must have had a bigger advertisement in the Today paper.
Explanation of Correct Answer:
- The logical structure in option A mirrors the one in the given statement by establishing a correlation between two factors and drawing a conclusion based on that correlation.
- Just like how the speaker in the given statement assumes Shawn listened more to classic music as a child, the conclusion in option A assumes the city store had a bigger advertisement in the Today paper.
- Therefore, option A most closely parallels the logical structure provided in the given statement.
A merchant who marked his goods up by 50% subsequently offered a discount of 20% on the marked price. What is the percentage profit that the merchant make after offering the discount?- a)30%
- b)125%
- c)25%
- d)20%
- e)16.66%
Correct answer is option 'D'. Can you explain this answer?
A merchant who marked his goods up by 50% subsequently offered a discount of 20% on the marked price. What is the percentage profit that the merchant make after offering the discount?
a)
30%
b)
125%
c)
25%
d)
20%
e)
16.66%
|
|
EduRev GMAT answered |
Step 1: Assume cost price and find marked price
Approach: Assume cost price as $100.
Let the cost price of the goods to be $ 100.
The merchant marks his goods up by 50%.
Therefore, his marked price = cost price + mark up.
Marked price = $100 + 50% of $100 = 100 + 50 = $150.
The merchant marks his goods up by 50%.
Therefore, his marked price = cost price + mark up.
Marked price = $100 + 50% of $100 = 100 + 50 = $150.
Step 2: Find the discount offered and Selling price
The merchant offers a discount of 20% on the marked price.
Discount offered = 20% of 150 = $30.
Therefore, the goods are finally sold at $150 − $30 = $ 120.
Discount offered = 20% of 150 = $30.
Therefore, the goods are finally sold at $150 − $30 = $ 120.
Cost price is $100 and final selling price is $120.
Therefore, profit made = $20 on the cost price of $ 100.
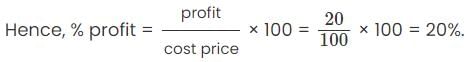
Merchant made a profit of 20%
Therefore, profit made = $20 on the cost price of $ 100.
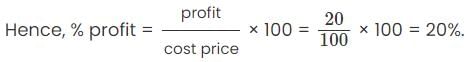
Merchant made a profit of 20%
Choice D is the correct answer.
Is y an integer?Statement 1: y3 is an integer
Statement 2: 3y is an integer- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
- c)Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
- d)EACH statement ALONE is sufficient
- e)Statements (1) and (2) TOGETHER are NOT sufficient
Correct answer is option 'C'. Can you explain this answer?
Is y an integer?
Statement 1: y3 is an integer
Statement 2: 3y is an integer
Statement 2: 3y is an integer
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
c)
Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
d)
EACH statement ALONE is sufficient
e)
Statements (1) and (2) TOGETHER are NOT sufficient
|
|
Kirti Roy answered |
Understanding the Problem
To determine whether y is an integer, we need to analyze the given statements separately and together.
Statement 1: y³ is an integer
- If y³ is an integer, it means that y could potentially be a rational number, but not necessarily an integer.
- For example, if y = 1/2, then y³ = (1/2)³ = 1/8, which is not an integer.
- Therefore, Statement 1 alone is insufficient.
Statement 2: 3y is an integer
- If 3y is an integer, then y must be of the form k/3, where k is an integer.
- For instance, if y = 1/3, then 3y = 1, which is an integer, but if y = 1/6, then 3y = 1/2, which is not an integer.
- Thus, Statement 2 alone is also insufficient.
Combining Both Statements
- From Statement 1, we know y³ is an integer, indicating y could be rational.
- From Statement 2, where 3y is an integer, we can deduce y must be a rational number of the form k/3.
- If we take the cube root of an integer (y³) and it must also satisfy the integer condition in Statement 2, we can analyze further:
- If 3y = m (an integer), then y = m/3, meaning for y³ to be an integer, m must be a multiple of 3.
- This ensures that y itself must be an integer.
Conclusion
- Therefore, when both statements are combined, they provide sufficient information to conclude that y must be an integer.
- The correct answer is option 'C': Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
To determine whether y is an integer, we need to analyze the given statements separately and together.
Statement 1: y³ is an integer
- If y³ is an integer, it means that y could potentially be a rational number, but not necessarily an integer.
- For example, if y = 1/2, then y³ = (1/2)³ = 1/8, which is not an integer.
- Therefore, Statement 1 alone is insufficient.
Statement 2: 3y is an integer
- If 3y is an integer, then y must be of the form k/3, where k is an integer.
- For instance, if y = 1/3, then 3y = 1, which is an integer, but if y = 1/6, then 3y = 1/2, which is not an integer.
- Thus, Statement 2 alone is also insufficient.
Combining Both Statements
- From Statement 1, we know y³ is an integer, indicating y could be rational.
- From Statement 2, where 3y is an integer, we can deduce y must be a rational number of the form k/3.
- If we take the cube root of an integer (y³) and it must also satisfy the integer condition in Statement 2, we can analyze further:
- If 3y = m (an integer), then y = m/3, meaning for y³ to be an integer, m must be a multiple of 3.
- This ensures that y itself must be an integer.
Conclusion
- Therefore, when both statements are combined, they provide sufficient information to conclude that y must be an integer.
- The correct answer is option 'C': Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
An analysis of the monthly incentives received by 5 salesmen : The mean and median of the incentives is $7000. The only mode among the observations is $12,000. Incentives paid to each salesman were in full thousands. What is the difference between the highest and the lowest incentive received by the 5 salesmen in the month?- a)$4000
- b)$13,000
- c)$9000
- d)$5000
- e)$11,000
Correct answer is option 'E'. Can you explain this answer?
An analysis of the monthly incentives received by 5 salesmen : The mean and median of the incentives is $7000. The only mode among the observations is $12,000. Incentives paid to each salesman were in full thousands. What is the difference between the highest and the lowest incentive received by the 5 salesmen in the month?
a)
$4000
b)
$13,000
c)
$9000
d)
$5000
e)
$11,000
|
|
EduRev GMAT answered |
Hints to solve this question:
- Mean and Median = $7000. So, find the third highest incentive.
- Only one mode; mode = $12,000.
- Use hint 1 and hint 2 to find how many executives have got $12,000.
- Now compute the sum of incentives got by those who got neither $7000 nor $12000.
Step 1: Understanding the given data
- The arithmetic mean of the incentives is $7000.
- The median of the incentives is also $7000.
- There is only one mode and the mode is $12,000.
Step 2: Decoding Mean and Median
Let their incentives be a, b, c, d, and e such that a ≤ b ≤ c ≤ d ≤ e
Therefore, the median of these values is 'c'.
The median incentive is $7000. So, c = $7000.
The median incentive is $7000. So, c = $7000.
Essentially, the incentives are __ __ 7000 __ __
The arithmetic mean of the incentives is $7000.
So, the sum of their incentives a + b + c + d + e = 5 * 7000 = $35,000
So, the sum of their incentives a + b + c + d + e = 5 * 7000 = $35,000
Step 3: Decoding Mode
There is only one mode amongst these 5 observations.
The mode is that value that appears with the maximum frequency.
Hence, $12,000 is the incentive received by the most number of salesmen.
The mode is that value that appears with the maximum frequency.
Hence, $12,000 is the incentive received by the most number of salesmen.
So, the incentives are __ __ 7000, 12000, 12000
Step 4: Putting it all together
The incentive that c has got is $7000
The incentive received by d and e are 12,000 each
The incentive received by d and e are 12,000 each
Therefore, c + d + e = 7000 + 12,000 + 12,000 = $31,000
Hence, a + b = 35,000 - 31,000 = $4000
Hence, a + b = 35,000 - 31,000 = $4000
As there is only one mode, the incentives received by a and b have to be different.
So, a received $1000 and b received $3000.
So, a received $1000 and b received $3000.
Maximum incentive: $12,000
Minimum incentive: $1000
Difference between maximum and minimum incentive: $11,000
Minimum incentive: $1000
Difference between maximum and minimum incentive: $11,000
Choice E is the correct answer.
Direction: Read the following Passage and Answer the following Question.In the world of modern technology, the race to develop quantum computers has become the new gold rush. While classical computers have driven the digital age, quantum computers hold the promise of solving problems beyond the reach of classical systems. This race, however, is not just about technological superiority; it's a strategic chess game involving national pride and potential economic supremacy.The United States and China have emerged as the front-runners in this race. The U.S., with its long history of technological innovation, has poured billions into research and development. Silicon Valley giants like Google and IBM are in a fierce competition to build the first fully functional quantum computer. On the other hand, China's ambitious national strategy has led to significant advancements, including the launch of the world's first quantum satellite.At the heart of this competition lies the principle of quantum supremacy - the point at which a quantum computer can perform a calculation that is impossible for a classical computer. Achieving this would not only be a scientific breakthrough but also have profound implications for cybersecurity, as quantum computers can potentially break many of the encryption methods currently in use.Despite the excitement, there are skeptics who question the practicality of quantum computing. They argue that these computers are incredibly sensitive to environmental factors and require extreme conditions to function, such as near-absolute zero temperatures. Moreover, the technology is still in its infancy, and real-world applications are years, if not decades, away.
As the race continues, one thing is certain: the arrival of quantum computing will mark a new era in the technological landscape, reshaping industries and possibly redefining global power dynamics.Q. Which of the following titles best encapsulates the main idea of the passage?- a)The Environmental Challenges of Quantum Computing
- b)The Global Race for Quantum Supremacy
- c)Silicon Valley's Dominance in Technological Innovation
- d)China's Strategies in Modern Technological Warfare
- e)The Impracticality of Quantum Computing
Correct answer is option 'B'. Can you explain this answer?
Direction: Read the following Passage and Answer the following Question.
In the world of modern technology, the race to develop quantum computers has become the new gold rush. While classical computers have driven the digital age, quantum computers hold the promise of solving problems beyond the reach of classical systems. This race, however, is not just about technological superiority; it's a strategic chess game involving national pride and potential economic supremacy.
The United States and China have emerged as the front-runners in this race. The U.S., with its long history of technological innovation, has poured billions into research and development. Silicon Valley giants like Google and IBM are in a fierce competition to build the first fully functional quantum computer. On the other hand, China's ambitious national strategy has led to significant advancements, including the launch of the world's first quantum satellite.
At the heart of this competition lies the principle of quantum supremacy - the point at which a quantum computer can perform a calculation that is impossible for a classical computer. Achieving this would not only be a scientific breakthrough but also have profound implications for cybersecurity, as quantum computers can potentially break many of the encryption methods currently in use.
Despite the excitement, there are skeptics who question the practicality of quantum computing. They argue that these computers are incredibly sensitive to environmental factors and require extreme conditions to function, such as near-absolute zero temperatures. Moreover, the technology is still in its infancy, and real-world applications are years, if not decades, away.
As the race continues, one thing is certain: the arrival of quantum computing will mark a new era in the technological landscape, reshaping industries and possibly redefining global power dynamics.
As the race continues, one thing is certain: the arrival of quantum computing will mark a new era in the technological landscape, reshaping industries and possibly redefining global power dynamics.
Q. Which of the following titles best encapsulates the main idea of the passage?
a)
The Environmental Challenges of Quantum Computing
b)
The Global Race for Quantum Supremacy
c)
Silicon Valley's Dominance in Technological Innovation
d)
China's Strategies in Modern Technological Warfare
e)
The Impracticality of Quantum Computing
|
|
Arka Basu answered |
Explanation:
Main Idea:
The passage discusses the global race for quantum supremacy between the United States and China, highlighting the technological advancements, strategic importance, and potential implications of quantum computing.
Key Points:
- The race for quantum computers is compared to a modern gold rush, with the promise of solving problems beyond classical systems.
- The competition involves national pride and economic supremacy, with the U.S. and China emerging as front-runners.
- The concept of quantum supremacy, where quantum computers outperform classical ones, is a central focus.
- While there are skeptics about the practicality of quantum computing due to environmental factors and technological infancy, the excitement and potential are undeniable.
- Quantum computing is expected to reshape industries and global power dynamics.
Conclusion:
The title "The Global Race for Quantum Supremacy" best encapsulates the main idea of the passage as it emphasizes the competitive nature, strategic implications, and potential breakthroughs associated with the development of quantum computers on a global scale.
Main Idea:
The passage discusses the global race for quantum supremacy between the United States and China, highlighting the technological advancements, strategic importance, and potential implications of quantum computing.
Key Points:
- The race for quantum computers is compared to a modern gold rush, with the promise of solving problems beyond classical systems.
- The competition involves national pride and economic supremacy, with the U.S. and China emerging as front-runners.
- The concept of quantum supremacy, where quantum computers outperform classical ones, is a central focus.
- While there are skeptics about the practicality of quantum computing due to environmental factors and technological infancy, the excitement and potential are undeniable.
- Quantum computing is expected to reshape industries and global power dynamics.
Conclusion:
The title "The Global Race for Quantum Supremacy" best encapsulates the main idea of the passage as it emphasizes the competitive nature, strategic implications, and potential breakthroughs associated with the development of quantum computers on a global scale.
Direction: Read the following Passage and Answer the following Question.Is there any knowledge in the world which is so certain that no reasonable man could doubt it? This question, which at first sight might not seem difficult, is really one of the most difficult that can be asked. When we have realized the obstacles in the way of a straightforward and confident answer, we shall be well launched on the study of philosophy—for philosophy is merely the attempt to answer such ultimate questions, not carelessly and dogmatically, as we do in ordinary life and even in the sciences, but critically, after exploring all that makes such questions puzzling, and after realizing all the vagueness and confusion that underlie our ordinary ideas.In daily life, we assume as certain many things which, on a closer scrutiny, are found to be so full of apparent contradictions that only a great amount of thought enables us to know what it is that we really may believe. In the search for certainty, it is natural to begin with our present experiences, and in some sense, no doubt, knowledge is to be derived from them. But any statement as to what it is that our immediate experiences make us know is very likely to be wrong. It seems to me that I am now sitting in a chair, at a table of a certain shape, on which I see sheets of paper with writing or print. By turning my head I see out of the window buildings and clouds and the sun. I believe that the sun is about ninety-three million miles from the earth; that it is a hot globe many times bigger than the earth; that, owing to the earth's rotation, it rises every morning, and will continue to do so for an indefinite time in the future. I believe that, if any other normal person comes into my room, he will see the same chairs and tables and books and papers as I see, and that the table which I see is the same as the table which I feel pressing against my arm. All this seems to be so evident as to be hardly worth stating, except in answer to a man who doubts whether I know anything. Yet all this may be reasonably doubted, and all of it requires much careful discussion before we can be sure that we have stated it in a form that is wholly true.Q. The first paragraph of the passage is primarily concerned with?- a)discussing what is the most difficult question to answer in this world
- b)defining and differentiating a field of study
- c)stating that we tend to get careless while answering difficult questions
- d)concluding that what appears to be a fact could actually be doubted
- e)proving the superiority of a particular field of study
Correct answer is option 'B'. Can you explain this answer?
Direction: Read the following Passage and Answer the following Question.
Is there any knowledge in the world which is so certain that no reasonable man could doubt it? This question, which at first sight might not seem difficult, is really one of the most difficult that can be asked. When we have realized the obstacles in the way of a straightforward and confident answer, we shall be well launched on the study of philosophy—for philosophy is merely the attempt to answer such ultimate questions, not carelessly and dogmatically, as we do in ordinary life and even in the sciences, but critically, after exploring all that makes such questions puzzling, and after realizing all the vagueness and confusion that underlie our ordinary ideas.
In daily life, we assume as certain many things which, on a closer scrutiny, are found to be so full of apparent contradictions that only a great amount of thought enables us to know what it is that we really may believe. In the search for certainty, it is natural to begin with our present experiences, and in some sense, no doubt, knowledge is to be derived from them. But any statement as to what it is that our immediate experiences make us know is very likely to be wrong. It seems to me that I am now sitting in a chair, at a table of a certain shape, on which I see sheets of paper with writing or print. By turning my head I see out of the window buildings and clouds and the sun. I believe that the sun is about ninety-three million miles from the earth; that it is a hot globe many times bigger than the earth; that, owing to the earth's rotation, it rises every morning, and will continue to do so for an indefinite time in the future. I believe that, if any other normal person comes into my room, he will see the same chairs and tables and books and papers as I see, and that the table which I see is the same as the table which I feel pressing against my arm. All this seems to be so evident as to be hardly worth stating, except in answer to a man who doubts whether I know anything. Yet all this may be reasonably doubted, and all of it requires much careful discussion before we can be sure that we have stated it in a form that is wholly true.
Q. The first paragraph of the passage is primarily concerned with?
a)
discussing what is the most difficult question to answer in this world
b)
defining and differentiating a field of study
c)
stating that we tend to get careless while answering difficult questions
d)
concluding that what appears to be a fact could actually be doubted
e)
proving the superiority of a particular field of study
|
|
EduRev GMAT answered |
The first para defines what is it that philosophy tries to do and also differentiates it from the other sciences. Thus (B) should be the correct answer.
A: While the passage does start off with this thought, the primary concern is to link this to the study of Philosophy
C: Too specific to be the main purpose
D: While the para does say this, this is not the main purpose but just a specific detail
E: The author is not proving anything in the 1st para
A: While the passage does start off with this thought, the primary concern is to link this to the study of Philosophy
C: Too specific to be the main purpose
D: While the para does say this, this is not the main purpose but just a specific detail
E: The author is not proving anything in the 1st para
What is the value of X, if X and Y are two distinct integers and their product is 30?Statement 1: X is an odd integerStatement 2: X > Y- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
- c)Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
- d)EACH statement ALONE is sufficient
- e)Statements (1) and (2) TOGETHER are NOT sufficient
Correct answer is option 'E'. Can you explain this answer?
What is the value of X, if X and Y are two distinct integers and their product is 30?
Statement 1: X is an odd integer
Statement 2: X > Y
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
c)
Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
d)
EACH statement ALONE is sufficient
e)
Statements (1) and (2) TOGETHER are NOT sufficient
|
|
EduRev GMAT answered |
Step 1: Understand the Question Stem
What kind of an answer will the question fetch?
The question is a "What is the value?" question. The answer has to be a value, a number for 'X'.
The question is a "What is the value?" question. The answer has to be a value, a number for 'X'.
When is the data sufficient?
The data is sufficient if we are able to get a UNIQUE answer for the value of 'X' from the information in the statements.
The data is sufficient if we are able to get a UNIQUE answer for the value of 'X' from the information in the statements.
Do we have any additional information about 'X' or 'Y' from the question stem?
From the question, we know that both X and Y are distinct integers and their product is 30.
30 can be obtained as a product of two distinct integers in the following ways.
From the question, we know that both X and Y are distinct integers and their product is 30.
30 can be obtained as a product of two distinct integers in the following ways.
Values that satisfy X × Y = 30
Step 2: Evaluate Statement (1) ALONE: X is an odd integer
From this statement, we know that the value of X is odd.
Therefore, X can be one of the following values: 1, -1, 3, -3, 5, -5.
So, using information in statement 1 we will not be able to deduce a UNIQUE value for X.
Therefore, X can be one of the following values: 1, -1, 3, -3, 5, -5.
So, using information in statement 1 we will not be able to deduce a UNIQUE value for X.
Statement 1 ALONE is NOT sufficient.
Eliminate choices A and D. Choices narrow down to B, C, or E.
Eliminate choices A and D. Choices narrow down to B, C, or E.
Step 3: Evaluate Statement (2) ALONE: X > Y
From this statement, we know that the value of X > Y.
From the combinations listed in the table above, X can take more than one value. Here are two possibilities: X could be 10 and Y could be 3. Or X could be 30 and Y could be 1.
Hence, using information in statement 2, we will not be able to find a UNIQUE value for X.
From the combinations listed in the table above, X can take more than one value. Here are two possibilities: X could be 10 and Y could be 3. Or X could be 30 and Y could be 1.
Hence, using information in statement 2, we will not be able to find a UNIQUE value for X.
Statement 2 ALONE is NOT sufficient.
Eliminate choice B. Choices narrow down to C or E.
Eliminate choice B. Choices narrow down to C or E.
Step 4: Evaluate Statements (1) & (2) Together: X is an odd integer and X > Y
Values of X and Y that satisfy both the conditions are
More than one value exists for X. Because we are not able to deduce a UNIQUE value for X using information provided in the two statements together, the given data is NOT sufficient.
Statements TOGETHER are NOT SUFFICIENT. Choice E is the answer.
In the twentieth century, the visual arts have embarked on major experimentation, from cubism to expressionism. While tastes always vary, there are certainly some people who find beautiful objects of each of the art movements of the first half of the twentieth century. In the latter half of the twentieth century, though, most works are so abstract or shocking that neither the critic nor the general public uses the word "beautiful" to describe them: indeed, sometimes late twentieth-century artists have, as one of their expressed goals, the creation of a work that no one could find beautiful. Whatever these artists are creating may be intellectually engaging at some level, but it is no longer art.Q. Which of the following is an assumption that supports drawing the conclusion above from the reasons given for that conclusion?- a)Art critics generally have a different appraisal of a work of art than does the general public
- b)The meaning of any work of art is defined entirely by the ideas of the artist who created it.
- c)Beauty is a defining quality of art.
- d)All art movements of the latter half of the twentieth century are responses to the movements of the first half of the century.
- e)It is not possible for any work to be simultaneously beautiful and intellectually engaging.
Correct answer is option 'C'. Can you explain this answer?
In the twentieth century, the visual arts have embarked on major experimentation, from cubism to expressionism. While tastes always vary, there are certainly some people who find beautiful objects of each of the art movements of the first half of the twentieth century. In the latter half of the twentieth century, though, most works are so abstract or shocking that neither the critic nor the general public uses the word "beautiful" to describe them: indeed, sometimes late twentieth-century artists have, as one of their expressed goals, the creation of a work that no one could find beautiful. Whatever these artists are creating may be intellectually engaging at some level, but it is no longer art.
Q. Which of the following is an assumption that supports drawing the conclusion above from the reasons given for that conclusion?
a)
Art critics generally have a different appraisal of a work of art than does the general public
b)
The meaning of any work of art is defined entirely by the ideas of the artist who created it.
c)
Beauty is a defining quality of art.
d)
All art movements of the latter half of the twentieth century are responses to the movements of the first half of the century.
e)
It is not possible for any work to be simultaneously beautiful and intellectually engaging.
|
|
Advait Roy answered |
Assumption Explanation:
Beauty is a defining quality of art:
- The assumption that beauty is a defining quality of art supports the conclusion that late twentieth-century works that are not considered beautiful are not art.
- If beauty is considered a defining quality of art, then works that do not possess this quality may not be classified as art.
- This assumption implies that art is intrinsically linked to beauty, and if a work does not possess this quality, it may not be considered art.
Therefore, the assumption that beauty is a defining quality of art supports the conclusion that late twentieth-century works that are not considered beautiful may not be classified as art.
Ann invested a certain sum of money in a bank that paid simple interest. The amount grew to $240 at the end of 2 years. She waited for another 3 years and got a final amount of $300. What was the principal amount that she invested at the beginning?- a)$200
- b)$150
- c)$210
- d)$175
- e)Insufficient data
Correct answer is option 'A'. Can you explain this answer?
Ann invested a certain sum of money in a bank that paid simple interest. The amount grew to $240 at the end of 2 years. She waited for another 3 years and got a final amount of $300. What was the principal amount that she invested at the beginning?
a)
$200
b)
$150
c)
$210
d)
$175
e)
Insufficient data
|
|
EduRev GMAT answered |
Concept: Simple interest earned remains same year after year.
At the end of 2 years: Value of investment (Amount) = $240
At the end of another 3 years: Value of investment (Amount) = $300
In 3 years, the sum grew by $60.
So interest for 3 years = $60.
Because Ann invested in simple interest, interest earned each year = $20.
At the end of another 3 years: Value of investment (Amount) = $300
In 3 years, the sum grew by $60.
So interest for 3 years = $60.
Because Ann invested in simple interest, interest earned each year = $20.
Interest earned in the first 2 years = 2 × 20 = $40.
Therefore, principal = Sum at the end of 2 years - $40 = $240 - $40 = $200.
Principal invested $200
Therefore, principal = Sum at the end of 2 years - $40 = $240 - $40 = $200.
Principal invested $200
Choice A is the correct answer.
A can complete a project in 20 days and B can complete the same project in 30 days. If A and B start working on the project together and A quits 10 days before the project is completed, in how many days will the project be completed?- a)18 days
- b)27 days
- c)26.67 days
- d)16 days
- e)12 days
Correct answer is option 'A'. Can you explain this answer?
A can complete a project in 20 days and B can complete the same project in 30 days. If A and B start working on the project together and A quits 10 days before the project is completed, in how many days will the project be completed?
a)
18 days
b)
27 days
c)
26.67 days
d)
16 days
e)
12 days
|
|
Ankita Chauhan answered |
Understanding the Problem
To solve this problem, we need to understand the individual work rates of A and B, and how their combined work rate changes when A quits 10 days before the project is completed.
Solving the Problem
1. Work Rates of A and B:
- A completes the project in 20 days, so A's work rate is 1/20 of the project per day.
- B completes the project in 30 days, so B's work rate is 1/30 of the project per day.
2. Combined Work Rate:
- When A and B work together, their combined work rate is the sum of their individual work rates.
- Therefore, A and B's combined work rate is 1/20 + 1/30 = 1/12 of the project per day.
3. Work Done by A before Quitting:
- Since A quits 10 days before the project is completed, A works for 10 days.
- In 10 days, A completes 10 * (1/20) = 1/2 of the project.
4. Remaining Work:
- After A quits, B is left to complete the remaining 1/2 of the project.
- With a combined work rate of 1/12 per day, B will take 1/2 / (1/12) = 6 days to complete the remaining work.
5. Total Time to Complete the Project:
- A worked for 10 days and B worked for 6 days after A quit, so the total time taken to complete the project is 10 + 6 = 16 days.
Therefore, the project will be completed in 16 days, which aligns with option 'A' as the correct answer.
To solve this problem, we need to understand the individual work rates of A and B, and how their combined work rate changes when A quits 10 days before the project is completed.
Solving the Problem
1. Work Rates of A and B:
- A completes the project in 20 days, so A's work rate is 1/20 of the project per day.
- B completes the project in 30 days, so B's work rate is 1/30 of the project per day.
2. Combined Work Rate:
- When A and B work together, their combined work rate is the sum of their individual work rates.
- Therefore, A and B's combined work rate is 1/20 + 1/30 = 1/12 of the project per day.
3. Work Done by A before Quitting:
- Since A quits 10 days before the project is completed, A works for 10 days.
- In 10 days, A completes 10 * (1/20) = 1/2 of the project.
4. Remaining Work:
- After A quits, B is left to complete the remaining 1/2 of the project.
- With a combined work rate of 1/12 per day, B will take 1/2 / (1/12) = 6 days to complete the remaining work.
5. Total Time to Complete the Project:
- A worked for 10 days and B worked for 6 days after A quit, so the total time taken to complete the project is 10 + 6 = 16 days.
Therefore, the project will be completed in 16 days, which aligns with option 'A' as the correct answer.
Ram, who is half as efficient as Krish, will take 24 days to complete a task if he worked alone. If Ram and Krish worked together, how long will they take to complete the task?- a)16 days
- b)12 days
- c)8 days
- d)6 days
- e)18 days
Correct answer is option 'C'. Can you explain this answer?
Ram, who is half as efficient as Krish, will take 24 days to complete a task if he worked alone. If Ram and Krish worked together, how long will they take to complete the task?
a)
16 days
b)
12 days
c)
8 days
d)
6 days
e)
18 days
|
|
EduRev GMAT answered |
Ram takes 24 days to complete the task, if he works alone.
Krish is twice as efficient as Ram is. So, working alone, Krish will take half the time to complete the task.i.e., 12 days.
Krish is twice as efficient as Ram is. So, working alone, Krish will take half the time to complete the task.i.e., 12 days.
Ram will complete 1/24th of the task in a day.
Krish will complete 1/12th of the task in a day.
When they work together, they will complete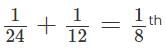
of the task in a day.
Krish will complete 1/12th of the task in a day.
When they work together, they will complete
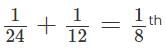of the task in a day.Therefore, when they work together they will complete the task in 8 days.
Choice C is the correct answer.
Direction: Read the following Passage and Answer the following Question.“Strange Bedfellows!” lamented the title of a recent letter to Museum News, in which a certain Harriet Sherman excoriated the National Gallery of Art in Washington for its handling of tickets to the much-ballyhooed “Van Gogh’s van Goghs” exhibit. A huge proportion of the 200,000 free tickets were snatched up by the opportunists in the dead of winter, who then scalped those tickets at $85 apiece to less hardy connoiseurs.Yet, Sherman’s bedfellows are far from strange. Art, despite its religious and magical origins, very soon became a commercial venture. From bourgeois patrons funding art they barely understood in order to share their protegee’s prestige, to museum curators stage-managing the cult of artists in order to enhance the market value of museum holdings, entrepreneurs have found validation and profit in big-name art. Speculators, thieves, and promoters long ago created and fed a market where cultural icons could be traded like commodities.This trend toward commodification of high-brow art took an ominous, if predictable, turn in the 1980s during the Japanese “bubble economy.” At a time when Japanese share prices more than doubled, individual tycoons and industrial giants alike invested record amounts in some of the West’s greatest masterpieces. Ryoei Saito, for example, purchased van Gogh’s Portrait of Dr. Gachet for a record-breaking $82.5 million. The work, then on loan to the Metropolitan Museum of Modern Art, suddenly vanished from the public domain. Later learning that he owed the Japanese government $24 million in taxes, Saito remarked that he would have the paining cremated with him to spare his heirs the inheritance tax. This statement, which he later dismissed as a joke, alarmed and enraged many. A representative of the Van Gogh museum, conceding that he had no legal redress, made an ethical appeal to Mr. Saito, asserting, “a work of art remains the possession of the world at large.”Ethical appeals notwithstanding, great art will increasingly devolve into big business. Firstly, great art can only be certified by its market value. Moreover, the “world at large” hasn’t the means of acquisition. Only one museum currently has the funding to contend for the best pieces–the J. Paul Getty Museum, founded by the billionaire oilman. The art may disappear into private hands, but its transfer will disseminate once static fortunes into the hands of various investors, collectors, and occasionally the artist.Q. It can be inferred from the passage that Harriet Sherman would be most likely to agree with which of the following statements regarding admission to museum exhibits?- a)Tickets should be available on a first-come-first-served basis.
- b)Those with a genuine interest in art should not have to pay inflated prices.
- c)Museums need the income from ticket sales in order to buy great art.
- d)Tickets should be distributed without prior announcement.
- e)No one should be able to purchase more than one or two tickets.
Correct answer is option 'B'. Can you explain this answer?
Direction: Read the following Passage and Answer the following Question.
“Strange Bedfellows!” lamented the title of a recent letter to Museum News, in which a certain Harriet Sherman excoriated the National Gallery of Art in Washington for its handling of tickets to the much-ballyhooed “Van Gogh’s van Goghs” exhibit. A huge proportion of the 200,000 free tickets were snatched up by the opportunists in the dead of winter, who then scalped those tickets at $85 apiece to less hardy connoiseurs.
Yet, Sherman’s bedfellows are far from strange. Art, despite its religious and magical origins, very soon became a commercial venture. From bourgeois patrons funding art they barely understood in order to share their protegee’s prestige, to museum curators stage-managing the cult of artists in order to enhance the market value of museum holdings, entrepreneurs have found validation and profit in big-name art. Speculators, thieves, and promoters long ago created and fed a market where cultural icons could be traded like commodities.
This trend toward commodification of high-brow art took an ominous, if predictable, turn in the 1980s during the Japanese “bubble economy.” At a time when Japanese share prices more than doubled, individual tycoons and industrial giants alike invested record amounts in some of the West’s greatest masterpieces. Ryoei Saito, for example, purchased van Gogh’s Portrait of Dr. Gachet for a record-breaking $82.5 million. The work, then on loan to the Metropolitan Museum of Modern Art, suddenly vanished from the public domain. Later learning that he owed the Japanese government $24 million in taxes, Saito remarked that he would have the paining cremated with him to spare his heirs the inheritance tax. This statement, which he later dismissed as a joke, alarmed and enraged many. A representative of the Van Gogh museum, conceding that he had no legal redress, made an ethical appeal to Mr. Saito, asserting, “a work of art remains the possession of the world at large.”
Ethical appeals notwithstanding, great art will increasingly devolve into big business. Firstly, great art can only be certified by its market value. Moreover, the “world at large” hasn’t the means of acquisition. Only one museum currently has the funding to contend for the best pieces–the J. Paul Getty Museum, founded by the billionaire oilman. The art may disappear into private hands, but its transfer will disseminate once static fortunes into the hands of various investors, collectors, and occasionally the artist.
Q. It can be inferred from the passage that Harriet Sherman would be most likely to agree with which of the following statements regarding admission to museum exhibits?
a)
Tickets should be available on a first-come-first-served basis.
b)
Those with a genuine interest in art should not have to pay inflated prices.
c)
Museums need the income from ticket sales in order to buy great art.
d)
Tickets should be distributed without prior announcement.
e)
No one should be able to purchase more than one or two tickets.
|
|
EduRev GMAT answered |
This is an INFERENCE question. It’s clear from the word ‘inferred’, of course, but the phrase ‘most likely to agree with’ is also a powerful indicator that you have encountered an Inference question on the GMAT. Use the notes that you have made for Topic, Scope, and Purpose, and look for an answer choice that is directly supported by the passage.
In order to answer this Inference question, use your passage map to locate where Sherman’s argument was presented – in the first paragraph. Sherman was angry because people with a genuine interest in art were forced to pay very high prices for tickets that were supposed to be free.
Choice (A) is a 180-degree reversal of her point: it was the first-come-first-served rule that allowed opportunists to get so many tickets.
Choice (B) is a strong choice, and is supported by the fact that Sherman was angry that those with a genuine interest in art had to pay high ticket prices.
Choice (C) may be true, but it is beyond the scope of this passage.
Choices (D) and (E) represent possible solutions to the problem raised by Sherman, but there is no support in the passage that either Sherman of the author would find them satisfactory.
Choice (B) is the correct answer.
Direction: Read the following Passage and Answer the following Question.“Strange Bedfellows!” lamented the title of a recent letter to Museum News, in which a certain Harriet Sherman excoriated the National Gallery of Art in Washington for its handling of tickets to the much-ballyhooed “Van Gogh’s van Goghs” exhibit. A huge proportion of the 200,000 free tickets were snatched up by the opportunists in the dead of winter, who then scalped those tickets at $85 apiece to less hardy connoiseurs.Yet, Sherman’s bedfellows are far from strange. Art, despite its religious and magical origins, very soon became a commercial venture. From bourgeois patrons funding art they barely understood in order to share their protegee’s prestige, to museum curators stage-managing the cult of artists in order to enhance the market value of museum holdings, entrepreneurs have found validation and profit in big-name art. Speculators, thieves, and promoters long ago created and fed a market where cultural icons could be traded like commodities.This trend toward commodification of high-brow art took an ominous, if predictable, turn in the 1980s during the Japanese “bubble economy.” At a time when Japanese share prices more than doubled, individual tycoons and industrial giants alike invested record amounts in some of the West’s greatest masterpieces. Ryoei Saito, for example, purchased van Gogh’s Portrait of Dr. Gachet for a record-breaking $82.5 million. The work, then on loan to the Metropolitan Museum of Modern Art, suddenly vanished from the public domain. Later learning that he owed the Japanese government $24 million in taxes, Saito remarked that he would have the paining cremated with him to spare his heirs the inheritance tax. This statement, which he later dismissed as a joke, alarmed and enraged many. A representative of the Van Gogh museum, conceding that he had no legal redress, made an ethical appeal to Mr. Saito, asserting, “a work of art remains the possession of the world at large.”Ethical appeals notwithstanding, great art will increasingly devolve into big business. Firstly, great art can only be certified by its market value. Moreover, the “world at large” hasn’t the means of acquisition. Only one museum currently has the funding to contend for the best pieces–the J. Paul Getty Museum, founded by the billionaire oilman. The art may disappear into private hands, but its transfer will disseminate once static fortunes into the hands of various investors, collectors, and occasionally the artist.Q. The passage supplies information for answering which of the following questions?- a)Who owned van Gogh’s Portrait of Dr. Gachet prior to its purchase by Saito?
- b)Where did Saito exhibit van Gogh’s Portrait of Dr. Gachet?
- c)Which museum proposed to purchase van Gogh’s Portrait of Dr. Gachet from Saito?
- d)Did the Van Gogh Museum threaten legal action in response to reports that Saito intended to destroy van Gogh’s Portrait of Dr. Gachet?
- e)Did Saito actually intend to destroy van Gogh’s Portrait of Dr. Gachet?
Correct answer is option 'D'. Can you explain this answer?
Direction: Read the following Passage and Answer the following Question.
“Strange Bedfellows!” lamented the title of a recent letter to Museum News, in which a certain Harriet Sherman excoriated the National Gallery of Art in Washington for its handling of tickets to the much-ballyhooed “Van Gogh’s van Goghs” exhibit. A huge proportion of the 200,000 free tickets were snatched up by the opportunists in the dead of winter, who then scalped those tickets at $85 apiece to less hardy connoiseurs.
Yet, Sherman’s bedfellows are far from strange. Art, despite its religious and magical origins, very soon became a commercial venture. From bourgeois patrons funding art they barely understood in order to share their protegee’s prestige, to museum curators stage-managing the cult of artists in order to enhance the market value of museum holdings, entrepreneurs have found validation and profit in big-name art. Speculators, thieves, and promoters long ago created and fed a market where cultural icons could be traded like commodities.
This trend toward commodification of high-brow art took an ominous, if predictable, turn in the 1980s during the Japanese “bubble economy.” At a time when Japanese share prices more than doubled, individual tycoons and industrial giants alike invested record amounts in some of the West’s greatest masterpieces. Ryoei Saito, for example, purchased van Gogh’s Portrait of Dr. Gachet for a record-breaking $82.5 million. The work, then on loan to the Metropolitan Museum of Modern Art, suddenly vanished from the public domain. Later learning that he owed the Japanese government $24 million in taxes, Saito remarked that he would have the paining cremated with him to spare his heirs the inheritance tax. This statement, which he later dismissed as a joke, alarmed and enraged many. A representative of the Van Gogh museum, conceding that he had no legal redress, made an ethical appeal to Mr. Saito, asserting, “a work of art remains the possession of the world at large.”
Ethical appeals notwithstanding, great art will increasingly devolve into big business. Firstly, great art can only be certified by its market value. Moreover, the “world at large” hasn’t the means of acquisition. Only one museum currently has the funding to contend for the best pieces–the J. Paul Getty Museum, founded by the billionaire oilman. The art may disappear into private hands, but its transfer will disseminate once static fortunes into the hands of various investors, collectors, and occasionally the artist.
Q. The passage supplies information for answering which of the following questions?
a)
Who owned van Gogh’s Portrait of Dr. Gachet prior to its purchase by Saito?
b)
Where did Saito exhibit van Gogh’s Portrait of Dr. Gachet?
c)
Which museum proposed to purchase van Gogh’s Portrait of Dr. Gachet from Saito?
d)
Did the Van Gogh Museum threaten legal action in response to reports that Saito intended to destroy van Gogh’s Portrait of Dr. Gachet?
e)
Did Saito actually intend to destroy van Gogh’s Portrait of Dr. Gachet?
|
|
EduRev GMAT answered |
This is a DETAIL question. To answer detail questions, use the passage map to find the appropriate paragraph to find the relevant details, then go back and research each answer choice to avoid distortions and other common wrong answer traps.
To answer this open-ended detail question, examine each choice. However, your passage map tells you that you can limit your research of all five options to Paragraph 3.
Choice (A): do you know who owned van Gogh’s Portrait of Dr. Gachet prior to its purchase by Saito? No, you are only told that it was on loan to a museum. You are told nothing about Saito’s exhibiting the portrait; in fact, it is implied that he did not exhibit it at all. Therefore, choice (B) is wrong.
Choice (C) is incorrect because there is no mention of anyone proposing to purchase the portrait from Saito.
Choice (D) is the correct answer.
You are told that the representative of the Van Gogh Museum admitted that “he had no legal redress”; this means that no legal action could be threatened. The passage offers us no information that would answer the question posed in choice (E): the author reports both the threat to destroy the portrait, and Saito’s dismissal of that threat as a “joke,” but the author does not tell you what to believe about this point.
A minor league baseball franchise experienced a drop in attendance this week after they suffered three losses by margins of ten runs or more last week. Many spectators of those games wrote letters to the editors of the local sporting news, complaining of the poor play of the team in those three losses. Nevertheless, the front office of this baseball franchise maintains that the team's poor play in those three losses has nothing to do with this week's decline in attendance.Q. Which of the following, if true, most strongly supports the position held by the front office of the baseball franchise?- a)The spectators who wrote letters to the local sporting news were long-standing fans of this minor league baseball team.
- b)Many minor league baseball franchises attribute a drop in attendance to the quality of play of the team only after a string of losses.
- c)Other minor league teams in that region of the state reported a similar drop in attendance this week.
- d)This was not the first time this team suffered multiple lopsided losses in a single week, prompting similar letters to the local sporting news.
- e)This minor league team is over four hours from the closest major league team, so many of the minor league team's fans do not often attend major league games.
Correct answer is option 'C'. Can you explain this answer?
A minor league baseball franchise experienced a drop in attendance this week after they suffered three losses by margins of ten runs or more last week. Many spectators of those games wrote letters to the editors of the local sporting news, complaining of the poor play of the team in those three losses. Nevertheless, the front office of this baseball franchise maintains that the team's poor play in those three losses has nothing to do with this week's decline in attendance.
Q. Which of the following, if true, most strongly supports the position held by the front office of the baseball franchise?
a)
The spectators who wrote letters to the local sporting news were long-standing fans of this minor league baseball team.
b)
Many minor league baseball franchises attribute a drop in attendance to the quality of play of the team only after a string of losses.
c)
Other minor league teams in that region of the state reported a similar drop in attendance this week.
d)
This was not the first time this team suffered multiple lopsided losses in a single week, prompting similar letters to the local sporting news.
e)
This minor league team is over four hours from the closest major league team, so many of the minor league team's fans do not often attend major league games.
|
|
Mihir Nambiar answered |
Supporting the front office's position
Explanation:
- Option C states that other minor league teams in the region reported a similar drop in attendance this week.
- This information suggests that the decline in attendance is not unique to this particular franchise and may be influenced by external factors affecting all teams in the area.
- If the drop in attendance is a trend seen across multiple teams, it supports the front office's claim that the recent poor play of their team is not the primary reason for the decline.
- Therefore, option C provides evidence that the drop in attendance is not solely due to the team's performance in the previous week but rather a broader issue affecting multiple minor league teams in the region.
Explanation:
- Option C states that other minor league teams in the region reported a similar drop in attendance this week.
- This information suggests that the decline in attendance is not unique to this particular franchise and may be influenced by external factors affecting all teams in the area.
- If the drop in attendance is a trend seen across multiple teams, it supports the front office's claim that the recent poor play of their team is not the primary reason for the decline.
- Therefore, option C provides evidence that the drop in attendance is not solely due to the team's performance in the previous week but rather a broader issue affecting multiple minor league teams in the region.
How is Bill related to Betty?Statement 1: Cindy, the wife of Bill's only brother Chris does not have any siblings.Statement 2: Betty is Cindy's brother in law's wife.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
- c)Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
- d)EACH statement ALONE is sufficient
- e)Statements (1) and (2) TOGETHER are NOT sufficient
Correct answer is option 'C'. Can you explain this answer?
How is Bill related to Betty?
Statement 1: Cindy, the wife of Bill's only brother Chris does not have any siblings.
Statement 2: Betty is Cindy's brother in law's wife.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
c)
Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
d)
EACH statement ALONE is sufficient
e)
Statements (1) and (2) TOGETHER are NOT sufficient
|
|
Nikhil Khanna answered |
Understanding the Relationship
To determine how Bill is related to Betty, we examine the information provided in both statements.
Statement 1: Cindy's Sibling Situation
- Cindy is the wife of Bill's only brother, Chris.
- Cindy does not have any siblings.
This statement tells us that Chris is Bill's only brother and that there are no other siblings in Cindy's family. However, it does not provide any direct information about Betty or her relationship to Bill.
Statement 2: Betty's Connection
- Betty is Cindy's brother-in-law's wife.
From this statement, we can infer that if Cindy is married to Chris (Bill's brother), then Betty must be married to Bill (because she is referred to as Cindy's brother-in-law's wife). This implies that Betty is Bill's wife.
Combining Both Statements
When we combine the insights from both statements:
- From Statement 1, we know Bill has only one brother (Chris).
- From Statement 2, we identify that Betty is likely Bill's wife.
Thus, both statements together confirm that Betty is Bill's wife.
Conclusion
- Each statement alone provides partial information.
- Statement 1 does not mention Betty, while Statement 2 does not clarify Bill's relationship to Betty without the context from Statement 1.
Therefore, the correct answer is that both statements together are sufficient to determine the relationship, but neither statement alone is sufficient. This leads us to option 'C'.
To determine how Bill is related to Betty, we examine the information provided in both statements.
Statement 1: Cindy's Sibling Situation
- Cindy is the wife of Bill's only brother, Chris.
- Cindy does not have any siblings.
This statement tells us that Chris is Bill's only brother and that there are no other siblings in Cindy's family. However, it does not provide any direct information about Betty or her relationship to Bill.
Statement 2: Betty's Connection
- Betty is Cindy's brother-in-law's wife.
From this statement, we can infer that if Cindy is married to Chris (Bill's brother), then Betty must be married to Bill (because she is referred to as Cindy's brother-in-law's wife). This implies that Betty is Bill's wife.
Combining Both Statements
When we combine the insights from both statements:
- From Statement 1, we know Bill has only one brother (Chris).
- From Statement 2, we identify that Betty is likely Bill's wife.
Thus, both statements together confirm that Betty is Bill's wife.
Conclusion
- Each statement alone provides partial information.
- Statement 1 does not mention Betty, while Statement 2 does not clarify Bill's relationship to Betty without the context from Statement 1.
Therefore, the correct answer is that both statements together are sufficient to determine the relationship, but neither statement alone is sufficient. This leads us to option 'C'.
Direction: Read the following Passage and Answer the following Question.In the world of modern technology, the race to develop quantum computers has become the new gold rush. While classical computers have driven the digital age, quantum computers hold the promise of solving problems beyond the reach of classical systems. This race, however, is not just about technological superiority; it's a strategic chess game involving national pride and potential economic supremacy.The United States and China have emerged as the front-runners in this race. The U.S., with its long history of technological innovation, has poured billions into research and development. Silicon Valley giants like Google and IBM are in a fierce competition to build the first fully functional quantum computer. On the other hand, China's ambitious national strategy has led to significant advancements, including the launch of the world's first quantum satellite.At the heart of this competition lies the principle of quantum supremacy - the point at which a quantum computer can perform a calculation that is impossible for a classical computer. Achieving this would not only be a scientific breakthrough but also have profound implications for cybersecurity, as quantum computers can potentially break many of the encryption methods currently in use.Despite the excitement, there are skeptics who question the practicality of quantum computing. They argue that these computers are incredibly sensitive to environmental factors and require extreme conditions to function, such as near-absolute zero temperatures. Moreover, the technology is still in its infancy, and real-world applications are years, if not decades, away.
As the race continues, one thing is certain: the arrival of quantum computing will mark a new era in the technological landscape, reshaping industries and possibly redefining global power dynamics.Q. The passage provides support for which of the following statements?- a)Quantum computing will likely replace classical computing in most common applications within a few years.
- b)The United States has already achieved quantum supremacy over China.
- c)Quantum computers have the potential to revolutionize cybersecurity.
- d)Most encryption methods used today are already resistant to quantum computing.
- e)Environmental factors do not significantly impact the functioning of quantum computers.
Correct answer is option 'C'. Can you explain this answer?
Direction: Read the following Passage and Answer the following Question.
In the world of modern technology, the race to develop quantum computers has become the new gold rush. While classical computers have driven the digital age, quantum computers hold the promise of solving problems beyond the reach of classical systems. This race, however, is not just about technological superiority; it's a strategic chess game involving national pride and potential economic supremacy.
The United States and China have emerged as the front-runners in this race. The U.S., with its long history of technological innovation, has poured billions into research and development. Silicon Valley giants like Google and IBM are in a fierce competition to build the first fully functional quantum computer. On the other hand, China's ambitious national strategy has led to significant advancements, including the launch of the world's first quantum satellite.
At the heart of this competition lies the principle of quantum supremacy - the point at which a quantum computer can perform a calculation that is impossible for a classical computer. Achieving this would not only be a scientific breakthrough but also have profound implications for cybersecurity, as quantum computers can potentially break many of the encryption methods currently in use.
Despite the excitement, there are skeptics who question the practicality of quantum computing. They argue that these computers are incredibly sensitive to environmental factors and require extreme conditions to function, such as near-absolute zero temperatures. Moreover, the technology is still in its infancy, and real-world applications are years, if not decades, away.
As the race continues, one thing is certain: the arrival of quantum computing will mark a new era in the technological landscape, reshaping industries and possibly redefining global power dynamics.
As the race continues, one thing is certain: the arrival of quantum computing will mark a new era in the technological landscape, reshaping industries and possibly redefining global power dynamics.
Q. The passage provides support for which of the following statements?
a)
Quantum computing will likely replace classical computing in most common applications within a few years.
b)
The United States has already achieved quantum supremacy over China.
c)
Quantum computers have the potential to revolutionize cybersecurity.
d)
Most encryption methods used today are already resistant to quantum computing.
e)
Environmental factors do not significantly impact the functioning of quantum computers.
|
|
Tejas Gupta answered |
Understanding the Answer: Quantum Computers and Cybersecurity
The passage highlights the potential impact of quantum computers, particularly on cybersecurity. Here’s a detailed explanation supporting option 'C':
Potential to Revolutionize Cybersecurity
- Quantum computers possess the capability to process information at unprecedented speeds. This characteristic enables them to conduct complex calculations that classical computers cannot handle.
- One significant implication of achieving quantum supremacy is its effect on encryption methods. Many current encryption systems rely on mathematical problems that are difficult for classical computers to solve. However, quantum computers could easily break these encryptions, posing a threat to data security.
Support from the Passage
- The passage explicitly states that achieving quantum supremacy would have "profound implications for cybersecurity," indicating that quantum computers may disrupt existing security protocols.
- The reference to quantum computers being able to "potentially break many of the encryption methods currently in use" reinforces the idea that they can revolutionize the field of cybersecurity.
Why Other Options Are Incorrect
- Option 'A': Quantum computing is still in its infancy, and widespread replacement of classical computing is not imminent.
- Option 'B': The passage does not confirm that the U.S. has achieved quantum supremacy; it discusses ongoing competition.
- Option 'D': It suggests that many encryption methods are vulnerable to quantum computing, contradicting the assertion that they are resistant.
- Option 'E': The passage mentions that quantum computers are sensitive to environmental factors, implying that such factors do significantly impact their functioning.
In conclusion, option 'C' is the correct choice as it accurately reflects the transformative potential of quantum computing in the realm of cybersecurity, as outlined in the passage.
The passage highlights the potential impact of quantum computers, particularly on cybersecurity. Here’s a detailed explanation supporting option 'C':
Potential to Revolutionize Cybersecurity
- Quantum computers possess the capability to process information at unprecedented speeds. This characteristic enables them to conduct complex calculations that classical computers cannot handle.
- One significant implication of achieving quantum supremacy is its effect on encryption methods. Many current encryption systems rely on mathematical problems that are difficult for classical computers to solve. However, quantum computers could easily break these encryptions, posing a threat to data security.
Support from the Passage
- The passage explicitly states that achieving quantum supremacy would have "profound implications for cybersecurity," indicating that quantum computers may disrupt existing security protocols.
- The reference to quantum computers being able to "potentially break many of the encryption methods currently in use" reinforces the idea that they can revolutionize the field of cybersecurity.
Why Other Options Are Incorrect
- Option 'A': Quantum computing is still in its infancy, and widespread replacement of classical computing is not imminent.
- Option 'B': The passage does not confirm that the U.S. has achieved quantum supremacy; it discusses ongoing competition.
- Option 'D': It suggests that many encryption methods are vulnerable to quantum computing, contradicting the assertion that they are resistant.
- Option 'E': The passage mentions that quantum computers are sensitive to environmental factors, implying that such factors do significantly impact their functioning.
In conclusion, option 'C' is the correct choice as it accurately reflects the transformative potential of quantum computing in the realm of cybersecurity, as outlined in the passage.
Maggie will either move into her old bedroom at her parents' house to save money or else she will share an apartment with her college roommate. However, she would not do either one unless she had accumulated excessive credit card debt during college. Maggie's parents will allow her to move into her old bedroom at their house if and only if they do not know that she has accumulated excessive credit card debt during college.Q. If all of the above statements are true, which of the following would allow the conclusion that Maggie will share an apartment with her college roommate only if her parents know that she has accumulated excessive credit card debt during college to be properly drawn?- a)Maggie's college roommate is willing to share an apartment only because Maggie accumulated excessive credit card debt during college.
- b)If Maggie shares an apartment with her college roommate, her parents will know that she accumulated excessive credit card debt during college.
- c)If Maggie had not accumulated excessive credit card debt in college, she would neither move into her old bedroom at her parents' house nor share an apartment with her college roommate.
- d)If Maggie's parents do not allow her to move into her old bedroom at their house, she will share an apartment with her college roommate.
- e)If Maggie's parents allow her to move into her old bedroom at their house, she will do so.
Correct answer is option 'E'. Can you explain this answer?
Maggie will either move into her old bedroom at her parents' house to save money or else she will share an apartment with her college roommate. However, she would not do either one unless she had accumulated excessive credit card debt during college. Maggie's parents will allow her to move into her old bedroom at their house if and only if they do not know that she has accumulated excessive credit card debt during college.
Q. If all of the above statements are true, which of the following would allow the conclusion that Maggie will share an apartment with her college roommate only if her parents know that she has accumulated excessive credit card debt during college to be properly drawn?
a)
Maggie's college roommate is willing to share an apartment only because Maggie accumulated excessive credit card debt during college.
b)
If Maggie shares an apartment with her college roommate, her parents will know that she accumulated excessive credit card debt during college.
c)
If Maggie had not accumulated excessive credit card debt in college, she would neither move into her old bedroom at her parents' house nor share an apartment with her college roommate.
d)
If Maggie's parents do not allow her to move into her old bedroom at their house, she will share an apartment with her college roommate.
e)
If Maggie's parents allow her to move into her old bedroom at their house, she will do so.
|
|
EduRev GMAT answered |
The question stem states that if the stimulus is true what will help draw the conclusion of the argument that: "Maggie will share an apartment with her college roommate only if her parents know that she has accumulated excessive credit card debt during college". This is turn means that we need to find the assumption that will help hold this conclusion true.
Analyzing answer options:
A. Maggie's college roommate is willing to share an apartment only because Maggie accumulated excessive credit card debt during college.( we already know this from the stimulus and keeping this as our assumption doesn't let us derive the conclusion that we need.)
B. If Maggie shares an apartment with her college roommate, her parents will know that she accumulated excessive credit card debt during college. (I considered this to be a contender initially but on thinking about a little more this option isn't a contender, what if Maggie's parents do not know about her credit card debt would she still move in with her room mate, this option doesn't answer this question.)
C. If Maggie had not accumulated excessive credit card debt in college, she would neither move into her old bedroom at her parents' house nor share an apartment with her college roommate. (irrelevant, the stimulus clearly helps us understand that if Maggie wouldn't have accumulated credit card debt she wouldn't have to consider either options in the first place.)
D. If Maggie's parents do not allow her to move into her old bedroom at their house, she will share an apartment with her college roommate. (This is the conclusion that we are trying to prove hence this definitely cannot be our assumption.)
E. If Maggie's parents allow her to move into her old bedroom at their house, she will do so. (This is our OA because if Maggie's parents are not aware that she has a huge credit card debt then they will let her move into her old bedroom but if they are aware that she has excessive credit card debt then she will have to move in with her college room mate, hence making the conclusion in the question stem hold true.)
Analyzing answer options:
A. Maggie's college roommate is willing to share an apartment only because Maggie accumulated excessive credit card debt during college.( we already know this from the stimulus and keeping this as our assumption doesn't let us derive the conclusion that we need.)
B. If Maggie shares an apartment with her college roommate, her parents will know that she accumulated excessive credit card debt during college. (I considered this to be a contender initially but on thinking about a little more this option isn't a contender, what if Maggie's parents do not know about her credit card debt would she still move in with her room mate, this option doesn't answer this question.)
C. If Maggie had not accumulated excessive credit card debt in college, she would neither move into her old bedroom at her parents' house nor share an apartment with her college roommate. (irrelevant, the stimulus clearly helps us understand that if Maggie wouldn't have accumulated credit card debt she wouldn't have to consider either options in the first place.)
D. If Maggie's parents do not allow her to move into her old bedroom at their house, she will share an apartment with her college roommate. (This is the conclusion that we are trying to prove hence this definitely cannot be our assumption.)
E. If Maggie's parents allow her to move into her old bedroom at their house, she will do so. (This is our OA because if Maggie's parents are not aware that she has a huge credit card debt then they will let her move into her old bedroom but if they are aware that she has excessive credit card debt then she will have to move in with her college room mate, hence making the conclusion in the question stem hold true.)
Window 1: Appraisal Letter
Dear Mr. and Mrs. Brown:We again want to thank you for choosing to work with the experts at Coin and Gem to settle your mother’s estate. After careful review of the coin collection in question, we found a total of 187 coins. Each coin has been appraised, packaged, and marked according to its grade.Each coin was ranked on a scale of 1 to 70 according to the Sheldon Scale of coin grading. We estimate the total value of the collection to be about $27,000. Most of the value resides in a few very rare American coins, which are in mint condition.We would be happy to further assist you in deciding how to handle this aspect of your mother’s estate. Please contact us with any questions or concerns you may have.Attached is a detailed appraisal that inventories each coin, its condition, and its value.Sincerely yours,
Charles Barker, Owner and Appraisal Expert
Coin and GemWindow 2: Inventory Appraisal: Very Fine and Mint Pieces
Window 3: Letter of Recommendation
Dear Mr. and Mrs. Brown:We highly recommend that the Extremely Fine and Mint pieces valued more than $350.00 each be sold at auction, with a reserve price that falls only slightly below their appraised value. Collectors will pay dearly for rare pieces in mint condition, especially if they will complete a collection.The remaining pieces of high value, 80 coins valued at $100.00 to $300.00 each, should be handled by a broker and sold individually. We would be more than willing to handle the sale of these pieces, at a commission of 2.7%.Finally, I recommend that the coins you have many of—like the wheat penny, which have a relatively low sale value—be sold off in lots. You will receive more for these coins from a prospector who wants to look through the lot for a specific coin of value than you would by selling them individually.Let us know of any way we can assist you in this matter.Sincerely,
Charles Barker, Owner and Appraisal Expert
Coin and GemQ: Consider each of the following statements. Does the information in the three sources support the inference as stated?
- a)No, No, No
- b)No, No, Yes
- c)Yes, No, Yes
- d)Yes, Yes, No
- e)Yes, Yes, Yes
Correct answer is option 'B'. Can you explain this answer?
Window 1: Appraisal Letter
Dear Mr. and Mrs. Brown:
Dear Mr. and Mrs. Brown:
We again want to thank you for choosing to work with the experts at Coin and Gem to settle your mother’s estate. After careful review of the coin collection in question, we found a total of 187 coins. Each coin has been appraised, packaged, and marked according to its grade.
Each coin was ranked on a scale of 1 to 70 according to the Sheldon Scale of coin grading. We estimate the total value of the collection to be about $27,000. Most of the value resides in a few very rare American coins, which are in mint condition.
We would be happy to further assist you in deciding how to handle this aspect of your mother’s estate. Please contact us with any questions or concerns you may have.
Attached is a detailed appraisal that inventories each coin, its condition, and its value.
Sincerely yours,
Charles Barker, Owner and Appraisal Expert
Coin and Gem
Charles Barker, Owner and Appraisal Expert
Coin and Gem
Window 2: Inventory Appraisal: Very Fine and Mint Pieces
Window 3: Letter of Recommendation
Dear Mr. and Mrs. Brown:
Dear Mr. and Mrs. Brown:
We highly recommend that the Extremely Fine and Mint pieces valued more than $350.00 each be sold at auction, with a reserve price that falls only slightly below their appraised value. Collectors will pay dearly for rare pieces in mint condition, especially if they will complete a collection.
The remaining pieces of high value, 80 coins valued at $100.00 to $300.00 each, should be handled by a broker and sold individually. We would be more than willing to handle the sale of these pieces, at a commission of 2.7%.
Finally, I recommend that the coins you have many of—like the wheat penny, which have a relatively low sale value—be sold off in lots. You will receive more for these coins from a prospector who wants to look through the lot for a specific coin of value than you would by selling them individually.
Let us know of any way we can assist you in this matter.
Sincerely,
Charles Barker, Owner and Appraisal Expert
Coin and Gem
Charles Barker, Owner and Appraisal Expert
Coin and Gem
Q: Consider each of the following statements. Does the information in the three sources support the inference as stated?
a)
No, No, No
b)
No, No, Yes
c)
Yes, No, Yes
d)
Yes, Yes, No
e)
Yes, Yes, Yes
|
|
EduRev GMAT answered |
The first inference is not supported by the information in the three sources. The appraiser does not imply a belief that the Browns will not receive full value for their coins.
In Source #3, the appraiser recommends that pieces valued at more than $350 be sold at auction. Source #2 shows that some of Brown’s Extremely Fine coins are valued at $350 or less. These pieces would not be sold at auction.
Source #1 shows that the Browns’ collection contains 187 coins. Source #2 lists 12 of these coins as valued at more than $350. Source #3 indicates that 80 coins have values from $100 to $300. That leaves 95
Top Trucks has two major custom lines: mud-truck improvements and low-rider packages. Last spring, the company completed roughly 200 customizations. This fall, market analysts suspect that the number of customizations will rise significantly. Specifically, they expect customizations to increase by roughly 170 customizations.For the first time, mud-truck improvement sales will exceed lowrider packages. In the table below, identify the minimum number of mud-truck improvements Top Truck’s employees should expect to complete during fall sales and the total number of customizations Top Trucks will complete next spring, if growth continues at its current pattern (an increase of 170). Make only two selections, one in each column.
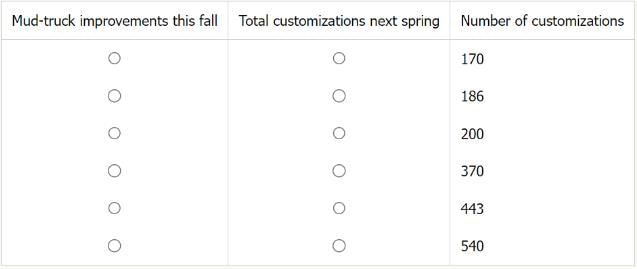
- a)Mud Truck 170, Total Customizations 370
- b) Mud Truck 186, Total Customizations 540
- c) Mud Truck 186, Total Customizations 443
- d)Mud Truck 200, Total Customizations 170
- e) Mud Truck 200, Total Customizations 540
Correct answer is option 'B'. Can you explain this answer?
Top Trucks has two major custom lines: mud-truck improvements and low-rider packages. Last spring, the company completed roughly 200 customizations. This fall, market analysts suspect that the number of customizations will rise significantly. Specifically, they expect customizations to increase by roughly 170 customizations.
For the first time, mud-truck improvement sales will exceed lowrider packages. In the table below, identify the minimum number of mud-truck improvements Top Truck’s employees should expect to complete during fall sales and the total number of customizations Top Trucks will complete next spring, if growth continues at its current pattern (an increase of 170). Make only two selections, one in each column.
a)
Mud Truck 170, Total Customizations 370
b)
Mud Truck 186, Total Customizations 540
c)
Mud Truck 186, Total Customizations 443
d)
Mud Truck 200, Total Customizations 170
e)
Mud Truck 200, Total Customizations 540
|
|
EduRev GMAT answered |
Last spring, the company completed roughly 200 customizations. This fall, the company expects to complete 170 more customizations than were completed last spring. The company should complete 370 total customizations this fall. Mud-truck improvement sales will exceed lowrider packages this fall. If Top Trucks sold an equal number of the two types of customizations, it would sell 185 of each type. If more mud truck improvements are sold, the minimum number of mud-truck improvements would be 186.
If growth continues at its current rate, Top Trucks will sell 200 + 170 customizations this fall, or 370. It will sell 370 + 170 customizations next spring, or 540.
Answer: Mud-truck improvements this fall: 186
Total customizations next spring: 540
Total customizations next spring: 540
If a salesman received a commission of 3% of the sales that he has booked in a month, what was the sales booked by the salesman in the month of November 2003?Statement 1: The sales booked by the salesman in the month of November 2003 minus salesman's commission was $245,000Statement 2: The selling price of the sales booked by the salesman in the month of November 2003 was 125 percent of the original purchase price of $225,000- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
- c)Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
- d)EACH statement ALONE is sufficient
- e)Statements (1) and (2) TOGETHER are NOT sufficient
Correct answer is option 'D'. Can you explain this answer?
If a salesman received a commission of 3% of the sales that he has booked in a month, what was the sales booked by the salesman in the month of November 2003?
Statement 1: The sales booked by the salesman in the month of November 2003 minus salesman's commission was $245,000
Statement 2: The selling price of the sales booked by the salesman in the month of November 2003 was 125 percent of the original purchase price of $225,000
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient
c)
Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
d)
EACH statement ALONE is sufficient
e)
Statements (1) and (2) TOGETHER are NOT sufficient
|
|
EduRev GMAT answered |
Step 1: Evaluate Statement 1 ALONE
Statement 1: The sales booked by the salesman in the month of November 2003 minus salesman's commission was $245,000
From statement 1, we know the value of sales after the salesman's commission is subtracted.
From the question stem, we know his commission is 3% of the sales booked. Then value of sales after subtracting his commission is 100 − 3 = 97% of the sales booked.
Putting the two together, we can deduce that 97% of sales booked = $245,000. So we can find out the sales booked.
Statement 1 ALONE is SUFFICIENT.
Eliminate choices B, C, and E.
Answers narrow down to choices (A) or (D).
From the question stem, we know his commission is 3% of the sales booked. Then value of sales after subtracting his commission is 100 − 3 = 97% of the sales booked.
Putting the two together, we can deduce that 97% of sales booked = $245,000. So we can find out the sales booked.
Statement 1 ALONE is SUFFICIENT.
Eliminate choices B, C, and E.
Answers narrow down to choices (A) or (D).
Step 2: Evaluate Statement 2 ALONE
Statement 2: The selling price of the sales booked by the salesman in the month of November 2003 was 125 percent of the original purchase price of $225,000.
From statement 2, we know that the original purchase of the products is $225,000.
We can compute the sales booked as 125% of 225,000 = 1.25 × 225,000.
Statement 2 ALONE is SUFFICIENT.
We can compute the sales booked as 125% of 225,000 = 1.25 × 225,000.
Statement 2 ALONE is SUFFICIENT.
Each statement is INDEPENDENTLY sufficient.
Choice D is the correct answer.
Each of the question below consists of a question and two statements numbered I and II are given below it You have to decide whether the data provided in the statements are sufficient to answer the question Read both the statement and answer the following question.What is the code for walks in the code language?
I. In the code language ‘she walks fast’ is written as ‘he ka to’
II. In the code language ‘she learns fast’ is written as ‘jo ka he’- a)If the data in Statement I alone are sufficient to answer the question while the data in Statement II alone are not sufficient to answer the question
- b)If the data in Statement II alone are sufficient to answer the question while the data in Statement I alone are not sufficient to answer the question
- c)If the data in Statement I alone or in Statement II alone are sufficient to answer the question
- d)If the data in both the Statement I and II are not sufficient to answer the question
- e)If the data in both the Statements I and II together are necessary to answer the question
Correct answer is option 'E'. Can you explain this answer?
Each of the question below consists of a question and two statements numbered I and II are given below it You have to decide whether the data provided in the statements are sufficient to answer the question Read both the statement and answer the following question.
What is the code for walks in the code language?
I. In the code language ‘she walks fast’ is written as ‘he ka to’
II. In the code language ‘she learns fast’ is written as ‘jo ka he’
I. In the code language ‘she walks fast’ is written as ‘he ka to’
II. In the code language ‘she learns fast’ is written as ‘jo ka he’
a)
If the data in Statement I alone are sufficient to answer the question while the data in Statement II alone are not sufficient to answer the question
b)
If the data in Statement II alone are sufficient to answer the question while the data in Statement I alone are not sufficient to answer the question
c)
If the data in Statement I alone or in Statement II alone are sufficient to answer the question
d)
If the data in both the Statement I and II are not sufficient to answer the question
e)
If the data in both the Statements I and II together are necessary to answer the question
|
|
EduRev GMAT answered |
Data in both statement is needed to find the code for ‘walks’
Now, ‘she walks fast’ is written as ‘he ka to’ and ‘she learns fast’ is written as ‘jo ka he’.
Therefore code for she, fast will be he and ka.
Code for walks is ‘to’.
Data in both statement is needed to answer teh question.
Therefore, the correct answer is option E.
Now, ‘she walks fast’ is written as ‘he ka to’ and ‘she learns fast’ is written as ‘jo ka he’.
Therefore code for she, fast will be he and ka.
Code for walks is ‘to’.
Data in both statement is needed to answer teh question.
Therefore, the correct answer is option E.
What is the smallest integer that satisfies the inequality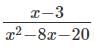
> 0?- a)-2
- b)10
- c)3
- d)-1
- e)0
Correct answer is option 'D'. Can you explain this answer?
What is the smallest integer that satisfies the inequality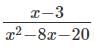 > 0?
> 0?a)
-2
b)
10
c)
3
d)
-1
e)
0
|
|
EduRev GMAT answered |
Let us factorize the denominator and rewrite the expression as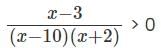 
Approach: Equate each of the terms of the expression to zero to identify the values of x in which the inequality holds good.
The values that are relevant to us are x = 3, x = 10 and x = -2.
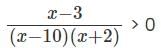
Approach: Equate each of the terms of the expression to zero to identify the values of x in which the inequality holds good.
The values that are relevant to us are x = 3, x = 10 and x = -2.
Let us arrange these values in ascending order: -2, 3 and 10.
The quickest way to solve inequalities questions after arriving at these values is verifying whether the inequality holds good at the following intervals.
The quickest way to solve inequalities questions after arriving at these values is verifying whether the inequality holds good at the following intervals.
Interval 1: x < -2.
Pick a value in that range and check whether the inequality holds good.
Let us take x = -10. When x = -10, the value of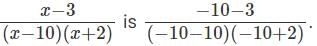
The value of the expression in this interval is negative; the inequality DOES NOT hold good in this interval.
Pick a value in that range and check whether the inequality holds good.
Let us take x = -10. When x = -10, the value of
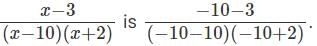
The value of the expression in this interval is negative; the inequality DOES NOT hold good in this interval.
Interval 2: -2 < x < 3.
Let us take x = 0. When x = 0,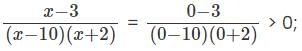
the inequality holds good in this interval.
We found that the inequality holds good in the interval -2 < x < 3
The least integer value that x can take in the interval -2 < x < 3 is x = -1.
Let us take x = 0. When x = 0,
the inequality holds good in this interval.We found that the inequality holds good in the interval -2 < x < 3
The least integer value that x can take in the interval -2 < x < 3 is x = -1.
So, the correct answer is -1.
Remember: We have to find out the least integer value. And we have arrived at -1.
Do not waste time computing the entire range of values of x that satisfy the inequality.
Note: In any inequality question, when the question asks us to determine the intervals in which the inequality holds good, we have to eliminate values of x that will result in the denominator becoming zero.
Do not waste time computing the entire range of values of x that satisfy the inequality.
Note: In any inequality question, when the question asks us to determine the intervals in which the inequality holds good, we have to eliminate values of x that will result in the denominator becoming zero.
Choice D is the correct answer.
The diagram shows, in two column groupings, various divisions of human gestation, with a total length of approximately 308 days. In the leftmost column, the full pregnancy is divided into its trimesters. In the second graphic area, the zygote stage is magnified and shown in greater detail. Select the best answer to fill in the blanks for each of the statements below, based on the data shown.Q. The second trimester is closest to ____ % as long as the first.- a)131
- b)135
- c)130
- d)133
- e)150
Correct answer is option 'D'. Can you explain this answer?
The diagram shows, in two column groupings, various divisions of human gestation, with a total length of approximately 308 days. In the leftmost column, the full pregnancy is divided into its trimesters. In the second graphic area, the zygote stage is magnified and shown in greater detail. Select the best answer to fill in the blanks for each of the statements below, based on the data shown.
Q. The second trimester is closest to ____ % as long as the first.
a)
131
b)
135
c)
130
d)
133
e)
150
|
|
EduRev GMAT answered |
First trimester = 84 days (ie, 0 to 84)
Second trimester = 112 days (ie. 85 to 196)
Hence, % = (112 / 84) * 100 % = 16/12 = 4/3 = 133 1/3%
133 is the CORRECT answer
Second trimester = 112 days (ie. 85 to 196)
Hence, % = (112 / 84) * 100 % = 16/12 = 4/3 = 133 1/3%
133 is the CORRECT answer
With elections around the corner, there has been a lot of debate on the policies formulated and implemented during the tenure of the incumbent government. One such policy is providing free and urgent health care at all major towns to all those families who have an yearly income at the most $10,000.Select for Government achievement the response that a government representative is likely to give as an achievement of the government and for Opposition Rebuttal the counter that the opposition can use as a flaw in the claim. Make two selections, one for each.
- a)Only A and B
- b)Only B and E
- c)Only A and C
- d)Only A , B and E
Correct answer is option 'B'. Can you explain this answer?
With elections around the corner, there has been a lot of debate on the policies formulated and implemented during the tenure of the incumbent government. One such policy is providing free and urgent health care at all major towns to all those families who have an yearly income at the most $10,000.
Select for Government achievement the response that a government representative is likely to give as an achievement of the government and for Opposition Rebuttal the counter that the opposition can use as a flaw in the claim. Make two selections, one for each.
a)
Only A and B
b)
Only B and E
c)
Only A and C
d)
Only A , B and E
|
|
EduRev GMAT answered |
Out of the given options:
Free Healthcare is provided through a network of preferred providers and hospitals resulting in higher cost to the exchequer.
This could be rebuttal of opposition as it indicates there has been corruption in implementing the policy by providing healthcare through preferred network of providers.
This could be rebuttal of opposition as it indicates there has been corruption in implementing the policy by providing healthcare through preferred network of providers.
80% of the population is benefited as the yearly income of almost 80% of the total population is below $10,000.
This would be government's achievement. As its policy has benefitted 80% of the population.
This would be government's achievement. As its policy has benefitted 80% of the population.
The free healthcare scheme is funded through taxes collected from 30% of the population.
It can't be either an achievement or rebuttal from the opposition.
It can't be either an achievement or rebuttal from the opposition.
The government has ensured that free healthcare is provided through a network of best hospitals.
This is of no use for opposition. For government also, it doesn't give any quantitative information that creates a +ve perception among the voters.
This is of no use for opposition. For government also, it doesn't give any quantitative information that creates a +ve perception among the voters.
More than 70% of the population stays in rural areas, which are underdeveloped with almost no connectivity.
This is irrelevant.
This is irrelevant.
Graph shows the number of unemployed (in thousands) over a five-month period, organized by level of education completed.
Q. The largest difference in the number of unemployed between any two groups was a difference of approximately _____
The greatest variation in the number of unemployed over this five month period occurred among ______
- a)August, Bachelor's degree and higher
- b)September, Bachelor's degree and higher
- c)September, high school diploma no college
- d)July, some college
- e)October, Bachelor's degree and higher
Correct answer is option 'B'. Can you explain this answer?
Graph shows the number of unemployed (in thousands) over a five-month period, organized by level of education completed.
Q. The largest difference in the number of unemployed between any two groups was a difference of approximately _____
The greatest variation in the number of unemployed over this five month period occurred among ______
a)
August, Bachelor's degree and higher
b)
September, Bachelor's degree and higher
c)
September, high school diploma no college
d)
July, some college
e)
October, Bachelor's degree and higher
|
|
EduRev GMAT answered |
Part 2: The only group that saw no rise in unemployment during this five month period was _____
Less than a high school diploma - rise in unemployment from September to October.
High School Diploma, no college - rise in unemployment from June to July.
Some College - rise in unemployment from September to October.
Bachelor's degree and higher - no rise in unemployment. (Steady - July to September or Decrease - September to October.)
Hence answer is Bachelor's degree and higher.
During the last 50 years in England, the national football team has had at least 60℅ of its players born during the months January to March. Similarly, in Germany, at least 50℅ of the team has been born during the first three months of the year. In fact, this statistic holds true for most European countries. This shows that in most European countries, parents with kids born early in the year are more likely to encourage a football career.Q. Which of the following best explains why the conclusion need not be the best explanation for the statistic?- a)Of the remaining members, 60℅ or more tend to be born between the months of April and June.
- b)Parents of kids born in the second half of the year have displayed a measurable intent to promote scholarly careers
- c)The age cut-off for kids to try out for a team in most European countries is calculated as on December 31 of any year and older the kid during trials, greater the chances of getting the right opportunities.
- d)The school year usually begins in April in most European countries and many parents are known to encourage students to work on their academics and not sports during the school year.
- e)During the last 50 years, on average 30℅ of the kids have been born during the first three months of the year.
Correct answer is option 'C'. Can you explain this answer?
During the last 50 years in England, the national football team has had at least 60℅ of its players born during the months January to March. Similarly, in Germany, at least 50℅ of the team has been born during the first three months of the year. In fact, this statistic holds true for most European countries. This shows that in most European countries, parents with kids born early in the year are more likely to encourage a football career.
Q. Which of the following best explains why the conclusion need not be the best explanation for the statistic?
a)
Of the remaining members, 60℅ or more tend to be born between the months of April and June.
b)
Parents of kids born in the second half of the year have displayed a measurable intent to promote scholarly careers
c)
The age cut-off for kids to try out for a team in most European countries is calculated as on December 31 of any year and older the kid during trials, greater the chances of getting the right opportunities.
d)
The school year usually begins in April in most European countries and many parents are known to encourage students to work on their academics and not sports during the school year.
e)
During the last 50 years, on average 30℅ of the kids have been born during the first three months of the year.
|
|
EduRev GMAT answered |
Step 1: Analyzing the Argument
The author believes that the parents who have kids in the first quarter of the new year are more likely to encourage their kids to have a football career.
The question asks to identify an option that points out that the author's reasoning may be flawed. Essentially, the correct option must provide an alternative explanation for the statistic that shows that a significant portion of the players on the teams were born in the first quarter.
Step 2: Process of Elimination
- The correct option must explain why more members of the team were born in the first quarter and not just talk about the number or percentage of births during the other months of the year. Therefore, Options (A) and (E) are irrelevant to the discussion and do not refute or support the author's reasoning.
- Option (B) adds strength to the argument. If the parents who had kids in the second half of the year prefer that their kids have scholarly careers, it stands to reason that the number of team members born in the first quarter is high because their parents encouraged their football careers.
- Option (D) is linking vacation months to encouragement to play football. The argument is discussing the link between birth month and encouragement to play football. The relationship discussed in the option has no ties to the argument and does not refute or strengthen the argument.
- Option (C) the cut-off dates for trials is December 31. If that were the scenario, the kids born earlier in any year would be older than kids born later in the year and will have an edge over the younger kids. The option implies that there are more players born in the first quarter because they had an edge over the other players, as kids, and not because of parental support. The option thus questions the author's argument.
Choice C is the correct answer.
The National Farm Administration (NFA) has been concerned over the last decade with the struggles of barley growers.Plan: In an effort to support these barley growers, two years ago, the NFA began a program of sending them, each autumn, a free special mix of fertilizer and enzymes designed to multiply barley yield, to be applied the following spring during first growth. This mix had been stunningly successful in multiplying the yield of barley in laboratory conditions.Results: Most barley growers reported little change in their economic status over this two year period.Further information: All barley growers received the shipments, and all used them. Weather conditions have been fair to optimal for barley growth over the past two years.Q. In light of the further information, which of the following, if true, does most to explain the result that followed the implementation of the plan?- a)During these two years, most of the barley growers reported using no other fertilizer besides the special mix sent by the government.
- b)The trucks that drove the special mix from the depot in Wisconsin to the individual farms sometime took as much as 4 or 5 days.
- c)Some of the enzymes in the special mix multiply the growth of a bacteria that feeds on the young barley plants.
- d)This program was implemented at a time when more than half of barley growers nationwide were reported barely breaking even in their yearly expenses.
- e)This was the second such NFA program to aid barley growers; the first one, 14 years ago, was started with high hopes, but did little to change their situation.
Correct answer is option 'C'. Can you explain this answer?
The National Farm Administration (NFA) has been concerned over the last decade with the struggles of barley growers.
Plan: In an effort to support these barley growers, two years ago, the NFA began a program of sending them, each autumn, a free special mix of fertilizer and enzymes designed to multiply barley yield, to be applied the following spring during first growth. This mix had been stunningly successful in multiplying the yield of barley in laboratory conditions.
Results: Most barley growers reported little change in their economic status over this two year period.
Further information: All barley growers received the shipments, and all used them. Weather conditions have been fair to optimal for barley growth over the past two years.
Q. In light of the further information, which of the following, if true, does most to explain the result that followed the implementation of the plan?
a)
During these two years, most of the barley growers reported using no other fertilizer besides the special mix sent by the government.
b)
The trucks that drove the special mix from the depot in Wisconsin to the individual farms sometime took as much as 4 or 5 days.
c)
Some of the enzymes in the special mix multiply the growth of a bacteria that feeds on the young barley plants.
d)
This program was implemented at a time when more than half of barley growers nationwide were reported barely breaking even in their yearly expenses.
e)
This was the second such NFA program to aid barley growers; the first one, 14 years ago, was started with high hopes, but did little to change their situation.
|
|
EduRev GMAT answered |
C is definitely the right answer. We're looking for some new information that could explain why the plan didn't help. If the special mix has a negative effect aside from the positive one, that could explain the problem. This doesn't require us to assume anything. Clearly, if it worked well under laboratory conditions, either the harmful bacteria was not present (entirely plausible) or something else in the laboratory conditions kept it from being a problem. In a CR problem, we don't even need to get into all that, and we certainly don't want to question the plausibility of this happening. We simply accept the given premises (the mix worked in the lab, everyone used it, but no one is better off financially). Once we accept all that, we just look for some reason for the continued trouble--the right answer could have been any source of financial trouble: invaders from another galaxy ate all the barley, every single barley grower was robbed by a team of hackers . . . it really doesn't matter what it is. We just need to know why the plan didn't leave the growers better off.
A, B, and E all require tremendous assumptions on our part. Is it bad not to use other fertilizer, or to have the mix sit in a truck for days? Perhaps, but we don't know, so it's impossible to say if this information makes any difference. D expands on what we already know--the barley growers were in financial trouble--but it does nothing to help us understand why they are no better off now that the plan has been put into action.
Chapter doubts & questions for Mock Test - 35 Days Preparation for GMAT 2025 is part of GMAT exam preparation. The chapters have been prepared according to the GMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for GMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Mock Test - 35 Days Preparation for GMAT in English & Hindi are available as part of GMAT exam.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
35 Days Preparation for GMAT
171 videos|269 docs|181 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup