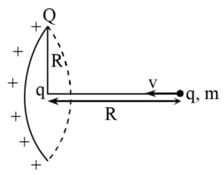
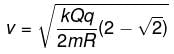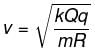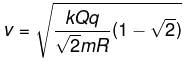All Exams >
MCAT >
MCAT Chemical and Physical Foundations >
All Questions
All questions of Electrostatics (PHY) for MCAT Exam
- a)0.5 J
- b)1.12 J
- c)1.2 J
- d)0.9 J
Correct answer is 'D'. Can you explain this answer?
|
Nikita Singh answered |
q=6x10-10 c
Q=-2x10-9c
r1=3x10-2m
r2=4x10-2m
△vQ=w/q
(1/4πεo)-2x10-9/10-2[(1/4)-(1/3)]=W/6x10-3
9x109x2x10-9x6x10-3/12x10-2=W
W=9x10-3x102
W=0.9J
Q=-2x10-9c
r1=3x10-2m
r2=4x10-2m
△vQ=w/q
(1/4πεo)-2x10-9/10-2[(1/4)-(1/3)]=W/6x10-3
9x109x2x10-9x6x10-3/12x10-2=W
W=9x10-3x102
W=0.9J
The amount of work done in moving a charge from one point to another along an equipotential line or surface charge is- a)Zero
- b)Infinity
- c)One
- d)Two
Correct answer is option 'A'. Can you explain this answer?
The amount of work done in moving a charge from one point to another along an equipotential line or surface charge is
a)
Zero
b)
Infinity
c)
One
d)
Two
|
Om Desai answered |
Since Potential difference between two points in equipotential surfaces is zero, the work done between two points in equipotential surface is also zero.
Work done in carrying 2C charge in a circular path of radius 2m around a charge of 10C is- a)6.67J
- b)60J
- c)Zero
- d)15J
Correct answer is option 'C'. Can you explain this answer?
Work done in carrying 2C charge in a circular path of radius 2m around a charge of 10C is
a)
6.67J
b)
60J
c)
Zero
d)
15J
|
Suresh Iyer answered |
The overall work performed in carrying a 2coulomb charge in a circular orbit of radius 3 m around a charge of 10 coulomb is calculated below.
It is a well-known fact that W=qdv.
Here dV is the change in overall potential. In the circular orbit of r potential at each point is similar.
Most significantly, the value of r is 3.
The value of dv=0 and hence W=q0=0.
It is a well-known fact that W=qdv.
Here dV is the change in overall potential. In the circular orbit of r potential at each point is similar.
Most significantly, the value of r is 3.
The value of dv=0 and hence W=q0=0.
Electric field intensity at point ‘B’ due to a point charge ‘Q’ kept at a point ‘A’ is 12 NC-1 and the electric potential at a point ‘B’ due to same charge is 6 JC-1. The distance between AB is- a)2 m
- b)1.5 m
- c)1 m
- d)0.5 m
Correct answer is option 'D'. Can you explain this answer?
Electric field intensity at point ‘B’ due to a point charge ‘Q’ kept at a point ‘A’ is 12 NC-1 and the electric potential at a point ‘B’ due to same charge is 6 JC-1. The distance between AB is
a)
2 m
b)
1.5 m
c)
1 m
d)
0.5 m
|
|
Nandini Patel answered |
As we know , E . l = V where,
E = electric field intensity = 12 N/C
V = electric potential = 6 J/C
=> distance between A and B ,
l = ( 6 / 12 ) m or ( 1 / 2 ) m = 0.5 m
Three concentric metallic spherical shells of radii R, 2R, 3R, are given charges Q1, Q2, Q3, respectively. It is found that the surface charge densities on the outer surfaces of the shells are equal. Then, the ratio of the charges given to the shells, Q1: Q2: Q3, is - a)it is 1:03:05
- b)it is 1:02:03
- c)it is 1:04:09
- d)it is 1:08:18
Correct answer is 'A'. Can you explain this answer?
Three concentric metallic spherical shells of radii R, 2R, 3R, are given charges Q1, Q2, Q3, respectively. It is found that the surface charge densities on the outer surfaces of the shells are equal. Then, the ratio of the charges given to the shells, Q1: Q2: Q3, is
a)
it is 1:03:05
b)
it is 1:02:03
c)
it is 1:04:09
d)
it is 1:08:18
|
|
Sanaya Kumar answered |
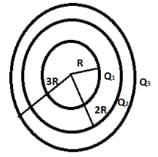
Since the charge goes to outer surface when given inside so the charges on concentri shells are respectively.
Q1, Q1 + Q2, Q1 + Q2 + Q3. Sine their charge densities are equal so σ1 = σ2 = σ3
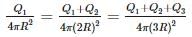
So Q1 = 3Q2 = 5Q3 so 1 : 3 : 5
If 100 J of work has to be done in moving an electric charge of 4C from a place where potential is -5 V to another place, where potential is V volt. The value of V is- a)15 V
- b)20 V
- c)25 V
- d)10 V
Correct answer is option 'B'. Can you explain this answer?
If 100 J of work has to be done in moving an electric charge of 4C from a place where potential is -5 V to another place, where potential is V volt. The value of V is
a)
15 V
b)
20 V
c)
25 V
d)
10 V
|
|
Suresh Iyer answered |
From the definition, the work done to a test charge ‘q0’ from one place to another place in an electric field is given by the formula
W=q0x[vfinal-vinitial ]
100=4x[v-(-5)]
v+5=25
v=20V
W=q0x[vfinal-vinitial ]
100=4x[v-(-5)]
v+5=25
v=20V
Can you explain the answer of this question below:Equal charges are given to two spheres of different radii. The potential will
- A:
be equal on both the spheres
- B:
be more on the smaller sphere
- C:
be more on the bigger sphere
- D:
depend on the material of the sphere
The answer is b.
Equal charges are given to two spheres of different radii. The potential will
be equal on both the spheres
be more on the smaller sphere
be more on the bigger sphere
depend on the material of the sphere
|
Ruchika Agarwal answered |
V(potential) is inversely proportional to r ( radius).so smaller sphere will have more potential as its radius will be small.
The electrostatic potential energy between two charges q1 and q2 separated by a distance by r is given by- a)
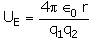
- b)
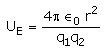
- c)
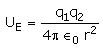
- d)
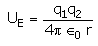
Correct answer is option 'D'. Can you explain this answer?
The electrostatic potential energy between two charges q1 and q2 separated by a distance by r is given by
a)
b)
c)
d)
|
Khushi Mittal answered |
Energy = force × distance U=Kq1q2/r^2 × r U=Kq1q2/r
A hollow metal sphere of radius 5cm is charged so that the potential on its surface is 10V. The potential at a distance of 2cm from the centre of the sphere is- a)4V
- b)zero
- c)10/3V
- d)10V
Correct answer is option 'D'. Can you explain this answer?
A hollow metal sphere of radius 5cm is charged so that the potential on its surface is 10V. The potential at a distance of 2cm from the centre of the sphere is
a)
4V
b)
zero
c)
10/3V
d)
10V
|
Ayush Joshi answered |
In the case of a hollow metal sphere (spherical shell), the electric field inside the shell is zero. This means that the potential inside the shell is constant. Therefore the potential at the centre of the sphere is the same as that on its surface, i.e. 10 V.
Can you explain the answer of this question below:It requires 4 J of work to move a charge of 20 C from point A to point B, separated by a distance of 0.2 cm. The potential difference between A and B in volts
- A:
0.2
- B:
16
- C:
5
- D:
80
The answer is a.
It requires 4 J of work to move a charge of 20 C from point A to point B, separated by a distance of 0.2 cm. The potential difference between A and B in volts
0.2
16
5
80
|
Mayank Singh answered |
As we know tha..v=w/q. .....1 so according to question w=4j and q=20c on putting value of w and q in equation 1 we find that v=0.2v
A hollow metal sphere of radius 10 cm is charged such that the potential on its surface is 80 volt. The potential at the centre of the sphere is- a)8 volt
- b)zero
- c)800 volt
- d)80 volt
Correct answer is option 'D'. Can you explain this answer?
A hollow metal sphere of radius 10 cm is charged such that the potential on its surface is 80 volt. The potential at the centre of the sphere is
a)
8 volt
b)
zero
c)
800 volt
d)
80 volt
|
Sunidhi Pandey answered |
Chage is uniformly distributed in an hollow sphere.
The linear charge densities of two infinitely long thin and parallel wires are 4Cm−1, 8Cm−1 and separation between them is 4 cm. Then the electric field intensity at mid point on the line joining them is- a)18 × 1011 NC−1
- b)36 × 1011NC−1
- c)9 × 1011NC−1
- d)72 × 1011 NC−1
Correct answer is option 'B'. Can you explain this answer?
The linear charge densities of two infinitely long thin and parallel wires are 4Cm−1, 8Cm−1 and separation between them is 4 cm. Then the electric field intensity at mid point on the line joining them is
a)
18 × 1011 NC−1
b)
36 × 1011NC−1
c)
9 × 1011NC−1
d)
72 × 1011 NC−1
|
Stepway Academy answered |
Electric Field Formula:
Electric field due to an infinitely long wire: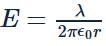
Calculate Electric Fields:
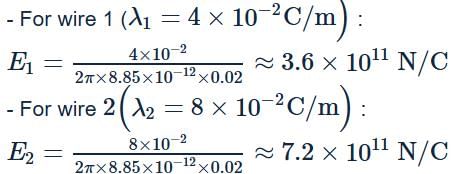
Net Electric Field at Midpoint:
- Since the fields are in opposite directions, the net field is:
E = E2 − E1 = 7.2 × 1011−3.6 × 1011 = 3.6 × 1011 N/C
Electric field due to an infinitely long wire:
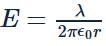
Calculate Electric Fields:
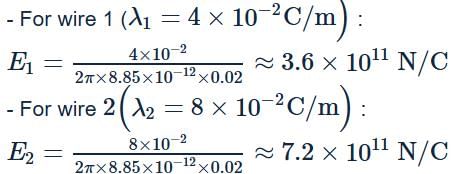
Net Electric Field at Midpoint:
- Since the fields are in opposite directions, the net field is:
E = E2 − E1 = 7.2 × 1011−3.6 × 1011 = 3.6 × 1011 N/C
When a negatively charged conductor is connected to earth,
- a)No charge flow occurs.
- b)Protons flow from the conductor to the earth.
- c)Electrons flow from the earth to the conductor.
- d)Electrons flow from the conductor to the earth.
Correct answer is option 'D'. Can you explain this answer?
When a negatively charged conductor is connected to earth,
a)
No charge flow occurs.
b)
Protons flow from the conductor to the earth.
c)
Electrons flow from the earth to the conductor.
d)
Electrons flow from the conductor to the earth.
|
Riya Banerjee answered |
Explanation:
When a negatively charged conductor is connected to the earth, electrons will flow from the conductor to the earth. This is because electrons have a negative charge and they will be repelled from the negatively charged conductor and attracted to the positively charged earth. As electrons flow from the conductor to the earth, the negative charge on the conductor will gradually decrease until it becomes neutral.
- Option A is incorrect because charge flow does occur when a negatively charged conductor is connected to the earth.
- Option B is incorrect because protons have a positive charge and they are not free to move in a conductor.
- Option C is incorrect because electrons flow from the earth to the conductor, not the other way around.
Electric potential is- a)scalar and dimensionless
- b)vector and dimensionless
- c)scalar with dimension
- d)vector with dimension
Correct answer is option 'C'. Can you explain this answer?
Electric potential is
a)
scalar and dimensionless
b)
vector and dimensionless
c)
scalar with dimension
d)
vector with dimension
|
Pooja Mehta answered |
He electric potential due to a system of point charges is equal to the sum of the point charges' individual potentials. This fact simplifies calculations significantly, since addition of potential (scalar) fields is much easier than addition of the electric (vector) fields.
The amount of work done in moving a unit positive charge through distance of 10 cm on an equipotential surface is- a)100 joule
- b)10 cm
- c)1/10 cm
- d)Zero
Correct answer is option 'D'. Can you explain this answer?
The amount of work done in moving a unit positive charge through distance of 10 cm on an equipotential surface is
a)
100 joule
b)
10 cm
c)
1/10 cm
d)
Zero
|
|
Anupam Singh answered |
Zero because at equipotential surface potential difference is zero
Can you explain the answer of this question below:The potential energy of a system containing only one point charge is
- A:
Zero
- B:
Infinity
- C:
Nonzero finite
- D:
None of the above
The answer is a.
The potential energy of a system containing only one point charge is
Zero
Infinity
Nonzero finite
None of the above
|
.mie. answered |
Answer is 0 as there are no other sources of electrostatic potential .... against which an external agent must do work.... in moving the point charge.... from infinity to its final location.... therefore correct opt is A
Consider a solid cube made up of insulating material having a uniform volume charge density. Assuming the electrostatic potential to be zero at infinity, the ratio of the potential at a corner of the cube to that at the centre will be - a)1:1
- b)1:2
- c)1:4
- d)1:8
Correct answer is option 'B'. Can you explain this answer?
Consider a solid cube made up of insulating material having a uniform volume charge density. Assuming the electrostatic potential to be zero at infinity, the ratio of the potential at a corner of the cube to that at the centre will be
a)
1:1
b)
1:2
c)
1:4
d)
1:8
|
|
Sanaya Kumar answered |
By dimensional analysis
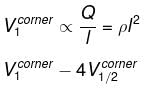
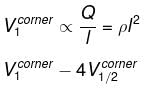
but by superposition
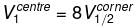
Because of the centre of the larger cube lies at a corner of the eight smaller cubes of which it is made
therefore,
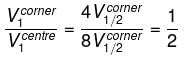
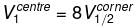
Because of the centre of the larger cube lies at a corner of the eight smaller cubes of which it is made
therefore,
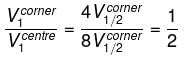
What is the direction of the lines of force at any point on the equipotential surface?- a)Parallel to it
- b)Perpendicular to it.
- c)Inclined at 45 degrees
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
What is the direction of the lines of force at any point on the equipotential surface?
a)
Parallel to it
b)
Perpendicular to it.
c)
Inclined at 45 degrees
d)
None of the above
|
Anjali Iyer answered |
When electric lines of force get perpendicular to equipotential surface then area vector and electric lines of force are parallel to each other.so angle between them is zero. due to that reason they get perpendicular to each other.
In bringing an electron towards another electron, the electrostatic potential energy of the system- a)becomes zero
- b)decreases
- c)remains same
- d)increases
Correct answer is option 'D'. Can you explain this answer?
In bringing an electron towards another electron, the electrostatic potential energy of the system
a)
becomes zero
b)
decreases
c)
remains same
d)
increases
|
|
Nandini Patel answered |
The electron has negative charge. When an electron is bringing towards another electron, then due to same negative charge repulsive force is produced between them. So, to bring them closer a work is done against this repulsive force. This work is stored in the form of electrostatic potential energy. Thus, electrostatic potential energy of system increases.
Alternative: Electrostatic potential energy of system of two electrons
U=[1/4πε0][(−e)(−e)/r] = [1/4πε0](e^2/r)
Thus, as r decreases, potential energy U increases.
Two insulated charged copper spheres A and B have their centres separated by a distance of 50 cm. What is the mutual force of electrostatic repulsion if the charge on each is 6.5×10−7C ? The radii of A and B are negligible compared to the distance of separation.- a)4.5×10−2N
- b)2.5×10−2N
- c)1.5×10−2N
- d)3.5×10−2N
Correct answer is option 'C'. Can you explain this answer?
Two insulated charged copper spheres A and B have their centres separated by a distance of 50 cm. What is the mutual force of electrostatic repulsion if the charge on each is 6.5×10−7C ? The radii of A and B are negligible compared to the distance of separation.
a)
4.5×10−2N
b)
2.5×10−2N
c)
1.5×10−2N
d)
3.5×10−2N
|
Kavya Das answered |
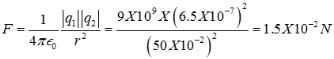
If a unit charge is taken from one part to another part over an equipotential surface, then what is the change in electrostatic potential energy of the charge?- a)10 J
- b)100 J
- c)1 J
- d)0 J
Correct answer is option 'D'. Can you explain this answer?
If a unit charge is taken from one part to another part over an equipotential surface, then what is the change in electrostatic potential energy of the charge?
a)
10 J
b)
100 J
c)
1 J
d)
0 J
|
Utsav Srivastava answered |
Equipotential surface means the potential on every. point on that surface is constant. it means the change in potential on equipotential surface is zero we know that... ( electrostatic potential energy = change in potential × charge.)... ... according to this electrostatic potential energy is zero
Can you explain the answer of this question below:Electric field lines can be said to be
- A:
lines of equal Electric field
- B:
drawing lines of electric fields
- C:
lines of equal Electric voltage
- D:
graphical representation of electric fields.
The answer is d.
Electric field lines can be said to be
lines of equal Electric field
drawing lines of electric fields
lines of equal Electric voltage
graphical representation of electric fields.
|
P. Poonia answered |
Simple they are imaginary line which be represent by graphical manner
A point charge of 2.0 μCμC is at the centre of a cubic Gaussian surface 9.0 cm on edge. What is the net electric flux through the surface?- a)1.7×105Nm2/C
- b)2.1×105Nm2/C
- c)2.2×105Nm2/C
- d)1.9×105Nm2/C
Correct answer is option 'C'. Can you explain this answer?
A point charge of 2.0 μCμC is at the centre of a cubic Gaussian surface 9.0 cm on edge. What is the net electric flux through the surface?
a)
1.7×105Nm2/C
b)
2.1×105Nm2/C
c)
2.2×105Nm2/C
d)
1.9×105Nm2/C
|
Princy Goyal answered |
This question is based on Gauss law. Net electric flux will be 1/Enot times the total charge enclosed
A hollow metal sphere of radius 20 cm is charged such that the potential on its surface is 120 Volt. The potential at the centre of the sphere is- a)80 V
- b)6 V
- c)120 V
- d)Zero
Correct answer is 'C'. Can you explain this answer?
A hollow metal sphere of radius 20 cm is charged such that the potential on its surface is 120 Volt. The potential at the centre of the sphere is
a)
80 V
b)
6 V
c)
120 V
d)
Zero
|
|
Anjana Sharma answered |
Potential inside the charged sphere is constant and equal to potential on the surface. Hence the potential at the centre of the sphere is 120 V.
The potential energy of a system containing only one point charge is
- a)Zero
- b)Infinity
- c)Non zero finite
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
The potential energy of a system containing only one point charge is
a)
Zero
b)
Infinity
c)
Non zero finite
d)
None of the above
|
Manoj Chauhan answered |
Explanation:
Potential energy is defined as the work done by an external force in bringing a system from infinity to its position. Hence, the potential energy of a system containing only one point charge is given by -
U = qV
where, q is the charge of the point charge and V is the potential at its position.
Now, let's consider the two cases -
Case 1: When the point charge is at infinity
At infinity, the potential is zero as the electric field due to a point charge decreases as we move away from it. Hence, the potential energy of the system containing only one point charge at infinity is zero.
U = qV = q x 0 = 0
Case 2: When the point charge is at a finite distance from infinity
In this case, the potential energy of the system will be non-zero finite as the potential at the position of the point charge will be non-zero.
U = qV ≠ 0
Conclusion:
Hence, the correct answer is option 'A' i.e. zero as the potential energy of a system containing only one point charge is zero when the point charge is at infinity.
Potential energy is defined as the work done by an external force in bringing a system from infinity to its position. Hence, the potential energy of a system containing only one point charge is given by -
U = qV
where, q is the charge of the point charge and V is the potential at its position.
Now, let's consider the two cases -
Case 1: When the point charge is at infinity
At infinity, the potential is zero as the electric field due to a point charge decreases as we move away from it. Hence, the potential energy of the system containing only one point charge at infinity is zero.
U = qV = q x 0 = 0
Case 2: When the point charge is at a finite distance from infinity
In this case, the potential energy of the system will be non-zero finite as the potential at the position of the point charge will be non-zero.
U = qV ≠ 0
Conclusion:
Hence, the correct answer is option 'A' i.e. zero as the potential energy of a system containing only one point charge is zero when the point charge is at infinity.
A point charge causes an electric flux of −1.0×103Nm2/C to pass through a spherical Gaussian surface of 10.0 cm radius centred on the charge. (a) If the radius of the Gaussian surface were doubled, how much flux would pass through the surface? (b) What is the value of the point charge? - a) 103Nm2/C,−7.8nC
- b) B 103Nm2/C,−8.8nC
- c) −103Nm2/C,−8.8nC
- d) −103Nm2/C,−6.8nC
Correct answer is option 'C'. Can you explain this answer?
A point charge causes an electric flux of −1.0×103Nm2/C to pass through a spherical Gaussian surface of 10.0 cm radius centred on the charge. (a) If the radius of the Gaussian surface were doubled, how much flux would pass through the surface? (b) What is the value of the point charge?
a)
103Nm2/C,−7.8nC
b)
B 103Nm2/C,−8.8nC
c)
−103Nm2/C,−8.8nC
d)
−103Nm2/C,−6.8nC
|
Mira Sharma answered |
A. Doubling the radius of Gaussian surface will not affect the electric flux since the charge enclosed is the same in both cases. Thus, the flux will remain the same i.e., –1.0 x 10^3 Nm^2/C
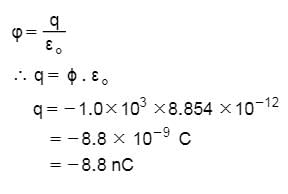
(b) Using gauss theorem,
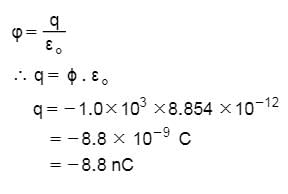
If 109electrons move out of a body to another body every second, how much time is approximately required to get a total charge of 1 C on the other body?- a)120 years
- b)220 years
- c)200 years
- d)180 years
Correct answer is option 'C'. Can you explain this answer?
If 109electrons move out of a body to another body every second, how much time is approximately required to get a total charge of 1 C on the other body?
a)
120 years
b)
220 years
c)
200 years
d)
180 years
|
|
Naina Bansal answered |
we know that 1 Coulomb = 6.242�10^18 eletrons
given 10^9 electrons take 1 secs
=> 10^9 electrons ------> 1 sec
=> 1 electrons ---------> 1/(10^9) secs
=> 6.242�10^18 ------> 6.242�10^18/ (10^9)
= 6.242�10^9 secs = 6.242�10^9/ (60*60*24*365) years
=197.93 years
Negative mutual potential energy corresponds to attraction between two charges- a)False
- b)True
- c)Can’t predict
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
Negative mutual potential energy corresponds to attraction between two charges
a)
False
b)
True
c)
Can’t predict
d)
None of the above
|
Soham Rastogi answered |
The formula for electric potential energy of system of 2 charges is (kq1q2)/r, if the result comes out to be negative,one of the charges has to be negative and one has to be positive, because there can be no other case in which it comes out to be negative. Since opposite charges attract each other,hence the answer is True.
A charge q = 1.0 C moves distance of 1.5 m in the direction of a uniform electric field E of magnitude 2.0 N/C. Find its change in electrostatic potential energy.- a)2 J
- b)3 J
- c)4 J
- d)1 J
Correct answer is option 'B'. Can you explain this answer?
A charge q = 1.0 C moves distance of 1.5 m in the direction of a uniform electric field E of magnitude 2.0 N/C. Find its change in electrostatic potential energy.
a)
2 J
b)
3 J
c)
4 J
d)
1 J
|
Anchal Maurya answered |
Force (F)=E•q=2×1=2,. Energy (E)=F•d=2×1.5=3 joule
At any point on S on an electric field line - a)the perpendicular to the line is in the direction of at that point
- b)the tangent to the line is in the direction of at that point
- c)the binormal to the line is in the direction of at that point
- d)the curvature is in the direction of at that point
Correct answer is option 'B'. Can you explain this answer?
At any point on S on an electric field line
a)
the perpendicular to the line is in the direction of at that point
b)
the tangent to the line is in the direction of at that point
c)
the binormal to the line is in the direction of at that point
d)
the curvature is in the direction of at that point
|
Amar Pillai answered |
When a tangent is drawn at any point on field line then that tangent gives the direction of electric field at that point
Equal charges are given to two spheres of different radii. The potential will- a)be equal on both the spheres
- b)be more on the smaller sphere
- c)be more on the bigger sphere
- d)depend on the material of the sphere
Correct answer is option 'B'. Can you explain this answer?
Equal charges are given to two spheres of different radii. The potential will
a)
be equal on both the spheres
b)
be more on the smaller sphere
c)
be more on the bigger sphere
d)
depend on the material of the sphere
|
Priya Chavan answered |
Explanation:
When equal charges are given to two spheres of different radii, the potential will be different on both spheres. This is because the potential depends on the radius of the sphere.
The formula for potential is given as:
V = kQ/r
Where,
V = potential
k = Coulomb's constant
Q = charge
r = radius
As we can see from the formula, the potential is inversely proportional to the radius. This means that the potential will be more on the smaller sphere and less on the bigger sphere.
Therefore, the correct answer is option B, i.e., the potential will be more on the smaller sphere.
To summarize:
- The potential depends on the radius of the sphere.
- The potential formula is V = kQ/r.
- The potential is inversely proportional to the radius.
- The potential will be more on the smaller sphere and less on the bigger sphere.
- Therefore, the correct answer is option B, i.e., the potential will be more on the smaller sphere.
When equal charges are given to two spheres of different radii, the potential will be different on both spheres. This is because the potential depends on the radius of the sphere.
The formula for potential is given as:
V = kQ/r
Where,
V = potential
k = Coulomb's constant
Q = charge
r = radius
As we can see from the formula, the potential is inversely proportional to the radius. This means that the potential will be more on the smaller sphere and less on the bigger sphere.
Therefore, the correct answer is option B, i.e., the potential will be more on the smaller sphere.
To summarize:
- The potential depends on the radius of the sphere.
- The potential formula is V = kQ/r.
- The potential is inversely proportional to the radius.
- The potential will be more on the smaller sphere and less on the bigger sphere.
- Therefore, the correct answer is option B, i.e., the potential will be more on the smaller sphere.
It requires 4 J of work to move a charge of 20 C from point A to point B, separated by a distance of 0.2 cm. The potential difference between A and B in volts- a)0.2
- b)16
- c)5
- d)80
Correct answer is 'A'. Can you explain this answer?
It requires 4 J of work to move a charge of 20 C from point A to point B, separated by a distance of 0.2 cm. The potential difference between A and B in volts
a)
0.2
b)
16
c)
5
d)
80
|
Ishani Yadav answered |
Potential difference between two points is given by
Va - Vb = W/q0
Work, W = 2 J
Charge, q0 = 20 C
Potential difference = 2/20 = 0.1 V
The correct option is C.
The work done in bringing a unit positive charge from infinite distance to a point at distance x from a positive charge Q is W. Then the potential ϕ at that point is- a)WQ/x
- b)W
- c)W/x
- d)WQ
Correct answer is option 'B'. Can you explain this answer?
The work done in bringing a unit positive charge from infinite distance to a point at distance x from a positive charge Q is W. Then the potential ϕ at that point is
a)
WQ/x
b)
W
c)
W/x
d)
WQ
|
Dev Patel answered |
Electric potential at a point in an electric field is defined as the work done in bringing a unit positive charge from infinity to that point.
Or, V = W/q
Since charge is of magnitude unity, Hence electric potential at that point will be equal to the workdone ∴ ϕ = W
Or, V = W/q
Since charge is of magnitude unity, Hence electric potential at that point will be equal to the workdone ∴ ϕ = W
Two equal positive charges q1 = q2 = 2.0 μC. μC are located at x = 0, y =0.3 and x =0 and y = -0.3 m respectively. What are the magnitude and direction of the total electric force (expressed in Newton and degrees counter clockwise w.r.t x - axis) that q1 and q2 exert on a third charge Q = 4.0 μC. μC at x =0.4 and y = 0 m- a)0.46,0.00
- b)0.44,2.00
- c)0.42,1.00
- d)0.48,3.00
Correct answer is option 'A'. Can you explain this answer?
Two equal positive charges q1 = q2 = 2.0 μC. μC are located at x = 0, y =0.3 and x =0 and y = -0.3 m respectively. What are the magnitude and direction of the total electric force (expressed in Newton and degrees counter clockwise w.r.t x - axis) that q1 and q2 exert on a third charge Q = 4.0 μC. μC at x =0.4 and y = 0 m
a)
0.46,0.00
b)
0.44,2.00
c)
0.42,1.00
d)
0.48,3.00
|
|
Ankita Datta answered |
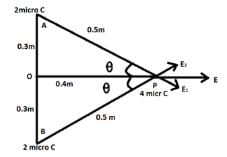
Side AP =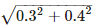 
= 0.5m Electric Field due to charge at A on point P = Elecric Field due to charge at B on 
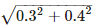= 0.5m Electric Field due to charge at A on point P = Elecric Field due to charge at B on point P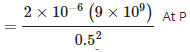 
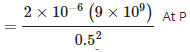
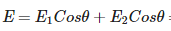
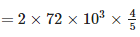
Where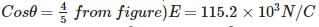 
So force due to this field on charge P
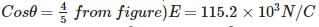So force due to this field on charge PF = qE = 4 x 10-6 x 115.2 x 103 F = 0.46N
Since this force in the direction of positive x axis so angle = 00
Find the electric field inside the sphere which carries a charge density proportional to the distance from the origin
ρ = kr- a)ρ/ε0
- b)ρr/ε0
- c) ρr2/ε0
- d)none of the above
Correct answer is option 'B'. Can you explain this answer?
Find the electric field inside the sphere which carries a charge density proportional to the distance from the origin
ρ = kr
ρ = kr
a)
ρ/ε0
b)
ρr/ε0
c)
ρr2/ε0
d)
none of the above
|
Geetika Tiwari answered |
We can start by using Gauss's Law to find the electric field. Gauss's Law states that the flux of the electric field through any closed surface is proportional to the charge enclosed by the surface. Mathematically, it can be written as:
∮E⋅dA = Qenc/ε0
where E is the electric field, dA is an infinitesimal area element on the surface, Qenc is the charge enclosed by the surface, and ε0 is the permittivity of free space.
In this case, we can choose a spherical Gaussian surface centered at the origin, with radius r. The charge enclosed by this surface is:
Qenc = ∫ρdV
where ρ is the charge density and dV is an infinitesimal volume element. Since the charge density is proportional to the distance from the origin, we can write:
ρ = k r
where k is a constant of proportionality. The integral becomes:
Qenc = ∫ρdV = k ∫r^2sinθdrdθdφ
where the limits of integration are 0 to r for r, 0 to π for θ, and 0 to 2π for φ. Evaluating the integral gives:
Qenc = (4/3)πk r^3
Now we can apply Gauss's Law to find the electric field. The flux of the electric field through the Gaussian surface is:
∮E⋅dA = E(4πr^2)
where we have used the fact that the surface area of a sphere is 4πr^2. Therefore, Gauss's Law gives us:
E(4πr^2) = (4/3)πk r^3/ε0
Solving for E, we get:
E = k r/3ε0
Therefore, the electric field inside the sphere is proportional to the distance from the origin, with a constant of proportionality k/3ε0.
∮E⋅dA = Qenc/ε0
where E is the electric field, dA is an infinitesimal area element on the surface, Qenc is the charge enclosed by the surface, and ε0 is the permittivity of free space.
In this case, we can choose a spherical Gaussian surface centered at the origin, with radius r. The charge enclosed by this surface is:
Qenc = ∫ρdV
where ρ is the charge density and dV is an infinitesimal volume element. Since the charge density is proportional to the distance from the origin, we can write:
ρ = k r
where k is a constant of proportionality. The integral becomes:
Qenc = ∫ρdV = k ∫r^2sinθdrdθdφ
where the limits of integration are 0 to r for r, 0 to π for θ, and 0 to 2π for φ. Evaluating the integral gives:
Qenc = (4/3)πk r^3
Now we can apply Gauss's Law to find the electric field. The flux of the electric field through the Gaussian surface is:
∮E⋅dA = E(4πr^2)
where we have used the fact that the surface area of a sphere is 4πr^2. Therefore, Gauss's Law gives us:
E(4πr^2) = (4/3)πk r^3/ε0
Solving for E, we get:
E = k r/3ε0
Therefore, the electric field inside the sphere is proportional to the distance from the origin, with a constant of proportionality k/3ε0.
The magnitude of electric field experienced by a charge at a certain distance from a source charge is equal to 64 N/C. What will be the magnitude of the electric field at four times that distance and with a source charge half as strong?- a)1 N/C
- b)2 N/C
- c)64 N/C
- d)128 N/C
Correct answer is option 'B'. Can you explain this answer?
The magnitude of electric field experienced by a charge at a certain distance from a source charge is equal to 64 N/C. What will be the magnitude of the electric field at four times that distance and with a source charge half as strong?
a)
1 N/C
b)
2 N/C
c)
64 N/C
d)
128 N/C
|
|
Ava Brown answered |
The magnitude of the electric field is given by Coulomb's Law, which states that the electric field (E) is directly proportional to the source charge (Q) and inversely proportional to the square of the distance (r) between the source charge and the point where the electric field is being measured. Mathematically, this can be expressed as:
E = k * (Q/r^2)
where k is the electrostatic constant.
In this question, we are given that the magnitude of the electric field at a certain distance (let's call it r1) is 64 N/C. Let's assume that the source charge at this distance is Q1.
So, we have:
64 = k * (Q1/r1^2) ...(1)
Now, we need to find the magnitude of the electric field at four times the distance (4r1) with a source charge half as strong (Q2 = Q1/2).
Using the same formula, we can write:
E' = k * (Q2/(4r1)^2) ...(2)
To find the magnitude of the electric field at 4r1, we can substitute 4r1 for r in equation (1):
64 = k * (Q1/(4r1)^2)
Simplifying this equation, we get:
64 = k * (Q1/16r1^2)
Multiplying both sides of the equation by 16, we get:
1024 = k * (Q1/r1^2)
This equation is equivalent to equation (1), which means that the magnitude of the electric field at 4r1 is also 64 N/C.
Now, let's substitute the values into equation (2) to find the magnitude of the electric field at 4r1 with a source charge half as strong:
E' = k * (Q2/(4r1)^2)
E' = k * ((Q1/2)/(4r1)^2)
E' = k * (Q1/8r1^2)
Since we know that the magnitude of the electric field at 4r1 is 64 N/C, we can write:
64 = k * (Q1/8r1^2)
Simplifying this equation, we get:
512 = k * (Q1/r1^2)
Comparing this equation with equation (1), we can see that the magnitude of the electric field at 4r1 with a source charge half as strong is 512 N/C.
Therefore, the correct answer is option B) 2 N/C.
E = k * (Q/r^2)
where k is the electrostatic constant.
In this question, we are given that the magnitude of the electric field at a certain distance (let's call it r1) is 64 N/C. Let's assume that the source charge at this distance is Q1.
So, we have:
64 = k * (Q1/r1^2) ...(1)
Now, we need to find the magnitude of the electric field at four times the distance (4r1) with a source charge half as strong (Q2 = Q1/2).
Using the same formula, we can write:
E' = k * (Q2/(4r1)^2) ...(2)
To find the magnitude of the electric field at 4r1, we can substitute 4r1 for r in equation (1):
64 = k * (Q1/(4r1)^2)
Simplifying this equation, we get:
64 = k * (Q1/16r1^2)
Multiplying both sides of the equation by 16, we get:
1024 = k * (Q1/r1^2)
This equation is equivalent to equation (1), which means that the magnitude of the electric field at 4r1 is also 64 N/C.
Now, let's substitute the values into equation (2) to find the magnitude of the electric field at 4r1 with a source charge half as strong:
E' = k * (Q2/(4r1)^2)
E' = k * ((Q1/2)/(4r1)^2)
E' = k * (Q1/8r1^2)
Since we know that the magnitude of the electric field at 4r1 is 64 N/C, we can write:
64 = k * (Q1/8r1^2)
Simplifying this equation, we get:
512 = k * (Q1/r1^2)
Comparing this equation with equation (1), we can see that the magnitude of the electric field at 4r1 with a source charge half as strong is 512 N/C.
Therefore, the correct answer is option B) 2 N/C.
The electric potential at a point (x,y) is given by: V=−Kxy. The electric field intensity a distance r from the origin varies as- a)r2
- b)r
- c)2r
- d)2r2
Correct answer is option 'B'. Can you explain this answer?
The electric potential at a point (x,y) is given by: V=−Kxy. The electric field intensity a distance r from the origin varies as
a)
r2
b)
r
c)
2r
d)
2r2
|
|
Mainak Patel answered |
Understanding Electric Potential
The electric potential (V) at a point (x,y) is given by the equation:
V = -Kxy
Here, K is a constant and the equation indicates that the potential is dependent on the product of the x and y coordinates.
Relationship Between Electric Field and Potential
The electric field intensity (E) can be derived from the electric potential using the relation:
E = -∇V
This means that the electric field is the negative gradient of the electric potential.
Calculating the Electric Field Components
1. Potential Function: Given V = -Kxy, we need to find the electric field components.
2. Gradient Calculation:
- The electric field components in the x and y directions are:
- Ex = -∂V/∂x = K*y
- Ey = -∂V/∂y = K*x
3. Magnitude of the Electric Field:
- The magnitude of the electric field E can be calculated as:
- E = √(Ex^2 + Ey^2) = √((Ky)^2 + (Kx)^2) = K√(x^2 + y^2)
Analyzing the Distance from the Origin
When we consider a distance r from the origin, we can express x and y in terms of r using polar coordinates:
- x = r*cos(θ)
- y = r*sin(θ)
Substituting these into the electric field expression gives:
E = K√(r^2) = Kr
Conclusion
Thus, the electric field intensity is directly proportional to the distance r from the origin, confirming that it varies as:
Option B: r
This shows that the electric field strength increases linearly with distance from the origin.
The electric potential (V) at a point (x,y) is given by the equation:
V = -Kxy
Here, K is a constant and the equation indicates that the potential is dependent on the product of the x and y coordinates.
Relationship Between Electric Field and Potential
The electric field intensity (E) can be derived from the electric potential using the relation:
E = -∇V
This means that the electric field is the negative gradient of the electric potential.
Calculating the Electric Field Components
1. Potential Function: Given V = -Kxy, we need to find the electric field components.
2. Gradient Calculation:
- The electric field components in the x and y directions are:
- Ex = -∂V/∂x = K*y
- Ey = -∂V/∂y = K*x
3. Magnitude of the Electric Field:
- The magnitude of the electric field E can be calculated as:
- E = √(Ex^2 + Ey^2) = √((Ky)^2 + (Kx)^2) = K√(x^2 + y^2)
Analyzing the Distance from the Origin
When we consider a distance r from the origin, we can express x and y in terms of r using polar coordinates:
- x = r*cos(θ)
- y = r*sin(θ)
Substituting these into the electric field expression gives:
E = K√(r^2) = Kr
Conclusion
Thus, the electric field intensity is directly proportional to the distance r from the origin, confirming that it varies as:
Option B: r
This shows that the electric field strength increases linearly with distance from the origin.
A long, hollow conducting cylinder is kept coaxially inside another long, hollow conducting cylinder of larger radius. Both the cylinders are initially electrically neutral.- a)No potential difference appears between the two cylinders when same charge density is given to both the cylinders.
- b)No potential difference appears between the two cylinders when a uniform line charge is kept along the axis of the cylinders.
- c)A potential difference appears between the two cylinders when a charge density is given to the outer cylinder.
- d)A potential difference appears between the two cylinders when a charge density is given to the inner cylinder.
Correct answer is option 'D'. Can you explain this answer?
A long, hollow conducting cylinder is kept coaxially inside another long, hollow conducting cylinder of larger radius. Both the cylinders are initially electrically neutral.
a)
No potential difference appears between the two cylinders when same charge density is given to both the cylinders.
b)
No potential difference appears between the two cylinders when a uniform line charge is kept along the axis of the cylinders.
c)
A potential difference appears between the two cylinders when a charge density is given to the outer cylinder.
d)
A potential difference appears between the two cylinders when a charge density is given to the inner cylinder.
|
Top Rankers answered |
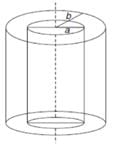
Let λ be the charge density on the inner cylinder.
For a < r < b, we get
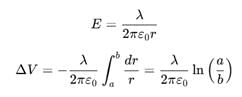
Hence, a potential difference appears between the two cylinders when a charge density is given to the inner cylinder.
Ionization of a neutral atom is the - a)only gain of one or more electrons
- b)only gain of one or more protons
- c)gain or loss of one or more electrons
- d)only gain of one or more neutrons
Correct answer is option 'C'. Can you explain this answer?
Ionization of a neutral atom is the
a)
only gain of one or more electrons
b)
only gain of one or more protons
c)
gain or loss of one or more electrons
d)
only gain of one or more neutrons
|
Ashwin Yadav answered |
Explanation:It is not possible to remove or add protons to atom, but electron can be added or removed by an atom easily so charge can be developed on an atom by removing or adding electrons, by adding electrons it becomes negative charged ,by removing electrons it becomes positive charged.
Electric field lines can be said to be - a)lines of equal Electric field
- b)drawing lines of electric fields
- c)lines of equal Electric voltage
- d)graphical representation of electric fields.
Correct answer is option 'D'. Can you explain this answer?
Electric field lines can be said to be
a)
lines of equal Electric field
b)
drawing lines of electric fields
c)
lines of equal Electric voltage
d)
graphical representation of electric fields.
|
|
Abhijeet Menon answered |
Explanation:Electric Field Lines can be defined as a curve which shows direction of electric field, when we draw tangent at its point. The concept of electric field was proposed by Michael Faraday, in the 19th century. He always thought that electric field lines can be used to describe and interpret the invisible electric field. Instead of using complex vector diagram every time, This pictorial representation or form is called electric field lines.Electric field lines can be used to describe electric field around a system of charges in a better way.
Three point charges +q, –2q and +q are placed at points (x = 0, y = a, z = 0), (x = 0, y = 0, z = 0) and (x = a, y = 0, z = 0) respectively. The magnitude and direction of the electric dipole moment vector of this charge assembly are- a)√2qa along the line joining points (x = 0, y = 0,
z = 0) and (x = a, y = a, z = 0) - b)qa along the line joining points (x = 0, y = 0,
z = 0) and (x = a, y = a, z = 0) - c)√2qa along + x direction
- d)√2qa along + y direction
Correct answer is option 'A'. Can you explain this answer?
Three point charges +q, –2q and +q are placed at points (x = 0, y = a, z = 0), (x = 0, y = 0, z = 0) and (x = a, y = 0, z = 0) respectively. The magnitude and direction of the electric dipole moment vector of this charge assembly are
a)
√2qa along the line joining points (x = 0, y = 0,
z = 0) and (x = a, y = a, z = 0)
z = 0) and (x = a, y = a, z = 0)
b)
qa along the line joining points (x = 0, y = 0,
z = 0) and (x = a, y = a, z = 0)
z = 0) and (x = a, y = a, z = 0)
c)
√2qa along + x direction
d)
√2qa along + y direction
|
|
Stepway Academy answered |
This consists of two dipoles, –q and +q with dipole moment along with the +y-direction and –q and +q along the x-direction.
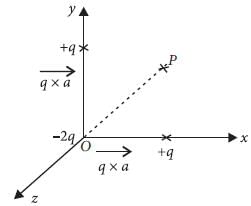
Along the direction 45° that is along OP, where P is (+a, +a, 0).
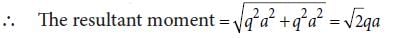
Along the direction 45° that is along OP, where P is (+a, +a, 0).
Two point charges A and B, having charges +Q and –Q respectively, are placed at certain distance apart and force acting between them is F. If 25% charge of A is transferred to B, then force between the charges becomes- a)4F/3
- b)F
- c)9F/16
- d)16F/9
Correct answer is option 'C'. Can you explain this answer?
Two point charges A and B, having charges +Q and –Q respectively, are placed at certain distance apart and force acting between them is F. If 25% charge of A is transferred to B, then force between the charges becomes
a)
4F/3
b)
F
c)
9F/16
d)
16F/9
|
Ambition Institute answered |
In case I :
In Case II :
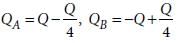
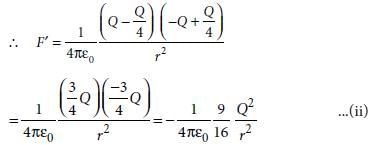
From equations (i) and (ii),
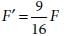
In Case II :
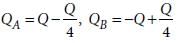
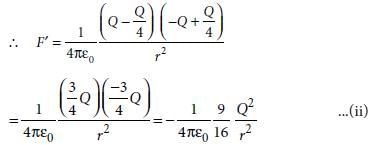
From equations (i) and (ii),
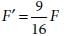
Chapter doubts & questions for Electrostatics (PHY) - MCAT Chemical and Physical Foundations 2025 is part of MCAT exam preparation. The chapters have been prepared according to the MCAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for MCAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Electrostatics (PHY) - MCAT Chemical and Physical Foundations in English & Hindi are available as part of MCAT exam.
Download more important topics, notes, lectures and mock test series for MCAT Exam by signing up for free.
MCAT Chemical and Physical Foundations
336 videos|223 docs|109 tests
|
