All questions of Communication System for Electronics and Communication Engineering (ECE) Exam
What is the carrier frequency in an AM wave when its highest frequency component is 850Hz and the bandwidth of the signal is 50Hz?- a)80 Hz
- b)695 Hz
- c)625 Hz
- d)825 Hz
Correct answer is option 'D'. Can you explain this answer?
What is the carrier frequency in an AM wave when its highest frequency component is 850Hz and the bandwidth of the signal is 50Hz?
a)
80 Hz
b)
695 Hz
c)
625 Hz
d)
825 Hz
|
|
Sarita Yadav answered |
Upper frequency = 850Hz
Bandwidth = 50Hz
Therefore lower Frequency = 850 - 50= 800 Hz
Carrier Frequency = (850-800)/2
= 825 Hz
Bandwidth = 50Hz
Therefore lower Frequency = 850 - 50= 800 Hz
Carrier Frequency = (850-800)/2
= 825 Hz
A 10 kW carrier is sinusoidally modulated by two carriers corresponding to a modulation index of 30% and 40% respectively. The total radiated power(is- a)11.25 kW
- b)12.5 kW
- c)15 kW
- d)17 kW
Correct answer is option 'A'. Can you explain this answer?
A 10 kW carrier is sinusoidally modulated by two carriers corresponding to a modulation index of 30% and 40% respectively. The total radiated power(is
a)
11.25 kW
b)
12.5 kW
c)
15 kW
d)
17 kW

|
Baishali Bajaj answered |
The required answer is 1 (1 + 0.42 + 0.32) or 11.25 kW.
A carrier is simultaneously modulated by two sine waves with modulation indices of 0.4 and 0.3. The resultant modulation index will be- a)1.0
- b)0.7
- c)0.5
- d)0.35
Correct answer is 'C'. Can you explain this answer?
A carrier is simultaneously modulated by two sine waves with modulation indices of 0.4 and 0.3. The resultant modulation index will be
a)
1.0
b)
0.7
c)
0.5
d)
0.35
|
|
Avinash Mehta answered |
Given: m1 = 0.4, m2 = 0.3
Resultant modulation index = α^2 = 0.3^2 + 0.4^2 = 0.5^2 or
α = 0.5.
A rate 1/2 convolution code with dfrec = 10 is used to encode a data requeence occurring at a rate of 1 kbps. The modulation is binary PSK. The DS spread spectrum sequence has a chip rate of 10 MHzQue: The coding gain is- a)7 dB
- b)12 dB
- c)14 dB
- d)24 dB
Correct answer is option 'A'. Can you explain this answer?
A rate 1/2 convolution code with dfrec = 10 is used to encode a data requeence occurring at a rate of 1 kbps. The modulation is binary PSK. The DS spread spectrum sequence has a chip rate of 10 MHz
Que: The coding gain is
a)
7 dB
b)
12 dB
c)
14 dB
d)
24 dB

|
Arjun Unni answered |
An amplifier has an operating spot noise figure of 10 dB when driven by a source of effective noise temperature 225 K.Que: In previous question what is the standard spot noisefigure of the cascade ?- a)10.3 dB
- b)12.2 dB
- c)14.9 dB
- d)17.6 dB
Correct answer is option 'B'. Can you explain this answer?
An amplifier has an operating spot noise figure of 10 dB when driven by a source of effective noise temperature 225 K.
Que: In previous question what is the standard spot noisefigure of the cascade ?
a)
10.3 dB
b)
12.2 dB
c)
14.9 dB
d)
17.6 dB

|
Subhankar Ghoshal answered |
A super heterodyne receiver is designed to receive transmitted signals between 5 and 10 MHz. High-side tuning is to be used. The tuning range of the local oscillator for IF frequency 500 kHz would be- a)4.5 MHz - 9.5 MHz
- b)5.5 MHz - 10.5 MHz
- c)4.5 MHz - 10.5 MHz
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
A super heterodyne receiver is designed to receive transmitted signals between 5 and 10 MHz. High-side tuning is to be used. The tuning range of the local oscillator for IF frequency 500 kHz would be
a)
4.5 MHz - 9.5 MHz
b)
5.5 MHz - 10.5 MHz
c)
4.5 MHz - 10.5 MHz
d)
None of the above

|
Varun Banerjee answered |
Since High-side tuning is used
In amplitude modulation, the modulation envelope has a peak value which is double the unmodulated carrier value. What is the value of the modulation index ?- a)25%
- b)50%
- c)75%
- d)100%
Correct answer is option 'D'. Can you explain this answer?
In amplitude modulation, the modulation envelope has a peak value which is double the unmodulated carrier value. What is the value of the modulation index ?
a)
25%
b)
50%
c)
75%
d)
100%

|
Pranavi Gupta answered |
The amplitude of a random signal is uniformly distributed between –5V and 5V. If the signal to quantization noise ratio required in uniformly quantizing the signal is 43.5dB, the step size of the quantization is approximately-- a)0.0333V
- b)0.05V
- c)0.0667V
- d)0.10V
Correct answer is option 'C'. Can you explain this answer?
The amplitude of a random signal is uniformly distributed between –5V and 5V. If the signal to quantization noise ratio required in uniformly quantizing the signal is 43.5dB, the step size of the quantization is approximately-
a)
0.0333V
b)
0.05V
c)
0.0667V
d)
0.10V

|
Imtiaz Ahmad answered |
Given; Signal to quantization noise = 43.5 dB
The amplitude of a random signal is uniformly distributed between –5V and 5V.
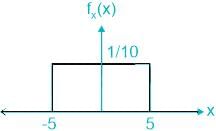
The amplitude of a random signal is uniformly distributed between –5V and 5V.

E[X2] = 52/3 = 25/3
E[XQE2] = δ2/12
SNR = (25/3)/ (δ2/12) = 100/ δ2
SNR (dB) = 10log(SNR)
⇒ 43.5 = 10log(SNR)
⇒ log(SNR) = 43.5/10
⇒ SNR= 104.35
Therefore
100/ δ2 = 104.35
⇒ δ2 = 100/104.35
⇒ δ = 0.0667
signal is sampled at 8 kHz and is quantized using 8 bit uniform quantizer. Assuming SNRq for a sinusoidal signal, the correct statement for PCM signal with a bit rate of R is- a)R = 32 kbps, SNRq = 25.8 dB
- b)R = 64 kbps, SNRq = 49.8 dB
- c)R = 64 kbps, SNRq = 55.8 dB
- d)R = 32 kbps, SNRq = 49.8 dB
Correct answer is option 'B'. Can you explain this answer?
signal is sampled at 8 kHz and is quantized using 8 bit uniform quantizer. Assuming SNRq for a sinusoidal signal, the correct statement for PCM signal with a bit rate of R is
a)
R = 32 kbps, SNRq = 25.8 dB
b)
R = 64 kbps, SNRq = 49.8 dB
c)
R = 64 kbps, SNRq = 55.8 dB
d)
R = 32 kbps, SNRq = 49.8 dB

|
Bhavya Rane answered |
Bit Rate = 8k x 8 = 64 kbps
Four signals g1(t) , g3(t), g2(t) and g4(t) are to be multiplexed and transmitted. g1(t) and g4(t) have a bandwidth of 4 kHz, and the remaining two signals have bandwidth of 8 kHz,. Each sample requires 8 bit for encoding. What is the minimum transmission bit rate of the system.- a)512 kbps
- b)16 kbps
- c)192 kbps
- d)384 kbps
Correct answer is option 'D'. Can you explain this answer?
Four signals g1(t) , g3(t), g2(t) and g4(t) are to be multiplexed and transmitted. g1(t) and g4(t) have a bandwidth of 4 kHz, and the remaining two signals have bandwidth of 8 kHz,. Each sample requires 8 bit for encoding. What is the minimum transmission bit rate of the system.
a)
512 kbps
b)
16 kbps
c)
192 kbps
d)
384 kbps

|
Subhankar Ghoshal answered |
signals g1(t) , g3(t), g2(t) and g4(t) will have 8 k, 8 k, 16 k and 16 k sample/sec at Nyquist rate. Thus 48000 sample/sec bit rate 48000 x 8 =384 kbps
The input to a linear delta modulator having fa step-size Δ = 0.628 is a sine wave with frequency fm and peak amplitude Em. If the sampling frequency fs = 40 kHz, the combination of the sinc-wave frequency and the peak amplitude, where slope overload will take place is- a)Em = 0.3V , fm = 8KHz
- b)Em = 1.5V , fm = 4kHz
- c)Em = 1.5 V , fm = 2kHz
- d)Em = 3.0V , fm = 1kHZ
Correct answer is option 'B'. Can you explain this answer?
The input to a linear delta modulator having fa step-size Δ = 0.628 is a sine wave with frequency fm and peak amplitude Em. If the sampling frequency fs = 40 kHz, the combination of the sinc-wave frequency and the peak amplitude, where slope overload will take place is
a)
Em = 0.3V , fm = 8KHz
b)
Em = 1.5V , fm = 4kHz
c)
Em = 1.5 V , fm = 2kHz
d)
Em = 3.0V , fm = 1kHZ

|
Mrinalini Chavan answered |
Linear Delta Modulation and Slope Overload
Linear Delta Modulation (LDM) is a type of analog-to-digital conversion technique used in communication systems. It is a variant of Delta Modulation (DM) in which the quantization step size is fixed and linearly proportional to the amplitude of the input signal.
Slope Overload is a phenomenon that occurs in LDM when the amplitude of the input signal exceeds the maximum permissible slope of the quantization step. This leads to distortion and errors in the output signal.
Given Parameters
In this question, we are given the following parameters:
- Fast step-size = 0.628
- Sampling frequency fs = 40 kHz
- Input signal = sine wave with frequency fm and peak amplitude Em
We need to determine the combination of frequency fm and peak amplitude Em, where slope overload will take place.
Solution Steps
To solve this problem, we need to use the formula for the maximum permissible slope of the LDM quantization step:
Smax = 2 * δ * fs
where Smax is the maximum permissible slope, δ is the fast step-size, and fs is the sampling frequency.
We know that the input signal is a sine wave with frequency fm and peak amplitude Em. Therefore, its maximum slope is given by:
S = Em * 2π * fm
To avoid slope overload, we need to ensure that Smax > S. Substituting the given values, we get:
2 * δ * fs > Em * 2π * fm
Simplifying, we get:
Em/fm < (2="" *="" δ="" *="" fs)="" />
Substituting the given values, we get:
Em/fm < (2="" *="" 0.628="" *="" 40,000)="" />
Em/fm < />
Therefore, the combination of frequency fm and peak amplitude Em, where slope overload will take place, is:
Em = 1.5 V, fm = 4 kHz
Option B is the correct answer.
Conclusion
In this question, we have learned about Linear Delta Modulation and Slope Overload. We have solved a numerical problem to determine the combination of frequency and amplitude where slope overload will occur in an LDM system.
Linear Delta Modulation (LDM) is a type of analog-to-digital conversion technique used in communication systems. It is a variant of Delta Modulation (DM) in which the quantization step size is fixed and linearly proportional to the amplitude of the input signal.
Slope Overload is a phenomenon that occurs in LDM when the amplitude of the input signal exceeds the maximum permissible slope of the quantization step. This leads to distortion and errors in the output signal.
Given Parameters
In this question, we are given the following parameters:
- Fast step-size = 0.628
- Sampling frequency fs = 40 kHz
- Input signal = sine wave with frequency fm and peak amplitude Em
We need to determine the combination of frequency fm and peak amplitude Em, where slope overload will take place.
Solution Steps
To solve this problem, we need to use the formula for the maximum permissible slope of the LDM quantization step:
Smax = 2 * δ * fs
where Smax is the maximum permissible slope, δ is the fast step-size, and fs is the sampling frequency.
We know that the input signal is a sine wave with frequency fm and peak amplitude Em. Therefore, its maximum slope is given by:
S = Em * 2π * fm
To avoid slope overload, we need to ensure that Smax > S. Substituting the given values, we get:
2 * δ * fs > Em * 2π * fm
Simplifying, we get:
Em/fm < (2="" *="" δ="" *="" fs)="" />
Substituting the given values, we get:
Em/fm < (2="" *="" 0.628="" *="" 40,000)="" />
Em/fm < />
Therefore, the combination of frequency fm and peak amplitude Em, where slope overload will take place, is:
Em = 1.5 V, fm = 4 kHz
Option B is the correct answer.
Conclusion
In this question, we have learned about Linear Delta Modulation and Slope Overload. We have solved a numerical problem to determine the combination of frequency and amplitude where slope overload will occur in an LDM system.
An amplifier has an average standard noise figure of 2.0 dB and an average operating noise figure of 6.5 dB when used with a source of average effective source temperature 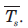 The
The 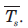 is
is - a)156.32 K
- b)100.81 K
- c)48.93 K
- d)None of the above
Correct answer is option 'D'. Can you explain this answer?
An amplifier has an average standard noise figure of 2.0 dB and an average operating noise figure of 6.5 dB when used with a source of average effective source temperature 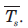 The
The  is
is
a)
156.32 K
b)
100.81 K
c)
48.93 K
d)
None of the above

|
Moumita Chopra answered |
An amplifier has three stages for which Te1 = 150 K (first stage), Te3 = 350 K, and Te3 = 600 K (output stage). Available power gain of the first stage is 10 and overall input effective noise temperature is 190 KQue: What is the cascade's operating spot noise figure when used with a source of noise temperature Ts = 50 K- a)1.34 dB
- b)3.96 dB
- c)6.81 dB
- d)None of the above.
Correct answer is option 'C'. Can you explain this answer?
An amplifier has three stages for which Te1 = 150 K (first stage), Te3 = 350 K, and Te3 = 600 K (output stage). Available power gain of the first stage is 10 and overall input effective noise temperature is 190 K
Que: What is the cascade's operating spot noise figure when used with a source of noise temperature Ts = 50 K
a)
1.34 dB
b)
3.96 dB
c)
6.81 dB
d)
None of the above.

|
Nitya Sharma answered |
A CDMA system consist of 15 equal power user that transmit information at a rate of 10 kbps, each using a DS spread spectrum signal operating at chip rate of 1 MHz. The modulation scheme is BPSKQue: The value of εb/Jb is- a)8.54 dB
- b)7.14 dB
- c)17.08 dB
- d)14.28 dB
Correct answer is option 'A'. Can you explain this answer?
A CDMA system consist of 15 equal power user that transmit information at a rate of 10 kbps, each using a DS spread spectrum signal operating at chip rate of 1 MHz. The modulation scheme is BPSK
Que: The value of εb/Jb is
a)
8.54 dB
b)
7.14 dB
c)
17.08 dB
d)
14.28 dB

|
Sameer Verma answered |
We have Nu = 15 users transmitting at a rate of 10,000 bps each, in a bandwidth of W =1MHz.
An amplifier has an operating spot noise figure of 10 dB when driven by a source of effective noise temperature 225 K.Que: If a matched attenuator with a loss of 3.2 dB isplaced between the source and the amplifier's input,what is the operating spot noise figure of the attenuator's amplifier cascade if the attenuator's physicaltemperature is 290 K ?- a)9 dB
- b)10.4 dB
- c)11.3 dB
- d)13.3 dB
Correct answer is option 'D'. Can you explain this answer?
An amplifier has an operating spot noise figure of 10 dB when driven by a source of effective noise temperature 225 K.
Que: If a matched attenuator with a loss of 3.2 dB isplaced between the source and the amplifier's input,what is the operating spot noise figure of the attenuator's amplifier cascade if the attenuator's physicaltemperature is 290 K ?
a)
9 dB
b)
10.4 dB
c)
11.3 dB
d)
13.3 dB

|
Aditya Majumdar answered |
In a fast FH spread spectrum system, the information is transmitted via FSK with non coherent detection. Suppose there are N = 3 hops/bit with hard decision decoding of the signal in each hop. The channel is AWGN with power spectral density 1/2 N0 and an SNR 20-13 dB (total SNR over the three hops)Que: The probability of error for this system is- a)0.013
- b)0.0013
- c)0.049
- d)0.0049
Correct answer is option 'B'. Can you explain this answer?
In a fast FH spread spectrum system, the information is transmitted via FSK with non coherent detection. Suppose there are N = 3 hops/bit with hard decision decoding of the signal in each hop. The channel is AWGN with power spectral density 1/2 N0 and an SNR 20-13 dB (total SNR over the three hops)
Que: The probability of error for this system is
a)
0.013
b)
0.0013
c)
0.049
d)
0.0049

|
Ankit Mukherjee answered |
The total SNR for three hops is 20 ~ 13 dB. Therefore the SNR per hop is 20/3. The probability of a chip error with non-coherent detection is
A joint sample space for two random variable X and Y has four elements (1, 1), (2, 2), (3, 3) and (4, 4). Probabilities of these elements are 0.1, 0.35, 0.05 and 0.5 respectively.Que: The probability of the event {X ≤ 2.5, Y ≤ 6} is- a)0.45
- b)0.50
- c)0.55
- d)0.60
Correct answer is option 'A'. Can you explain this answer?
A joint sample space for two random variable X and Y has four elements (1, 1), (2, 2), (3, 3) and (4, 4). Probabilities of these elements are 0.1, 0.35, 0.05 and 0.5 respectively.
Que: The probability of the event {X ≤ 2.5, Y ≤ 6} is
a)
0.45
b)
0.50
c)
0.55
d)
0.60

|
Om Pillai answered |
A rate 1/2 convolution code with dfrec = 10 is used to encode a data requeence occurring at a rate of 1 kbps. The modulation is binary PSK. The DS spread spectrum sequence has a chip rate of 10 MHzQue: The processing gain is- a)14 dB
- b)37 dB
- c)58 dB
- d)104 dB
Correct answer is option 'B'. Can you explain this answer?
A rate 1/2 convolution code with dfrec = 10 is used to encode a data requeence occurring at a rate of 1 kbps. The modulation is binary PSK. The DS spread spectrum sequence has a chip rate of 10 MHz
Que: The processing gain is
a)
14 dB
b)
37 dB
c)
58 dB
d)
104 dB

|
Rutuja Deshpande answered |
The processing gain
Three identical amplifier, each having a spot effective input noise temperature of 125 K and available power G are cascaded. The overall spot effective input noise temperature of the cascade is 155 K. The G is- a)3
- b)5
- c)7
- d)9
Correct answer is option 'B'. Can you explain this answer?
Three identical amplifier, each having a spot effective input noise temperature of 125 K and available power G are cascaded. The overall spot effective input noise temperature of the cascade is 155 K. The G is
a)
3
b)
5
c)
7
d)
9

|
Aditya Patel answered |
Suppose we wish to transmit the signal x(t) = sin 200πt + 2 sin 400πt using a modulation that create the signal g(t) = x(t) sin 400πt. If the product g(t) sin 400πt is passed through an ideal LPF with cutoff frequency 400π and pass band gain of 2, the signal obtained at the output of the LPF is- a)sin200πt
- b)1/2 sin200πt
- c)2sin 200πt
- d)0
Correct answer is option 'A'. Can you explain this answer?
Suppose we wish to transmit the signal x(t) = sin 200πt + 2 sin 400πt using a modulation that create the signal g(t) = x(t) sin 400πt. If the product g(t) sin 400πt is passed through an ideal LPF with cutoff frequency 400π and pass band gain of 2, the signal obtained at the output of the LPF is
a)
sin200πt
b)
1/2 sin200πt
c)
2sin 200πt
d)
0

|
Manisha Chavan answered |
In a DSB-SC system with 100% modulation, the power saving is- a)50%
- b)66%
- c)75%
- d)100%
Correct answer is option 'B'. Can you explain this answer?
In a DSB-SC system with 100% modulation, the power saving is
a)
50%
b)
66%
c)
75%
d)
100%

|
Shivam Sharma answered |
This is so because the power is suppressed by two thirds of the total. hence the power saving is 66%.
A CDMA system consist of 15 equal power user that transmit information at a rate of 10 kbps, each using a DS spread spectrum signal operating at chip rate of 1 MHz. The modulation scheme is BPSKQue: The Processing gain is- a)0.01
- b)100
- c)0.1
- d)10
Correct answer is option 'B'. Can you explain this answer?
A CDMA system consist of 15 equal power user that transmit information at a rate of 10 kbps, each using a DS spread spectrum signal operating at chip rate of 1 MHz. The modulation scheme is BPSK
Que: The Processing gain is
a)
0.01
b)
100
c)
0.1
d)
10

|
Shivani Choudhury answered |
A diode detector has a load of 1 kΩ shunted by a 10000 pF capacitor. The diode has a forward resistance of 1 Ω. The maximum permissible depth of modulation,so as to avoid diagonal clipping, with modulating signal frequency fo 10 kHz will be- a)0.847
- b)0.628
- c)0.734
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
A diode detector has a load of 1 kΩ shunted by a 10000 pF capacitor. The diode has a forward resistance of 1 Ω. The maximum permissible depth of modulation,so as to avoid diagonal clipping, with modulating signal frequency fo 10 kHz will be
a)
0.847
b)
0.628
c)
0.734
d)
None of the above

|
Diya Dasgupta answered |
The mean value of the random variableW = (X + 3Y)2 + 2X + 3 is- a)98 + √3
- b)98 - √3
- c)49 - √3
- d)49 + √3
Correct answer is option 'B'. Can you explain this answer?
The mean value of the random variable
W = (X + 3Y)2 + 2X + 3 is
a)
98 + √3
b)
98 - √3
c)
49 - √3
d)
49 + √3
|
|
Rajat Kapoor answered |
Mean Value of Random Variable
The mean value of a random variable is a measure of its central tendency. It represents the average value that the random variable takes on over a large number of trials.
In this question, we are given a random variable W which is defined as follows:
W = (X + 3Y)^2 - 2X + 3
We need to find the mean value of this random variable.
Breaking down the Random Variable
To find the mean value of a random variable, we need to calculate the expected value of that variable. In this case, we need to calculate the expected value of W.
To do this, we need to break down the random variable W into its constituent random variables X and Y.
W = (X + 3Y)^2 - 2X + 3
Expanding the square term, we get:
W = (X^2 + 6XY + 9Y^2) - 2X + 3
Simplifying further, we get:
W = X^2 + 6XY + 9Y^2 - 2X + 3
Now, we can calculate the expected value of W by taking the expected value of each term separately.
Calculating the Expected Value
To calculate the expected value, we need to know the probability distribution of the random variables X and Y. Without this information, we cannot calculate the mean value of W accurately.
However, we can make some assumptions about the probability distribution to simplify the calculation. Let's assume that X and Y are independent and identically distributed random variables with a mean of 0 and a variance of 1.
Using these assumptions, we can calculate the expected value of each term in the random variable W.
E(X^2) = Var(X) + E(X)^2 = 1 + 0^2 = 1
E(6XY) = E(X) * E(Y) * 6 = 0 * 0 * 6 = 0
E(9Y^2) = Var(Y) + E(Y)^2 = 1 + 0^2 = 1
E(-2X) = -2 * E(X) = -2 * 0 = 0
E(3) = 3
Summing up these expected values, we get:
E(W) = E(X^2) + E(6XY) + E(9Y^2) + E(-2X) + E(3)
= 1 + 0 + 1 + 0 + 3
= 5
Therefore, the mean value of the random variable W is 5.
Conclusion
The mean value of the random variable W, given by W = (X + 3Y)^2 - 2X + 3, is 5. Therefore, none of the given options (a), b), c), d)) is the correct answer.
The mean value of a random variable is a measure of its central tendency. It represents the average value that the random variable takes on over a large number of trials.
In this question, we are given a random variable W which is defined as follows:
W = (X + 3Y)^2 - 2X + 3
We need to find the mean value of this random variable.
Breaking down the Random Variable
To find the mean value of a random variable, we need to calculate the expected value of that variable. In this case, we need to calculate the expected value of W.
To do this, we need to break down the random variable W into its constituent random variables X and Y.
W = (X + 3Y)^2 - 2X + 3
Expanding the square term, we get:
W = (X^2 + 6XY + 9Y^2) - 2X + 3
Simplifying further, we get:
W = X^2 + 6XY + 9Y^2 - 2X + 3
Now, we can calculate the expected value of W by taking the expected value of each term separately.
Calculating the Expected Value
To calculate the expected value, we need to know the probability distribution of the random variables X and Y. Without this information, we cannot calculate the mean value of W accurately.
However, we can make some assumptions about the probability distribution to simplify the calculation. Let's assume that X and Y are independent and identically distributed random variables with a mean of 0 and a variance of 1.
Using these assumptions, we can calculate the expected value of each term in the random variable W.
E(X^2) = Var(X) + E(X)^2 = 1 + 0^2 = 1
E(6XY) = E(X) * E(Y) * 6 = 0 * 0 * 6 = 0
E(9Y^2) = Var(Y) + E(Y)^2 = 1 + 0^2 = 1
E(-2X) = -2 * E(X) = -2 * 0 = 0
E(3) = 3
Summing up these expected values, we get:
E(W) = E(X^2) + E(6XY) + E(9Y^2) + E(-2X) + E(3)
= 1 + 0 + 1 + 0 + 3
= 5
Therefore, the mean value of the random variable W is 5.
Conclusion
The mean value of the random variable W, given by W = (X + 3Y)^2 - 2X + 3, is 5. Therefore, none of the given options (a), b), c), d)) is the correct answer.
Suppose Y is a random variable representing the number of successes in 5 independent Bernoulli trials with success probability p = 0.6. What is the probability that Y equals 3?- a)0.3456
- b)0.303
- c)0.031
- d)0.009
Correct answer is option 'A'. Can you explain this answer?
Suppose Y is a random variable representing the number of successes in 5 independent Bernoulli trials with success probability p = 0.6. What is the probability that Y equals 3?
a)
0.3456
b)
0.303
c)
0.031
d)
0.009

|
Starcoders answered |
Y follows a Binomial distribution with parameters n = 5 (number of trials) and p = 0.6 (probability of success).
The probability mass function for a binomial random variable is:
P(Y = k) = C(n, k) * p^k * (1 - p)^(n - k)
Where C(n, k) is the combination of n items taken k at a time.
For Y = 3:
C(5, 3) = 10
P(Y = 3) = 10 * (0.6)^3 * (0.4)^2
Calculate:
(0.6)3 = 0.216
(0.4)2 = 0.16
P(Y = 3) = 10 * 0.216 * 0.16 = 10 * 0.03456 = 0.3456
A random process consists of three samples function X(t, s1 ) = 2, X(t, s2 ) = 2cos t1 and X(t, s3 ) = 3sint - each occurring with equal probability. The process is- a)First order stationary
- b)Second order stationary
- c)Wide-sense stationary
- d)Not stationary in any sense
Correct answer is option 'D'. Can you explain this answer?
A random process consists of three samples function X(t, s1 ) = 2, X(t, s2 ) = 2cos t1 and X(t, s3 ) = 3sint - each occurring with equal probability. The process is
a)
First order stationary
b)
Second order stationary
c)
Wide-sense stationary
d)
Not stationary in any sense

|
Navya Sarkar answered |
The mean value is time dependent so X (t) is not stationary in any sense.
An amplifier has a standard spot noise figure F0 = 6.31 (8.0 dB). The amplifier, that is used to amplify the output of an antenna have antenna temperature of Ta = 180 KQue: The effective input noise temperature of this amplifier is- a)2520 K
- b)2120 K
- c)2710 K
- d)1540 K
Correct answer is option 'D'. Can you explain this answer?
An amplifier has a standard spot noise figure F0 = 6.31 (8.0 dB). The amplifier, that is used to amplify the output of an antenna have antenna temperature of Ta = 180 K
Que: The effective input noise temperature of this amplifier is
a)
2520 K
b)
2120 K
c)
2710 K
d)
1540 K

|
Moumita Chopra answered |
The number of cars arriving at ICICI bank drive-in window during 10-min period is Poisson random variable X with b = 2.Que : The probability that more than 3 cars will arrive during any 10 min period is- a)0.249
- b)0.143
- c)0.346
- d)0.543
Correct answer is option 'B'. Can you explain this answer?
The number of cars arriving at ICICI bank drive-in window during 10-min period is Poisson random variable X with b = 2.
Que : The probability that more than 3 cars will arrive during any 10 min period is
a)
0.249
b)
0.143
c)
0.346
d)
0.543

|
Kritika Shah answered |
A signal having a bandwidth of 5 MHz is transmitted using the Pulse code modulation (PCM) scheme as follows. The signal is sampled at a rate of 50% above the Nyquist rate and quantized into 256 levels. The binary pulse rate of the PCM signal in Mbits per second is ___.- a)120
- b)134
- c)340
- d)145
Correct answer is option 'A'. Can you explain this answer?
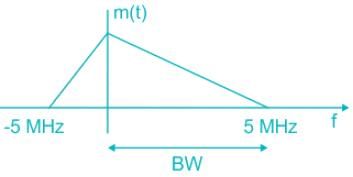
A signal having a bandwidth of 5 MHz is transmitted using the Pulse code modulation (PCM) scheme as follows. The signal is sampled at a rate of 50% above the Nyquist rate and quantized into 256 levels. The binary pulse rate of the PCM signal in Mbits per second is ___.
a)
120
b)
134
c)
340
d)
145

|
Starcoders answered |


A sinusoidal message signal is converted to a PCM signal using a uniform quantizer. The required signal-to-quantization noise ratio (SQNR) at the output of the quantizer is 40 dB. The minimum number of bits per sample needed to achieve the desired SQNR is __________ . - a)7
- b)10
- c)5
- d)3
Correct answer is option 'A'. Can you explain this answer?
A sinusoidal message signal is converted to a PCM signal using a uniform quantizer. The required signal-to-quantization noise ratio (SQNR) at the output of the quantizer is 40 dB. The minimum number of bits per sample needed to achieve the desired SQNR is __________ .
a)
7
b)
10
c)
5
d)
3
|
|
Diya Choudhary answered |
Calculation of Minimum Number of Bits per Sample
Given:
Signal-to-quantization noise ratio (SQNR) = 40 dB
Formula:
SQNR = 6.02 * N + 1.76 dB, where N is the number of bits per sample
Calculation:
40 = 6.02 * N + 1.76
38.24 = 6.02 * N
N ≈ 6.35
Minimum number of bits per sample needed = 7
Therefore, the minimum number of bits per sample needed to achieve the desired SQNR of 40 dB is 7.
Given:
Signal-to-quantization noise ratio (SQNR) = 40 dB
Formula:
SQNR = 6.02 * N + 1.76 dB, where N is the number of bits per sample
Calculation:
40 = 6.02 * N + 1.76
38.24 = 6.02 * N
N ≈ 6.35
Minimum number of bits per sample needed = 7
Therefore, the minimum number of bits per sample needed to achieve the desired SQNR of 40 dB is 7.
Consider a linear DM system designed to accommodate analog message signals limited to bandwidth of 3.5 kHz. A sinusoidal test signals of amplitude Amax = 1 V and frequency fm = 800 Hz is applied to system. The sampling rate of the system is 64 kHz.Que: The granular-noise power would be- a)1.68 x 10-3 W
- b)2.86 x 10-4 W
- c)2.48 x 10-3 W
- d)1.12 x 10-4 W
Correct answer is option 'D'. Can you explain this answer?
Consider a linear DM system designed to accommodate analog message signals limited to bandwidth of 3.5 kHz. A sinusoidal test signals of amplitude Amax = 1 V and frequency fm = 800 Hz is applied to system. The sampling rate of the system is 64 kHz.
Que: The granular-noise power would be
a)
1.68 x 10-3 W
b)
2.86 x 10-4 W
c)
2.48 x 10-3 W
d)
1.12 x 10-4 W

|
Nidhi Tiwari answered |
A slow FH binary FSK system with non coherent detection operates at ε0/J0 10, with hopping bandwidth of 2 GHz, and a bit rate of 10 kbps.Que: The minimum hop rate for a FH spread spectrum system that will prevent a jammer from operating five onives away from the receiver is- a)3.2 bHz
- b)3.2 MHz
- c)18.6 MHz
- d)18.6 kHz
Correct answer is option 'D'. Can you explain this answer?
A slow FH binary FSK system with non coherent detection operates at ε0/J0 10, with hopping bandwidth of 2 GHz, and a bit rate of 10 kbps.
Que: The minimum hop rate for a FH spread spectrum system that will prevent a jammer from operating five onives away from the receiver is
a)
3.2 bHz
b)
3.2 MHz
c)
18.6 MHz
d)
18.6 kHz
|
|
Jai Kapoor answered |
Minimum Hop Rate Calculation:
- The minimum hop rate required to prevent a jammer from operating five onives away from the receiver can be calculated using the formula:
f_min = 2 * bandwidth * (d_c / λ_c)
where:
f_min = minimum hop rate
bandwidth = hopping bandwidth (2 GHz in this case)
d_c = distance from the jammer to the receiver (5 onives in this case)
λ_c = speed of light (3 * 10^8 m/s)
- Substituting the given values into the formula:
f_min = 2 * 2 * 10^9 * (5 * 0.010) / (3 * 10^8)
f_min ≈ 0.0667 GHz ≈ 66.7 MHz
Therefore, the minimum hop rate required to prevent a jammer from operating five onives away from the receiver is approximately 66.7 MHz, which is closest to option 'd' (18.6 kHz).
- The minimum hop rate required to prevent a jammer from operating five onives away from the receiver can be calculated using the formula:
f_min = 2 * bandwidth * (d_c / λ_c)
where:
f_min = minimum hop rate
bandwidth = hopping bandwidth (2 GHz in this case)
d_c = distance from the jammer to the receiver (5 onives in this case)
λ_c = speed of light (3 * 10^8 m/s)
- Substituting the given values into the formula:
f_min = 2 * 2 * 10^9 * (5 * 0.010) / (3 * 10^8)
f_min ≈ 0.0667 GHz ≈ 66.7 MHz
Therefore, the minimum hop rate required to prevent a jammer from operating five onives away from the receiver is approximately 66.7 MHz, which is closest to option 'd' (18.6 kHz).
Delhi averages three murder per week and their occurrences follow a poission distribution.Que:How many weeds per year (average) can the Delhi expect the number of murders per week to equal orexceed the average number per week ?- a)15
- b)20
- c)25
- d)30
Correct answer is option 'D'. Can you explain this answer?
Delhi averages three murder per week and their occurrences follow a poission distribution.
Que:How many weeds per year (average) can the Delhi expect the number of murders per week to equal orexceed the average number per week ?
a)
15
b)
20
c)
25
d)
30

|
Arya Kaur answered |
Average number of weeks per year that number of murder exceeds the average
An amplifier has three stages for which Te1 = 200 K (first stage), Te2 = 450 K, and Te3 = 1000K (last stage). If the available power gain of the second stage is 5, what gain must the first stage have to guarantee an effective input noise temperature of 250 K ?- a)10
- b)13
- c)16
- d)19
Correct answer is option 'B'. Can you explain this answer?
An amplifier has three stages for which Te1 = 200 K (first stage), Te2 = 450 K, and Te3 = 1000K (last stage). If the available power gain of the second stage is 5, what gain must the first stage have to guarantee an effective input noise temperature of 250 K ?
a)
10
b)
13
c)
16
d)
19

|
Subhankar Ghoshal answered |
A CDMA system consist of 15 equal power user that transmit information at a rate of 10 kbps, each using a DS spread spectrum signal operating at chip rate of 1 MHz. The modulation scheme is BPSKQue: How much should the processing gain be increased to allow for doubling the number of users with affecting the autopad SNR- a)1.46 MHz
- b)2.07 MHz
- c)4.93 MHz
- d)2.92 MHz
Correct answer is option 'B'. Can you explain this answer?
A CDMA system consist of 15 equal power user that transmit information at a rate of 10 kbps, each using a DS spread spectrum signal operating at chip rate of 1 MHz. The modulation scheme is BPSK
Que: How much should the processing gain be increased to allow for doubling the number of users with affecting the autopad SNR
a)
1.46 MHz
b)
2.07 MHz
c)
4.93 MHz
d)
2.92 MHz

|
Srishti Chopra answered |
A slow FH binary FSK system with non coherent detection operates at ε0/J0 10, with hopping bandwidth of 2 GHz, and a bit rate of 10 kbps.Que: If the jammer operates as a partial band jammar, the bandwidth occupancy for worst case jamming is- a)0.4 GHz
- b)0.6 GHz
- c)0.7 GHz
- d)0.9 GHz
Correct answer is option 'A'. Can you explain this answer?
A slow FH binary FSK system with non coherent detection operates at ε0/J0 10, with hopping bandwidth of 2 GHz, and a bit rate of 10 kbps.
Que: If the jammer operates as a partial band jammar, the bandwidth occupancy for worst case jamming is
a)
0.4 GHz
b)
0.6 GHz
c)
0.7 GHz
d)
0.9 GHz

|
Sparsh Unni answered |
The bandwidth of the worst partial-band jammer is α * W , where
An amplifier has three stages for which Te1 = 150 K (first stage), Te3 = 350 K, and Te3 = 600 K (output stage). Available power gain of the first stage is 10 and overall input effective noise temperature is 190 KQue: The cascade's standard spot noise figure is- a)1.3 dB
- b)2.2 dB
- c)4.3 dB
- d)5.3 dB
Correct answer is option 'B'. Can you explain this answer?
An amplifier has three stages for which Te1 = 150 K (first stage), Te3 = 350 K, and Te3 = 600 K (output stage). Available power gain of the first stage is 10 and overall input effective noise temperature is 190 K
Que: The cascade's standard spot noise figure is
a)
1.3 dB
b)
2.2 dB
c)
4.3 dB
d)
5.3 dB

|
Manisha Chavan answered |
An FH binary orthogonal FSK system employs an m = 15 stage liner feedback shift register that generates an ML sequence. Each state of the shift register selects one of L non over lapping frequency bands in the hopping pattern. The bit rate is 100 bits/s. The demodulator employ non coherent detection.Que: If the hop rate is one per bit, the hopping band width for this channel is- a)6.5534 MHz
- b)9.4369 MHz
- c)2.6943 MHz
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
An FH binary orthogonal FSK system employs an m = 15 stage liner feedback shift register that generates an ML sequence. Each state of the shift register selects one of L non over lapping frequency bands in the hopping pattern. The bit rate is 100 bits/s. The demodulator employ non coherent detection.
Que: If the hop rate is one per bit, the hopping band width for this channel is
a)
6.5534 MHz
b)
9.4369 MHz
c)
2.6943 MHz
d)
None of the above

|
Mrinalini Chavan answered |
The length of the shift-register sequence is
L = 2m - 1215 - 1 = 32767 bits
For binary FSK modulation, the minimum frequency separation is 2/T, where 1/T is the symbol (bit) rate.
The hop rate is 100 hops/sec. Since the shift register has L = 32767 states and each state utilizes a bandwidth of 2/T = 200 Hz, then the total bandwidth for the FH signal is 6.5534 MHz.
The hop rate is 100 hops/sec. Since the shift register has L = 32767 states and each state utilizes a bandwidth of 2/T = 200 Hz, then the total bandwidth for the FH signal is 6.5534 MHz.
The output signal-to-quantization-noise ratio of a 10-bit PCM was found to be 30 dB. The desired SNR is 42 dB. It can be increased by increasing the number of quantization level.In this way the fractional increase in the transmission bandwidth would be (assume log210 = 0.3)- a)20%
- b)30%
- c)40%
- d)50%
Correct answer is option 'A'. Can you explain this answer?
The output signal-to-quantization-noise ratio of a 10-bit PCM was found to be 30 dB. The desired SNR is 42 dB. It can be increased by increasing the number of quantization level.In this way the fractional increase in the transmission bandwidth would be (assume log210 = 0.3)
a)
20%
b)
30%
c)
40%
d)
50%

|
Varun Banerjee answered |
= log C
+ 20 nlog2 =
α + 6 ndB. This equation shows that increasing n by one bits increase the by 6 dB.
Hence an increase in the SNR by 12 dB can be accomplished by increasing 9is form 10 to 12, the transmission bandwidth would be increased by 20%
Hence an increase in the SNR by 12 dB can be accomplished by increasing 9is form 10 to 12, the transmission bandwidth would be increased by 20%
Three analog signals, having bandwidths 1200 Hz, 600 Hz and 600 Hz, are sampled at their respective Nyquist rates, encoded with 12 bit words, and time division multiplexed. The bit rate for the multiplexed signal is- a)115.2 kbps
- b)28.8 kbps
- c)57.6 kbps
- d)38.4 kbps
Correct answer is option 'C'. Can you explain this answer?
Three analog signals, having bandwidths 1200 Hz, 600 Hz and 600 Hz, are sampled at their respective Nyquist rates, encoded with 12 bit words, and time division multiplexed. The bit rate for the multiplexed signal is
a)
115.2 kbps
b)
28.8 kbps
c)
57.6 kbps
d)
38.4 kbps

|
Pranavi Gupta answered |
Analog signals, having bandwidth 1200 Hz, 600 Hz and 600 Hz have 2400, 1200 samples/sec at Nyquist rate. Hence 48000 sample/sec
bit rate = 48000 sample/sec x 12 = 57.6 kbps
The random variables X and Y have variances 0.2 and 0.5 respectively. Let Z= 5X-2Y. The variance of Z is?- a)7
- b)5
- c)4
- d)3
Correct answer is option 'A'. Can you explain this answer?
The random variables X and Y have variances 0.2 and 0.5 respectively. Let Z= 5X-2Y. The variance of Z is?
a)
7
b)
5
c)
4
d)
3

|
Bhaskar Joshi answered |
Var(X) = 0.2, Var(Y) = 0.5
Z = 5X – 2Y
Var(Z) = Var(5X-2Y)
= Var(5X) + Var(2Y)
= 25Var(X) + 4Var(Y)
Var(Z) = 7.
Chapter doubts & questions for Communication System - RRB JE for Electronics & Communication Engineering 2025 is part of Electronics and Communication Engineering (ECE) exam preparation. The chapters have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Electronics and Communication Engineering (ECE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Communication System - RRB JE for Electronics & Communication Engineering in English & Hindi are available as part of Electronics and Communication Engineering (ECE) exam.
Download more important topics, notes, lectures and mock test series for Electronics and Communication Engineering (ECE) Exam by signing up for free.
RRB JE for Electronics & Communication Engineering
3 videos|68 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily















