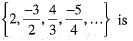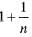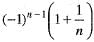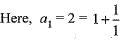All Exams >
Mathematics >
Topic-wise Tests & Solved Examples for Mathematics >
All Questions
All questions of Sequences and Series of Real Numbers for Mathematics Exam
If 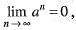 then
then
a)| a | ≥ 1 b)| a | ≤ 1c)| a | > 1d)| a | < 1Correct answer is option 'D'. Can you explain this answer?
|
|
Chirag Verma answered |
Correct Answer :- D
Explanation : For |a|<1
b = 1/a, |b|>1
lim (n→∞) an = lim (n→∞) (1/b)n
= lim(n→∞) 1/bn
= 1/(±∞)
= 0
A convergent sequence is a Cauchy sequence, if it is a- a)sequence of real numbers
- b)sequence of rational numbers
- c)sequence of irrational numbers
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
A convergent sequence is a Cauchy sequence, if it is a
a)
sequence of real numbers
b)
sequence of rational numbers
c)
sequence of irrational numbers
d)
None of the above
|
|
Chirag Verma answered |
ANSWER :- b
Solution :- If {an}∞n=1 is a cauchy sequence of real numbers and if there is a sub-sequence of this sequence, {anj}∞j=1 which converges to a real number L, then I need to show that the sequence {an}∞n=1 converges to the real number L.
The sequence {xn}, where xn = nl/n, converge to- a)1
- b)0
- c)1/2
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The sequence {xn}, where xn = nl/n, converge to
a)
1
b)
0
c)
1/2
d)
None of these

|
Om Pavan Koushik answered |
One can view the sequence as a function and take log on both sides and evaluate using l'hospital rule.
The sequence <sn> = 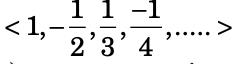 is
is - a)not monotonic but bounded
- b)not monotonic and not bounded
- c)monotonic but not bounded
- d)monotonic and bounded
Correct answer is option 'A'. Can you explain this answer?
The sequence <sn> = 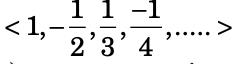 is
is
a)
not monotonic but bounded
b)
not monotonic and not bounded
c)
monotonic but not bounded
d)
monotonic and bounded
|
|
Chirag Verma answered |
Here lower bound = l = − 1/2 , & upper bounded u = 1. But the given sequence is neither increasing nor decreasing. Thus, <sn> is bounded but not monotonic.
Let ∑un be a series of positive terms such that 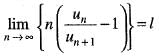 Then,
Then,
(i) if l > 1, the series converges;
(ii) if l < 1, the series diverges;
(iii) if l = 1, the series may either converge or diverge and therefore the test fails;
This theorem is known as
- a)Raabe’s test
- b)Cauchy test
- c)d’Alembert’s tes
- d)Kummer’s test
Correct answer is option 'A'. Can you explain this answer?
Let ∑un be a series of positive terms such that 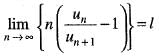 Then,
Then,
(i) if l > 1, the series converges;
(ii) if l < 1, the series diverges;
(iii) if l = 1, the series may either converge or diverge and therefore the test fails;
This theorem is known as
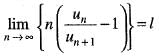 Then,
Then,(i) if l > 1, the series converges;
(ii) if l < 1, the series diverges;
(iii) if l = 1, the series may either converge or diverge and therefore the test fails;
This theorem is known as
a)
Raabe’s test
b)
Cauchy test
c)
d’Alembert’s tes
d)
Kummer’s test

|
Laxmi Choudhary answered |
C answer is right
Let San be a convergent series of positive terms and let Sbn be a divergent series of positive terms. Then,
- a)the sequence < an > is convergent and < bn > is not convergent
- b)the sequence < an > converges to 0
- c)the sequence < bn > does not converge to 0
- d)the sequence < bn > diverges to ∞
Correct answer is option 'B'. Can you explain this answer?
Let San be a convergent series of positive terms and let Sbn be a divergent series of positive terms. Then,
a)
the sequence < an > is convergent and < bn > is not convergent
b)
the sequence < an > converges to 0
c)
the sequence < bn > does not converge to 0
d)
the sequence < bn > diverges to ∞

|
Chhotu Yadav answered |
Answer is abc
The sequence {xn}, where 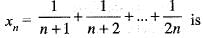
- a)increasing but not bounded
- b)increasing and bounded
- c)decreasing and bounded
- d)decreasing but not bounded
Correct answer is option 'A'. Can you explain this answer?
The sequence {xn}, where 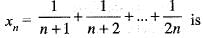
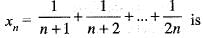
a)
increasing but not bounded
b)
increasing and bounded
c)
decreasing and bounded
d)
decreasing but not bounded
|
|
Chirag Verma answered |
If a sequence is eventually increasing and not bounded above, then it is divergent to positive infinity. If a sequence is eventually decreasing and not bounded below, then it is divergent to negative infinity.
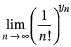 is equal to
is equal to- a)0
- b)1
- c)e
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
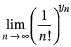 is equal to
is equal toa)
0
b)
1
c)
e
d)
None of these

|
Ibrahim Parekh answered |
Take log on both the sides.
If Sn denoted the sum of n term of the series 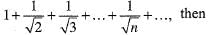
- a)Sn > n2
- b)Sn > n
- c)
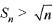
- d)Sn = ∞
Correct answer is option 'C'. Can you explain this answer?
If Sn denoted the sum of n term of the series 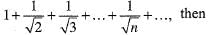
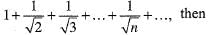
a)
Sn > n2
b)
Sn > n
c)
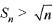
d)
Sn = ∞
|
|
Chirag Verma answered |
If Sn denote the sum of n terms of the series 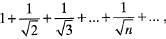 then Sn will be >
then Sn will be > 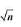 Explanation:
Explanation:
A: Sn > n^2
- The given comparison tells us that the sum of the first n terms of the series is greater than n^2.
- This could be true for certain series where the sum of terms grows faster than n^2, such as series with exponential growth.
- However, this comparison alone does not provide enough information to determine the behavior of the series for all values of n.
B: Sn > n
- This comparison indicates that the sum of the first n terms of the series is greater than n itself.
- Similar to the first comparison, this could be true for certain series with increasing terms.
- Again, this comparison alone does not give a definitive answer about the convergence or divergence of the series.
C: Sn = ∞
- This comparison suggests that the sum of the terms of the series diverges to infinity.
- If the sum of the series approaches infinity as n increases, it indicates that the series does not converge.
- This comparison implies that the series may be divergent and does not have a finite sum.
D: Sn = ∞
- This comparison reiterates the previous point that the sum of the series diverges to infinity.
- It reinforces the idea that the series does not have a finite sum and diverges as n increases.
Conclusion:
- Based on the comparisons provided, it is most likely that the series described does not converge and has an infinite sum. This is indicated by the comparisons stating that the sum of the terms exceeds n^2 and n, and ultimately diverges to infinity.
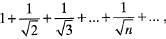 then Sn will be >
then Sn will be > 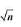 Explanation:
Explanation:A: Sn > n^2
- The given comparison tells us that the sum of the first n terms of the series is greater than n^2.
- This could be true for certain series where the sum of terms grows faster than n^2, such as series with exponential growth.
- However, this comparison alone does not provide enough information to determine the behavior of the series for all values of n.
B: Sn > n
- This comparison indicates that the sum of the first n terms of the series is greater than n itself.
- Similar to the first comparison, this could be true for certain series with increasing terms.
- Again, this comparison alone does not give a definitive answer about the convergence or divergence of the series.
C: Sn = ∞
- This comparison suggests that the sum of the terms of the series diverges to infinity.
- If the sum of the series approaches infinity as n increases, it indicates that the series does not converge.
- This comparison implies that the series may be divergent and does not have a finite sum.
D: Sn = ∞
- This comparison reiterates the previous point that the sum of the series diverges to infinity.
- It reinforces the idea that the series does not have a finite sum and diverges as n increases.
Conclusion:
- Based on the comparisons provided, it is most likely that the series described does not converge and has an infinite sum. This is indicated by the comparisons stating that the sum of the terms exceeds n^2 and n, and ultimately diverges to infinity.
Consider the following statement- a)every convergent sequence is a Cauchy sequence
- b)every Cauchy sequence of rational number is convergent
- c)every Cauchy sequence of real number is convergent
- d)every convergent sequence is bounded
Correct answer is option 'C'. Can you explain this answer?
Consider the following statement
a)
every convergent sequence is a Cauchy sequence
b)
every Cauchy sequence of rational number is convergent
c)
every Cauchy sequence of real number is convergent
d)
every convergent sequence is bounded
|
|
Vedika Sharma answered |
Explanation:
In order to determine the correct option, let's analyze each statement one by one.
a) Every convergent sequence is a Cauchy sequence:
A convergent sequence is one in which the terms of the sequence approach a specific limit as the sequence progresses. It means that for any given positive value ε, there exists a positive integer N such that for all n ≥ N, the distance between the terms of the sequence and the limit is less than ε.
On the other hand, a Cauchy sequence is a sequence in which the terms become arbitrarily close to each other as the sequence progresses. It means that for any given positive value ε, there exists a positive integer N such that for all n, m ≥ N, the distance between the terms of the sequence is less than ε.
While it is true that every convergent sequence is a Cauchy sequence, the converse is not true. There are Cauchy sequences that do not converge. Therefore, option a) is not correct.
b) Every Cauchy sequence of rational numbers is convergent:
This statement is false. There exist Cauchy sequences of rational numbers that do not converge to a rational number. An example of such a sequence is the sequence of decimal approximations of the square root of 2. This sequence is a Cauchy sequence of rational numbers, but it does not converge to a rational number. Therefore, option b) is not correct.
c) Every Cauchy sequence of real numbers is convergent:
This statement is true. In the real number system, every Cauchy sequence is guaranteed to converge to a real number. This property is known as the completeness of the real numbers. The completeness of the real numbers distinguishes them from the rational numbers. Therefore, option c) is correct.
d) Every convergent sequence is bounded:
This statement is also true. A convergent sequence is bounded because there exists a finite interval around the limit of the sequence that contains all the terms of the sequence. This interval serves as a bound for the sequence. Therefore, option d) is correct.
To summarize, the correct option is c) "every Cauchy sequence of real numbers is convergent".
In order to determine the correct option, let's analyze each statement one by one.
a) Every convergent sequence is a Cauchy sequence:
A convergent sequence is one in which the terms of the sequence approach a specific limit as the sequence progresses. It means that for any given positive value ε, there exists a positive integer N such that for all n ≥ N, the distance between the terms of the sequence and the limit is less than ε.
On the other hand, a Cauchy sequence is a sequence in which the terms become arbitrarily close to each other as the sequence progresses. It means that for any given positive value ε, there exists a positive integer N such that for all n, m ≥ N, the distance between the terms of the sequence is less than ε.
While it is true that every convergent sequence is a Cauchy sequence, the converse is not true. There are Cauchy sequences that do not converge. Therefore, option a) is not correct.
b) Every Cauchy sequence of rational numbers is convergent:
This statement is false. There exist Cauchy sequences of rational numbers that do not converge to a rational number. An example of such a sequence is the sequence of decimal approximations of the square root of 2. This sequence is a Cauchy sequence of rational numbers, but it does not converge to a rational number. Therefore, option b) is not correct.
c) Every Cauchy sequence of real numbers is convergent:
This statement is true. In the real number system, every Cauchy sequence is guaranteed to converge to a real number. This property is known as the completeness of the real numbers. The completeness of the real numbers distinguishes them from the rational numbers. Therefore, option c) is correct.
d) Every convergent sequence is bounded:
This statement is also true. A convergent sequence is bounded because there exists a finite interval around the limit of the sequence that contains all the terms of the sequence. This interval serves as a bound for the sequence. Therefore, option d) is correct.
To summarize, the correct option is c) "every Cauchy sequence of real numbers is convergent".
The series 2 + 4 + 6 + 8 + ...is
- a)divergent
- b)convergent
- c)Both of these
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The series 2 + 4 + 6 + 8 + ...is
a)
divergent
b)
convergent
c)
Both of these
d)
None of these
|
|
Chirag Verma answered |
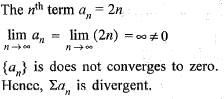
The sequence of n th partial sum of given series is unbounded and goes to infinity.
since sequence of n th partial sum is unbounded, it is not convergent therefore the given series
is not convergent i.e. divergent.
 is equal to
is equal to
- a)1
- b)0
- c)e
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
 is equal to
is equal to a)
1
b)
0
c)
e
d)
None of these
|
|
Chirag Verma answered |
Correct Answer:- A
Explanation : 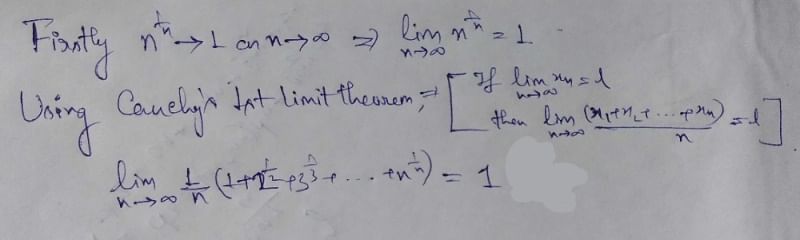
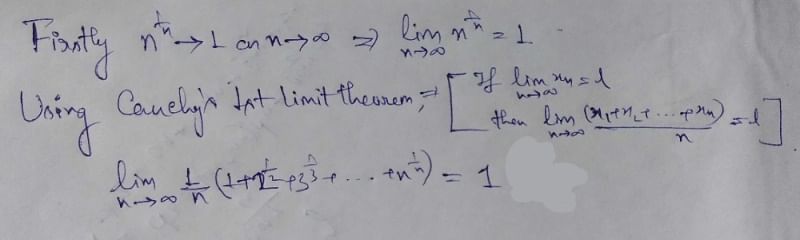
For the sequence 1, 7, 25, 79, 241, 727 … simple formula for {an} is ____________ - a)3n+1 – 2
- b)(-3)n + 4
- c)n2 – 2
- d)3n – 2
Correct answer is option 'D'. Can you explain this answer?
For the sequence 1, 7, 25, 79, 241, 727 … simple formula for {an} is ____________
a)
3n+1 – 2
b)
(-3)n + 4
c)
n2 – 2
d)
3n – 2
|
|
Chirag Verma answered |
The ratio of consecutive numbers is close to 3. Comparing these terms with the sequence of {3n} which is 3, 9, 27 …. Comparing these terms with the corresponding terms of sequence {3n} and the nth term is 2 less than the corresponding power of 3.
Let < an> —> a. Let for every positive integer k, Ak be the set of all positive integer n such that | an- a | < —1/k. Then,- a)Ak is finite for all k
- b)Ak is finite for some k
- c)every Ak contains all but finitely many positive integers
- d)Ak contains all positive integers
Correct answer is option 'D'. Can you explain this answer?
Let < an> —> a. Let for every positive integer k, Ak be the set of all positive integer n such that | an- a | < —1/k. Then,
a)
Ak is finite for all k
b)
Ak is finite for some k
c)
every Ak contains all but finitely many positive integers
d)
Ak contains all positive integers
|
|
Tapas Bhowmik answered |
I think C is correct
Let {an} and {bn} be sequences of real numbers defined as a1 = 1 and for n ≥ 1, an+1 = an + (–1)n 2–n, bn =  . Then
. Then- a){an} converges to zero and {bn} is Cauchy sequence
- b){an} converges to zero and {bn} is not a convergent sequence
- c){an} converges to a non-zero number and {bn} is a Cauchy sequence
- d){an} converges to a non-zero number and {bn} is not a convergent sequence
Correct answer is option 'C'. Can you explain this answer?
Let {an} and {bn} be sequences of real numbers defined as a1 = 1 and for n ≥ 1, an+1 = an + (–1)n 2–n, bn =  . Then
. Then
a)
{an} converges to zero and {bn} is Cauchy sequence
b)
{an} converges to zero and {bn} is not a convergent sequence
c)
{an} converges to a non-zero number and {bn} is a Cauchy sequence
d)
{an} converges to a non-zero number and {bn} is not a convergent sequence

|
Veda Institute answered |
Let {an} & {bn} be sequences of real numbers defined as a1 = 1
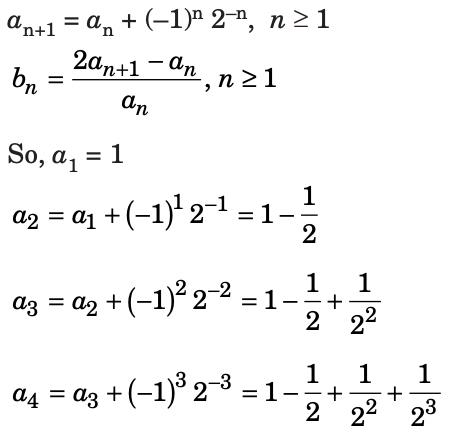
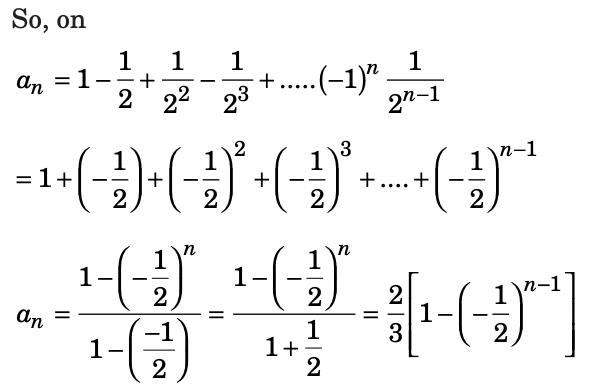

⇒ {bn} converges to 1.
Hence {bn} will be a Cauchy sequence.
⇒ {bn} converges to 1.
Hence {bn} will be a Cauchy sequence.
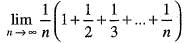 is equal to
is equal to- a)1
- b)0
- c)e
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
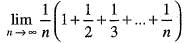 is equal to
is equal toa)
1
b)
0
c)
e
d)
None of these

|
Sakshi Jain answered |
Yes, B is the correct ans from Cauchy first theorem on limit .
The radius of convergent of the series 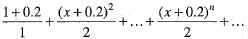
- a)1
- b)∞
- c)zero
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The radius of convergent of the series 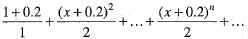
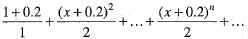
a)
1
b)
∞
c)
zero
d)
None of these
|
|
Radhika Varma answered |
The series can be written as:
∑[(x * 0.2)^n / n!]
To find the radius of convergence, we can use the ratio test. Let's apply the ratio test to the series:
lim(n→∞) |[(x * 0.2)^(n+1) / (n+1)!] / [(x * 0.2)^n / n!]|
= lim(n→∞) |(x * 0.2)^(n+1) * n! / [(n+1)! * (x * 0.2)^n]|
= lim(n→∞) |(x * 0.2) / (n+1)|
Since (x * 0.2) is a constant and n! grows faster than (n+1)!, the limit will approach zero as n goes to infinity. Therefore, the series converges for all values of x.
The radius of convergence is infinite, so the answer is:
b) Infinite.
∑[(x * 0.2)^n / n!]
To find the radius of convergence, we can use the ratio test. Let's apply the ratio test to the series:
lim(n→∞) |[(x * 0.2)^(n+1) / (n+1)!] / [(x * 0.2)^n / n!]|
= lim(n→∞) |(x * 0.2)^(n+1) * n! / [(n+1)! * (x * 0.2)^n]|
= lim(n→∞) |(x * 0.2) / (n+1)|
Since (x * 0.2) is a constant and n! grows faster than (n+1)!, the limit will approach zero as n goes to infinity. Therefore, the series converges for all values of x.
The radius of convergence is infinite, so the answer is:
b) Infinite.
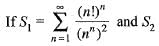
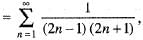 then which one of the following statement is correct?
then which one of the following statement is correct?- a)Both S1 and S2 are convergent
- b)S1 is divergent and S2 is convergent
- c)S1 is convergent and S2 is divergent
- d)Both S1 and S2 are divergent
Correct answer is option 'B'. Can you explain this answer?
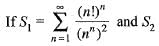
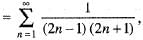 then which one of the following statement is correct?
then which one of the following statement is correct?a)
Both S1 and S2 are convergent
b)
S1 is divergent and S2 is convergent
c)
S1 is convergent and S2 is divergent
d)
Both S1 and S2 are divergent

|
Veda Institute answered |
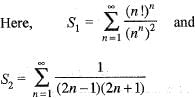
So, we can see that from S1 and S2 that is divergent and S2 is convergent.
Which of the following series is divergent?- a)
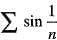
- b)
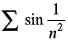
- c)
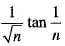
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Which of the following series is divergent?
a)
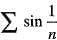
b)
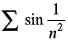
c)
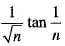
d)
None of these
|
|
Chirag Verma answered |
The series Sigma [sin(1/n)] is a divergent series, because
lim(n-->inf.)[sin(1/n)]/(1/n) = 1, which is nonzero, which in turn is a consequence of lim(x-->0)[sin(x)]/x = 1. Hence the two series Sigma [sin(1/n)] and Sigma(1/n) have the same convergence behaviour by limit comparison test, for series of positive terms But we know that the harmonic series Sigma(1/n) diverges. Hence the given series Sigma[sin(1/n) also diverges.
Note that for all 1 </= n, 0 < (1/n) </= 1 < π, and so sin(1/n) is positive i.e. the given series is of positive terms.
Match list I with list II and select the correct answer


- a)a
- b)b
- c)c
- d)d
Correct answer is option 'C'. Can you explain this answer?
Match list I with list II and select the correct answer




a)
a
b)
b
c)
c
d)
d
|
|
Chirag Verma answered |
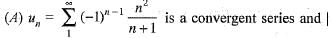
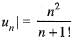
is also convergent series.
∴ un is also convergent series.
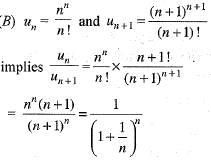
Hence, by d’Alembert test
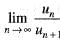
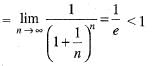
implies un is divergent series.
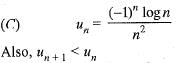
By Cauchy condensation test, ∑μn is convergent series.
(D)
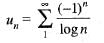
By Leibnitz’s test, the series is convergent.
Also,
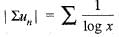 is divergent series.
is divergent series. So, the given series is converges conditionally.
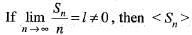
- a)is not bounded
- b)may or may not be bounded
- c)convergent
- d)may or may not be convergent
Correct answer is option 'A'. Can you explain this answer?
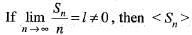
a)
is not bounded
b)
may or may not be bounded
c)
convergent
d)
may or may not be convergent

|
Kartikey Mehrotra answered |
Simply by cauchy second theorem on limits if lim Sn = l, then lim Sn/n= l also.
Therefore here Sn= l and is convergent to L. option c is correct
Therefore here Sn= l and is convergent to L. option c is correct
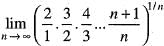 is equal to
is equal to
- a)0
- b)1
- c)e
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
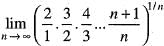 is equal to
is equal toa)
0
b)
1
c)
e
d)
None of these

|
Supriya Tiwari answered |
Option b...by Cauchy's second theorem
The series 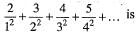
- a)conditional convergent
- b)absolutely convergent
- c)divergent
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
The series 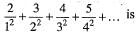
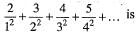
a)
conditional convergent
b)
absolutely convergent
c)
divergent
d)
None of the above
|
|
Chirag Verma answered |
Let the given series be denoted by ∑μn, then
∑|μn|
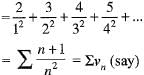
Compare this series ∑vn with the auxiliary series,
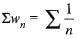
Then,
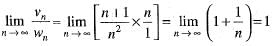
which is finite quantity.
Hence, ∑un and ∑wn are either both convergent or both divergent. But ∑wn
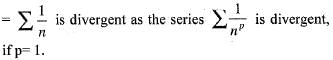
Hence, the series ∑vn is divergent.
Also, in the series ∑un, we find that its term are alternately positive and negative, its terms are continuously decreasing and
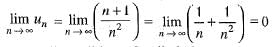
Thus, all condition of Leibnitz’s test are satisfied and as such ∑un is convergent. H ence, the given series ∑un is conditionally convergent.
∑|μn|
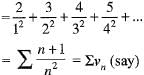
Compare this series ∑vn with the auxiliary series,
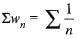
Then,
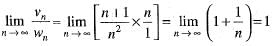
which is finite quantity.
Hence, ∑un and ∑wn are either both convergent or both divergent. But ∑wn
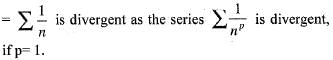
Hence, the series ∑vn is divergent.
Also, in the series ∑un, we find that its term are alternately positive and negative, its terms are continuously decreasing and
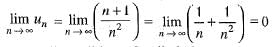
Thus, all condition of Leibnitz’s test are satisfied and as such ∑un is convergent. H ence, the given series ∑un is conditionally convergent.
The sequence 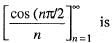
- a)divergent
- b)convergent to 0
- c)convergent to 1
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The sequence 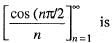
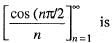
a)
divergent
b)
convergent to 0
c)
convergent to 1
d)
None of these
|
|
Chirag Verma answered |
Correct Answer :- b
Explanation : Suppose otherwise, that there exists a number L implies R and a positive integer N such that
| f(n) - L | < e {for all } e > 0 {for all } n > N.
Since N is a positive integer, we know 4N > N and 4N+2 > N.
But,
f(4N) = cos (2N pi) = 1 and f(4N+2) = cos((2N+1)pi) = -1
Taking e = 1/2
= |1 - L| < 1/2 and |-1-L| < 1/2
=> |1+L| < 1/2
But, these imply
|1-L| + |1+L| < 1.
By the triangle inequality we then have
|1 - L + 1 + L | < 1
=> 2 < 1
a contradiction. Hence, there is no such limit L.
Therefore, the sequence converges to zero.
The sequence {xn}, where 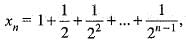
- a)increasing but not bounded
- b)increasing and bounded
- c)decreasing but not bounded
- d)decreasing and bounded
Correct answer is option 'B'. Can you explain this answer?
The sequence {xn}, where 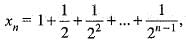
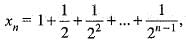
a)
increasing but not bounded
b)
increasing and bounded
c)
decreasing but not bounded
d)
decreasing and bounded

|
Veda Institute answered |
as it is a gp so as n increase sum will be more
xn = a(rn-1)/(r-1)
xn = (1)(1/2n-1)/(1/2-1)
xn will be terminating
xn = a(rn-1)/(r-1)
xn = (1)(1/2n-1)/(1/2-1)
xn will be terminating
For what value of x the infinite series 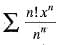 diverges?
diverges?- a)x < e
- b)x > e
- c)
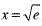
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
For what value of x the infinite series 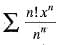 diverges?
diverges?
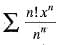 diverges?
diverges?a)
x < e
b)
x > e
c)
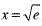
d)
None of these
|
|
Chirag Verma answered |
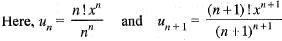
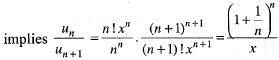
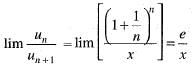
If e/x > 1 i.e.., x < e, then the given series diverges.
If {xn} and {yn} are two convergent sequence such that xn < yn, 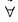 n ∈ N, then
n ∈ N, then- a)
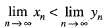
- b)
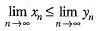
- c)
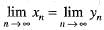
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If {xn} and {yn} are two convergent sequence such that xn < yn, 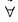 n ∈ N, then
n ∈ N, then
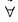 n ∈ N, then
n ∈ N, thena)
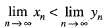
b)
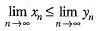
c)
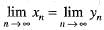
d)
None of these
|
|
Chirag Verma answered |
The correct option is Option A.
Let lim xn = x and lim yn = y and zn = yn - xn
n->∞ n->∞
Then (zn) is a convergent sequence such that zn > 0 ∇ n ∊N
and lim zn = y - x.
n->∞
Now (zn) is a convergent sequence of real numbers and zn > 0 ∇ n ∊N
So, lim zn ≥ 0
n->∞
So, y - x ≥ 0
=> y ≥ x
=> lim yn ≥ lim xn
n->∞ n->∞
Hence, proved.
Consider the following statement
I. Every Cauchy sequence contains convergent subsequence
II. If a subsequence of a Cauchy sequence converges to a real numbers l, then the original sequence also converge to l.
III. Every monotone sequence contains a convergent subsequence.
IV. Every bounded sequence contains a convergent subsequence.
Select the correct answer using the codes given below:
- a)II, III and IV
- b)I, II and IV
- c)I, III and IV
- d)I, II, and III
Correct answer is option 'B'. Can you explain this answer?
Consider the following statement
I. Every Cauchy sequence contains convergent subsequence
II. If a subsequence of a Cauchy sequence converges to a real numbers l, then the original sequence also converge to l.
III. Every monotone sequence contains a convergent subsequence.
IV. Every bounded sequence contains a convergent subsequence.
I. Every Cauchy sequence contains convergent subsequence
II. If a subsequence of a Cauchy sequence converges to a real numbers l, then the original sequence also converge to l.
III. Every monotone sequence contains a convergent subsequence.
IV. Every bounded sequence contains a convergent subsequence.
Select the correct answer using the codes given below:
a)
II, III and IV
b)
I, II and IV
c)
I, III and IV
d)
I, II, and III
|
|
Rohan Mathur answered |
Explanation:
To determine the correct answer, we need to evaluate each statement individually and see if it holds true.
I. Every Cauchy sequence contains a convergent subsequence:
This statement is true. A Cauchy sequence is a sequence in which the terms become arbitrarily close to each other as the sequence progresses. This means that for any positive tolerance, there exists a point in the sequence beyond which all the terms lie within that tolerance. This property allows us to select a subsequence that is convergent. By selecting terms from the original sequence that lie within each tolerance, we can construct a subsequence that converges to a specific limit.
II. If a subsequence of a Cauchy sequence converges to a real number l, then the original sequence also converges to l:
This statement is true. If a subsequence converges to a real number l, it means that all the terms beyond a certain index in the subsequence are arbitrarily close to l. Since the original sequence contains all the terms of the subsequence, it follows that all the terms beyond the same index in the original sequence are also arbitrarily close to l. Therefore, the original sequence also converges to l.
III. Every monotone sequence contains a convergent subsequence:
This statement is true. A monotone sequence is a sequence that is either non-decreasing or non-increasing. If the sequence is non-decreasing, we can choose a subsequence that consists of the terms at odd indices (1, 3, 5, ...), which is also non-decreasing. By the monotone convergence theorem, a bounded non-decreasing sequence must converge. Similarly, if the sequence is non-increasing, we can choose a subsequence that consists of the terms at even indices (2, 4, 6, ...), which is also non-increasing. Again, by the monotone convergence theorem, a bounded non-increasing sequence must converge. Therefore, every monotone sequence contains a convergent subsequence.
IV. Every bounded sequence contains a convergent subsequence:
This statement is true. A bounded sequence is a sequence in which all the terms lie within a certain range. By the Bolzano-Weierstrass theorem, any bounded sequence in a metric space has a convergent subsequence. Therefore, every bounded sequence contains a convergent subsequence.
Based on the evaluation of each statement, the correct answer is option 'B': I, II, and IV.
To determine the correct answer, we need to evaluate each statement individually and see if it holds true.
I. Every Cauchy sequence contains a convergent subsequence:
This statement is true. A Cauchy sequence is a sequence in which the terms become arbitrarily close to each other as the sequence progresses. This means that for any positive tolerance, there exists a point in the sequence beyond which all the terms lie within that tolerance. This property allows us to select a subsequence that is convergent. By selecting terms from the original sequence that lie within each tolerance, we can construct a subsequence that converges to a specific limit.
II. If a subsequence of a Cauchy sequence converges to a real number l, then the original sequence also converges to l:
This statement is true. If a subsequence converges to a real number l, it means that all the terms beyond a certain index in the subsequence are arbitrarily close to l. Since the original sequence contains all the terms of the subsequence, it follows that all the terms beyond the same index in the original sequence are also arbitrarily close to l. Therefore, the original sequence also converges to l.
III. Every monotone sequence contains a convergent subsequence:
This statement is true. A monotone sequence is a sequence that is either non-decreasing or non-increasing. If the sequence is non-decreasing, we can choose a subsequence that consists of the terms at odd indices (1, 3, 5, ...), which is also non-decreasing. By the monotone convergence theorem, a bounded non-decreasing sequence must converge. Similarly, if the sequence is non-increasing, we can choose a subsequence that consists of the terms at even indices (2, 4, 6, ...), which is also non-increasing. Again, by the monotone convergence theorem, a bounded non-increasing sequence must converge. Therefore, every monotone sequence contains a convergent subsequence.
IV. Every bounded sequence contains a convergent subsequence:
This statement is true. A bounded sequence is a sequence in which all the terms lie within a certain range. By the Bolzano-Weierstrass theorem, any bounded sequence in a metric space has a convergent subsequence. Therefore, every bounded sequence contains a convergent subsequence.
Based on the evaluation of each statement, the correct answer is option 'B': I, II, and IV.
If a sequence is not a Cauchy sequence, then it is a
- a)divergent sequence
- b)convergent sequence
- c)bounded sequence
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
If a sequence is not a Cauchy sequence, then it is a
a)
divergent sequence
b)
convergent sequence
c)
bounded sequence
d)
None of the above
|
|
Dronacharya Institute answered |
A sequence that is not a Cauchy sequence is called a divergent sequence. A Cauchy sequence is a sequence whose elements get closer and closer together as the sequence progresses.
Which of the following series is divergent?- a)
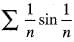
- b)
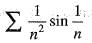
- c)
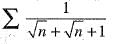
- d)
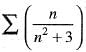
Correct answer is option 'B'. Can you explain this answer?
Which of the following series is divergent?
a)
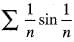
b)
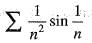
c)
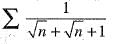
d)
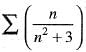

|
Supriya Tiwari answered |
Option b is convergent not divergent.
The series
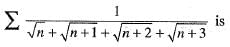
- a)convergent
- b)divergent
- c)oscillatory
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The series
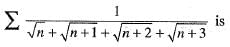
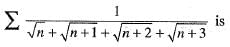
a)
convergent
b)
divergent
c)
oscillatory
d)
None of these
|
|
Chirag Verma answered |
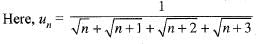
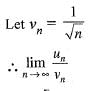
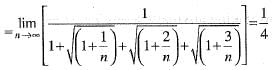
which is finite and non-zero.
Since, ∑vn is divergent, therefore, ∑un is also divergent.
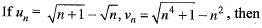
- a)
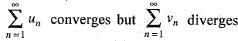
- b)
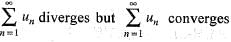
- c)
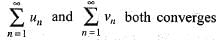
- d)
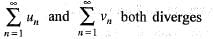
Correct answer is option 'C'. Can you explain this answer?
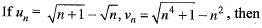
a)
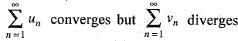
b)
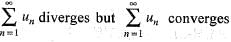
c)
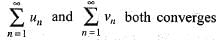
d)
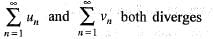

|
Veda Institute answered |
Here, it is given that
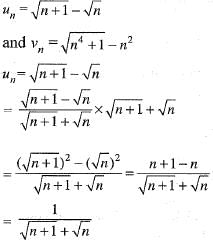
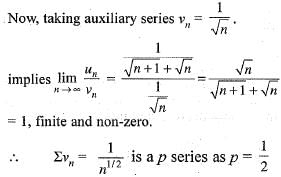
Hence, ∑vn is divergent and ∑un is also divergent and
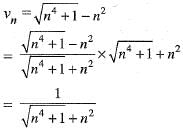
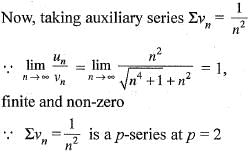

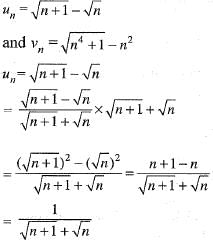
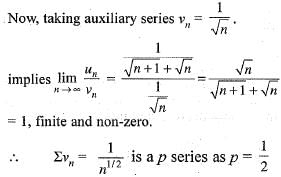
Hence, ∑vn is divergent and ∑un is also divergent and
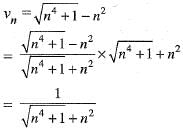
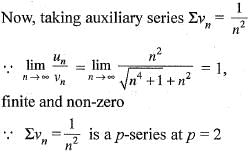

The series  convergent for
convergent for- a)all real value o f x
- b)| x | < 1 only
- c)| x | ≤ 1
- d)-1 < x ≤ 1
Correct answer is option 'D'. Can you explain this answer?
The series  convergent for
convergent for
 convergent for
convergent fora)
all real value o f x
b)
| x | < 1 only
c)
| x | ≤ 1
d)
-1 < x ≤ 1

|
Veda Institute answered |
The series x 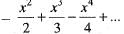 is convergent.
is convergent.
If -1 <x ≤ 1.
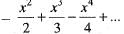 is convergent.
is convergent.If -1 <x ≤ 1.
Find the sum of the series. 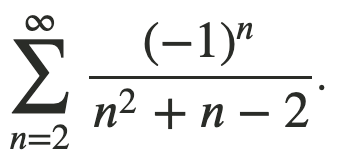
- a)
(1/3)ln2−5/18 - b) (1/3)ln2−5/6
- c) (2/3)ln2−5/18
- d) (2/3)ln2−5/6
Correct answer is option 'C'. Can you explain this answer?
Find the sum of the series. 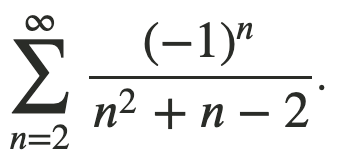
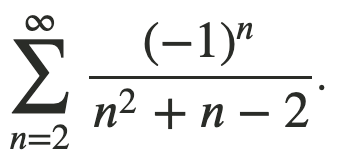
a)
(1/3)ln2−5/18
b)
(1/3)ln2−5/6
c)
(2/3)ln2−5/18
d)
(2/3)ln2−5/6

|
Pie Academy answered |
This problem is a very basic one, this problem can easily be solved by step by step solution. The steps are:
Step 1 : First we will ignore the summation part. We will factorize the denominator, because we are going step by step so our aim is to simplify the given problem first.
Step 2: After factorizing the the denominator we will reach to a position where we have to use partial fraction to go forward.
Step 3: In this step we will take care of the (−1)�� part, like how it will affect the series.
Step 4: After taking care of the (−1)�� we will now expand the summation (breaking it into infinite sum).
Step 5 : So after 4 steps we are halfway done now just the last simplification is left we will use the value
ln2=1−1/2+1/3−1/4+…
The series 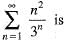
- a)divergent
- b)convergent
- c)unbounded
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The series 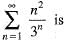
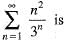
a)
divergent
b)
convergent
c)
unbounded
d)
None of these
|
|
Chirag Verma answered |
We have 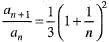
implies
Hence, series is convergent.
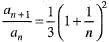
implies

Hence, series is convergent.
Let < an > and < bn> be two sequences of real numbers such that an = bn - bn + 1 for n = 1, 2 , 3 , 4 , . . . if Sbn is convergent, then which is always true?- a)San may not be convergent
- b)San is convergent and San = b1
- c)San is convergent and San = 0
- d)San is convergent and San = a1 - b1
- e)
Correct answer is option 'B'. Can you explain this answer?
Let < an > and < bn> be two sequences of real numbers such that an = bn - bn + 1 for n = 1, 2 , 3 , 4 , . . . if Sbn is convergent, then which is always true?
a)
San may not be convergent
b)
San is convergent and San = b1
c)
San is convergent and San = 0
d)
San is convergent and San = a1 - b1
e)
|
|
Chirag Verma answered |
The series 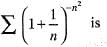
- a)convergent
- b)divergent
- c)oscillatory
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The series 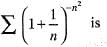
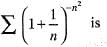
a)
convergent
b)
divergent
c)
oscillatory
d)
None of these
|
|
Chirag Verma answered |
The nth term of the given series is
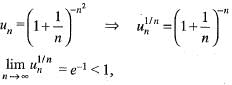
Hence, ∑un is convergent.
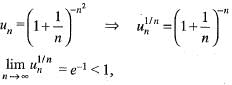
Hence, ∑un is convergent.
The sequence 1, 1, 1, 1, 1…. is?- a)Absolutely summable
- b)Can’t say
- c)Is not absolutely summable
- d)None of the mentioned
Correct answer is option 'C'. Can you explain this answer?
The sequence 1, 1, 1, 1, 1…. is?
a)
Absolutely summable
b)
Can’t say
c)
Is not absolutely summable
d)
None of the mentioned
|
|
Chirag Verma answered |
For limit n tending to infinity the sum also tends to infinity and thus it is not summable.
Let f(x) = (x – 2)17 (x + 5)24. Then- a)f does not have a critical point at 2
- b)f has a minimum at 2
- c)f has neither minimum nor a maximum at x = 2
- d)f has a maximum at 2
Correct answer is option 'C'. Can you explain this answer?
Let f(x) = (x – 2)17 (x + 5)24. Then
a)
f does not have a critical point at 2
b)
f has a minimum at 2
c)
f has neither minimum nor a maximum at x = 2
d)
f has a maximum at 2
|
|
Pranav Sharma answered |
Understanding the Function f(x)
The function given is f(x) = (x - 2)^17 * (x + 5)^24. To analyze the behavior of f(x) at x = 2, we need to investigate its critical points and local extrema.
Critical Points
- A critical point occurs where the derivative f'(x) is zero or undefined.
- To find f'(x), we apply the product rule and analyze the behavior near x = 2.
Behavior at x = 2
- At x = 2, the term (x - 2)^17 equals zero, making f(2) = 0.
- The derivative f'(x) will also involve (x - 2) terms, leading to f'(2) = 0.
Local Extrema Analysis
- To determine the nature of the critical point at x = 2, we examine f(x) around this point.
- As x approaches 2 from the left, f(x) is negative (since (x - 2)^17 is negative).
- As x approaches 2 from the right, f(x) is still negative (since (x - 2)^17 is positive).
- Therefore, f(x) does not change sign around x = 2, indicating that it is neither a maximum nor a minimum.
Conclusion
- Since f(x) does not have a change in direction around x = 2, it confirms that:
- f has neither a minimum nor a maximum at x = 2.
Thus, the correct answer is option 'C'.
The function given is f(x) = (x - 2)^17 * (x + 5)^24. To analyze the behavior of f(x) at x = 2, we need to investigate its critical points and local extrema.
Critical Points
- A critical point occurs where the derivative f'(x) is zero or undefined.
- To find f'(x), we apply the product rule and analyze the behavior near x = 2.
Behavior at x = 2
- At x = 2, the term (x - 2)^17 equals zero, making f(2) = 0.
- The derivative f'(x) will also involve (x - 2) terms, leading to f'(2) = 0.
Local Extrema Analysis
- To determine the nature of the critical point at x = 2, we examine f(x) around this point.
- As x approaches 2 from the left, f(x) is negative (since (x - 2)^17 is negative).
- As x approaches 2 from the right, f(x) is still negative (since (x - 2)^17 is positive).
- Therefore, f(x) does not change sign around x = 2, indicating that it is neither a maximum nor a minimum.
Conclusion
- Since f(x) does not have a change in direction around x = 2, it confirms that:
- f has neither a minimum nor a maximum at x = 2.
Thus, the correct answer is option 'C'.
The series 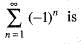
- a)oscillating
- b)convergent
- c)unbounded
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The series 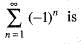
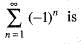
a)
oscillating
b)
convergent
c)
unbounded
d)
None of these
|
|
Chirag Verma answered |
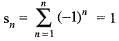 or 0 as n is odd or even implies {Sn} - { 1 , 0 , 1 , 0 , . . . }
or 0 as n is odd or even implies {Sn} - { 1 , 0 , 1 , 0 , . . . }It is an oscillating sequence
The series x 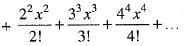 is convergent, if
is convergent, if
- a)0 <x < l/e
- b)x> l/e
- c)2/e <x< 3e
- d)3/e < x < 4/e
Correct answer is option 'A'. Can you explain this answer?
The series x 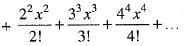 is convergent, if
is convergent, if
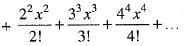 is convergent, if
is convergent, ifa)
0 <x < l/e
b)
x> l/e
c)
2/e <x< 3e
d)
3/e < x < 4/e

|
Veda Institute answered |
If ∑μn be the given series, then we have
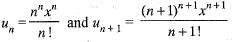
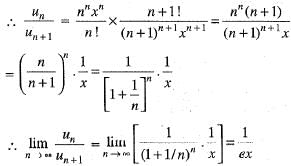
∴ From ratio test, the given series ∑μn is convergent or divergent according as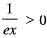
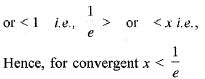
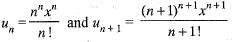

∴ From ratio test, the given series ∑μn is convergent or divergent according as
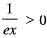
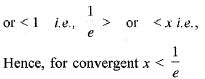
Chapter doubts & questions for Sequences and Series of Real Numbers - Topic-wise Tests & Solved Examples for Mathematics 2025 is part of Mathematics exam preparation. The chapters have been prepared according to the Mathematics exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mathematics 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Sequences and Series of Real Numbers - Topic-wise Tests & Solved Examples for Mathematics in English & Hindi are available as part of Mathematics exam.
Download more important topics, notes, lectures and mock test series for Mathematics Exam by signing up for free.
Topic-wise Tests & Solved Examples for Mathematics
27 docs|150 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup

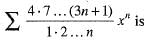 convergent, if
convergent, if
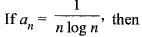
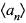 is convergent
is convergent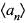 does not converges to 0
does not converges to 0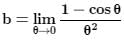 then the value of
then the value of 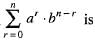
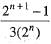
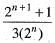
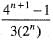

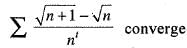


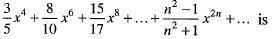

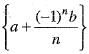
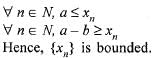
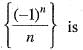
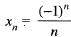
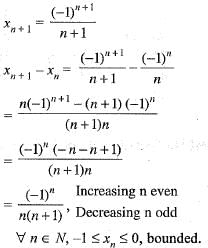
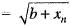 for all n e N, then sequence {xn} converges to the positive root of the equation
for all n e N, then sequence {xn} converges to the positive root of the equation