All Exams >
Mechanical Engineering >
Topicwise Question Bank for Mechanical Engineering >
All Questions
All questions of Heat Transfer for Mechanical Engineering Exam
Choose the correct statement about thermaf conductivity- a)thermal conductivity for metals decreases with increase in temperature
- b)thermal conductivity for gases and insulating material decreases with increase in temperature
- c)thermal conductivity is not a function of temperature
- d)thermal conductivity increases with increase in temperature irrespective of material
Correct answer is option 'A'. Can you explain this answer?
Choose the correct statement about thermaf conductivity
a)
thermal conductivity for metals decreases with increase in temperature
b)
thermal conductivity for gases and insulating material decreases with increase in temperature
c)
thermal conductivity is not a function of temperature
d)
thermal conductivity increases with increase in temperature irrespective of material
|
|
Sarita Yadav answered |
Due to increase in lattice vibratioh the thermal conductivity of metals decreases with increase in temperature.
The ratio of total emissive power of body to the total emissive power of a black body at the same temperature is called- a)Absorptivity
- b)Transmissivity
- c)Reflectivity
- d)Emissivity
Correct answer is option 'D'. Can you explain this answer?
The ratio of total emissive power of body to the total emissive power of a black body at the same temperature is called
a)
Absorptivity
b)
Transmissivity
c)
Reflectivity
d)
Emissivity

|
Amar Desai answered |
Emissivity for any body is given by
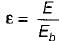
Where
E = Emissive power of a body
Eb = Emissive power of a black body
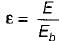
Where
E = Emissive power of a body
Eb = Emissive power of a black body
The temperature gradient through the two layer composite wall consisting of two metals A and B is as shown in figure. It can be concluded that
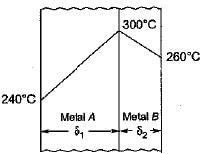
- a)metal A is better conductor of heat than metal B
- b)heat flows from metal B to metal A
- c)heat is being generated at the interface of metals A and B
- d)free surface of metals A and B are being heated
Correct answer is option 'C'. Can you explain this answer?
The temperature gradient through the two layer composite wall consisting of two metals A and B is as shown in figure. It can be concluded that


a)
metal A is better conductor of heat than metal B
b)
heat flows from metal B to metal A
c)
heat is being generated at the interface of metals A and B
d)
free surface of metals A and B are being heated
|
|
Sarita Yadav answered |
According to the figure, the temperature at the interface of metal A and metal B is observed to be 300 degrees centigrade. This temperature is the highest recorded during the entire process. Additionally, the flow of heat is observed to be from a higher temperature to a lower temperature. Therefore, it can be deduced that the heat must have been generated at the interface of metal A and metal B.
Therefore option C is correct.
Which of the following changes in temperature during unsteady state follow a periodic variation?
- a)Temperature variations in cycle of an internal combustion engine.
- b)Cooling of bars, blanks and metal billets in steel works.
- c)Variation of temperature of a building during a full day period of 24 hours.
- d)Heat processing of regenerators whose packings are alternately heated by flue gases and cooled by air
Correct answer is option 'A'. Can you explain this answer?
Which of the following changes in temperature during unsteady state follow a periodic variation?
a)
Temperature variations in cycle of an internal combustion engine.
b)
Cooling of bars, blanks and metal billets in steel works.
c)
Variation of temperature of a building during a full day period of 24 hours.
d)
Heat processing of regenerators whose packings are alternately heated by flue gases and cooled by air

|
Gauri Roy answered |
Temperature variations in cycle of an internal combustion engine.
- An internal combustion engine undergoes a series of processes in a cycle, including intake, compression, combustion, and exhaust.
- These processes result in changes in temperature within the engine.
- During the intake stroke, the air-fuel mixture enters the combustion chamber, causing a decrease in temperature.
- In the compression stroke, the mixture is compressed, leading to an increase in temperature.
- The combustion of the mixture during the power stroke produces high temperatures.
- Finally, during the exhaust stroke, the combustion products are expelled, leading to a decrease in temperature.
- This cycle repeats continuously as the engine operates.
Cooling of bars, blanks and metal billets in steel works.
- When bars, blanks, and metal billets are produced in steel works, they are often heated to high temperatures for shaping and processing.
- After the shaping process, these metal components need to be cooled down to ambient temperature for further handling or storage.
- The cooling process involves transferring heat from the hot metal to the surrounding environment.
- However, this cooling process is typically not periodic but rather a continuous and gradual decrease in temperature.
- The rate of cooling depends on various factors such as the initial temperature of the metal, the ambient temperature, and the surface area-to-volume ratio of the metal.
- The cooling rate can be controlled by adjusting the cooling medium, such as air or water, and their flow rates.
- While the temperature of the metal may change over time during the cooling process, it does not exhibit a periodic variation.
Variation of temperature of a building during a full day period of 24 hours.
- The temperature of a building can vary throughout the day due to various factors such as solar radiation, outdoor temperature, and HVAC system operation.
- During the day, when the sun is up, the building may experience an increase in temperature due to solar heat gain.
- As the sun sets and the outdoor temperature drops, the building may start to lose heat and the temperature may decrease.
- However, this temperature variation is not periodic as it is influenced by external factors such as weather conditions and the time of year.
- The temperature of the building may also be affected by the operation of heating, ventilation, and air conditioning (HVAC) systems.
- The HVAC system may be programmed to maintain a constant temperature or to follow a specific temperature schedule, but this schedule is typically not a perfect periodic variation.
Heat processing of regenerators whose packings are alternately heated by flue gases and cooled by air.
- Regenerators are heat exchangers used in various industrial processes, including combustion systems.
- In some regenerators, the packings or beds are designed to alternate between being heated by hot flue gases and cooled by air.
- This alternating heating and cooling process can result in a periodic variation of temperature within the regenerator.
- When the packings are exposed to flue gases, they absorb heat and their temperature increases.
- After a certain period, the flow is switched, and the packings are exposed to cooling air, causing their temperature to decrease.
- This alternating heating and cooling cycle repeats, resulting in a periodic variation of temperature within the regenerator.
- The purpose of this process is to efficiently transfer heat between the flue gases and the air, maximizing the energy efficiency of the system.
Therefore, among the given options
- An internal combustion engine undergoes a series of processes in a cycle, including intake, compression, combustion, and exhaust.
- These processes result in changes in temperature within the engine.
- During the intake stroke, the air-fuel mixture enters the combustion chamber, causing a decrease in temperature.
- In the compression stroke, the mixture is compressed, leading to an increase in temperature.
- The combustion of the mixture during the power stroke produces high temperatures.
- Finally, during the exhaust stroke, the combustion products are expelled, leading to a decrease in temperature.
- This cycle repeats continuously as the engine operates.
Cooling of bars, blanks and metal billets in steel works.
- When bars, blanks, and metal billets are produced in steel works, they are often heated to high temperatures for shaping and processing.
- After the shaping process, these metal components need to be cooled down to ambient temperature for further handling or storage.
- The cooling process involves transferring heat from the hot metal to the surrounding environment.
- However, this cooling process is typically not periodic but rather a continuous and gradual decrease in temperature.
- The rate of cooling depends on various factors such as the initial temperature of the metal, the ambient temperature, and the surface area-to-volume ratio of the metal.
- The cooling rate can be controlled by adjusting the cooling medium, such as air or water, and their flow rates.
- While the temperature of the metal may change over time during the cooling process, it does not exhibit a periodic variation.
Variation of temperature of a building during a full day period of 24 hours.
- The temperature of a building can vary throughout the day due to various factors such as solar radiation, outdoor temperature, and HVAC system operation.
- During the day, when the sun is up, the building may experience an increase in temperature due to solar heat gain.
- As the sun sets and the outdoor temperature drops, the building may start to lose heat and the temperature may decrease.
- However, this temperature variation is not periodic as it is influenced by external factors such as weather conditions and the time of year.
- The temperature of the building may also be affected by the operation of heating, ventilation, and air conditioning (HVAC) systems.
- The HVAC system may be programmed to maintain a constant temperature or to follow a specific temperature schedule, but this schedule is typically not a perfect periodic variation.
Heat processing of regenerators whose packings are alternately heated by flue gases and cooled by air.
- Regenerators are heat exchangers used in various industrial processes, including combustion systems.
- In some regenerators, the packings or beds are designed to alternate between being heated by hot flue gases and cooled by air.
- This alternating heating and cooling process can result in a periodic variation of temperature within the regenerator.
- When the packings are exposed to flue gases, they absorb heat and their temperature increases.
- After a certain period, the flow is switched, and the packings are exposed to cooling air, causing their temperature to decrease.
- This alternating heating and cooling cycle repeats, resulting in a periodic variation of temperature within the regenerator.
- The purpose of this process is to efficiently transfer heat between the flue gases and the air, maximizing the energy efficiency of the system.
Therefore, among the given options
Metals are good conductors of heat because of
- a)all of the below
- b)their atoms are relatively far apart
- c)their atoms collide frequently
- d)free electrons are present
Correct answer is option 'D'. Can you explain this answer?
Metals are good conductors of heat because of
a)
all of the below
b)
their atoms are relatively far apart
c)
their atoms collide frequently
d)
free electrons are present
|
|
Sarita Yadav answered |
- The thermal conductivity of the liquids is more than the gasses and the metals have the highest.
- Metals have valence electrons that are free to move around the surface. When heated, these free electrons collide with each other and the majority of the Kinetic energy is transformed into heat energy, making metals a good conductor of heat.
- In the gaseous state, the molecules of a substance are spaced relatively far away, and their motion is random. This means that energy transfer by the molecular impact is much slower than in the case of a liquid, in which the motion is still random but in liquids, the molecules are more closely packed. The same is true concerning the difference between the thermal conductivity of the liquid and solid phases.
In case of hollow cylinder, as the ratio of outer radius to inner radius increases, the heat transfer- a)decreases
- b)increases
- c)remains constant
- d)may increase or decrease depending upon cylinder material
Correct answer is option 'A'. Can you explain this answer?
In case of hollow cylinder, as the ratio of outer radius to inner radius increases, the heat transfer
a)
decreases
b)
increases
c)
remains constant
d)
may increase or decrease depending upon cylinder material

|
Rajat Sen answered |
In case of hollow cylinder
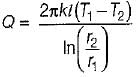
as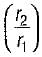 increases Q decreases
increases Q decreases
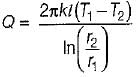
as
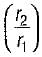 increases Q decreases
increases Q decreasesWhich of the following parameter is a measure of the relative importance of natural convection in relation to forced convection?
All empirical parameters have their usual meaning.- a)Re
- b)Gr
- c)Gr/Re2
- d)Nu/Re2
Correct answer is option 'C'. Can you explain this answer?
Which of the following parameter is a measure of the relative importance of natural convection in relation to forced convection?
All empirical parameters have their usual meaning.
All empirical parameters have their usual meaning.
a)
Re
b)
Gr
c)
Gr/Re2
d)
Nu/Re2

|
Bibek Mukherjee answered |
Explanation:
Gr/Re2
The parameter Gr/Re2 is a measure of the relative importance of natural convection in relation to forced convection.
Gr
The Grashof number (Gr) is a dimensionless number in fluid dynamics that is used to determine the relative strength of buoyancy and viscous forces in a fluid flow. It is defined as the ratio of buoyancy forces to viscous forces within a fluid.
Re
The Reynolds number (Re) is a dimensionless number that describes the flow of a fluid. It is the ratio of inertial forces to viscous forces within the fluid.
Interpretation
When the Gr/Re2 parameter is high, natural convection is more dominant compared to forced convection. Conversely, when this parameter is low, forced convection is more significant.
Conclusion
Therefore, by calculating the Gr/Re2 parameter, one can determine the relative importance of natural convection in relation to forced convection in a given fluid flow situation.
Gr/Re2
The parameter Gr/Re2 is a measure of the relative importance of natural convection in relation to forced convection.
Gr
The Grashof number (Gr) is a dimensionless number in fluid dynamics that is used to determine the relative strength of buoyancy and viscous forces in a fluid flow. It is defined as the ratio of buoyancy forces to viscous forces within a fluid.
Re
The Reynolds number (Re) is a dimensionless number that describes the flow of a fluid. It is the ratio of inertial forces to viscous forces within the fluid.
Interpretation
When the Gr/Re2 parameter is high, natural convection is more dominant compared to forced convection. Conversely, when this parameter is low, forced convection is more significant.
Conclusion
Therefore, by calculating the Gr/Re2 parameter, one can determine the relative importance of natural convection in relation to forced convection in a given fluid flow situation.
The concept of overall heat transfer is used in the heat transfer in the case of- a)conduction
- b)convection
- c)radiation
- d)combined mode of conduction and convection
Correct answer is option 'D'. Can you explain this answer?
The concept of overall heat transfer is used in the heat transfer in the case of
a)
conduction
b)
convection
c)
radiation
d)
combined mode of conduction and convection

|
Anuj Chakraborty answered |
Note that the concept of overall heat transfer is useful in combined mode of heat transfer like conduction and convection
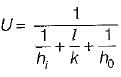
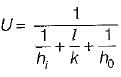
The effectiveness of a fin will be maximum in an environment with- a)free convection
- b)forced convection
- c)radiation
- d)convection and radiation
Correct answer is option 'A'. Can you explain this answer?
The effectiveness of a fin will be maximum in an environment with
a)
free convection
b)
forced convection
c)
radiation
d)
convection and radiation
|
|
Aditya Chavan answered |
Effectiveness of the fin is given by
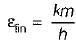
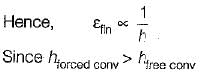
Hence, Effectiveness of the fin will be more in free convection than forced convection.
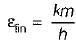

Hence, Effectiveness of the fin will be more in free convection than forced convection.
The time constant of a thermocouple is the time taken to attain- a)the final value to be measured
- b)50% of the value of the initial temperature differenc
- c)63.2% of the value of the initial temperature difference
- d)98.8% of the value of the initial temperature differenc
Correct answer is option 'C'. Can you explain this answer?
The time constant of a thermocouple is the time taken to attain
a)
the final value to be measured
b)
50% of the value of the initial temperature differenc
c)
63.2% of the value of the initial temperature difference
d)
98.8% of the value of the initial temperature differenc
|
|
Hiral Jain answered |
Time Constant of a Thermocouple
The time constant of a thermocouple refers to the time taken for the temperature reading to reach a certain percentage of the final value after a sudden change in temperature.
Explanation of the Correct Answer
Option C: 63.2% of the value of the initial temperature difference
- The correct answer is 63.2% because this percentage corresponds to one time constant in a first-order system.
- In a first-order system, it takes approximately 63.2% of the total time constant to reach 63.2% of the final value.
- After one time constant, the temperature reading of the thermocouple will be about 63.2% of the final value.
Other Options Explained
- Option A: The final value to be measured is not relevant to the time constant. The time constant is about how quickly the temperature reading approaches the final value.
- Option B: 50% of the value of the initial temperature difference is not the correct choice for the time constant of a thermocouple.
- Option D: 98.8% of the value of the initial temperature difference is too close to the final value and does not correspond to a standard time constant in a first-order system.
In conclusion, the time constant of a thermocouple is the time it takes for the temperature reading to reach approximately 63.2% of the final value after a sudden change in temperature.
The time constant of a thermocouple refers to the time taken for the temperature reading to reach a certain percentage of the final value after a sudden change in temperature.
Explanation of the Correct Answer
Option C: 63.2% of the value of the initial temperature difference
- The correct answer is 63.2% because this percentage corresponds to one time constant in a first-order system.
- In a first-order system, it takes approximately 63.2% of the total time constant to reach 63.2% of the final value.
- After one time constant, the temperature reading of the thermocouple will be about 63.2% of the final value.
Other Options Explained
- Option A: The final value to be measured is not relevant to the time constant. The time constant is about how quickly the temperature reading approaches the final value.
- Option B: 50% of the value of the initial temperature difference is not the correct choice for the time constant of a thermocouple.
- Option D: 98.8% of the value of the initial temperature difference is too close to the final value and does not correspond to a standard time constant in a first-order system.
In conclusion, the time constant of a thermocouple is the time it takes for the temperature reading to reach approximately 63.2% of the final value after a sudden change in temperature.
Nusselt number in case of free convection is the function of- a)Reynolds number and Prandtl number
- b)Reynolds number only
- c)Grashoff number only
- d)Grashoff number and Prandtl numbe
Correct answer is option 'D'. Can you explain this answer?
Nusselt number in case of free convection is the function of
a)
Reynolds number and Prandtl number
b)
Reynolds number only
c)
Grashoff number only
d)
Grashoff number and Prandtl numbe

|
Prerna Menon answered |
Nusselt number in case of free convection is the function of Grashoff number and Prandtl number. Let us understand why.
Free Convection:
When heat transfer takes place due to buoyancy forces, it is referred to as free convection. In free convection, the fluid moves due to the density differences caused by temperature differences.
Nusselt Number:
Nusselt number is a dimensionless number that represents the ratio of convective to conductive heat transfer across a boundary. It is defined as:
Nu = hL/k
Where h is the convective heat transfer coefficient, L is the characteristic length, and k is the thermal conductivity of the fluid.
Grashoff Number:
Grashoff number is a dimensionless number that represents the ratio of buoyancy to viscous forces in a fluid. It is defined as:
Gr = gβΔTL^3/ν^2
Where g is the acceleration due to gravity, β is the coefficient of thermal expansion, ΔT is the temperature difference, L is the characteristic length, and ν is the kinematic viscosity.
Prandtl Number:
Prandtl number is a dimensionless number that represents the ratio of momentum diffusivity to thermal diffusivity in a fluid. It is defined as:
Pr = ν/α
Where ν is the kinematic viscosity and α is the thermal diffusivity.
Relationship between Nusselt Number, Grashoff Number, and Prandtl Number:
The Nusselt number in case of free convection is dependent on the Grashoff number and Prandtl number. The relationship between these numbers is given by the following equation:
Nu = C(GrPr)^n
Where C and n are constants that depend on the geometry of the system. The above equation shows that the Nusselt number is directly proportional to the Grashoff number and Prandtl number raised to the power of n. Thus, the Nusselt number in case of free convection is the function of Grashoff number and Prandtl number.
Free Convection:
When heat transfer takes place due to buoyancy forces, it is referred to as free convection. In free convection, the fluid moves due to the density differences caused by temperature differences.
Nusselt Number:
Nusselt number is a dimensionless number that represents the ratio of convective to conductive heat transfer across a boundary. It is defined as:
Nu = hL/k
Where h is the convective heat transfer coefficient, L is the characteristic length, and k is the thermal conductivity of the fluid.
Grashoff Number:
Grashoff number is a dimensionless number that represents the ratio of buoyancy to viscous forces in a fluid. It is defined as:
Gr = gβΔTL^3/ν^2
Where g is the acceleration due to gravity, β is the coefficient of thermal expansion, ΔT is the temperature difference, L is the characteristic length, and ν is the kinematic viscosity.
Prandtl Number:
Prandtl number is a dimensionless number that represents the ratio of momentum diffusivity to thermal diffusivity in a fluid. It is defined as:
Pr = ν/α
Where ν is the kinematic viscosity and α is the thermal diffusivity.
Relationship between Nusselt Number, Grashoff Number, and Prandtl Number:
The Nusselt number in case of free convection is dependent on the Grashoff number and Prandtl number. The relationship between these numbers is given by the following equation:
Nu = C(GrPr)^n
Where C and n are constants that depend on the geometry of the system. The above equation shows that the Nusselt number is directly proportional to the Grashoff number and Prandtl number raised to the power of n. Thus, the Nusselt number in case of free convection is the function of Grashoff number and Prandtl number.
If heat and mass transfer takes place simultaneously, then the ratio of heat transfer coefficient to mass transfer coefficient is a function of the ratio of- a)Schmidt and Reynolds number
- b)Schmidt and Prandtl number
- c)Nusselt and Lewis number
- d)Reynolds and Lewis numbers
Correct answer is option 'A'. Can you explain this answer?
If heat and mass transfer takes place simultaneously, then the ratio of heat transfer coefficient to mass transfer coefficient is a function of the ratio of
a)
Schmidt and Reynolds number
b)
Schmidt and Prandtl number
c)
Nusselt and Lewis number
d)
Reynolds and Lewis numbers

|
Arshiya Roy answered |
Analogy of heat and mass transfer is given by Sh = 0.023 Re0. 8 Sc0.33
Fins are used to increase heat transfer rate from a surface by
1. increasing the temperature difference
2. increasing the effective surface area
3. increasing the convective heat transfer coefficient
4. decreasing the thermal conductivityWhich of the above are true?- a)1 and 2
- b)1,3 and 4
- c)2 only
- d)4 only
Correct answer is option 'C'. Can you explain this answer?
Fins are used to increase heat transfer rate from a surface by
1. increasing the temperature difference
2. increasing the effective surface area
3. increasing the convective heat transfer coefficient
4. decreasing the thermal conductivity
1. increasing the temperature difference
2. increasing the effective surface area
3. increasing the convective heat transfer coefficient
4. decreasing the thermal conductivity
Which of the above are true?
a)
1 and 2
b)
1,3 and 4
c)
2 only
d)
4 only
|
|
Sagnik Choudhary answered |
Explanation:
Fins are widely used in various engineering applications for enhancing the heat transfer rate from a surface. The primary function of fins is to increase the effective surface area of a heat transfer surface so that more heat can be transferred from the surface. However, fins can also affect other parameters that affect heat transfer rate. Let's discuss each of the given options one by one:
1. Increasing the Temperature Difference:
Increasing the temperature difference between the surface and the surrounding fluid can enhance the heat transfer rate. However, fins do not directly affect the temperature difference between the surface and the fluid. Therefore, option 1 is incorrect.
2. Increasing the Effective Surface Area:
Fins are designed to increase the effective surface area of a heat transfer surface. By increasing the surface area, the contact area between the surface and the fluid increases, which enhances the heat transfer rate. Therefore, option 2 is correct.
3. Increasing the Convective Heat Transfer Coefficient:
Convective heat transfer coefficient is a measure of the efficiency of heat transfer between a surface and a fluid. Fins can enhance the convective heat transfer coefficient by promoting fluid flow and turbulence around the surface. However, fins do not directly affect the convective heat transfer coefficient. Therefore, option 3 is incorrect.
4. Decreasing the Thermal Conductivity:
Thermal conductivity is a measure of the ability of a material to conduct heat. Fins do not affect the thermal conductivity of the surface material. Therefore, option 4 is incorrect.
Conclusion:
From the above explanation, it is clear that option 2 is correct, and options 1, 3, and 4 are incorrect. Therefore, the correct answer is option C, i.e., 2 only.
Fins are widely used in various engineering applications for enhancing the heat transfer rate from a surface. The primary function of fins is to increase the effective surface area of a heat transfer surface so that more heat can be transferred from the surface. However, fins can also affect other parameters that affect heat transfer rate. Let's discuss each of the given options one by one:
1. Increasing the Temperature Difference:
Increasing the temperature difference between the surface and the surrounding fluid can enhance the heat transfer rate. However, fins do not directly affect the temperature difference between the surface and the fluid. Therefore, option 1 is incorrect.
2. Increasing the Effective Surface Area:
Fins are designed to increase the effective surface area of a heat transfer surface. By increasing the surface area, the contact area between the surface and the fluid increases, which enhances the heat transfer rate. Therefore, option 2 is correct.
3. Increasing the Convective Heat Transfer Coefficient:
Convective heat transfer coefficient is a measure of the efficiency of heat transfer between a surface and a fluid. Fins can enhance the convective heat transfer coefficient by promoting fluid flow and turbulence around the surface. However, fins do not directly affect the convective heat transfer coefficient. Therefore, option 3 is incorrect.
4. Decreasing the Thermal Conductivity:
Thermal conductivity is a measure of the ability of a material to conduct heat. Fins do not affect the thermal conductivity of the surface material. Therefore, option 4 is incorrect.
Conclusion:
From the above explanation, it is clear that option 2 is correct, and options 1, 3, and 4 are incorrect. Therefore, the correct answer is option C, i.e., 2 only.
Which of the following statements is not correct?In a transient flow process- a)the rates of inflow and outflow of mass are different.
- b)the state of matter inside the control volume varies with time.
- c)there can be work and heat interactions across the control volume.
- d)there is no accumulation of energy inside the control volume.
Correct answer is option 'D'. Can you explain this answer?
Which of the following statements is not correct?
In a transient flow process
a)
the rates of inflow and outflow of mass are different.
b)
the state of matter inside the control volume varies with time.
c)
there can be work and heat interactions across the control volume.
d)
there is no accumulation of energy inside the control volume.
|
|
Ishaan Malik answered |
Assumption: Change in internal energy of the billet during time
dt = Net heat flow from the billet to the bath or air during time dt
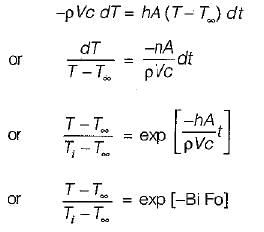
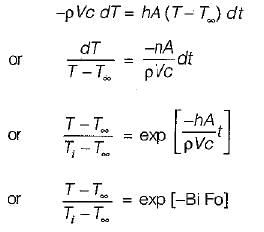
For a thin steel sheet, total emissive power is given as 32 W/m2, insolation as 93 W/m2. If thin sheet has reflectivity = 0,6, absorbtivity = 0.1 and transmissivity = 0.3. Then radiosity in W/m2- a)87.8 W/m2
- b)41.3 W/m2
- c)112.2 W/m2
- d)102.6 W/m2
Correct answer is option 'A'. Can you explain this answer?
For a thin steel sheet, total emissive power is given as 32 W/m2, insolation as 93 W/m2. If thin sheet has reflectivity = 0,6, absorbtivity = 0.1 and transmissivity = 0.3. Then radiosity in W/m2
a)
87.8 W/m2
b)
41.3 W/m2
c)
112.2 W/m2
d)
102.6 W/m2
|
|
Ashutosh Sharma answered |
Given Data:
- Total emissive power (E) = 32 W/m2
- Insolation (I) = 93 W/m2
- Reflectivity (R) = 0.6
- Absorptivity (A) = 0.1
- Transmissivity (T) = 0.3
Calculating the Radiosity:
The radiosity (J) can be calculated using the following equation:
J = A * I + E - R * E
Substituting the given values:
J = 0.1 * 93 + 32 - 0.6 * 32
J = 9.3 + 32 - 19.2
J = 22.1
Therefore, the radiosity is 22.1 W/m2.
Comparing with the Answer Options:
The correct answer is given as option 'A' (87.8 W/m2), but our calculated radiosity is 22.1 W/m2. This means that the given answer is incorrect.
Conclusion:
The correct answer to the given question cannot be determined based on the provided information.
- Total emissive power (E) = 32 W/m2
- Insolation (I) = 93 W/m2
- Reflectivity (R) = 0.6
- Absorptivity (A) = 0.1
- Transmissivity (T) = 0.3
Calculating the Radiosity:
The radiosity (J) can be calculated using the following equation:
J = A * I + E - R * E
Substituting the given values:
J = 0.1 * 93 + 32 - 0.6 * 32
J = 9.3 + 32 - 19.2
J = 22.1
Therefore, the radiosity is 22.1 W/m2.
Comparing with the Answer Options:
The correct answer is given as option 'A' (87.8 W/m2), but our calculated radiosity is 22.1 W/m2. This means that the given answer is incorrect.
Conclusion:
The correct answer to the given question cannot be determined based on the provided information.
A copper block and an air mass block having similar dimensions are subjected to symmetrical heat transfer from one face of each block will reach to the same temperature at a rate- a)faster in air block
- b)faster in copper block
- c)equal in air as well as copper block
- d)cannot predicted with given information
Correct answer is option 'B'. Can you explain this answer?
A copper block and an air mass block having similar dimensions are subjected to symmetrical heat transfer from one face of each block will reach to the same temperature at a rate
a)
faster in air block
b)
faster in copper block
c)
equal in air as well as copper block
d)
cannot predicted with given information
|
|
Aditya Chavan answered |
Since thermal conductivity of copper is far greater than air.
In order to achieve maximum heat dissipation the fin should be designed in such a way that it has- a)maximum lateral surface at the root side of fin
- b)maximum lateral surface towards the tip side of fin
- c)maximum lateral surface near the center of fin
- d)minimum lateral surface near the center of fin
Correct answer is option 'A'. Can you explain this answer?
In order to achieve maximum heat dissipation the fin should be designed in such a way that it has
a)
maximum lateral surface at the root side of fin
b)
maximum lateral surface towards the tip side of fin
c)
maximum lateral surface near the center of fin
d)
minimum lateral surface near the center of fin

|
Aditi Sarkar answered |
Fins are provided to a heat exchanger surface in such a way- that lateral surface area at root is maximum.
Consider the following statements regarding fin of minimum weight
1. The weight saved by using the triangular fin is 44%.
2. The difference in weight between a fin in shape of circular arc and the fin of triangular shape is very large.
3. The triangular shape fin is regarded as best shape as it is much easier to manufacture.
4. Weight of fin is of paramount importance for the design of cooling device used in aircraft.Which of the above are correct?- a)1, 2 and 4
- b)1, 3 and 4
- c)2, 3 and 4
- d)1, 2 and
Correct answer is option 'B'. Can you explain this answer?
Consider the following statements regarding fin of minimum weight
1. The weight saved by using the triangular fin is 44%.
2. The difference in weight between a fin in shape of circular arc and the fin of triangular shape is very large.
3. The triangular shape fin is regarded as best shape as it is much easier to manufacture.
4. Weight of fin is of paramount importance for the design of cooling device used in aircraft.
1. The weight saved by using the triangular fin is 44%.
2. The difference in weight between a fin in shape of circular arc and the fin of triangular shape is very large.
3. The triangular shape fin is regarded as best shape as it is much easier to manufacture.
4. Weight of fin is of paramount importance for the design of cooling device used in aircraft.
Which of the above are correct?
a)
1, 2 and 4
b)
1, 3 and 4
c)
2, 3 and 4
d)
1, 2 and
|
|
Ameya Kaur answered |
Understanding the Statements on Fin Design
To analyze the correctness of each statement about fins of minimum weight, let's break down the provided information.
1. Weight Savings of Triangular Fins
- The claim that a triangular fin saves 44% of the weight compared to other shapes is generally supported by empirical studies. Triangular fins are often found to minimize material usage while maintaining efficiency.
2. Weight Difference Between Fin Shapes
- The assertion that the weight difference between a fin shaped like a circular arc and a triangular fin is very large may not hold universally true. While there can be differences, they are not always significant enough to deem one shape vastly superior in all applications.
3. Manufacturing Ease of Triangular Fins
- The statement that triangular fins are easier to manufacture is accurate. Their simple geometric shape allows for straightforward fabrication processes, making them a preferred choice in many applications.
4. Importance of Fin Weight in Aircraft Cooling Devices
- This statement is valid. In aircraft design, minimizing weight is crucial for overall performance, fuel efficiency, and payload capacity. Thus, the weight of fins in cooling systems is indeed of paramount importance.
Conclusion
Based on the evaluations:
- Statement 1 is correct.
- Statement 2 is misleading as the differences may not always be "very large."
- Statement 3 is correct.
- Statement 4 is correct.
Thus, the correct options are 1, 3, and 4, aligning with option 'B'.
To analyze the correctness of each statement about fins of minimum weight, let's break down the provided information.
1. Weight Savings of Triangular Fins
- The claim that a triangular fin saves 44% of the weight compared to other shapes is generally supported by empirical studies. Triangular fins are often found to minimize material usage while maintaining efficiency.
2. Weight Difference Between Fin Shapes
- The assertion that the weight difference between a fin shaped like a circular arc and a triangular fin is very large may not hold universally true. While there can be differences, they are not always significant enough to deem one shape vastly superior in all applications.
3. Manufacturing Ease of Triangular Fins
- The statement that triangular fins are easier to manufacture is accurate. Their simple geometric shape allows for straightforward fabrication processes, making them a preferred choice in many applications.
4. Importance of Fin Weight in Aircraft Cooling Devices
- This statement is valid. In aircraft design, minimizing weight is crucial for overall performance, fuel efficiency, and payload capacity. Thus, the weight of fins in cooling systems is indeed of paramount importance.
Conclusion
Based on the evaluations:
- Statement 1 is correct.
- Statement 2 is misleading as the differences may not always be "very large."
- Statement 3 is correct.
- Statement 4 is correct.
Thus, the correct options are 1, 3, and 4, aligning with option 'B'.
A critical radius of insulated pipe leads to- a)minimum heat transfer
- b)no effect on heat transfer
- c)no heat transfer at all
- d)maximum heat transfe
Correct answer is option 'D'. Can you explain this answer?
A critical radius of insulated pipe leads to
a)
minimum heat transfer
b)
no effect on heat transfer
c)
no heat transfer at all
d)
maximum heat transfe

|
Aarav Kulkarni answered |
From the above figure one can analyse that at critical radius heat transfer is maximum.
Thermal conductivity of wood depends on- a)moisture
- b)density
- c)temperature
- d)all of these
Correct answer is option 'D'. Can you explain this answer?
Thermal conductivity of wood depends on
a)
moisture
b)
density
c)
temperature
d)
all of these
|
|
Sanskriti Chakraborty answered |
Thermal conductivity of wood is affected by several factors, including moisture content, density, and temperature. Let's discuss each of these factors in detail:
Moisture content:
- Wood is a hygroscopic material, which means it can absorb or release moisture from the environment.
- Moisture content in wood can affect its thermal conductivity because water has a much higher thermal conductivity than wood.
- As the moisture content in wood increases, its thermal conductivity also increases. This is because the water molecules conduct heat better than the wood molecules.
Density:
- The density of wood can also affect its thermal conductivity.
- Generally, the denser the wood, the higher its thermal conductivity. This is because denser wood has more atoms per unit volume, which means there are more pathways for heat transfer to occur.
Temperature:
- The temperature of wood can also affect its thermal conductivity.
- As the temperature of wood increases, its thermal conductivity also increases. This is because the wood molecules vibrate more rapidly at higher temperatures, which means they can transfer heat more efficiently.
Overall, the thermal conductivity of wood is influenced by these three factors: moisture content, density, and temperature. Therefore, option D, "all of these," is the correct answer.
Moisture content:
- Wood is a hygroscopic material, which means it can absorb or release moisture from the environment.
- Moisture content in wood can affect its thermal conductivity because water has a much higher thermal conductivity than wood.
- As the moisture content in wood increases, its thermal conductivity also increases. This is because the water molecules conduct heat better than the wood molecules.
Density:
- The density of wood can also affect its thermal conductivity.
- Generally, the denser the wood, the higher its thermal conductivity. This is because denser wood has more atoms per unit volume, which means there are more pathways for heat transfer to occur.
Temperature:
- The temperature of wood can also affect its thermal conductivity.
- As the temperature of wood increases, its thermal conductivity also increases. This is because the wood molecules vibrate more rapidly at higher temperatures, which means they can transfer heat more efficiently.
Overall, the thermal conductivity of wood is influenced by these three factors: moisture content, density, and temperature. Therefore, option D, "all of these," is the correct answer.
The Fourier law of heat conduction is valid for- a)One dimensional only
- b)Two dimensional only
- c)Three dimensional only
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The Fourier law of heat conduction is valid for
a)
One dimensional only
b)
Two dimensional only
c)
Three dimensional only
d)
None of these
|
|
Nayanika Yadav answered |
While deriving Fourier law of heat conduction some assumptions are made, which are
1. Steady-state condition
2. One-directional heat transfer
3. No heat generation
4. Material is homogeneous and isotropic
1. Steady-state condition
2. One-directional heat transfer
3. No heat generation
4. Material is homogeneous and isotropic
Transient three-dimensional heat conduction is governed by ONE of the following differential equations (α - thermal diffusivity, k - thermal conductivity and ψ - volumetric rate of heat generation)- a)
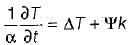
- b)
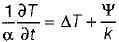
- c)
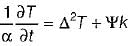
- d)
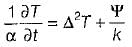
Correct answer is option 'D'. Can you explain this answer?
Transient three-dimensional heat conduction is governed by ONE of the following differential equations (α - thermal diffusivity, k - thermal conductivity and ψ - volumetric rate of heat generation)
a)
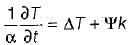
b)
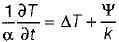
c)
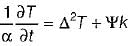
d)
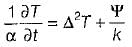

|
Swati Gupta answered |
Fourier equation
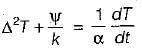
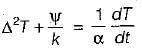
All the three modes of heat transfer are involved in- a)melting of ice
- b)Cooling of a small metal casting in a quenching bath
- c)heat flow through the walls of a refrigerator
- d)automobile engine equipped with a thermosyphon cooling system
Correct answer is option 'D'. Can you explain this answer?
All the three modes of heat transfer are involved in
a)
melting of ice
b)
Cooling of a small metal casting in a quenching bath
c)
heat flow through the walls of a refrigerator
d)
automobile engine equipped with a thermosyphon cooling system
|
|
Nayanika Yadav answered |
Heat Transfer in Different Processes
Melting of Ice:
- Involves only one mode of heat transfer, i.e. latent heat transfer
- Heat is absorbed by the ice to break the bonds between molecules and change the phase from solid to liquid
- No conduction or convection involved
Cooling of a Small Metal Casting in a Quenching Bath:
- Involves two modes of heat transfer, i.e. convection and conduction
- Metal casting is immersed in a quenching bath to cool it quickly
- Convection occurs as the cooler liquid in the bath comes in contact with the hot metal casting and carries away the heat
- Conduction occurs as heat is transferred from the hot metal casting to the cooler liquid in the bath
Heat Flow Through the Walls of a Refrigerator:
- Involves only one mode of heat transfer, i.e. conduction
- Heat flows from the warmer environment outside the refrigerator to the cooler environment inside the refrigerator
- The walls of the refrigerator act as a barrier to the heat flow through conduction
Automobile Engine Equipped with a Thermosyphon Cooling System:
- Involves all three modes of heat transfer, i.e. conduction, convection, and radiation
- Heat is generated in the engine due to combustion and friction
- Conduction occurs as the heat is transferred from the engine to the coolant in the engine block
- Convection occurs as the heated coolant rises and cooler coolant sinks, creating a natural circulation of the fluid
- Radiation occurs as the heat is transferred from the engine to the surrounding environment
- The thermosyphon cooling system helps in the efficient transfer of heat and keeps the engine cool
Therefore, option 'D' is the correct answer as it involves all three modes of heat transfer.
Melting of Ice:
- Involves only one mode of heat transfer, i.e. latent heat transfer
- Heat is absorbed by the ice to break the bonds between molecules and change the phase from solid to liquid
- No conduction or convection involved
Cooling of a Small Metal Casting in a Quenching Bath:
- Involves two modes of heat transfer, i.e. convection and conduction
- Metal casting is immersed in a quenching bath to cool it quickly
- Convection occurs as the cooler liquid in the bath comes in contact with the hot metal casting and carries away the heat
- Conduction occurs as heat is transferred from the hot metal casting to the cooler liquid in the bath
Heat Flow Through the Walls of a Refrigerator:
- Involves only one mode of heat transfer, i.e. conduction
- Heat flows from the warmer environment outside the refrigerator to the cooler environment inside the refrigerator
- The walls of the refrigerator act as a barrier to the heat flow through conduction
Automobile Engine Equipped with a Thermosyphon Cooling System:
- Involves all three modes of heat transfer, i.e. conduction, convection, and radiation
- Heat is generated in the engine due to combustion and friction
- Conduction occurs as the heat is transferred from the engine to the coolant in the engine block
- Convection occurs as the heated coolant rises and cooler coolant sinks, creating a natural circulation of the fluid
- Radiation occurs as the heat is transferred from the engine to the surrounding environment
- The thermosyphon cooling system helps in the efficient transfer of heat and keeps the engine cool
Therefore, option 'D' is the correct answer as it involves all three modes of heat transfer.
A fin will be necessary and effective only when
where k = thermal conductivity of fin material, h = convective heat transfer coefficient between the fin surface and environment temperature- a)k is small and h is large
- b)k is large and h is also large
- c)k is small and h is also small
- d)k is large and h is small
Correct answer is option 'D'. Can you explain this answer?
A fin will be necessary and effective only when
where k = thermal conductivity of fin material, h = convective heat transfer coefficient between the fin surface and environment temperature
where k = thermal conductivity of fin material, h = convective heat transfer coefficient between the fin surface and environment temperature
a)
k is small and h is large
b)
k is large and h is also large
c)
k is small and h is also small
d)
k is large and h is small
|
|
Hrishikesh Chakraborty answered |

so, for more effectiveness, k should be large and h should be small.
Arrangement of silver, air, aluminium and lead in order of increasing thermal conductivity at room temperature yields- a)Air, Aluminium,'Silver, Lead
- b)Air, Aluminium, Lead, Silver
- c)Lead, Air, Aluminium, Silver
- d)Air, Lead, Aluminium, Silver
Correct answer is option 'D'. Can you explain this answer?
Arrangement of silver, air, aluminium and lead in order of increasing thermal conductivity at room temperature yields
a)
Air, Aluminium,'Silver, Lead
b)
Air, Aluminium, Lead, Silver
c)
Lead, Air, Aluminium, Silver
d)
Air, Lead, Aluminium, Silver

|
Anuj Verma answered |
According to their thermal conductivity for Air, k = 0.022 W/mK
for Aluminium, k = 205 W/mK
for Silver, k = 407 W/mK
Hence correct sequence is
Air, Lead, Aluminium, Silve
for Aluminium, k = 205 W/mK
for Silver, k = 407 W/mK
Hence correct sequence is
Air, Lead, Aluminium, Silve
Consider the following statements:
1. The thermal conductivity of a material is it’s ability to conduct heat.
2. The thermal conductivity can be defined as the rate of heat transfer through a unit thickness of the material per unit area.
3. In solids, heat conduction is due to lattice vibrational energy as well as energy transported via free flow of electrons.
4. Convection involves combined effect of conduction and fluid motion.
Which of the above statements are valid?- a)1 and 2
- b)2, 3 and 4
- c)1, 3 and 4
- d)3 and 4
Correct answer is option 'C'. Can you explain this answer?
Consider the following statements:
1. The thermal conductivity of a material is it’s ability to conduct heat.
2. The thermal conductivity can be defined as the rate of heat transfer through a unit thickness of the material per unit area.
3. In solids, heat conduction is due to lattice vibrational energy as well as energy transported via free flow of electrons.
4. Convection involves combined effect of conduction and fluid motion.
Which of the above statements are valid?
1. The thermal conductivity of a material is it’s ability to conduct heat.
2. The thermal conductivity can be defined as the rate of heat transfer through a unit thickness of the material per unit area.
3. In solids, heat conduction is due to lattice vibrational energy as well as energy transported via free flow of electrons.
4. Convection involves combined effect of conduction and fluid motion.
Which of the above statements are valid?
a)
1 and 2
b)
2, 3 and 4
c)
1, 3 and 4
d)
3 and 4

|
Simran Saha answered |
S ability to conduct heat.
2. Materials with high thermal conductivity are good conductors of heat.
3. Metals generally have high thermal conductivity.
4. Insulators have low thermal conductivity.
All of these statements are true.
2. Materials with high thermal conductivity are good conductors of heat.
3. Metals generally have high thermal conductivity.
4. Insulators have low thermal conductivity.
All of these statements are true.
A large concrete slab 1 m thick has one dimensional temperature distribution:
T = 4 - 10x + 20x2 + 10x3
where T is temperature and x is distance from one face towards other face of wail. If the slab material has thermal diffusivity of 2 x 10-3m2/hr, what is the rate of change of temperature at the other face of the wall?- a)0.1°C/h
- b)0.2°C/h
- c)0.3°C/h
- d)0.4°C/h
Correct answer is option 'B'. Can you explain this answer?
A large concrete slab 1 m thick has one dimensional temperature distribution:
T = 4 - 10x + 20x2 + 10x3
where T is temperature and x is distance from one face towards other face of wail. If the slab material has thermal diffusivity of 2 x 10-3m2/hr, what is the rate of change of temperature at the other face of the wall?
T = 4 - 10x + 20x2 + 10x3
where T is temperature and x is distance from one face towards other face of wail. If the slab material has thermal diffusivity of 2 x 10-3m2/hr, what is the rate of change of temperature at the other face of the wall?
a)
0.1°C/h
b)
0.2°C/h
c)
0.3°C/h
d)
0.4°C/h

|
Samridhi Choudhary answered |
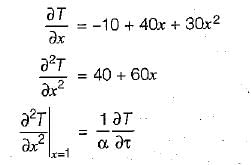
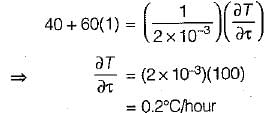
Thermal conductivity of air with rise in temperature- a)increases
- b)remains constant
- c)decreases
- d)may increase or decrease depending on temperature
Correct answer is option 'A'. Can you explain this answer?
Thermal conductivity of air with rise in temperature
a)
increases
b)
remains constant
c)
decreases
d)
may increase or decrease depending on temperature
|
|
Stuti Bajaj answered |
Thermal conductivity of air with rise in temperature
The correct answer is option 'A', which states that the thermal conductivity of air increases with a rise in temperature. This can be explained by the following factors:
1. Increase in molecular motion:
As the temperature of a gas (such as air) increases, the average kinetic energy of its molecules also increases. This leads to an increase in molecular motion, resulting in more frequent collisions between the molecules. These collisions facilitate the transfer of thermal energy from one molecule to another, thereby increasing the thermal conductivity of the gas.
2. Increase in collision frequency:
With the increase in temperature, the frequency of collisions between gas molecules also increases. This is due to the higher molecular velocity resulting from increased kinetic energy. As a result, there is a greater probability of energy transfer through collisions, leading to higher thermal conductivity.
3. Decrease in mean free path:
The mean free path is the average distance a molecule travels between successive collisions. With the rise in temperature, the mean free path of air molecules decreases. This is because the increased molecular motion leads to more frequent collisions, reducing the average distance traveled by the molecules. A shorter mean free path implies that the molecules have less distance to travel before they collide and transfer thermal energy. Consequently, the thermal conductivity of air increases.
4. Impact of molecular structure:
The molecular structure of air remains relatively unchanged with temperature variations. Therefore, the increase in thermal conductivity is primarily influenced by the factors mentioned above, such as increased molecular motion and collision frequency.
In summary, the thermal conductivity of air increases with a rise in temperature due to enhanced molecular motion, higher collision frequency, and reduced mean free path. These factors contribute to a more efficient transfer of thermal energy within the gas.
The correct answer is option 'A', which states that the thermal conductivity of air increases with a rise in temperature. This can be explained by the following factors:
1. Increase in molecular motion:
As the temperature of a gas (such as air) increases, the average kinetic energy of its molecules also increases. This leads to an increase in molecular motion, resulting in more frequent collisions between the molecules. These collisions facilitate the transfer of thermal energy from one molecule to another, thereby increasing the thermal conductivity of the gas.
2. Increase in collision frequency:
With the increase in temperature, the frequency of collisions between gas molecules also increases. This is due to the higher molecular velocity resulting from increased kinetic energy. As a result, there is a greater probability of energy transfer through collisions, leading to higher thermal conductivity.
3. Decrease in mean free path:
The mean free path is the average distance a molecule travels between successive collisions. With the rise in temperature, the mean free path of air molecules decreases. This is because the increased molecular motion leads to more frequent collisions, reducing the average distance traveled by the molecules. A shorter mean free path implies that the molecules have less distance to travel before they collide and transfer thermal energy. Consequently, the thermal conductivity of air increases.
4. Impact of molecular structure:
The molecular structure of air remains relatively unchanged with temperature variations. Therefore, the increase in thermal conductivity is primarily influenced by the factors mentioned above, such as increased molecular motion and collision frequency.
In summary, the thermal conductivity of air increases with a rise in temperature due to enhanced molecular motion, higher collision frequency, and reduced mean free path. These factors contribute to a more efficient transfer of thermal energy within the gas.
A steel plate of thermal conductivity 50 W/m-K and thickness 10 cm passes a heat flux by conduction of 25 kW/m2. If the temperature of the hot surface of the plate is 100°C then what is the temperature of the cooler side of the plate?- a)30°C
- b)40°C
- c)50°C
- d)60°C
Correct answer is option 'C'. Can you explain this answer?
A steel plate of thermal conductivity 50 W/m-K and thickness 10 cm passes a heat flux by conduction of 25 kW/m2. If the temperature of the hot surface of the plate is 100°C then what is the temperature of the cooler side of the plate?
a)
30°C
b)
40°C
c)
50°C
d)
60°C

|
Prasad Desai answered |

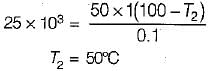
Two long parallel surfaces each of emissivity 07 are maintained at different temperature and accordingly have radiation heat exchange between them. It is desirable to reduce 75% of this radiant heat transfer by inserting thin parallel shields of equal emissivity on both sides. The number of shields should be- a)one
- b)two
- c)three
- d)four
Correct answer is option 'C'. Can you explain this answer?
Two long parallel surfaces each of emissivity 07 are maintained at different temperature and accordingly have radiation heat exchange between them. It is desirable to reduce 75% of this radiant heat transfer by inserting thin parallel shields of equal emissivity on both sides. The number of shields should be
a)
one
b)
two
c)
three
d)
four
|
|
Anshul Basu answered |
Explanation:
Given:
- Two long parallel surfaces with emissivity 0.7
- Desired reduction in radiant heat transfer: 75%
- Thin parallel shields with equal emissivity on both sides
- Number of shields required: ?
Solution:
Step 1: Calculate the initial radiant heat transfer
- Let's assume the initial radiant heat transfer between the two surfaces is Q.
- The radiant heat transfer between two surfaces can be calculated using the Stefan-Boltzmann Law:
Q = εσA(T1^4 - T2^4)
where ε is the emissivity, σ is the Stefan-Boltzmann constant, A is the surface area, T1 is the temperature of the first surface, and T2 is the temperature of the second surface.
- Since the emissivity of both surfaces is 0.7, we can simplify the equation as:
Q = 0.7σA(T1^4 - T2^4)
Step 2: Calculate the desired reduction in radiant heat transfer
- The desired reduction in radiant heat transfer is 75%.
- Therefore, the radiant heat transfer after inserting the shields should be 25% of the initial radiant heat transfer.
- Let's assume the radiant heat transfer after inserting the shields is Q'.
- Hence, Q' = 0.25Q
Step 3: Calculate the number of shields required
- Let's assume the number of shields required is n.
- When n shields are inserted between the two surfaces, the radiant heat transfer between each shield is reduced by a factor of 0.7 (emissivity of the shields).
- Therefore, the radiant heat transfer between the shields can be calculated as:
Q'' = (0.7)^nQ
- Since there are two sides to each shield, the total reduction in radiant heat transfer is:
Q''' = (0.7)^{2n}Q
- The radiant heat transfer after inserting the shields is given by:
Q' = Q - Q'''
- Substituting the values of Q' and Q''', we get:
0.25Q = Q - (0.7)^{2n}Q
- Simplifying the equation, we get:
(0.7)^{2n} = 0.75
- Taking the logarithm on both sides of the equation, we get:
2n log(0.7) = log(0.75)
n = log(0.75) / (2 log(0.7))
n ≈ 2.45
Conclusion:
- The number of shields required to reduce 75% of the radiant heat transfer is approximately 2.
- Therefore, the correct answer is option 'C' (two shields).
Given:
- Two long parallel surfaces with emissivity 0.7
- Desired reduction in radiant heat transfer: 75%
- Thin parallel shields with equal emissivity on both sides
- Number of shields required: ?
Solution:
Step 1: Calculate the initial radiant heat transfer
- Let's assume the initial radiant heat transfer between the two surfaces is Q.
- The radiant heat transfer between two surfaces can be calculated using the Stefan-Boltzmann Law:
Q = εσA(T1^4 - T2^4)
where ε is the emissivity, σ is the Stefan-Boltzmann constant, A is the surface area, T1 is the temperature of the first surface, and T2 is the temperature of the second surface.
- Since the emissivity of both surfaces is 0.7, we can simplify the equation as:
Q = 0.7σA(T1^4 - T2^4)
Step 2: Calculate the desired reduction in radiant heat transfer
- The desired reduction in radiant heat transfer is 75%.
- Therefore, the radiant heat transfer after inserting the shields should be 25% of the initial radiant heat transfer.
- Let's assume the radiant heat transfer after inserting the shields is Q'.
- Hence, Q' = 0.25Q
Step 3: Calculate the number of shields required
- Let's assume the number of shields required is n.
- When n shields are inserted between the two surfaces, the radiant heat transfer between each shield is reduced by a factor of 0.7 (emissivity of the shields).
- Therefore, the radiant heat transfer between the shields can be calculated as:
Q'' = (0.7)^nQ
- Since there are two sides to each shield, the total reduction in radiant heat transfer is:
Q''' = (0.7)^{2n}Q
- The radiant heat transfer after inserting the shields is given by:
Q' = Q - Q'''
- Substituting the values of Q' and Q''', we get:
0.25Q = Q - (0.7)^{2n}Q
- Simplifying the equation, we get:
(0.7)^{2n} = 0.75
- Taking the logarithm on both sides of the equation, we get:
2n log(0.7) = log(0.75)
n = log(0.75) / (2 log(0.7))
n ≈ 2.45
Conclusion:
- The number of shields required to reduce 75% of the radiant heat transfer is approximately 2.
- Therefore, the correct answer is option 'C' (two shields).
The convective heat transfer coefficient from a hot cylindrical surface exposed to still air varies in accordance with
Where ΔT is the temperature difference between the hot surface and surrounding ambient air.- a)(ΔT)0.25
- b)(ΔT)0.5
- c)(ΔT)0.75
- d)(ΔT)1.25
Correct answer is option 'A'. Can you explain this answer?
The convective heat transfer coefficient from a hot cylindrical surface exposed to still air varies in accordance with
Where ΔT is the temperature difference between the hot surface and surrounding ambient air.
Where ΔT is the temperature difference between the hot surface and surrounding ambient air.
a)
(ΔT)0.25
b)
(ΔT)0.5
c)
(ΔT)0.75
d)
(ΔT)1.25

|
Sneha Roy answered |
Is h: convective heat transfer coefficient (W/m^2·K)
k: thermal conductivity of the fluid (W/m·K)
Nu: Nusselt number (dimensionless)
D: diameter of the cylinder (m)
L: characteristic length of the cylinder (e.g. diameter or length) (m)
Pr: Prandtl number (dimensionless)
Re: Reynolds number (dimensionless)
μ: dynamic viscosity of the fluid (Pa·s)
v: velocity of the fluid (m/s)
c: specific heat capacity of the fluid (J/kg·K)
ρ: density of the fluid (kg/m^3)
β: thermal expansion coefficient of the fluid (1/K)
g: acceleration due to gravity (m/s^2)
ΔT: temperature difference between the surface and the fluid (K)
k: thermal conductivity of the fluid (W/m·K)
Nu: Nusselt number (dimensionless)
D: diameter of the cylinder (m)
L: characteristic length of the cylinder (e.g. diameter or length) (m)
Pr: Prandtl number (dimensionless)
Re: Reynolds number (dimensionless)
μ: dynamic viscosity of the fluid (Pa·s)
v: velocity of the fluid (m/s)
c: specific heat capacity of the fluid (J/kg·K)
ρ: density of the fluid (kg/m^3)
β: thermal expansion coefficient of the fluid (1/K)
g: acceleration due to gravity (m/s^2)
ΔT: temperature difference between the surface and the fluid (K)
The surface hardening of a mild steel component by the diffusion of carbon molecules is a- a)transient mass diffusion process
- b)steady mass diffusion process
- c)pressure diffusion process
- d)Ordinary diffusion process
Correct answer is option 'A'. Can you explain this answer?
The surface hardening of a mild steel component by the diffusion of carbon molecules is a
a)
transient mass diffusion process
b)
steady mass diffusion process
c)
pressure diffusion process
d)
Ordinary diffusion process

|
Manisha Chavan answered |
Understanding Surface Hardening of Mild Steel
Surface hardening of mild steel through carbon diffusion is a crucial process in mechanical engineering. It enhances wear resistance and strength by altering the material's surface properties.
Transient Mass Diffusion Process
- Definition: A transient mass diffusion process occurs when the concentration of diffusing species changes with time. In this case, carbon atoms diffuse into the steel surface, gradually increasing the carbon concentration.
- Mechanism: Initially, the carbon concentration at the surface is higher than that within the steel. Over time, carbon atoms move into the steel, leading to a gradient in concentration that changes as the process continues.
- Factors Affecting Transience:
- Temperature: Higher temperatures increase the diffusion rate.
- Time: The longer the component is exposed, the deeper carbon can diffuse into the steel.
- Concentration Gradient: As the carbon diffuses, the gradient diminishes, affecting the diffusion rate.
Comparison with Other Processes
- Steady Mass Diffusion Process: In contrast, a steady-state process implies that the concentration remains constant over time, which is not the case in carbon diffusion during surface hardening.
- Pressure Diffusion Process: This refers to diffusion driven by pressure differences, which is not applicable in the context of carbon diffusion in mild steel.
- Ordinary Diffusion Process: While carbon diffusion can be considered ordinary, it specifically refers to the transient nature in this scenario due to changing concentration over time.
Conclusion
In conclusion, the surface hardening of mild steel through carbon diffusion is a transient mass diffusion process, characterized by time-dependent changes in carbon concentration, which effectively enhances the mechanical properties of the steel.
Surface hardening of mild steel through carbon diffusion is a crucial process in mechanical engineering. It enhances wear resistance and strength by altering the material's surface properties.
Transient Mass Diffusion Process
- Definition: A transient mass diffusion process occurs when the concentration of diffusing species changes with time. In this case, carbon atoms diffuse into the steel surface, gradually increasing the carbon concentration.
- Mechanism: Initially, the carbon concentration at the surface is higher than that within the steel. Over time, carbon atoms move into the steel, leading to a gradient in concentration that changes as the process continues.
- Factors Affecting Transience:
- Temperature: Higher temperatures increase the diffusion rate.
- Time: The longer the component is exposed, the deeper carbon can diffuse into the steel.
- Concentration Gradient: As the carbon diffuses, the gradient diminishes, affecting the diffusion rate.
Comparison with Other Processes
- Steady Mass Diffusion Process: In contrast, a steady-state process implies that the concentration remains constant over time, which is not the case in carbon diffusion during surface hardening.
- Pressure Diffusion Process: This refers to diffusion driven by pressure differences, which is not applicable in the context of carbon diffusion in mild steel.
- Ordinary Diffusion Process: While carbon diffusion can be considered ordinary, it specifically refers to the transient nature in this scenario due to changing concentration over time.
Conclusion
In conclusion, the surface hardening of mild steel through carbon diffusion is a transient mass diffusion process, characterized by time-dependent changes in carbon concentration, which effectively enhances the mechanical properties of the steel.
The earth receive at its surface radiation from the sun at the rate of 1400 W/m2. The distance of the centre of sun from the surface of earth is 1.5 x 1011 m and the radius of the sun is 7 x 108 m. Treating the sun as black body, it follows from the above data that sun's surface temperature is about- a)3650 K
- b)4520 K
- c)5800 K
- d)6150 K[
Correct answer is option 'C'. Can you explain this answer?
The earth receive at its surface radiation from the sun at the rate of 1400 W/m2. The distance of the centre of sun from the surface of earth is 1.5 x 1011 m and the radius of the sun is 7 x 108 m. Treating the sun as black body, it follows from the above data that sun's surface temperature is about
a)
3650 K
b)
4520 K
c)
5800 K
d)
6150 K[
|
|
Atharva Majumdar answered |
Solution:
Given:
Radiation received at the surface of the Earth from the sun = 1400 W/m²
Distance between the center of the sun and the surface of the Earth = 1.5 x 10^11 m
Radius of the sun = 7 x 10^8 m
To find:
Surface temperature of the sun
Formula:
The power radiated by a black body is given by the Stefan-Boltzmann law:
P = σAT^4
where P is the power, σ is the Stefan-Boltzmann constant (5.67 x 10^-8 W/m²K⁴), A is the surface area, and T is the temperature.
Step-by-step solution:
1. Calculate the surface area of the sun:
The surface area of a sphere is given by the formula:
A = 4πr²
where r is the radius.
Substituting the given radius of the sun:
A = 4π(7 x 10^8)²
A = 1.54 x 10^18 m²
2. Calculate the power radiated by the sun:
Given power received at the surface of the Earth = 1400 W/m²
Area of the Earth's surface = A = 4πr²
where r is the distance between the center of the sun and the surface of the Earth.
Substituting the given distance:
A = 4π(1.5 x 10^11)²
A = 2.83 x 10^23 m²
The power radiated by the sun can be calculated using the formula:
P = 1400 W/m² x 2.83 x 10^23 m²
P = 3.96 x 10^26 W
3. Calculate the temperature of the sun:
Using the Stefan-Boltzmann law:
P = σAT^4
Rearranging the formula to solve for T:
T^4 = P / (σA)
T = (P / (σA))^(1/4)
Substituting the calculated values:
T = (3.96 x 10^26) / (5.67 x 10^-8 x 1.54 x 10^18)^(1/4)
T ≈ 5800 K
Therefore, the surface temperature of the sun is approximately 5800 K, which corresponds to option C.
Given:
Radiation received at the surface of the Earth from the sun = 1400 W/m²
Distance between the center of the sun and the surface of the Earth = 1.5 x 10^11 m
Radius of the sun = 7 x 10^8 m
To find:
Surface temperature of the sun
Formula:
The power radiated by a black body is given by the Stefan-Boltzmann law:
P = σAT^4
where P is the power, σ is the Stefan-Boltzmann constant (5.67 x 10^-8 W/m²K⁴), A is the surface area, and T is the temperature.
Step-by-step solution:
1. Calculate the surface area of the sun:
The surface area of a sphere is given by the formula:
A = 4πr²
where r is the radius.
Substituting the given radius of the sun:
A = 4π(7 x 10^8)²
A = 1.54 x 10^18 m²
2. Calculate the power radiated by the sun:
Given power received at the surface of the Earth = 1400 W/m²
Area of the Earth's surface = A = 4πr²
where r is the distance between the center of the sun and the surface of the Earth.
Substituting the given distance:
A = 4π(1.5 x 10^11)²
A = 2.83 x 10^23 m²
The power radiated by the sun can be calculated using the formula:
P = 1400 W/m² x 2.83 x 10^23 m²
P = 3.96 x 10^26 W
3. Calculate the temperature of the sun:
Using the Stefan-Boltzmann law:
P = σAT^4
Rearranging the formula to solve for T:
T^4 = P / (σA)
T = (P / (σA))^(1/4)
Substituting the calculated values:
T = (3.96 x 10^26) / (5.67 x 10^-8 x 1.54 x 10^18)^(1/4)
T ≈ 5800 K
Therefore, the surface temperature of the sun is approximately 5800 K, which corresponds to option C.
Two long rods A and B of the same diameter have thermal conductivities k and 4 k and have attached by one side of their ends inserted into a furnace at 400 K. At a section 1 m away from the furnace, the temperature of rod B is 120°C. At what distance from the furnace end, the same temperature would be reached in the rod A?- a)0.2 m
- b)0.25 m
- c)0.5 m
- d)0.75 m
Correct answer is option 'C'. Can you explain this answer?
Two long rods A and B of the same diameter have thermal conductivities k and 4 k and have attached by one side of their ends inserted into a furnace at 400 K. At a section 1 m away from the furnace, the temperature of rod B is 120°C. At what distance from the furnace end, the same temperature would be reached in the rod A?
a)
0.2 m
b)
0.25 m
c)
0.5 m
d)
0.75 m
|
|
Sagarika Dey answered |

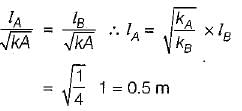
A stagnant liquid film of 0.4 mm thickness is held between two parallel plates. The top plate is maintained at 40°C and the bottom plate is maintained at 30°C. if the thermal conductivity of the liquid is 0.14 W/(m K), then the steady state heat flux (in W/m2) assuming one dimensional heat transfer is- a)3.5
- b)350
- c)3500
- d)7000
Correct answer is option 'C'. Can you explain this answer?
A stagnant liquid film of 0.4 mm thickness is held between two parallel plates. The top plate is maintained at 40°C and the bottom plate is maintained at 30°C. if the thermal conductivity of the liquid is 0.14 W/(m K), then the steady state heat flux (in W/m2) assuming one dimensional heat transfer is
a)
3.5
b)
350
c)
3500
d)
7000

|
Ashwin Gupta answered |
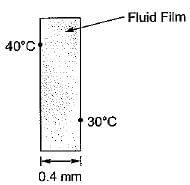
From Fourier’s law of heat conduction
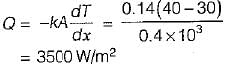
Which one of the following is correct, in context of thermal diffusivity of liquid and gas- a)αgas > αliquid
- b)αgas < αliquid
- c)αgas = αliquid
- d)Depend on other factors
Correct answer is option 'A'. Can you explain this answer?
Which one of the following is correct, in context of thermal diffusivity of liquid and gas
a)
αgas > αliquid
b)
αgas < αliquid
c)
αgas = αliquid
d)
Depend on other factors

|
Akshat Datta answered |
Since thermal diffusivity, α = k/ρc
(ρC)liquid > (ρC)gas
αgas > αliquid
(ρC)liquid > (ρC)gas
αgas > αliquid
A steam pipe is covered with two layers of insulating materials, with the better insulating material forming the outer part. If the two layers are interchanged, the heat conducted
- a)will decrease
- b)will increase
- c)will remain unaffected
- d)may increase or decrease depending upon the thickness of the each layer
Correct answer is option 'A'. Can you explain this answer?
A steam pipe is covered with two layers of insulating materials, with the better insulating material forming the outer part. If the two layers are interchanged, the heat conducted
a)
will decrease
b)
will increase
c)
will remain unaffected
d)
may increase or decrease depending upon the thickness of the each layer
|
|
Shruti Bose answered |
k1 < k2 [k1 better insulator]
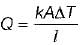
Q ∝ k. This means that the material having better insulating materia! should be inside to minimize the heat flux hence if better insulating materia! is placed inside, it will reduce the heat transfer.
In unsteady state heat conduction the two significant dimensionless parameter used are- a)Fourier number and Reynolds number
- b)Reynolds number and Prandtl number
- c)Biot number and Fourier number
- d)Reynolds number and Biot number
Correct answer is option 'C'. Can you explain this answer?
In unsteady state heat conduction the two significant dimensionless parameter used are
a)
Fourier number and Reynolds number
b)
Reynolds number and Prandtl number
c)
Biot number and Fourier number
d)
Reynolds number and Biot number
|
|
Pritam Jain answered |
In case of unsteady state conduction
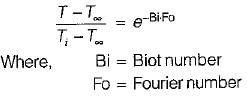
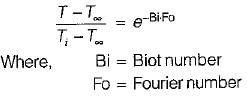
The temperature distribution for a sphere for steady state heat flow and constant value of thermal conductivity is- a)logarithmic
- b)parabolic
- c)hyperbolic
- d)exponential
Correct answer is option 'C'. Can you explain this answer?
The temperature distribution for a sphere for steady state heat flow and constant value of thermal conductivity is
a)
logarithmic
b)
parabolic
c)
hyperbolic
d)
exponential

|
Milan Saha answered |
Understanding Steady State Heat Flow in a Sphere
In a sphere with steady-state heat conduction and constant thermal conductivity, the temperature distribution is derived from the principles of heat transfer.
Key Concepts
- Steady-State Condition: This implies that the temperature within the sphere does not change with time. The heat entering a volume equals the heat leaving it.
- Spherical Coordinates: The analysis is conducted in spherical coordinates (r, θ, φ), where 'r' represents the radial distance from the center of the sphere.
Mathematical Derivation
- Heat Equation: The heat conduction equation in spherical coordinates leads to a differential equation where the radial temperature distribution depends only on the radial distance 'r'.
- Boundary Conditions: By applying appropriate boundary conditions (such as temperatures at the surface or center), we can solve the differential equation to find the temperature profile.
Temperature Distribution
- Hyperbolic Nature: The solution to the differential equation results in a hyperbolic relationship, typically represented as:
- T(r) = A + B * ln(r), where A and B are constants determined by boundary conditions.
- Physical Interpretation: This hyperbolic behavior indicates that as one moves from the center to the surface of the sphere, the temperature decreases logarithmically, which is characteristic of heat conduction in spherical bodies.
Conclusion
The temperature distribution in a sphere under steady-state conditions and constant thermal conductivity indeed exhibits a hyperbolic nature, making option 'C' the correct answer. Understanding this concept is crucial for applications in thermal management and engineering designs involving spherical geometries.
In a sphere with steady-state heat conduction and constant thermal conductivity, the temperature distribution is derived from the principles of heat transfer.
Key Concepts
- Steady-State Condition: This implies that the temperature within the sphere does not change with time. The heat entering a volume equals the heat leaving it.
- Spherical Coordinates: The analysis is conducted in spherical coordinates (r, θ, φ), where 'r' represents the radial distance from the center of the sphere.
Mathematical Derivation
- Heat Equation: The heat conduction equation in spherical coordinates leads to a differential equation where the radial temperature distribution depends only on the radial distance 'r'.
- Boundary Conditions: By applying appropriate boundary conditions (such as temperatures at the surface or center), we can solve the differential equation to find the temperature profile.
Temperature Distribution
- Hyperbolic Nature: The solution to the differential equation results in a hyperbolic relationship, typically represented as:
- T(r) = A + B * ln(r), where A and B are constants determined by boundary conditions.
- Physical Interpretation: This hyperbolic behavior indicates that as one moves from the center to the surface of the sphere, the temperature decreases logarithmically, which is characteristic of heat conduction in spherical bodies.
Conclusion
The temperature distribution in a sphere under steady-state conditions and constant thermal conductivity indeed exhibits a hyperbolic nature, making option 'C' the correct answer. Understanding this concept is crucial for applications in thermal management and engineering designs involving spherical geometries.
Consider the following materials:
1. Carbon
2. Mica
3. Bakelite
4. Fibreglass
Q. Which of these materials are good conductors- of heat, but bad conductors of electricity- a)1 only
- b)2 only
- c)2 and 3
- d)3 and 4
Correct answer is option 'A'. Can you explain this answer?
Consider the following materials:
1. Carbon
2. Mica
3. Bakelite
4. Fibreglass
Q. Which of these materials are good conductors- of heat, but bad conductors of electricity
1. Carbon
2. Mica
3. Bakelite
4. Fibreglass
Q. Which of these materials are good conductors- of heat, but bad conductors of electricity
a)
1 only
b)
2 only
c)
2 and 3
d)
3 and 4

|
Aditya Jain answered |
Mica, Bakelite and fibre glass are insulator material and carbon in the form of diamond is the good conductor of heat but bad conductor of electricity
The nusselt number of convective heat transfer between a horizontal tube and water surrounding it is prescribed by the relation Nu = 0.52 (Gr Pr)0.25 for a 5 cm diameter tube, the heat transfer coefficient is 6000 W/m2-K. Subsequently, the tube is replaced by one with 20 cm diameter tube. If the temperature and surface of the fluid remain same, the heat transfer coefficient will change to- a)4142W/m2-K
- b)4342W/m2-K
- c)4242 W/m2-K
- d)4042W/m2-K
Correct answer is option 'C'. Can you explain this answer?
The nusselt number of convective heat transfer between a horizontal tube and water surrounding it is prescribed by the relation Nu = 0.52 (Gr Pr)0.25 for a 5 cm diameter tube, the heat transfer coefficient is 6000 W/m2-K. Subsequently, the tube is replaced by one with 20 cm diameter tube. If the temperature and surface of the fluid remain same, the heat transfer coefficient will change to
a)
4142W/m2-K
b)
4342W/m2-K
c)
4242 W/m2-K
d)
4042W/m2-K
|
|
Akshara Rane answered |
∴
∴
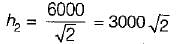
= 4242W/m2-K
For a given heat flow and for the same thickness the temperature drop across the material will be maximum for- a)Copper
- b)Steel
- c)Glass-wool
- d)Refractory Brick
Correct answer is option 'C'. Can you explain this answer?
For a given heat flow and for the same thickness the temperature drop across the material will be maximum for
a)
Copper
b)
Steel
c)
Glass-wool
d)
Refractory Brick

|
Sameer Verma answered |
The correct answer is option 'C' - Glass-wool.
Explanation:
In order to understand why the temperature drop across the material will be maximum for glass-wool, let's consider the concept of thermal conductivity.
Thermal conductivity is a property of a material that determines how well it can conduct heat. Materials with high thermal conductivity can transfer heat more easily, while materials with low thermal conductivity transfer heat slowly.
1. Copper:
- Copper is a metal that has a very high thermal conductivity, which means it can conduct heat very well.
- When heat flows through copper, the temperature drop across the material will be relatively small because it can easily transfer heat from one side to the other.
2. Steel:
- Steel is also a metal, but it has a lower thermal conductivity compared to copper.
- When heat flows through steel, the temperature drop across the material will be higher than copper, but still relatively small compared to other materials.
3. Glass-wool:
- Glass-wool is an insulating material commonly used for thermal insulation purposes.
- It has a very low thermal conductivity, which means it does not conduct heat well.
- When heat flows through glass-wool, the temperature drop across the material will be higher compared to copper and steel.
- This is because glass-wool resists the transfer of heat, causing a larger temperature difference between the two sides of the material.
4. Refractory Brick:
- Refractory brick is a material designed to withstand high temperatures and is commonly used in furnaces and kilns.
- It has a low thermal conductivity, similar to glass-wool.
- When heat flows through refractory brick, the temperature drop across the material will also be higher compared to copper and steel.
Conclusion:
The temperature drop across a material is related to its thermal conductivity. Materials with low thermal conductivity, such as glass-wool and refractory brick, will have a higher temperature drop compared to materials with high thermal conductivity, such as copper and steel. Therefore, the temperature drop will be maximum for glass-wool (option 'C') in this scenario.
Explanation:
In order to understand why the temperature drop across the material will be maximum for glass-wool, let's consider the concept of thermal conductivity.
Thermal conductivity is a property of a material that determines how well it can conduct heat. Materials with high thermal conductivity can transfer heat more easily, while materials with low thermal conductivity transfer heat slowly.
1. Copper:
- Copper is a metal that has a very high thermal conductivity, which means it can conduct heat very well.
- When heat flows through copper, the temperature drop across the material will be relatively small because it can easily transfer heat from one side to the other.
2. Steel:
- Steel is also a metal, but it has a lower thermal conductivity compared to copper.
- When heat flows through steel, the temperature drop across the material will be higher than copper, but still relatively small compared to other materials.
3. Glass-wool:
- Glass-wool is an insulating material commonly used for thermal insulation purposes.
- It has a very low thermal conductivity, which means it does not conduct heat well.
- When heat flows through glass-wool, the temperature drop across the material will be higher compared to copper and steel.
- This is because glass-wool resists the transfer of heat, causing a larger temperature difference between the two sides of the material.
4. Refractory Brick:
- Refractory brick is a material designed to withstand high temperatures and is commonly used in furnaces and kilns.
- It has a low thermal conductivity, similar to glass-wool.
- When heat flows through refractory brick, the temperature drop across the material will also be higher compared to copper and steel.
Conclusion:
The temperature drop across a material is related to its thermal conductivity. Materials with low thermal conductivity, such as glass-wool and refractory brick, will have a higher temperature drop compared to materials with high thermal conductivity, such as copper and steel. Therefore, the temperature drop will be maximum for glass-wool (option 'C') in this scenario.
The curve for unsteady state cooling or heating of bodies is- a)parabolic curve asymptotic to time axis
- b)exponential curve asymptotic to time axis
- c)exponential curve asymptotic both to time and temperature axes
- d)hyperbolic curve asymptotic both to time and temperature axes
Correct answer is option 'B'. Can you explain this answer?
The curve for unsteady state cooling or heating of bodies is
a)
parabolic curve asymptotic to time axis
b)
exponential curve asymptotic to time axis
c)
exponential curve asymptotic both to time and temperature axes
d)
hyperbolic curve asymptotic both to time and temperature axes
|
|
Avik Ghosh answered |

Which one of the following have a highest thermal conductivity?- a)Boiling water
- b)Steam
- c)Solid ice
- d)Rainwa
Correct answer is option 'C'. Can you explain this answer?
Which one of the following have a highest thermal conductivity?
a)
Boiling water
b)
Steam
c)
Solid ice
d)
Rainwa
|
|
Sanskriti Chakraborty answered |
Understanding Thermal Conductivity
Thermal conductivity is a measure of a material's ability to conduct heat. It varies significantly across different states of matter (solid, liquid, gas).
Factors Affecting Thermal Conductivity
- State of Matter: Solids generally have higher thermal conductivity than liquids and gases due to closely packed molecules.
- Molecular Structure: The arrangement and bonding of atoms affect how easily heat can be transferred.
Comparison of Options
- Boiling Water: While water can conduct heat, its thermal conductivity is lower than that of solids. Its value is about 0.6 W/m·K.
- Steam: As a gas, steam has a lower thermal conductivity compared to liquids and solids. The thermal conductivity of steam is around 0.02 W/m·K.
- Solid Ice: Ice, being a solid, has a higher thermal conductivity than water in liquid form. The thermal conductivity of ice is approximately 2.2 W/m·K.
- Rainwater: Similar to boiling water, rainwater has low thermal conductivity, comparable to that of boiling water.
Conclusion
Based on the comparison, solid ice (option C) possesses the highest thermal conductivity among the listed options. This is due to its solid state, which allows for efficient heat transfer through tightly packed molecular structures. In contrast, the other options (boiling water, steam, and rainwater) are either in liquid or gaseous states, resulting in lower thermal conductivity.
Thus, the correct answer is indeed option C: Solid Ice.
Thermal conductivity is a measure of a material's ability to conduct heat. It varies significantly across different states of matter (solid, liquid, gas).
Factors Affecting Thermal Conductivity
- State of Matter: Solids generally have higher thermal conductivity than liquids and gases due to closely packed molecules.
- Molecular Structure: The arrangement and bonding of atoms affect how easily heat can be transferred.
Comparison of Options
- Boiling Water: While water can conduct heat, its thermal conductivity is lower than that of solids. Its value is about 0.6 W/m·K.
- Steam: As a gas, steam has a lower thermal conductivity compared to liquids and solids. The thermal conductivity of steam is around 0.02 W/m·K.
- Solid Ice: Ice, being a solid, has a higher thermal conductivity than water in liquid form. The thermal conductivity of ice is approximately 2.2 W/m·K.
- Rainwater: Similar to boiling water, rainwater has low thermal conductivity, comparable to that of boiling water.
Conclusion
Based on the comparison, solid ice (option C) possesses the highest thermal conductivity among the listed options. This is due to its solid state, which allows for efficient heat transfer through tightly packed molecular structures. In contrast, the other options (boiling water, steam, and rainwater) are either in liquid or gaseous states, resulting in lower thermal conductivity.
Thus, the correct answer is indeed option C: Solid Ice.
A composite wall of a furnace has 3 layers of equal thickness having thermal conductivities the ratio of 1 : 2 : 4. What will be the temperature drop ratio across the three respective layer- a)1 : 2 : 4
- b)4: 2: 1
- c)1 : 1 : 1
- d)log 4 : log 2 : log 1
Correct answer is option 'B'. Can you explain this answer?
A composite wall of a furnace has 3 layers of equal thickness having thermal conductivities the ratio of 1 : 2 : 4. What will be the temperature drop ratio across the three respective layer
a)
1 : 2 : 4
b)
4: 2: 1
c)
1 : 1 : 1
d)
log 4 : log 2 : log 1

|
Anmol Menon answered |
From the fourier law of heat conduction
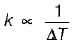
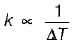
Which of the followings is wrong value of characteristic length l which appears in the Biot number hl/k cand the Fourier number αζ / l2 ?- a)l = R/3 in case of sphere of radius R.
- b)l = R/2 in case of a cylinder of radius Rand length L.
- c)l = L/6 in case of a cube with each side of length L
- d)l = b/2 for a flat plate of thickness δ, breadth b and height h.
Correct answer is option 'D'. Can you explain this answer?
Which of the followings is wrong value of characteristic length l which appears in the Biot number hl/k cand the Fourier number αζ / l2 ?
a)
l = R/3 in case of sphere of radius R.
b)
l = R/2 in case of a cylinder of radius Rand length L.
c)
l = L/6 in case of a cube with each side of length L
d)
l = b/2 for a flat plate of thickness δ, breadth b and height h.

|
Muskaan Sen answered |
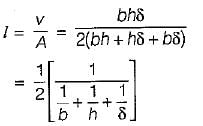
b and h >> δ
∴ l = δ/2
An aluminium sheet of 10 mm thickness is brought into contact with an iron sheet of 20 mm thickness. The outer surface of aluminium is kept at 100°C. Where as the outer surface of iron is maintained at 0°C. if the ratio of thermal conductivity of aluminium and iron is 3 : 1, then the interface temperature in °C is- a)40
- b)60
- c)75.7
- d)85.7
Correct answer is option 'D'. Can you explain this answer?
An aluminium sheet of 10 mm thickness is brought into contact with an iron sheet of 20 mm thickness. The outer surface of aluminium is kept at 100°C. Where as the outer surface of iron is maintained at 0°C. if the ratio of thermal conductivity of aluminium and iron is 3 : 1, then the interface temperature in °C is
a)
40
b)
60
c)
75.7
d)
85.7

|
Rohan Singh answered |
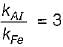

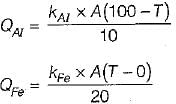
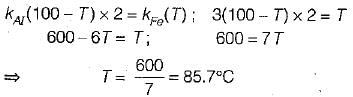
An electronic device in the form of a wire is found to dissipate maximum heat when its outer most diameter = 32 mm. Keeping all the parameter same, it is proposed to use the same device in spherical form. The ideal diameter would be
- a)64 mm
- b)16 mm
- c)32 mm
- d)8 mm
Correct answer is option 'A'. Can you explain this answer?
An electronic device in the form of a wire is found to dissipate maximum heat when its outer most diameter = 32 mm. Keeping all the parameter same, it is proposed to use the same device in spherical form. The ideal diameter would be
a)
64 mm
b)
16 mm
c)
32 mm
d)
8 mm

|
Akash Mukherjee answered |
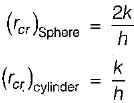

One end of iron rod of cross-sectional area A and length L is kept in a steambath. After same time steady state conditions prevail and Q unit of heat per second passes through any cross- section of the rod. The heat flow rate will be adversely affected if- a)room temperature is decreased
- b)cross-sectional area of the rod increases
- c)rod is made longer
- d)iron rod is replaced by a copper rod of the same area and length.
Correct answer is option 'C'. Can you explain this answer?
One end of iron rod of cross-sectional area A and length L is kept in a steambath. After same time steady state conditions prevail and Q unit of heat per second passes through any cross- section of the rod. The heat flow rate will be adversely affected if
a)
room temperature is decreased
b)
cross-sectional area of the rod increases
c)
rod is made longer
d)
iron rod is replaced by a copper rod of the same area and length.
|
|
Mrinalini Sharma answered |
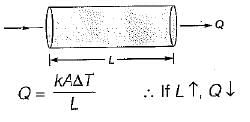
Chapter doubts & questions for Heat Transfer - Topicwise Question Bank for Mechanical Engineering 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Heat Transfer - Topicwise Question Bank for Mechanical Engineering in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Topicwise Question Bank for Mechanical Engineering
45 videos|314 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily










