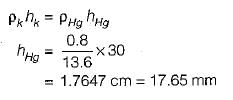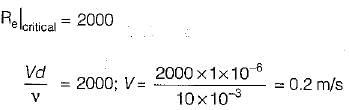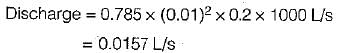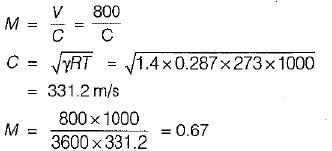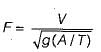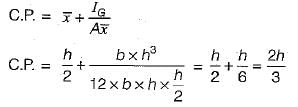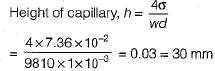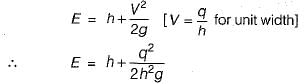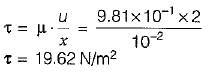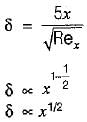All Exams >
Mechanical Engineering >
Topicwise Question Bank for Mechanical Engineering >
All Questions
All questions of Fluid Mechanics for Mechanical Engineering Exam
Which one of the dimensionless numbers identifies the compressibility effect of a fluid- a)Euler number
- b)Fraud number
- c)Mach number
- d)Weber number
Correct answer is option 'C'. Can you explain this answer?
Which one of the dimensionless numbers identifies the compressibility effect of a fluid
a)
Euler number
b)
Fraud number
c)
Mach number
d)
Weber number
|
|
Sanya Agarwal answered |
At higher Mach number the compressibility effect is predominant.
Which one of the following is defined as force per unit length?- a)surface tension
- b)compressibility
- c)capillarity
- d)viscosity
Correct answer is option 'A'. Can you explain this answer?
Which one of the following is defined as force per unit length?
a)
surface tension
b)
compressibility
c)
capillarity
d)
viscosity
|
|
Avinash Sharma answered |
Surface tension is defined as line force per unit length.
A hydraulic press has a ram of 30 cm diameter and a plunger of 4.5 cm diameter. What is the weight lifted by the hydraulic press when the force applied at the plunger is 600 N?- a)25.67 kN
- b)26.67 kN
- c)28.67 kN
- d)24.67 kN
Correct answer is option 'B'. Can you explain this answer?
A hydraulic press has a ram of 30 cm diameter and a plunger of 4.5 cm diameter. What is the weight lifted by the hydraulic press when the force applied at the plunger is 600 N?
a)
25.67 kN
b)
26.67 kN
c)
28.67 kN
d)
24.67 kN

|
Sreemoyee Chauhan answered |

A real fluid is any fluid which
- a)has surface tension and is compressible
- b)has zero shear stress
- c)has constant viscosity and density
- d)has viscosity
Correct answer is option 'D'. Can you explain this answer?
A real fluid is any fluid which
a)
has surface tension and is compressible
b)
has zero shear stress
c)
has constant viscosity and density
d)
has viscosity
|
|
Saranya Saha answered |
Real Fluids in Mechanical Engineering
Real Fluids are fluids that have viscosity, which is the property of a fluid that causes it to resist flow. Real fluids are common in everyday life, and they are found in many industrial applications.
Viscosity
Viscosity is the measure of a fluid's resistance to deformation or flow. It is a property of the fluid, and it determines how easily the fluid can flow. Real fluids have viscosity, which means that they resist flow.
Examples of Real Fluids
Some examples of real fluids include:
- Water
- Oil
- Gasoline
- Honey
- Blood
Properties of Real Fluids
Real fluids have properties that are different from ideal fluids. Some of the properties of real fluids include:
- Viscosity
- Density
- Compressibility
Applications of Real Fluids
Real fluids are used in many applications in mechanical engineering. Some examples include:
- Lubrication of machine parts
- Cooling of engines
- Hydraulic systems
- Pneumatic systems
Conclusion
Real fluids are an important part of mechanical engineering. They have properties that make them different from ideal fluids, and they are used in many applications. Understanding the properties of real fluids is essential for designing and operating mechanical systems.
Real Fluids are fluids that have viscosity, which is the property of a fluid that causes it to resist flow. Real fluids are common in everyday life, and they are found in many industrial applications.
Viscosity
Viscosity is the measure of a fluid's resistance to deformation or flow. It is a property of the fluid, and it determines how easily the fluid can flow. Real fluids have viscosity, which means that they resist flow.
Examples of Real Fluids
Some examples of real fluids include:
- Water
- Oil
- Gasoline
- Honey
- Blood
Properties of Real Fluids
Real fluids have properties that are different from ideal fluids. Some of the properties of real fluids include:
- Viscosity
- Density
- Compressibility
Applications of Real Fluids
Real fluids are used in many applications in mechanical engineering. Some examples include:
- Lubrication of machine parts
- Cooling of engines
- Hydraulic systems
- Pneumatic systems
Conclusion
Real fluids are an important part of mechanical engineering. They have properties that make them different from ideal fluids, and they are used in many applications. Understanding the properties of real fluids is essential for designing and operating mechanical systems.
The velocity distribution in a viscous flow over a plate is given by
u = 4y - y2 for y ≤ 2m
where, u = velocity in m/s at a point distant y from the plate. If the coefficient of dynamic viscosity is 1.5 Pa-s, what is the shear stress at y= 1.2 m?- a)1.4 Pa
- b)1.8 Pa
- c)2 Pa
- d)2.4 Pa
Correct answer is option 'D'. Can you explain this answer?
The velocity distribution in a viscous flow over a plate is given by
u = 4y - y2 for y ≤ 2m
where, u = velocity in m/s at a point distant y from the plate. If the coefficient of dynamic viscosity is 1.5 Pa-s, what is the shear stress at y= 1.2 m?
u = 4y - y2 for y ≤ 2m
where, u = velocity in m/s at a point distant y from the plate. If the coefficient of dynamic viscosity is 1.5 Pa-s, what is the shear stress at y= 1.2 m?
a)
1.4 Pa
b)
1.8 Pa
c)
2 Pa
d)
2.4 Pa
|
|
Bhargavi Chauhan answered |

When a shear stress is applied to a substance, it is found to resist it by static deformation, the substance is - a)liquid
- b)solid
- c)gas
- d)fluid
Correct answer is option 'B'. Can you explain this answer?
When a shear stress is applied to a substance, it is found to resist it by static deformation, the substance is
a)
liquid
b)
solid
c)
gas
d)
fluid
|
|
Neha Joshi answered |
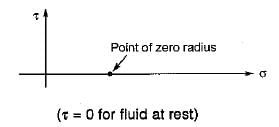
- A solid can resist shear stress by a static deformation; a fluid cannot
- Any shear stress applied to a fluid, no matter how small, will result in motion of that fluid
- The fluid moves and deforms continuously as long as the shear stress is applied
- So, a fluid at rest must be in a state of zero shear stress
A perfect fluid is- a)a real fluid is
- b)the one which obeys perfect gas laws
- c)compressive and gaseous
- d)incompressible and frictionless
Correct answer is option 'D'. Can you explain this answer?
A perfect fluid is
a)
a real fluid is
b)
the one which obeys perfect gas laws
c)
compressive and gaseous
d)
incompressible and frictionless

|
Cstoppers Instructors answered |
- A perfect fluid is incompressible and frictionless and it is explained with the help of Euler's equation.
Euler's equation of motion:
- The Euler's equation for a steady flow of an ideal fluid along a streamline is a relation between the velocity, pressure, and density of a moving fluid.
- It is based on Newton's Second Law of Motion which states that if the external force is zero, linear momentum is conserved.
- The integration of the equation gives Bernoulli's equation in the form of energy per unit weight of the following fluid.
It is based on the following assumptions:
- The fluid is non-viscous (i,e., the frictional losses are zero)
- The fluid is homogeneous and incompressible (i.e., the mass density of the fluid is constant)
- The flow is continuous, steady, and along the streamline.
- The velocity of the flow is uniform over the section.
- No energy or force (except gravity and pressure forces) is involved in the flow.
Newton’s law of viscosity for a fluid states that the shear stress is
- a)proportional to angular deformation
- b)proportional to rate of angular deformation
- c)inversely proportional to angular deformation
- d)inversely proportional to rate of angular deformation
Correct answer is option 'B'. Can you explain this answer?
Newton’s law of viscosity for a fluid states that the shear stress is
a)
proportional to angular deformation
b)
proportional to rate of angular deformation
c)
inversely proportional to angular deformation
d)
inversely proportional to rate of angular deformation
|
|
Samarth Chaudhary answered |

Boundary layer separation is caused by- a)adverse pressure gradient
- b)laminar flow changing to turbulent flow
- c)reduction in pressure to vapour pressure
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Boundary layer separation is caused by
a)
adverse pressure gradient
b)
laminar flow changing to turbulent flow
c)
reduction in pressure to vapour pressure
d)
none of these
|
|
Lavanya Menon answered |
Boundary layer separation is caused due to adverse pressure gradient or positive pressure gradient.
The concept of continuum in fluid flow assumes that the characteristics length of the flow is - a)smaller than the mean free path of the molecules.
- b)larger than the mean free path of the molecule
- c)larger than the dimensions of the suspended particles
- d)larger than the wavelength of sound in the medium.
Correct answer is option 'B'. Can you explain this answer?
The concept of continuum in fluid flow assumes that the characteristics length of the flow is
a)
smaller than the mean free path of the molecules.
b)
larger than the mean free path of the molecule
c)
larger than the dimensions of the suspended particles
d)
larger than the wavelength of sound in the medium.
|
|
Neha Joshi answered |
- The concept of the continuum is a kind of idealization of the continuous description of matter where the properties of the matter are considered as continuous functions of space variables.
- In this approach, the matter is continuously distributed with no void present continuum concept be applied if the mean free path is much less than the system dimensions.
- Although any matter is composed of several molecules, the concept of continuum assumes a continuous distribution of mass within the matter or system with no empty space, instead of the actual conglomeration of separate molecules.
- Describing a fluid flow quantitatively makes it necessary to assume that flow variables (pressure, velocity etc.) and fluid properties vary continuously from one point to another.
- One of the factors considered important in determining the validity of the continuum model is molecular density. It is the distance between the molecules which is characterized by a mean free path ( λ ). It is calculated by finding statistical average distance the molecules travel between two successive collisions.
- If the mean free path is very small as compared with some characteristic length in the flow domain (i.e., the molecular density is very high) then the gas can be treated as a continuous medium.
- If the mean free path is large in comparison to some characteristic length, the gas cannot be considered continuous and it should be analysed by the molecular theory.
- A dimensionless parameter is known as Knudsen number, Kn = λ/L, where λ is the mean free path and L is the characteristic length. It describes the degree of departure from the continuum.
- Usually when Kn > 0.01, the concept of the continuum does not hold good and when Kn < 0.01, the concept of the continuum does hold good.
- In the continuum approach, fluid properties such as density, viscosity, thermal conductivity, temperature, etc. can be expressed as continuous functions of space and time.
Gauge pressure at a point is equal to- a)absolute pressure plus atmospheric pressure
- b)absolute pressure minus atmospheric pressure
- c)vacuum pressure plus absolute pressure
- d)vacuum pressure minus absolute pressure
Correct answer is option 'B'. Can you explain this answer?
Gauge pressure at a point is equal to
a)
absolute pressure plus atmospheric pressure
b)
absolute pressure minus atmospheric pressure
c)
vacuum pressure plus absolute pressure
d)
vacuum pressure minus absolute pressure
|
|
Nandini Basak answered |
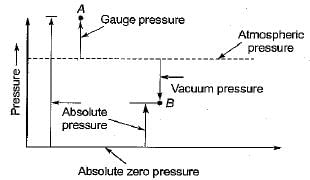
∴ Gauge pressure = Absolute minus atmospheric pressure
When a cylindrical vessel containing a liquid is revolved at constant angular velocity about its vertical axis, the pressure- a)varies as the square of the inverse of radial distance
- b)decreases as the square of angular velocity
- c)increases as the square of angular velocity
- d)remains same
Correct answer is option 'C'. Can you explain this answer?
When a cylindrical vessel containing a liquid is revolved at constant angular velocity about its vertical axis, the pressure
a)
varies as the square of the inverse of radial distance
b)
decreases as the square of angular velocity
c)
increases as the square of angular velocity
d)
remains same
|
|
Lavanya Menon answered |

The space between two parallel plates kept 4 mm apart is filled with an oil of dynamic viscosity 0.2 Pa-s. What is the shear stress on the lower fixed plate, if the upper one is moved with a velocity of 1.6 m/s? .- a)100 Pa
- b)90 Pa
- c)80 Pa
- d)60 Pa
Correct answer is option 'C'. Can you explain this answer?
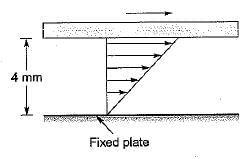
The space between two parallel plates kept 4 mm apart is filled with an oil of dynamic viscosity 0.2 Pa-s. What is the shear stress on the lower fixed plate, if the upper one is moved with a velocity of 1.6 m/s? .
a)
100 Pa
b)
90 Pa
c)
80 Pa
d)
60 Pa

|
Ashish Chakraborty answered |
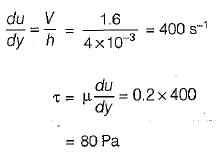
The metacentric height of a passenger ship is kept water lower than that of a naval or a cargo ship. This is because- a)apparent weight will increase
- b)otherwise it will be in neutral equilibrium
- c)it will decrease the frequency of rolling
- d)otherwise it will sink and get totally immersed
Correct answer is option 'C'. Can you explain this answer?
The metacentric height of a passenger ship is kept water lower than that of a naval or a cargo ship. This is because
a)
apparent weight will increase
b)
otherwise it will be in neutral equilibrium
c)
it will decrease the frequency of rolling
d)
otherwise it will sink and get totally immersed
|
|
Moumita Sharma answered |
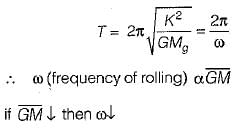
The specific gravity of a liquid has
- a)the same unit as that of mass density
- b)the same unit as that of weight density
- c)no unit
- d)the same unit as that of specific volume
Correct answer is option 'C'. Can you explain this answer?
The specific gravity of a liquid has
a)
the same unit as that of mass density
b)
the same unit as that of weight density
c)
no unit
d)
the same unit as that of specific volume
|
|
Avinash Sharma answered |
The specific gravity of a liquid is the ratio of two similar quantities (densities) which makes it unitless.
In the phenomenon of cavitation, the characteristic fluid property involved is- a)Surface tension
- b)Viscosity
- c)Bulk modulus of elasticity
- d)Vapour pressure
Correct answer is option 'D'. Can you explain this answer?
In the phenomenon of cavitation, the characteristic fluid property involved is
a)
Surface tension
b)
Viscosity
c)
Bulk modulus of elasticity
d)
Vapour pressure
|
|
Avantika Sen answered |
In any flow system, if the pressure at any point in the liquid approaches the vapour pressure, vaporization of liquid starts, resulting in the pockets of dissolved gasses and vapours. The bubbles of vapour thus formed are carried by the flowing liquid into a region of high pressure where they collapse, giving rise to high impact pressure. This phenomenon is known as cavitation.
In a turbulent flow in a pipe, the shear stress is- a)maximum at the center and decreases linearly towards the wall
- b)maximum at the center and decreases logarithmically towards the wall
- c)maximum midway between the centerline and the wall
- d)maximum at the wall and decreases linearly to a zero value at the center
Correct answer is option 'D'. Can you explain this answer?
In a turbulent flow in a pipe, the shear stress is
a)
maximum at the center and decreases linearly towards the wall
b)
maximum at the center and decreases logarithmically towards the wall
c)
maximum midway between the centerline and the wall
d)
maximum at the wall and decreases linearly to a zero value at the center

|
Pallabi Kulkarni answered |
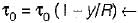 shear stress variation where y is distance from pipe wall, so, the shear stress varies linearly with the distance from the boundary to become zero at the center.
shear stress variation where y is distance from pipe wall, so, the shear stress varies linearly with the distance from the boundary to become zero at the center.The potential lines in case of a doublet are- a)circles tangent to the x-axis
- b)circles tangent to the y-axis
- c)concentric circles with center on the x-axis
- d)concentric circles with center on the y-axis
Correct answer is option 'B'. Can you explain this answer?
The potential lines in case of a doublet are
a)
circles tangent to the x-axis
b)
circles tangent to the y-axis
c)
concentric circles with center on the x-axis
d)
concentric circles with center on the y-axis
|
|
Sagarika Mukherjee answered |
Understanding Doublets in Fluid Mechanics
In fluid mechanics, a doublet is a combination of a source and a sink of equal strength very close to each other. The potential lines or streamlines associated with a doublet reveal important characteristics of fluid flow.
Potential Lines of a Doublet
When analyzing the potential lines of a doublet, we consider how these lines behave in relation to the axes in a Cartesian coordinate system.
Option Analysis
- a) Circles Tangent to the X-axis
This option suggests circular paths that touch the x-axis. However, doublets do not create such potential lines.
- b) Circles Tangent to the Y-axis
This is the correct answer. The potential lines resulting from a doublet resemble circles that are tangent to the y-axis. As the doublet is oriented along the x-axis, the flow lines exhibit this circular characteristic.
- c) Concentric Circles with Center on the X-axis
While concentric circles indicate uniform flow, they do not accurately represent the potential lines of a doublet.
- d) Concentric Circles with Center on the Y-axis
Similar to option c, these circles would not represent the nature of the flow induced by a doublet.
Conclusion
In summary, the potential lines of a doublet are best represented by circles that are tangent to the y-axis. This behavior illustrates the unique flow characteristics created by the interaction of a source and sink, confirming option 'b' as the correct choice. Understanding these flow patterns is essential in fluid mechanics and applications like aerodynamics and hydrodynamics.
In fluid mechanics, a doublet is a combination of a source and a sink of equal strength very close to each other. The potential lines or streamlines associated with a doublet reveal important characteristics of fluid flow.
Potential Lines of a Doublet
When analyzing the potential lines of a doublet, we consider how these lines behave in relation to the axes in a Cartesian coordinate system.
Option Analysis
- a) Circles Tangent to the X-axis
This option suggests circular paths that touch the x-axis. However, doublets do not create such potential lines.
- b) Circles Tangent to the Y-axis
This is the correct answer. The potential lines resulting from a doublet resemble circles that are tangent to the y-axis. As the doublet is oriented along the x-axis, the flow lines exhibit this circular characteristic.
- c) Concentric Circles with Center on the X-axis
While concentric circles indicate uniform flow, they do not accurately represent the potential lines of a doublet.
- d) Concentric Circles with Center on the Y-axis
Similar to option c, these circles would not represent the nature of the flow induced by a doublet.
Conclusion
In summary, the potential lines of a doublet are best represented by circles that are tangent to the y-axis. This behavior illustrates the unique flow characteristics created by the interaction of a source and sink, confirming option 'b' as the correct choice. Understanding these flow patterns is essential in fluid mechanics and applications like aerodynamics and hydrodynamics.
When a body, floating in a liquid is given a small angular displacement, it starts oscillating about a point known as- a)center of pressure
- b)center of gravity
- c)center of buoyancy
- d)meta center
Correct answer is option 'D'. Can you explain this answer?
When a body, floating in a liquid is given a small angular displacement, it starts oscillating about a point known as
a)
center of pressure
b)
center of gravity
c)
center of buoyancy
d)
meta center

|
Ameya Sen answered |
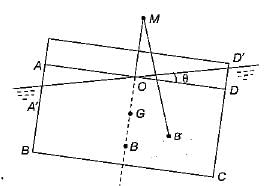
Where M is metacentre and θ is small angle of hill through which a body is tilted.
Hence metacenter is a point about which a body oscillate when tilted or given a small angular displacement.
The shear stress between two fixed parallel plates with a laminar flow between them- a)varies directly as distance from the mid-plane
- b)varies inversely as distance from the midplane
- c)varies parabolically across the gap
- d)remains constant across the gap
Correct answer is option 'A'. Can you explain this answer?
The shear stress between two fixed parallel plates with a laminar flow between them
a)
varies directly as distance from the mid-plane
b)
varies inversely as distance from the midplane
c)
varies parabolically across the gap
d)
remains constant across the gap

|
Sai Sarkar answered |

A pipe of diameter 1.5 m is required to transport an oil of relative density 0,9 and kinematic viscosity = 3 x 10-2 stoke at a rate of 3 m3/s. if a 15 cm diameter pipe with water at 20°C (n = 0.01 stoke) is used to model the above flow, the discharge in the model is- a)0.1 m3/s
- b)0.15 m3/s
- c)0.2 m3/s
- d)0.25 m3/s
Correct answer is option 'A'. Can you explain this answer?
A pipe of diameter 1.5 m is required to transport an oil of relative density 0,9 and kinematic viscosity = 3 x 10-2 stoke at a rate of 3 m3/s. if a 15 cm diameter pipe with water at 20°C (n = 0.01 stoke) is used to model the above flow, the discharge in the model is
a)
0.1 m3/s
b)
0.15 m3/s
c)
0.2 m3/s
d)
0.25 m3/s
|
|
Gargi Reddy answered |
The Reynolds number must be the same in the model and prototype for similar pipe flows
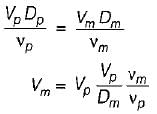

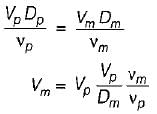

An airplane is flying at an altitude where the pressure is 20 kPa (absolute) and the density is 0.28 kg/m3. If the plane has attained a mach number of 1,8, what is the speed of plane in km/hr?- a)1550
- b)1709
- c)2049
- d)216
Correct answer is option 'C'. Can you explain this answer?
An airplane is flying at an altitude where the pressure is 20 kPa (absolute) and the density is 0.28 kg/m3. If the plane has attained a mach number of 1,8, what is the speed of plane in km/hr?
a)
1550
b)
1709
c)
2049
d)
216
|
|
Niharika Iyer answered |
Velocity of sound,

A sprue in a sand mould has a top diameter of 20 mm and height of 200 mm. The velocity of the molten metal at entry of the sprue is 0.5 m/s. Assume acceleration due to gravity as 9.8 m/s2 and neglect all losses. If the mould is well ventilated the velocity (upto 3 decimal points accuracy) of the molten metal at the bottom of the sprue is ____m/s.Correct answer is '2.042'. Can you explain this answer?
A sprue in a sand mould has a top diameter of 20 mm and height of 200 mm. The velocity of the molten metal at entry of the sprue is 0.5 m/s. Assume acceleration due to gravity as 9.8 m/s2 and neglect all losses. If the mould is well ventilated the velocity (upto 3 decimal points accuracy) of the molten metal at the bottom of the sprue is ____m/s.

|
Baishali Chopra answered |
Understanding the Problem
To calculate the velocity of the molten metal at the bottom of the sprue, we can use the principle of conservation of energy, specifically Bernoulli's equation. The equation relates the velocity and height of the fluid in motion.
Given Data
- Top Diameter of Sprue: 20 mm
- Height of Sprue: 200 mm
- Initial Velocity (V1): 0.5 m/s
- Acceleration due to Gravity (g): 9.8 m/s²
- Density and viscosity are neglected due to the assumption of ideal conditions.
Key Concepts
- Potential Energy: At the top of the sprue, the molten metal possesses gravitational potential energy due to its height.
- Kinetic Energy: As it descends, potential energy converts into kinetic energy, increasing the velocity of the molten metal.
Applying Bernoulli's Equation
1. Initial State (Top of the Sprue):
- Velocity (V1) = 0.5 m/s
- Height (h1) = 0.2 m (200 mm)
2. Final State (Bottom of the Sprue):
- Velocity (V2) = ?
- Height (h2) = 0 m
Using Bernoulli’s equation:
V1²/2 + g*h1 = V2²/2 + g*h2
Simplifying, we find:
0.5²/2 + 9.8*0.2 = V2²/2
3. Calculating V2:
- Solve for V2, applying the values.
- V2 = √(0.5² + 2*9.8*0.2)
This gives us V2 ≈ 2.042 m/s.
Conclusion
Thus, the velocity of the molten metal at the bottom of the sprue, considering ideal conditions and neglecting losses, is approximately 2.042 m/s.
To calculate the velocity of the molten metal at the bottom of the sprue, we can use the principle of conservation of energy, specifically Bernoulli's equation. The equation relates the velocity and height of the fluid in motion.
Given Data
- Top Diameter of Sprue: 20 mm
- Height of Sprue: 200 mm
- Initial Velocity (V1): 0.5 m/s
- Acceleration due to Gravity (g): 9.8 m/s²
- Density and viscosity are neglected due to the assumption of ideal conditions.
Key Concepts
- Potential Energy: At the top of the sprue, the molten metal possesses gravitational potential energy due to its height.
- Kinetic Energy: As it descends, potential energy converts into kinetic energy, increasing the velocity of the molten metal.
Applying Bernoulli's Equation
1. Initial State (Top of the Sprue):
- Velocity (V1) = 0.5 m/s
- Height (h1) = 0.2 m (200 mm)
2. Final State (Bottom of the Sprue):
- Velocity (V2) = ?
- Height (h2) = 0 m
Using Bernoulli’s equation:
V1²/2 + g*h1 = V2²/2 + g*h2
Simplifying, we find:
0.5²/2 + 9.8*0.2 = V2²/2
3. Calculating V2:
- Solve for V2, applying the values.
- V2 = √(0.5² + 2*9.8*0.2)
This gives us V2 ≈ 2.042 m/s.
Conclusion
Thus, the velocity of the molten metal at the bottom of the sprue, considering ideal conditions and neglecting losses, is approximately 2.042 m/s.
A smooth pipe of diameter 200 mm carries water. The pressure in the pipe at section S1 (elevation:10 m) is 50 kPa. At section S2 (elevation:12 m) the pressure is 20 kPa and velocity is 2 ms-1. Density of water is 1000 kgm-3 and acceleration due to gravity is 9.8 ms-2. Which of the following is TRUE- a)Flow is from S1 to S2 and head loss is 0.53 m
- b)Flow is from S2 to S1 and head loss is 0.53 m
- c)Flow is from S1 to S2 and head loss is 1.06 m
- d)Flow is from S2 to S1 and head loss is 1.06 m
Correct answer is option 'C'. Can you explain this answer?
A smooth pipe of diameter 200 mm carries water. The pressure in the pipe at section S1 (elevation:10 m) is 50 kPa. At section S2 (elevation:12 m) the pressure is 20 kPa and velocity is 2 ms-1. Density of water is 1000 kgm-3 and acceleration due to gravity is 9.8 ms-2. Which of the following is TRUE
a)
Flow is from S1 to S2 and head loss is 0.53 m
b)
Flow is from S2 to S1 and head loss is 0.53 m
c)
Flow is from S1 to S2 and head loss is 1.06 m
d)
Flow is from S2 to S1 and head loss is 1.06 m
|
|
Hrishikesh Chakraborty answered |
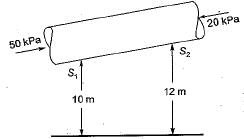
Applying Bernoulli’s equation between section S1 and S2
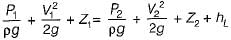
as area is constant velocity head will be same
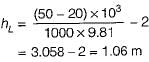
thus flow from S1 to S2 and head loss is 1.06 m.
Dimensional analysis is useful inDimensional analysis deals with the process whereby all the important factors involved in a physical phenomenon are systematically arranged into dimensional group.- a)checking the correctness of a physical equation
- b)determining the number of variables involved in a particular phenomenon
- c)determining the dimensionless groups from the given variables
- d)the exact formulation of a physical phenomenon
Correct answer is option 'C'. Can you explain this answer?
Dimensional analysis is useful in
Dimensional analysis deals with the process whereby all the important factors involved in a physical phenomenon are systematically arranged into dimensional group.
a)
checking the correctness of a physical equation
b)
determining the number of variables involved in a particular phenomenon
c)
determining the dimensionless groups from the given variables
d)
the exact formulation of a physical phenomenon
|
|
Kirti Bose answered |
Dimensional analysis is a powerful tool used in the field of physics and engineering to analyze and understand the relationships between different physical variables involved in a phenomenon. It involves systematically arranging the important factors into dimensional groups, which helps in simplifying and solving complex equations. Dimensional analysis is particularly useful in determining dimensionless groups from given variables. Let's explore why option 'C' is the correct answer.
1. Checking the correctness of a physical equation:
Dimensional analysis can be used to check the correctness of a physical equation by ensuring that the dimensions of the variables on both sides of the equation are consistent. Each physical quantity has a specific dimension (e.g., length, mass, time), and if the dimensions on both sides of the equation do not match, then it indicates an error or inconsistency in the equation.
2. Determining the number of variables involved in a particular phenomenon:
Dimensional analysis can also help in determining the number of variables involved in a particular phenomenon. By analyzing the dimensions of the physical quantities, we can identify the independent variables that affect the phenomenon. This understanding is crucial in simplifying the problem and focusing on the key variables that need to be considered.
3. Determining the dimensionless groups from the given variables:
One of the primary applications of dimensional analysis is to determine dimensionless groups from given variables. Dimensionless groups are ratios of physical quantities with the same dimensions, and they have special significance in many physical phenomena. These dimensionless groups often represent fundamental relationships and can provide insights into the behavior of the system under study. By identifying and analyzing these dimensionless groups, engineers and scientists can derive meaningful conclusions and make predictions about the phenomenon.
4. The exact formulation of a physical phenomenon:
While dimensional analysis helps in simplifying and understanding the relationships between variables, it does not provide the exact formulation of a physical phenomenon. The exact formulation typically involves mathematical modeling, experimentation, and theoretical analysis. However, dimensional analysis can serve as a valuable initial step in formulating the problem and identifying the key variables and their relationships.
In conclusion, dimensional analysis is a powerful tool that can be used in various ways, including checking the correctness of a physical equation, determining the number of variables involved, and most importantly, determining dimensionless groups from given variables. This analysis helps in simplifying complex equations, understanding the behavior of the system, and making predictions about the phenomenon under study.
1. Checking the correctness of a physical equation:
Dimensional analysis can be used to check the correctness of a physical equation by ensuring that the dimensions of the variables on both sides of the equation are consistent. Each physical quantity has a specific dimension (e.g., length, mass, time), and if the dimensions on both sides of the equation do not match, then it indicates an error or inconsistency in the equation.
2. Determining the number of variables involved in a particular phenomenon:
Dimensional analysis can also help in determining the number of variables involved in a particular phenomenon. By analyzing the dimensions of the physical quantities, we can identify the independent variables that affect the phenomenon. This understanding is crucial in simplifying the problem and focusing on the key variables that need to be considered.
3. Determining the dimensionless groups from the given variables:
One of the primary applications of dimensional analysis is to determine dimensionless groups from given variables. Dimensionless groups are ratios of physical quantities with the same dimensions, and they have special significance in many physical phenomena. These dimensionless groups often represent fundamental relationships and can provide insights into the behavior of the system under study. By identifying and analyzing these dimensionless groups, engineers and scientists can derive meaningful conclusions and make predictions about the phenomenon.
4. The exact formulation of a physical phenomenon:
While dimensional analysis helps in simplifying and understanding the relationships between variables, it does not provide the exact formulation of a physical phenomenon. The exact formulation typically involves mathematical modeling, experimentation, and theoretical analysis. However, dimensional analysis can serve as a valuable initial step in formulating the problem and identifying the key variables and their relationships.
In conclusion, dimensional analysis is a powerful tool that can be used in various ways, including checking the correctness of a physical equation, determining the number of variables involved, and most importantly, determining dimensionless groups from given variables. This analysis helps in simplifying complex equations, understanding the behavior of the system, and making predictions about the phenomenon under study.
The transition Reynolds number for flow over a flat plate is 5 x 105. What is the distance from the leading edge at which transition will occur for flow of water with a uniform velocity of 1 m/s (for water the kinematic viscosity v = 0.86 x 10-6m2/s)- a)0.43 m
- b)1 m
- c)43 m
- d)103 m
Correct answer is option 'A'. Can you explain this answer?
The transition Reynolds number for flow over a flat plate is 5 x 105. What is the distance from the leading edge at which transition will occur for flow of water with a uniform velocity of 1 m/s (for water the kinematic viscosity v = 0.86 x 10-6m2/s)
a)
0.43 m
b)
1 m
c)
43 m
d)
103 m
|
|
Sparsh Chakraborty answered |
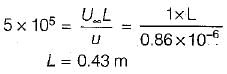
The gap between a -horizontal shaft and a concentric sleeve is filled with viscous oil. The sleeve moves with a constant velocity of 1.5 m/s when a force of 1500 N is applied parallel to the axis of the shaft. If it was required to move the sleeve at a velocity of 2 m/s, what should have been the force?- a)1250 N
- b)1500 N
- c)1750 N
- d)2000 N
Correct answer is option 'D'. Can you explain this answer?
The gap between a -horizontal shaft and a concentric sleeve is filled with viscous oil. The sleeve moves with a constant velocity of 1.5 m/s when a force of 1500 N is applied parallel to the axis of the shaft. If it was required to move the sleeve at a velocity of 2 m/s, what should have been the force?
a)
1250 N
b)
1500 N
c)
1750 N
d)
2000 N
|
|
Sinjini Bose answered |
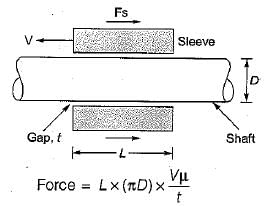
for the given problem, L, D, μ and fare constant
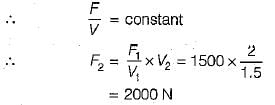
If B = Center of buoyancy, G = Center of gravity and M= Metacenter, of afloating body, the body will be in stable equilibrium if- a)MG = 0
- b)M is below G
- c)BG = 0
- d)M is above G
Correct answer is option 'D'. Can you explain this answer?
If B = Center of buoyancy, G = Center of gravity and M= Metacenter, of afloating body, the body will be in stable equilibrium if
a)
MG = 0
b)
M is below G
c)
BG = 0
d)
M is above G
|
|
Akshita Desai answered |
For a floating body
Metacentre above centre of gravity→ Stable Equilibrium
Metacentre coincides centre of gravity→ Neutral Equilibrium
Metacentre below centre of gravity→ Unstable Equilibrium
For a submerged body
Centre of buoyancy above centre of gravity→ Stable Equilibrium
Centre of buoyancy coincides centre of gravity→ Neutral Equilibrium
Centre of buoyancy below centre of gravity→ Unstable Equilibrium
Metacentre above centre of gravity→ Stable Equilibrium
Metacentre coincides centre of gravity→ Neutral Equilibrium
Metacentre below centre of gravity→ Unstable Equilibrium
For a submerged body
Centre of buoyancy above centre of gravity→ Stable Equilibrium
Centre of buoyancy coincides centre of gravity→ Neutral Equilibrium
Centre of buoyancy below centre of gravity→ Unstable Equilibrium
Consider the following statements:
A tube, with the section diverging in the direction of flow, can be used as
1. Supersonic nozzle
2. Subsonic nozzle
3. Supersonic diffuser
4. Subsonic diffuserSelect the correct answer using the codes given below:- a)1 alone
- b)2 alone
- c)1 and 4
- d)2 and 3
Correct answer is option 'C'. Can you explain this answer?
Consider the following statements:
A tube, with the section diverging in the direction of flow, can be used as
1. Supersonic nozzle
2. Subsonic nozzle
3. Supersonic diffuser
4. Subsonic diffuser
A tube, with the section diverging in the direction of flow, can be used as
1. Supersonic nozzle
2. Subsonic nozzle
3. Supersonic diffuser
4. Subsonic diffuser
Select the correct answer using the codes given below:
a)
1 alone
b)
2 alone
c)
1 and 4
d)
2 and 3
|
|
Anshul Sharma answered |
Supersonic and Subsonic Flow in Nozzles and Diffusers
Introduction:
In fluid dynamics, a nozzle is a device that accelerates the flow of a fluid (usually a gas) by increasing its velocity. A diffuser, on the other hand, is a device that slows down the flow of a fluid by increasing its pressure. Both nozzles and diffusers can operate in either subsonic or supersonic flow conditions. Let us analyze the given statements and determine which options are correct.
Analysis:
1. Supersonic Nozzle: A supersonic nozzle is designed to accelerate the flow of a fluid to supersonic speeds. It is characterized by a converging-diverging shape. As the fluid passes through the converging section, its velocity increases, and it reaches its maximum velocity at the throat of the nozzle. After passing through the throat, the flow expands in the diverging section, maintaining supersonic speeds. Therefore, a tube with a section diverging in the direction of flow can be used as a supersonic nozzle. Hence, Statement 1 is correct.
2. Subsonic Nozzle: A subsonic nozzle is designed to accelerate the flow of a fluid to subsonic speeds. It is characterized by a converging shape. The fluid passes through the converging section, and its velocity increases. However, it does not reach supersonic speeds. Therefore, a tube with a section diverging in the direction of flow cannot be used as a subsonic nozzle. Hence, Statement 2 is incorrect.
3. Supersonic Diffuser: A supersonic diffuser is designed to slow down the flow of a supersonic fluid by increasing its pressure. It is characterized by a converging-diverging shape, similar to a supersonic nozzle but in the opposite direction. As the supersonic flow enters the diffuser, it expands in the diverging section, decreasing its velocity and increasing its pressure. Therefore, a tube with a section diverging in the direction of flow can be used as a supersonic diffuser. Hence, Statement 3 is incorrect.
4. Subsonic Diffuser: A subsonic diffuser is designed to slow down the flow of a subsonic fluid by increasing its pressure. It is characterized by a diverging shape. As the fluid enters the diffuser, it expands in the diverging section, decreasing its velocity and increasing its pressure. Therefore, a tube with a section diverging in the direction of flow can be used as a subsonic diffuser. Hence, Statement 4 is correct.
Conclusion:
From the analysis, we can conclude that a tube with a section diverging in the direction of flow can be used as a supersonic nozzle and a subsonic diffuser. Therefore, the correct answer is option 'C' (1 and 4).
Introduction:
In fluid dynamics, a nozzle is a device that accelerates the flow of a fluid (usually a gas) by increasing its velocity. A diffuser, on the other hand, is a device that slows down the flow of a fluid by increasing its pressure. Both nozzles and diffusers can operate in either subsonic or supersonic flow conditions. Let us analyze the given statements and determine which options are correct.
Analysis:
1. Supersonic Nozzle: A supersonic nozzle is designed to accelerate the flow of a fluid to supersonic speeds. It is characterized by a converging-diverging shape. As the fluid passes through the converging section, its velocity increases, and it reaches its maximum velocity at the throat of the nozzle. After passing through the throat, the flow expands in the diverging section, maintaining supersonic speeds. Therefore, a tube with a section diverging in the direction of flow can be used as a supersonic nozzle. Hence, Statement 1 is correct.
2. Subsonic Nozzle: A subsonic nozzle is designed to accelerate the flow of a fluid to subsonic speeds. It is characterized by a converging shape. The fluid passes through the converging section, and its velocity increases. However, it does not reach supersonic speeds. Therefore, a tube with a section diverging in the direction of flow cannot be used as a subsonic nozzle. Hence, Statement 2 is incorrect.
3. Supersonic Diffuser: A supersonic diffuser is designed to slow down the flow of a supersonic fluid by increasing its pressure. It is characterized by a converging-diverging shape, similar to a supersonic nozzle but in the opposite direction. As the supersonic flow enters the diffuser, it expands in the diverging section, decreasing its velocity and increasing its pressure. Therefore, a tube with a section diverging in the direction of flow can be used as a supersonic diffuser. Hence, Statement 3 is incorrect.
4. Subsonic Diffuser: A subsonic diffuser is designed to slow down the flow of a subsonic fluid by increasing its pressure. It is characterized by a diverging shape. As the fluid enters the diffuser, it expands in the diverging section, decreasing its velocity and increasing its pressure. Therefore, a tube with a section diverging in the direction of flow can be used as a subsonic diffuser. Hence, Statement 4 is correct.
Conclusion:
From the analysis, we can conclude that a tube with a section diverging in the direction of flow can be used as a supersonic nozzle and a subsonic diffuser. Therefore, the correct answer is option 'C' (1 and 4).
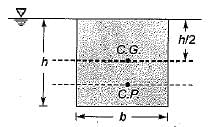
A hemispherical bulge of diameter 1.5 m is provided in the bottom of a tank. If the depth of water above the horizontal floor of the tank is 5.0 m, what is the magnitude and direction of the resultant force on the hemisphere?- a)78 kN
- b)77 kN
- c)76 kN
- d)75 kN
Correct answer is option 'A'. Can you explain this answer?
A hemispherical bulge of diameter 1.5 m is provided in the bottom of a tank. If the depth of water above the horizontal floor of the tank is 5.0 m, what is the magnitude and direction of the resultant force on the hemisphere?
a)
78 kN
b)
77 kN
c)
76 kN
d)
75 kN
|
|
Neha Joshi answered |
Net horizontal force = 0
Fv = weight of fluid above the hemisphere
Fv = weight of fluid above the hemisphere

The drag coefficient for laminar flow varies with reynolds number (Re) as- a)Re1/2
- b)Re
- c)Re-1
- d)Re-1/2
Correct answer is option 'D'. Can you explain this answer?
The drag coefficient for laminar flow varies with reynolds number (Re) as
a)
Re1/2
b)
Re
c)
Re-1
d)
Re-1/2
|
|
Anshul Basu answered |
Explanation:
The drag coefficient is a dimensionless quantity that characterizes the resistance of an object to movement through a fluid. The drag coefficient for laminar flow can be determined by the Reynold's number (Re), which is the ratio of inertial forces to viscous forces in a fluid flow.
The drag coefficient for laminar flow varies with Reynolds number (Re) as Re-1/2. This means that as the Reynolds number increases, the drag coefficient decreases.
The Reynolds number is given by the formula:
Re = (ρVD)/μ
where,
ρ = density of the fluid
V = velocity of the object
D = characteristic length of the object
μ = viscosity of the fluid
The drag coefficient for laminar flow can be determined using the following formula:
Cd = (2F)/(ρV2A)
where,
F = drag force
A = reference area
The drag coefficient for laminar flow is dependent on the shape of the object and the Reynolds number.
Conclusion:
In conclusion, the drag coefficient for laminar flow varies with Reynolds number (Re) as Re-1/2. This means that as the Reynolds number increases, the drag coefficient decreases. The drag coefficient for laminar flow is dependent on the shape of the object and the Reynolds number.
The drag coefficient is a dimensionless quantity that characterizes the resistance of an object to movement through a fluid. The drag coefficient for laminar flow can be determined by the Reynold's number (Re), which is the ratio of inertial forces to viscous forces in a fluid flow.
The drag coefficient for laminar flow varies with Reynolds number (Re) as Re-1/2. This means that as the Reynolds number increases, the drag coefficient decreases.
The Reynolds number is given by the formula:
Re = (ρVD)/μ
where,
ρ = density of the fluid
V = velocity of the object
D = characteristic length of the object
μ = viscosity of the fluid
The drag coefficient for laminar flow can be determined using the following formula:
Cd = (2F)/(ρV2A)
where,
F = drag force
A = reference area
The drag coefficient for laminar flow is dependent on the shape of the object and the Reynolds number.
Conclusion:
In conclusion, the drag coefficient for laminar flow varies with Reynolds number (Re) as Re-1/2. This means that as the Reynolds number increases, the drag coefficient decreases. The drag coefficient for laminar flow is dependent on the shape of the object and the Reynolds number.
Three parallel pipes connected at the two ends have flowrates Q1, Q2, and Q3, respectively, and the corresponding frictional head losses are hL1, hL2, and hL3 respectively. The correct expressions for total flow rate (Q) and frictional head loss across the two ends (hL) are- a)Q = Q1 + Q2 + Q3; hL = hL1 + hL2 + hL3
- b)Q = Q1 + Q2 + Q3; hL = hL1 = hL2 = hL3
- c)Q = Q1 = Q2 = Q3; hL = hL1 + hL2 + hL3
- d)Q = Q1 = Q2 = Q3; hL = hL1 = hL2 = hL3
Correct answer is option 'B'. Can you explain this answer?
Three parallel pipes connected at the two ends have flowrates Q1, Q2, and Q3, respectively, and the corresponding frictional head losses are hL1, hL2, and hL3 respectively. The correct expressions for total flow rate (Q) and frictional head loss across the two ends (hL) are
a)
Q = Q1 + Q2 + Q3; hL = hL1 + hL2 + hL3
b)
Q = Q1 + Q2 + Q3; hL = hL1 = hL2 = hL3
c)
Q = Q1 = Q2 = Q3; hL = hL1 + hL2 + hL3
d)
Q = Q1 = Q2 = Q3; hL = hL1 = hL2 = hL3

|
Constructing Careers answered |
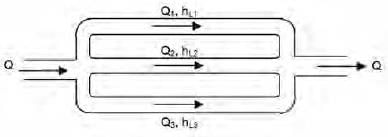
Total flow rate, Q = Q1 + Q2 + Q3 and frictional head loss,
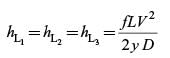
An odd shaped body weighing 7.5 kg and occupying 0.01 m3 volume wiil be completely submerged in a fluid having specific gravity of- a)1
- b)1.2
- c)0.8
- d)0.75
Correct answer is option 'D'. Can you explain this answer?
An odd shaped body weighing 7.5 kg and occupying 0.01 m3 volume wiil be completely submerged in a fluid having specific gravity of
a)
1
b)
1.2
c)
0.8
d)
0.75
|
|
Aniket Saini answered |
Submergence of Odd Shaped Body in Fluid
Given:
Weight of the body, W = 7.5 kg
Volume of the body, V = 0.01 m3
Specific gravity of the fluid, S.G. = ρ/ρw
where, ρ = Density of the fluid
ρw = Density of water
a) If S.G. = 1
Density of water, ρw = 1000 kg/m3
Weight of the displaced water, WD = V × ρw = 0.01 × 1000 = 10 kg
As the weight of the body (7.5 kg) is less than the weight of the displaced water (10 kg), the body will float on the surface of the fluid. Therefore, the answer is incorrect.
b) If S.G. = 1.2
Density of the fluid, ρ = S.G. × ρw = 1.2 × 1000 = 1200 kg/m3
Weight of the displaced water, WD = V × ρw = 0.01 × 1000 = 10 kg
Buoyancy force acting on the body, FB = WD × g = 10 × 9.81 = 98.1 N
Weight of the body, W = 7.5 × 9.81 = 73.58 N
As the buoyancy force (98.1 N) is greater than the weight of the body (73.58 N), the body will float on the surface of the fluid. Therefore, the answer is incorrect.
c) If S.G. = 0.8
Density of the fluid, ρ = S.G. × ρw = 0.8 × 1000 = 800 kg/m3
Weight of the displaced water, WD = V × ρw = 0.01 × 1000 = 10 kg
Buoyancy force acting on the body, FB = WD × g = 10 × 9.81 = 98.1 N
Weight of the body, W = 7.5 × 9.81 = 73.58 N
As the buoyancy force (98.1 N) is greater than the weight of the body (73.58 N), the body will float on the surface of the fluid. Therefore, the answer is incorrect.
d) If S.G. = 0.75
Density of the fluid, ρ = S.G. × ρw = 0.75 × 1000 = 750 kg/m3
Weight of the displaced water, WD = V × ρw = 0.01 × 1000 = 10 kg
Buoyancy force acting on the body, FB = WD × g = 10 × 9.81 = 98.1 N
Weight of the body, W = 7.5 × 9.81 = 73.58 N
As the buoyancy force (98.1 N) is greater than the weight of the body (73.58 N), the body will sink and be completely submerged in the fluid. Therefore, the correct answer is option 'D'.
Given:
Weight of the body, W = 7.5 kg
Volume of the body, V = 0.01 m3
Specific gravity of the fluid, S.G. = ρ/ρw
where, ρ = Density of the fluid
ρw = Density of water
a) If S.G. = 1
Density of water, ρw = 1000 kg/m3
Weight of the displaced water, WD = V × ρw = 0.01 × 1000 = 10 kg
As the weight of the body (7.5 kg) is less than the weight of the displaced water (10 kg), the body will float on the surface of the fluid. Therefore, the answer is incorrect.
b) If S.G. = 1.2
Density of the fluid, ρ = S.G. × ρw = 1.2 × 1000 = 1200 kg/m3
Weight of the displaced water, WD = V × ρw = 0.01 × 1000 = 10 kg
Buoyancy force acting on the body, FB = WD × g = 10 × 9.81 = 98.1 N
Weight of the body, W = 7.5 × 9.81 = 73.58 N
As the buoyancy force (98.1 N) is greater than the weight of the body (73.58 N), the body will float on the surface of the fluid. Therefore, the answer is incorrect.
c) If S.G. = 0.8
Density of the fluid, ρ = S.G. × ρw = 0.8 × 1000 = 800 kg/m3
Weight of the displaced water, WD = V × ρw = 0.01 × 1000 = 10 kg
Buoyancy force acting on the body, FB = WD × g = 10 × 9.81 = 98.1 N
Weight of the body, W = 7.5 × 9.81 = 73.58 N
As the buoyancy force (98.1 N) is greater than the weight of the body (73.58 N), the body will float on the surface of the fluid. Therefore, the answer is incorrect.
d) If S.G. = 0.75
Density of the fluid, ρ = S.G. × ρw = 0.75 × 1000 = 750 kg/m3
Weight of the displaced water, WD = V × ρw = 0.01 × 1000 = 10 kg
Buoyancy force acting on the body, FB = WD × g = 10 × 9.81 = 98.1 N
Weight of the body, W = 7.5 × 9.81 = 73.58 N
As the buoyancy force (98.1 N) is greater than the weight of the body (73.58 N), the body will sink and be completely submerged in the fluid. Therefore, the correct answer is option 'D'.
The critical value of reynolds number for transition from laminar to turbulent boundary layer in external flows is taken as- a)2300
- b)4000
- c)5 x 105
- d)3 x 106
Correct answer is option 'C'. Can you explain this answer?
The critical value of reynolds number for transition from laminar to turbulent boundary layer in external flows is taken as
a)
2300
b)
4000
c)
5 x 105
d)
3 x 106

|
Arjun Menon answered |
Critical Reynolds number for external flow
(Re)Cr = 5 x 105
(Re)Cr = 5 x 105
Chapter doubts & questions for Fluid Mechanics - Topicwise Question Bank for Mechanical Engineering 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Fluid Mechanics - Topicwise Question Bank for Mechanical Engineering in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Topicwise Question Bank for Mechanical Engineering
45 videos|314 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup