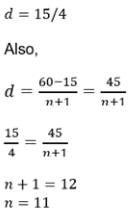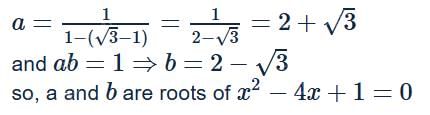All Exams >
JEE >
Mathematics (Maths) for JEE Main & Advanced >
All Questions
All questions of Sequences and Series for JEE Exam
What is the 50th term of the sequence √3, 3, 3√3, 9, ......- a)(√3)49
- b)(√3)50
- c)349
- d)350
Correct answer is option 'B'. Can you explain this answer?
What is the 50th term of the sequence √3, 3, 3√3, 9, ......
a)
(√3)49
b)
(√3)50
c)
349
d)
350

|
Infinity Academy answered |
an = ar(n-1)
Given, a = √3, r = 3/√3
r = √3
a50 = ar(n-1)
= (√3)(√3)(50-1)
= (√3)(√3)49
= (√3)50
Given, a = √3, r = 3/√3
r = √3
a50 = ar(n-1)
= (√3)(√3)(50-1)
= (√3)(√3)49
= (√3)50
Find the missing number. 1, 4, 9, 16, 25, 36, 49, (....)- a)64
- b)54
- c)56
- d)81
Correct answer is option 'A'. Can you explain this answer?
Find the missing number. 1, 4, 9, 16, 25, 36, 49, (....)
a)
64
b)
54
c)
56
d)
81
|
|
Anjana Sharma answered |
The given number series as follow as 1^2, 2^2, 3^2, 4^2, 5^2, 6^2, 7^2, 8^2, ...
So the next number is 8^2 = 64.
The terms of an A.P. are doubled, then the resulting sequence is- a)An A.P. with common difference equal to the common difference of the original A.P
- b)An A.P. with common difference thrice the common difference of the original A.P.
- c)An A.P. with common difference double the common difference of the original A.P.
- d)An A.P. with common difference half the common difference of the original A.P.
Correct answer is option 'C'. Can you explain this answer?
The terms of an A.P. are doubled, then the resulting sequence is
a)
An A.P. with common difference equal to the common difference of the original A.P
b)
An A.P. with common difference thrice the common difference of the original A.P.
c)
An A.P. with common difference double the common difference of the original A.P.
d)
An A.P. with common difference half the common difference of the original A.P.
|
|
Lavanya Menon answered |
The general form of an AP is a, a+d, a+2d,.....
where a is the first term and d is the common difference
If we double the terms, the new sequence would be
A , a+2d, a+4d,......
We can observe that this sequence is also an AP
First term is a
Common difference is 2d nth term= 2a+(n-1)2d
= 2[a+(n-1)d]
where a is the first term and d is the common difference
If we double the terms, the new sequence would be
A , a+2d, a+4d,......
We can observe that this sequence is also an AP
First term is a
Common difference is 2d nth term= 2a+(n-1)2d
= 2[a+(n-1)d]
The sum of the first hundred even natural numbers divisible by 5 is- a)55005
- b)55000
- c)50000
- d)50500
Correct answer is option 'D'. Can you explain this answer?
The sum of the first hundred even natural numbers divisible by 5 is
a)
55005
b)
55000
c)
50000
d)
50500
|
|
Preeti Iyer answered |
first even no. divisible by 5= 10
d=10
Sn = n/2(2a + (n-1) d)
S100= 100/2 (2(10) + (100-1)10)
S100=50(20 + 990)
S100= 50(1010)
S100 = 50500
The first negative term of the A.P.62,57,52…. is the- a)10th term
- b)14th term
- c)12th term
- d)18th term
Correct answer is option 'B'. Can you explain this answer?
The first negative term of the A.P.62,57,52…. is the
a)
10th term
b)
14th term
c)
12th term
d)
18th term
|
|
Naina Sharma answered |
a = 62 d = 57 - 62 = -5
tn = a + (n-1)d
= 62 + (n-1)(-5)
= 62 - 5n + 5
= 67 - 5n
From the options, we take '14'
= 67 - 5(14)
= 67 - 70
= -3 (The first negative term will be at the 14th term)
tn = a + (n-1)d
= 62 + (n-1)(-5)
= 62 - 5n + 5
= 67 - 5n
From the options, we take '14'
= 67 - 5(14)
= 67 - 70
= -3 (The first negative term will be at the 14th term)
How many terms of the series
24,20,16,…are required so that their sum is 72?- a)8 or 6
- b)12
- c)9 or 4
- d)11
Correct answer is option 'C'. Can you explain this answer?
How many terms of the series
24,20,16,…are required so that their sum is 72?
24,20,16,…are required so that their sum is 72?
a)
8 or 6
b)
12
c)
9 or 4
d)
11
|
|
Naina Bansal answered |
As given above we can clearly see that the given series forms an AP. So we can use the sum formula to calculate it.
= Sn = n / 2 [ 2a + ( n-1 ) d ]
So the values are :
a = 24
d = -4
n = ?
Sn = 72
So substitute in the formula to get the answer:
= 72 = n / 2 [ 2 ( 24 ) + ( n - 1 ) -4 ]
= 72 = n / 2 [ 48 - 4n + 4 ]
= 72 * 2 = n [ 52 - 4n ]
= 144 = 52n - 4n^2
= 4n^2 - 52n + 144 = 0 ------ Dividing by 4 throughout the equation we get,
= n^2 - 13n + 36
Factorizing the above quadratic equation we get,
= n^2 - 9n - 4n + 36 = 0
= n ( n - 9 ) -4 ( n - 9 ) = 0
= ( n - 4 ) ( n - 9 ) = 0
= n = 4 , 9
So the number of terms can be both 4 terms and 9 terms. This is because since the AP is decreasing.
Hope it helps !!
The 5th term of the sequence 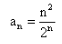 is
is- a)1
- b)5/16
- c)25/16
- d)25/32
Correct answer is option 'D'. Can you explain this answer?
The 5th term of the sequence 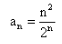 is
is
a)
1
b)
5/16
c)
25/16
d)
25/32
|
|
Riya Banerjee answered |
an = (n2)/2n
⇒ a5 = [(5)2]/2(5)
⇒ a5 = 25/32
⇒ a5 = [(5)2]/2(5)
⇒ a5 = 25/32
What is the 10th term of the sequence defined by an = (n-1)(2-n)(3+n)?
a) 792
b) -936
c) -924
d) -792
The answer is b.
|
|
Naina Sharma answered |
an = (n-1)(2-n)(3+n)
Put n = 10
an = 9×(-8)×13
= - 936
Put n = 10
an = 9×(-8)×13
= - 936
Three terms in A.P. are such that their sum is 45. What is the middle term?- a)25
- b)30
- c)15
- d)10
Correct answer is option 'C'. Can you explain this answer?
Three terms in A.P. are such that their sum is 45. What is the middle term?
a)
25
b)
30
c)
15
d)
10
|
|
Pooja Shah answered |
Let the three numbers be a-d, a, a+d
ATQ,
a - d + a + a + 2d = 45
3a = 45
a = 15
Middle term is 15
ATQ,
a - d + a + a + 2d = 45
3a = 45
a = 15
Middle term is 15
A man saved Rs 21700 in 14 years. In each year after the first he saved Rs 100 more than he did in the preceding year. How much did he save in the first year?- a)Rs 2100
- b)Rs 1300
- c)Rs 900
- d)Rs 600
Correct answer is option 'C'. Can you explain this answer?
A man saved Rs 21700 in 14 years. In each year after the first he saved Rs 100 more than he did in the preceding year. How much did he save in the first year?
a)
Rs 2100
b)
Rs 1300
c)
Rs 900
d)
Rs 600
|
|
Gaurav Kumar answered |
d = 100
Sn = 21700
n = 14
Sn = n/2[2a + (n-1)d]
21700 = 14/2[2a + (14-1)100]
= 21700 = 7[2a + 1300]
= 3100 = 2a + 1300
⇒ 3100 - 1300 = 2a
⇒ 1800 = 2a
⇒ a = 900
Sn = 21700
n = 14
Sn = n/2[2a + (n-1)d]
21700 = 14/2[2a + (14-1)100]
= 21700 = 7[2a + 1300]
= 3100 = 2a + 1300
⇒ 3100 - 1300 = 2a
⇒ 1800 = 2a
⇒ a = 900
If A1, A2, A3,…., An are n numbers between a and b, such that a, A1, A2, A3,…, An, b are in A.P., then nth term from beginning is:- a)b
- b)An-1
- c)An
- d)A1
Correct answer is option 'B'. Can you explain this answer?
If A1, A2, A3,…., An are n numbers between a and b, such that a, A1, A2, A3,…, An, b are in A.P., then nth term from beginning is:
a)
b
b)
An-1
c)
An
d)
A1
|
|
Krishna Iyer answered |
A1,A2,......, An are inserted between a and b then the series will become
a, A1,A2,A3,......, An,b. Now a becomes the first term, A1 will be second, A2 will become third term
An will become A(n+1)th term
therefore A(n-1) will become nth term.
a, A1,A2,A3,......, An,b. Now a becomes the first term, A1 will be second, A2 will become third term
An will become A(n+1)th term
therefore A(n-1) will become nth term.
The digits of a positive integer having three digits are in AP and sum of their digits is 21. The number obtained by reversing the digits is 396 less than the original number. Find the original number.- a)876
- b)579
- c)975
- d)678
Correct answer is option 'C'. Can you explain this answer?
The digits of a positive integer having three digits are in AP and sum of their digits is 21. The number obtained by reversing the digits is 396 less than the original number. Find the original number.
a)
876
b)
579
c)
975
d)
678

|
Trisha Vashisht answered |
Let the digits at ones, tens and hundreds place be (a−d)a and (a+d) respectively. The, the number is
(a+d)×100+a×10+(a−d) = 111a+99d
The number obtained by reversing the digits is
(a−d)×+a×10+(a+d) = 111a−99d
It is given that the sum of the digits is 21.
(a−d)+a+(a+d) = 21 ...(i)
Also it is given that the number obtained by reversing the digits is 594 less than the original number.
∴111a−99d = 111a+99d−396 ...(ii)
⟹ 3a = 21 and 198d = 396
⟹ a = 7 and d = -2
Original number = (a−d)×+a×10+(a+d)
= 100(9) + 10(7) + 5
= 975
(a+d)×100+a×10+(a−d) = 111a+99d
The number obtained by reversing the digits is
(a−d)×+a×10+(a+d) = 111a−99d
It is given that the sum of the digits is 21.
(a−d)+a+(a+d) = 21 ...(i)
Also it is given that the number obtained by reversing the digits is 594 less than the original number.
∴111a−99d = 111a+99d−396 ...(ii)
⟹ 3a = 21 and 198d = 396
⟹ a = 7 and d = -2
Original number = (a−d)×+a×10+(a+d)
= 100(9) + 10(7) + 5
= 975
The first 4 terms of the sequence 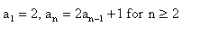 are
are- a)2, 6, 13, 27
- b)2, 5, 11, 23
- c)2, 6, 11, 24
- d)2, 5, 12, 37
Correct answer is option 'B'. Can you explain this answer?
The first 4 terms of the sequence 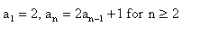 are
are
a)
2, 6, 13, 27
b)
2, 5, 11, 23
c)
2, 6, 11, 24
d)
2, 5, 12, 37
|
|
Geetika Shah answered |
a1 = 2
a2 = 2a1 + 1
=> 2(2) + 1 = 5
a3 = 2a2 + 1
=> 2(5) + 1 = 11
a4 = 2a3 + 1
=> 2(11) + 1 = 23
Hence, the required series is : 2,5,11,23………
a2 = 2a1 + 1
=> 2(2) + 1 = 5
a3 = 2a2 + 1
=> 2(5) + 1 = 11
a4 = 2a3 + 1
=> 2(11) + 1 = 23
Hence, the required series is : 2,5,11,23………
The arithmetic mean between 6 and – 12 is:- a)6
- b)-3
- c)-6
- d)9
Correct answer is option 'B'. Can you explain this answer?
The arithmetic mean between 6 and – 12 is:
a)
6
b)
-3
c)
-6
d)
9
|
|
Geetika Shah answered |
6, x, -12
x = (6-12)/2
x = -6/2
x = -3
x = (6-12)/2
x = -6/2
x = -3
What is the 10th A.M between 2 and 57 if 10 A.M s are inserted between these numbers?
- a)54
- b)53
- c)52
- d)55
Correct answer is option 'C'. Can you explain this answer?
What is the 10th A.M between 2 and 57 if 10 A.M s are inserted between these numbers?
a)
54
b)
53
c)
52
d)
55
|
|
Aryan Khanna answered |
2 and 57 have 10 terms between them so including them there would be 12 terms
an = 57, a = 2, n = 12
an = a + (n-1)d
=> 57 = 2 + (12 - 1)d
=> 55 = 11d
d = 5
T10 = a + 10d
=> 2 + 10(5)
= 52
an = 57, a = 2, n = 12
an = a + (n-1)d
=> 57 = 2 + (12 - 1)d
=> 55 = 11d
d = 5
T10 = a + 10d
=> 2 + 10(5)
= 52
If we want to insert 8 numbers between the numbers 4 and 31 such that the resulting sequence is an AP.The difference between the consecutive numbers will be- a)4
- b)3
- c)2
- d)5
Correct answer is option 'B'. Can you explain this answer?
If we want to insert 8 numbers between the numbers 4 and 31 such that the resulting sequence is an AP.The difference between the consecutive numbers will be
a)
4
b)
3
c)
2
d)
5

|
New Words answered |
a = 4, l = 31, n = 8
(l-a)/(n+1) = (31-4)/(8+1)
= 27/9
= 3
(l-a)/(n+1) = (31-4)/(8+1)
= 27/9
= 3
If the sums of n, 2n and 3n terms of an AP are S1, S2 and S3 respectively, then 
- a)
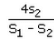
- b)
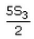
- c)3
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If the sums of n, 2n and 3n terms of an AP are S1, S2 and S3 respectively, then
a)
b)
c)
3
d)
none of these
|
|
Pooja Shah answered |
Given x 2 - 3x = 0
Factor x out in the expression on the left.
x (x - 3) = 0
For the product x (x - 3) to be equal to zero we nedd to have
x = 0 or x - 3 = 0
Solve the above simple equations to obtain the solutions.
x = 0
or
x = 3
Factor x out in the expression on the left.
x (x - 3) = 0
For the product x (x - 3) to be equal to zero we nedd to have
x = 0 or x - 3 = 0
Solve the above simple equations to obtain the solutions.
x = 0
or
x = 3
The sum of the series 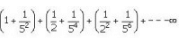
- a)49/25
- b)49/24
- c)47/24
- d)49/29
Correct answer is option 'B'. Can you explain this answer?
The sum of the series 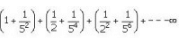
a)
49/25
b)
49/24
c)
47/24
d)
49/29

|
Knowledge Hub answered |
(1 + 1/52) + (1/2 + 1/52) + (1/22 + 1/54)+......
= (1 + 1/2 + 1/22 +....) + (1/52 + 1/54 + 1/56 +......)
= r = (1/4)/(1/2) , r = (1/54)/(1/52)
⇒ r = 1/2 + 1/25
⇒ S = 1 + [(1/2)/(1-1/2)], S = [(1/25)/(1-1/25)]
⇒ S = 1 + 1, S = 1/24
Total sum = 2 + 1/24
⇒ 49/24
= (1 + 1/2 + 1/22 +....) + (1/52 + 1/54 + 1/56 +......)
= r = (1/4)/(1/2) , r = (1/54)/(1/52)
⇒ r = 1/2 + 1/25
⇒ S = 1 + [(1/2)/(1-1/2)], S = [(1/25)/(1-1/25)]
⇒ S = 1 + 1, S = 1/24
Total sum = 2 + 1/24
⇒ 49/24
If the 10 times of the 10th term of an AP is equal to 15 times to the 15th term, then the 25th term is:- a)25 times of 25th term
- b)zero
- c)1
- d)2
Correct answer is option 'B'. Can you explain this answer?
If the 10 times of the 10th term of an AP is equal to 15 times to the 15th term, then the 25th term is:
a)
25 times of 25th term
b)
zero
c)
1
d)
2
|
|
Nandini Patel answered |
According to question ,
10 x 10th term =15 x 15th term
let a is the first term and d is the common difference .
10 (a+9d)=15 (a+14d)
5a+120d=0
a +24d=0
now ,
25th term =a+(25-1) d=a+24d=0
hence 25th term=0
How many terms of the G.P. 4 + 16 + 64 + … will make the sum 5460?- a)9
- b)7
- c)8
- d)6
Correct answer is option 'D'. Can you explain this answer?
How many terms of the G.P. 4 + 16 + 64 + … will make the sum 5460?
a)
9
b)
7
c)
8
d)
6
|
|
Nandini Iyer answered |
Sum (Sn) = a x (rn -1)/(r-1)
5460 = 4 x (4n -1)/3
16380 = 4n+1 - 4
5460 = 4 x (4n -1)/3
16380 = 4n+1 - 4
16384 = 4n+1
47 = 4n+1
7 = n + 1
n = 6
The 10th term of an G.P. is 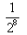 and the 5th term is
and the 5th term is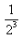 .What is the Common Ratio?
.What is the Common Ratio?- a)1/4
- b)1/16
- c)1/2
- d)1/8
Correct answer is option 'C'. Can you explain this answer?
The 10th term of an G.P. is 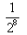 and the 5th term is
and the 5th term is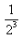 .What is the Common Ratio?
.What is the Common Ratio?
a)
1/4
b)
1/16
c)
1/2
d)
1/8

|
Praveen Kumar answered |
ar9 = 1/(2)8 -----------------------(1)
ar3 = 1/(2)2 ------------------------------(2)
Comparing eq (1) & (2)
1/(2)8 r9 = 1/(2)^2 r4
1/r5 = (2)5
r5 = 1/(2)5
r = 1/2
ar3 = 1/(2)2 ------------------------------(2)
Comparing eq (1) & (2)
1/(2)8 r9 = 1/(2)^2 r4
1/r5 = (2)5
r5 = 1/(2)5
r = 1/2

- a)4
- b)6
- c)8
- d)2
Correct answer is option 'B'. Can you explain this answer?
a)
4
b)
6
c)
8
d)
2
|
|
Preeti Iyer answered |
6 + 6 + 6.........∞
61/2 * 61/4 * 61/8………..∞
= 61/2 + 1/(2*2) + 1/(2*2*2) (sum of infinte G.P.= a/(1−r))
= (1/2)/(6(1-½))
= (1/2)/(61/2)
= 6
61/2 * 61/4 * 61/8………..∞
= 61/2 + 1/(2*2) + 1/(2*2*2) (sum of infinte G.P.= a/(1−r))
= (1/2)/(6(1-½))
= (1/2)/(61/2)
= 6
Which term of the following sequence is 64?2 , 2√2, 4, .....- a)12
- b)10
- c)11
- d)8
Correct answer is option 'C'. Can you explain this answer?
Which term of the following sequence is 64?
2 , 2√2, 4, .....
a)
12
b)
10
c)
11
d)
8
|
|
Krishna Iyer answered |
Given sequence : 2, 2√2, 4….
First term a1 = a = 2 and 2nd term a2 = 2√2, then
Common ratio r = a2/a = (2√2)/2
Let an = 64
∴ ar(n-1) = 64
⇒ 2.(√2)(n-1) = 32
⇒ (2)(n-1)/2 = 32
∴ (2)(n-1)/2 = (2)5
⇒ (n − 1)/2 = 5,
⇒ n = 11
First term a1 = a = 2 and 2nd term a2 = 2√2, then
Common ratio r = a2/a = (2√2)/2
Let an = 64
∴ ar(n-1) = 64
⇒ 2.(√2)(n-1) = 32
⇒ (2)(n-1)/2 = 32
∴ (2)(n-1)/2 = (2)5
⇒ (n − 1)/2 = 5,
⇒ n = 11
If a, b, c are in A.P., then- a)b - a = b - c
- b)b is the arithmetic mean of a and c.
- c)2a = b + c
- d)a - b = c - b
Correct answer is option 'B'. Can you explain this answer?
If a, b, c are in A.P., then
a)
b - a = b - c
b)
b is the arithmetic mean of a and c.
c)
2a = b + c
d)
a - b = c - b
|
|
Anirban Sharma answered |
Understanding Arithmetic Progression (A.P.)
When three numbers a, b, and c are in Arithmetic Progression (A.P.), it means they have a specific relationship. A.P. is characterized by a constant difference between consecutive terms.
Key Definition
- In A.P., the middle term is the average of the two outer terms. Hence, for numbers a, b, and c:
- b = (a + c) / 2
This implies that b is the arithmetic mean of a and c.
Analyzing the Options
Let's break down each option to see their validity:
- Option a) b - a = b - c
This implies a + c = 2b, which is true.
- Option b) b is the arithmetic mean of a and c
This directly aligns with the definition of A.P., making it correct.
- Option c) 2a = b + c
Rearranging gives b = 2a - c. This is not a general rule for A.P.
- Option d) a - b = c - b
Rearranging gives a + c = 2b, which is true but doesn't define A.P. directly.
Conclusion
The correct answer is Option b) because it succinctly captures the essence of A.P., where b is indeed the arithmetic mean of a and c. This fundamental property is central to understanding and solving problems related to Arithmetic Progression.
In summary, when a, b, and c are in A.P., b perfectly represents the mean of the outer terms a and c, confirming that Option b is the correct choice.
When three numbers a, b, and c are in Arithmetic Progression (A.P.), it means they have a specific relationship. A.P. is characterized by a constant difference between consecutive terms.
Key Definition
- In A.P., the middle term is the average of the two outer terms. Hence, for numbers a, b, and c:
- b = (a + c) / 2
This implies that b is the arithmetic mean of a and c.
Analyzing the Options
Let's break down each option to see their validity:
- Option a) b - a = b - c
This implies a + c = 2b, which is true.
- Option b) b is the arithmetic mean of a and c
This directly aligns with the definition of A.P., making it correct.
- Option c) 2a = b + c
Rearranging gives b = 2a - c. This is not a general rule for A.P.
- Option d) a - b = c - b
Rearranging gives a + c = 2b, which is true but doesn't define A.P. directly.
Conclusion
The correct answer is Option b) because it succinctly captures the essence of A.P., where b is indeed the arithmetic mean of a and c. This fundamental property is central to understanding and solving problems related to Arithmetic Progression.
In summary, when a, b, and c are in A.P., b perfectly represents the mean of the outer terms a and c, confirming that Option b is the correct choice.
The common ratio of a G.P. is -4/5 and the sum to infinity is 80/9, then its first term is - a)32
- b)24
- c)8
- d)16
Correct answer is option 'D'. Can you explain this answer?
The common ratio of a G.P. is -4/5 and the sum to infinity is 80/9, then its first term is
a)
32
b)
24
c)
8
d)
16
|
|
Naina Sharma answered |
S(infinity) = a/(1-r)
80/9 = a/(1 + 4/5)
80/9 = a/(9/5)
a = 16
80/9 = a/(1 + 4/5)
80/9 = a/(9/5)
a = 16
The sum of n terms of the sequence 8, 88, 888,…. is:- a)
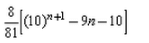
- b)
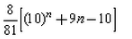
- c)
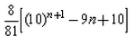
- d)
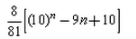
Correct answer is option 'A'. Can you explain this answer?
The sum of n terms of the sequence 8, 88, 888,…. is:
a)
b)
c)
d)

|
Infinity Academy answered |
8(1) + 8(11) + 8(111) + 8(1111) +........up to n times
= 8{ 1 + 11 + 111 + 1111 + ....... up to n times}
= 8/9{9 + 99 + 999 + 9999 + ..... up to n times}
= 8/9 {(10-1 )+ (100-1) + (1000-1) + (10000-1) + ........up to n times}
= 8/9 {(10 + 100 + 1000 + 10000 +...... n times) - (n×1)}
= 8/9{( (10×(10n -1))/(10-1)) -n}
= 80/81(10n - 1) - n
= 8/81(10n+1 - 10 -9n)
= 8{ 1 + 11 + 111 + 1111 + ....... up to n times}
= 8/9{9 + 99 + 999 + 9999 + ..... up to n times}
= 8/9 {(10-1 )+ (100-1) + (1000-1) + (10000-1) + ........up to n times}
= 8/9 {(10 + 100 + 1000 + 10000 +...... n times) - (n×1)}
= 8/9{( (10×(10n -1))/(10-1)) -n}
= 80/81(10n - 1) - n
= 8/81(10n+1 - 10 -9n)
The G.M. of 5 and 8 is- a)40
- b)2√10
- c)10√2
- d)20
Correct answer is option 'B'. Can you explain this answer?
The G.M. of 5 and 8 is
a)
40
b)
2√10
c)
10√2
d)
20
|
|
Hansa Sharma answered |
The geometric mean of two numbers, say x, and y is the square root of their product x * y.
Mean = [x * y]1/2
= [5 * 8]1/2
= [40]1/2
= 2(10)1/2
Mean = [x * y]1/2
= [5 * 8]1/2
= [40]1/2
= 2(10)1/2
If we want to insert 8 numbers between the numbers 4 and 31 such that the resulting sequence is an AP.The difference between the consecutive numbers will be- a)4
- b)3
- c)2
- d)5
Correct answer is 'B'. Can you explain this answer?
If we want to insert 8 numbers between the numbers 4 and 31 such that the resulting sequence is an AP.The difference between the consecutive numbers will be
a)
4
b)
3
c)
2
d)
5
|
|
Lavanya Menon answered |
a = 4, l = 31, n = 8
(l-a)/(n+1) = (31-4)/(8+1)
= 27/9
= 3
(l-a)/(n+1) = (31-4)/(8+1)
= 27/9
= 3
For what value of n, 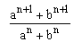 is the arithmetic mean (AM) of a and b?
is the arithmetic mean (AM) of a and b?- a)1
- b)1/2
- c)-1/2
- d)zero
Correct answer is option 'D'. Can you explain this answer?
For what value of n, 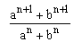 is the arithmetic mean (AM) of a and b?
is the arithmetic mean (AM) of a and b?
a)
1
b)
1/2
c)
-1/2
d)
zero
|
|
Neha Joshi answered |
(aⁿ⁺¹ + bⁿ⁺¹)/(aⁿ + bⁿ) is mean between a & b
Mean of a & b = ( a + b)/2
=> (aⁿ⁺¹ + bⁿ⁺¹)/(aⁿ + bⁿ) = ( a + b)/2
=> 2aⁿ⁺¹ + 2bⁿ⁺¹ = aⁿ⁺¹ + bⁿ⁺¹ + baⁿ + bⁿa
=> aⁿ⁺¹ + bⁿ⁺¹ = baⁿ + bⁿa
=> aⁿ(a - b) = bⁿ(a - b)
=> aⁿ = bⁿ
=> (a/b)ⁿ = 1
=> n = 0 or a = b
Mean of a & b = ( a + b)/2
=> (aⁿ⁺¹ + bⁿ⁺¹)/(aⁿ + bⁿ) = ( a + b)/2
=> 2aⁿ⁺¹ + 2bⁿ⁺¹ = aⁿ⁺¹ + bⁿ⁺¹ + baⁿ + bⁿa
=> aⁿ⁺¹ + bⁿ⁺¹ = baⁿ + bⁿa
=> aⁿ(a - b) = bⁿ(a - b)
=> aⁿ = bⁿ
=> (a/b)ⁿ = 1
=> n = 0 or a = b
For a G.P. the ratio of the 7th and the third terms is 16. The sum of 9 terms is 2555.
What is the first term?- a)7
- b)5
- c)4
- d)9
Correct answer is 'B'. Can you explain this answer?
For a G.P. the ratio of the 7th and the third terms is 16. The sum of 9 terms is 2555.
What is the first term?
What is the first term?
a)
7
b)
5
c)
4
d)
9
|
|
Jyoti Sengupta answered |
ar6/ar2 = 16
r4 = 16
r4 = (2)4
r = 2
S9 = a(rn - 1)
2555 = a((2)9 - 1)
2555 = a(512-1)
2555/511 = a
a = 5
r4 = 16
r4 = (2)4
r = 2
S9 = a(rn - 1)
2555 = a((2)9 - 1)
2555 = a(512-1)
2555/511 = a
a = 5
Which of the following sequeces in GP will have common ratio 3,where n is an Integer?- a)gn = 6(3n-1)
- b)gn = 3n2 + 3n
- c)gn = 2n2 + 3
- d)gn = 2n2 + 3n
Correct answer is option 'A'. Can you explain this answer?
Which of the following sequeces in GP will have common ratio 3,where n is an Integer?
a)
gn = 6(3n-1)
b)
gn = 3n2 + 3n
c)
gn = 2n2 + 3
d)
gn = 2n2 + 3n
|
|
Preethi Desai answered |
gn = 6( 3n-1) it is a geometric expression with coefficient of constant as 3n-1.So it is GP with common ratio 3.
7th term of Geometric Progression 2, 6, 18, ... is
- a)5832
- b)2919
- c)1458
- d)729
Correct answer is option 'C'. Can you explain this answer?
7th term of Geometric Progression 2, 6, 18, ... is
a)
5832
b)
2919
c)
1458
d)
729
|
|
Saptarshi Sen answered |
The 7th term of a geometric progression (GP) can be found using the formula:
Tn=a⋅rn−1
Where:
- Tn is the n-th term,
- a is the first term,
- r is the common ratio,
- n is the term number.
In the given GP: 2, 6, 18, ...
- The first term a=2
- The common ratio r=6/2=3
Now, substitute into the formula for the 7th term:
T7 = 2⋅37−1 = 2⋅36 = 2⋅729 = 1458
So, the 7th term is 1458
If a, b, c are in A. P., then (a + 2b − c)(2b + c − a)(c + a − b) equals- a)1/2 abc
- b)abc
- c)2abc
- d)4abc
Correct answer is option 'D'. Can you explain this answer?
If a, b, c are in A. P., then (a + 2b − c)(2b + c − a)(c + a − b) equals
a)
1/2 abc
b)
abc
c)
2abc
d)
4abc

|
KP Classes answered |
2 b = a + c, so the given expression is (a + a + c − c)(a + c + c − a)(2b − b) = 4abc
Consider the sequence 8 A + 2 B,6 A + B,4 A 2 A−B,……., Which term of this sequence will have a coefficient of A which is twice the coefficient of B?- a)10th
- b)14th
- c)16th
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
Consider the sequence 8 A + 2 B,6 A + B,4 A 2 A−B,……., Which term of this sequence will have a coefficient of A which is twice the coefficient of B?
a)
10th
b)
14th
c)
16th
d)
None of these

|
Harsh Mehta answered |
Understanding the Sequence
The sequence provided is:
- 8A + 2B
- 6A + B
- 4A^2 - B
- ...
To determine which term has a coefficient of A that is twice the coefficient of B, we need to analyze the pattern in the coefficients of A and B in the sequence.
Identifying the Coefficients
Let's denote the coefficient of A in the nth term as A_n, and the coefficient of B as B_n. The terms are:
- 1st term: A_1 = 8, B_1 = 2
- 2nd term: A_2 = 6, B_2 = 1
- 3rd term: A_3 = 4 (from 4A^2), B_3 = -1
Pattern Analysis
To find a general formula, we can observe:
- A decreases by 2 for the first two terms and then changes form in the third term.
- B decreases by 1 and then becomes negative.
Let's analyze the coefficients further:
- The potential formula is not straightforward, but we can check manually for the provided options.
Finding Terms Where A = 2B
We need to find when A_n = 2B_n. Testing the first few terms:
- For the 1st term: 8 ≠ 2(2)
- For the 2nd term: 6 ≠ 2(1)
- For the 3rd term: 4 ≠ 2(-1)
Continue this process for higher terms until reaching higher values.
Conclusion
By observing the trends, it becomes clear that none of the terms in the sequence will satisfy the condition where the coefficient of A is precisely double that of B. Therefore, the answer is:
Correct Answer: None of these
The sequence provided is:
- 8A + 2B
- 6A + B
- 4A^2 - B
- ...
To determine which term has a coefficient of A that is twice the coefficient of B, we need to analyze the pattern in the coefficients of A and B in the sequence.
Identifying the Coefficients
Let's denote the coefficient of A in the nth term as A_n, and the coefficient of B as B_n. The terms are:
- 1st term: A_1 = 8, B_1 = 2
- 2nd term: A_2 = 6, B_2 = 1
- 3rd term: A_3 = 4 (from 4A^2), B_3 = -1
Pattern Analysis
To find a general formula, we can observe:
- A decreases by 2 for the first two terms and then changes form in the third term.
- B decreases by 1 and then becomes negative.
Let's analyze the coefficients further:
- The potential formula is not straightforward, but we can check manually for the provided options.
Finding Terms Where A = 2B
We need to find when A_n = 2B_n. Testing the first few terms:
- For the 1st term: 8 ≠ 2(2)
- For the 2nd term: 6 ≠ 2(1)
- For the 3rd term: 4 ≠ 2(-1)
Continue this process for higher terms until reaching higher values.
Conclusion
By observing the trends, it becomes clear that none of the terms in the sequence will satisfy the condition where the coefficient of A is precisely double that of B. Therefore, the answer is:
Correct Answer: None of these
If |3x−1|,3,|x−3| are the first three terms of an arithmetic progression, then the sum of the first five terms can be- a)5
- b)10
- c)20
- d)30
Correct answer is option 'A'. Can you explain this answer?
If |3x−1|,3,|x−3| are the first three terms of an arithmetic progression, then the sum of the first five terms can be
a)
5
b)
10
c)
20
d)
30

|
Nipun Tuteja answered |
Case-I: x<1/3 ⇒ −3x+1,3,−x+3 are in A.P.
⇒ 6 = −3x + 1 − x + 3
⇒ 4x = −2 ⇒ x = −1/2
⇒ terms are 5/2, 3, 7/2, 4, 9/2
⇒ sum =35/2
Case-II: 1/3 ≤ x < 3
3x − 1,3, −x + 3 are in A.P.
⇒ 6 = 3x − 1 − x + 3 = 2x + 2 ⇒ x = 2
⇒ terms are 5, 3, 1, –1, –3
⇒ sum = 5
Case-III: x ≥ 3
⇒ terms are 3x − 1,3,x − 3
⇒ 6 = 3x − 1 + x − 3 = 4x − 4
⇒ 4x = 10 ⇒ x = 5/2 not possible
⇒ 6 = −3x + 1 − x + 3
⇒ 4x = −2 ⇒ x = −1/2
⇒ terms are 5/2, 3, 7/2, 4, 9/2
⇒ sum =35/2
Case-II: 1/3 ≤ x < 3
3x − 1,3, −x + 3 are in A.P.
⇒ 6 = 3x − 1 − x + 3 = 2x + 2 ⇒ x = 2
⇒ terms are 5, 3, 1, –1, –3
⇒ sum = 5
Case-III: x ≥ 3
⇒ terms are 3x − 1,3,x − 3
⇒ 6 = 3x − 1 + x − 3 = 4x − 4
⇒ 4x = 10 ⇒ x = 5/2 not possible
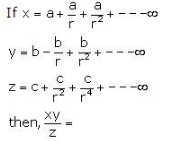
- a)ac/b
- b)bc/a
- c)ab/c
- d)cb/a
Correct answer is option 'C'. Can you explain this answer?
a)
ac/b
b)
bc/a
c)
ab/c
d)
cb/a

|
Anshu Joshi answered |
x = a + a/r + a/r² + .....................+ ∞
First term = a , Common Ratio = 1/r
=> x = a/(1 - 1/r) = ra/(r - 1)
y = b - b/r + b/r² + .....................+ ∞
First term = b , Common Ratio = -1/r
=> y = b/(1 - (-1/r)) = rb/(r + 1)
z=c+c/r²+c/r⁴+..........................+ ∞
First term = c , Common Ratio = 1/r²
z = c/(1 - (1/r²) = r²c/(r² - 1)
LHS = xy/z
= (ra/(r - 1) )( rb/(r + 1)) / ( r²c/(r² - 1))
= r²ab(r² - 1)/ r²c/(r² - 1)
= ab/c
First term = a , Common Ratio = 1/r
=> x = a/(1 - 1/r) = ra/(r - 1)
y = b - b/r + b/r² + .....................+ ∞
First term = b , Common Ratio = -1/r
=> y = b/(1 - (-1/r)) = rb/(r + 1)
z=c+c/r²+c/r⁴+..........................+ ∞
First term = c , Common Ratio = 1/r²
z = c/(1 - (1/r²) = r²c/(r² - 1)
LHS = xy/z
= (ra/(r - 1) )( rb/(r + 1)) / ( r²c/(r² - 1))
= r²ab(r² - 1)/ r²c/(r² - 1)
= ab/c
If the pth term of an A.P. be 1/q and qth term be 1/p, then the sum of its pqth terms will be- a)
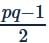
- b)
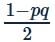
- c)
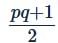
- d)
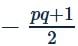
Correct answer is option 'C'. Can you explain this answer?
If the pth term of an A.P. be 1/q and qth term be 1/p, then the sum of its pqth terms will be
a)
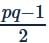
b)
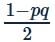
c)
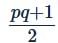
d)
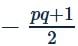

|
Sai Kulkarni answered |
Given ap = 1/q
a + (p − 1)d = 1/q
aq + (pq − q)d=1…(1)
Similarly, we get
ap + (pq − p)d = 1…(2)
From (1) and (2), we get
aq + (pq − q)d = ap + (pq − p)d
aq − ap = d[pq − p − pq + q]
a(q − p) = d(q − p)
∴ a = d
Equation (1) becomes,
dq + pqd − dq = 1

a + (p − 1)d = 1/q
aq + (pq − q)d=1…(1)
Similarly, we get
ap + (pq − p)d = 1…(2)
From (1) and (2), we get
aq + (pq − q)d = ap + (pq − p)d
aq − ap = d[pq − p − pq + q]
a(q − p) = d(q − p)
∴ a = d
Equation (1) becomes,
dq + pqd − dq = 1

Chapter doubts & questions for Sequences and Series - Mathematics (Maths) for JEE Main & Advanced 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Sequences and Series - Mathematics (Maths) for JEE Main & Advanced in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily


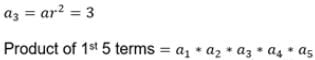


 Therefore
Therefore