All Exams >
Electronics and Communication Engineering (ECE) >
Communication System >
All Questions
All questions of Digital Communication for Electronics and Communication Engineering (ECE) Exam
The error probability of QPSK is
- a)better than BPSK
- b)inferior to BPSK
- c)same as BPSK
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The error probability of QPSK is
a)
better than BPSK
b)
inferior to BPSK
c)
same as BPSK
d)
none of these

|
Manisha Chavan answered |
The error probability of QPSK is same as BPSK.
The bit error probability is determined when the signal interference and Gaussian noise are applied to the input of the QPSK receiver. The interference is approximated by a sum of sine waves with constant amplitudes and uniformly distributed phases.
The bit error probability is determined when the signal interference and Gaussian noise are applied to the input of the QPSK receiver. The interference is approximated by a sum of sine waves with constant amplitudes and uniformly distributed phases.
In a digital continuous-time communication system, the bit rate of NRZ data stream is 1 Mbps and carrier frequency of transmission is 100 MHz. What is the bandwidth requirement of the channel in BPSK and QPSK systems respectively?- a)2 MHz and 4 MHz
- b)1 MHz and 2 MHz
- c)4 MHz and 2 MHz
- d)2 MHz and 1 MHz
Correct answer is option 'D'. Can you explain this answer?
In a digital continuous-time communication system, the bit rate of NRZ data stream is 1 Mbps and carrier frequency of transmission is 100 MHz. What is the bandwidth requirement of the channel in BPSK and QPSK systems respectively?
a)
2 MHz and 4 MHz
b)
1 MHz and 2 MHz
c)
4 MHz and 2 MHz
d)
2 MHz and 1 MHz

|
Diya Patel answered |
The bit period of NRZ data stream is
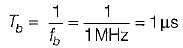
In BPSK, each binary bit is a symbol, therefore symbol duration Ts = Tb = 1 μs.
∴ The bandwidth required for BPSK system is
∴ The bandwidth required for BPSK system is
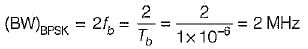
In QPSK, we group two successive bits to form one symbol, therefore symbol duration,
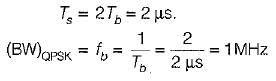
The representation of 4 bit code 1101 into 7 bit, even parity Hamming code is- a)(1010101)
- b)(1111001)
- c)(1011101)
- d)(1110000)
Correct answer is option 'A'. Can you explain this answer?
The representation of 4 bit code 1101 into 7 bit, even parity Hamming code is
a)
(1010101)
b)
(1111001)
c)
(1011101)
d)
(1110000)
|
|
Vihaan Gupta answered |
Hamming Code:
Hamming code is an error detection and correction technique used in digital communication systems. It allows the receiver to detect and correct errors that may occur during transmission.
Even Parity Hamming Code:
Even parity Hamming code is a type of Hamming code that uses an additional parity bit to ensure that the total number of ones in a code word is always even. This allows the receiver to detect and correct single-bit errors.
Given Code:
The given code is a 4-bit code represented as 1101. We need to convert this code into a 7-bit even parity Hamming code.
Procedure:
To convert the given 4-bit code into a 7-bit code, we need to add three parity bits to ensure even parity.
Step 1: Identify Parity Bits Positions:
In a 7-bit even parity Hamming code, the positions of the parity bits are 1, 2, and 4. These positions are determined by the power of 2 (starting from 1) where the bit positions are 2^0, 2^1, and 2^2.
Step 2: Insert Data Bits:
Insert the data bits into the remaining positions (3, 5, 6, and 7) of the 7-bit code.
The given 4-bit code 1101 can be inserted into the 7-bit code as follows:
- Position 1: Parity bit
- Position 2: Parity bit
- Position 3: Data bit (1)
- Position 4: Parity bit
- Position 5: Data bit (1)
- Position 6: Data bit (0)
- Position 7: Data bit (1)
So far, the code looks like: _ _ 1 _ 1 0 1
Step 3: Calculate Parity Bits:
Calculate the parity bits based on the data bits in their respective positions.
Parity Bit 1:
The parity bit at position 1 should be calculated based on the data bits at positions 3, 5, and 7.
The positions involved in the calculation of parity bit 1 are 3, 5, and 7. The bits at these positions are 1, 1, and 1, respectively. Since the total number of ones is 3 (odd), the parity bit 1 should be 0 to ensure even parity.
Parity Bit 2:
The parity bit at position 2 should be calculated based on the data bits at positions 3, 6, and 7.
The positions involved in the calculation of parity bit 2 are 3, 6, and 7. The bits at these positions are 1, 0, and 1, respectively. Since the total number of ones is 2 (even), the parity bit 2 should be 1 to ensure even parity.
Parity Bit 4:
The parity bit at position 4 should be calculated based on the data bits at positions 5, 6, and 7.
The positions involved in the calculation of parity bit 4 are 5, 6, and 7. The bits at these positions are 1, 0
Hamming code is an error detection and correction technique used in digital communication systems. It allows the receiver to detect and correct errors that may occur during transmission.
Even Parity Hamming Code:
Even parity Hamming code is a type of Hamming code that uses an additional parity bit to ensure that the total number of ones in a code word is always even. This allows the receiver to detect and correct single-bit errors.
Given Code:
The given code is a 4-bit code represented as 1101. We need to convert this code into a 7-bit even parity Hamming code.
Procedure:
To convert the given 4-bit code into a 7-bit code, we need to add three parity bits to ensure even parity.
Step 1: Identify Parity Bits Positions:
In a 7-bit even parity Hamming code, the positions of the parity bits are 1, 2, and 4. These positions are determined by the power of 2 (starting from 1) where the bit positions are 2^0, 2^1, and 2^2.
Step 2: Insert Data Bits:
Insert the data bits into the remaining positions (3, 5, 6, and 7) of the 7-bit code.
The given 4-bit code 1101 can be inserted into the 7-bit code as follows:
- Position 1: Parity bit
- Position 2: Parity bit
- Position 3: Data bit (1)
- Position 4: Parity bit
- Position 5: Data bit (1)
- Position 6: Data bit (0)
- Position 7: Data bit (1)
So far, the code looks like: _ _ 1 _ 1 0 1
Step 3: Calculate Parity Bits:
Calculate the parity bits based on the data bits in their respective positions.
Parity Bit 1:
The parity bit at position 1 should be calculated based on the data bits at positions 3, 5, and 7.
The positions involved in the calculation of parity bit 1 are 3, 5, and 7. The bits at these positions are 1, 1, and 1, respectively. Since the total number of ones is 3 (odd), the parity bit 1 should be 0 to ensure even parity.
Parity Bit 2:
The parity bit at position 2 should be calculated based on the data bits at positions 3, 6, and 7.
The positions involved in the calculation of parity bit 2 are 3, 6, and 7. The bits at these positions are 1, 0, and 1, respectively. Since the total number of ones is 2 (even), the parity bit 2 should be 1 to ensure even parity.
Parity Bit 4:
The parity bit at position 4 should be calculated based on the data bits at positions 5, 6, and 7.
The positions involved in the calculation of parity bit 4 are 5, 6, and 7. The bits at these positions are 1, 0
An amplifier has an operating spot noise figure of 10 dB when driven by a source of effective noise temperature 225 K.Que: In previous question what is the standard spot noisefigure of the cascade ?- a)10.3 dB
- b)12.2 dB
- c)14.9 dB
- d)17.6 dB
Correct answer is option 'B'. Can you explain this answer?
An amplifier has an operating spot noise figure of 10 dB when driven by a source of effective noise temperature 225 K.
Que: In previous question what is the standard spot noisefigure of the cascade ?
a)
10.3 dB
b)
12.2 dB
c)
14.9 dB
d)
17.6 dB

|
Subhankar Ghoshal answered |
The bit rate of a digital communication system is 34 Mbps. The modulation scheme is QPSK. The baud rate of the system is- a)68 Mbps
- b)34 Mbps
- c)17 Mbps
- d)85 Mbps
Correct answer is option 'C'. Can you explain this answer?
The bit rate of a digital communication system is 34 Mbps. The modulation scheme is QPSK. The baud rate of the system is
a)
68 Mbps
b)
34 Mbps
c)
17 Mbps
d)
85 Mbps

|
Rounak Choudhary answered |
In BPSK, baud rate is half the bit rate due to which there is more effective utilization of the available bandwidth of the transmission channel. Given, bit rate = 34 Mbps


The error probability of QPSK is- a)better than BPSK
- b)inferior to BPSK
- c)same as BPSK
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The error probability of QPSK is
a)
better than BPSK
b)
inferior to BPSK
c)
same as BPSK
d)
none of these
|
|
Shlok Sengupta answered |
Introduction:
QPSK (Quadrature Phase Shift Keying) and BPSK (Binary Phase Shift Keying) are two common digital modulation schemes used in communication systems. The error probability refers to the likelihood of incorrect symbol detection or bit error in the received signal. In this question, we need to determine the error probability of QPSK compared to BPSK.
Explanation:
To understand why the error probability of QPSK is the same as BPSK, let's discuss both modulation schemes and their error probabilities individually.
BPSK (Binary Phase Shift Keying):
- In BPSK, two different phases (0 and π) are used to represent the two binary symbols (0 and 1).
- The received signal is compared with a decision threshold to determine the transmitted symbol.
- The error probability in BPSK is affected by noise and interference.
- The probability of error can be calculated using the formula: P(error) = Q(sqrt(2Eb/N0)), where Eb/N0 is the signal-to-noise ratio per bit.
QPSK (Quadrature Phase Shift Keying):
- In QPSK, four different phases (0, π/2, π, and 3π/2) are used to represent four possible symbols (00, 01, 10, and 11).
- QPSK uses two carrier signals, one in-phase (I) and one quadrature (Q), to transmit symbols.
- The error probability in QPSK is also affected by noise and interference.
- The probability of error can be calculated using the formula: P(error) = 1 - (1 - P(error in BPSK))^2, where P(error in BPSK) is the error probability of BPSK.
Comparison and Conclusion:
- The error probability of QPSK is derived from the error probability of BPSK.
- In QPSK, each symbol represents two bits, so the error probability is squared to calculate the overall error probability.
- Therefore, the error probability of QPSK is the same as BPSK, but it represents twice the amount of information per symbol.
- Option 'C' is correct because the error probability of QPSK is the same as BPSK.
- QPSK offers higher spectral efficiency compared to BPSK as it transmits more bits per symbol.
- However, in terms of error probability, both modulation schemes have the same performance.
Summary:
The error probability of QPSK is the same as BPSK. Although QPSK offers higher spectral efficiency by transmitting more bits per symbol, the error probability is derived from BPSK and remains the same.
QPSK (Quadrature Phase Shift Keying) and BPSK (Binary Phase Shift Keying) are two common digital modulation schemes used in communication systems. The error probability refers to the likelihood of incorrect symbol detection or bit error in the received signal. In this question, we need to determine the error probability of QPSK compared to BPSK.
Explanation:
To understand why the error probability of QPSK is the same as BPSK, let's discuss both modulation schemes and their error probabilities individually.
BPSK (Binary Phase Shift Keying):
- In BPSK, two different phases (0 and π) are used to represent the two binary symbols (0 and 1).
- The received signal is compared with a decision threshold to determine the transmitted symbol.
- The error probability in BPSK is affected by noise and interference.
- The probability of error can be calculated using the formula: P(error) = Q(sqrt(2Eb/N0)), where Eb/N0 is the signal-to-noise ratio per bit.
QPSK (Quadrature Phase Shift Keying):
- In QPSK, four different phases (0, π/2, π, and 3π/2) are used to represent four possible symbols (00, 01, 10, and 11).
- QPSK uses two carrier signals, one in-phase (I) and one quadrature (Q), to transmit symbols.
- The error probability in QPSK is also affected by noise and interference.
- The probability of error can be calculated using the formula: P(error) = 1 - (1 - P(error in BPSK))^2, where P(error in BPSK) is the error probability of BPSK.
Comparison and Conclusion:
- The error probability of QPSK is derived from the error probability of BPSK.
- In QPSK, each symbol represents two bits, so the error probability is squared to calculate the overall error probability.
- Therefore, the error probability of QPSK is the same as BPSK, but it represents twice the amount of information per symbol.
- Option 'C' is correct because the error probability of QPSK is the same as BPSK.
- QPSK offers higher spectral efficiency compared to BPSK as it transmits more bits per symbol.
- However, in terms of error probability, both modulation schemes have the same performance.
Summary:
The error probability of QPSK is the same as BPSK. Although QPSK offers higher spectral efficiency by transmitting more bits per symbol, the error probability is derived from BPSK and remains the same.
Bandwidth of BPSK is ___ than that of BFSK.- a)higher
- b)equal
- c)lower
- d)either lower or higher
Correct answer is option 'C'. Can you explain this answer?
Bandwidth of BPSK is ___ than that of BFSK.
a)
higher
b)
equal
c)
lower
d)
either lower or higher

|
Anshu Kumar answered |
Minimum bandwidth required in BPSK = 2fb.
Minimum bandwidth required in BFSK = 4fb.
Hence, bandwidth of BPSK is lower than that of BFSK.
Minimum bandwidth required in BFSK = 4fb.
Hence, bandwidth of BPSK is lower than that of BFSK.
The amplitude of a random signal is uniformly distributed between –5V and 5V. If the signal to quantization noise ratio required in uniformly quantizing the signal is 43.5dB, the step size of the quantization is approximately-- a)0.0333V
- b)0.05V
- c)0.0667V
- d)0.10V
Correct answer is option 'C'. Can you explain this answer?
The amplitude of a random signal is uniformly distributed between –5V and 5V. If the signal to quantization noise ratio required in uniformly quantizing the signal is 43.5dB, the step size of the quantization is approximately-
a)
0.0333V
b)
0.05V
c)
0.0667V
d)
0.10V

|
Imtiaz Ahmad answered |
Given; Signal to quantization noise = 43.5 dB
The amplitude of a random signal is uniformly distributed between –5V and 5V.
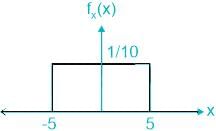
The amplitude of a random signal is uniformly distributed between –5V and 5V.

E[X2] = 52/3 = 25/3
E[XQE2] = δ2/12
SNR = (25/3)/ (δ2/12) = 100/ δ2
SNR (dB) = 10log(SNR)
⇒ 43.5 = 10log(SNR)
⇒ log(SNR) = 43.5/10
⇒ SNR= 104.35
Therefore
100/ δ2 = 104.35
⇒ δ2 = 100/104.35
⇒ δ = 0.0667
signal is sampled at 8 kHz and is quantized using 8 bit uniform quantizer. Assuming SNRq for a sinusoidal signal, the correct statement for PCM signal with a bit rate of R is- a)R = 32 kbps, SNRq = 25.8 dB
- b)R = 64 kbps, SNRq = 49.8 dB
- c)R = 64 kbps, SNRq = 55.8 dB
- d)R = 32 kbps, SNRq = 49.8 dB
Correct answer is option 'B'. Can you explain this answer?
signal is sampled at 8 kHz and is quantized using 8 bit uniform quantizer. Assuming SNRq for a sinusoidal signal, the correct statement for PCM signal with a bit rate of R is
a)
R = 32 kbps, SNRq = 25.8 dB
b)
R = 64 kbps, SNRq = 49.8 dB
c)
R = 64 kbps, SNRq = 55.8 dB
d)
R = 32 kbps, SNRq = 49.8 dB

|
Bhavya Rane answered |
Bit Rate = 8k x 8 = 64 kbps
Four signals g1(t) , g3(t), g2(t) and g4(t) are to be multiplexed and transmitted. g1(t) and g4(t) have a bandwidth of 4 kHz, and the remaining two signals have bandwidth of 8 kHz,. Each sample requires 8 bit for encoding. What is the minimum transmission bit rate of the system.- a)512 kbps
- b)16 kbps
- c)192 kbps
- d)384 kbps
Correct answer is option 'D'. Can you explain this answer?
Four signals g1(t) , g3(t), g2(t) and g4(t) are to be multiplexed and transmitted. g1(t) and g4(t) have a bandwidth of 4 kHz, and the remaining two signals have bandwidth of 8 kHz,. Each sample requires 8 bit for encoding. What is the minimum transmission bit rate of the system.
a)
512 kbps
b)
16 kbps
c)
192 kbps
d)
384 kbps

|
Subhankar Ghoshal answered |
signals g1(t) , g3(t), g2(t) and g4(t) will have 8 k, 8 k, 16 k and 16 k sample/sec at Nyquist rate. Thus 48000 sample/sec bit rate 48000 x 8 =384 kbps
The input to a linear delta modulator having fa step-size Δ = 0.628 is a sine wave with frequency fm and peak amplitude Em. If the sampling frequency fs = 40 kHz, the combination of the sinc-wave frequency and the peak amplitude, where slope overload will take place is- a)Em = 0.3V , fm = 8KHz
- b)Em = 1.5V , fm = 4kHz
- c)Em = 1.5 V , fm = 2kHz
- d)Em = 3.0V , fm = 1kHZ
Correct answer is option 'B'. Can you explain this answer?
The input to a linear delta modulator having fa step-size Δ = 0.628 is a sine wave with frequency fm and peak amplitude Em. If the sampling frequency fs = 40 kHz, the combination of the sinc-wave frequency and the peak amplitude, where slope overload will take place is
a)
Em = 0.3V , fm = 8KHz
b)
Em = 1.5V , fm = 4kHz
c)
Em = 1.5 V , fm = 2kHz
d)
Em = 3.0V , fm = 1kHZ

|
Kiran Gupta answered |
An amplifier has an average standard noise figure of 2.0 dB and an average operating noise figure of 6.5 dB when used with a source of average effective source temperature 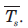 The
The 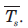 is
is - a)156.32 K
- b)100.81 K
- c)48.93 K
- d)None of the above
Correct answer is option 'D'. Can you explain this answer?
An amplifier has an average standard noise figure of 2.0 dB and an average operating noise figure of 6.5 dB when used with a source of average effective source temperature 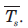 The
The 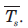 is
is
a)
156.32 K
b)
100.81 K
c)
48.93 K
d)
None of the above

|
Moumita Chopra answered |
An amplifier has three stages for which Te1 = 150 K (first stage), Te3 = 350 K, and Te3 = 600 K (output stage). Available power gain of the first stage is 10 and overall input effective noise temperature is 190 KQue: What is the cascade's operating spot noise figure when used with a source of noise temperature Ts = 50 K- a)1.34 dB
- b)3.96 dB
- c)6.81 dB
- d)None of the above.
Correct answer is option 'C'. Can you explain this answer?
An amplifier has three stages for which Te1 = 150 K (first stage), Te3 = 350 K, and Te3 = 600 K (output stage). Available power gain of the first stage is 10 and overall input effective noise temperature is 190 K
Que: What is the cascade's operating spot noise figure when used with a source of noise temperature Ts = 50 K
a)
1.34 dB
b)
3.96 dB
c)
6.81 dB
d)
None of the above.

|
Nitya Sharma answered |
An amplifier has an operating spot noise figure of 10 dB when driven by a source of effective noise temperature 225 K.Que: If a matched attenuator with a loss of 3.2 dB isplaced between the source and the amplifier's input,what is the operating spot noise figure of the attenuator's amplifier cascade if the attenuator's physicaltemperature is 290 K ?- a)9 dB
- b)10.4 dB
- c)11.3 dB
- d)13.3 dB
Correct answer is option 'D'. Can you explain this answer?
An amplifier has an operating spot noise figure of 10 dB when driven by a source of effective noise temperature 225 K.
Que: If a matched attenuator with a loss of 3.2 dB isplaced between the source and the amplifier's input,what is the operating spot noise figure of the attenuator's amplifier cascade if the attenuator's physicaltemperature is 290 K ?
a)
9 dB
b)
10.4 dB
c)
11.3 dB
d)
13.3 dB

|
Aditya Majumdar answered |
A digital transmission system uses a (7, 4) systematic linear Hamming code for transmitting data over a noisy channel. If three of the message-codeword pairs in this code (mi ; ci), where ci is the codeword corresponding to the ith message mi, are known to be (1 1 0 0 ; 0 1 0 1 1 0 0), (1 1 1 0 ; 0 0 1 1 1 1 0) and (0 1 1 0 ; 1 0 0 0 1 1 0), then which of the following is a valid codeword in this code?- a)1 0 1 1 0 1 0
- b)0 1 1 0 1 0 0
- c)0 0 0 1 0 1 1
- d)1 1 0 1 0 0 1
Correct answer is option 'C'. Can you explain this answer?
A digital transmission system uses a (7, 4) systematic linear Hamming code for transmitting data over a noisy channel. If three of the message-codeword pairs in this code (mi ; ci), where ci is the codeword corresponding to the ith message mi, are known to be (1 1 0 0 ; 0 1 0 1 1 0 0), (1 1 1 0 ; 0 0 1 1 1 1 0) and (0 1 1 0 ; 1 0 0 0 1 1 0), then which of the following is a valid codeword in this code?
a)
1 0 1 1 0 1 0
b)
0 1 1 0 1 0 0
c)
0 0 0 1 0 1 1
d)
1 1 0 1 0 0 1

|
Starcoders answered |
Let d = (d1, d2 …. dk)
Codeword C can be written as:
Codeword C can be written as:
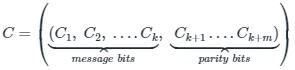
Cd = d1
C2 = d2
C3 = d3
⋮
Ck = dk
Ck = dk
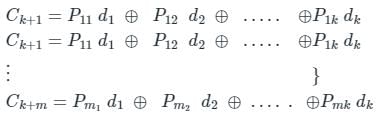
Note: The parity bits are generated by a linear combination of message bits.
Application:
Given (7, 4) linear Hamming code.
(mi, ci) given are:
(1100 ; 0101100)
(1110 ; 0011110)
(0110 ; 1000110)
Clearly, we can observe that the first 3 bits are parity bits and the last 4 bits are message bits.
Clearly, we can observe that the first 3 bits are parity bits and the last 4 bits are message bits.
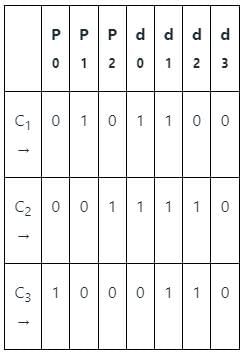
Observe when P0, P1, and P2 are one, and write their combination, i.e.
P0 = d0 ⊕ d1 ⊕ d3
P1 = d1 ⊕ d2 ⊕ d3
P2 = d0 ⊕ d1 ⊕ d2
Now checking each of the options:
Option (1): 1011010
Message bits are:
Message bits are:
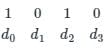
P0 = d0 ⊕ d1 ⊕ d3 = 1
P1 = d1 ⊕ d2 ⊕ d3 = 1
P2 = d0 ⊕ d1 ⊕ d2 = 0
So, the codeword is 1101010.
Hence option (1) is invalid codeword.
Option (2): 0110100
Message bits are:
Message bits are:
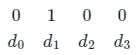
P0 = d0 ⊕ d1 ⊕ d3 = 1
P1 = d1 ⊕ d2 ⊕ d3 = 1
P2 = d0 ⊕ d1 ⊕ d2 = 1
So, the valid codeword is 1110100
Hence option (2) is an invalid codeword.
Option (3): 0001011
Message bits are:
Message bits are:
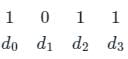
P0 = d0 ⊕ d1 ⊕ d3 = 0
P1 = d1 ⊕ d2 ⊕ d3 = 0
P2 = d0 ⊕ d1 ⊕ d2 = 0
So the valid codeword is 0001011
Hence option (3) is a valid codeword.
Three identical amplifier, each having a spot effective input noise temperature of 125 K and available power G are cascaded. The overall spot effective input noise temperature of the cascade is 155 K. The G is- a)3
- b)5
- c)7
- d)9
Correct answer is option 'B'. Can you explain this answer?
Three identical amplifier, each having a spot effective input noise temperature of 125 K and available power G are cascaded. The overall spot effective input noise temperature of the cascade is 155 K. The G is
a)
3
b)
5
c)
7
d)
9

|
Aditya Patel answered |
What is the hamming distance between the codes '11001011' and ‘10000111'- a)2
- b)3
- c)4
- d)5
Correct answer is option 'B'. Can you explain this answer?
What is the hamming distance between the codes '11001011' and ‘10000111'
a)
2
b)
3
c)
4
d)
5

|
Starcoders answered |
Given code words are: 11001011 and 10000111
Hamming distance can also be calculated by taking XOR of two code words.
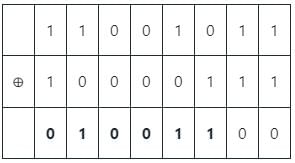
The number of 1’s in XOR result is 3
∴ Minimum Hamming distance is 3 only
Hamming distance can also be calculated by taking XOR of two code words.

The number of 1’s in XOR result is 3
∴ Minimum Hamming distance is 3 only
An amplifier has a standard spot noise figure F0 = 6.31 (8.0 dB). The amplifier, that is used to amplify the output of an antenna have antenna temperature of Ta = 180 KQue: The effective input noise temperature of this amplifier is- a)2520 K
- b)2120 K
- c)2710 K
- d)1540 K
Correct answer is option 'D'. Can you explain this answer?
An amplifier has a standard spot noise figure F0 = 6.31 (8.0 dB). The amplifier, that is used to amplify the output of an antenna have antenna temperature of Ta = 180 K
Que: The effective input noise temperature of this amplifier is
a)
2520 K
b)
2120 K
c)
2710 K
d)
1540 K

|
Moumita Chopra answered |
A signal having a bandwidth of 5 MHz is transmitted using the Pulse code modulation (PCM) scheme as follows. The signal is sampled at a rate of 50% above the Nyquist rate and quantized into 256 levels. The binary pulse rate of the PCM signal in Mbits per second is ___.- a)120
- b)134
- c)340
- d)145
Correct answer is option 'A'. Can you explain this answer?
A signal having a bandwidth of 5 MHz is transmitted using the Pulse code modulation (PCM) scheme as follows. The signal is sampled at a rate of 50% above the Nyquist rate and quantized into 256 levels. The binary pulse rate of the PCM signal in Mbits per second is ___.
a)
120
b)
134
c)
340
d)
145
|
|
Naman Khanna answered |
Given Information:
- Bandwidth of the signal = 5 MHz
- Sampling rate = 50% above the Nyquist rate
- Quantization levels = 256
Calculation:
Step 1: Nyquist Rate Calculation
Nyquist rate is twice the bandwidth of the signal. Hence,
Nyquist rate = 2 x 5 MHz = 10 MHz
Step 2: Sampling Rate Calculation
Sampling rate = 1.5 x Nyquist rate = 1.5 x 10 MHz = 15 MHz
Step 3: Number of bits per sample Calculation
Given that the signal is quantized into 256 levels, we need log2(256) = 8 bits per sample.
Step 4: Binary Pulse Rate Calculation
Binary pulse rate = Sampling rate x Number of bits per sample
Binary pulse rate = 15 MHz x 8 = 120 Mbits per second
Therefore, the binary pulse rate of the PCM signal is 120 Mbits per second. So, the correct answer is option 'A'.
- Bandwidth of the signal = 5 MHz
- Sampling rate = 50% above the Nyquist rate
- Quantization levels = 256
Calculation:
Step 1: Nyquist Rate Calculation
Nyquist rate is twice the bandwidth of the signal. Hence,
Nyquist rate = 2 x 5 MHz = 10 MHz
Step 2: Sampling Rate Calculation
Sampling rate = 1.5 x Nyquist rate = 1.5 x 10 MHz = 15 MHz
Step 3: Number of bits per sample Calculation
Given that the signal is quantized into 256 levels, we need log2(256) = 8 bits per sample.
Step 4: Binary Pulse Rate Calculation
Binary pulse rate = Sampling rate x Number of bits per sample
Binary pulse rate = 15 MHz x 8 = 120 Mbits per second
Therefore, the binary pulse rate of the PCM signal is 120 Mbits per second. So, the correct answer is option 'A'.
A sinusoidal message signal is converted to a PCM signal using a uniform quantizer. The required signal-to-quantization noise ratio (SQNR) at the output of the quantizer is 40 dB. The minimum number of bits per sample needed to achieve the desired SQNR is __________ . - a)7
- b)10
- c)5
- d)3
Correct answer is option 'A'. Can you explain this answer?
A sinusoidal message signal is converted to a PCM signal using a uniform quantizer. The required signal-to-quantization noise ratio (SQNR) at the output of the quantizer is 40 dB. The minimum number of bits per sample needed to achieve the desired SQNR is __________ .
a)
7
b)
10
c)
5
d)
3

|
Starcoders answered |
Concept:
SNR (Signal to Noise Ratio) for a sinusoidal message signal Quantized uniformly with ‘n’ bits in given by; SNRAB = 6n + 1.8
Calculation: Given, SNR = 40 dB, required at the output;
So, 40 ≤ 6n + 1.8
6n ≥ 40 – 1.8
n ≥ 6.366
So, the minimum number of bits per sample needed to achieve the derived SQNR is 7 bits
Consider a linear DM system designed to accommodate analog message signals limited to bandwidth of 3.5 kHz. A sinusoidal test signals of amplitude Amax = 1 V and frequency fm = 800 Hz is applied to system. The sampling rate of the system is 64 kHz.Que: The granular-noise power would be- a)1.68 x 10-3 W
- b)2.86 x 10-4 W
- c)2.48 x 10-3 W
- d)1.12 x 10-4 W
Correct answer is option 'D'. Can you explain this answer?
Consider a linear DM system designed to accommodate analog message signals limited to bandwidth of 3.5 kHz. A sinusoidal test signals of amplitude Amax = 1 V and frequency fm = 800 Hz is applied to system. The sampling rate of the system is 64 kHz.
Que: The granular-noise power would be
a)
1.68 x 10-3 W
b)
2.86 x 10-4 W
c)
2.48 x 10-3 W
d)
1.12 x 10-4 W

|
Nidhi Tiwari answered |
Consider binary data transmission at a rate of 56 kbps using baseband binary pulse amplitude modulation (PAM) that is designed to have a raised-cosine spectrum. The transmission bandwidth (in kHz) required for a roll-off factor of 0.25 is ________∙Correct answer is '35'. Can you explain this answer?
Consider binary data transmission at a rate of 56 kbps using baseband binary pulse amplitude modulation (PAM) that is designed to have a raised-cosine spectrum. The transmission bandwidth (in kHz) required for a roll-off factor of 0.25 is ________∙
|
|
Khushi Jain answered |
Bandwidth Calculation for Raised-Cosine Spectrum
- The formula to calculate the required bandwidth for a raised-cosine spectrum is given by:
Bandwidth = (1 + α) * Bit Rate
where α is the roll-off factor and Bit Rate is the data transmission rate.
- Given that the data transmission rate is 56 kbps and the roll-off factor is 0.25, we can substitute these values into the formula to find the required bandwidth:
Bandwidth = (1 + 0.25) * 56 kHz
= 1.25 * 56 kHz
= 70 kHz
Answer: 35 kHz
- Therefore, the transmission bandwidth required for a roll-off factor of 0.25 in this scenario is 35 kHz.
- The formula to calculate the required bandwidth for a raised-cosine spectrum is given by:
Bandwidth = (1 + α) * Bit Rate
where α is the roll-off factor and Bit Rate is the data transmission rate.
- Given that the data transmission rate is 56 kbps and the roll-off factor is 0.25, we can substitute these values into the formula to find the required bandwidth:
Bandwidth = (1 + 0.25) * 56 kHz
= 1.25 * 56 kHz
= 70 kHz
Answer: 35 kHz
- Therefore, the transmission bandwidth required for a roll-off factor of 0.25 in this scenario is 35 kHz.
A speech signal is sampled at 8 kHz and encoded into PCM format using 8 bits/sample. The PCM data is transmitted through a baseband channel via 4-level PAM. The minimum bandwidth (in kHz) required for transmission is ________Correct answer is between '15.9,16.1'. Can you explain this answer?
A speech signal is sampled at 8 kHz and encoded into PCM format using 8 bits/sample. The PCM data is transmitted through a baseband channel via 4-level PAM. The minimum bandwidth (in kHz) required for transmission is ________

|
Starcoders answered |
Baseband communication is given.
Minimum Bandwidth will be required if transmission of data takes place using sinc pulses and the bandwidth is given by:
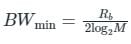
Where Rb = n fs
n = number of bits used to represent samples
fs = sampling rate.
Calculation:
In the Question, it is asked about minimum Bandwidth. ∴ we will consider that the transmission of data is taking place through sinc pulses.
Given fs = 8 kHz
n = 8 bits/sample
M = 4
Rb = nfs
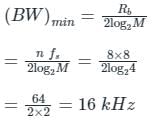
Minimum Bandwidth will be required if transmission of data takes place using sinc pulses and the bandwidth is given by:
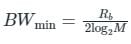
Where Rb = n fs
n = number of bits used to represent samples
fs = sampling rate.
Calculation:
In the Question, it is asked about minimum Bandwidth. ∴ we will consider that the transmission of data is taking place through sinc pulses.
Given fs = 8 kHz
n = 8 bits/sample
M = 4
Rb = nfs
If Eb, the energy per bit of a binary digital signal, is 10-5 Ws (Watt-Second) and the one-sided power spectral density of the white noise, N0 = 10-6 W/Hz, then the output SNR of the matched filter is- a)26 dB
- b)10 dB
- c)20 dB
- d)13 dB
Correct answer is option 'D'. Can you explain this answer?
If Eb, the energy per bit of a binary digital signal, is 10-5 Ws (Watt-Second) and the one-sided power spectral density of the white noise, N0 = 10-6 W/Hz, then the output SNR of the matched filter is
a)
26 dB
b)
10 dB
c)
20 dB
d)
13 dB

|
Starcoders answered |
The output SNR is given by:
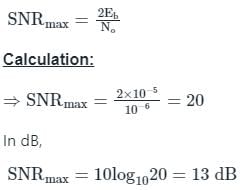
In a matched filter the filter response is shaped according to the input signal waveform.
The peak amplitude of the output of the filter is proportional to the input signal energy, hence the probability of error depends on the signal energy.
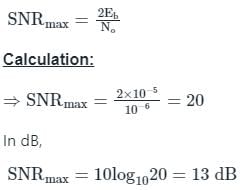
In a matched filter the filter response is shaped according to the input signal waveform.
The peak amplitude of the output of the filter is proportional to the input signal energy, hence the probability of error depends on the signal energy.
The bit rate of a digital communication system is R Kbits/sec. The modulation used is 32-QAM. The minimum band width for intersymbol interference free transmission is –- a)(R/10)Hz
- b)(R/10)KHz
- c)(R/5)Hz
- d)(R/5)KHz
Correct answer is option 'D'. Can you explain this answer?
The bit rate of a digital communication system is R Kbits/sec. The modulation used is 32-QAM. The minimum band width for intersymbol interference free transmission is –
a)
(R/10)Hz
b)
(R/10)KHz
c)
(R/5)Hz
d)
(R/5)KHz
|
|
Tanay Singh answered |
To determine the minimum bandwidth for intersymbol interference (ISI)-free transmission, we need to consider the modulation scheme used and the bit rate of the digital communication system.
In 32-QAM modulation, each symbol represents 5 bits (log2(32) = 5). Therefore, the symbol rate (Rs) can be calculated by dividing the bit rate (R) by the number of bits per symbol:
Rs = R / log2(M)
Where M is the number of symbols in the modulation scheme.
For 32-QAM, M = 32, so the symbol rate is given by:
Rs = R / log2(32) = R / 5
To avoid ISI, the Nyquist criterion states that the bandwidth (B) should be equal to or greater than the symbol rate (Rs). Therefore, the minimum bandwidth for ISI-free transmission is:
B = Rs = R / 5
So, the minimum bandwidth required for ISI-free transmission in this digital communication system is R/5 Kbits/sec.
In 32-QAM modulation, each symbol represents 5 bits (log2(32) = 5). Therefore, the symbol rate (Rs) can be calculated by dividing the bit rate (R) by the number of bits per symbol:
Rs = R / log2(M)
Where M is the number of symbols in the modulation scheme.
For 32-QAM, M = 32, so the symbol rate is given by:
Rs = R / log2(32) = R / 5
To avoid ISI, the Nyquist criterion states that the bandwidth (B) should be equal to or greater than the symbol rate (Rs). Therefore, the minimum bandwidth for ISI-free transmission is:
B = Rs = R / 5
So, the minimum bandwidth required for ISI-free transmission in this digital communication system is R/5 Kbits/sec.
An amplifier has three stages for which Te1 = 200 K (first stage), Te2 = 450 K, and Te3 = 1000K (last stage). If the available power gain of the second stage is 5, what gain must the first stage have to guarantee an effective input noise temperature of 250 K ?- a)10
- b)13
- c)16
- d)19
Correct answer is option 'B'. Can you explain this answer?
An amplifier has three stages for which Te1 = 200 K (first stage), Te2 = 450 K, and Te3 = 1000K (last stage). If the available power gain of the second stage is 5, what gain must the first stage have to guarantee an effective input noise temperature of 250 K ?
a)
10
b)
13
c)
16
d)
19

|
Subhankar Ghoshal answered |
The representation of 4 bit code 1101 into 7 bit, even parity Hamming code is- a)(1010101)
- b)(1111001)
- c)(1011101)
- d)(1110000)
Correct answer is option 'A'. Can you explain this answer?
The representation of 4 bit code 1101 into 7 bit, even parity Hamming code is
a)
(1010101)
b)
(1111001)
c)
(1011101)
d)
(1110000)

|
Starcoders answered |
To represent the 4-bit code 1101 into a 7-bit, even parity Hamming code, we first need to add 3 parity bits to the 4 data bits. The parity bits are chosen so that the total number of 1's in each group of bits (including the parity bit) is even.
Hamming Code:

Given data 1101
i.e. d1 = 1, d2 = 1, d3 = 0, d4 = 1
We can write:
P1 = d1 ⊕ d2 ⊕ d4 = 1 ⊕ 1 ⊕ 1 = 1
P2 = d1 ⊕ d4 ⊕ d3 = 1 ⊕ 1 ⊕ 0 = 0
P3 = d2 ⊕ d4 ⊕ d3 = 1 ⊕ 1 ⊕ 0 = 0
Then transmitted final code is P1 P2 d1 P4 d2 d3 d4 which is 1010101
Hamming Code:

Given data 1101
i.e. d1 = 1, d2 = 1, d3 = 0, d4 = 1
We can write:
P1 = d1 ⊕ d2 ⊕ d4 = 1 ⊕ 1 ⊕ 1 = 1
P2 = d1 ⊕ d4 ⊕ d3 = 1 ⊕ 1 ⊕ 0 = 0
P3 = d2 ⊕ d4 ⊕ d3 = 1 ⊕ 1 ⊕ 0 = 0
Then transmitted final code is P1 P2 d1 P4 d2 d3 d4 which is 1010101
Which of the following statements about the matched filter in a communication receiver are correct ?
(A) It may produce phase error if synchronization is improper
(B) Its impulse response depends on the singal shape
(C) The characteristics of the matched filter is matched with the transmitted data
(D) It produces inter symbol interference
(E) It measures the correlation between incoming received message and its impulse response
Choose the correct answer from the options given below : - a)(B), (C), (E) only
- b)(A), (B), (C) only
- c)(C), (D), (E) only
- d)(A), (D), (E) only
Correct answer is option 'A'. Can you explain this answer?
Which of the following statements about the matched filter in a communication receiver are correct ?
(A) It may produce phase error if synchronization is improper
(B) Its impulse response depends on the singal shape
(C) The characteristics of the matched filter is matched with the transmitted data
(D) It produces inter symbol interference
(E) It measures the correlation between incoming received message and its impulse response
Choose the correct answer from the options given below :
(A) It may produce phase error if synchronization is improper
(B) Its impulse response depends on the singal shape
(C) The characteristics of the matched filter is matched with the transmitted data
(D) It produces inter symbol interference
(E) It measures the correlation between incoming received message and its impulse response
Choose the correct answer from the options given below :
a)
(B), (C), (E) only
b)
(A), (B), (C) only
c)
(C), (D), (E) only
d)
(A), (D), (E) only
|
|
Utkarsh Patel answered |
Matched Filter in a Communication Receiver
Matched filter is an important component in a communication receiver that plays a crucial role in detecting the transmitted signal. Below are the correct statements about the matched filter:
Impulse Response and Signal Shape
- The impulse response of a matched filter depends on the shape of the signal being transmitted. It is designed to maximize the signal-to-noise ratio by aligning with the shape of the transmitted signal.
Characteristics of Matched Filter
- The characteristics of the matched filter are specifically matched with the transmitted data to achieve optimal performance. This ensures that the filter can detect the signal accurately in the presence of noise.
Measuring Correlation
- The matched filter measures the correlation between the incoming received message and its impulse response. By calculating this correlation, the filter can determine the presence of the transmitted signal in the received data.
Therefore, the correct statements about the matched filter in a communication receiver are that its impulse response depends on the signal shape, its characteristics are matched with the transmitted data, and it measures the correlation between the incoming received message and its impulse response.
Matched filter is an important component in a communication receiver that plays a crucial role in detecting the transmitted signal. Below are the correct statements about the matched filter:
Impulse Response and Signal Shape
- The impulse response of a matched filter depends on the shape of the signal being transmitted. It is designed to maximize the signal-to-noise ratio by aligning with the shape of the transmitted signal.
Characteristics of Matched Filter
- The characteristics of the matched filter are specifically matched with the transmitted data to achieve optimal performance. This ensures that the filter can detect the signal accurately in the presence of noise.
Measuring Correlation
- The matched filter measures the correlation between the incoming received message and its impulse response. By calculating this correlation, the filter can determine the presence of the transmitted signal in the received data.
Therefore, the correct statements about the matched filter in a communication receiver are that its impulse response depends on the signal shape, its characteristics are matched with the transmitted data, and it measures the correlation between the incoming received message and its impulse response.
Four messages are band limited to W, W, 2W & 3W are to be multiplexed using TDM. The minimum B.W required for transmission is- a)W
- b)3W
- c)6W
- d)7W
Correct answer is option 'D'. Can you explain this answer?
Four messages are band limited to W, W, 2W & 3W are to be multiplexed using TDM. The minimum B.W required for transmission is
a)
W
b)
3W
c)
6W
d)
7W

|
Starcoders answered |
During sampling:
We sample at 2W. With this rate signal of bandwidth, W gets sampled properly.
The signal of bandwidth 2W is sampled properly by being fed twice in the commutator switch.
And signal with bandwidth 3W is fed thrice into the commutator switch in order to get sampled at an effective rate of 6W. So, the total bit rate is Rb = 14W
Now, the minimum bandwidth required is: Rb/2 = 7W.
We sample at 2W. With this rate signal of bandwidth, W gets sampled properly.
The signal of bandwidth 2W is sampled properly by being fed twice in the commutator switch.
And signal with bandwidth 3W is fed thrice into the commutator switch in order to get sampled at an effective rate of 6W. So, the total bit rate is Rb = 14W
Now, the minimum bandwidth required is: Rb/2 = 7W.
An amplifier has three stages for which Te1 = 150 K (first stage), Te3 = 350 K, and Te3 = 600 K (output stage). Available power gain of the first stage is 10 and overall input effective noise temperature is 190 KQue: The cascade's standard spot noise figure is- a)1.3 dB
- b)2.2 dB
- c)4.3 dB
- d)5.3 dB
Correct answer is option 'B'. Can you explain this answer?
An amplifier has three stages for which Te1 = 150 K (first stage), Te3 = 350 K, and Te3 = 600 K (output stage). Available power gain of the first stage is 10 and overall input effective noise temperature is 190 K
Que: The cascade's standard spot noise figure is
a)
1.3 dB
b)
2.2 dB
c)
4.3 dB
d)
5.3 dB

|
Manisha Chavan answered |
Consider a binary channel code in which each code word has a fixed length of 5 bits. The Hamming distance between any pair of distinct code words in this code is at least 2. The maximum number of code words such a code can contain is ________.Correct answer is '16'. Can you explain this answer?
Consider a binary channel code in which each code word has a fixed length of 5 bits. The Hamming distance between any pair of distinct code words in this code is at least 2. The maximum number of code words such a code can contain is ________.

|
Imtiaz Ahmad answered |
Concept: Hamming distance gives minimum positions at which the corresponding symbols are different.
Calculation: Fixed length code n = 5
Minimum harming distance d min = 2
Hamming distance gives minimum positions at which the corresponding symbols are different.
The table shows all possible codewords having a minimum hamming distance of 2.
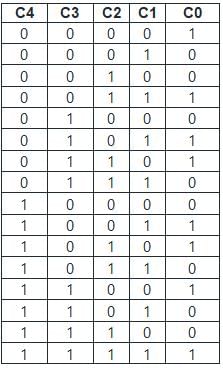
Hence there are 16 such codes where minimum Hamming distance 2 is possible.
Calculation: Fixed length code n = 5
Minimum harming distance d min = 2
Hamming distance gives minimum positions at which the corresponding symbols are different.
The table shows all possible codewords having a minimum hamming distance of 2.

Hence there are 16 such codes where minimum Hamming distance 2 is possible.
The output signal-to-quantization-noise ratio of a 10-bit PCM was found to be 30 dB. The desired SNR is 42 dB. It can be increased by increasing the number of quantization level.In this way the fractional increase in the transmission bandwidth would be (assume log210 = 0.3)- a)20%
- b)30%
- c)40%
- d)50%
Correct answer is option 'A'. Can you explain this answer?
The output signal-to-quantization-noise ratio of a 10-bit PCM was found to be 30 dB. The desired SNR is 42 dB. It can be increased by increasing the number of quantization level.In this way the fractional increase in the transmission bandwidth would be (assume log210 = 0.3)
a)
20%
b)
30%
c)
40%
d)
50%

|
Varun Banerjee answered |
= log C
+ 20 nlog2 =
α + 6 ndB. This equation shows that increasing n by one bits increase the by 6 dB.
Hence an increase in the SNR by 12 dB can be accomplished by increasing 9is form 10 to 12, the transmission bandwidth would be increased by 20%
Hence an increase in the SNR by 12 dB can be accomplished by increasing 9is form 10 to 12, the transmission bandwidth would be increased by 20%
Three analog signals, having bandwidths 1200 Hz, 600 Hz and 600 Hz, are sampled at their respective Nyquist rates, encoded with 12 bit words, and time division multiplexed. The bit rate for the multiplexed signal is- a)115.2 kbps
- b)28.8 kbps
- c)57.6 kbps
- d)38.4 kbps
Correct answer is option 'C'. Can you explain this answer?
Three analog signals, having bandwidths 1200 Hz, 600 Hz and 600 Hz, are sampled at their respective Nyquist rates, encoded with 12 bit words, and time division multiplexed. The bit rate for the multiplexed signal is
a)
115.2 kbps
b)
28.8 kbps
c)
57.6 kbps
d)
38.4 kbps

|
Pranavi Gupta answered |
Analog signals, having bandwidth 1200 Hz, 600 Hz and 600 Hz have 2400, 1200 samples/sec at Nyquist rate. Hence 48000 sample/sec
bit rate = 48000 sample/sec x 12 = 57.6 kbps
Comparison of MSKand QPSK scheme shows that- a)MSK requires less power
- b)QPSK requires less power
- c)filtering is simple in MSK
- d)there is no comparison between them
Correct answer is option 'A'. Can you explain this answer?
Comparison of MSKand QPSK scheme shows that
a)
MSK requires less power
b)
QPSK requires less power
c)
filtering is simple in MSK
d)
there is no comparison between them

|
Nitya Sharma answered |
More energy (or power) is contained in the main lobe of MSK (about 99% of the total energy or power) as compared to the QPSK (about 90% of the total energy or power).
The evolution of cell phone standards are from 1 G to 5 G, what this G indicates?- a)Gross
- b)Generation
- c)General
- d)Gap
Correct answer is option 'B'. Can you explain this answer?
The evolution of cell phone standards are from 1 G to 5 G, what this G indicates?
a)
Gross
b)
Generation
c)
General
d)
Gap
|
|
Bhumi Patel answered |
The meaning of 'G' in cell phone standards
The 'G' in cell phone standards stands for 'Generation'. It is used to denote the different generations of cellular network technology that have been developed over the years. Each generation represents a significant advancement in terms of speed, capacity, and functionality.
Evolution of cell phone standards from 1G to 5G
1. 1G (First Generation):
- 1G refers to the first generation of analog cellular network technology that was introduced in the 1980s.
- It provided basic voice calling capabilities and had limited coverage.
- The key technology used in 1G was Advanced Mobile Phone System (AMPS).
2. 2G (Second Generation):
- 2G refers to the second generation of cellular network technology and was introduced in the early 1990s.
- It brought digital technology into play and enabled not only voice calling but also text messaging (SMS).
- The key standards used in 2G were Global System for Mobile Communications (GSM) and Code Division Multiple Access (CDMA).
3. 3G (Third Generation):
- 3G represents the third generation of cellular network technology and was introduced in the early 2000s.
- It marked a significant leap in terms of data transfer speed, enabling the use of mobile internet and video calling.
- The key standards used in 3G were Universal Mobile Telecommunications System (UMTS) and CDMA2000.
4. 4G (Fourth Generation):
- 4G denotes the fourth generation of cellular network technology and was introduced in the late 2000s.
- It provided faster data speeds, lower latency, and improved capacity compared to 3G.
- The key standards used in 4G were Long Term Evolution (LTE) and WiMAX.
5. 5G (Fifth Generation):
- 5G represents the fifth generation of cellular network technology and is being rolled out in the 2020s.
- It offers significantly faster data speeds, ultra-low latency, and massive device connectivity.
- The key technologies used in 5G include millimeter wave (mmWave) frequencies, massive MIMO (Multiple-Input Multiple-Output), and network slicing.
Conclusion
The 'G' in cell phone standards stands for 'Generation'. It indicates the different generations of cellular network technology, with each generation representing a major advancement in terms of speed, capacity, and functionality. The evolution of cell phone standards has progressed from 1G to 5G, with each generation introducing new technologies and capabilities.
The 'G' in cell phone standards stands for 'Generation'. It is used to denote the different generations of cellular network technology that have been developed over the years. Each generation represents a significant advancement in terms of speed, capacity, and functionality.
Evolution of cell phone standards from 1G to 5G
1. 1G (First Generation):
- 1G refers to the first generation of analog cellular network technology that was introduced in the 1980s.
- It provided basic voice calling capabilities and had limited coverage.
- The key technology used in 1G was Advanced Mobile Phone System (AMPS).
2. 2G (Second Generation):
- 2G refers to the second generation of cellular network technology and was introduced in the early 1990s.
- It brought digital technology into play and enabled not only voice calling but also text messaging (SMS).
- The key standards used in 2G were Global System for Mobile Communications (GSM) and Code Division Multiple Access (CDMA).
3. 3G (Third Generation):
- 3G represents the third generation of cellular network technology and was introduced in the early 2000s.
- It marked a significant leap in terms of data transfer speed, enabling the use of mobile internet and video calling.
- The key standards used in 3G were Universal Mobile Telecommunications System (UMTS) and CDMA2000.
4. 4G (Fourth Generation):
- 4G denotes the fourth generation of cellular network technology and was introduced in the late 2000s.
- It provided faster data speeds, lower latency, and improved capacity compared to 3G.
- The key standards used in 4G were Long Term Evolution (LTE) and WiMAX.
5. 5G (Fifth Generation):
- 5G represents the fifth generation of cellular network technology and is being rolled out in the 2020s.
- It offers significantly faster data speeds, ultra-low latency, and massive device connectivity.
- The key technologies used in 5G include millimeter wave (mmWave) frequencies, massive MIMO (Multiple-Input Multiple-Output), and network slicing.
Conclusion
The 'G' in cell phone standards stands for 'Generation'. It indicates the different generations of cellular network technology, with each generation representing a major advancement in terms of speed, capacity, and functionality. The evolution of cell phone standards has progressed from 1G to 5G, with each generation introducing new technologies and capabilities.
An amplifier has three stages for which Te1 = 150 K (first stage), Te3 = 350 K, and Te3 = 600 K (output stage). Available power gain of the first stage is 10 and overall input effective noise temperature is 190 KQue: The available power gain of the second stage is- a)12
- b)14
- c)16
- d)18
Correct answer is option 'A'. Can you explain this answer?
An amplifier has three stages for which Te1 = 150 K (first stage), Te3 = 350 K, and Te3 = 600 K (output stage). Available power gain of the first stage is 10 and overall input effective noise temperature is 190 K
Que: The available power gain of the second stage is
a)
12
b)
14
c)
16
d)
18

|
Ananya Saha answered |
Assertion (A): Binary phase shift keying (BPSK) is the most efficient of the three digital modulation, i.e., ASK, FSK and PSK.
Reason (R): In BPSK, phase of sinusoidal carrier is changed according to the data bit to be transmitted.- a)Both A and R are true and R is the correct explanation of A.
- b)Both A and R are true but R is not the correct explanation of A.
- c)A is true but R is false.
- d)A is false but R is true.
Correct answer is option 'B'. Can you explain this answer?
Assertion (A): Binary phase shift keying (BPSK) is the most efficient of the three digital modulation, i.e., ASK, FSK and PSK.
Reason (R): In BPSK, phase of sinusoidal carrier is changed according to the data bit to be transmitted.
Reason (R): In BPSK, phase of sinusoidal carrier is changed according to the data bit to be transmitted.
a)
Both A and R are true and R is the correct explanation of A.
b)
Both A and R are true but R is not the correct explanation of A.
c)
A is true but R is false.
d)
A is false but R is true.
|
|
Saanvi Joshi answered |
Answer:
Binary Phase Shift Keying (BPSK) is a digital modulation technique that uses two different phases of a sinusoidal carrier wave to represent binary information (0 and 1). The phase of the carrier wave is changed according to the data bit to be transmitted, resulting in a phase shift of either 0 degrees or 180 degrees.
Assertion (A): Binary phase shift keying (BPSK) is the most efficient of the three digital modulation techniques, i.e., ASK, FSK, and PSK.
Reason (R): In BPSK, the phase of the sinusoidal carrier is changed according to the data bit to be transmitted.
Explanation:
Efficiency of Digital Modulation Techniques:
The efficiency of a digital modulation technique refers to its ability to transmit the maximum amount of information (bits) per unit bandwidth or power. In other words, it measures how well a modulation scheme utilizes the available resources.
Types of Digital Modulation:
1. Amplitude Shift Keying (ASK): In ASK, the amplitude of the carrier wave is changed according to the data bit to be transmitted.
2. Frequency Shift Keying (FSK): In FSK, the frequency of the carrier wave is changed according to the data bit to be transmitted.
3. Phase Shift Keying (PSK): In PSK, the phase of the carrier wave is changed according to the data bit to be transmitted.
Comparison of BPSK with ASK and FSK:
1. BPSK vs ASK: BPSK is more efficient than ASK because it uses the phase of the carrier wave to represent binary information, which allows for a higher data rate and better spectral efficiency. ASK, on the other hand, uses the amplitude of the carrier wave, which is more susceptible to noise and interference.
2. BPSK vs FSK: BPSK is also more efficient than FSK because it uses the phase of the carrier wave, which allows for a higher data rate and better spectral efficiency. FSK, on the other hand, uses the frequency of the carrier wave, which requires a larger bandwidth to transmit the same amount of information.
Explanation of Assertion (A):
Binary Phase Shift Keying (BPSK) is indeed the most efficient of the three digital modulation techniques (ASK, FSK, and PSK). This is because BPSK uses the phase of the carrier wave to represent binary information, which allows for a higher data rate and better spectral efficiency compared to ASK and FSK.
Explanation of Reason (R):
The reason given for the assertion is correct. In BPSK, the phase of the sinusoidal carrier wave is changed according to the data bit to be transmitted. This means that a phase shift of either 0 degrees or 180 degrees is applied to the carrier wave, depending on whether the data bit is 0 or 1. By changing the phase of the carrier wave, BPSK is able to represent binary information.
Conclusion:
Both the assertion and the reason are true, and the reason is the correct explanation of the assertion. Therefore, the correct answer is option 'B' - Both A and R are true, but R is not the correct explanation of A.
Binary Phase Shift Keying (BPSK) is a digital modulation technique that uses two different phases of a sinusoidal carrier wave to represent binary information (0 and 1). The phase of the carrier wave is changed according to the data bit to be transmitted, resulting in a phase shift of either 0 degrees or 180 degrees.
Assertion (A): Binary phase shift keying (BPSK) is the most efficient of the three digital modulation techniques, i.e., ASK, FSK, and PSK.
Reason (R): In BPSK, the phase of the sinusoidal carrier is changed according to the data bit to be transmitted.
Explanation:
Efficiency of Digital Modulation Techniques:
The efficiency of a digital modulation technique refers to its ability to transmit the maximum amount of information (bits) per unit bandwidth or power. In other words, it measures how well a modulation scheme utilizes the available resources.
Types of Digital Modulation:
1. Amplitude Shift Keying (ASK): In ASK, the amplitude of the carrier wave is changed according to the data bit to be transmitted.
2. Frequency Shift Keying (FSK): In FSK, the frequency of the carrier wave is changed according to the data bit to be transmitted.
3. Phase Shift Keying (PSK): In PSK, the phase of the carrier wave is changed according to the data bit to be transmitted.
Comparison of BPSK with ASK and FSK:
1. BPSK vs ASK: BPSK is more efficient than ASK because it uses the phase of the carrier wave to represent binary information, which allows for a higher data rate and better spectral efficiency. ASK, on the other hand, uses the amplitude of the carrier wave, which is more susceptible to noise and interference.
2. BPSK vs FSK: BPSK is also more efficient than FSK because it uses the phase of the carrier wave, which allows for a higher data rate and better spectral efficiency. FSK, on the other hand, uses the frequency of the carrier wave, which requires a larger bandwidth to transmit the same amount of information.
Explanation of Assertion (A):
Binary Phase Shift Keying (BPSK) is indeed the most efficient of the three digital modulation techniques (ASK, FSK, and PSK). This is because BPSK uses the phase of the carrier wave to represent binary information, which allows for a higher data rate and better spectral efficiency compared to ASK and FSK.
Explanation of Reason (R):
The reason given for the assertion is correct. In BPSK, the phase of the sinusoidal carrier wave is changed according to the data bit to be transmitted. This means that a phase shift of either 0 degrees or 180 degrees is applied to the carrier wave, depending on whether the data bit is 0 or 1. By changing the phase of the carrier wave, BPSK is able to represent binary information.
Conclusion:
Both the assertion and the reason are true, and the reason is the correct explanation of the assertion. Therefore, the correct answer is option 'B' - Both A and R are true, but R is not the correct explanation of A.
Consider the following statements;
1. BPSK has a bandwidth which is lower than that of a BFSK signal.
2. BPSK yields the maximum value of probability of error compared to ail the three digital modulation techniques i.e. ASK, FSK and PSK.
3. Binary FSK has the highest system complexity.
4. Binary ASK is demodulated using coherent detection while binary FSK and PSK are demodulated using envelope detectionWhich of the statements given above are correct?- a)1 and 3
- b)1,2 and 4
- c)2 and 3
- d)2, 3 and 4
Correct answer is option 'A'. Can you explain this answer?
Consider the following statements;
1. BPSK has a bandwidth which is lower than that of a BFSK signal.
2. BPSK yields the maximum value of probability of error compared to ail the three digital modulation techniques i.e. ASK, FSK and PSK.
3. Binary FSK has the highest system complexity.
4. Binary ASK is demodulated using coherent detection while binary FSK and PSK are demodulated using envelope detection
1. BPSK has a bandwidth which is lower than that of a BFSK signal.
2. BPSK yields the maximum value of probability of error compared to ail the three digital modulation techniques i.e. ASK, FSK and PSK.
3. Binary FSK has the highest system complexity.
4. Binary ASK is demodulated using coherent detection while binary FSK and PSK are demodulated using envelope detection
Which of the statements given above are correct?
a)
1 and 3
b)
1,2 and 4
c)
2 and 3
d)
2, 3 and 4

|
Diya Chopra answered |
- Statement-1 is correct.
- BPSK has the best performance of all the three digital modulation techniques in presence of noise, it yields the minimum value of probability of error compared to ASK, FSK and PSK. Hence, statement-2 is false.
- Statement-3 is correct since binary FSK has highest system complexity while binary ASK has least system complexity.
- Binary ASK is demodulated using envelope detection while binary FSK and PSK are demodulated using coherent detection.
Hence, statement-4 is fals
The final code after encoding data bits 1101 into 7-bit even parity Hamming Code is- a)1110101
- b)1011101
- c)1010101
- d)0110101
Correct answer is option 'C'. Can you explain this answer?
The final code after encoding data bits 1101 into 7-bit even parity Hamming Code is
a)
1110101
b)
1011101
c)
1010101
d)
0110101

|
Imtiaz Ahmad answered |
Hamming (7, 4) code: It is a linear error-correcting code that encodes four bits of data into seven bits, by adding three parity bits.
Example: It is used in the Bell-Telephone laboratory, error-prone punch caret reader to detect the error and correct them.
Hamming code:

P1 = d1 ⊕ d2 ⊕ d4
P2 = d1 ⊕ d4 ⊕ d3
P3 = d2 ⊕ d4 ⊕ d3
Example: It is used in the Bell-Telephone laboratory, error-prone punch caret reader to detect the error and correct them.
Hamming code:

P1 = d1 ⊕ d2 ⊕ d4
P2 = d1 ⊕ d4 ⊕ d3
P3 = d2 ⊕ d4 ⊕ d3
Given data 1101 i.e.
d1 = 1, d2 = 1, d3 = 0, d4 = 1
We can write:
P1 = d1 ⊕ d2 ⊕ d4 = 1 ⊕ 1 ⊕ 1 = 1
P2 = d1 ⊕ d4 ⊕ d3 = 1 ⊕ 1 ⊕ 0 = 0
P3 = d2 ⊕ d4 ⊕ d3 = 1 ⊕ 1 ⊕ 0 = 0
Then transmitted final code is
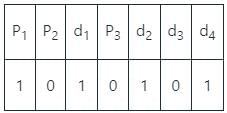
i.e. 1010101
Option 3 correct.
d1 = 1, d2 = 1, d3 = 0, d4 = 1
We can write:
P1 = d1 ⊕ d2 ⊕ d4 = 1 ⊕ 1 ⊕ 1 = 1
P2 = d1 ⊕ d4 ⊕ d3 = 1 ⊕ 1 ⊕ 0 = 0
P3 = d2 ⊕ d4 ⊕ d3 = 1 ⊕ 1 ⊕ 0 = 0
Then transmitted final code is

i.e. 1010101
Option 3 correct.
Data rate of 12 kbps is to be transmitted over a channel of bandwidth 8 kHz by using Nyquist criterion pulses. The value of the roll-off factor ‘ α’ that can be used is ______. (Correct up to 2 decimal places)Correct answer is between '0.32,0.34'. Can you explain this answer?
Data rate of 12 kbps is to be transmitted over a channel of bandwidth 8 kHz by using Nyquist criterion pulses. The value of the roll-off factor ‘ α’ that can be used is ______. (Correct up to 2 decimal places)

|
Starcoders answered |
The transmission bandwidth for Nyquist criteria (raised cosine pulse) with roll-off factor α is given by:


A linear delta modulator is designed to operate on speech signals limited to 3.4 kHz. The sampling rate is 10 time the Nyquist rate of the speech signal. The step size δ is 100 mV. The modulator is tested with a this test signal required to avoid slope overload is- a)2.04 V
- b)1.08 V
- c)4.08 V
- d)2.16 V
Correct answer is option 'B'. Can you explain this answer?
A linear delta modulator is designed to operate on speech signals limited to 3.4 kHz. The sampling rate is 10 time the Nyquist rate of the speech signal. The step size δ is 100 mV. The modulator is tested with a this test signal required to avoid slope overload is
a)
2.04 V
b)
1.08 V
c)
4.08 V
d)
2.16 V

|
Rounak Choudhary answered |
Consider a linear DM system designed to accommodate analog message signals limited to bandwidth of 3.5 kHz. A sinusoidal test signals of amplitude Amax = 1 V and frequency fm = 800 Hz is applied to system. The sampling rate of the system is 64 kHz.
Que: The minimum value of the step size to avoid overload is
- a)240 mV
- b)120 mV
- c)670 mV
- d)78.5 mV
Correct answer is option 'D'. Can you explain this answer?
Consider a linear DM system designed to accommodate analog message signals limited to bandwidth of 3.5 kHz. A sinusoidal test signals of amplitude Amax = 1 V and frequency fm = 800 Hz is applied to system. The sampling rate of the system is 64 kHz.
Que: The minimum value of the step size to avoid overload is
a)
240 mV
b)
120 mV
c)
670 mV
d)
78.5 mV
|
|
Omkar Rao answered |
Given information:
- Bandwidth of the analog message signals: 3.5 kHz
- Amplitude of the sinusoidal test signal (Amax): 1 V
- Frequency of the sinusoidal test signal (fm): 800 Hz
- Sampling rate of the system: 64 kHz
Explanation:
The minimum value of the step size is determined by the Nyquist criterion, which states that the sampling rate should be at least twice the bandwidth of the signal to avoid aliasing.
Step 1: Calculate the maximum frequency component of the analog message signal:
The maximum frequency component of the analog message signal can be calculated using the formula:
Maximum frequency component (fmax) = fm + bandwidth/2
Given: fm = 800 Hz, bandwidth = 3.5 kHz
Substituting the values, we get:
fmax = 800 Hz + 3.5 kHz/2
= 800 Hz + 1.75 kHz
= 2550 Hz
Step 2: Calculate the minimum sampling rate:
According to the Nyquist criterion, the minimum sampling rate should be at least twice the maximum frequency component of the analog message signal. Therefore,
Minimum sampling rate = 2 * fmax
Substituting the value of fmax, we get:
Minimum sampling rate = 2 * 2550 Hz
= 5100 Hz
Step 3: Calculate the maximum step size:
The maximum step size is determined by the quantization range of the analog-to-digital converter (ADC). In this case, the maximum amplitude of the sinusoidal test signal is given as Amax = 1 V.
The maximum step size (Δ) can be calculated using the formula:
Δ = (2 * Amax) / (2^N)
Where N is the number of bits used by the ADC.
Step 4: Calculate the number of bits required:
To determine the number of bits required, we need to calculate the quantization levels using the formula:
Quantization levels (L) = 2^N
The number of quantization levels is determined by the quantization range, which is given by:
Quantization range = 2 * Amax
Substituting the value of Amax, we get:
Quantization range = 2 * 1 V
= 2 V
Since the quantization range is divided into quantization levels, we have:
Quantization levels = 2^N
Substituting the value of the quantization range, we get:
2 V = 2^N
Taking the logarithm of both sides, we get:
log2(2 V) = log2(2^N)
Simplifying the equation, we get:
1 = N
Therefore, the number of bits required (N) is 1.
Step 5: Calculate the maximum step size:
Substituting the values of Amax and N into the formula, we get:
Δ = (2 * Amax) / (2^N)
= (2 * 1 V) / (2^1)
= 2 V / 2
= 1 V
Step 6: Calculate the minimum step size:
The minimum step size is equal to half
- Bandwidth of the analog message signals: 3.5 kHz
- Amplitude of the sinusoidal test signal (Amax): 1 V
- Frequency of the sinusoidal test signal (fm): 800 Hz
- Sampling rate of the system: 64 kHz
Explanation:
The minimum value of the step size is determined by the Nyquist criterion, which states that the sampling rate should be at least twice the bandwidth of the signal to avoid aliasing.
Step 1: Calculate the maximum frequency component of the analog message signal:
The maximum frequency component of the analog message signal can be calculated using the formula:
Maximum frequency component (fmax) = fm + bandwidth/2
Given: fm = 800 Hz, bandwidth = 3.5 kHz
Substituting the values, we get:
fmax = 800 Hz + 3.5 kHz/2
= 800 Hz + 1.75 kHz
= 2550 Hz
Step 2: Calculate the minimum sampling rate:
According to the Nyquist criterion, the minimum sampling rate should be at least twice the maximum frequency component of the analog message signal. Therefore,
Minimum sampling rate = 2 * fmax
Substituting the value of fmax, we get:
Minimum sampling rate = 2 * 2550 Hz
= 5100 Hz
Step 3: Calculate the maximum step size:
The maximum step size is determined by the quantization range of the analog-to-digital converter (ADC). In this case, the maximum amplitude of the sinusoidal test signal is given as Amax = 1 V.
The maximum step size (Δ) can be calculated using the formula:
Δ = (2 * Amax) / (2^N)
Where N is the number of bits used by the ADC.
Step 4: Calculate the number of bits required:
To determine the number of bits required, we need to calculate the quantization levels using the formula:
Quantization levels (L) = 2^N
The number of quantization levels is determined by the quantization range, which is given by:
Quantization range = 2 * Amax
Substituting the value of Amax, we get:
Quantization range = 2 * 1 V
= 2 V
Since the quantization range is divided into quantization levels, we have:
Quantization levels = 2^N
Substituting the value of the quantization range, we get:
2 V = 2^N
Taking the logarithm of both sides, we get:
log2(2 V) = log2(2^N)
Simplifying the equation, we get:
1 = N
Therefore, the number of bits required (N) is 1.
Step 5: Calculate the maximum step size:
Substituting the values of Amax and N into the formula, we get:
Δ = (2 * Amax) / (2^N)
= (2 * 1 V) / (2^1)
= 2 V / 2
= 1 V
Step 6: Calculate the minimum step size:
The minimum step size is equal to half
If one of the code words of a Hamming (7, 4) code is 0001011, which of the following cannot be the valid codeword in the same group?- a)0011101
- b)0101100
- c)0011010
- d)1110100
Correct answer is option 'C'. Can you explain this answer?
If one of the code words of a Hamming (7, 4) code is 0001011, which of the following cannot be the valid codeword in the same group?
a)
0011101
b)
0101100
c)
0011010
d)
1110100

|
Imtiaz Ahmad answered |
The minimum bits change between any valid Hamming codes is 3.
Analysis:
The change of bits between the given code: 0001011 and option C code: 0011010 is two bits change only.
So 0011010 can’t be a valid Hamming code of the same group.
Analysis:
The change of bits between the given code: 0001011 and option C code: 0011010 is two bits change only.
So 0011010 can’t be a valid Hamming code of the same group.
An amplifier has a standard spot noise figure F0 = 6.31 (8.0 dB). The amplifier, that is used to amplify the output of an antenna have antenna temperature of Ta = 180 KQue: The operating spot noise figure is- a)3.2 dB
- b)6.4 dB
- c)9.8 dB
- d)11.9 dB
Correct answer is option 'C'. Can you explain this answer?
An amplifier has a standard spot noise figure F0 = 6.31 (8.0 dB). The amplifier, that is used to amplify the output of an antenna have antenna temperature of Ta = 180 K
Que: The operating spot noise figure is
a)
3.2 dB
b)
6.4 dB
c)
9.8 dB
d)
11.9 dB

|
Mira Sharma answered |
Chapter doubts & questions for Digital Communication - Communication System 2025 is part of Electronics and Communication Engineering (ECE) exam preparation. The chapters have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Electronics and Communication Engineering (ECE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Digital Communication - Communication System in English & Hindi are available as part of Electronics and Communication Engineering (ECE) exam.
Download more important topics, notes, lectures and mock test series for Electronics and Communication Engineering (ECE) Exam by signing up for free.
Communication System
14 videos|44 docs|30 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup















