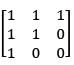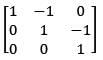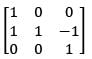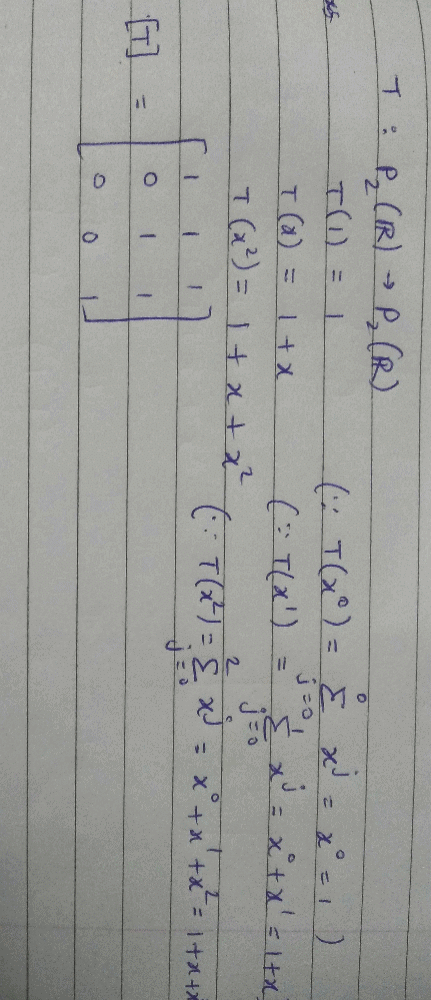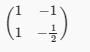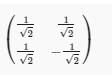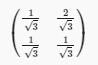All Exams >
Mathematics >
Mathematics for Competitive Exams >
All Questions
All questions of Vector Space & Linear Transformation for Mathematics Exam
If T : V → V be a linear operator for dim V = n and T has n distinct eigenvalues then- a)T must be invertible.
- b)T must be diagonalizable.
- c)T must be invertible as well as diagonalizable.
- d)T is not diagonalizable.
Correct answer is option 'B'. Can you explain this answer?
If T : V → V be a linear operator for dim V = n and T has n distinct eigenvalues then
a)
T must be invertible.
b)
T must be diagonalizable.
c)
T must be invertible as well as diagonalizable.
d)
T is not diagonalizable.
|
|
Kanika Verma answered |
It seems that your question got cut off. Could you please provide more information or complete your question?
Let T : R2 → R2 be a linear transformation such that T((1, 2)) = (2, 3) and T((0, 1)) = (1, 4).Then T((5, -4)) is
- a)(-4, -41)
- b)(-1, 6)
- c)(-6, 1)
- d)(1, -6)
Correct answer is option 'A'. Can you explain this answer?
Let T : R2 → R2 be a linear transformation such that T((1, 2)) = (2, 3) and T((0, 1)) = (1, 4).Then T((5, -4)) is
a)
(-4, -41)
b)
(-1, 6)
c)
(-6, 1)
d)
(1, -6)

|
Edurev.iitjam answered |
Given, T((1, 2)) = (2, 3) and
T((0, 1)) = (1, 4)
As T is the linear transformation
⇒ T(av1 + bv2) = a T(v1) + b T(v2).


Consider the two linear mapsT1 and T2 on V3 defined as T1(x1, x2, x3) = (0, x2, x3) and T2(x1, x2, x3) = (x1, 0,0)- a)T is idempotent but T2 is not idempotent
- b)T2 is idempotent but T1 is not idempotent
- c)Both T1 and T2 are idempotent
- d)Neither T1 norT2 are idempotent.
Correct answer is option 'C'. Can you explain this answer?
Consider the two linear mapsT1 and T2 on V3 defined as T1(x1, x2, x3) = (0, x2, x3) and T2(x1, x2, x3) = (x1, 0,0)
a)
T is idempotent but T2 is not idempotent
b)
T2 is idempotent but T1 is not idempotent
c)
Both T1 and T2 are idempotent
d)
Neither T1 norT2 are idempotent.

|
Om Pavan Koushik answered |
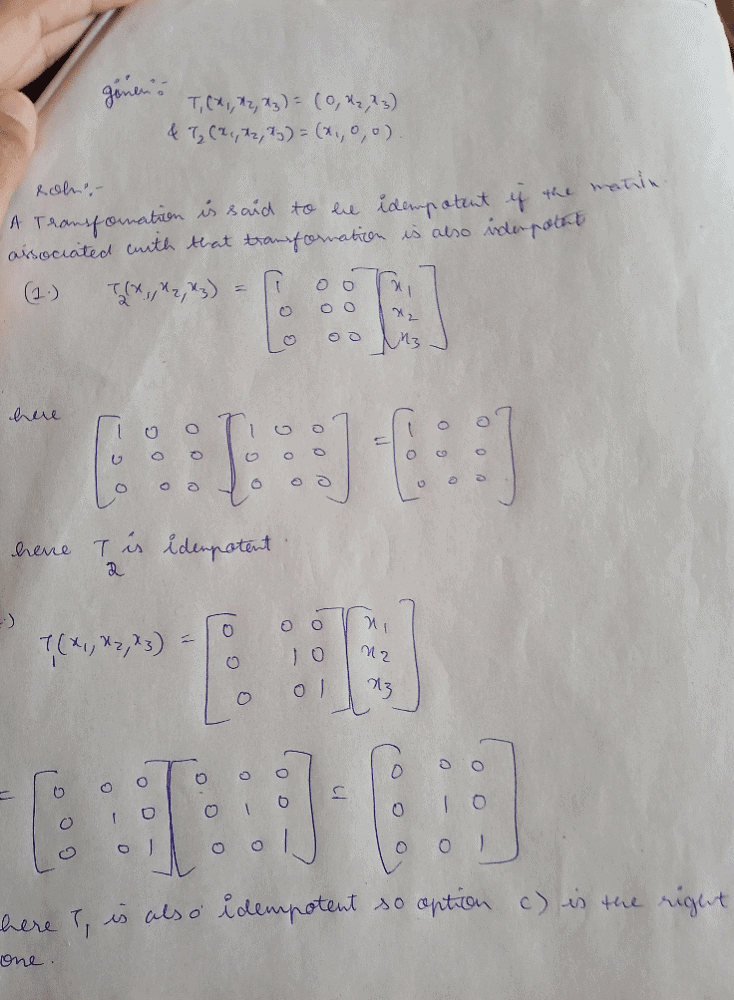
Let T be a linear transformation from a vector space 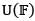 into a vector space
into a vector space 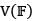 with U as finite dimensional. The rank of T is the dimension of the
with U as finite dimensional. The rank of T is the dimension of the
- a)null space of T
- b)range of T
- c)vector space U
- d)vector space V
Correct answer is option 'B'. Can you explain this answer?
Let T be a linear transformation from a vector space 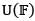 into a vector space
into a vector space 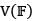 with U as finite dimensional. The rank of T is the dimension of the
with U as finite dimensional. The rank of T is the dimension of the
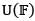 into a vector space
into a vector space 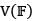 with U as finite dimensional. The rank of T is the dimension of the
with U as finite dimensional. The rank of T is the dimension of thea)
null space of T
b)
range of T
c)
vector space U
d)
vector space V

|
Vivek Singh answered |
Option A is correct
Let T: R3 → R3 be a linear transformation and I be the identify transformation of R3. If there is a scalar C and a non-zero vector x ∈ R3 such that T(x) = Cx, then rank (T – CI) - a)cannot be 0
- b)cannot be 2
- c)cannot be 3
- d)cannot be 1
Correct answer is option 'C'. Can you explain this answer?
Let T: R3 → R3 be a linear transformation and I be the identify transformation of R3. If there is a scalar C and a non-zero vector x ∈ R3 such that T(x) = Cx, then rank (T – CI)
a)
cannot be 0
b)
cannot be 2
c)
cannot be 3
d)
cannot be 1

|
Veda Institute answered |
By rank-nullity is theorem,
dim(T) = Rank(T) + Nullity (T)
Here dim(T) = 3 Now, (T – CI)x = T(x) – (T(x) = cx – cx
= 0
(I is identity transformation)
⇒ Nullity of T – CI cannot be zero
⇒ Hence, Rank of T – CI cannot be 3.
dim(T) = Rank(T) + Nullity (T)
Here dim(T) = 3 Now, (T – CI)x = T(x) – (T(x) = cx – cx
= 0
(I is identity transformation)
⇒ Nullity of T – CI cannot be zero
⇒ Hence, Rank of T – CI cannot be 3.
Let T be linear transformation on 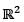 into itself such that T(1,0) = (1,2) and T (1, 1) = (0, 2) .Then T(a, b) is equal to
into itself such that T(1,0) = (1,2) and T (1, 1) = (0, 2) .Then T(a, b) is equal to
- a)(a, 2b)
- b)(2a, b)
- c)(a - b, 2a)
- d)(a - b, 2b)
Correct answer is option 'C'. Can you explain this answer?
Let T be linear transformation on 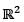 into itself such that T(1,0) = (1,2) and T (1, 1) = (0, 2) .Then T(a, b) is equal to
into itself such that T(1,0) = (1,2) and T (1, 1) = (0, 2) .Then T(a, b) is equal to
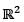 into itself such that T(1,0) = (1,2) and T (1, 1) = (0, 2) .Then T(a, b) is equal to
into itself such that T(1,0) = (1,2) and T (1, 1) = (0, 2) .Then T(a, b) is equal toa)
(a, 2b)
b)
(2a, b)
c)
(a - b, 2a)
d)
(a - b, 2b)
|
|
Pijush De answered |
As {(1,0),(1,1)} form a basis for R^2 so, (a,b) can be written as Linear combination of (1,0) &(1,1).
(a,b) = (a-b)(1,0) + b(1,1)
So, T(a,b) = T(b(1,1) + (a-b)(1,0))
= b T(1,1) + (a-b) T(1,0)
= b (0,2) + (a-b) (1,2)
= (a-b, 2a) [Option C]
(a,b) = (a-b)(1,0) + b(1,1)
So, T(a,b) = T(b(1,1) + (a-b)(1,0))
= b T(1,1) + (a-b) T(1,0)
= b (0,2) + (a-b) (1,2)
= (a-b, 2a) [Option C]
Let the linear transform ations S and 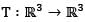 be defined by
S(x, y, z) = (2x, 4x - y, 2x + 3y - z)
be defined by
S(x, y, z) = (2x, 4x - y, 2x + 3y - z)
T(x, y, z) = (x cosθ - y sinθ, sinθ + y cos θ, z) where 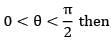
- a)S is one one but not T
- b)Both S and T are one one
- c)T is one one but not S
- d)neither S nor T is one one
Correct answer is option 'B'. Can you explain this answer?
Let the linear transform ations S and 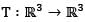 be defined by
be defined by
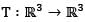 be defined by
be defined by S(x, y, z) = (2x, 4x - y, 2x + 3y - z)
T(x, y, z) = (x cosθ - y sinθ, sinθ + y cos θ, z) where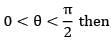
T(x, y, z) = (x cosθ - y sinθ, sinθ + y cos θ, z) where
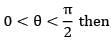
a)
S is one one but not T
b)
Both S and T are one one
c)
T is one one but not S
d)
neither S nor T is one one

|
Vivek Singh answered |
Option C is correct.
Let T (x, y, z) = xy2 + 2z – x2z2 be the temperature at the point (x, y, z). The unit vector in the direction in which the temperature decrease most rapidly at (1, 0, – 1) is- a)
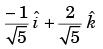
- b)
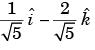
- c)
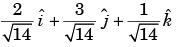
- d)

Correct answer is option 'B'. Can you explain this answer?
Let T (x, y, z) = xy2 + 2z – x2z2 be the temperature at the point (x, y, z). The unit vector in the direction in which the temperature decrease most rapidly at (1, 0, – 1) is
a)
b)
c)
d)
|
|
Chirag Verma answered |
Let T(x, y), z) = xy2 + 2z – x2z2 be the temperature at a point (x, y, z).
Temperature increase most rapidly in the direction of gradient i.e., ∇T
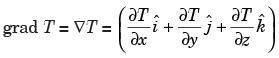
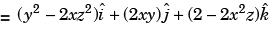
At point (1, 0, – 1), = ∇T(1, 0,1) =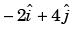
unit vector in direction of ∇T is
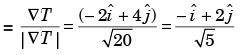
So, temperature decreases most rapidly in the direction of –∇T i.e.,
At point (1, 0, – 1), = ∇T(1, 0,1) =
unit vector in direction of ∇T is
So, temperature decreases most rapidly in the direction of –∇T i.e.,
Let T:R2 -> R2 be the transformation T(x1,x2) = (x1,0). The null space (or kernel) N(T) of T is- a)(x1,0) : x1 is real
- b)1
- c)(0,1)
- d)(0,x2) : x2 is real
Correct answer is option 'D'. Can you explain this answer?
Let T:R2 -> R2 be the transformation T(x1,x2) = (x1,0). The null space (or kernel) N(T) of T is
a)
(x1,0) : x1 is real
b)
1
c)
(0,1)
d)
(0,x2) : x2 is real
|
|
Kiara Kapoor answered |
R2 be a linear transformation. Let's denote the standard basis vectors in R2 as e1 = (1, 0) and e2 = (0, 1). Then any vector x in R2 can be written as x = x1e1 + x2e2, where x1 and x2 are scalars.
Since T is a linear transformation, we have:
T(x) = T(x1e1 + x2e2) = x1T(e1) + x2T(e2)
Let's denote the images of the standard basis vectors under T as T(e1) = (a, b) and T(e2) = (c, d), where a, b, c, and d are scalars.
Then the transformation T can be represented by the matrix:
[T] = | a c |
| b d |
This matrix is called the standard matrix of the linear transformation T. Each column of the matrix represents the image of the corresponding basis vector under T.
Note that the standard matrix of T depends on the choice of basis vectors in R2. If we choose a different set of basis vectors, the standard matrix representation of T will change accordingly.
Since T is a linear transformation, we have:
T(x) = T(x1e1 + x2e2) = x1T(e1) + x2T(e2)
Let's denote the images of the standard basis vectors under T as T(e1) = (a, b) and T(e2) = (c, d), where a, b, c, and d are scalars.
Then the transformation T can be represented by the matrix:
[T] = | a c |
| b d |
This matrix is called the standard matrix of the linear transformation T. Each column of the matrix represents the image of the corresponding basis vector under T.
Note that the standard matrix of T depends on the choice of basis vectors in R2. If we choose a different set of basis vectors, the standard matrix representation of T will change accordingly.
T is non singular iff- a)nullity T ≠ 0
- b)nullity (T) = 0
- c)Nullity T = rank T
- d)rank T = 0
Correct answer is option 'B'. Can you explain this answer?
T is non singular iff
a)
nullity T ≠ 0
b)
nullity (T) = 0
c)
Nullity T = rank T
d)
rank T = 0
|
|
Eesha Mehta answered |
The statement is incomplete. Can you please provide the complete statement?
Let A and B he nxn matrices with the same minimal polynomial. Then- a)A is similar to B.
- b)A is diagonalizable if B is diagonalizable.
- c)A - B is singular.
- d)A and B is commute.
Correct answer is option 'B'. Can you explain this answer?
Let A and B he nxn matrices with the same minimal polynomial. Then
a)
A is similar to B.
b)
A is diagonalizable if B is diagonalizable.
c)
A - B is singular.
d)
A and B is commute.
|
|
Pranavi Kapoor answered |
Explanation:
a) A is similar to B:
If A and B have the same minimal polynomial, it means that they have the same characteristic polynomial, and therefore the same eigenvalues. This implies that A and B have the same eigenvalue multiplicities.
Since A and B have the same eigenvalues and eigenvalue multiplicities, it follows that they have the same Jordan canonical form. The Jordan canonical form is unique up to the order of the Jordan blocks, so A and B must be similar.
b) A is diagonalizable if B is diagonalizable:
If B is diagonalizable, it means that it can be written as B = PDP^-1, where D is a diagonal matrix and P is an invertible matrix. Since A and B have the same minimal polynomial, they have the same characteristic polynomial, and therefore the same eigenvalues.
If A is diagonalizable, it means that it can be written as A = QDQ^-1, where D is a diagonal matrix and Q is an invertible matrix. Since A and B have the same eigenvalues, it follows that D is the same diagonal matrix for both A and B.
Therefore, if B is diagonalizable, A can also be written as A = PDQ^-1, where D is the same diagonal matrix as in the diagonalization of B. This implies that A is also diagonalizable.
c) A - B is singular:
Since A and B have the same minimal polynomial, they have the same characteristic polynomial, and therefore the same eigenvalues. Let λ be an eigenvalue of A and B. Then A - B has eigenvalues given by λ - λ = 0.
If A - B has eigenvalue 0, it means that A - B is not invertible, and therefore it is singular.
d) A and B commute:
To show that A and B commute, we need to show that AB = BA. Since A and B have the same minimal polynomial, they have the same characteristic polynomial, and therefore the same eigenvalues.
Let λ be an eigenvalue of A and B. Then we have:
ABv = BA v = λ Bv
where v is an eigenvector corresponding to the eigenvalue λ. This implies that ABv and BA v are scalar multiples of Bv. Since A and B have the same eigenvalues, ABv and BA v are scalar multiples of v as well.
Therefore, ABv = BA v for all eigenvalues λ and corresponding eigenvectors v, which implies that A and B commute.
Therefore, the correct answer is option 'B' - A is diagonalizable if B is diagonalizable.
a) A is similar to B:
If A and B have the same minimal polynomial, it means that they have the same characteristic polynomial, and therefore the same eigenvalues. This implies that A and B have the same eigenvalue multiplicities.
Since A and B have the same eigenvalues and eigenvalue multiplicities, it follows that they have the same Jordan canonical form. The Jordan canonical form is unique up to the order of the Jordan blocks, so A and B must be similar.
b) A is diagonalizable if B is diagonalizable:
If B is diagonalizable, it means that it can be written as B = PDP^-1, where D is a diagonal matrix and P is an invertible matrix. Since A and B have the same minimal polynomial, they have the same characteristic polynomial, and therefore the same eigenvalues.
If A is diagonalizable, it means that it can be written as A = QDQ^-1, where D is a diagonal matrix and Q is an invertible matrix. Since A and B have the same eigenvalues, it follows that D is the same diagonal matrix for both A and B.
Therefore, if B is diagonalizable, A can also be written as A = PDQ^-1, where D is the same diagonal matrix as in the diagonalization of B. This implies that A is also diagonalizable.
c) A - B is singular:
Since A and B have the same minimal polynomial, they have the same characteristic polynomial, and therefore the same eigenvalues. Let λ be an eigenvalue of A and B. Then A - B has eigenvalues given by λ - λ = 0.
If A - B has eigenvalue 0, it means that A - B is not invertible, and therefore it is singular.
d) A and B commute:
To show that A and B commute, we need to show that AB = BA. Since A and B have the same minimal polynomial, they have the same characteristic polynomial, and therefore the same eigenvalues.
Let λ be an eigenvalue of A and B. Then we have:
ABv = BA v = λ Bv
where v is an eigenvector corresponding to the eigenvalue λ. This implies that ABv and BA v are scalar multiples of Bv. Since A and B have the same eigenvalues, ABv and BA v are scalar multiples of v as well.
Therefore, ABv = BA v for all eigenvalues λ and corresponding eigenvectors v, which implies that A and B commute.
Therefore, the correct answer is option 'B' - A is diagonalizable if B is diagonalizable.
Let  be a linear transformation. Which of the following statement implies that T is bijective?
be a linear transformation. Which of the following statement implies that T is bijective?
- a)Nullity(T) = n
- b)Rank(T) + Nullity(T) = n
- c)Rank(T) = - n
- d)Rank(T) - nullity(T) = n
Correct answer is option 'D'. Can you explain this answer?
Let  be a linear transformation. Which of the following statement implies that T is bijective?
be a linear transformation. Which of the following statement implies that T is bijective?
 be a linear transformation. Which of the following statement implies that T is bijective?
be a linear transformation. Which of the following statement implies that T is bijective?a)
Nullity(T) = n
b)
Rank(T) + Nullity(T) = n
c)
Rank(T) = - n
d)
Rank(T) - nullity(T) = n
|
|
Dronacharya Institute answered |
Option D is correct because this is the only option which implies rank is n and nullity is 0.
Find the inverse Fourier transform of 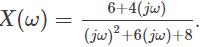
- a)e-2t u(t) – 5e-4t u(t)
- b)e-2t u(t) + 5e-4t u(t)
- c)-e-2t u(t) + 5e-4t u(t)
- d)-e-2t u(t) – 5e-4t u(t)
Correct answer is option 'C'. Can you explain this answer?
Find the inverse Fourier transform of 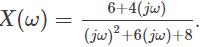
a)
e-2t u(t) – 5e-4t u(t)
b)
e-2t u(t) + 5e-4t u(t)
c)
-e-2t u(t) + 5e-4t u(t)
d)
-e-2t u(t) – 5e-4t u(t)
|
|
Chirag Verma answered |
Applying inverse Fourier transform, we get
x(t) = -e-2t u(t) + 5e-4t u(t).
The matrix A is represented as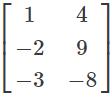 The transpose of the matrix of this matrix is represented as?
The transpose of the matrix of this matrix is represented as?- a)

- b)
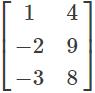
- c)
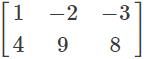
- d)
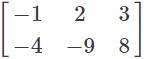
Correct answer is option 'C'. Can you explain this answer?
The matrix A is represented as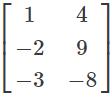 The transpose of the matrix of this matrix is represented as?
The transpose of the matrix of this matrix is represented as?
a)
b)
c)
d)
|
|
Chirag Verma answered |
Given matrix is a 3 × 2 matrix and the transpose of the matrix is 3×2 matrix.
The values of matrix are not changed but, the elements are interchanged, as row elements of a given matrix to the column elements of the transpose matrix and vice versa but the polarities of the elements remains same.
The values of matrix are not changed but, the elements are interchanged, as row elements of a given matrix to the column elements of the transpose matrix and vice versa but the polarities of the elements remains same.
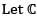 be the vector space of all complex numbers over complex field
be the vector space of all complex numbers over complex field 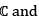
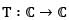 be defined by T(z) =
be defined by T(z) = 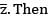
- a)T is linear
- b)T is not linear but a well defined map
- c)T is not well defined
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
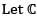 be the vector space of all complex numbers over complex field
be the vector space of all complex numbers over complex field 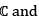
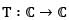 be defined by T(z) =
be defined by T(z) = 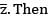
a)
T is linear
b)
T is not linear but a well defined map
c)
T is not well defined
d)
None of the above

|
Praveen Sharma answered |
It does not satisfy scalar multiplication property on a sacalar when u check . so not linear
Let T be a linear operator on a finite dimensional vector space V. If m(λ) = λr + ar-1λr-1 + ... + a1λ + a0 (a0 ≠ 0) be a minimal polynomial of T then- a)T is invertible
- b)0 is an eigenvalue of T
- c)T is singular
- d)0 is root of m(λ)
Correct answer is option 'A'. Can you explain this answer?
Let T be a linear operator on a finite dimensional vector space V. If m(λ) = λr + ar-1λr-1 + ... + a1λ + a0 (a0 ≠ 0) be a minimal polynomial of T then
a)
T is invertible
b)
0 is an eigenvalue of T
c)
T is singular
d)
0 is root of m(λ)
|
|
Rudra Sethi answered |
To prove that T is diagonalizable, we need to show that its minimal polynomial has distinct linear factors.
First, let's define the minimal polynomial of T as the monic polynomial of least degree that annihilates T. This means that the minimal polynomial p(x) satisfies p(T) = 0, where p(x) = (x - λ₁)^(m₁)(x - λ₂)^(m₂)...(x - λₖ)^(mₖ) for distinct eigenvalues λ₁, λ₂, ..., λₖ and positive integers m₁, m₂, ..., mₖ.
Now, let's assume that the minimal polynomial p(x) has repeated linear factors. Without loss of generality, assume that (x - λ)^(m) is a repeated linear factor, where λ is an eigenvalue of T and m > 1.
Since p(T) = 0, we have (T - λI)^(m) = 0, where I is the identity operator on V. This means that for any vector v in V, we have (T - λI)^(m)(v) = 0.
Now, let's consider the subspace W = Ker((T - λI)^(m-1)). Since (T - λI)^(m-1)(v) = 0 for any v in W, we have W ⊆ Ker((T - λI)^(m-1)).
Next, let's consider the vector u = (T - λI)^(m-1)(v) for some v in V. Since (T - λI)(u) = (T - λI)((T - λI)^(m-1)(v)) = (T - λI)^(m)(v) = 0, we have u in Ker(T - λI) = E(λ), the eigenspace of T corresponding to the eigenvalue λ. Therefore, u is an eigenvector of T corresponding to the eigenvalue λ.
However, since (T - λI)^(m-1)(v) = u, this means that u is a generalized eigenvector of T corresponding to the eigenvalue λ with a generalized eigenvector degree of m-1.
This contradicts the assumption that λ is diagonalizable, because a diagonalizable operator should have each eigenvalue associated with a unique eigenvector.
Therefore, our assumption that the minimal polynomial p(x) has repeated linear factors is false. This implies that the minimal polynomial of T has distinct linear factors, and thus T is diagonalizable.
First, let's define the minimal polynomial of T as the monic polynomial of least degree that annihilates T. This means that the minimal polynomial p(x) satisfies p(T) = 0, where p(x) = (x - λ₁)^(m₁)(x - λ₂)^(m₂)...(x - λₖ)^(mₖ) for distinct eigenvalues λ₁, λ₂, ..., λₖ and positive integers m₁, m₂, ..., mₖ.
Now, let's assume that the minimal polynomial p(x) has repeated linear factors. Without loss of generality, assume that (x - λ)^(m) is a repeated linear factor, where λ is an eigenvalue of T and m > 1.
Since p(T) = 0, we have (T - λI)^(m) = 0, where I is the identity operator on V. This means that for any vector v in V, we have (T - λI)^(m)(v) = 0.
Now, let's consider the subspace W = Ker((T - λI)^(m-1)). Since (T - λI)^(m-1)(v) = 0 for any v in W, we have W ⊆ Ker((T - λI)^(m-1)).
Next, let's consider the vector u = (T - λI)^(m-1)(v) for some v in V. Since (T - λI)(u) = (T - λI)((T - λI)^(m-1)(v)) = (T - λI)^(m)(v) = 0, we have u in Ker(T - λI) = E(λ), the eigenspace of T corresponding to the eigenvalue λ. Therefore, u is an eigenvector of T corresponding to the eigenvalue λ.
However, since (T - λI)^(m-1)(v) = u, this means that u is a generalized eigenvector of T corresponding to the eigenvalue λ with a generalized eigenvector degree of m-1.
This contradicts the assumption that λ is diagonalizable, because a diagonalizable operator should have each eigenvalue associated with a unique eigenvector.
Therefore, our assumption that the minimal polynomial p(x) has repeated linear factors is false. This implies that the minimal polynomial of T has distinct linear factors, and thus T is diagonalizable.
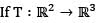 is a linear transformation T(1,0) = (2,3,l) and T(1,1) = (3,0,2) then which one of the following statement is correct?
is a linear transformation T(1,0) = (2,3,l) and T(1,1) = (3,0,2) then which one of the following statement is correct?- a)T(x,y) = (x + y, 2x + y, 3x - 3y)
- b)T(x,y) = (2x + y, 3x - 3y, x + y)
- c)T (x , y) = (2x - y, 3x + 3y, x - y)
- d)T (x , y) = (x - y,2x - y . 3x + 3y)
Correct answer is option 'B'. Can you explain this answer?
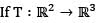 is a linear transformation T(1,0) = (2,3,l) and T(1,1) = (3,0,2) then which one of the following statement is correct?
is a linear transformation T(1,0) = (2,3,l) and T(1,1) = (3,0,2) then which one of the following statement is correct?a)
T(x,y) = (x + y, 2x + y, 3x - 3y)
b)
T(x,y) = (2x + y, 3x - 3y, x + y)
c)
T (x , y) = (2x - y, 3x + 3y, x - y)
d)
T (x , y) = (x - y,2x - y . 3x + 3y)

|
Dass Dass Dass answered |
Find the product of two train tense A
2
Given 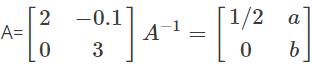 then find a + b.
then find a + b.- a)6 / 20
- b)7 / 20
- c)8 / 20
- d)5 / 20
Correct answer is option 'B'. Can you explain this answer?
Given 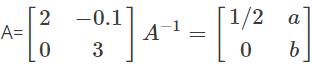 then find a + b.
then find a + b.
a)
6 / 20
b)
7 / 20
c)
8 / 20
d)
5 / 20

|
Veda Institute answered |
AA-1 = I = 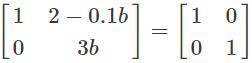
Therefore, a = 1 / 60 and b = 1 / 3 and a + b = 7 / 20.
Therefore, a = 1 / 60 and b = 1 / 3 and a + b = 7 / 20.
Consider the basis S = {v1, v2, v3} for 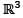 where v1 = (1,1,1) and v2 = (1,1,0), v3 = (1,0,0) and let
where v1 = (1,1,1) and v2 = (1,1,0), v3 = (1,0,0) and let 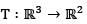 be a linear transformation such that T(v1) = (1,0), T (v2) = (2, -1), T (v3) = (4, 3). Then T (2, - 3, 5) is
be a linear transformation such that T(v1) = (1,0), T (v2) = (2, -1), T (v3) = (4, 3). Then T (2, - 3, 5) is- a)(- 1, 5)
- b)(3,4)
- c)(0,0)
- d)(9,23)
Correct answer is option 'D'. Can you explain this answer?
Consider the basis S = {v1, v2, v3} for 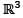 where v1 = (1,1,1) and v2 = (1,1,0), v3 = (1,0,0) and let
where v1 = (1,1,1) and v2 = (1,1,0), v3 = (1,0,0) and let 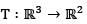 be a linear transformation such that T(v1) = (1,0), T (v2) = (2, -1), T (v3) = (4, 3). Then T (2, - 3, 5) is
be a linear transformation such that T(v1) = (1,0), T (v2) = (2, -1), T (v3) = (4, 3). Then T (2, - 3, 5) is
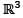 where v1 = (1,1,1) and v2 = (1,1,0), v3 = (1,0,0) and let
where v1 = (1,1,1) and v2 = (1,1,0), v3 = (1,0,0) and let 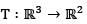 be a linear transformation such that T(v1) = (1,0), T (v2) = (2, -1), T (v3) = (4, 3). Then T (2, - 3, 5) is
be a linear transformation such that T(v1) = (1,0), T (v2) = (2, -1), T (v3) = (4, 3). Then T (2, - 3, 5) isa)
(- 1, 5)
b)
(3,4)
c)
(0,0)
d)
(9,23)
|
|
Vishal Thakur answered |
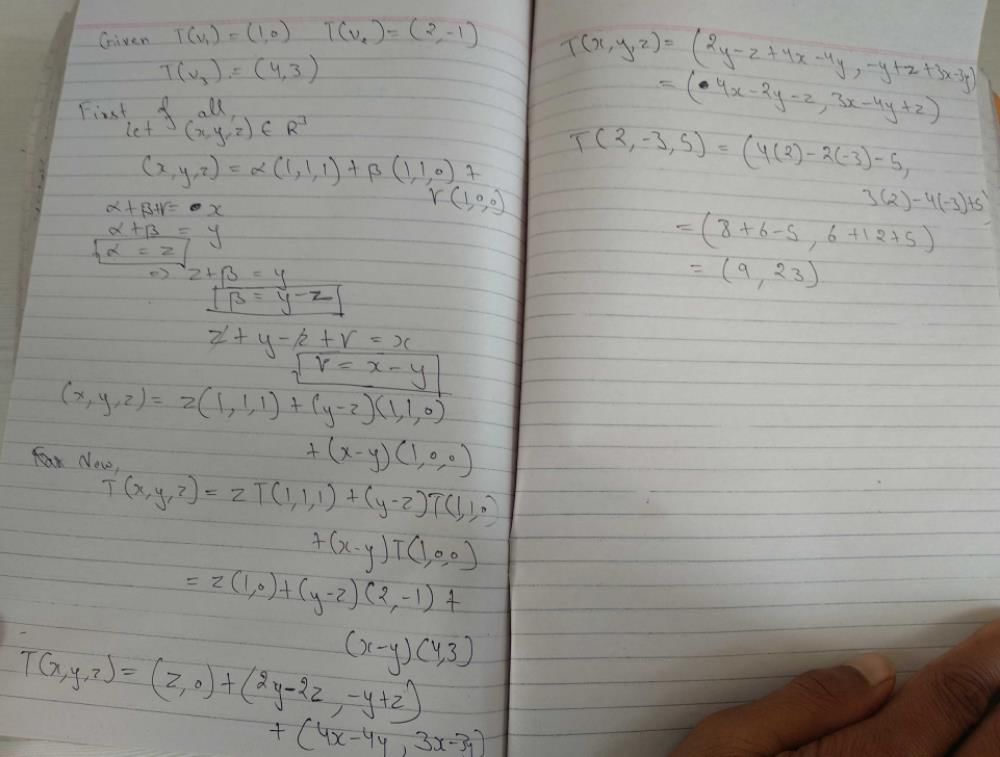
Let T: R4 → R4 be a linear transformation satisfy T3 + 3T2 = 4I, where I is the identity - a)one-one but not onto
- b)non-invertible
- c)onto but not one-one
- d)invertible
Correct answer is option 'B'. Can you explain this answer?
Let T: R4 → R4 be a linear transformation satisfy T3 + 3T2 = 4I, where I is the identity
a)
one-one but not onto
b)
non-invertible
c)
onto but not one-one
d)
invertible
|
|
Chirag Verma answered |
Here, L.T T : R4 → R4 satisfy
T3 + 3T2 = 4I, where I is identity transformation one of the eigenvalues of T is I
⇒ One of eigenvalue of S = T4 + 3T3 – 4I is zero
⇒ S is non-invertible
T3 + 3T2 = 4I, where I is identity transformation one of the eigenvalues of T is I
⇒ One of eigenvalue of S = T4 + 3T3 – 4I is zero
⇒ S is non-invertible
Let A be a 3 × 3 matrix with eigenvalues 1, –1 and 3. Then
- a)A2 + 3A is non-singular
- b)A2 + A is singular
- c)A2 – A is non-singular
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Let A be a 3 × 3 matrix with eigenvalues 1, –1 and 3. Then
a)
A2 + 3A is non-singular
b)
A2 + A is singular
c)
A2 – A is non-singular
d)
None of these
|
|
Chirag Verma answered |
A be a 3 × 3 matrix with eigenvalues of 1, –1 & 3.
For eigenvalues λ = 1, the characteristic equation is
|A – λI| = 0 ⇒ |A – I| = 0
⇒ |A2 – A|= 0 ⇒ A2 – A is singular
For λ = –1, the characteristic equation is |A + I| = 0 ⇒ |A2 + A| = 0 ⇒ A2 + A is singular
Similarly, for
λ = 3,
|A – 3I| = 0
⇒ |A2 – 3A| = 0 ⇒ A – 3A is singular
Since 0 & –3 are not eigenvalues,
So,|A| ≠ 0 & |A + 3I| ≠ 0
Hence |A2 + 3A| ≠ 0 ⇒ A2 + 3A is non-singular
For eigenvalues λ = 1, the characteristic equation is
|A – λI| = 0 ⇒ |A – I| = 0
⇒ |A2 – A|= 0 ⇒ A2 – A is singular
For λ = –1, the characteristic equation is |A + I| = 0 ⇒ |A2 + A| = 0 ⇒ A2 + A is singular
Similarly, for
λ = 3,
|A – 3I| = 0
⇒ |A2 – 3A| = 0 ⇒ A – 3A is singular
Since 0 & –3 are not eigenvalues,
So,|A| ≠ 0 & |A + 3I| ≠ 0
Hence |A2 + 3A| ≠ 0 ⇒ A2 + 3A is non-singular
Let S = {T: R3 → R3; T is a linear transformation with T (1, 0, 1) = (1, 2, 3) and T (1, 2, 3) = (1, 0, 1). Then S is - a)an uncountable set
- b)a singleton set
- c)a finite set containing more than one element
- d)a countable infinite set
Correct answer is option 'A'. Can you explain this answer?
Let S = {T: R3 → R3; T is a linear transformation with T (1, 0, 1) = (1, 2, 3) and T (1, 2, 3) = (1, 0, 1). Then S is
a)
an uncountable set
b)
a singleton set
c)
a finite set containing more than one element
d)
a countable infinite set
|
|
Chirag Verma answered |
Here, L.T. is T : R3 → R3 s.t.
T (1, 0) = (1, 2, 3)
T (1, 2, 3) = (1, 0, 1)
We can define a transformation for the third in depend vector in any way. So accordingly we get infinitely many linear transformations.
T (1, 0) = (1, 2, 3)
T (1, 2, 3) = (1, 0, 1)
We can define a transformation for the third in depend vector in any way. So accordingly we get infinitely many linear transformations.
Let T : R2 → R2 be a linear transformation such that T((1, 2)) = (2, 3) and T((0, 1)) = (1, 4).Then T((5, -4)) is- a)(-4, -41)
- b)(-6, 1)
- c)(-1, 6)
- d)(1, -6)
Correct answer is option 'A'. Can you explain this answer?
Let T : R2 → R2 be a linear transformation such that T((1, 2)) = (2, 3) and T((0, 1)) = (1, 4).Then T((5, -4)) is
a)
(-4, -41)
b)
(-6, 1)
c)
(-1, 6)
d)
(1, -6)

|
Veda Institute answered |
Given, T((1, 2)) = (2, 3) and
T((0, 1)) = (1, 4)
As T is the linear transformation
⇒ T(av1 + bv2) = a T(v1) + b T(v2).
Let T: R3 → R3 be a linear transformation and I be the identity transformation of R3. If there is a scalar C and a non-zero vector x ∈ R3 such that T(x) = Cx, then rank (T – CI)- a)cannot be 3
- b)cannot be 2
- c)cannot be 1
- d)cannot be 0
Correct answer is option 'A'. Can you explain this answer?
Let T: R3 → R3 be a linear transformation and I be the identity transformation of R3. If there is a scalar C and a non-zero vector x ∈ R3 such that T(x) = Cx, then rank (T – CI)
a)
cannot be 3
b)
cannot be 2
c)
cannot be 1
d)
cannot be 0
|
|
Chirag Verma answered |
By rank-nullity is theorem,
dim(T) = Rank(T) + Nullity (T)
Here dim(T) = 3
Now, (T – CI)x = T(x) – (T(x) = cx – cx = 0 (I is identity transformation)
⇒ Nullity of T – CI cannot be zero
⇒ Hence, Rank of T – CI cannot be 3.
dim(T) = Rank(T) + Nullity (T)
Here dim(T) = 3
Now, (T – CI)x = T(x) – (T(x) = cx – cx = 0 (I is identity transformation)
⇒ Nullity of T – CI cannot be zero
⇒ Hence, Rank of T – CI cannot be 3.
Which one of the following is not a criterion for linearity of an equation? - a)The dependent variable y should be of second order
- b)Each coefficient does not depend on the independent variable
- c)The derivatives of the dependent variable should be of second order
- d)Each coefficient depends only on the independent variable
Correct answer is option 'B'. Can you explain this answer?
Which one of the following is not a criterion for linearity of an equation?
a)
The dependent variable y should be of second order
b)
Each coefficient does not depend on the independent variable
c)
The derivatives of the dependent variable should be of second order
d)
Each coefficient depends only on the independent variable
|
|
Chirag Verma answered |
The two criterions for linearity of an equation are: The dependent variable y and its derivatives of first degree. Each coefficient depends only on the independent variable.
Which of the following Linear Transformations is not correct for the given matrix?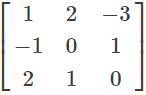
- a)x1 = 1y1 - 2y2 - 3y3
- b)x2 = -1y1 + 1y3
- c)x1 = 1y1 - 3y2 - 3y3
- d)x3 = 2y1 + y2
Correct answer is option 'C'. Can you explain this answer?
Which of the following Linear Transformations is not correct for the given matrix?
a)
x1 = 1y1 - 2y2 - 3y3
b)
x2 = -1y1 + 1y3
c)
x1 = 1y1 - 3y2 - 3y3
d)
x3 = 2y1 + y2

|
Veda Institute answered |
In the given question,
Thus,
x1 = 1y1 - 2y2 - 3y3
x2 = -1y1 + 1y3
x3 = 2y1 + y2.
Find the sum of the Eigen values of the matrix
- a)8
- b)7
- c)9
- d)10
Correct answer is option 'A'. Can you explain this answer?
Find the sum of the Eigen values of the matrix
a)
8
b)
7
c)
9
d)
10
|
|
Chirag Verma answered |
According to the property of the Eigen values, the sum of the Eigen values of a matrix is its trace that is the sum of the elements of the principal diagonal.
Therefore, the sum of the Eigen values = 3 + 4 + 1 = 8.
Therefore, the sum of the Eigen values = 3 + 4 + 1 = 8.
Let A be an n × n matrix such that the set of all its nonzero eigenvalues has exactly r elements. Which of the following statements is true?- a)rank A ≥ r
- b)A2 has r distinct nonzero eigenvalues
- c)If r = 0, then rank A < n - 1
- d)rank A ≤ r
Correct answer is option 'A'. Can you explain this answer?
Let A be an n × n matrix such that the set of all its nonzero eigenvalues has exactly r elements. Which of the following statements is true?
a)
rank A ≥ r
b)
A2 has r distinct nonzero eigenvalues
c)
If r = 0, then rank A < n - 1
d)
rank A ≤ r

|
Veda Institute answered |
Calculation:
Let A be an n × n matrix such that the set of all its nonzero eigenvalues has exactly r elements.
let E = { a1 , a2 , . . . . . ar}
for each non zero eigen values there is at least one eigen vector .
for r non zero distinct eigenvector .
range space is at least r .
Hence option 3 is correct .
Hence option 3 is correct .
Option (1):
Let A =
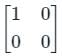 then eigenvalues are 0, 0 ⇒ r = 0
then eigenvalues are 0, 0 ⇒ r = 0
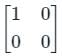 then eigenvalues are 0, 0 ⇒ r = 0
then eigenvalues are 0, 0 ⇒ r = 0rank(A) = 1 = 2 - 1 ≮ 2 - 1
Option (2) is false
Rank(A) = 1 ≮ r = 0
Option (1) is false
Option (4):
A has r non-zero eigenvalues
⇒ A2 has r non-zero eigenvalues
But if A has r distinct eigenvalues does not imply A2 has r distinct eigenvalues.
Let A =
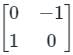
then eigenvalues of A are i, -1
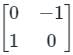
then eigenvalues of A are i, -1
but A2 has eigenvalues -1, -1 which are not distinct.
Option (4) is false.
Let us consider a 3×3 matrix A with Eigen values of λ1, λ2, λ3 and the Eigen values of A-1 are?- a)λ1, λ2, λ3
- b)1 / λ1, 1 / λ2, 1 / λ3
- c)-λ1, -λ2, -λ3
- d)λ1, 0, 0
Correct answer is option 'B'. Can you explain this answer?
Let us consider a 3×3 matrix A with Eigen values of λ1, λ2, λ3 and the Eigen values of A-1 are?
a)
λ1, λ2, λ3
b)
1 / λ1, 1 / λ2, 1 / λ3
c)
-λ1, -λ2, -λ3
d)
λ1, 0, 0
|
|
Chirag Verma answered |
According to the property of the Eigen values, if is the Eigen value of A, then 1 / λ is the Eigen value of A-1. So the Eigen values of A-1 are 1 / λ1, 1 / λ2, 1 / λ3.
Which of the following Linear Transformations is not correct for the given matrix?
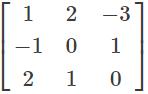
- a)x1 = 1y1 + 2y2 - 3y3
- b)x2 = -1y1 + 1y3
- c)x1 = 1y1 - 3y2 - 3y3
- d)x3 = 2y1 + y2
Correct answer is option 'C'. Can you explain this answer?
Which of the following Linear Transformations is not correct for the given matrix?
a)
x1 = 1y1 + 2y2 - 3y3
b)
x2 = -1y1 + 1y3
c)
x1 = 1y1 - 3y2 - 3y3
d)
x3 = 2y1 + y2
|
|
Chirag Verma answered |
In the given question,
Thus, x1 = 1y1 - 2y2 - 3y3
x2 = -1y1 + 1y3
x3 = 2y1 + y2.
Let A be 3 x 3 matrix with real entries such that det(A) = 6 and the trace of A is 0. lf det(A + I) = 0 where I denotes the 3 x 3 identity matrix, then the eigenvalues of A are- a)-1, 2, 3
- b)-1, 2, -3
- c)1, 2, -3
- d)-1, -2, 3
Correct answer is option 'D'. Can you explain this answer?
Let A be 3 x 3 matrix with real entries such that det(A) = 6 and the trace of A is 0. lf det(A + I) = 0 where I denotes the 3 x 3 identity matrix, then the eigenvalues of A are
a)
-1, 2, 3
b)
-1, 2, -3
c)
1, 2, -3
d)
-1, -2, 3
|
|
Mohit Desai answered |
Given Information:
- A is a 3x3 matrix with real entries.
- det(A) = 6
- The trace of A is 0.
- det(A + I) = 0, where I denotes the 3x3 identity matrix.
To Find:
The eigenvalues of matrix A.
Solution:
1. Trace of a Matrix:
The trace of a square matrix is the sum of its diagonal elements. Given that the trace of matrix A is 0, we have:
Trace(A) = 0
2. Eigenvalues and Determinant:
The determinant of a matrix is equal to the product of its eigenvalues. We are given that det(A) = 6. Since the matrix A is 3x3, it has three eigenvalues (possibly repeated).
3. Determinant of (A + I):
We are given that det(A + I) = 0. The determinant of a matrix is also equal to the product of its eigenvalues. So, the product of the eigenvalues of (A + I) is 0.
4. Product of Eigenvalues:
Let the eigenvalues of A be λ1, λ2, and λ3. The eigenvalues of (A + I) will be (λ1 + 1), (λ2 + 1), and (λ3 + 1). Since the product of the eigenvalues of (A + I) is 0, we have:
(λ1 + 1) * (λ2 + 1) * (λ3 + 1) = 0
5. Eigenvalues of A:
Since the product of the eigenvalues of (A + I) is 0, at least one of the eigenvalues of (A + I) must be 0. This means at least one of the eigenvalues of A must be -1.
6. Eigenvalues of A:
The determinant of A is equal to the product of its eigenvalues. We are given that det(A) = 6. Since one eigenvalue is -1, the product of the other two eigenvalues must be -6.
7. Possible Eigenvalues of A:
Considering the product of the other two eigenvalues of A is -6, and the eigenvalues are real, the possible eigenvalues are:
-1, -2, 3
-1, 2, -3
1, -2, 3
1, 2, -3
8. Eigenvalues of A:
Since the trace of A is 0, the sum of its eigenvalues is 0. Among the possible eigenvalues, only the set -1, -2, 3 satisfies this condition.
Final Answer:
Therefore, the eigenvalues of matrix A are -1, -2, and 3, which matches option 'D'.
- A is a 3x3 matrix with real entries.
- det(A) = 6
- The trace of A is 0.
- det(A + I) = 0, where I denotes the 3x3 identity matrix.
To Find:
The eigenvalues of matrix A.
Solution:
1. Trace of a Matrix:
The trace of a square matrix is the sum of its diagonal elements. Given that the trace of matrix A is 0, we have:
Trace(A) = 0
2. Eigenvalues and Determinant:
The determinant of a matrix is equal to the product of its eigenvalues. We are given that det(A) = 6. Since the matrix A is 3x3, it has three eigenvalues (possibly repeated).
3. Determinant of (A + I):
We are given that det(A + I) = 0. The determinant of a matrix is also equal to the product of its eigenvalues. So, the product of the eigenvalues of (A + I) is 0.
4. Product of Eigenvalues:
Let the eigenvalues of A be λ1, λ2, and λ3. The eigenvalues of (A + I) will be (λ1 + 1), (λ2 + 1), and (λ3 + 1). Since the product of the eigenvalues of (A + I) is 0, we have:
(λ1 + 1) * (λ2 + 1) * (λ3 + 1) = 0
5. Eigenvalues of A:
Since the product of the eigenvalues of (A + I) is 0, at least one of the eigenvalues of (A + I) must be 0. This means at least one of the eigenvalues of A must be -1.
6. Eigenvalues of A:
The determinant of A is equal to the product of its eigenvalues. We are given that det(A) = 6. Since one eigenvalue is -1, the product of the other two eigenvalues must be -6.
7. Possible Eigenvalues of A:
Considering the product of the other two eigenvalues of A is -6, and the eigenvalues are real, the possible eigenvalues are:
-1, -2, 3
-1, 2, -3
1, -2, 3
1, 2, -3
8. Eigenvalues of A:
Since the trace of A is 0, the sum of its eigenvalues is 0. Among the possible eigenvalues, only the set -1, -2, 3 satisfies this condition.
Final Answer:
Therefore, the eigenvalues of matrix A are -1, -2, and 3, which matches option 'D'.
A is any nxn matrix with all entries equal to 1 then 0 is an eigenvalue of A and- a)multiplicity of 0 is n - 1
- b)multiplicity of 0 is 1
- c)multiplicity of 0 is n
- d)multiplicity of 0 is 0
Correct answer is option 'A'. Can you explain this answer?
A is any nxn matrix with all entries equal to 1 then 0 is an eigenvalue of A and
a)
multiplicity of 0 is n - 1
b)
multiplicity of 0 is 1
c)
multiplicity of 0 is n
d)
multiplicity of 0 is 0
|
|
Qiana Sharma answered |
Explanation:
To prove that 0 is an eigenvalue of matrix A, we need to show that there exists a nonzero vector x such that Ax = 0.
Let's consider the matrix A with all entries equal to 1.
Matrix A:
[1 1 1 ... 1]
[1 1 1 ... 1]
[1 1 1 ... 1]
...
[1 1 1 ... 1]
Step 1:
To find the eigenvalues of matrix A, we need to solve the equation (A - λI)x = 0, where λ is the eigenvalue and I is the identity matrix.
Step 2:
Substituting A and I into the equation, we get:
[1-λ 1 1 ... 1]
[1 1-λ 1 ... 1]
[1 1 1-λ ... 1]
...
[1 1 1 ... 1-λ] * [x1, x2, x3, ..., xn] = 0
Step 3:
Expanding this equation, we get n equations:
(1-λ)x1 + x2 + x3 + ... + xn = 0
x1 + (1-λ)x2 + x3 + ... + xn = 0
x1 + x2 + (1-λ)x3 + ... + xn = 0
...
x1 + x2 + x3 + ... + (1-λ)xn = 0
Step 4:
Simplifying these equations, we get:
(1-λ)(x1 + x2 + x3 + ... + xn) = 0
Step 5:
Since all entries of matrix A are equal to 1, the sum of all elements in each row is n.
Step 6:
Therefore, the equation becomes:
(1-λ)(n) = 0
Step 7:
Solving this equation, we get:
1-λ = 0
λ = 1
Conclusion:
From the above steps, we can see that the only eigenvalue of matrix A is 1. Therefore, 0 is an eigenvalue of A with multiplicity n-1.
Hence, the correct answer is option A) multiplicity of 0 is n - 1.
To prove that 0 is an eigenvalue of matrix A, we need to show that there exists a nonzero vector x such that Ax = 0.
Let's consider the matrix A with all entries equal to 1.
Matrix A:
[1 1 1 ... 1]
[1 1 1 ... 1]
[1 1 1 ... 1]
...
[1 1 1 ... 1]
Step 1:
To find the eigenvalues of matrix A, we need to solve the equation (A - λI)x = 0, where λ is the eigenvalue and I is the identity matrix.
Step 2:
Substituting A and I into the equation, we get:
[1-λ 1 1 ... 1]
[1 1-λ 1 ... 1]
[1 1 1-λ ... 1]
...
[1 1 1 ... 1-λ] * [x1, x2, x3, ..., xn] = 0
Step 3:
Expanding this equation, we get n equations:
(1-λ)x1 + x2 + x3 + ... + xn = 0
x1 + (1-λ)x2 + x3 + ... + xn = 0
x1 + x2 + (1-λ)x3 + ... + xn = 0
...
x1 + x2 + x3 + ... + (1-λ)xn = 0
Step 4:
Simplifying these equations, we get:
(1-λ)(x1 + x2 + x3 + ... + xn) = 0
Step 5:
Since all entries of matrix A are equal to 1, the sum of all elements in each row is n.
Step 6:
Therefore, the equation becomes:
(1-λ)(n) = 0
Step 7:
Solving this equation, we get:
1-λ = 0
λ = 1
Conclusion:
From the above steps, we can see that the only eigenvalue of matrix A is 1. Therefore, 0 is an eigenvalue of A with multiplicity n-1.
Hence, the correct answer is option A) multiplicity of 0 is n - 1.
Which of the following statement is correct?- a)The matrix A and its transpose AT have the same characteristic polynomial.
- b)Similar matrices have not the same characteristic polynomial.
- c)The trace of two similar matrices are not same.
- d)The determinant of two similar matrices is not same.
Correct answer is option 'A'. Can you explain this answer?
Which of the following statement is correct?
a)
The matrix A and its transpose AT have the same characteristic polynomial.
b)
Similar matrices have not the same characteristic polynomial.
c)
The trace of two similar matrices are not same.
d)
The determinant of two similar matrices is not same.

|
Abhishek Nambiar answered |
Explanation:
Characteristic polynomial:
The characteristic polynomial of a square matrix A is defined as the polynomial det(A - λI) where det denotes the determinant, I is the identity matrix, and λ is a scalar variable.
Statement (a):
The matrix A and its transpose AT have the same characteristic polynomial.
This statement is true. The proof is given below:
- Let A be a square matrix of order n.
- Then, the characteristic polynomial of A is det(A - λI) where I is the n × n identity matrix.
- Now, consider the transpose of A, denoted by AT.
- The characteristic polynomial of AT is det(AT - λI).
- We know that (AT - λI) = (A - λI)T.
- Therefore, det(AT - λI) = det((A - λI)T) = det(A - λI).
- Hence, the matrix A and its transpose AT have the same characteristic polynomial.
Statement (b):
Similar matrices have not the same characteristic polynomial.
This statement is false. Similar matrices have the same characteristic polynomial.
- Two matrices A and B are said to be similar if there exists an invertible matrix P such that B = P-1AP.
- If A and B are similar matrices, then they have the same eigenvalues.
- The eigenvalues of a matrix are the roots of its characteristic polynomial.
- Hence, similar matrices have the same characteristic polynomial.
Statement (c):
The trace of two similar matrices are not same.
This statement is false. Similar matrices have the same trace.
- The trace of a matrix is the sum of its diagonal elements.
- If A and B are similar matrices, then they have the same characteristic polynomial and hence the same eigenvalues.
- The sum of the eigenvalues of a matrix is equal to its trace.
- Therefore, similar matrices have the same trace.
Statement (d):
The determinant of two similar matrices is not same.
This statement is false. Similar matrices have the same determinant.
- If A and B are similar matrices, then they have the same characteristic polynomial and hence the same eigenvalues.
- The determinant of a matrix is equal to the product of its eigenvalues.
- Therefore, similar matrices have the same determinant.
Characteristic polynomial:
The characteristic polynomial of a square matrix A is defined as the polynomial det(A - λI) where det denotes the determinant, I is the identity matrix, and λ is a scalar variable.
Statement (a):
The matrix A and its transpose AT have the same characteristic polynomial.
This statement is true. The proof is given below:
- Let A be a square matrix of order n.
- Then, the characteristic polynomial of A is det(A - λI) where I is the n × n identity matrix.
- Now, consider the transpose of A, denoted by AT.
- The characteristic polynomial of AT is det(AT - λI).
- We know that (AT - λI) = (A - λI)T.
- Therefore, det(AT - λI) = det((A - λI)T) = det(A - λI).
- Hence, the matrix A and its transpose AT have the same characteristic polynomial.
Statement (b):
Similar matrices have not the same characteristic polynomial.
This statement is false. Similar matrices have the same characteristic polynomial.
- Two matrices A and B are said to be similar if there exists an invertible matrix P such that B = P-1AP.
- If A and B are similar matrices, then they have the same eigenvalues.
- The eigenvalues of a matrix are the roots of its characteristic polynomial.
- Hence, similar matrices have the same characteristic polynomial.
Statement (c):
The trace of two similar matrices are not same.
This statement is false. Similar matrices have the same trace.
- The trace of a matrix is the sum of its diagonal elements.
- If A and B are similar matrices, then they have the same characteristic polynomial and hence the same eigenvalues.
- The sum of the eigenvalues of a matrix is equal to its trace.
- Therefore, similar matrices have the same trace.
Statement (d):
The determinant of two similar matrices is not same.
This statement is false. Similar matrices have the same determinant.
- If A and B are similar matrices, then they have the same characteristic polynomial and hence the same eigenvalues.
- The determinant of a matrix is equal to the product of its eigenvalues.
- Therefore, similar matrices have the same determinant.
Let 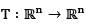 such that T(x1, x2, ...., xn) = (0, x1, x2, ..... xn - 1) then
such that T(x1, x2, ...., xn) = (0, x1, x2, ..... xn - 1) then- a)T is diagonalizable
- b)T is invertible
- c)T is nilpotent
- d)Either diagonalizable or nilpotent
Correct answer is option 'C'. Can you explain this answer?
Let 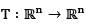 such that T(x1, x2, ...., xn) = (0, x1, x2, ..... xn - 1) then
such that T(x1, x2, ...., xn) = (0, x1, x2, ..... xn - 1) then
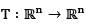 such that T(x1, x2, ...., xn) = (0, x1, x2, ..... xn - 1) then
such that T(x1, x2, ...., xn) = (0, x1, x2, ..... xn - 1) thena)
T is diagonalizable
b)
T is invertible
c)
T is nilpotent
d)
Either diagonalizable or nilpotent
|
|
Tanuja Sharma answered |
When we make it's started basis then one row / Colmans all elements are zero so it is nilpotent matrix.
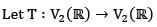 where T be the reflection of the points through the line y = -x then the matrix of T with respect to standard basis is
where T be the reflection of the points through the line y = -x then the matrix of T with respect to standard basis is- a)
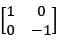
- b)

- c)
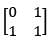
- d)
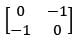
Correct answer is option 'D'. Can you explain this answer?
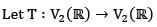 where T be the reflection of the points through the line y = -x then the matrix of T with respect to standard basis is
where T be the reflection of the points through the line y = -x then the matrix of T with respect to standard basis isa)
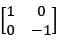
b)

c)
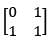
d)
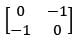

|
Shubha Madevi answered |
The reflection of the point (x,y) across the line y= -x is (-y,-x).
The transformation is defined by T(x,y)=(-y,-x).
Find the basis for this transformation w.r.t standard basis you will get the solution
The transformation is defined by T(x,y)=(-y,-x).
Find the basis for this transformation w.r.t standard basis you will get the solution
If T be a linear operator on a vector space V such that T2 - T + 1 = 0 then- a)T is one-one but may not be onto.
- b)T is onto but may not be one-one.
- c)T is invertible.
- d)No such T exists.
Correct answer is option 'C'. Can you explain this answer?
If T be a linear operator on a vector space V such that T2 - T + 1 = 0 then
a)
T is one-one but may not be onto.
b)
T is onto but may not be one-one.
c)
T is invertible.
d)
No such T exists.
|
|
Eesha Mehta answered |
To prove that the correct answer is option 'C', we need to show that if T is a linear operator on a vector space V such that T^2 - T + 1 = 0, then T is invertible.
Given: T^2 - T + 1 = 0
To prove: T is invertible
Proof:
1. Assume that T is not invertible. This means that there exists a nonzero vector v in V such that T(v) = 0.
2. Applying T to both sides of the given equation, we get:
T(T^2 - T + 1) = T(0)
T^3 - T^2 + T = 0
3. Rearranging the terms, we have:
T(T^2 - T) = T^2
4. Since T(v) = 0, we can substitute T(v) with 0 in the above equation:
T(0) = T^2
0 = T^2
5. Multiplying both sides by T, we get:
T(0) = T(T^2)
0 = T^3
6. Substituting T^3 with T^2 - T in the above equation (from step 2), we have:
0 = T^2 - T
T^2 = T
7. Substituting T^2 with T in the given equation, we get:
T - T + 1 = 0
1 = 0
8. This is a contradiction, as 1 cannot be equal to 0.
9. Therefore, our assumption that T is not invertible is incorrect, and T must be invertible.
Hence, the correct answer is option 'C': T is invertible.
Given: T^2 - T + 1 = 0
To prove: T is invertible
Proof:
1. Assume that T is not invertible. This means that there exists a nonzero vector v in V such that T(v) = 0.
2. Applying T to both sides of the given equation, we get:
T(T^2 - T + 1) = T(0)
T^3 - T^2 + T = 0
3. Rearranging the terms, we have:
T(T^2 - T) = T^2
4. Since T(v) = 0, we can substitute T(v) with 0 in the above equation:
T(0) = T^2
0 = T^2
5. Multiplying both sides by T, we get:
T(0) = T(T^2)
0 = T^3
6. Substituting T^3 with T^2 - T in the above equation (from step 2), we have:
0 = T^2 - T
T^2 = T
7. Substituting T^2 with T in the given equation, we get:
T - T + 1 = 0
1 = 0
8. This is a contradiction, as 1 cannot be equal to 0.
9. Therefore, our assumption that T is not invertible is incorrect, and T must be invertible.
Hence, the correct answer is option 'C': T is invertible.
Chapter doubts & questions for Vector Space & Linear Transformation - Mathematics for Competitive Exams 2025 is part of Mathematics exam preparation. The chapters have been prepared according to the Mathematics exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mathematics 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Vector Space & Linear Transformation - Mathematics for Competitive Exams in English & Hindi are available as part of Mathematics exam.
Download more important topics, notes, lectures and mock test series for Mathematics Exam by signing up for free.
Mathematics for Competitive Exams
98 videos|37 docs|32 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup
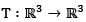 be the linear transformation defined by T(x1, x2, x3) = (x1 + 3x2 + 2x3, 4x2 + x3, 2x + x2 - x3). The dimension of null space of T3 is
be the linear transformation defined by T(x1, x2, x3) = (x1 + 3x2 + 2x3, 4x2 + x3, 2x + x2 - x3). The dimension of null space of T3 is

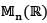 denotes the space of all n x n real matrices. If
denotes the space of all n x n real matrices. If 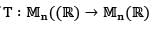 is a linear transformation such thatT(A) = 0 whenever
is a linear transformation such thatT(A) = 0 whenever 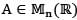 is symmetric or skew symmetric then the rank of T is
is symmetric or skew symmetric then the rank of T is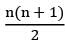

 satisfying f" - 2f' + f = 0. Define
satisfying f" - 2f' + f = 0. Define  by T(f) = (f'(0), f(0)).Then T is
by T(f) = (f'(0), f(0)).Then T is
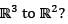
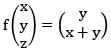
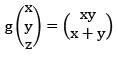
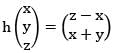

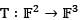 be defined by T(x1, x2) = (x1, x2 + x2, x2). Then the nullity of T is
be defined by T(x1, x2) = (x1, x2 + x2, x2). Then the nullity of T is
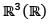 defined as T(x,y,z) = (2y + z, x - 4y, 3x) with respect to the basis β = {(1,1,1), (1,1,0), (1,0,0)} is
defined as T(x,y,z) = (2y + z, x - 4y, 3x) with respect to the basis β = {(1,1,1), (1,1,0), (1,0,0)} is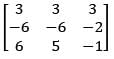
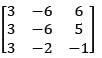
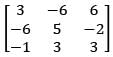

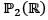 be the polynomial space with basis {1, x, x2} then matrix representation of
be the polynomial space with basis {1, x, x2} then matrix representation of 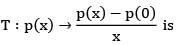



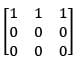
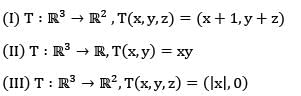
 and the maps
and the maps 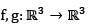 defined by f(x,y,z) = (x, |y|,z) and g(x,y,z) = (x + 1,y - 1, z).Then
defined by f(x,y,z) = (x, |y|,z) and g(x,y,z) = (x + 1,y - 1, z).Then 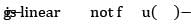
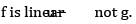
 is not a linear mapping?
is not a linear mapping?
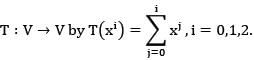 The matrix of T-1 with respect to the basis {1, x, x2} is
The matrix of T-1 with respect to the basis {1, x, x2} is