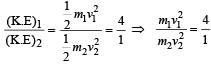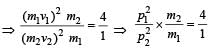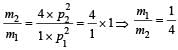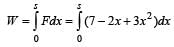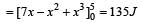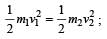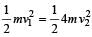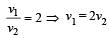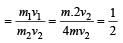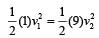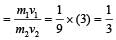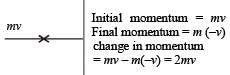All Exams >
NEET >
NEET Past Year Papers >
All Questions
All questions of Work, Energy and Power for NEET Exam
Two identical balls A and B moving with velocities +0.5 m/s and –0.3 m/s respectively, collide head on elastically. The velocities of the balls A and B after collision, will be, respectively [1991]- a)+0.5 m/s and +0.3 m/s
- b)– 0.3 m/s and +0.5 m/s
- c)+0.3 m/s and 0.5 m/s
- d)–0.5 m/s and +0.3 m/s
Correct answer is option 'B'. Can you explain this answer?
Two identical balls A and B moving with velocities +0.5 m/s and –0.3 m/s respectively, collide head on elastically. The velocities of the balls A and B after collision, will be, respectively [1991]
a)
+0.5 m/s and +0.3 m/s
b)
– 0.3 m/s and +0.5 m/s
c)
+0.3 m/s and 0.5 m/s
d)
–0.5 m/s and +0.3 m/s

|
Kajal Bose answered |
When the identical balls collide head-on, their velocities are exchanged.
Water falls from a height of 60 m at the rate of 15 kg/s to operate a turbine. The losses due to frictional force are 10% of energy. How much power is generated by the turbine?( g = 10 m/s2) [2008]
- a)8.1 kW
- b)10.2 kW
- c)12.3 kW
- d)7.0 kW
Correct answer is option 'A'. Can you explain this answer?
Water falls from a height of 60 m at the rate of 15 kg/s to operate a turbine. The losses due to frictional force are 10% of energy. How much power is generated by the turbine?( g = 10 m/s2) [2008]
a)
8.1 kW
b)
10.2 kW
c)
12.3 kW
d)
7.0 kW

|
Arnav Iyer answered |
Given, h = 60m, g = 10 ms–2, Rate of flow of water = 15 kg/s
∴ Power of the falling water = 15 kgs–1 × 10 ms–2 × 60 m = 900 watt.
Loss in energy due to friction
Loss in energy due to friction
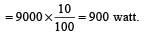
∴ Power generated by the turbine = ( 9000 – 900) watt = 8100 watt = 8.1 kW
A bomb of mass 30 kg at rest explodes into two pieces of masses 18 kg and 12 kg. The velocity of 18 kg mass is 6 ms–1. The kinetic energy of the other mass is [2005]- a)324 J
- b)486 J
- c)256 J
- d)524 J
Correct answer is option 'B'. Can you explain this answer?
A bomb of mass 30 kg at rest explodes into two pieces of masses 18 kg and 12 kg. The velocity of 18 kg mass is 6 ms–1. The kinetic energy of the other mass is [2005]
a)
324 J
b)
486 J
c)
256 J
d)
524 J

|
Sarthak Saini answered |
From conservation of linear momentum
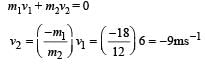
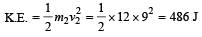
The potential energy of a system increases if work is done [2011]- a)upon the system by a n on conser vative force
- b)upon the system by a conservative force
- c)by the system against a non conservative force
- d)by the system against a conservative force
Correct answer is option 'D'. Can you explain this answer?
The potential energy of a system increases if work is done [2011]
a)
upon the system by a n on conser vative force
b)
upon the system by a conservative force
c)
by the system against a non conservative force
d)
by the system against a conservative force
|
|
Avantika Kumar answered |
Explanation:
When work is done on a system against a conservative force, the potential energy of the system increases.
- Conservative Force: A force is said to be conservative if the work done by the force on a particle moving from one point to another depends only on the initial and final positions of the particle and not on the path followed by the particle.
- Potential Energy: Potential energy is the energy possessed by a system due to the relative positions of its components. It is a scalar quantity and is measured in joules (J).
In the given options, only option D mentions work done by the system against a conservative force, which is the correct answer.
When a system does work against a conservative force, the energy is stored in the system as potential energy. This potential energy can be released later when the system returns to its original position or configuration.
For example, when a spring is compressed by an external force, the system stores potential energy. When the external force is removed, the spring returns to its original position and releases the stored potential energy.
Hence, the potential energy of a system increases when work is done by the system against a conservative force.
When work is done on a system against a conservative force, the potential energy of the system increases.
- Conservative Force: A force is said to be conservative if the work done by the force on a particle moving from one point to another depends only on the initial and final positions of the particle and not on the path followed by the particle.
- Potential Energy: Potential energy is the energy possessed by a system due to the relative positions of its components. It is a scalar quantity and is measured in joules (J).
In the given options, only option D mentions work done by the system against a conservative force, which is the correct answer.
When a system does work against a conservative force, the energy is stored in the system as potential energy. This potential energy can be released later when the system returns to its original position or configuration.
For example, when a spring is compressed by an external force, the system stores potential energy. When the external force is removed, the spring returns to its original position and releases the stored potential energy.
Hence, the potential energy of a system increases when work is done by the system against a conservative force.
If the kinetic energy of a particle is increased by 300%, the momentum of the particle will increase by[2002]- a)20%
- b)200%
- c)100%
- d)50%
Correct answer is option 'C'. Can you explain this answer?
If the kinetic energy of a particle is increased by 300%, the momentum of the particle will increase by[2002]
a)
20%
b)
200%
c)
100%
d)
50%

|
Pooja Saha answered |
New K.E., E' = 4E
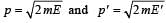
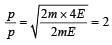
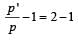
[on substrating 1 in both sides.]
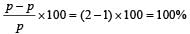
A 0.5 kg ball moving with speed of 12 m/s strikes a hard wall at an angle of 30° with the wall. It is reflected with the same speed and at the same angle. If the ball is in contact with the wall for 0.25 seconds, the average force acting on the wall is[2006]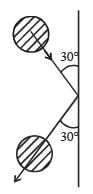
- a)24 N
- b)12 N
- c)96 N
- d)48 N
Correct answer is option 'A'. Can you explain this answer?
A 0.5 kg ball moving with speed of 12 m/s strikes a hard wall at an angle of 30° with the wall. It is reflected with the same speed and at the same angle. If the ball is in contact with the wall for 0.25 seconds, the average force acting on the wall is[2006]

a)
24 N
b)
12 N
c)
96 N
d)
48 N

|
Ias Masters answered |
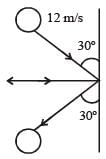
Resolving the velocities in vertical and horizontal directions, resolved parts of first velocity
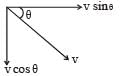
v cosθ perpendicular to the wall and v sinθ parallel to the wall. In the second case, they are –v sinθ & v cosθ respectively. Here, –ve sign is because direction is opposite to the earlier ones. So we see a net change in velocity perpendicular to way = v sinθ – (–v sinθ) = 2v sinθ
This change has occured in 0.25 sec, so, rate of change of velocity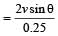
This change has occured in 0.25 sec, so, rate of change of velocity
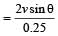
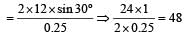
Thus, acceleration a = 48 m/sec2
Force applied = m . a = 0.5 × 48 = 24 N
A shell of mass 200 gm is ejected from a gun of mass 4 kg by an explosion that generates 1.05 kJ of energy. The initial velocity of the shell is:- a)100 ms–1
- b)80 ms–1 [2008]
- c)40 ms–1
- d)120 ms–1
Correct answer is option 'A'. Can you explain this answer?
A shell of mass 200 gm is ejected from a gun of mass 4 kg by an explosion that generates 1.05 kJ of energy. The initial velocity of the shell is:
a)
100 ms–1
b)
80 ms–1 [2008]
c)
40 ms–1
d)
120 ms–1
|
|
Rajeev Saxena answered |
Solution: Option A is correct option.
Explanation is given as follows.
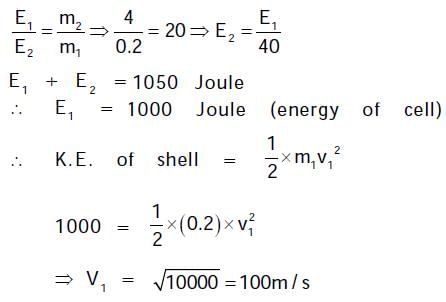
If the momentum of a body is increased by 50%, then the percentage increase in its kinetic energy is[1995]- a)50%
- b)100%
- c)125%
- d)200%
Correct answer is option 'C'. Can you explain this answer?
If the momentum of a body is increased by 50%, then the percentage increase in its kinetic energy is[1995]
a)
50%
b)
100%
c)
125%
d)
200%
|
|
Anand Chaudhary answered |
Explanation:
Let the initial momentum (P) of the body be P and its initial kinetic energy (K) be K.
According to the question, the momentum of the body is increased by 50%.
Therefore, the new momentum (P') of the body is:
P' = P + (50/100) * P = 1.5P
The kinetic energy of a body is given by:
K = (1/2) * m * v^2
where m is the mass of the body and v is its velocity.
Since the mass of the body remains constant, the kinetic energy is directly proportional to the square of its velocity.
Let the initial velocity (v) of the body be v and its new velocity (v') be v'.
Since momentum is given by:
P = m * v
and
P' = m * v'
we can write:
m * v' = 1.5 * m * v
or
v' = (3/2) * v
Therefore, the new kinetic energy (K') of the body is:
K' = (1/2) * m * v'^2
Substituting the value of v' in the above equation, we get:
K' = (1/2) * m * (3/2)^2 * v^2
K' = (9/8) * K
Therefore, the percentage increase in kinetic energy is:
(K' - K)/K * 100%
= [(9/8)K - K]/K * 100%
= (1/8) * 100%
= 12.5%
Hence, the correct option is (c) 125%.
A body projected ver tically fr om the ear th reaches a height equal to earth's radius before returning to the earth. The power exerted by the gravitational force is greatest [2011]- a)at the highest position of the body
- b)at the instant just before the body hits the earth
- c)it remains constant all through
- d)at the instant just after the body is projected
Correct answer is option 'B'. Can you explain this answer?
A body projected ver tically fr om the ear th reaches a height equal to earth's radius before returning to the earth. The power exerted by the gravitational force is greatest [2011]
a)
at the highest position of the body
b)
at the instant just before the body hits the earth
c)
it remains constant all through
d)
at the instant just after the body is projected
|
|
Anshika Roy answered |
**Answer:**
The power exerted by the gravitational force can be calculated using the formula:
Power = force x velocity
When a body is projected vertically upwards, the only force acting on it is the gravitational force. The gravitational force is given by:
F = mg
Where:
F = gravitational force
m = mass of the body
g = acceleration due to gravity
Since the body reaches a height equal to the Earth's radius, the distance traveled by the body is 2 times the Earth's radius. Let's assume the Earth's radius is R.
Therefore, the work done against the gravitational force is given by:
Work = force x distance
= mg x 2R
= 2mgR
Now, the time taken to reach the maximum height is given by:
t = (2u sinθ) / g
Where:
t = time taken
u = initial velocity
θ = angle of projection
g = acceleration due to gravity
Since the body is projected vertically upwards, the angle of projection is 90° and the sine of 90° is 1.
Therefore, the time taken to reach the maximum height is:
t = (2u) / g
Now, the power exerted by the gravitational force can be calculated using the formula:
Power = Work / time
= (2mgR) / [(2u) / g]
= mg^2R/u
From this equation, we can see that the power exerted by the gravitational force is inversely proportional to the initial velocity (u). As the body reaches the highest position, the velocity becomes zero. Therefore, the power exerted by the gravitational force is greatest at the highest position of the body.
Hence, the correct answer is option 'A' - at the highest position of the body.
The power exerted by the gravitational force can be calculated using the formula:
Power = force x velocity
When a body is projected vertically upwards, the only force acting on it is the gravitational force. The gravitational force is given by:
F = mg
Where:
F = gravitational force
m = mass of the body
g = acceleration due to gravity
Since the body reaches a height equal to the Earth's radius, the distance traveled by the body is 2 times the Earth's radius. Let's assume the Earth's radius is R.
Therefore, the work done against the gravitational force is given by:
Work = force x distance
= mg x 2R
= 2mgR
Now, the time taken to reach the maximum height is given by:
t = (2u sinθ) / g
Where:
t = time taken
u = initial velocity
θ = angle of projection
g = acceleration due to gravity
Since the body is projected vertically upwards, the angle of projection is 90° and the sine of 90° is 1.
Therefore, the time taken to reach the maximum height is:
t = (2u) / g
Now, the power exerted by the gravitational force can be calculated using the formula:
Power = Work / time
= (2mgR) / [(2u) / g]
= mg^2R/u
From this equation, we can see that the power exerted by the gravitational force is inversely proportional to the initial velocity (u). As the body reaches the highest position, the velocity becomes zero. Therefore, the power exerted by the gravitational force is greatest at the highest position of the body.
Hence, the correct answer is option 'A' - at the highest position of the body.
One coolie takes 1 minute to raise a suitcase through a height of 2 m but the second coolie takes 30 s to raise the same suitcase to the same height. The powers of two coolies are in the ratio of [NEET Kar. 2013]- a)1 : 2
- b)1 : 3
- c)2 : 1
- d)3 : 1
Correct answer is option 'A'. Can you explain this answer?
One coolie takes 1 minute to raise a suitcase through a height of 2 m but the second coolie takes 30 s to raise the same suitcase to the same height. The powers of two coolies are in the ratio of [NEET Kar. 2013]
a)
1 : 2
b)
1 : 3
c)
2 : 1
d)
3 : 1

|
Rajeev Sharma answered |
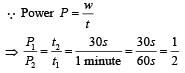
(t1 = 1 minute; t2 = 30 second given)
An explosion blows a rock into three parts. Two parts go off at right angles to each other. These two are, 1 kg first part moving with a velocity of 12 ms–1 and 2 kg second part moving with a velocity of 8 ms–1. If the third part flies off with a velocity of 4 ms–1, its mass would be: [2009]- a)7 kg
- b)17 kg
- c)3 kg
- d)5 kg
Correct answer is option 'D'. Can you explain this answer?
An explosion blows a rock into three parts. Two parts go off at right angles to each other. These two are, 1 kg first part moving with a velocity of 12 ms–1 and 2 kg second part moving with a velocity of 8 ms–1. If the third part flies off with a velocity of 4 ms–1, its mass would be: [2009]
a)
7 kg
b)
17 kg
c)
3 kg
d)
5 kg
|
|
Anoushka Kaur answered |
$^{-1}$ and 2 kg second part moving with a velocity of 8 ms$^{-1}$. What is the mass and velocity of the third part?
To solve this problem, we need to use the law of conservation of momentum. According to this law, the total momentum of a system of objects remains constant if there are no external forces acting on the system. In other words, the sum of the momenta of all the objects before the explosion is equal to the sum of the momenta of all the objects after the explosion.
Before the explosion, the rock had zero velocity, so its momentum was zero. After the explosion, the two parts that went off at right angles to each other have the following momenta:
First part: momentum = mass x velocity = 1 kg x 12 ms$^{-1}$ = 12 kg ms$^{-1}$
Second part: momentum = mass x velocity = 2 kg x 8 ms$^{-1}$ = 16 kg ms$^{-1}$
The total momentum of these two parts is:
Total momentum = 12 kg ms$^{-1}$ + 16 kg ms$^{-1}$ = 28 kg ms$^{-1}$
According to the law of conservation of momentum, the momentum of the third part must be equal and opposite to the total momentum of the first two parts. Let's call the mass of the third part "m" and its velocity "v". Then we have:
Momentum of third part = -28 kg ms$^{-1}$
Momentum = mass x velocity
Therefore:
-mv = -28 kg ms$^{-1}$
Solving for "m", we get:
m = 28/v
Now we can use the law of conservation of energy to find the velocity of the third part. According to this law, the total kinetic energy of a system of objects remains constant if there are no external forces acting on the system. In other words, the sum of the kinetic energies of all the objects before the explosion is equal to the sum of the kinetic energies of all the objects after the explosion.
Before the explosion, the rock had zero kinetic energy, so its total kinetic energy was zero. After the explosion, the two parts that went off at right angles to each other have the following kinetic energies:
First part: KE = 0.5 x mass x velocity$^2$ = 0.5 x 1 kg x (12 ms$^{-1}$)$^2$ = 72 J
Second part: KE = 0.5 x mass x velocity$^2$ = 0.5 x 2 kg x (8 ms$^{-1}$)$^2$ = 64 J
The total kinetic energy of these two parts is:
Total KE = 72 J + 64 J = 136 J
According to the law of conservation of energy, the kinetic energy of the third part must be equal to the difference between the total kinetic energy of the first two parts and the initial kinetic energy of the rock. The initial kinetic energy of the rock was zero, so we have:
KE of third part = Total KE - 0 = 136 J
Using the formula for kinetic energy, we can write:
0.5mv$^2$ = 136 J
Solving for "v", we get:
v = $\sqrt{\frac{272}{m}}$
Substituting
To solve this problem, we need to use the law of conservation of momentum. According to this law, the total momentum of a system of objects remains constant if there are no external forces acting on the system. In other words, the sum of the momenta of all the objects before the explosion is equal to the sum of the momenta of all the objects after the explosion.
Before the explosion, the rock had zero velocity, so its momentum was zero. After the explosion, the two parts that went off at right angles to each other have the following momenta:
First part: momentum = mass x velocity = 1 kg x 12 ms$^{-1}$ = 12 kg ms$^{-1}$
Second part: momentum = mass x velocity = 2 kg x 8 ms$^{-1}$ = 16 kg ms$^{-1}$
The total momentum of these two parts is:
Total momentum = 12 kg ms$^{-1}$ + 16 kg ms$^{-1}$ = 28 kg ms$^{-1}$
According to the law of conservation of momentum, the momentum of the third part must be equal and opposite to the total momentum of the first two parts. Let's call the mass of the third part "m" and its velocity "v". Then we have:
Momentum of third part = -28 kg ms$^{-1}$
Momentum = mass x velocity
Therefore:
-mv = -28 kg ms$^{-1}$
Solving for "m", we get:
m = 28/v
Now we can use the law of conservation of energy to find the velocity of the third part. According to this law, the total kinetic energy of a system of objects remains constant if there are no external forces acting on the system. In other words, the sum of the kinetic energies of all the objects before the explosion is equal to the sum of the kinetic energies of all the objects after the explosion.
Before the explosion, the rock had zero kinetic energy, so its total kinetic energy was zero. After the explosion, the two parts that went off at right angles to each other have the following kinetic energies:
First part: KE = 0.5 x mass x velocity$^2$ = 0.5 x 1 kg x (12 ms$^{-1}$)$^2$ = 72 J
Second part: KE = 0.5 x mass x velocity$^2$ = 0.5 x 2 kg x (8 ms$^{-1}$)$^2$ = 64 J
The total kinetic energy of these two parts is:
Total KE = 72 J + 64 J = 136 J
According to the law of conservation of energy, the kinetic energy of the third part must be equal to the difference between the total kinetic energy of the first two parts and the initial kinetic energy of the rock. The initial kinetic energy of the rock was zero, so we have:
KE of third part = Total KE - 0 = 136 J
Using the formula for kinetic energy, we can write:
0.5mv$^2$ = 136 J
Solving for "v", we get:
v = $\sqrt{\frac{272}{m}}$
Substituting
Two spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction.
- a)Same as that of B [2012]
- b)Opposite to that of B
- c)θ = tan–1 (1/2) to the x-axis
- d)θ = tan–1 (–1/2) to the x-axis
Correct answer is option 'C'. Can you explain this answer?
Two spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction.
a)
Same as that of B [2012]
b)
Opposite to that of B
c)
θ = tan–1 (1/2) to the x-axis
d)
θ = tan–1 (–1/2) to the x-axis
|
|
Kavya Choudhury answered |
Perpendicular to the original direction of B
d)Cannot be determined
Answer:
c) Perpendicular to the original direction of B
Explanation:
We can solve this problem using conservation of momentum and conservation of kinetic energy.
Before the collision, the total momentum of the system is:
p = m2v
Since sphere A is at rest, its momentum is zero.
The total kinetic energy of the system before the collision is:
K = (1/2)m2v^2
After the collision, the spheres move in different directions. Let the velocity of sphere A be u and the velocity of sphere B be w. Then, the total momentum of the system after the collision is:
p' = m1u + m2w
Since sphere B moves perpendicular to its original direction, we can write:
w = 2v
Using conservation of momentum, we have:
m2v = m1u + m2(2v)
Simplifying, we get:
u = (m2 - 2m1)v / m1
Now, using conservation of kinetic energy, we have:
(1/2)m1u^2 + (1/2)m2w^2 = (1/2)m2v^2
Substituting the values of u and w, we get:
(m2 - 2m1)v^2 = m1u^2
Simplifying, we get:
u = sqrt((m2 - 2m1)/m1) v
Since m1 and m2 are positive, (m2 - 2m1)/m1 is negative. Therefore, u is imaginary, which means that sphere A moves in a direction perpendicular to the original direction of sphere B. Hence, the answer is option c) Perpendicular to the original direction of B.
d)Cannot be determined
Answer:
c) Perpendicular to the original direction of B
Explanation:
We can solve this problem using conservation of momentum and conservation of kinetic energy.
Before the collision, the total momentum of the system is:
p = m2v
Since sphere A is at rest, its momentum is zero.
The total kinetic energy of the system before the collision is:
K = (1/2)m2v^2
After the collision, the spheres move in different directions. Let the velocity of sphere A be u and the velocity of sphere B be w. Then, the total momentum of the system after the collision is:
p' = m1u + m2w
Since sphere B moves perpendicular to its original direction, we can write:
w = 2v
Using conservation of momentum, we have:
m2v = m1u + m2(2v)
Simplifying, we get:
u = (m2 - 2m1)v / m1
Now, using conservation of kinetic energy, we have:
(1/2)m1u^2 + (1/2)m2w^2 = (1/2)m2v^2
Substituting the values of u and w, we get:
(m2 - 2m1)v^2 = m1u^2
Simplifying, we get:
u = sqrt((m2 - 2m1)/m1) v
Since m1 and m2 are positive, (m2 - 2m1)/m1 is negative. Therefore, u is imaginary, which means that sphere A moves in a direction perpendicular to the original direction of sphere B. Hence, the answer is option c) Perpendicular to the original direction of B.
An engine pumps water through a hose pipe.Water passes through the pipe and leaves it with a velocity of 2 m/s. The mass per unit length of water in the pipe is 100 kg/m. What is the power of the engine? [2010]
- a)400 W
- b)200 W
- c)100 W
- d)800 W
Correct answer is option 'D'. Can you explain this answer?
An engine pumps water through a hose pipe.Water passes through the pipe and leaves it with a velocity of 2 m/s. The mass per unit length of water in the pipe is 100 kg/m. What is the power of the engine? [2010]
a)
400 W
b)
200 W
c)
100 W
d)
800 W
|
|
Nitya Shah answered |
Given:
Velocity of water, v = 2 m/s
Mass per unit length of water, m = 100 kg/m
To find:
Power of the engine
Formula used:
Power = Force × Velocity
Force = mass × acceleration = mass × change in velocity / time
Change in velocity = final velocity - initial velocity = v - 0 = v
Time taken to move out of the pipe, t = length of the pipe / velocity of water
Let the length of the pipe be L.
Therefore, t = L / v
Force = m × v / t = m × v² / L
Power = Force × Velocity = m × v² / L × v = m × v² / L
Substituting the given values, we get:
Power = 100 kg/m × (2 m/s)² / L = 400 W
Therefore, the power of the engine is 400 W.
Velocity of water, v = 2 m/s
Mass per unit length of water, m = 100 kg/m
To find:
Power of the engine
Formula used:
Power = Force × Velocity
Force = mass × acceleration = mass × change in velocity / time
Change in velocity = final velocity - initial velocity = v - 0 = v
Time taken to move out of the pipe, t = length of the pipe / velocity of water
Let the length of the pipe be L.
Therefore, t = L / v
Force = m × v / t = m × v² / L
Power = Force × Velocity = m × v² / L × v = m × v² / L
Substituting the given values, we get:
Power = 100 kg/m × (2 m/s)² / L = 400 W
Therefore, the power of the engine is 400 W.
How much water, a pump of 2 kW can raise in one minute to a height of 10 m, take g = 10 m/s2? [1990]- a)1000 litres
- b)1200 litres
- c)100 litres
- d)2000 litres
Correct answer is option 'B'. Can you explain this answer?
How much water, a pump of 2 kW can raise in one minute to a height of 10 m, take g = 10 m/s2? [1990]
a)
1000 litres
b)
1200 litres
c)
100 litres
d)
2000 litres

|
Pooja Saha answered |
 Here, P = 2kW = 2000 W..
Here, P = 2kW = 2000 W..W = Mgh = M × 10 × 10 = 100 M and t = 60 s.
This gives, M = 1200 kg Its volume = 1200 litre as 1 litre of water contains 1 kg of its mass.
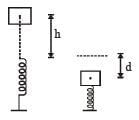
A vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring so that the spring is compressed by a distance d. The net work done in the process is [2007]- a)
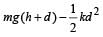
- b)
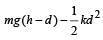
- c)
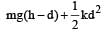
- d)
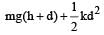
Correct answer is option 'A'. Can you explain this answer?
A vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring so that the spring is compressed by a distance d. The net work done in the process is [2007]
a)
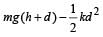
b)
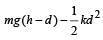
c)
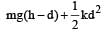
d)
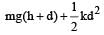

|
Diya Datta answered |
Gravitational potential energy of ball gets converted into elastic potential energy of the spring.
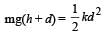
Net work done 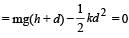
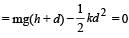
A person holding a rifle (mass of person and rifle together is 100 kg) stands on a smooth surface and fires 10 shots horizontally, in 5 s.Each bullet has a mass of 10 g with a muzzle velocity of 800 ms–1. The final velocity acquired by the person and the average force exerted on the person are [NEET Kar. 2013]- a)–1.6 ms–1; 8 N
- b)–0.08 ms–1; 16 N
- c)– 0.8 ms–1; 16 N
- d)–1.6 ms–1; 16 N
Correct answer is option 'C'. Can you explain this answer?
A person holding a rifle (mass of person and rifle together is 100 kg) stands on a smooth surface and fires 10 shots horizontally, in 5 s.Each bullet has a mass of 10 g with a muzzle velocity of 800 ms–1. The final velocity acquired by the person and the average force exerted on the person are [NEET Kar. 2013]
a)
–1.6 ms–1; 8 N
b)
–0.08 ms–1; 16 N
c)
– 0.8 ms–1; 16 N
d)
–1.6 ms–1; 16 N
|
|
Ananya Basak answered |
We have to use the Law of momentum conservation:
P ( initial ) = P ( final )
0 = n · m · u + ( M - n · m ) · v
where: n = 10, m = 10 g = 0.01 kg, u = 800 m/s, M = 100 kg.
0 = 10 · 0.01 kg · 800 m/s + ( 100 kg - 10 · 0.01 kg ) · v
v = - 80 kgm/s / 99.9 kgm/s
v = 0.8 m/s
Then : F = Δ P / Δ t = ( 10 · 0.01 kg · 800 m/s ) : 5 s = 16 N
Answer: The average force exerted on the person is 16 N.
A bomb of mass 1 kg is thr own vertically upwards with a speed of 100 m/s. After 5 seconds it explodes into two fragments. One fragment of mass 400 gm is found to go down with a speed of 25 m/s. What will happen to the second fragment just after the explosion? (g = 10 m/s2) [2000]- a)It will go upward with speed 40 m/s
- b)It will go upward with speed 100 m/s
- c)It will go upward with speed 60 m/s
- d)It will also go downward with speed 40m/s
Correct answer is option 'B'. Can you explain this answer?
A bomb of mass 1 kg is thr own vertically upwards with a speed of 100 m/s. After 5 seconds it explodes into two fragments. One fragment of mass 400 gm is found to go down with a speed of 25 m/s. What will happen to the second fragment just after the explosion? (g = 10 m/s2) [2000]
a)
It will go upward with speed 40 m/s
b)
It will go upward with speed 100 m/s
c)
It will go upward with speed 60 m/s
d)
It will also go downward with speed 40m/s

|
Aman Sharma answered |
Speed of bomb after 5 second, v = u – gt = 100 –10×5 = 50m/s
Momentum of 400 g fragment
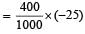 [downward]
[downward]Momentum of 600g fragment 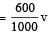
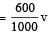
Momentum of bomb = 1 × 50 = 50
From conservation of momentum Total momentum before splitting = total momentum after splitting.
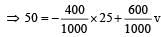
⇒ v = 100 m/s [upward]
A particle with total energy E is moving in a potential energy region U(x). Motion of the particle is restricted to the region when [NEET Kar. 2013]- a)U(x) > E
- b)U(x) < E
- c)U(x) = O
- d)U(x) ≤ E
Correct answer is option 'D'. Can you explain this answer?
A particle with total energy E is moving in a potential energy region U(x). Motion of the particle is restricted to the region when [NEET Kar. 2013]
a)
U(x) > E
b)
U(x) < E
c)
U(x) = O
d)
U(x) ≤ E

|
Krish Patel answered |
As the particle is moving in a potential energy region.
∴ Kinetic energy ≥ 0 And, total energy E = K.E. + P.E.
⇒ U(x) ≤ E
A ball moving with velocity 2 m/s collides head on with another stationary ball of double the mass. If the coefficient of restitution is 0.5, then their velocities (in m/s) after collision will be:- a)0, 1
- b)1, 1 [2010]
- c)1, 0.5
- d)0, 2
Correct answer is option 'A'. Can you explain this answer?
A ball moving with velocity 2 m/s collides head on with another stationary ball of double the mass. If the coefficient of restitution is 0.5, then their velocities (in m/s) after collision will be:
a)
0, 1
b)
1, 1 [2010]
c)
1, 0.5
d)
0, 2

|
Abhishek Choudhary answered |
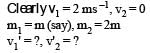
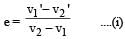
By conservation of momentum, 2m = mv1' + 2mv2' ... (ii) From (i),
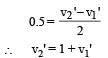
From (ii), 2 = v1'+ 2 + 2 v1'
⇒ v1 = 0 and v2 = 1 ms–1
A solid cylinder of mass 3 kg is rolling on a horizontal surface with velocity 4 ms–1. It collides with a horizontal spring of force constant 200 Nm–1 . The maximum compression produced in the spring will be : [2012]- a)0.5 m
- b)0.6 m
- c)0.7 m
- d)0.2 m
Correct answer is option 'B'. Can you explain this answer?
A solid cylinder of mass 3 kg is rolling on a horizontal surface with velocity 4 ms–1. It collides with a horizontal spring of force constant 200 Nm–1 . The maximum compression produced in the spring will be : [2012]
a)
0.5 m
b)
0.6 m
c)
0.7 m
d)
0.2 m
|
|
Maheshwar Iyer answered |
-1. The radius of the cylinder is 0.5 m. Calculate the kinetic energy of the cylinder.
First, we need to calculate the angular velocity of the cylinder, which can be found using the formula:
v = ωr
where v is the linear velocity, ω is the angular velocity, and r is the radius of the cylinder. Rearranging this formula, we get:
ω = v/r
Substituting the given values, we get:
ω = 4/0.5 = 8 rad/s
The kinetic energy of the cylinder can be calculated using the formula:
KE = (1/2)Iω^2 + (1/2)mv^2
where I is the moment of inertia of the cylinder, m is the mass of the cylinder, and v is the linear velocity.
The moment of inertia of a solid cylinder is given by:
I = (1/2)mr^2
Substituting the given values, we get:
I = (1/2)×3×(0.5)^2 = 0.375 kg m^2
Substituting all the values in the formula for KE, we get:
KE = (1/2)×0.375×8^2 + (1/2)×3×4^2
= 12 + 24
= 36 J
Therefore, the kinetic energy of the cylinder is 36 Joules.
First, we need to calculate the angular velocity of the cylinder, which can be found using the formula:
v = ωr
where v is the linear velocity, ω is the angular velocity, and r is the radius of the cylinder. Rearranging this formula, we get:
ω = v/r
Substituting the given values, we get:
ω = 4/0.5 = 8 rad/s
The kinetic energy of the cylinder can be calculated using the formula:
KE = (1/2)Iω^2 + (1/2)mv^2
where I is the moment of inertia of the cylinder, m is the mass of the cylinder, and v is the linear velocity.
The moment of inertia of a solid cylinder is given by:
I = (1/2)mr^2
Substituting the given values, we get:
I = (1/2)×3×(0.5)^2 = 0.375 kg m^2
Substituting all the values in the formula for KE, we get:
KE = (1/2)×0.375×8^2 + (1/2)×3×4^2
= 12 + 24
= 36 J
Therefore, the kinetic energy of the cylinder is 36 Joules.
An explosion breaks a rock into three parts in a horizontal plane. Two of them go off at right angles to each other. The first part of mass 1 kg moves with a speed of 12 ms–1 and the second part of mass 2 kg moves with speed 8 ms–1. If the third part flies off with speed 4 ms–1 then its mass is [NEET 2013]- a)5 kg
- b)7 kg
- c)17 kg
- d)3 kg
Correct answer is option 'A'. Can you explain this answer?
An explosion breaks a rock into three parts in a horizontal plane. Two of them go off at right angles to each other. The first part of mass 1 kg moves with a speed of 12 ms–1 and the second part of mass 2 kg moves with speed 8 ms–1. If the third part flies off with speed 4 ms–1 then its mass is [NEET 2013]
a)
5 kg
b)
7 kg
c)
17 kg
d)
3 kg

|
Moumita Khanna answered |
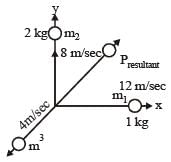
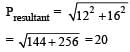
m3v3 = 20 (momentum of third part)
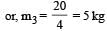
A bullet of mass 10g leaves a rifle at an initial velocity of 1000 m/s and strikes the earth at the same level with a velocity of 500 m/s. The work done in joules overcoming the resistance of air will be[1989]- a)375
- b)3750
- c)5000
- d)500
Correct answer is option 'B'. Can you explain this answer?
A bullet of mass 10g leaves a rifle at an initial velocity of 1000 m/s and strikes the earth at the same level with a velocity of 500 m/s. The work done in joules overcoming the resistance of air will be[1989]
a)
375
b)
3750
c)
5000
d)
500

|
Sarthak Saini answered |
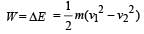
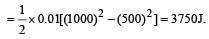
A force acts on a 30 gm particle in such a way that the position of the particle as a function of time is given by x = 3t – 4t2 + t3, where x is in metres and t is in seconds. The work done during the first 4 seconds is [1998]- a)576 mJ
- b)450 mJ
- c)490 mJ
- d)530 mJ
Correct answer is option 'A'. Can you explain this answer?
A force acts on a 30 gm particle in such a way that the position of the particle as a function of time is given by x = 3t – 4t2 + t3, where x is in metres and t is in seconds. The work done during the first 4 seconds is [1998]
a)
576 mJ
b)
450 mJ
c)
490 mJ
d)
530 mJ

|
Charvi Shah answered |
x = 3t –4t2 + t3
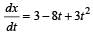
Acceleration 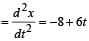
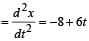
Acceleration after 4sec = –8 + 6 × 4 = 16 ms–2
Displacement in 4sec = 3 ×4 – 4 × 42 + 43 = 12 m
Displacement in 4sec = 3 ×4 – 4 × 42 + 43 = 12 m
∴ Work = Force × displacement = Mass × acc. × disp. = 3 × 10–3 × 16 × 12 = 576 mJ
A body of mass 1 kg is thrown upwards with a velocity 20 m/s. It momentarily comes to rest after attaining a height of 18 m. How much energy is lost due to air friction? (g = 10 m/s2)- a)30 J
- b)40 J [2009]
- c)10 J
- d)20 J
Correct answer is option 'D'. Can you explain this answer?
A body of mass 1 kg is thrown upwards with a velocity 20 m/s. It momentarily comes to rest after attaining a height of 18 m. How much energy is lost due to air friction? (g = 10 m/s2)
a)
30 J
b)
40 J [2009]
c)
10 J
d)
20 J

|
Lekshmi Banerjee answered |
When the body is thrown upwards. its K.E is converted into P.E. The loss of energy due to air friction is the difference of K.E and P.E.
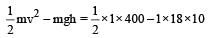
= 200 – 180 = 20 J
Consider a car moving along a straight horizantal road with a speed of 72 km/h. If the coefficient of static friction between road and tyres is 0.5, the shortest distance in which the car can be stopped is[1994]- a)30 m
- b)40 m
- c)72 m
- d)20 m
Correct answer is option 'B'. Can you explain this answer?
Consider a car moving along a straight horizantal road with a speed of 72 km/h. If the coefficient of static friction between road and tyres is 0.5, the shortest distance in which the car can be stopped is[1994]
a)
30 m
b)
40 m
c)
72 m
d)
20 m

|
Shanaya Rane answered |
Force due to friction = kinetic energy
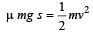
[Here, v = 72 km/h
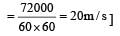
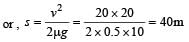
A stationary particle explodes into two particles of masses m1 and m2 which move in opposite directions with velocities v1 and v2. The ratio of their kinetic energies E1/E2 is [2003]- a)m1v2/m2v1
- b)m2/m1
- c)m1/m2
- d)1
Correct answer is option 'B'. Can you explain this answer?
A stationary particle explodes into two particles of masses m1 and m2 which move in opposite directions with velocities v1 and v2. The ratio of their kinetic energies E1/E2 is [2003]
a)
m1v2/m2v1
b)
m2/m1
c)
m1/m2
d)
1

|
Deepak Joshi answered |
From conservation law of momentum, before collision and after collision linear momentum (p) will be same. That is, initial momentum = final momentum.
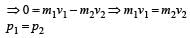
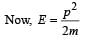
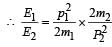
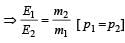
A body of mass 3 kg is under a constant force which causes a displacements in metres in it, given by the relation 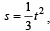 , where t is in seconds.
, where t is in seconds.
Work done by the force in 2 seconds is [2006]- a)
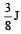
- b)
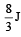
- c)
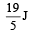
- d)
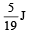
Correct answer is option 'B'. Can you explain this answer?
A body of mass 3 kg is under a constant force which causes a displacements in metres in it, given by the relation 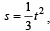 , where t is in seconds.
, where t is in seconds.
Work done by the force in 2 seconds is [2006]
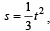 , where t is in seconds.
, where t is in seconds.Work done by the force in 2 seconds is [2006]
a)
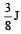
b)
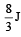
c)
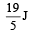
d)
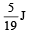
|
|
Gaurav Kumar answered |
Acceleration 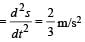
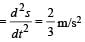
Force acting on the body
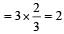 newton
newtonDisplacement in 2 secs 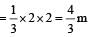
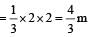
Work done 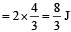
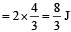
A uniform force of 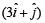 newton acts on a particle of mass 2 kg. The particle is displaced from position
newton acts on a particle of mass 2 kg. The particle is displaced from position 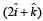 meter to position
meter to position 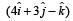 meter. The work done by the force on the particle is [NEET 2013]
meter. The work done by the force on the particle is [NEET 2013]- a)6 J
- b)13 J
- c)15 J
- d)9 J
Correct answer is option 'D'. Can you explain this answer?
A uniform force of 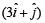 newton acts on a particle of mass 2 kg. The particle is displaced from position
newton acts on a particle of mass 2 kg. The particle is displaced from position 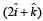 meter to position
meter to position 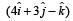 meter. The work done by the force on the particle is [NEET 2013]
meter. The work done by the force on the particle is [NEET 2013]
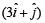 newton acts on a particle of mass 2 kg. The particle is displaced from position
newton acts on a particle of mass 2 kg. The particle is displaced from position 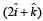 meter to position
meter to position 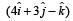 meter. The work done by the force on the particle is [NEET 2013]
meter. The work done by the force on the particle is [NEET 2013]a)
6 J
b)
13 J
c)
15 J
d)
9 J
|
|
Vijay Bansal answered |
Explanation:
Given : F = 3i + j
r1 = (2i + k), r2= (4i + 3j – k)
R = r2 – r1= (4i + 3j – k) – (2i + k)
or R = 2i + 3j – 2k
so, work done by the given force w = F.R
= (3i + j) x (2i + 3j – 2k) = 6 + 3 = 9 J
r1 = (2i + k), r2= (4i + 3j – k)
R = r2 – r1= (4i + 3j – k) – (2i + k)
or R = 2i + 3j – 2k
so, work done by the given force w = F.R
= (3i + j) x (2i + 3j – 2k) = 6 + 3 = 9 J
A force F acting on an object varies with distance x as shown here. The force is in N and x in m. The work done by the force in moving the object fr om x = 0 to x = 6 m is [2005]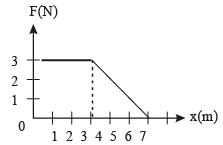
- a)18.0 J
- b)13.5 J
- c)9.0 J
- d)4.5 J
Correct answer is option 'B'. Can you explain this answer?
A force F acting on an object varies with distance x as shown here. The force is in N and x in m. The work done by the force in moving the object fr om x = 0 to x = 6 m is [2005]

a)
18.0 J
b)
13.5 J
c)
9.0 J
d)
4.5 J

|
Dipanjan Mehta answered |
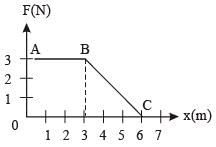
Work done = area under F-x graph = area of trapezium OABC
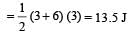
The kinetic energy acquired by a mass (m) in travelling distance (s) starting from rest under the action of a constant force is directly proportional to [1994, 1996]- a)
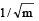
- b)1/m
- c)
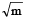
- d)m0
Correct answer is option 'D'. Can you explain this answer?
The kinetic energy acquired by a mass (m) in travelling distance (s) starting from rest under the action of a constant force is directly proportional to [1994, 1996]
a)
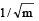
b)
1/m
c)
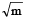
d)
m0

|
Sneha Basak answered |
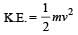
Further, v2 = u2 + 2as = 0 + 2ad = 2ad = 2(F/m)d
Hence, K.E. = 

or, K.E. acquired = Work done
= F × d = constant.i.e., it is independent of mass m.
When a long sprin g is stretched by 2 cm, its potential energy is U. If the spring is stretched by 10 cm, the potential energy stored in it will be[2003]- a)25 U
- b)U/5
- c)5 U
- d)10 U
Correct answer is option 'A'. Can you explain this answer?
When a long sprin g is stretched by 2 cm, its potential energy is U. If the spring is stretched by 10 cm, the potential energy stored in it will be[2003]
a)
25 U
b)
U/5
c)
5 U
d)
10 U

|
Arindam Khanna answered |
If k be the spring constant, then
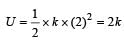
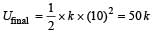
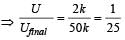
⇒ U final = 25U
The co-efficient of restitution e for a perfectly elastic collision is [1988]- a)1
- b)0
- c)∞
- d)–1
Correct answer is option 'A'. Can you explain this answer?
The co-efficient of restitution e for a perfectly elastic collision is [1988]
a)
1
b)
0
c)
∞
d)
–1

|
Sneha Basak answered |
e = | v1 – v2 |/ | u1 – u2 | which is 1 for a perfectly elastic collision.
A metal ball of mass 2 kg moving with a velocity of 36 km/h has a head on collision with a stationary ball of mass 3 kg. If after the collision, the two balls move together, the loss in kinetic energy due to collision is [1997]- a)140 J
- b)100 J
- c)60 J
- d)40 J
Correct answer is option 'C'. Can you explain this answer?
A metal ball of mass 2 kg moving with a velocity of 36 km/h has a head on collision with a stationary ball of mass 3 kg. If after the collision, the two balls move together, the loss in kinetic energy due to collision is [1997]
a)
140 J
b)
100 J
c)
60 J
d)
40 J

|
Jatin Chakraborty answered |
Applying conservation of momen tum,
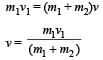
Here, v1 = 36 km/hr = 10 m/s m1 = 2 kg, m2 = 3 kg
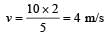
K.E. (initial) =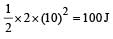
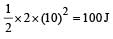
K.E. (Final) =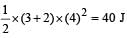
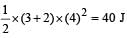
Loss in K.E. = 100 – 40 = 60 J
A mass m moving horizontally (along the x-axis) with velocity v collides and sticks to mass of 3m moving vertically upward (along the y-axis) with velocity 2v. The final velocity of the combination is [2011M]- a)
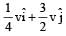
- b)
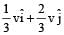
- c)
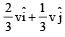
- d)
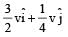
Correct answer is option 'A'. Can you explain this answer?
A mass m moving horizontally (along the x-axis) with velocity v collides and sticks to mass of 3m moving vertically upward (along the y-axis) with velocity 2v. The final velocity of the combination is [2011M]
a)
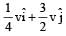
b)
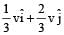
c)
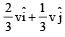
d)
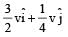

|
Ayush Choudhury answered |
As the two masses stick together after collision, hence it is inelastic collision.
Therefore, only momentum is conserved.
Therefore, only momentum is conserved.
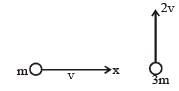
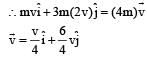
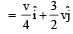
A car of mass m starts from rest and accelerates so that the instantaneous power delivered to the car has a constant magnitude P0. The instantaneous velocity of this car is proportional to : [2012M]- a)t2P0
- b)t1/2
- c)t– 1/2
- d)
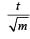
Correct answer is option 'B'. Can you explain this answer?
A car of mass m starts from rest and accelerates so that the instantaneous power delivered to the car has a constant magnitude P0. The instantaneous velocity of this car is proportional to : [2012M]
a)
t2P0
b)
t1/2
c)
t– 1/2
d)
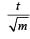
|
|
Surendra Bishnoi answered |
A particle of mass m1 is moving with a velocity v1 and another particle of mass m2 is moving with a velocity v2. Both of them have the same momentum but their different kinetic energies are E1 and E2 respectively. If m1 > m2 then [2004]- a)E1 = E2
- b)E1 < E2
- c)
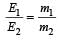
- d)E1 > E2
Correct answer is option 'B'. Can you explain this answer?
A particle of mass m1 is moving with a velocity v1 and another particle of mass m2 is moving with a velocity v2. Both of them have the same momentum but their different kinetic energies are E1 and E2 respectively. If m1 > m2 then [2004]
a)
E1 = E2
b)
E1 < E2
c)
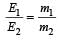
d)
E1 > E2

|
Aashna Mukherjee answered |
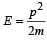
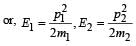

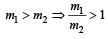
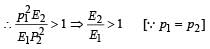
or, E2 > E1
A mass of 0.5 kg moving with a speed of 1.5 m/ s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k = 50 N/m. The maximum compression of the spring would be [2004]
- a)0.5 m
- b)0.15 m
- c)0.12 m
- d)1.5 m
Correct answer is option 'B'. Can you explain this answer?
A mass of 0.5 kg moving with a speed of 1.5 m/ s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k = 50 N/m. The maximum compression of the spring would be [2004]

a)
0.5 m
b)
0.15 m
c)
0.12 m
d)
1.5 m

|
Ishaan Menon answered |
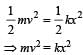
or 0.5 × (1.5)2 = 50×x2
∴ x = 0.15 m
A 3 kg ball strikes a heavy rigid wall with a speed of 10 m/s at an angle of 60º. It gets reflected with the same speed and angle as shown here. If the ball is in contact with the wall for 0.20s, what is the average force exerted on the ball by the wall? [2000]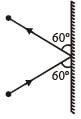
- a)150 N
- b)zero
- c)
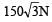
- d)300 N
Correct answer is option 'C'. Can you explain this answer?
A 3 kg ball strikes a heavy rigid wall with a speed of 10 m/s at an angle of 60º. It gets reflected with the same speed and angle as shown here. If the ball is in contact with the wall for 0.20s, what is the average force exerted on the ball by the wall? [2000]

a)
150 N
b)
zero
c)
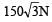
d)
300 N

|
Aashna Mukherjee answered |
Change in momentum along the wall = mv cos60º – mv cos 60º = 0
Change in momentum perpendicular to the wall
= mv sin60º – (– mv sin60º) = 2mv sin60º
Change in momentum perpendicular to the wall
= mv sin60º – (– mv sin60º) = 2mv sin60º
∴ Applied force = 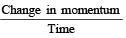
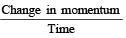
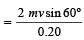
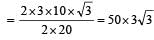
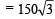 newton
newtonIn a simple pendulum of length l the bob is pulled aside from its equilibrium position through an angle θ and then released. The bob passes through the equilibrium position with speed. [2000]- a)
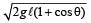
- b)
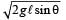
- c)
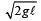
- d)
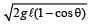
Correct answer is option 'D'. Can you explain this answer?
In a simple pendulum of length l the bob is pulled aside from its equilibrium position through an angle θ and then released. The bob passes through the equilibrium position with speed. [2000]
a)
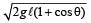
b)
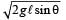
c)
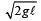
d)
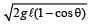

|
Akshat Chavan answered |
If l is length of pendulum and θ be angular amplitude then height
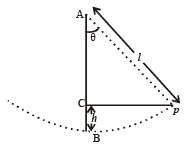
h = AB AC = l – l cosθ = l(1 – cosθ)
At extreme position, potential energy is maximum and kinetic energy is zero; At mean (equilibrium) position potential energy is zero and kinetic energy is maximum, so from principle of conservation of energy. (KE + PE ) at P = (KE + PE) at B
At extreme position, potential energy is maximum and kinetic energy is zero; At mean (equilibrium) position potential energy is zero and kinetic energy is maximum, so from principle of conservation of energy. (KE + PE ) at P = (KE + PE) at B
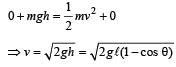
An explosion breaks a rock into three parts in a horizontal plane. Two of them go off at right angles to each other. The first part of mass 1 kg moves with a speed of 12 ms–1 and the second part of mass 2 kg moves with speed 8 ms–1. If the third part flies off with speed 4 ms–1 then its mass is [NEET 2013]- a)5 kg
- b)7 kg
- c)17 kg
- d)3 kg
Correct answer is option 'A'. Can you explain this answer?
An explosion breaks a rock into three parts in a horizontal plane. Two of them go off at right angles to each other. The first part of mass 1 kg moves with a speed of 12 ms–1 and the second part of mass 2 kg moves with speed 8 ms–1. If the third part flies off with speed 4 ms–1 then its mass is [NEET 2013]
a)
5 kg
b)
7 kg
c)
17 kg
d)
3 kg
|
|
Partho Khanna answered |
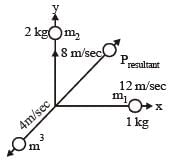
m3v3 = 20 (momentum of third part)
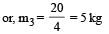
A force of 250 N is required to lift a 75 kg mass through a pulley system. In order to lift the mass through 3 m, the rope has to be pulled through 12m. Th e efficiency of system is [2001]- a)50%
- b)75%
- c)33%
- d)90%
Correct answer is option 'B'. Can you explain this answer?
A force of 250 N is required to lift a 75 kg mass through a pulley system. In order to lift the mass through 3 m, the rope has to be pulled through 12m. Th e efficiency of system is [2001]
a)
50%
b)
75%
c)
33%
d)
90%

|
Jatin Chakraborty answered |
Efficiency = 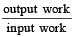
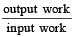
i.e. Efficiency
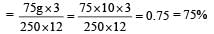
The upper half of an inclined plane of inclination θ is perfectly smooth while lower half is rough.
A block starting from rest at the top of the plane will again come to rest at the bottom, if the coefficient of friction between the block and lower half of the plane is given by [NEET 2013]- a)
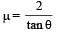
- b)μ = 2 tanθ
- c)μ = tanθ
- d)
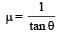
Correct answer is option 'B'. Can you explain this answer?
The upper half of an inclined plane of inclination θ is perfectly smooth while lower half is rough.
A block starting from rest at the top of the plane will again come to rest at the bottom, if the coefficient of friction between the block and lower half of the plane is given by [NEET 2013]
A block starting from rest at the top of the plane will again come to rest at the bottom, if the coefficient of friction between the block and lower half of the plane is given by [NEET 2013]
a)
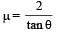
b)
μ = 2 tanθ
c)
μ = tanθ
d)
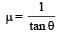

|
Raghav Khanna answered |
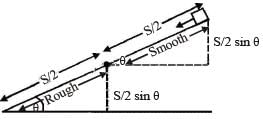
For upper half of inclined plane v2 = u2 + 2a S/2 = 2 (g sinθ) S/2 = gS sinθ
For lower half of inclined plane
For lower half of inclined plane
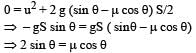

Two equal masses m1 and m2 moving along the same straight line with velocities + 3 m/s and – 5m/s respectively, collide elastically.Their velocities after the collision will be respectively. [1998]- a)–3 m/s & +5 m/s
- b)+ 4 m/s for both
- c)–4 m/s & +4 m/s
- d)–5m/s & +3 m/s
Correct answer is option 'D'. Can you explain this answer?
Two equal masses m1 and m2 moving along the same straight line with velocities + 3 m/s and – 5m/s respectively, collide elastically.Their velocities after the collision will be respectively. [1998]
a)
–3 m/s & +5 m/s
b)
+ 4 m/s for both
c)
–4 m/s & +4 m/s
d)
–5m/s & +3 m/s

|
Krish Khanna answered |
In elastic collision, the velocities get in ter changed if the colliding objects have equal masses.
A rubber ball is dropped from a height of 5m on a plane, where the acceleration due to gravity is not shown. On bouncing it rises to 1.8 m. The ball loses its velocity on bouncing by a factor of [1998]- a)

- b)
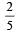
- c)

- d)
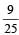
Correct answer is option 'B'. Can you explain this answer?
A rubber ball is dropped from a height of 5m on a plane, where the acceleration due to gravity is not shown. On bouncing it rises to 1.8 m. The ball loses its velocity on bouncing by a factor of [1998]
a)

b)
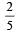
c)

d)
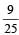

|
Arindam Khanna answered |
Accordin g to principle of conservation of energy Loss in potential energy = Gain in kinetic energy
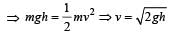
If h1 and h2 are initial and final heights, then
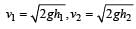
Loss in velocity
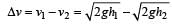
∴ Fractional loss in velocity

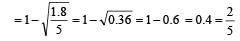
A body of mass m moving with velocity 3 km/h collides with a body of mass 2 m at rest. Now the coalesced mass starts to move with a velocity [1996]- a)1 km/h
- b)2 km/h
- c)3 km/h
- d)4 km/h
Correct answer is option 'A'. Can you explain this answer?
A body of mass m moving with velocity 3 km/h collides with a body of mass 2 m at rest. Now the coalesced mass starts to move with a velocity [1996]
a)
1 km/h
b)
2 km/h
c)
3 km/h
d)
4 km/h

|
Dipanjan Mehta answered |
Applying law of conservation of momentum,
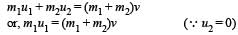
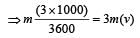
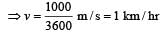
Chapter doubts & questions for Work, Energy and Power - NEET Past Year Papers 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Work, Energy and Power - NEET Past Year Papers in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup